Abstract
In this study, we propose a system-theoretic approach to the analysis and quantitative modeling of the TNFα-mediated NF-κB-signaling pathway. Tumor necrosis factor α (TNFα) is a potent proinflammatory cytokine that plays an important role in immunity and inflammation, in the control of cell proliferation, differentiation, and apoptosis. To date, there have been numerous approaches to model cellular dynamics. The most prominent uses ordinary differential equations (ODEs) to describe biochemical reactions. This approach can provide us with mathematically well-founded and tractable interpretations regarding pathways, especially those best described by enzyme reactions. This work first introduces a graphical method to intuitively represent the TNFα-mediated NF-κB-signaling pathway and then utilizes ODEs to quantitatively model the pathway. The simulation study shows qualitative validation of the proposed model compared with experimental results for this pathway. The proposed system-theoretic approach is expected to be further applicable to predict the signaling behavior of NF-κB in a quantitative manner for any variation of the ligand, TNFα.
Tumor necrosis factor α (TNFα) is a potent proinflammatory cytokine that plays an important role in immunity and inflammation and in the control of cell proliferation, differentiation, and apoptosis. Binding of TNFα to its two receptors, TNFR1 and TNFR2, results in recruitment of signal transducers that activate at least three distinct effectors. Through complicated signaling cascades and networks, these effectors lead to the activation of caspases and two transcription factors, AP-1 and NF-κB (Francis et al. 2000; Swaroop and David 2001; Veronique and Michael 2001; Michael and Anning 2002). This study is to propose a system-theoretic approach for the analysis and quantitative modeling of the TNFα-mediated NF-κB-signaling pathway.
We can find numerous approaches in the literature for the modeling of cellular dynamics (Robert 1997; Upinder and Ravi 1999; Anand and Douglas 2000; Douglas 2000; Jeff et al. 2001; Robert and Tom 2001; Tyson et al. 2001; Wolkenhauer 2001). The most prominent approach uses ordinary differential equations (ODEs) to model biochemical reactions. This can provide us with mathematically well-founded and tractable interpretations for biological pathways, especially those best described by enzyme reactions. Recently, Hoffmann et al. (2002) presented a remarkable computational model that describes the temporal control of NF-κB activation by the coordinated degradation and synthesis of IκB proteins. The focus of the model was the central-signaling module composed of IKK, three mammalian IκB isoforms, and NF-κB to address the role of different IκB isoforms in controlling the dynamic response of the pathway to transient and persistent stimulation. The model was developed in a heuristic way considering a simple differential equations approximation of a biochemical system with negative feedback and provided valuable conclusions regarding the respective functions of IκB isoforms, the bimodal signal-processing characteristics, and the newly revealed mechanism for specificity in gene expression. In this work, we first focus on developing a general modeling framework for signal-transduction pathways on the basis of a system-theoretic approach from complemented enzyme-reaction kinetics, and then apply the developed methodology to the TNFα-mediated NF-κB-signaling pathway. The model also captures the dynamics regarding generation and degradation of the enzyme and provides a basis for sensitivity analysis of the pathway with respect to the variation of initial concentrations (TNFα) in a three-dimensional graphical representation. Specifically, this study first introduces a graphical method to intuitively represent the TNFα-mediated NF-κB-signaling pathway and then utilizes ODEs to quantitatively model the pathway dynamics. For this purpose, we complement the enzyme kinetics to incorporate the restoring process into the steady-state concentration of substrates. We then model the pathway step-by-step, on the basis of these complemented enzyme kinetics. By integrating individual ODE models into a whole, the quantitative model of the signaling pathway is established. The simulation study shows qualitative validation of the proposed model on the basis of current experimental results. Each parameter value for the computer simulation is derived via inference on the basis of the experimental reaction time.
The work is organized as follows. Section I briefly introduces some preliminaries on mathematical modeling of reaction kinetics are described above. Section II describes the TNFα-mediated NF-κB-signaling pathway. Section III presents the proposed graphical and mathematical modeling of the TNFα-mediated NF-κB-signaling pathway on the basis of ODEs. Section IV illustrates simulation studies. Finally, conclusions are made in Section V.
METHODS AND RESULTS
Preliminaries
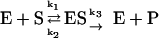 |
1 |
Equation 1 is a very well-known simple model for enzyme kinetics. It is often used to account for typical kinetic properties of various kinds of enzymes. In equation 1, E is the concentration of an enzyme that combines with a substrate S to form an enzyme-substrate complex ES with a rate constant k1. The complex ES holds two possible outcomes in the next step. It can be dissociated into E and S with a rate constant k2, or it can further proceed to form a product P with a rate constant k3. It is assumed that none of the products reverts to the initial substrate. It is necessary to express the relations between the rate of catalysis and the change of concentration for the substrate, the enzyme, the complex, and the product. These relations are usually represented by the following set of ODEs. The reaction kinetics we develop in the remainder of this work are based on these ODEs.
 |
2 |
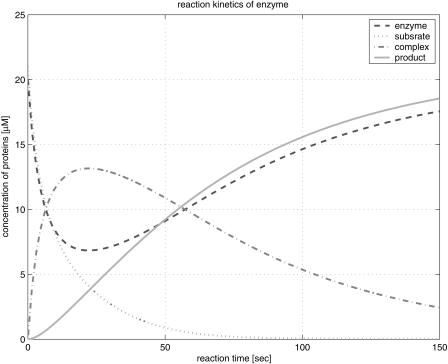
Figure 1 illustrates the reaction profile of the basic enzyme kinetics in equation 1 evolving in time. It shows that the formation of an enzyme-substrate complex is the first step in enzyme catalysis. Initially, both the concentration of the substrate and the enzyme decrease until after 25 sec; the concentration of the enzyme increases before settling to its steady state. On the other hand, the concentration of the complex reaches its maximum at 25 sec, and then decreases exponentially. The curve for the concentration of the product increases and reaches its steady state long after these transitional changes. In reaction kinetics, the change of each concentration implies a signal transfer, passing information to other agonists. The trail of this signal transfer constitutes a signaling pathway. Some signals in a signaling pathway can be merged and amplified or reduced due to interference among signals.
Figure 1.
Reaction profile of the basic enzyme kinetics.
A popular way to intuitively describe a signaling pathway utilizes a graphical representation, akin to diagrams familiar to, or popular with biologists. These cartoons are usually insufficiently descriptive to explain molecular dynamics quantitatively, but they provide an intuition of the overall dynamics and information processing in cellular systems. Here, we propose both a graphical method and a mathematical method on the basis of ODEs to investigate the analysis and modeling of TNFα-mediated NF-κB-signaling pathway.
The graphical tool is based on a bipartite-directed multigraph, in which structure of the bipartite graph consists of two types of nodes and directed arcs; a circle represents a state for the concentration of a protein, a bar represents a rate of reaction, and directed arcs (arrows) connect the circles and the bar. The signal flow in a signaling pathway can then be qualitatively described by this graphical tool.
Equation 2 shows the differential equation model of the reaction kinetics outlined in equation 1, and Figure 2 illustrates the graphical representation for the kinetics in equations 1 and 2. In Figure 2, the bar represents the rate of formation and breakdown of the complex or the product.
Figure 2.
Graphical representation of the reaction kinetics.
Beause the dynamics regarding generation and degradation of the enzyme is not included in the conventional representation of equations 1 and 2, we complement the enzyme kinetic model 2 by considering these dynamics. The main idea is based on the observation that the signal-transduction system usually behaves as a slowly time-varying nonlinear system during the reaction period. Figure 3 illustrates the complemented model of an enzyme (or protein) including the generation and degradation, whose role is to maintain the steady-state concentration of the enzyme (or protein). In Figure 3, the two bars for kf(t) and kr(t) represent the rates of generation and degradation, respectively. If we consider the fact that the steady state of enzymes or proteins depends upon the local environment in the cell, it is reasonable to model the rate as a function of time.
Figure 3.
The complemented graphical model of an enzyme.
Hence, the concentration of an enzyme (or protein) can be modeled as follows.
 |
3 |
On the basis of assumption of slowly time-varying processes, we can approximate the rates for the generation and degradation as constant during the reaction period, which means that the steady-state concentration of the enzyme (or protein) is independent of time. Thus,
 |
4 |
By substituting equation 4 into equation 3 and solving the resultant differential equation, we have
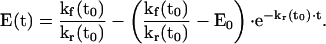 |
5 |
Taking the limit in equation 5, we obtain the following steady-state value for E(t),
 |
6 |
Finally, we have obtained the following complemented reaction kinetics model on the basis of ODEs, including the rate of generation and degradation for an enzyme (or protein): 
In the extreme, if kr(t0) >> kf(t0), then E(t) 0. This implies a case when the signal flow is blocked, as there is no more signaling protein involved in its signaling pathway. The case depends wholly upon the cell environment.
Figures 4 and 5 provide a graphical representation of the complemented model for the reaction kinetics and the corresponding simulation results for equation 7.
Figure 4.
Graphical representation of the complemented model of the reaction kinetics.
Figure 5.
Simulation results of the complemented reaction kinetics.
Figure 5 shows a similar behavior to Figure 1, on the basis of equation 2. Note that the curve for the enzyme returns to its steady state more quickly in Figure 5. If we reduce the rate of generation or raise the rate of degradation for the enzyme, the response would be slowed down. This implies that the steady state of an enzyme (or protein) can modulate the response of the signal.
TNFα-Mediated NF-κB-Signaling Pathway
TNFα is a potent cytokine often produced by various cell types including macrophage, monocytes, lymphocytes, keratinocytes, and fibroblasts in response to inflammation, infection, injury, and other environmental challenges (Veronique and Michael 2001). Exposure of cells to TNFα can recruit an activation of a caspase cascade that leads to apoptosis. However, more commonly, the binding of TNFα to its receptor causes an activation of two major transcriptional factors, AP-1 and NF-κB; these, in turn, induce genes involved in chronic and acute inflammatory responses. NF-κB is regulated primarily by phosphorylation of inhibitory proteins, the IκBs, which are retained in the cytoplasm of nonstimulated cells. In response to TNFα and other agonists, the IκBs are phosphorylated by the IκB kinase (IKK) complex, resulting in their ubiquitination, degradation, and the nuclear translocation of the freed NF-κB. Generally, TNFα exerts its effects through two distinct receptors, TNFR1 and TNFR2. Binding of the inherently trimeric TNFα to TNFR1 induces receptor trimerization and recruitment of several signaling proteins to the cytoplasmic domains of the receptors as shown in Figure 6. The first protein recruited to TNFR1 is TNFR1-associated death-domain protein (TRADD), which serves as a platform to recruit at least three additional mediators, a receptor-interacting protein (RIP), a Fas-associated death-domain protein (FADD), and a TNF-receptor-associated factor 2(TRAF2). TRAF2 plays a central role in early events, common to TNFR1 and TNFR2, which leads to the IKK activation (Veronique and Michael 2001).
Figure 6.
Graphical model of the TNFα-mediated NF-κB-signaling pathway.
Figure 6 shows the graphical model of the TNFα-mediated FN-κB-signaling pathway.
Mathematical Modeling of TNFα-Mediated NF-κB-Signaling Pathway
Applying the previous complemented model 7 of the reaction kinetics to each pathway step-by-step and integrating each model into a whole, the final mathematical model of the TNFα-mediated NF-κB-signaling pathway, on the basis of a set of ODEs, is summarized in the Appendix. Moreover, all of the relevant definitions of variables and parameters appearing in the ODE model, together with nominal values for simulation studies in the Simulation Studies section, are given in Tables 1 and 2. The terminology of the dependent variables and their acronyms follows the conventional biological description, for which the symbols are based on common use of mathematical notation. It is assumed that the cell keeps the concentration of each signaling protein constant before and after each signaling, that is, the concentration of these proteins returns to a steady state after the reaction. Note that this assumption reflects the biological observation. In addition, we assume that the signaling pathway behaves as a slowly time-varying system as described in the Preliminaries section.
Table 1.
Definition of Variables and Nominal Values for Signaling Proteins at Steady State
| Dependent variables | Acronym | Symbol | Concentration [μM] | Independent variables | [μMsec−1]/[sec−1] |
|---|---|---|---|---|---|
| TNF Necrosis Factor | TNF | m1 | 20 | — | — |
| TNF Receptor 1 | TNFR1 | m2 | 25 | k2f/k2r | 0.139/0.00556 |
| TNFR1-complex | — | m3 | 0 | — | — |
| TNFR1-associated death domain protein | TRADD | m4 | 25 | k4f/k4r | 0.139/0.00556 |
| TRADD-complex | — | m5 | 0 | — | — |
| Fas-associated death domain | FADD | m6 | 0 | k6f/k6r | 0.139/0.00556 |
| FADD-complex | — | m9 | 0 | — | — |
| Receptor-interacting protein | RIP | m7 | 25 | k7f/k7r | 0.139/0.00556 |
| RIP-complex | — | m10 | 0 | — | — |
| TNF-Receptor-associated factor 2 | TRAF2 | m8 | 12 | k8f/k8r | 0.139/0.00556 |
| TRAF2-complex | — | m11 | 0 | — | — |
| IκB kinase | IKK | m9 | 25 | k9f/k9r | 0.139/0.00556 |
| NF-κB Inhibitor/Nuclear factor κB | IkB/NF-κB | m14 | 25 | k14f/k14r | 0.139/0.00556 |
| IKK-complex | — | m12 | 0 | — | — |
| NF-κB Inhibitor | IκB | m16 | 0 | — | — |
| Nuclear factor κB | NK-κB | m17 | 0 | — | — |
Table 2.
Definition of Variables and Nominal Values for Parameters in Reaction Kinetics
| Independent variables | Symbol | [μM−1sec−1]/[sec−1] |
|---|---|---|
| TNF/TNFR1 ratio | k12_3/k3_12 | 0.00096/0.004 |
| TNFR1/TRADD ratio | k34_5/k5_34 | 0.00096/0.004 |
| TRADD/FADD ratio | k56_9/k9_56 | 0.00096/0.004 |
| TRADD/RIP ratio | k57_10/k10_57 | 0.00096/0.004 |
| RIP/TRAF2 | k810_11/K11_810 | 0.00096/0.004 |
| TRAF2/IKK ratio | k911_12/K12_911 | 0.00096/0.004 |
| IKK activation ratio | K12_13 | 0.1 |
| IKK_act/(IκB/NF-κB) ratio | K1314_15/k15_1314 | 0.00096/0.004 |
| NF-κB activated ratio | k15-1617 | 0.00096/0.004 |
| Degradation ratio | k16 | 0.1 |
The exact value of parameters, such as the concentration of each signaling protein, the rate constants for the generation and degradation, etc., are difficult to obtain because their numerical value not only depends on the species and tissue, but also on the physiological state of the cells/organism. Hence, we derive the nominal value for each parameter from the reaction time. For instance, it is well known that it takes several seconds for two proteins to interact in the signaling pathway. We therefore make a reasonable quantitative inference from the reaction time. In this way, we summarize the derived nominal value for each parameter in Tables 1 and 2. Note that whenever we can get more specific information regarding the reaction time in a particular experimental condition, for example, the measured time for TNFα returning to the steady state after a reaction from its initial state, we can then modify more exact parameter values for the rate of generation, the rate of degradation, and so forth, on the basis of new information about the reaction time.
In Table 2, the rate of formation for the complex is assumed to be 0.00096 (µM-1sec-1), the rate of dissociation from the complex is assumed to be 0.004 (sec-1), and the rate of production is assumed to be 0.1 (sec-1).
Simulation Studies
The computer simulation is carried out with a 2GHz Pentium 4 PC. The differential equations in the model of the signaling pathway are solved by utilizing MATLAB library functions (ode45, etc.). The results can be classified into two groups as follows: one group for protein interactions, and the other group for three-dimensional profiles along with time and the concentration for TNFα. The latter group is to be called the sensitivity to TNFα.
As in the Preliminaries and the Mathematical Modeling sections, it is assumed that the cell keeps the concentration of each signaling protein constant before and after signaling takes place. Figure 7, 8, 9, 10, 11, 12 illustrates the formation process for the complex from TNFα and TNFR1. The concentration of the complex reaches its maximum in about 10 sec, and then decreases exponentially to the initial condition zero. TNFα reduces to 8 µM, and then increases gradually. After a while, it returns to its steady state. Here, we consider the change of concentration of the complex as a signal. This signal is transferred to the next stage in Figure 8, in which TRADD is recruited and bound to the TNFR1 complex, forming a TRADD complex. The concentration change of the TRADD complex can be considered as another biochemical signal transferred from the previous stage. Similarly, the signal is transferred to IKK in Figure 11, below (for intermediate procedures, refer to Figs. 8, 9, 10, 11). The signal activates IKK, and then the activated IKK finally phosphorylates IκB, which, in turn, releases NF-κB. Thereupon, the concentration of released NF-κB increases to its maximum value as illustrated in Figure 12. Finally, the released NF-κB translocates into the nucleus and initiates transcription of the gene that responds to the variation of the ligand TNFα.
Figure 7.
Binding of TNFα to TNFR1.
Figure 8.
Recruitment of TRADD.
Figure 9.
Recruitment of RIP.
Figure 10.
Recruitment of TRAF2.
Figure 11.
Activation of IKK.
Figure 12.
Activation of NF-κB.
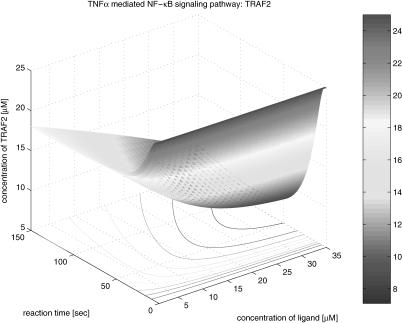
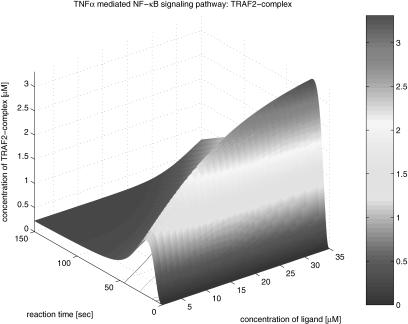
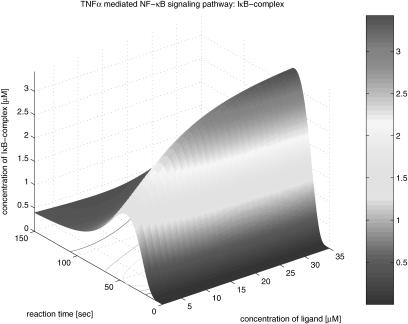
The second group of the results is the three-dimensional graphical representation that illustrates the profile as function time and the concentration of TNFα in Figure 13. The concentration varies form 0 to 35 µM. From the three-dimensional representation, we obtain information about the dynamics of signaling components involved in the pathway, dependent on variations of the initial TNFα concentration. In Figure 14, TNFR1 is very quickly (<20 sec) occupied by TNFα at its highest density, and then, after a while, TNFR1 turns to its steady state; however, it takes a longer period of time to recover its steady state. This implies that TNFR1 becomes more desensitized to the external stimulation as the initial TNFα concentration increases. That is, if the same stimulation is given consecutively to the cell receptor, then a lower signal transduces through the pathway. Figure 15 shows the profile of TNFR1-complex, in which the concentration increases along with time and the concentration of TNFα. This shows that TNFR1 also becomes desensitized to the external stimulation, as the number of receptor molecules trapped in TNFR1 complex becomes larger as the initial TNFα concentration is higher. The TNFα complex recruits TRADD in Figure 16, and its concentration decreases during the recruiting, whereas the concentration of the TRADD complex increases along with time and the concentration of TNFα as shown in Figure 17. The increase of the TRADD complex, anchored in the upstream-signaling component, implies that the apoptosis mechanism and the cell-proliferation mechanism become activated in accordance with the increase of the initial TNFα concentration, as TRADD serves as a platform in which FADD (responsible for apoptosis) and RIP (responsible for proliferation) are recruited as shown in Figure 18. However, it depends on the internal mechanism as to whether the apoptosis or the proliferation mainly affects the fate of the cell. Figures 19, 20, 21, 22, 23 illustrate the dynamics of the activated IKK. We note that the concentration of IKK increases only about 2.2 times, whereas the initial TNFα concentration increases 35 times. This indicates that IKK is relatively insensitive to the change of the initial TNFα concentration. Figures 24, 25, 26, 27 show the signaling profile of the free NF-κB in a cytoplasm released from the NF-κB/IκB complex. We can also find the insensitive change of the free NF-κB in a cytoplasm according to the variation of the initial TNFα concentration. That is, we note that the NF-κB concentration varies 2.5 times as the initial TNFα concentration increases 35 times. The sensitivity characteristics of the signaling components with respect to the initial TNFα concentration (i.e., input to the system) is related to the stability and robustness of the signal transduction system in view of systems theory.
Figure 13.
TNFα.
Figure 14.
TNFR1.
Figure 15.
TNFR1 complex.
Figure 16.
TRADD.
Figure 17.
TRADD complex.
Figure 18.
RIP.
Figure 19.
RIP complex.
Figure 20.
TRAF2.
Figure 21.
TRAF2 complex.
Figure 22.
IKK complex.
Figure 23.
Activated IKK.
Figure 24.
NFκB/IkB.
Figure 25.
IκB complex.
Figure 26.
Phosphorylated IκB.
Figure 27.
NFκB.
Another interesting observation from these three-dimensional simulation results relates to the signal propagation delay. We note that the time delay of each component in the pathway increases for downstream components as shown in the contours depicted in the bottom planes of Figures 14, 16, 18, 20, and 24. The signal propagation delay of the pathway with multiple inputs (i.e., different kinds of stimulations and corresponding receptors, etc.) can result in various dynamics such as signaling discontinuity through merging and amplification. Figs. 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27
DISCUSSION
In this work, we have investigated a system-theoretic approach to analysis and quantitative modeling of the TNFα-mediated NF-κB-signaling pathway. The quantitative model was complemented with a qualitative model. We proposed an intuitive graphical representation of the signaling pathway on the basis of a bipartite-directed multigraph, and then presented the mathematical model of the signal pathway via a set of ODEs on the basis of complemented reaction kinetics. For simulation studies, we have derived the nominal value for each parameter through inference on the basis of reaction time. The simulation studies have illustrated the process of variation of each protein concentration along with the TNFα-mediated NF-κB-signaling pathway as the concentration of the ligand TNFα varies. Moreover, the computer simulation, on the basis of the proposed quantitative model, has revealed the transient behavior of the signaling pathway. The proposed signaling-pathway model based on a system-theoretic approach can be extended and is applicable to other signaling pathways in the same manner. As a next step, it will be useful to include more detailed elements of the pathway excluded in the current study. This may lead to hybrid systems, combining discrete event systems with continuous dynamics in order to model the switching or decision making in signaling pathways. Feedback control and time delays are further challenges for an extended model. As yet, the model produces hypotheses and can guide the biologist in experimental design. To predict quantitative behavior from the proposed model and to apply the predicted results in biotechnological application, the proposed model needs to be supplemented by more accurate nominal values for each parameter on the basis of in vivo experiments. The experimental validation of the quantitative predictions made by the simulation studies also remains as important further research.
Acknowledgments
This work was supported by the Post-doctoral Fellowship Program of the Korea Science & Engineering Foundation (KOSEF) and by a grant from the SRC Fund to IRC at University of Ulsan from the KOSEF and the Ministry of Science and Technology, Korea.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
APPENDIX
The mathematical model of the TNFα-mediated NF-κB-signaling pathway on the basis of complemented reaction kinetics. This appendix summarizes the mathematical model of the TNFα-mediated NF-κB-signaling pathway on the basis of the complemented reaction kinetics in the Preliminaries section. For the nominal value of each parameter, refer to Tables 1 and 2.
 |
 |
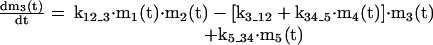 |
 |
 |
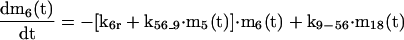 |
 |
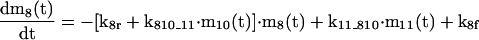 |
 |
 |
 |
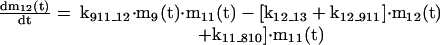 |
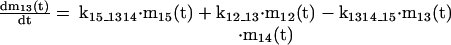 |
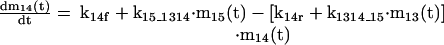 |
 |
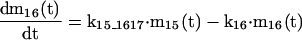 |
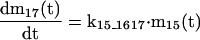 |
 |
Footnotes
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.1195703. Article published online before print in October 2003.
References
- Anand, R.A. and Douglas, A.L. 2000. Bioengineering models of cell signaling. Annu. Rev. Biomed. Eng. 2: 31-53. [DOI] [PubMed] [Google Scholar]
- Douglas, A.L. 2000. Cell signaling pathways as control modules: Complexity for simplicity? Proc. Natl. Acad. Soc. 97: 5031-5033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Francis, K.C., Richard, M.S., and Michael, J.L. 2000. Signaling by the TNF receptor super family and T cell homeostasis. Immunity 13: 419-422. [DOI] [PubMed] [Google Scholar]
- Hoffmann, A., Levchenko, A., Scott, M.L., and Baltimore, D. 2002. The IκB-NF-κB signaling module: Temporal control and selective gene activation. Science 298: 1241-1245. [DOI] [PubMed] [Google Scholar]
- Jeff, H., David, M., Farren, I., and James, J.C. 2001. Computational studies of gene regulatory networks: In numero molecular biology. Nat. Rev. Genet. 2: 268-279. [DOI] [PubMed] [Google Scholar]
- Michael, K. and Anning, L. 2002. NF-κB at the cross roads of life and death. Nat. Immun. 3: 221-227. [Google Scholar]
- Robert, D.P. 1997. Development of kinetic models in the nonlinear world of molecular cell biology. Metabolism 46: 1489-1495. [DOI] [PubMed] [Google Scholar]
- Robert, D.P. and Tom, M. 2001. Kinetic modeling approaches to in vivo imaging. Nat. Rev. Mol. Cell Biol. 2: 898-907. [DOI] [PubMed] [Google Scholar]
- Swaroop, A. and David, L.N. 2001. NF-κB signaling and human disease. Curr. Opin. Genet. Dev. 11: 300-306. [DOI] [PubMed] [Google Scholar]
- Tyson, J.J., Kathy, C., and Bela, N. 2001. Network dynamics and cell physiology. Nat. Rev. Mol. Cell Biol. 2: 908-916. [DOI] [PubMed] [Google Scholar]
- Upinder, S.B. and Ravi, I. 1999. Emergent properties of networks of biological signaling pathways. Science 283: 381-387. [DOI] [PubMed] [Google Scholar]
- Veronique, B. and Michael, K. 2001. Signal transduction by tumor necrosis factor and its relatives. Trends Cell Biol. 11: 372-377. [DOI] [PubMed] [Google Scholar]
- Wolkenhauer, O. 2001. Systems biology: The reincarnation of systems theory applied in biology? Briefings in Bioinformatics 2: 258-270. [DOI] [PubMed] [Google Scholar]