Skip to main content
PMC home page
Genome Research logoLink to Genome Research
. 2003 Nov;13(11):2467–2474. doi: 10.1101/gr.1262503

Parameter Estimation in Biochemical Pathways: A Comparison of Global Optimization Methods

Carmen G Moles 1, Pedro Mendes 2, Julio R Banga 1,3
PMCID: PMC403766  PMID: 14559783

Abstract

Here we address the problem of parameter estimation (inverse problem)of nonlinear dynamic biochemical pathways. This problem is stated as a nonlinear programming (NLP)problem subject to nonlinear differential-algebraic constraints. These problems are known to be frequently ill-conditioned and multimodal. Thus, traditional (gradient-based)local optimization methods fail to arrive at satisfactory solutions. To surmount this limitation, the use of several state-of-the-art deterministic and stochastic global optimization methods is explored. A case study considering the estimation of 36 parameters of a nonlinear biochemical dynamic model is taken as a benchmark. Only a certain type of stochastic algorithm, evolution strategies (ES), is able to solve this problem successfully. Although these stochastic methods cannot guarantee global optimality with certainty, their robustness, plus the fact that in inverse problems they have a known lower bound for the cost function, make them the best available candidates.

Mathematical optimization can be used as a computational engine to arrive at the best solution for a given problem in a systematic and efficient way. In the context of biochemical systems, coupling optimization with suitable simulation modules opens a whole new avenue of possibilities. Mendes and Kell (1998) highlight two types of important applications:

  1. Design problems: How to rationally design improved metabolic pathways to maximize the flux of interesting products and minimize the production of undesired by-products (metabolic engineering and biochemical evolution studies);

  2. Parameter estimation: Given a set of experimental data, calibrate the model so as to reproduce the experimental results in the best possible way.

This contribution considers the latter case, that is, the so-called inverse problem. The correct solution of inverse problems plays a key role in the development of dynamic models, which, in turn, can promote functional understanding at the systems level, as shown by, for example, Swameye et al. (2003) and Cho et al. (2003) for signaling pathways.

The paper is structured as follows: In the next section, we state the mathematical problem, highlighting its main characteristics, and very especially its challenging nature for traditional local optimization methods. Next, global optimization (GO) is presented as an alternative to surmount those difficulties. A brief review of GO methods is given, and a selection of the presently most promising alternatives is presented. The following section outlines a case study considering the estimation of 36 parameters of a three-step pathway, which will be used as a benchmark to compare the different GO methods selected. A Results and Discussion section follows, ending with a set of Conclusions.

METHODS

Statement of the Inverse Problem

Parameter estimation problems of nonlinear dynamic systems are stated as minimizing a cost function that measures the goodness of the fit of the model with respect to a given experimental data set, subject to the dynamics of the system (acting as a set of differential equality constraints) plus possibly other algebraic constraints. Mathematically, the formulation is that of a nonlinear programming problem (NLP) with differential-algebraic constraints:

Find p to minimize

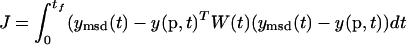graphic file with name M1.gif 1

subject to

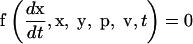graphic file with name M2.gif 2
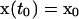graphic file with name M3.gif 3
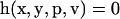graphic file with name M4.gif 4
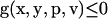graphic file with name M5.gif 5
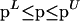graphic file with name M6.gif 6

where J is the cost function to be minimized, p is the vector of decision variables of the optimization problem, the set of parameters to be estimated, ymsd is the experimental measure of a subset of the (so-called) output state variables, y(p, t) is the model prediction for those outputs, W(t) is a weighting (or scaling) matrix, x is the differential state variables, v is a vector of other (usually time-invariant) parameters that are not estimated, f is the set of differential and algebraic equality constraints describing the system dynamics (i.e., the nonlinear process model), and h and g are the possible equality and inequality path and point constraints that express additional requirements for the system performance. Finally, p is subject to upper and lower bounds acting as inequality constraints.

The formulation above is that of a nonlinear programming problem (NLP) with differential-algebraic (DAEs) constraints. Because of the nonlinear and constrained nature of the system dynamics, these problems are very often multimodal (nonconvex). Therefore, if this NLP-DAEs is solved via standard local methods, such as the standard Levenberg-Marquardt method, it is very likely that the solution found will be of local nature, as discussed by Mendes and Kell (1998), for example.

The earliest and simplest attempt to surmount the nonconvexity of many optimization problems was based on the idea of using a local method repeatedly, starting from a number of different initial decision vectors, which is the so-called multistart strategy (Guus et al. 1995). However, the approach usually does not work for realistic applications, because it exhibits a major drawback: When many starting points are used, the same minimum will eventually be determined several times (Törn 1973; Guus et al. 1995), thus, the method becomes very inefficient. Clustering methods and other so-called global optimization (GO) methods (more details given below) have been developed to ensure better efficiency and robustness.

Mendes and Kell (1998) considered the parameter estimation of several rate constants of the mechanism of irreversible inhibition of HIV proteinase. This problem has a total of 20 parameters to estimate, and these authors obtained the best fit using the simulated annealing (SA) method. However, they highlighted the huge computational effort associated with this method, noting that the topic deserves more detailed study.

More recently, Mendes (2001) considered a larger inverse problem regarding a three-step pathway, finding that gradient methods could not converge to the solution from any arbitrary starting vector. After comparing a number of stochastic methods, evolutionary programming (EP) was found to be the best performing algorithm, with a final refined solution that replicated the true dynamics rather well. As a drawback, the needed computation time was again excessive.

In this contribution, we have considered this same three-step pathway as a benchmark, and we have attempted to solve the associated inverse problem using several state-of-the-art deterministic and stochastic global optimization (GO) algorithms. Our main objective was to investigate if the present state of GO can provide us with a more efficient and reliable method for this class of problems.

Global Optimization Methods

Global optimization methods can be roughly classified as deterministic (Horst and Tuy 1990; Grossmann 1996; Pinter 1996; Esposito and Floudas 2000) and stochastic strategies (Guus et al. 1995; Ali et al. 1997; Törn et al. 1999).

Stochastic methods for global optimization ultimately rely on probabilistic approaches. Given that random elements are involved, these methods only have weak theoretical guarantees of convergence to the global solution. Deterministic methods are those that can provide a level of assurance that the global optimum will be located, and several important advances in the GO of certain types of nonlinear dynamic systems have been made recently (Esposito and Floudas 2000; Singer et al. 2001; Papamichail and Adjiman 2002). However, it should be noted that, although deterministic methods can guarantee global optimality for certain GO problems, no algorithm can solve general GO problems with certainty in finite time (Guus et al. 1995). In fact, although several classes of deterministic methods (e.g., branch and bound) have sound theoretical convergence properties, the associated computational effort increases very rapidly (often exponentially) with the problem size.

In contrast, many stochastic methods can locate the vicinity of global solutions with relative efficiency, but the cost to pay is that global optimality cannot be guaranteed. However, in practice, the user can be satisfied if these methods provide a very good (often, the best available) solution in modest computation times. Furthermore, stochastic methods are usually quite simple to implement and use, and they do not require transformation of the original problem, which can be treated as a black box. This characteristic is especially interesting because very often the researcher must link the optimizer with a third-party software package in which the process dynamic model has been implemented.

Stochastic GO Methods

There are many different kinds of stochastic methods for global optimization, but the following groups must be highlighted:

  • Adaptive stochastic methods (or adaptive random search), which were originally developed in the domains of electrical and control engineering and applied mathematics in the 1950s and 1960s (Brooks 1958; Matyas 1965; Rastrigin and Rubinstein 1969).

  • Clustering methods (Törn 1973; Rinnooy-Kan and Timmer 1987) were derived from the initial concepts of multistart methods, that is, local methods started from different initial points. Clustering methods are more efficient and robust than multistart methods because they try to identify the vicinity of local optima, thus increasing efficiency by avoiding the repeated determination of the same local solutions. However, they do not seem to work well for a large number of decision variables.

  • Evolutionary computation (EC), also known as biologically inspired methods, or population-based stochastic methods. This is a very popular class of methods based on the ideas of biological evolution (Fogel 2000), which is driven by the mechanisms of reproduction, mutation, and the principle of survival of the fittest (Darwin 1859). Similarly to biological evolution, evolutionary computing methods generate better and better solutions by iteratively creating new “generations” by means of those mechanisms in numerical form. EC methods are usually classified into three groups: Genetic Algorithms (GAs; Goldberg 1989; Holland 1992; Michalewicz 1996), Evolutionary Programming (EP; Fogel et al. 1966), and Evolution Strategies (ES; Schwefel 1995; Beyer and Schwefel 2002).

  • Simulated annealing (SA; and other similar physically inspired methods) is another extremely popular class of methods. These methods were created by simulating certain natural phenomena taking place in, for example, the cooling of metals, where atoms adopt the most stable configuration as slow cooling of a metal takes place (Kirkpatrick et al. 1983; van Laarhoven and Aarts 1987).

  • Other meta-heuristics: Several stochastic methods have been presented during recent years that are mostly based on other biological or physical phenomena, and with combinatorial optimization as their original domain of application. Examples of these more recent methods are Taboo Search (TS), Ant Colony Optimization (ACO), and particle swarm methods. A thorough review of these and other recent techniques can be found in Corne et al. (1999).

GO Methods Used

In this study, we have considered a set of selected stochastic and deterministic GO methods that can handle black-box models. The selection has been made based on their published performance and on our own experiences considering their results for a set of GO benchmark problems. Although none of these methods can guarantee optimality, at least the researcher can solve a given problem with different methods and make a decision based on the set of solutions found. Usually, several of the methods will converge to essentially the same (best) solution. It should be noted that although this result can not be regarded as a confirmation of global optimality (it might be the same local optimum), it does give the user some extra confidence. Furthermore, it is usually possible to have estimates of lower bounds for the cost function and its different terms, so the goodness of the “global” solution can be evaluated (sometimes a “good enough” solution is sufficient).

The GO methods that we have considered are:

GBLSOLVE

A deterministic GO method, implemented in Matlab as part of the optimization environment TOMLAB (Holmström 1999). It is a version of the DIRECT algorithm (Jones et al. 1993; Jones 2001) that handles nonlinear and integer constraints. GBLSOLVE runs for a predefined number of iterations and considers the best function value found as the global optimum.

MCS

The Multilevel Coordinate Search algorithm by Huyer and Neumaier (1999), also inspired by the DIRECT method (Jones 2001), is an intermediate between purely heuristic methods and those allowing an assessment of the quality of the minimum obtained. It has an initial global phase after which a local procedure, based on an SQP algorithm, is launched. These local enhancements lead to quick convergence once the global step has found a point in the basin of attraction of a global minimizer.

ICRS

An adaptive stochastic presented by Banga and Casares (1987), improving the Controlled Random Search (CRS) method of Goulcher and Casares (1978). Basically, ICRS is a sequential (one trial vector at a time), adaptive random search method that can handle inequality constraints via penalty functions, and which has been successfully applied to a number of dynamic optimization problems (Banga and Seider 1996; Banga et al. 1997).

DE

The Differential Evolution method as presented by Storn and Price (1997). DE is a heuristic, population-based approach to GO. The original code of the DE algorithm (Storn and Price 1997) did not check if the new generated vectors were within their bound constraints, therefore we have slightly modified the code for that purpose.

uES

The unconstrained Evolution Strategy (uES) is a (µ, λ)-ES evolutionary optimization algorithm (based on Schwefel 1995) for problems only constrained by bounds on the decision variables.

SRES

The Evolution Strategy using Stochastic Ranking (Runarsson and Yao 2000) is a (µ, λ)-ES evolutionary optimization algorithm that uses stochastic ranking as the constraint handling technique. The stochastic ranking is based on the bubble-sort algorithm and is supported by the idea of dominance. It adjusts the balance between the objective and penalty functions automatically during the evolutionary search.

CMA-ES

Another Evolution Strategy method. To improve the convergence rates, especially on nonseparable and/or badly scaled functions, this method introduces in the evolution strategy the intermediate (center of mass) recombination with derandomized covariance matrix adaptation (CMA). This is a generalized individual step-size control approach independent of the orientation and permutation of the coordinate axes (Hansen and Ostermeier 1997).

Justification of the Selection

The above set of GO methods should be regarded as a balanced selection of competitive algorithms trying to reflect the state of the art for each type of approach:

Deterministic methods

GBLSOLVE was chosen as a recent method with good reported results for several challenging problems. Similarly, the related and similarly recent MCS method was included as a qualified representative of those methods combining deterministic approaches with some heuristics.

Adaptive stochastic methods

The ICRS algorithm, the oldest in the set, was taken as a representative of the adaptive random search methods. Although this type of algorithm is not as popular as, for example, Evolutionary Computation methods, they have been shown to exhibit nice properties especially regarding their good scaling with the problem size (Zabinsky and Smith 1992). In fact, Evolutionary Computation methods can be regarded as population-based extensions of adaptive random search methods.

Evolutionary Computation (EC) methods

The rest of the selected methods, DE, uES, SRES, and CMA-ES, have been included as the most competitive representatives of EC methods. DE (Storn and Price 1997) can be considered as a hybrid between adaptive random search methods and genetic algorithms (GAs). Although pure GAs are by far the most popular EC methods, an increasing amount of literature during recent years has consistently shown that ES methods, closely followed by EP, are usually more efficient and robust than GAs, especially for continuous problems (Hoffmeister and Bäck 1991; Saravanan et al. 1995; Bäck 1996; Balsa-Canto et al. 1998). For this reason, we have selected SRES and CMA-ES as recent and competitive ES methods. Their superiority over more traditional GAs has been shown considering many different test problems (Hansen and Ostermeier 1997; Runarsson and Yao 2000).

It should be noted that we have not included any representative of the type of GO methods known as Simulated Annealing (SA), which are almost as popular as GAs. As in the case of GAs, the decision to exclude SA-based methods was based on its reported poor performance with respect to the above selected methods. It should be noted that both GAs and SA were originally devised for combinatorial optimization problems (i.e., those with discrete decision variables), and later adapted for global optimization in real valued search spaces. In contrast, the above methods were designed with real (continuous) decision variables in mind, and this could be one of the main reasons for their better efficiency and robustness for this class of problems.

Implementation Details

For the sake of fair comparison, we have considered Matlab (http://www.mathworks.com) implementations of all these methods. The main reason to use Matlab is that it is a convenient environment to postprocess and visualize all the information arising from the optimization runs of the different solvers, allowing careful comparisons with little programming effort. Furthermore, new methods (or modifications to existing ones) can be easily prototyped and evaluated. However, as a drawback, it is well known that Matlab programs usually are one order of magnitude (or more) slower than equivalent compiled Fortran or C codes. To minimize this effect, we have implemented the more costly part of the problem (i.e., system dynamic simulation plus objective function evaluation) in a compiled Fortran-77 module, using LSODA as the initial value solver (Hindmarsh 1983). This solver is able to solve both stiff and nonstiff systems with automatic switching between the necessary numerical schemes. The resulting module (a dynamic link library) is callable from the Matlab solvers via suitable gateways. Because most stochastic methods use 90% (or more) of the computation time in system simulations (especially if their complexity level is medium to large), this procedure ensures good efficiency while retaining the main advantages of the Matlab environment. Table 1 shows the internal search parameters used for the different algorithms, which were selected according to either published recommendations and/or our personal experience with several preliminary runs.

Table 1.

Search Parameters Utilized in the Different Algorithms

SRES uES DE CMA-ES
Search parameters G = 8000 G = 8000 VTR = 0.0; st = 6 N = 36
lambda = 350 lambda = 350 D = 36; NP = 450 lambda = 15
μ = 30; pf = 0.450 μ = 30 iterMax = 5000 μ = 7; xlow = xl; xup = xu
varphi = 1 varphi = 1 F = 0.5; CR = 0.55 MaxFunEvals = 3000N2
ICRS MCS GBLSOLVE
Search parameters e = 10−3 n = 36; smax = 370 eps_x = eps_f = 10−4
kl = 1 nf = 600 n2; stop(2) = 0 Iterations = 1500
k2 = 1/2 stop(1) = n + 2000
maxfsd = 4 iinit = 3; local = 15
Open in a new tab

Finally, to illustrate the comparative performance of multistart local methods for this type of problem, a multistart code (named ms-FMINCON) was also implemented in Matlab making use of the FMINCON code, which is part of the MATLAB Optimization Toolbox (Anonymous 2000). FMINCON is a gradient-based solver indicated for unconstrained functions. Its default algorithm is a quasi-Newtonian method that uses the BFGS formula for updating the approximation of the Hessian matrix. Its default line search algorithm is a safeguarded mixed quadratic and cubic polynomial interpolation and extrapolation method.

Case Study: A Three-Step Pathway

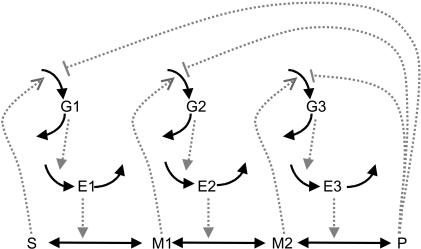
The optimization problem consists of the estimation of 36 kinetic parameters of a nonlinear biochemical dynamic model formed by 8 ODEs that describe the variation of the metabolite concentrations with time (see Fig. 1).

Figure 1.

Figure 1

Open in a new tab

The model metabolic pathway used in these studies. Solid arrows represent mass flow, dashed arrows represent kinetic regulation; arrow ends represent activation, blunt ends inhibition. S and P are the pathway substrate and product and are held at constant concentrations; M1 and M2 are intermediate metabolites of the pathway; E1, E2, and E3 are the enzymes; G1, G2, and G3 are the mRNA species for the enzymes.

The mathematical formulation of the nonlinear dynamic model is:

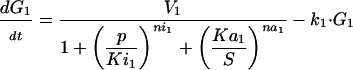graphic file with name M7.gif 7
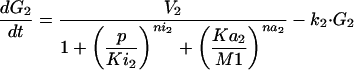graphic file with name M8.gif 8
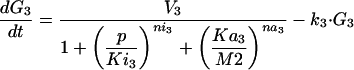graphic file with name M9.gif 9
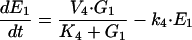graphic file with name M10.gif 10
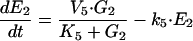graphic file with name M11.gif 11
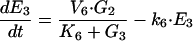graphic file with name M12.gif 12
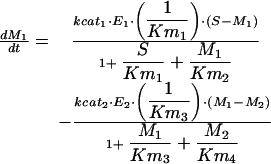graphic file with name M13.gif 13
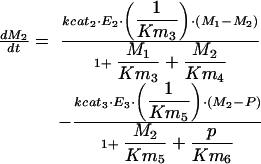graphic file with name M14.gif 14

where M1, M2, E1, E2, E3, G1, G2, and G3 represent the concentrations of the species involved in the different biochemical reactions and S and P keep fixed initial values for each experiment (i.e., parameters under our control). The optimization problem is then to fit the 36 remaining parameters, which are divided into two different classes: Hill coefficients, allowed to vary within the range (0.1, 10) and all the others, allowed to vary within the range (10 -12, 10+12).

The global optimization problem is stated as the minimization of a weighted distance measure J between experimental and predicted values of the 8 state variables, represented by the vector y:

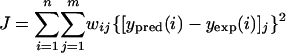graphic file with name M15.gif 15

where n is the number of data for each experiment, m is the number of experiments, yexp represents the known experimental data, and ypred is the vector of states that corresponds to the predicted theoretical evolution using the model with a given set of the 36 parameters. Furthermore, wij corresponds to the different weights taken to normalize the contributions of each term (i.e., wij = {1/max[yexp(i)]j}2).

To better assess the performance of the GO techniques for the solution of the inverse problem, pseudoexperimental data were generated by simulation from a set of chosen parameters (to be considered as the true, or nominal, values). Thus, pseudomeasurements of the concentrations of metabolites, proteins, and messenger RNA species were the result of 16 different experiments (simulations) in which the initial concentrations of the pathway substrate, S, and product, P, were varied (see Table 2 to examine S and P values for each experimental design, plus the nominal values considered for the parameters). These simulated data represent exact results, that is, devoid of measurement noise.

Table 2.

Experiment Generation

P value 0.05 0.13572 0.36840 1.0
S value 0.1 0.46416 2.1544 10
Parameter Element of decision variables vector Nominal value
V1 p1 1
Ki1 p2 1
ni1 p3 2
Ka1 p4 1
na1 p5 2
k1 p6 1
V2 p7 1
Ki2 p8 1
ni2 p9 2
Ka2 p10 1
na2 p11 2
k2 p12 1
V3 p13 1
Ki3 p14 1
ni3 p15 2
Ka3 p16 1
na3 p17 2
k3 p18 1
V4 p19 0.1
K4 p20 1
k4 p21 0.1
V5 p22 0.1
K5 p23 1
k5 p24 0.1
V6 p25 0.1
K6 p26 1
k6 p27 0.1
kcat1 p28 1
Km1 p29 1
Km2 p30 1
kcat2 p31 1
Km3 p32 1
Km4 p33 1
kcat3 p34 1
Km5 p35 1
Km6 p36 1
Open in a new tab

S and P values were combined to generate a total of 16 sets of pseudoexperimental measurements, and nominal values of the parameters, also indicating the corresponding element of the decision variables vector (p).

RESULTS AND DISCUSSION

All the computations were performed using a PC/Pentium III (866 MHz) platform running Windows 2000. The best result (J = 0.0013) was obtained using the SRES method (Runarsson and Yao 2000) after a total computation time of 39.42 h. However, it should be noted that this large computational effort was the consequence of the very tight convergence criteria used, but from a practical point of view, an almost equally good result was reached in a few hours. The second best method was the uES method, which converged to a very close value of J = 0.0109. Thus, uES can be regarded as a very close second winner. Detailed results are given in Table 3 with the best solution vector shown in Table 4. Table 3 shows that none of the other algorithms tested, neither deterministic nor stochastic, could arrive at the vicinity of the abovementioned solutions. This is, indeed, a clear sign of the very challenging nature of these problems. The results in Table 3 also reveal an interesting result that might be surprising at first sight: The MCS and GBLSOLVE methods present a larger computation time per function evaluation than the rest of the algorithms. However, this is simply a consequence of the larger overhead introduced by these methods to generate each new decision vector.

Table 3.

Results of the Global Optimization Methods

SRES uES DE ICRS CMA-ES MCS GBLSOLVE
J 0.0013 0.0109 151.779 183.579 37.881 364.139 1179.464
Neval 28e5 28e5 22.5e5 16515 756135 327698 649431
CPU time (h) 39.42 41.27 46.03 0.41 17.31 39.06 114.69
Open in a new tab

Objective function, J, number of function evaluations, Neval, and computation time, in hours of a PC/Pentium III 866 MHz.

Table 4.

Decision Vector for the Best Solution (Found by SRES)

Elements of best vector
p1-p4 0.8360 0.9997 1.9990 1.0000
p5-p8 1.9989 0.8359 1.0387 1.0001
p9-p12 1.9980 0.9992 2.0012 1.0390
p13-p16 0.9321 1.0007 2.0028 0.9995
p17-p20 2.0019 0.9329 0.1026 1.0000
p21-p24 0.1026 0.0995 1.0025 0.0993
p25-p28 0.1008 0.9990 0.1008 1.0076
p29-p32 0.9996 0.9678 1.0124 1.0036
p33-p36 0.9514 1.0021 1.0041 0.9856
Open in a new tab

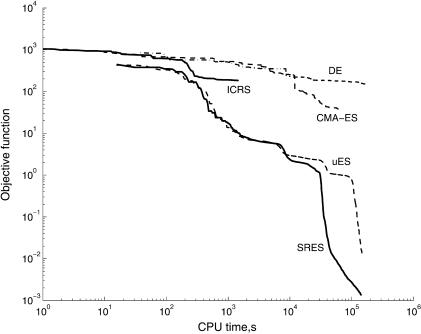
Simply comparing the final cost function values and the overall computation times can be misleading. In Figure 2, the convergence curves (objective function versus computation time) of the best five methods, all of them stochastic, are plotted (note the log-log scales). It is quite clear that SRES and uES presented the best convergence rates at all times.

Figure 2.

Figure 2

Open in a new tab

Convergence curves (objective function versus computation time, in seconds, using a PC/Pentium III 866 MHz).

It is, indeed, surprising to note that several global optimization methods (e.g., DE, ICRS), which in the past presented a very good performance dealing with a number of hard GO problems, have clearly failed here. This is probably because of the greater complexity of this parameter estimation problem (i.e., a very large number of local solutions) and/or its relatively large dimensionality. In the case of ICRS, its reported CPU time in Table 3 is much shorter that those of the other algorithms, but this is only a consequence of its early stop at a local minimum. In fact, the true story about comparative performance is told in Figure 2 (convergence curves), where it can be seen that the uES and SRES methods were better than ICRS at all times. Moreover, by the time ICRS stopped (0.41 h), the running ES-based methods had already arrived at much better objective function values, as shown in Figure 2.

In the case of the MCS and GBLSOLVE methods, which are both inspired by the DIRECT method of Jones (2001), the results are probably due to the dimensionality of the problem, but also to implementation issues, at least in the case of GBLSOLVE, because more efficient implementations have been reported in the latest version of the TOMLAB library (Holmström 2001).

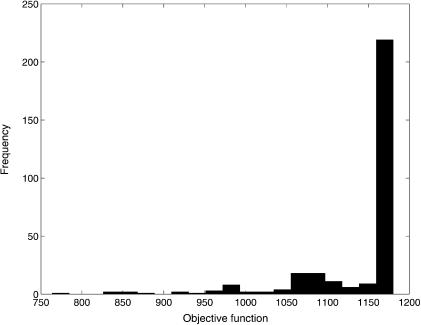
Regarding the multistart local search, the ms-FMINCON method was executed starting from >300 random initial points. The best result was J = 763.72, very far from the best solution obtained with SRES. Furthermore, most of the other local solutions obtained were much worse. Figure 3 shows a histogram with the distribution of all the local solutions found with this method. Clearly, and in contrast with popular belief (or “folklore,” in the words of Guus et al. 1995), multistart local methods are unsatisfactory for hard parameter estimation problems like this one.

Figure 3.

Figure 3

Open in a new tab

Histogram of the results obtained with the multistart local method.

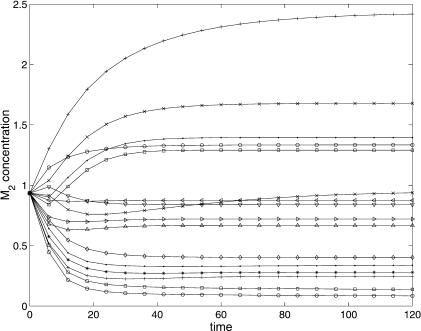
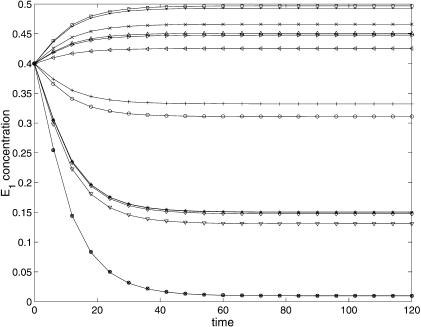
Figures 4 and 5 show a comparison (between the predicted and experimental data) for the best decision vector (found with SRES) of the concentrations M2 and E1. It is worth noting the very good correlation between the experimental and predicted data. The representation of the dynamic behavior for the other variables is quite similar and is not included here for the sake of brevity.

Figure 4.

Figure 4

Open in a new tab

M2 predicted (continuous line) and experimental (marker) behavior for the 16 experiments.

Figure 5.

Figure 5

Open in a new tab

E1 predicted (continuous line) and experimental (marker) behavior for the 16 experiments.

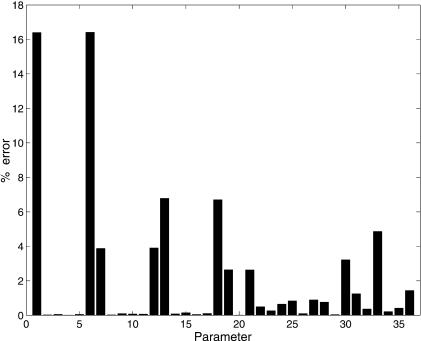
Finally, to underline the merit of the best solution obtained by the SRES optimizer, the error values, that is, the relative differences between the known (real) and the estimated parameters are shown in Figure 6. Only parameters 1 and 6 were estimated with an error >16%. All the other errors were below 7%, with the majority being below 3%, which is a very remarkable result. The earlier study had not been able to achieve such good results (Mendes 2001). We believe that this is because here we used the results of 16 different experiments, rather than just a single one. The data used in the earlier study reflected a greater level of underdetermination, and this resulted in the somewhat imperfect solution obtained. By covering a larger set of dynamics that the model is capable of, we have been able to obtain near-exact results (convergence to the global optimum). We stress that these excellent results were obtained (as before) in conditions in which measurement noise is absent, whereas in reality, one expects it to be present to some extent, sometimes even in considerable magnitudes (e.g., microarray data). Nevertheless, the problem was already sufficiently hard that most algorithms did not perform satisfactorily. Later we intend to repeat this study in the presence of measurement noise.

Figure 6.

Figure 6

Open in a new tab

Relative error (%) for the estimated parameters (for the best solution, obtained by SRES).

Conclusions

Only evolutionary strategies, namely, the SRES and uES methods, were able to successfully solve the inverse problem associated with a three-step pathway. This result is in agreement with other recent global optimization studies (Rechenberg 2000; Runarsson and Yao 2000; Costa and Oliveira 2001), some of them dealing with nonlinear dynamic systems (Moles et al. 2001; Banga et al. 2002), which indicate that evolution strategies might be the most competitive stochastic optimization method, especially for large problems.

A possible drawback of ES methods, in spite of these good results, is the computational effort required, which is on the order of hours using low-cost PC platforms. However, it is well known that many stochastic methods, including ES, lend themselves to parallelization very easily, which means that this problem could be handled in reasonable wallclock time by suitable parallel versions. Present technologies for cluster computing (e.g., http://www.beowulf.org) or grid computing (e.g., http://www.globus.org) can greatly facilitate the development of such versions.

One of us (P.M.) wrote and distributes a biochemical simulation package, Gepasi (http://www.gepasi.org, Mendes 1993), which implements several numerical optimization methods, including GO. Although that software is easily extensible, most of the methods implemented and tested here are not yet included in that software. Given the superior performance of SRES and uES, these are now being implemented in that package, which will make them available to the biochemical modeling community at large.

Acknowledgments

P.M. thanks the National Science Foundation (grants BES-0120306, DBI-0109732, and DBI-0217653), the Commonwealth of Virginia, and Sun Microsystems for financial support. J.R.B. thanks the Spanish Government (MCyT project AGL2001-2610-C02-02) for financial support.

The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.

Footnotes

Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.1262503. Article published online before print in October 2003.

References

  1. Ali, M.M., Storey, C., and Törn, A. 1997. Application of stochastic global optimization algorithms to practical problems. J. Optim. Theory Appl. 95: 545-563. [Google Scholar]
  2. Anonymous. 2000. Optimization toolbox user's guide. The Math Works Inc., Natick, MA.
  3. Bäck, T. 1996. Evolution strategies: An alternative evolutionary algorithm. In Artificial evolution (eds. J.M. Alliott et al.), pp. 3-20. Springer, Berlin.
  4. Balsa-Canto, E., Alonso, A.A., and Banga, J.R. 1998. Dynamic optimization of bioprocesses: Deterministic and stochastic strategies. In Proceedings of ACoFop IV (Automatic Control of Food and Biological Processes), (eds. C. Skjoldebremd and G. Trystrom), pp. 2-23. Göteborg, Sweden.
  5. Banga, J.R. and Casares, J.J. 1987. ICRS: Application to a wastewater treatment plant model. In IChemE Symposium Series No. 100, pp. 183-192. Pergamon Press, Oxford, UK.
  6. Banga, J.R. and Seider, W.D. 1996. Global optimization of chemical processes using stochastic algorithms. In State of the art in global optimization (eds. C.A. Floudas and P.M. Pardalos), pp. 563-583. Kluwer Academic Publishers, Dordrecht, The Netherlands.
  7. Banga, J.R., Alonso, A.A., and Singh, R.P. 1997. Stochastic dynamic optimization of batch and semicontinuous bioprocesses. Biotechnology Prog. 13: 326-335. [Google Scholar]
  8. Banga, J.R., Alonso, A.A., Moles, C.G., and Balsa-Canto, E. 2002. Efficient and robust numerical strategies for the optimal control of non-linear bio-processes. In Proceedings of the Mediterranean Conference on Control and Automation (MED2002), (eds. J.S. Sentievio and M. Attrans), CD-ROM. IEEE CSS, Lisbon, Portugal.
  9. Beyer, H.G. and Schwefel, H.P. 2002. Evolution strategies—A comprehensive introduction. Natural Computing 1: 3-52. [Google Scholar]
  10. Brooks, S.H. 1958. A discussion of random methods for seeking maxima. Op. Res. 6: 244-251. [Google Scholar]
  11. Cho, K.H., Shin, S.Y., Kim, H.W., Wolkenhauer, O., McFerran, B., and Kolch, W. 2003. Mathematical modelling of the influence of RKIP on the ERK signalling pathway. In Computational methods in systems biology (ed. C. Priami), pp. 127-141. Lecture Notes in Computer Science (LNCS) 2602. Springer Verlag, New York.
  12. Corne, D., Dorigo, M., and Glover, F. 1999. New ideas in optimization. McGraw-Hill, New York.
  13. Costa, L. and Oliveira, P. 2001. Evolutionary algorithms approach to the solution of mixed integer non-linear programming problems. Comput. Chem. Eng. 25: 257-266. [Google Scholar]
  14. Darwin, C.R. 1859. On the origin of species by means of natural selection. J. Murray, London.
  15. Esposito, W.R. and Floudas, C.A. 2000. Global optimization for the parameter estimation of differential-algebraic systems. Indust. Eng. Chem. Res. 39: 1291-1310. [Google Scholar]
  16. Fogel, D.B. 2000. Evolutionary computation: Toward a new philosophy of machine intelligence. IEEE Press, New York.
  17. Fogel, L.J., Owens, A.J., and Walsh, M.J. 1966. Artificial intelligence through simulated evolution. Wiley, New York.
  18. Goldberg, D.E. 1989. Genetic algorithms in search, optimization and machine learning. Addison Wesley Longman, London.
  19. Goulcher, R. and Casares, J.J. 1978. The solution of steady-state chemical engineering optimisation problems using a random-search algorithm. Comput. Chem. Eng. 2: 33-36. [Google Scholar]
  20. Grossmann, I.E. 1996. Global optimization in engineering design. Kluwer Academic Publishers, Dordrecht, The Netherlands.
  21. Guus, C., Boender, E., and Romeijn, H.E. 1995. Stochastic methods. In Handbook of global optimization (eds. R. Horst and P.M. Pardalos), pp. 829-869. Kluwer Academic Publishers, Dordrecht, The Netherlands.
  22. Hansen, N. and Ostermeier, A. 1997. Convergence properties of evolution strategies with the derandomized covariance matrix adaptation: the (µ/µI, λ)-CMA-ES. In Proceedings of the 5th European Congress on Intelligent Techniques and Soft Computing, EUFIT '97 pp. 650-654. Verlag Maing, Auchen, Germany.
  23. Hindmarsh, A.C. 1983. ODEPACK, a systematized collection of ODE solvers. In Scientific computing (ed. R.S. Stepleman), pp. 55-64. North-Holland, Amsterdam.
  24. Hoffmeister, F. and Bäck, T. 1991. Genetic algorithms and evolution strategies: Similarities and differences. In Proceedings of Parallel Problem Solving from Nature—1st Workshop, PPSN 1 (eds. H.-P. Schwefel and R. Männer), pp. 455-469. Lecture Notes in Computer Science, Vol. 496. Springer-Verlag, Berlin. [Google Scholar]
  25. Holland, J.H. 1992. Adaptation in natural and artificial systems: An introductory analysis with applications to biology, control, and artificial intelligence. MIT Press, Cambridge, MA.
  26. Holmström, K. 1999. The TOMLAB optimization environment in Matlab. Adv. Model. Optim. 1: 47-69. [Google Scholar]
  27. ____. 2001. Practical optimization with the TOMLAB environment in Matlab. In Proceedings of the 42nd SIMS Conference, pp. 89-108, Telemark University College, Porsgrunn, Norway.
  28. Horst, R. and Tuy, H. 1990. Global optimization: Deterministic approaches. Springer-Verlag, Berlin.
  29. Huyer, W. and Neumaier, A. 1999. A global optimization by multilevel coordinate search. J. Global Optim. 14: 331-355. [Google Scholar]
  30. Jones, D.R. 2001. DIRECT global optimization algorithm. In Encyclopedia of optimization (eds. C.A. Floudas and P.M. Pardalos), pp. 431-440. Kluwer Academic Publishers, Dordrecht, The Netherlands.
  31. Jones, D.R., Perttunen, C.D., and Stuckman, B.E. 1993. Lipschitzian optimization without the Lipschitz constant. J. Optimization Theory Appl. 79: 157-181. [Google Scholar]
  32. Kirkpatrick, S., Gellatt, C.D., and Vecchi, M.P. 1983. Optimization by simulated annealing. Science 220: 671-680. [DOI] [PubMed] [Google Scholar]
  33. Matyas, J. 1965. Random optimization. Automat. Remote Control 26: 246-253. [Google Scholar]
  34. Mendes, P. 1993. GEPASI: A software package for modelling the dynamics, steady states and control of biochemical and other systems. Comput. Appl. Biosci. 9: 563-571. [DOI] [PubMed] [Google Scholar]
  35. ____. 2001. Modeling large biological systems from functional genomic data: Parameter estimation. In Foundations of systems biology (ed. H. Kitano), pp. 163-186. MIT Press, Cambridge, MA.
  36. Mendes, P. and Kell, D.B. 1998. Non-linear optimization of biochemical pathways: Applications to metabolic engineering and parameter estimation. Bioinformatics 14: 869-883. [DOI] [PubMed] [Google Scholar]
  37. Michalewicz, Z. 1996. Genetic algorithms + data structures = evolution programs. Springer-Verlag, Berlin, New York.
  38. Moles, C.G., Gutierrez, G., Alonso, A.A., and Banga, J.R. 2001. Integrated process design and control via global optimization: A wastewater treatment plant case study. In Proceedings of the European Control Conference (ECC) 2001, 4-7 September (ed. J.L. Martins), CD-ROM, EUCA, Porto, Portugal.
  39. Papamichail, I. and Adjiman, C.S. 2002. A rigorous global optimization algorithm for problems with ordinary differential equations. J. Global Optim. 24: 1-33. [Google Scholar]
  40. Pinter, J. 1996. Global optimization in action. Continuous and Lipschitz optimization: Algorithms, implementations and applications. Kluwer Academics Publishers, Dordrecht, The Netherlands.
  41. Rastrigin, L.A. and Rubinstein, Y. 1969. The comparison of random search and stochastic approximation while solving the problem of optimization. Automat. Control 2: 23-29. [Google Scholar]
  42. Rechenberg, I. 2000. Case studies in evolutionary experimentation and computation. Computer Meth. Appl. Mech. Eng. 186: 125-140. [Google Scholar]
  43. Rinnooy-Kan, A.H.G. and Timmer, G.T. 1987. Stochastic global optimization methods. Part I: Clustering methods. Math. Prog. 39: 27-56. [Google Scholar]
  44. Runarsson, T.P. and Yao, X. 2000. Stochastic ranking for constrained evolutionary optimization. IEEE Trans. Evol. Comput. 4: 284-294. [Google Scholar]
  45. Saravanan, N., Fogel, D.B., and Nelson, K.M. 1995. A comparison of methods for self-adaptation in evolutionary algorithms. Biosystems 36: 157-166. [DOI] [PubMed] [Google Scholar]
  46. Schwefel, H.P. 1995. Evolution and optimum seeking. Wiley, New York.
  47. Singer, A.B., Bok, J.K., and Barton, P.I. 2001. Convex underestimators for variational and optimal control problems. Comput. Aided Chem. Eng. 9: 767-772. [Google Scholar]
  48. Storn, R. and Price, K. 1997. Differential Evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Global Optim. 11: 341-359. [Google Scholar]
  49. Swameye, I., Muller, T.G., Timmer, J., Sandra, O., and Klingmuller, U. 2003. Identification of nucleocytoplasmic cycling as a remote sensor in cellular signaling by databased modeling. Proc. Natl. Acad. Sci. 100: 1028-1033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Törn, A.A. 1973. Global optimization as a combination of global and local search. Proceedings of computer simulation versus analytical solutions for business and economic models, pp. 191-206. Gothenburg, Sweden.
  51. Törn, A., Ali, M., and Viitanen, S. 1999. Stochastic global optimization: Problem classes and solution techniques. J. Global Opt. 14: 437-447. [Google Scholar]
  52. van Laarhoven, P.J.M. and Aarts, E.H.L. 1987. Simulated annealing: Theory and applications. Reidel, Dordrecht, The Netherlands.
  53. Zabinsky, Z.B. and Smith, R.L. 1992. Pure adaptive search in global optimization. Math. Prog. 53: 323-338. [Google Scholar]

WEB SITE REFERENCES

  1. http://www.beowulf.org; technology for cluster computing.
  2. http://www.gepasi.org; Gepasi biochemical simulation package.
  3. http://www.globus.org; technology for grid computing.
  4. http://www.mathworks.com; Matlab.

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES