Decay Rates of Human mRNAs: Correlation With Functional Characteristics and Sequence Attributes

Abstract

Although mRNA decay rates are a key determinant of the steady-state concentration for any given mRNA species, relatively little is known, on a population level, about what factors influence turnover rates and how these rates are integrated into cellular decisions. We decided to measure mRNA decay rates in two human cell lines with high-density oligonucleotide arrays that enable the measurement of decay rates simultaneously for thousands of mRNA species. Using existing annotation and the Gene Ontology hierarchy of biological processes, we assign mRNAs to functional classes at various levels of resolution and compare the decay rate statistics between these classes. The results show statistically significant organizational principles in the variation of decay rates among functional classes. In particular, transcription factor mRNAs have increased average decay rates compared with other transcripts and are enriched in “fast-decaying” mRNAs with half-lives <2 h. In contrast, we find that mRNAs for biosynthetic proteins have decreased average decay rates and are deficient in fast-decaying mRNAs. Our analysis of data from a previously published study of Saccharomyces cerevisiae mRNA decay shows the same functional organization of decay rates, implying that it is a general organizational scheme for eukaryotes. Additionally, we investigated the dependence of decay rates on sequence composition, that is, the presence or absence of short mRNA motifs in various regions of the mRNA transcript. Our analysis recovers the positive correlation of mRNA decay with known AU-rich mRNA motifs, but we also uncover further short mRNA motifs that show statistically significant correlation with decay. However, we also note that none of these motifs are strong predictors of mRNA decay rate, indicating that the regulation of mRNA decay is more complex and may involve the cooperative binding of several RNA-binding proteins at different sites.

In a living cell, mRNA is synthesized by polymerases and destroyed by nucleases. When these two events occur at a constant rate, they give rise to a steady-state mRNA population for each unique transcript (Ross 1995; Wilusz et al. 2001). Although variations in mRNA transcription rates are generally recognized for their central importance in regulating gene expression, the regulatory role of variations in mRNA decay rates has been left relatively unexplored, in particular on a genome-wide scale. Most gene array experiments have focused on measuring the fluctuations in steady-state mRNA concentrations, from which the separate contributions of synthesis and decay cannot be disentangled. More recently, however, measurements of mRNA decay for the entire set of expressed mRNAs (the “transcriptome”) have been carried out in Saccharomyces cerevisiae and Escherichia coli (Holstege et al. 1998; Bernstein et al. 2002; Wang et al. 2002). These studies found some evidence that mRNA decay rates may differ by functional group or membership in certain protein complexes, implying that variations in mRNA decay rate, indeed, play a functional and possibly regulatory role. As mentioned in the Discussion, there have also been some recent efforts to collect mRNA decay data in human cells (Lam et al. 2001; Raghavan et al. 2002; Frevel et al. 2003). However, a comprehensive, functional analysis of decaying mRNA transcripts has not yet been performed.

In this work, we sought to examine several facets of mRNA degradation in human cells. First, we created a database of decay rates of individual mRNA transcripts in human cells that have significantly increased doubling times (24–48 h) in comparison to yeast and bacteria. Using 2–3 h of Actinomycin D treatment, a compound documented to quantitatively halt RNA polymerases in human cells (Scherrer et al. 1963), we measured decreases in mRNA levels with oligonucleotide arrays for the hepatocellular carcinoma cell line HepG2 and the primary fibroblast cell line Bud8.

Secondly, we systematically investigated the functional organization of decay rates and compared this organization between eukaryotes at opposite ends of the spectrum of biological complexity, that is, yeast and humans. Using available annotation of human and yeast genes, and the Gene Ontology (GO) hierarchy of biological processes, we assigned our transcripts to functional classes at various levels of resolution and compared the average decay rates and fractions of fast-decaying transcripts between these classes. As described below, we found clear statistical evidence for a functional organization in mRNA decay rates that is reproduced between yeast and humans. Third, we wanted to investigate and quantify the dependence of decay rates on mRNA sequence composition, in particular the presence and absence of short mRNA sequence motifs in the 3′-UTR, the coding sequence, and the 5′-UTR of the sequence.

Our addition of rigorous statistical methodology and automated annotation methodology enables a definitive, high-resolution evaluation of the connection between mRNA transcript function and decay rate. As described below, these statistical inference procedures led to an intriguing observation about the connection of mRNA decay to the regulation of gene expression. We also make full use of the available sequence information to analyze the impact of existing and new mRNA decay motifs when located in different segments of the mRNA transcript. Together, these results provide information essential for a global understanding of mRNA decay in human cells.

RESULTS

Overall Features of mRNA Turnover in Cultured Human Cells

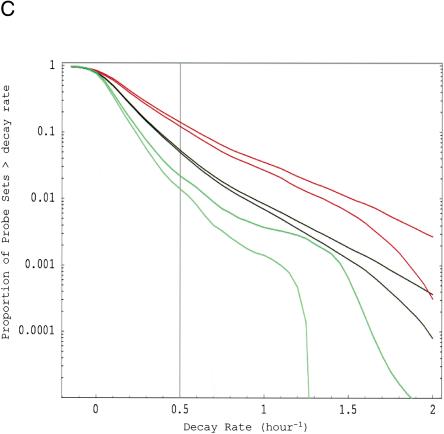
To study the rates of mRNA degradation (“decay”) in human cells, we measured changes in mRNA levels following application of the RNA polymerase inhibitor Actinomycin D with Affymetrix U95Av2 high-density oligonucleotide arrays. We collected RNA from cells after 2–3 h of inhibition and used the Affymetrix Microarray Suite (MAS) 5.0 to analyze the changes from the untreated state. Four experiments (i.e., eight hybridizations) were performed in HepG2 cells, and we conducted an additional experiment in Bud8 primary cells to exclude the possibility of cancer-cell-specific artifacts. We estimated the average decay rate for each unique GenBank accession expressed (p < 0.04) at both the baseline and experimental time point in the HepG2 experiments by combining all probe sets i for each gene (including replicate probe sets on a single chip and across the four replicate decay experiments). In this way, we obtained decay rate estimates for 5245 accessions, which we collected in a database that is available at www.genome.org and http://genomes.rockefeller.edu/~yange/ as Supplemental Table 9. Combining the decay rate for all probe sets present in the initial and final conditions, we find that the median half-life in both cell types was ∼10 h (Supplemental Table 9; E. van Nimwegen and E. Yang, unpubl.). It should be noted, however, that, in contrast to the relative decay rates of different transcripts (discussed below), the absolute decay rates that we infer are sensitive to the overall normalization of the arrays. With our normalization based on β-actin expression, we find roughly 10% variation of the average overall absolute decay rate between the replicates. We thus believe that our 10-h median half-life figure is accurate to within 10%. Comparing this median half-life with the median half-lives of transcripts in yeast and bacteria, it appears that the half-life of the mRNA pool of a cell scales roughly in proportion to the length of the cell cycle: cell cycle lengths of 20, 90, and 3000 min correspond to median half-lives of 5, 21, and 600 min, respectively, for E. coli, S. cerevisiae, and human HepG2/Bud8 cells (Bernstein et al. 2002; Wang et al. 2002). The reverse cumulative distribution of decay rates for the HepG2 cells is shown in Figure 1C. As indicated in the cumulative distribution plot, a small percentage (∼5%) of expressed transcripts have “fast” decay rates (which we define as r > 0.5 h^-1 or a half-life < 2 h). A similar percentage of rapidly decaying genes was observed when we re-ran an HepG2 experiment with U95B arrays, which are predominantly expressed sequence tags (E. van Nimwegen and E. Yang, unpubl.). The percent of fast-decaying mRNAs also agrees with data obtained from studies of human lymphoma cells (Lam et al. 2001). Although total length of cDNA did not correlate with decay rate, we did find evidence that mRNAs with 3′-UTR sequence >1 kb decayed at a significantly faster rate than shorter 3′-UTRs (E. van Nimwegen and E. Yang, unpubl.).

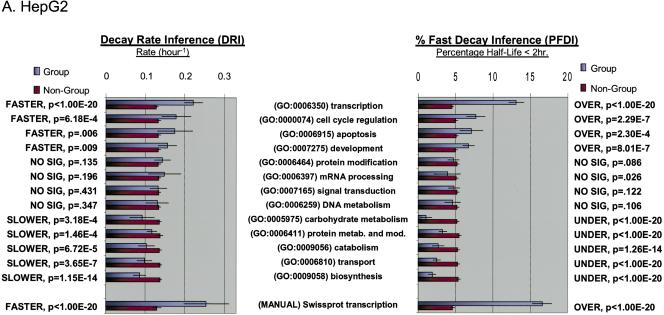
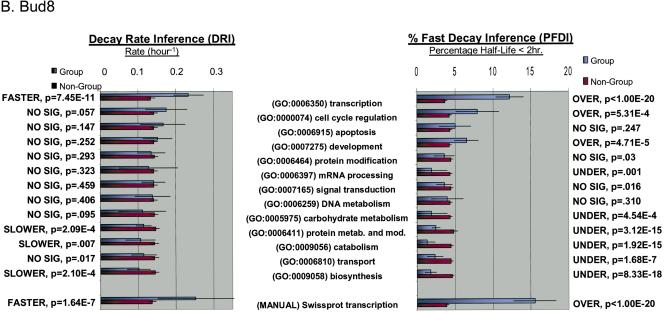
Figure 1.

Functional analysis of decaying transcripts in human cells. (A,B) Probe sets from the HepG2 experiments (A) or the Bud8 experiment (B) were grouped by functional (i.e., Gene Ontology, GO) category, and both decay rate and the percentage of fast decayers were inferred using procedures we call DRI and PFDI (see Methods: Statistical Analysis and Decay Rate Calculations). For DRI, the average decay rates were calculated (error bars denote 99% posterior probability interval (PPI)) for probe sets corresponding to the functional category listed in the center (Group, blue). If the GO category in question was separated from the rest of the probe sets (Nongroup, purple) with >99% probability (see p-values to left), the distribution was described as “FASTER” or “SLOWER” as appropriate. Otherwise, the GO distribution was said to be “NO SIG” (not significantly) different from the other probe sets. For PFDI, the percentage of probe sets (error bars again denote 99% PPI) decaying with a rate >0.5 h^-1 (2 h half-life) were calculated for probe sets inside of the stated GO category (Group) or outside the category (Nongroup). If the GO category's probe sets were enriched/depleted in the rapid turnover pool with at least 99% probability (see p-values to the right), the category was said to be “OVER” (overrepresented) or “UNDER” (underrepresented), respectively. Otherwise, the category was listed as “NO SIG” (no significant) enrichment. For comparison, the same analysis (“MANUAL”) was performed using a set of probe sets corresponding to SWISS-PROT entries annotated as transcription-related (see Methods). (C) Reverse cumulative distribution of decay rates for probe sets in different functional classes (HepG2 experiments). Decay rate r is shown horizontally, while vertically the fraction of probe sets with decay rates higher than r is plotted on a logarithmicscale. The pairs of lines show the 98% posterior probability intervals for the fraction at each value of r. (Red) GO process transcription; (black) all probe sets; (green) biosynthesis. The gray line indicates the decay rate r = 0.5 h^-1, which is our cutoff for fast decay in PFDI.

Correlation of Gene Function With Decay Rate

To determine whether the function of a gene product influenced the rate of decay, we coupled all probe sets in our experiments to Gene Ontology (GO) codes (see Methods). GO codes provide a standardized, hierarchical classification for describing gene products agreed to by the public genome sequencing projects. For reference, we provide the list of gene products associated with the GO process codes for “transcription” and “biosynthesis” in Supplemental Tables 7 and 8. We then determined the decay rate r (h^-1) and percentage of “fast-decaying” transcripts for each GO category containing more than 25 probe sets. Each GO category was then analyzed for average decay rate (decay rate inference, DRI) or over/underrepresentation of fast turnover transcripts among the probe sets in the category (percentage fast decay inference, PFDI). Thus, an unbiased search for statistically significant changes in mRNA decay rate was possible for hundreds of functional categories at various levels of detail. A graphical summary of the results for selected GO categories is provided as Figure 1, A and B, for HepG2 and Bud8, respectively. The results for all GO categories analyzed are provided as Supplemental Tables 1 and 2.

For both Bud8 and HepG2 data sets, we observed several GO categories with significant increases or decreases in average decay rate (see Supplemental Tables 1 and 2). In particular, we noted a marked increase of average decay rate for transcription-related transcripts (HepG2: 0.221 h^-1 vs. 0.127 h^-1 for nontranscriptional transcripts, p < 10^-20). This trend for the GO transcription category matched results obtained from a “manual” classification method (see Methods). Notably, other regulatory functional groups (e.g., signal transduction, mRNA processing) were not significantly altered compared with other transcripts. We also observed a significant decrease in the decay rate of biosynthesis-related transcripts (HepG2: 0.085 h^-1 vs. 0.137 h^-1 for nonbiosynthesis transcripts; p < 10^-13). Similar decreases in average decay rate were observed for other “housekeeping” categories such as catabolism and carbohydrate metabolism. These changes are mirrored by the changes in percentage of transcripts that turn over rapidly (i.e., half-life < 2 h, PFDI) for these groups. In the case of the HepG2 experiment (Fig. 1A), the percent of all probe sets with fast decay was ∼5%, but 13.1% of the transcriptional transcripts are fast decaying (i.e., overrepresentation; p < 10^-20). Similarly, only 1.9% of the biosynthetic transcripts are rapidly decaying (i.e., underrepresentation; p < 10^-20). We also noted increased decay of transcription-related transcripts and decreased decay of metabolic genes in a previously published yeast data set, indicating a general organizing principle for eukaryotic cells (see Supplemental Table 3). Thus, transcript function is associated with differences in the mean decay rate as well as the proportion of transcripts with fast turnover. These features are illustrated in Figure 1C; for “transcription” and “biosynthesis,” the decay rate distribution has the same general shape but is shifted away from the distribution for probe sets over a wide range of decay rates.

Correlation of RNA Motifs With Decay Rate

Mammalian mRNA stability is regulated, in part, by RNA motifs that correlate with rapid transcript destruction (Wilusz et al. 2001). However, the impact of these motifs on the decay behavior of large, heterogeneous populations of transcripts is not well understood. In analogy to our functional analysis, we matched probe sets on our microarray to sequences corresponding to their 3′-UTR, 5′-UTR, open reading frame (ORF), or whole cDNA. These sequences were subjected to quality control procedures and had poly(A)s removed from the 3′-UTR and whole cDNA sequences (see Methods). Using previously described AU-rich motif variants and novel motifs detected in the course of this study (see Methods), we accumulated a list of several RNA motifs that we had reason to believe correlated with changes in RNA decay rate. We then determined the average decay rate r (h^-1) and percentage of “fast-decaying” transcripts for each combination of motif and sequence position. After discarding combinations represented by <26 probe sets, the same two statistical procedures used above (i.e., DRI and PFDI) were performed for these motifs. The number of probe sets contributing to calculations for each motif–location combination is shown in Supplemental Table 4. Average decay rates and percentages of fast decayers are summarized in Supplemental Tables 5 and 6 for HepG2 and Bud8, respectively.

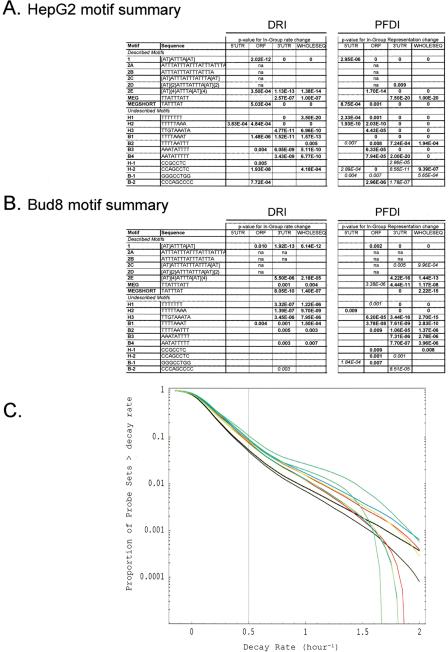
Figures 2, A and B, show the results of our analysis of the correlation between decay rate and the occurrence of particular sequence motifs at different positions in the transcript. Significant correlations are indicated with their p-values, and the entries corresponding to motif–location combinations that are not significant are left blank. Several of the motifs examined (both previously described and new motifs) correlate significantly with increased average rates of decay and overrepresentation in the fast-decaying mRNA population: motifs 1, 2E, MEG, B1-4, and H1-3. However, contrary to conventional wisdom (Shaw and Kamen 1986; Ross 1995), transcripts bearing these decay motifs were far from guaranteed to decay rapidly: in the case of HepG2, at most 10%–15% of transcripts with AU-rich motifs decayed with a half-life <2 h (vs. ∼5% for motifless transcripts; see Supplemental Table 5D). This association between AU-rich motifs and mRNA decay has also been observed in the previously mentioned studies (Lam et al. 2001; Raghavan et al. 2002; Frevel et al. 2003). Although these shifts toward greater average decay rates were most strongly associated with presence in the 3′-UTR sequence, there was also evidence for an ability of motifs to alter decay rates when located in the ORF or even 5′-UTR of a sequence (e.g., motifs 1 and H2). We also found that a few motifs were associated with reduced average decay rates in both HepG2 and Bud8 experiments (e.g., H-1, B-1), but some of these “stabilization” motifs had inconsistent behaviors when located in different parts of the cDNA (e.g., H-2, B-2) and in the different cell types. In particular, the H-2 motif correlates with enhanced decay when located in the ORF, and reduced decay when located in the 3′-UTR.

Figure 2.

Motif analysis of decaying transcripts in human cells. (A,B) The probe sets from the four HepG2 experiments (A) or the Bud8 experiment (B) were analyzed for the relationship between transcript decay and the presence of particular sequence motifs. The results of DRI and PFDI (same procedures used in Fig. 1) are summarized in A and B. For the motif analysis, we performed separate inferences for portions of the sequence (3′-UTR, 5′-UTR, ORF) and the cDNA sequence considered as a whole. For DRI, we compared the average decay rate of the probe sets from genes containing the motif in a specified location with rates of all other probe sets: significant (99% probability or greater) increases are shown in bold and significant decreases in italics. For PFDI, motifs that are overrepresented in the rapidly decaying transcript pool (r > 0.5 h^-1) when located in a given position are shown in bold; underrepresented transcripts are shown in italics (again, 99% probability cutoff for both). Motif–location combinations without statistically significant changes are shown as blank, and combinations with too few probe pairs for inference (≤25 probe pairs) are indicated with “n.a.” For more details on the motif analysis (e.g., extent of shift in average decay rate, percent enrichment), see Supplemental Tables 4–6. (C) Reverse cumulative distribution of decay rates for probe sets from genes that contain particular sequence motifs in their 3′-UTR (HepG2 experiment). Decay rate r is shown horizontally, while vertically the fraction of probe sets with decay rates higher than r is plotted on a logarithmicscale. The pairs of lines show the 98% posterior probability intervals for the fraction at each value of r. (Red) Motif 1; (blue) motif MEGSHORT; (green) Motif 2E; (light green) Motif H1; (black) all probe sets. “Described” AU-rich decay motifs (1–2E, MEG, MEGSHORT) and “undescribed” motifs were derived from the sources mentioned in Methods.

Although PFDI (percentage of fast decayers) picked up more high-probability changes than DRI, the reverse cumulative plot (Fig. 2C) shows that the motif-associated decay rate increases occur over nearly all decay rates. In other words, there is no evidence for a bimodal distribution of decay rates for AU-rich motif-associated transcripts. Together, these observations show that the examined RNA motifs correlate with shifts in the distribution of decay rates, but that they do not reliably predict turnover behavior. It thus seems that the regulation of mRNA decay is more complicated and might involve combinatorial interactions, that is, cooperative binding between different RNA-binding proteins that bind at different sites in the mRNA. This might also explain why the effect on decay rate is context-dependent for certain motifs (such as H-2).

DISCUSSION

The relevance of mRNA stability to steady-state mRNA concentration has long been appreciated (Darnell Jr. 1982; Ross 1995; Wilusz et al. 2001). Indeed, the proposal of messenger RNA as an entity led to speculation about regulation at the level of transcript stability (Jacob and Monod 1961). The earliest attempts to understand the population characteristics of decaying transcripts predated the availability of modern molecular genetic techniques and generally came to the conclusion that the average mRNA half-life in mammalian cells is on the order of several hours (Singer and Penman 1973; Harpold et al. 1981). It was also appreciated that rapidly destroyed mRNAs (half-life <2 h) existed and may yield insights into the organizing principles behind RNA metabolism (e.g., half-life as an indicator of transcript function; Puckett et al. 1975; Harpold et al. 1981). Yet accurate measurements of mRNA decay for large numbers of genes and correlation with biological function were not possible until the advent of microarray technology and biological annotation databases.

After performing the experiments and analysis presented in this paper, we became aware of a preliminary study in this direction using human cells and the cyclin-dependent kinases inhibitor flavopiridol (Lam et al. 2001). On the basis of small, manually curated lists of functional groups, this study found some evidence of differences in decay rate for mRNAs belonging to different functional groups. Although the flavopiridol study did check for correlations with AU-rich motifs, it did not mine the data set for position-specific effects (e.g., 3′-UTR vs. ORF) or new decay motifs. Like other recent microarray studies of several hundred sequences bearing AU-rich motifs (Raghavan et al. 2002; Frevel et al. 2003), this study notes that such motifs do not necessarily predict fast mRNA turnover.

In our series of experiments, we determined thousands of decay rates for transcripts in human cells. Our estimated median mRNA half-life in human cells is 10 h, a number that scales linearly relative to division time when compared with bacteria and yeast (Bernstein et al. 2002; Wang et al. 2002). And, we found that the number of transcripts with short half-lives (i.e., <2 h) is ∼5% in both a cancer cell line (HepG2) and a primary cell line (Bud8).

Having determined these decay rates, we then devised a scheme that uses the global decay rate data for automated inference of decay rate for any set of functionally related genes. We used Gene Ontology (GO) terminology to define classes of functionally related genes and obtained results consistent with a more conservative method that “manually” searches gene product descriptions for keywords. Using this automated functional assignment, we showed that the mRNA decay rate distribution for several functional groups is shifted relative to the decay rate distribution of all other transcripts. All functional groups that show a significant shift in the HepG2 cell line show the same qualitative behavior in the Bud8 cell line. However, because only one experiment was performed with the Bud8 cell line, not all of these changes are statistically significant. The most notable functional organization evident in our human data is that transcripts associated with transcription regulation decay faster and those associated with biosynthesis decay slower. This organization is also found in a previously published yeast data set.

The transcriptome of a single cell contains thousands of individual mRNA species. Clearly, efficient production and use of these transcripts requires some basic organizing principles. Previous analysis of a yeast data set (Wang et al. 2002) revealed that transcripts involved in the same pathway (e.g., pheromone signaling) or multiprotein complex decay at similar rates. Our reanalysis of their data along with our own data uncovers a second organizing principle of transcriptomes: rapid turnover of gene-regulatory transcripts and reduced turnover of transcripts related to biosynthesis or metabolism.

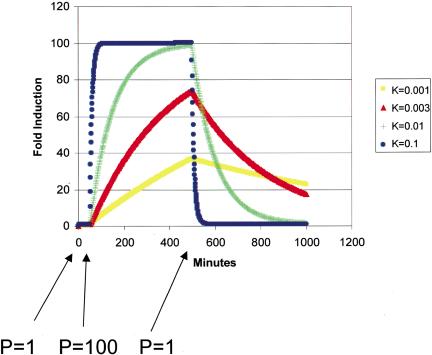
These observations can be partially explained by the relationship of decay rate to changes in steady-state mRNA concentration after a transcriptional stimulus (see Methods: Simulation of Steady State mRNA Dynamics, below). As shown in Figure 3, transcripts that are destroyed rapidly are also induced more rapidly. If the time to reach steady state exceeds the time of the RNA synthesis increase (e.g., k = 0.001, k = 0.003), transcripts with a higher decay rate will also experience a larger fold induction. Together, these properties enable a rapidly destroyed transcript's concentration to be changed more quickly and dramatically than a slowly destroyed transcript. Thus, it appears that both yeast cells and human cells are evolved to allow rapid changes in the levels of transcription regulatory factors, a property that makes sense given the primacy of transcriptional regulation in the control of gene expression (Lodish et al. 1995). Similarly, the relatively long half-lives of biosynthesis transcripts circumvent the self-defeating process of continuously destroying transcripts needed only at relatively constant levels. Additionally, it damps the response to noise fluctuations in the induction level of these genes.

Figure 3.

Simulation of the effect of decay rate on gene induction. Equation 6 (Methods) was solved for a step function RNA synthesis impulse: the synthesis rate was increased from 1 copy/(min · cell) to 100 copies/(min · cell) from 50–550 min. Using the indicated first-order decay constant (in units of 1/minute), the steady-state concentration of RNA was calculated and divided by initial concentration to determine the fold induction.

Although the mechanistic basis for targeted destruction of certain transcripts bearing AU-rich motifs by the exosome has been established biochemically (Chen et al. 2001; Mukherjee et al. 2002), many major questions remain unanswered about this critical biological process. Work with synthetic decay motifs (Zubiaga et al. 1995) and bioinformatic comparisons (Bakheet et al. 2001) have focused attention on several common UUAUUUAUU-type motifs, and, as mentioned earlier, a collection of sequences bearing these motifs has been examined with microarray studies (Frevel et al. 2003). In our studies, we were able to combine our large quantity of decay data with sequence information and showed that certain AU-rich motifs are associated with an increased average decay rate, especially when found in the 3′-UTR of a gene. These motifs include both the known motifs as well as a set of newly uncovered motifs. Our findings also confirm that nonamer-based motifs are not sufficient on their own to direct transcript destruction because many transcripts with decay motifs do not decay at a rapid rate. Vice versa, many transcripts without these motifs do decay at a high rate. Additionally, the new decay motifs we have detected (i.e., H-series, B-series) resemble known AU-rich motifs and suggest that they may be recognized by a common protein. SELEX (serial enrichment of ligands exponentially) could be performed to better characterize the sequence preferences of AU-binding proteins and other proteins associated with rapid mRNA decay. We further suspect that mRNA decay regulation cannot be accurately described in terms of single motifs and might involve cooperative binding at multiple sites by different RNA-binding proteins. This might also explain the intriguing observation that three of our novel motifs (H-2, B-1, B-2) appeared to slow or hasten mRNA decay depending on sequence context. In this respect, our data set will greatly facilitate future experiments that examine the relationship of sequence composition to mRNA turnover.

Finally, it is important to consider the importance of mRNA dynamics to global studies of gene regulation. Microarray experiments generate gene expression clusters that presumably contain genes coregulated at the transcriptional level (Roth et al. 1998; Pilpel et al. 2001). However, such clusters may contain fluctuations with a posttranscriptional component or that differ vastly in terms of RNA synthesis rates. Clearly the differences in half-lives for groups of coregulated mRNAs remain a major potential variable in the interpretation of such experiments. Ideally, one would compare only genes that have quantitatively similar rates of RNA synthesis (i.e., genes with identical enhanceosome composition might be expected to have identical rates of synthesis). Theoretically, one could obtain steady-state measurements of transcription rates through the comparison of mRNA decay rates (as performed here) and quantitative measurements of RNA concentration. However, the cost of doing such an experiment is presently limiting for an individual laboratory, even though methodologies exist to perform such measurements (Dudley et al. 2002). Perhaps the ultimate solution to this problem will require adaptation of the nuclear run-on assay to the microarray format, something that has already been attempted in prototype form (Fan et al. 2002).

METHODS

Data Acquisition

HepG2 Decay Measurements

HepG2 cells (ATCC) were seeded at 5–7 × 10⁶ cells per 10-cm dish and allowed to recover in 10% FCS, Modified Eagle's Medium for 24 h. Following overnight serum starvation (0.2% FCS, MEM), Actinomycin D treatments (5 μg/mL) were performed for 2–3 h either without IL-6 treatment or after 30 min of IL-6 (2.5 ng/mL) treatment (exact times of treatment were recorded and used for calculations). Thus, four decay data sets were accumulated for HepG2: two with and two without IL-6 treatment. Treatments were quenched by addition of Trizol (GIBCO/Life Technologies) RNA harvesting agent. Total RNA was then carried through the standard Affymetrix labeling protocol, which uses a T7-oligo(dT) reverse transcription primer. Following verification of high-quality reverse transcription and biotinylated cRNA synthesis by RT-PCR and Test Chip hybridization, the fragmented biotinylated cRNA was applied to human U95Av2 Affymetrix chips that contain 12,625 probe sets, mostly of characterized genes. In one case, sample was reapplied to the U95B Affymetrix chip, which contains mostly expressed sequence tags (ESTs). Scanning and data processing were performed on an Affymetrix scanner post-PMT adjustment running Affymetrix Microarray Suite (MAS) 5.0 (core facilities of Weill Medical College of Cornell University and The Rockefeller University). Decay experiments were normalized using three probe sets of the β-actin gene, whose transcript is known to decay extremely slowly compared with the timescale of our experiments (Reuner et al. 1995).

Bud8 Decay Measurements

The primary, diploid human fibroblast line Bud8 (ATCC) was grown to confluence in four 15-cm tissue culture plates in 10% FCS Dulbecco's Modified Eagle's Medium. Two plates of Bud8 were left untreated, and two plates were treated with Actinomycin D for ∼2 h. Samples were then harvested and analyzed as for HepG2 cells.

Yeast Decay Data

Published data regarding yeast transcriptome stability were obtained from the Web site of the Pat Brown group (http://genome-www.stanford.edu/turnover). This data set contains cDNA microarray data generated using exponentially growing S. cerevisiae and monitored with spotted cDNA microarrays containing 6184 open reading frames. The yeast strain used, Y262, contains a temperature-sensitive mutation in the major RNA polymerase II subunit RPB1 that stops mRNA synthesis upon a shift to 37°C. The data set consists of three independent nine-point time courses (0, 5, 10, 15, 20, 30, 40, 50, and 60 min after the switch to the nonpermissive temperature; Wang et al. 2002).

Functional Assignment

To determine decay rate statistics for collections of transcripts belonging to different functional groups, automated analysis of gene function was required. Functional assignments of the genes on the human and yeast chips were obtained by the following methods.

Gene Ontology (GO)

Before actually assigning genes to different functional classes, we first have to define the functional classes that we want to consider. For this, we used the Gene Ontology (GO) hierarchy. The GO Consortium (http://www.geneontology.org) is composed of all the major genome projects and seeks to create a hierarchical classification of genes by function, process, or subcellular localization. In this paper, we only used the classes that are defined under the biological process hierarchy. The Saccharomyces Genome Project GO resource is fairly complete in that assignments to GO classes exist for almost all annotated genes. We used this resource directly as downloaded: the GO codes were simply matched to the gene names of the cDNAs on the array. For human genes, the assignment of genes to GO classes is less complete and relies heavily on proprietary computational methods from the Compugen corporation. Version 0.3.1 of the Compugen human GO resource (∼144,000 GO assignments) was used to match the Affymetrix-supplied GenBank accession numbers to GO process codes. In cases in which an accession matched both Curagen's GenBank-based GO list and Curagen's SWISS-PROT-based GO list, we used the SWISS-PROT-based assignment.

Because the GO is a hierarchical structure, the collection A_g of all accessions belonging to a GO category g consists of all accessions that are directly mapped to g together with all accessions that are mapped to any of the GO categories g′ that occur below category g in the GO hierarchy. We only analyzed decay rate statistics for GO categories that contain >25 probe sets. For reference, the lists of genes grouped under “transcription” and the lists of genes grouped under “biosynthesis” are provided as Supplemental Tables 7 and 8, respectively.

Manual

We also “manually” collected a set of genes for the functional class “transcription.” For both yeast and human analyses, the manually curated SWISS-PROT (version 39) database was searched for all accessions of the correct species with keyword or function referencing “transc” or “RNA Pol” word fragments. Entries that were cross-referenced to the TRANSFAC transcription factor database were also flagged. Because this method occasionally picked up alternatively spliced gene products, genes with keyword “alternative splicing” were removed from the list of accessions “manually” associated with the process of transcription: the group of remaining accessions is referred to as “Swissprot transcription.” For the yeast genes, this keyword search was also performed on the description line from the Saccharomyces Genome Database (http://genome-www.stanford.edu/Saccharomyces) to derive a second list of manual transcription assignments: this group of accessions is referred to as “Description Line Transcription.”

Decay Motifs

RNA motif searches were performed on microarray sequences derived from two sources: Affymetrix “exemplar” sequences from http://www.affymetrix.com/analysis/index.affx and a list of 10,995 sequences downloaded from the Sequence Retrieval System (SRS) based on the accession numbers provided by Affymetrix. The latter set was screened to remove large genomic sequences or redundant accession numbers and therefore contains fewer sequences than the 12,625 probes on the U95Av2 microarray. For each of the 10,995 nonredundant accessions, the sequence containing the longest ORF corresponding to a given accession number (between the “exemplar” and SRS sequences) was used for analysis. The sequence was then further subdivided into 5′-UTR, ORF, or 3′-UTR sections for analysis in addition to the whole cDNA sequence. The sequences used for analysis omitted any sequence with one or more of the following deficits: UTR sequence <8 bp, ORF <90 bp, or sequence containing >10% Ns. Finally, poly(A) stretches were removed from the 3′-end of the whole sequence and 3′-UTR sequence. If only one component (e.g., 3′-UTR) failed a quality control test, the other parts of the sequence are still retained for analysis (provided they pass their tests). Therefore, there are different numbers of total entries for 5′-UTR, ORF, 3′-UTR, and whole sequences in the “sequence sets” used to search for motifs: 10,059, 9913, 10,085, and 10,603 sequences, respectively.

The sequence sets were then searched for various motifs to generate lists of accessions bearing particular motifs in their 5′-UTR, ORF, 3′-UTR, and so on. The known AU-rich motifs were extracted from published wet lab (MEG, MEGSHORT; Zubiaga et al. 1995) and bioinformatic studies (class 1–2E; Bakheet et al. 2001). New motifs were derived as described in the following. We collect sets of accessions containing the known or new motifs in their 5′-UTR, ORF, or 3′-UTR for analysis of decay rate statistics as described in Methods: Statistical Analysis and Decay Rate Calculations (below).

To uncover novel/unknown motifs that correlate with decay rate, we used a program that was originally designed to compare two genomes for enrichment of oligonucleotides of specified length (N. Rajewsky and E.D. Siggia, in prep.). We collected the 3′-UTR sequences of all genes with a half-life of <2 h (determined by MAS 4.0) in each of four HepG2 experiments or the single Bud8 experiment. This collection of sequences was then compared with a “background” sequence set that consists of all “present” genes expressed in each of the four HepG2 experiments or the one Bud8 experiment. In particular, the algorithm searches for 5–9-nt nucleotides such that the number of occurrences of the 5–9-nt nucleotide and its single-mismatch neighbors is significantly over- or underrepresented in the “fast-decaying” sequence population. This search identified a number of motifs enriched (H1, H2, etc.) or underrepresented (H[-1], H[-2], etc.) in the HepG2 (H-series) or Bud8 (B-series) experiments (Fig. 2). We further validate the significance of both the known as well as the new motifs by independently, for each motif, comparing the decay rate statistics of those transcripts containing the motif, and those not containing the motif as described in the next section.

Statistical Analysis and Decay Rate Calculations

Overview

Our objective is to use the data from the microarray experiments to infer transcriptome-wide decay rates of mRNAs and to use these rates to determine (1) whether the average decay rate of a particular group of transcripts differs significantly from the transcripts outside this group (decay rate inference, or DRI) and (2) whether there is an overrepresentation of transcripts with a half-life of <2 h for a particular group of transcripts (percentage fast decay inference, or PFDI). These groups of transcripts are either transcripts of genes from a common functional category, or transcripts that all contain a particular sequence motif in a specified location (e.g., 3′-UTR, 5′-UTR, ORF, or the whole cDNA sequence).

First, we use the data provided by the Affymetrix MAS 5.0 software to infer, for each probe set i, a posterior distribution P(r_i|D_i) for its decay rate r_i given the data D_i for this probe set. We use this distribution to calculate, for each probe set i, the probability q_i that the half-life of its transcript is <2 h. We refer to this probability q_i as the probability that i is a “fast decayer.” Then, to estimate the average decay rate of all the probe sets for a given category (i.e., having a particular function or motif) of accessions, we assume that the posterior distribution for this average can be approximated by a Gaussian. We then simply add the means and variances of the posterior distributions P(r_i|D_i) for all probe sets i in the category to obtain the mean and variance of this Gaussian. We similarly calculate the posterior distribution of the average decay rate of all probe sets representing genes outside the category. Finally, by considering the distribution of the difference between these two average decay rates, we can assess if probe sets in a particular category decay at a significantly faster or slower rate than all other probe sets (i.e., DRI). We perform analogous computations for the percentage of probe sets in a category that are fast decayers (i.e., PFDI).

We also provide reverse-cumulative distributions of the decay rates of all probe sets for a few selected GO categories and motifs. As described below, obtaining these distributions involves the calculation of a large number of definite integrals of the posterior distributions P(r_i|D_i) for all the probe sets in each selected functional category.

Finally, we also determine the average decay rate for each unique GenBank accession expressed (p < 0.04) at both the baseline and experimental time point in the HepG2 experiments. These rates were determined by gathering all probe sets i for each gene (including replicate probe sets on a single chip and across the four replicate decay experiments) and combining them in the same way that we combine other groups of probe sets.

Inferring the Decay Rate of a Probe Set

To infer decay rates of mRNA, transcriptome-wide expression levels of “baseline” experiments (i.e., resting, untreated cells) were compared with expression levels after transcription had been turned off for a certain time t (“experimental” condition). If a transcript is decaying at a rate r, then after t hours, the expression level should be lower by a factor8 of 2^-rt.

When comparing an experimental condition against a baseline condition, the Affymetrix MAS 5.0 software reports several statistics based on comparing the expression levels on a probe-by-probe basis. For each probe, the logarithm of the ratio of intensities in experimental and baseline conditions is calculated. If, for a probe set i, the log ratio is x_i, then the decay rate of probe set i is

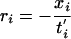with t_i the amount of time that transcription was halted. The half-life of probe set i is 1/r_i. The Affymetrix software reports the mean log ratio 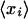over all probes in a probe set, along with a confidence interval 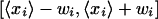for this log ratio. This confidence interval is based on the assumption that the measured log ratios for the different probes in the probe set each differ from the “real” log ratio by Gaussian noise of unknown variance. Integrating out the unknown variance, one obtains a Student-t distribution for the posterior. Formally, let 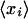be the observed average log ratio of the probes, and let (σ_i)² be the observed variance of the log ratio among the n_i probes in the probe set.9 The posterior density for the log ratio is then:

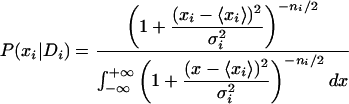1

The 95% confidence interval that the Affymetrix software reports is given by the symmetric interval around the mean 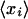that contains 95% of the posterior probability. Thus, using the confidence interval that Affymetrix reports, we may calculate σ_i by inverting the cumulative distribution.10 We then convert the distribution over x_i into a distribution over the decay rate r_i. Let 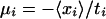and τ = σ_i/t_i. We then have for the posterior of the decay rate:

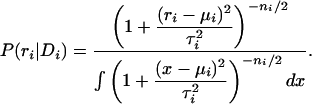2

The expected value of r_i is 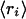= μ_i, and the variance of this posterior is given by 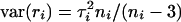. Below, we also require the probabilities p_i(c) that the transcript of probe set i is decaying at a rate that is larger than c. This is simply given by

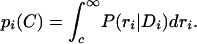3

We consider transcripts that decay with a half-life of <2 h to be fast decayers. Thus, the probability q_i of probe set i being a fast decayer is given by q_i = p_i(½).

Presence Statistics

For many probe sets on the chip, the corresponding transcript may not be present in the cells, and these probe sets will only be recording background noise. We want to exclude such absent transcripts from our analysis as much as possible.

For each probe set, the Affymetrix software reports a p-value for the absence/presence of the transcript. Here, we interpret this p-value as giving the probability that the transcript is absent. In all the analyses that we report, we only included probe sets that were present with a probability >0.96 in both conditions (i.e., before and after halting the polymerase with Actinomycin D). In principle, this may result in excluding transcripts that decay to undetectable levels on the timescale of our experiment (2–3 h). However, we have found that relaxing this presence condition does not significantly alter our results.

Estimating Decay Rates of Individual GenBank Accessions

Let S_a be the set of all probe sets i (both from single chips as well as over all replicates) that belong to GenBank accession a, and let r_a denote the average decay rate of accession a. Formally, we have

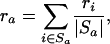where |S_a| is the number of probe sets in the set S_a. The posterior distribution for r_a has a mean

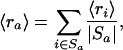and variance

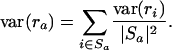We report for each accession the mean and the standard deviation

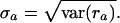Note that r_a is the average decay rate of accession a; there is no guarantee that accession a decayed at roughly equal rates in all replicates. We therefore checked, for each accession a, if the measured values r_i for all probe sets i ∈ S_a are consistent with a single decay rate for all probe sets. For each i ∈ S_a, we calculate the 0.999 posterior probability interval I_i. We then take the intersection of all intervals I_i. If this intersection is empty, we characterize the probe sets for accession a as “inconsistent” with a single decay rate for all probe sets. These calculations are summarized in Supplemental Table 9 for the HepG2 experiment.

Statistics for Sets of Accessions

In complete analogy to the estimation of the average decay rate r_a of all probe sets belonging to accession a, we can estimate the average decay rate of all probe sets for a group of accessions. For example, let S_g denote the set of all probe sets that belong to accessions that match functional category g in the GO hierarchy, and let S_⌝g denote all other probe sets (i.e., those not matching functional category g). In complete analogy with the previous section, we calculate 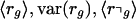, and var(r_⌝g). We report the 99% probability intervals given by

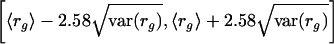and similarly for r_⌝g.

We then calculate the probability P(r_g > r_⌝g) that r_g is larger than r_⌝g. Because we assume that the distributions for r_g and r_⌝g take on an approximately Gaussian form, the normalized difference

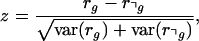will also be distributed normally with mean 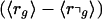and variance 1. The probability P(r_g > r_⌝g) is thus given by

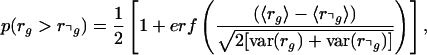4

with erf(x) the error function. When P(r_g > r_⌝g) > 0.99, we classify g as decaying significantly faster than the set of accessions outside of g, and when P(r_g > r_⌝g) < 0.01, we classify g as decaying significantly slower. In between these limits, we do not consider the difference between r_g and r_⌝g as significant, and we classify g as “NO SIG.” In the text and figures, we refer to these procedures as “DRI” for decay rate inference.

Apart from these statistics, we also report the fraction f_g of probe sets in class g that are decaying “fast” (half-life < 2 h). Let n_g be the number of probe sets in S_g that are decaying fast (defined as half-life < 2 h). Obviously, we have f_g = n_g/|S_g|. Because each probe set i ∈ S_g has a probability q_i to be a fast decayer, we find for the expected fraction

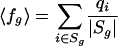and the variance of this fraction is given by

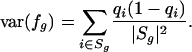We then report 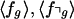, the probability P(f_g > f_⌝g), and make a call when this probability is >0.99 or <0.01 (overrepresented or underrepresented for class g, respectively). These comparisons are referred to as “PFDI” for percent fast decay inference.

We calculate the same statistics for a set of motifs m in complete analogy with the above procedures. In the case of motifs, the set S_m includes all probe sets for accessions that contain motif m in their “sequence.” The sequence is the 3′-UTR of a gene, the 5′-UTR of a gene, the ORF, or the whole sequence. We thus have four sets of statistics for each motif m.

Cumulative Distributions

For a few selected functional groups g and motifs m, we plot the reversed cumulative distribution of decay rates. That is, we plot as a function of c, the proportion p_g(c) of probe sets in the set S_g (or p_m(c) of probe sets in S_m) that has a decay rate larger than c. Using equation 3, and in analogy with the results for f_g above, the expected proportion p_g(c) is

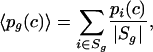and its variance is

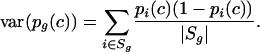With 98% probability, the real value of p_g(c) lies in the interval

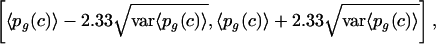which is the interval that we show in the figures of the reverse cumulative distributions (Figs. 1C and 2C).

Simulation of Steady-State mRNA Dynamics

Assuming a time scale on which cell growth rates are negligible, a time-varying RNA production rate P(t), and the well-known first-order decay rate for an mRNA species (Ross 1995; Wang et al. 2002) with rate k (where k = 1/τ), one arrives at the relationship:

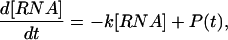5

with solution:

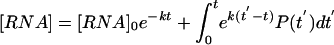6

Equation 6 allows for determination of the RNA concentration at any given time for a known decay constant k and production curve P(t). Note that the rate constant k in equation 6 is related to the rate constant r described above by r = k/ln 2. At steady state, the production rate equals the degradation rate, and the RNA concentration equals the production rate divided by the decay rate k. Using equation 6, the induction curves for different degradation rates (r = 0.001, 0.003, 0.01, and 0.1 min^-1) were calculated for a square wave transcriptional impulse going from 1 to 100 and back to 1 copy/(min · cell) over a 500-min period (Fig. 3).