Abstract
Patient-specific absorbed dose calculation for nuclear medicine therapy is a topic of increasing interest. 3D dosimetry at the voxel level is one of the major improvements for the development of more accurate calculation techniques, as compared to the standard dosimetry at the organ level. This study aims to use the FLUKA Monte Carlo code to perform patient-specific 3D dosimetry through direct Monte Carlo simulation on PET-CT and SPECT-CT images. To this aim, dedicated routines were developed in the FLUKA environment. Two sets of simulations were performed on model and phantom images. Firstly, the correct handling of PET and SPECT images was tested under the assumption of homogeneous water medium by comparing FLUKA results with those obtained with the voxel kernel convolution method and with other Monte Carlo-based tools developed to the same purpose (the EGS-based 3D-RD software and the MCNP5-based MCID). Afterwards, the correct integration of the PET/SPECT and CT information was tested, performing direct simulations on PET/CT images for both homogeneous (water) and non-homogeneous (water with air, lung and bone inserts) phantoms. Comparison was performed with the other Monte Carlo tools performing direct simulation as well. The absorbed dose maps were compared at the voxel level. In the case of homogeneous water, by simulating 108 primary particles a 2% average difference with respect to the kernel convolution method was achieved; such difference was lower than the statistical uncertainty affecting the FLUKA results. The agreement with the other tools was within 3–4%, partially ascribable to the differences among the simulation algorithms. Including the CT-based density map, the average difference was always within 4% irrespective of the medium (water, air, bone), except for a maximum 6% value when comparing FLUKA and 3D-RD in air. The results confirmed that the routines were properly developed, opening the way for the use of FLUKA for patient-specific, image-based dosimetry in nuclear medicine.
1. Introduction
Patient-specific dosimetry for nuclear medicine therapy with radiolabeled compounds is fundamental to maximize the treatment efficacy while minimizing normal tissue damage, and to inspect the correlation between the delivered absorbed dose and the observed effect, which would allow one to better plan the future treatments.
Dosimetry can be performed at different levels of accuracy according to the specific situation and to the available resources. The use of more sophisticated techniques for absorbed dose calculation must go ahead together with the consciousness of their limitations to assure the pertinence of their application.
The most widespread method for image-based dosimetry relies on the use of planar (two-dimensional (2D)) images, exhibiting unavoidable approximations due to the organs superimposition and further complicating the difficult task of quantification.
One major improvement is represented by the absorbed dose calculation at the voxel level—known as three-dimensional (3D) voxel dosimetry—with respect to the average calculation at the organ level. The big potentiality of the voxel dosimetry is the availability of a 3D absorbed dose map, allowing to plan a treatment in terms of absorbed dose–volume constraints and to take into account the absorbed dose inhomogeneity from the dosimetric and radiobiological point of view. On the other side, some aspects of the methodology are still a matter of debate, in particular regarding the possibility to accurately assess the activity and the cumulated activity at the voxel level.
Different methods have been proposed to perform 3D voxel dosimetry, including the voxel kernel convolution (VKC) method and the direct Monte Carlo (DMC) simulation method (Bolch et al 1999). Both require the cumulated activity distribution at the voxel level as input data, provided by the functional images (SPECT or PET) associated with the information coming from biokinetic studies. From this common starting point, the VKC method performs calculation under the hypothesis of homogeneous medium, whereas the DMC method also employs the CT data to take into account the real spatial distribution of tissue density and composition.
The DMC method appears as the most advanced technique and, at least theoretically, the most accurate, taking into account patient specificity from any point of view (Furhang et al 1996, 1997). Many different tools were developed to implement the DMC method, including the EGS-based 3D-RD software by Prideaux et al (2007), the OEDIPE tool by Chiavassa et al (2005) based on the MCNPX code, the DOSIMG program based on the EGS4 code (Liu et al 2001), the DPM program (Wilderman and Dewaraja 2007), other tools based on the MCNP-4B code (Yoriyaz et al 2001) or the GEANT4 code (Kost et al 2011), and, most recently, the RAYDOSE software based on the GEANT4 code (Marcatili et al 2013) and the MCID tool based on MCNP5 (Vergara Gil et al 2012).
This study aimed to implement the DMC methodology utilizing the FLUKA MC code (Ferrari et al 2005, Battistoni et al 2007), with the final goal of personalized internal dosimetry.
To this purpose, dedicated routines have been developed in the FLUKA environment to import the patient images in the code and opportunely use them as an input for the simulation.
To confirm that the new routines have been properly developed and integrated in the FLUKA simulation workflow, the first results—regarding DMC simulation on model and phantom images—have been compared to those obtained with other tools performing the same image-based dosimetry on the same images.
More specifically, the comparison was performed with a home-made tool performing VKC (Pacilio et al 2012), limited to the case of perfectly homogeneous water medium, and with two of the above listed MC-based tools, 3D-RD and MCID. Different scenarios, including both homogeneous and non-homogeneous density patterns, have been examined.
The results of such comparison are presented here.
2. Material and methods
2.1. FLUKA for direct Monte Carlo simulation on nuclear medicine images
2.1.1. Development of FLUKA routines
To perform patient-specific absorbed dose calculation by MC simulation, two basic pieces of information are needed: (a) the properties of the tissue where radiation travels and interacts; (b) the radiation source, i.e. the amount of radioactivity retained in the body, and its spatial distribution.
-
(a)
The first information is expressed in terms of tissue mass density and elemental composition and can be derived from CT images, so CT data need to be conveniently interpreted and imported in the code. A program was previously developed in FLUKA (Parodi et al 2007) to convert the CT number (expressed in Hounsfield Unit, HU) into the corresponding tissue density and composition, according to the method described by Schneider et al (2000), which in the following will be denoted by `Schneider segmentation'. This same program has been used in this study, after developing a dedicated routine in Matlab® (version 7.7.0, R2008b) to list the CT data in a format readable by the program. Schneider's segmentation divides the HU range from –1000 to 1600 into 24 intervals and assigns the density and elemental composition to each interval based on a specific calibration of the CT scanner. In this study, experimental measurements were performed to compare the response of the CT scanners used in our institute (8 and 16 slices CT, Discovery ST and Discovery 600 PET-CT scanners, GE Healthcare) with that of Schneider study. If the responses of the CT scanners are consistent, the same segmentation reported in Schneider's study can be adopted for our images as well. To this aim, images of the Catphan® 500 phantom have been acquired, and the measured CT numbers for different materials have been compared to those predicted using the same formulation and parameters as Schneider et al.
The CT data are imported in FLUKA by means of the voxel geometry routine to represent the patient and the surrounding region as a 3D matrix with the same size as the CT image.
-
(b)
The second information is provided by SPECT or PET images together with the data obtained from biokinetic studies. The therapy is performed with a pharmaceutical labelled with a beta emitter isotope, aiming to depose energy locally and kill the tumour cells. For image acquisition, instead, gamma emission is necessary to be detected outside the patient. If the beta emitter does not also have a gamma emission, SPECT/PET images are obtained by injecting a tracer amount of radiopharmaceutical labelled with a gamma/positron emitting isotope. This can be done under the assumption that the radiopharmaceutical has the same biokinetic when labelled with either the gamma/positron emitter used to acquire images or with the beta emitter used for the therapy. The collection of such images can be done before the therapy or in concomitance with the therapy itself.
In this study 99mTc SPECT images and 18F PET images have been used as examples. 90Y, a pure beta emitter, has been considered as an example of isotope used for therapy. This choice appeared to be convenient for the purpose of this study, which is to test the routines developed in the FLUKA environment by comparison with the results obtained with other tools. In fact, the use of a pure beta emitter and not an isotope with both beta and gamma emissions, often used in the clinical practice as well, makes the result less dependent on the simulation algorithm used by each code, especially considering that the calculation is performed at the voxel level. On the other side, if the routines work properly with a pure beta emitter, they will with any other isotope as well.
Dedicated routines have been developed in order to convert the images into a source distribution readable by FLUKA. A routine was firstly developed in Matlab® to sort the source voxels by the voxel value. If images are acquired on a calibrated scanner, the voxel content is expressed in terms of activity (SPECT) or activity concentration (PET) and the simulation will provide an absorbed dose-rate map (Gy s−1). Without calibration, as in this study, the voxel content is generically expressed in terms of counts and the simulation output will be in terms of absorbed dose for a single disintegration (Gy GBq−1 s−1). Then, the FLUKA routine source.f was modified to import such list and select the voxel for the starting position of each decaying particle, the frequency of each voxel being proportional to its relative counts with respect to the total image counts. During the first stage, the cumulative probability discrete function is stored for each slice, so that the probability to select a slice is proportional to the number of events in that slice. For each simulated particle, the corresponding slice is sampled according to this distribution after random number generation. Similarly, in a following step the voxel index within that slice is sampled according to a 2D counts distribution so that the probability to select a voxel is proportional to the number of events in that voxel with respect to the total events in the slice. Finally, the starting coordinates of the decaying nucleus are sampled uniformly within the selected voxel.
The isotope to be simulated is selected in the FLUKA input file. The type of radiation emitted and its energy are sampled from the isotope spectrum internally calculated by FLUKA. When comparing FLUKA results with the other two MC codes, instead of using the spectrum internally calculated by FLUKA the same beta spectrum implemented in 3D-RD software was used (see section 2.4), by properly modifying the FLUKA source.f routine.
The particle path is simulated and energy deposition is scored at the voxel level and converted into absorbed dose for a single disintegration. The output is a text file providing the absorbed dose/disintegration voxel by voxel, together with its statistical uncertainty. The physical details of particles transport are reported in section 2.1.2.
2.1.2. FLUKA simulation parameters
FLUKA performs electron transport using a multiple scattering approach with a special algorithm (Ferrari et al 1992, Aarnio et al 1994, Fassò et al 1997, 2001, Böhlen et al 2012) based on Molière's theory improved by Bethe (Molière 1948, 1955, Bethe 1953). Further information about the FLUKA code and its simulation algorithms has been reported in detail elsewhere (Ferrari et al 2005, Battistoni et al 2007).
Transport and production cuts for both electrons and photons were set at 1 keV, the closest value comparable to the settings of the other considered MC models (see sections 2.4 and 2.5). It is to point out, however, that it is in general sufficient to fix the minimum energy threshold to that corresponding to an electron range equivalent to the voxel size.
With this setting, the average CPU time for simulating a MC history in water was around 4.7 × 10−3 s on a 2.133 GHz Intel® Core™ Duo processor.
2.2. Simulations on model and phantom images
A two-step approach was adopted to verify the correct working of the newly developed FLUKA routines. At each step, FLUKA simulations were performed on model and phantom images, and the results were compared to those obtained with the other tools (see in the following, sections 2.3, 2.4 and 2.5).
2.2.1. First step: DMC simulation in a homogeneous water medium
The first step aims to check the routine handling the SPECT or PET images. For this reason, the structure and material composition was not derived from the CT images, in order to avoid introducing the two routines simultaneously. Instead, the structure and material composition was defined by the user in the input file; in particular, a perfectly homogeneous medium (water with 1 g cm−3 density) was defined both inside and outside the model/phantom.
Two different 99mTc-SPECT studies were generated using the SIMIND MC code (Ljungberg and Strand 1989). SPECT_1 study is a model representing a cylinder (10 cm radius, 16 cm height) having a 3 cm radius sphere at its centre. SPECT_2 study represents the same cylinder having three different spheres (2, 2.5 and 4 cm radii) inside. Both the spheres and the cylinder are uniformly filled with activity, with a higher activity concentration in the spheres than in the cylinder (5:1 ratio in the case of SPECT_1, 3:1 ratio in case of SPECT_2). The total phantom activity is 4.5 MBq in both cases. SIMIND simulates each projection assuming 1s acquisition. 107 photons were simulated for each projection.
The simulated images have a 128 × 128 matrix size and 4.42 mm side cubic voxel.
18F-PET images were experimentally acquired on a hybrid scanner (Discovery ST, GE Healthcare). A cylindrical Jaszczak phantom was filled with water and seven hollow spheres (volume ranging from 0.3 cm3 to 16.3 cm3) were embedded in it (PET_1). The spheres were filled with 18F-FDG solution, 20 kBq ml−1 activity concentration, ninefold higher than the activity concentration in the cylinder. The PET matrix size was 256 × 256, with 2.73 × 2.73 × 3.27 mm3 voxel dimensions.
SPECT_1, SPECT_2 and PET_1 images were used as input for the FLUKA simulation, as if they were representing the radiopharmaceutical distribution inside a `patient' undergoing 90Y therapy. Thus, 90Y emission was simulated by FLUKA to compute the absorbed dose distribution. A total of 108 primary particles were simulated for each of the three cases analysed (SPECT_1, SPECT_2 and PET_1, respectively), representing an acceptable compromise between the precision of the results (statistical uncertainty of about 2–3% at the voxel level) and the simulation time.
FLUKA-absorbed dose maps were compared (section 2.6) to those obtained with the VKC method, which calculates the absorbed dose distribution in the case of homogeneous medium as well. Details on the VKC method are given in section 2.3.
In addition, for the PET_1 phantom, simulations were also performed with the EGS-based 3DRD software (section 2.4) and with the MCNP5-based MCID tool (section 2.5) under the same assumption of a homogeneous water medium. The results from 108 primary particle simulations were compared. For this last comparison, the three codes used the 90Y beta spectrum implemented in the 3D-RD software (section 2.4) to avoid introducing differences among the results due to different spectra.
2.2.2. Second step: DMC simulation with CT-based density map
While in the first step a homogeneous medium has been used, in the second step the structure and the material composition is derived from the voxelized CT-based density map. The source description is still taken from SPECT/PET images. Thus, in this step the two routines, the one dealing with the SPECT/PET images and the one dealing with the CT images, are both included in the simulation workflow.
Test simulations have been performed with (18F)PET-CT images, the results being valid for SPECT-CT images likewise. PET-CT images have been experimentally acquired on a hybrid scanner (Discovery ST, GE Healthcare), so they are intrinsically registered.
Two water phantoms were used to this purpose. The first phantom is the same PET_1 phantom as before. The second phantom (PET_2) is a cylindrical phantom containing three different inserts, filled respectively with water, air and a material resembling the bone. This phantom was used to explore also the case of non-homogeneous tissue. The cylinder was filled with water and a low amount of activity (2 kBq ml−1). Activity was also injected in the water insert to obtain a higher activity concentration than the surrounding background (about threefold). Conversely, the air and bone inserts did not contain activity. The CT images were resized to the PET matrix (from 512 × 512 to 256 × 256) for the simulation.
FLUKA absorbed dose maps were compared to those obtained with the other MC software (3D-RD, MCID) performing DMC simulation on the same PET-CT images. As previously, results from 108 primary particle simulations were compared.
The three software packages were used by three different groups who independently developed their own tool. In particular, each group already implemented a different method to associate the tissue properties (density, elemental composition) to the CT number.
The three methods are coherent among them in the water region, so in the case of the PET_1 phantom, each group performed the simulation implementing his own method.
Conversely, in the case of air and bone regions the three methods present differences that could have an impact on the absorbed dose results; thus, a segmentation standardization was adopted for PET_2 phantom simulation to work under comparable conditions. To this aim, the same simplified segmentation named `air–water–bone segmentation' was implemented in each of the three software packages: HU (−1000, −920), density 0.00129 g cm−3, air; HU (−919, 156), density 1 g cm−3, water; HU (157, 992), density 1.92 g cm−3, bone. Material compositions were derived from ICRU Report 44 (ICRU 1989).
In addition, considering that in the clinical practice the absorbed dose to air is normally not an issue, another set of simulations was performed on the same PET_2 phantom, but fictitiously assigning to the air insert the density and composition of the lung (the dosimetry of lung lesions, for example, is a matter of interest for clinical applications). This was done as an expedient due to the unavailability of lung-equivalent inserts to be included in the phantom. The so-obtained `lung—water–bone segmentation' was the following: HU (−1000, −920), density 0.296 g cm−3, lung; HU (−919, 156), density 1 g cm−3, water; HU (157, 992), density 1.92 g cm−3, bone. Lung density and composition were derived from the lung ORNL MIRD phantom (Akkurt et al 2007). Obviously in the case of patient dosimetry a correct segmentation would be implemented adequately assigning the lung properties to the correct HU range.
Additionally, comparison between FLUKA and 3D-RD both implementing the Schneider segmentation was also performed.
2.3. Voxel kernel convolution (VKC)
The VKC, described in the MIRD Pamphlet No. 17 (Bolch et al 1999), allows one to calculate the 3D absorbed dose distribution starting from the 3D activity distribution.
The average absorbed dose inside each voxel is calculated by adding the contributions of the voxel itself and the surrounding ones, as follows:
| (1) |
where Dvoxel,t is the average absorbed dose in the voxel `t' (target voxel), Ãvoxel,s (Bq s) is the cumulative number of nuclear transformations in the voxel `s' (source voxel) and Svoxel t ← voxel,s(Gy GBq−1 s−1) is the average absorbed dose in the voxel `t' per unit transformation in the voxel `s'. The sum is performed over all the source voxels deposing energy in the target voxel. The à value inside each voxel can be derived from the PET or SPECT image after converting the image counts into activity (by means of a calibration procedure), and taking into account the kinetic behaviour of activity over time (Bolch et al 2009).
To perform the convolution between the PET or SPECT image and the S factors, equation (1), a dedicated tool was developed in Matlab®. The tool accepts the PET or SPECT images as input and provides the absorbed dose distribution in the matrix format. The consistency of its results had been previously verified by comparison with an analogue tool developed on IDL support (Pacilio et al 2012).
By definition, the VKC method assumes all the voxels to have the same density and composition, corresponding to that used for the calculation of the S factors. Thus, if the S factors are calculated in the water medium (1 g cm−3 density), the same conditions are matched as for the FLUKA simulations described in section 2.2.1. In this way, a comparison can be done between two different ways to get to the same result: convolution with a voxel kernel in one case, direct simulation in the other. A good agreement between the two absorbed dose maps, within the statistical uncertainty, can be an indication that the FLUKA routine developed to handle the PET or SPECT images is working properly.
For this study, the S factors were in fact calculated with FLUKA in water (1 g cm−3 density) for 90Y and for the voxel dimensions of the SPECT (cubic, 4.42 mm side) and PET (2.73 · 2.73 · 3.27 mm3) images. The source voxel was considered to be uniformly filled. The physical settings for the radiation transport were the same as reported in section 2.1.2, and the same 90Y spectrum as for the DMC simulations was used. Considering that the maximum range of beta particles emitted by 90Y is about 11 mm, in the case of SPECT the S factors were calculated up to 5 voxels from the source voxel (a cube of 11 voxels side, the source voxel being in the centre), whereas in case of PET 6, 6 and 5 voxels from the source voxel were considered in x, y and z directions respectively (a parallelepiped with 13, 13 and 11 voxels sides, the source voxel being in the centre).
2.4. 3D-RD
3D-RD is a well-established 3D personalized dosimetry package (Prideaux et al 2007) based on the EGSnrc MC code. It is an extension of a prior dosimetry package 3D-ID, which was one of the earliest 3D imaging-based targeted radionuclide dosimetry package described in the literature (Sgouros and Kolbert 2002). 3D-RD was applied in a variety of cases, including a real time clinical implementation for 131I therapy of thyroid cancer (Hobbs et al 2009) and represented a baseline standard for comparison for more recent software packages (Dieudonné et al 2010). A more complete description of 3D-RD was previously provided in the literature (Prideaux et al 2007).
As applied to the current case, the air–water–bone, lung–water–bone and Schneider segmentations were implemented for comparison with the other codes. In case of the Schneider segmentation implementation, the HU numbers were converted to density using a bi-linear fit to the Schneider segmentation data. A material map based on density thresholds was made: for density <0.8 g cm−3, air was assigned to the voxel, for a density between 0.8 and 1.15 g cm−3, the voxel was assigned to water and for a density >1.15 g cm−3, the voxel was designated as bone. The air, water and bone compositions were the same as reported for Schneider segmentation.
The absorption threshold for photon and electron transport was 1 keV for all the simulations.
The density, materials and activity distribution maps are loaded into the EGSnrc MC code where 90Y β-decay is simulated using the decay probability spectra from the RADTABS program (Eckerman and Endo 2008). EGSnrc outputs the energy deposition per disintegration per voxel, which is returned to 3D-RD to be converted to the absorbed dose rate by dividing by the voxel mass and then to absorbed dose by assuming physical decay (i.e. no re-localization of the radiopharmaceutical).
2.5. MCID
A dosimetry tool named MCID (MC integration Internal Dosimetric tool) was developed to calculate patient-specific absorbed dose in nuclear medicine applications, based on DMC simulation performed with the MCNP5 code (Vergara Gil et al 2012, X-5 Monte Carlo Team 2008a, 2008b).
Coregistered PET-CT and SPECT-CT images can be read by the tool as input for the simulation. The functional images (PET, SPECT) must correspond to the cumulative activity map at the voxel level. In MCID original version, the anatomical images (CT) are converted into a density map by dividing the (−1000, 1000) HU range into a maximum of 12 intervals: air, lung, skin, water, breast, brain, muscle, testis, ovaries, blood, soft tissue and bone, with density and composition derived from Mc Conn et al (2011). The number of intervals and their boundaries can be selected by the user through the MCID interface.
As applied to the current case, the air–water–bone and lung–water–bone segmentations were implemented for comparison with the other codes.
The latest electron transport algorithm (DBCN 17j 2), implementing a detailed electron energy-loss straggling logic, was adopted (Koivunoro et al 2012). The absorption threshold for photon and electron transport was 1 keV for all the simulations. No variance reduction techniques were implemented.
The output from MCNP5 simulation is converted into an absorbed dose image, together with a report file where the main dosimetric results are summarized.
2.6. Absorbed dose map comparison
The following procedures were adopted to compare the absorbed dose maps obtained with FLUKA, VKC, 3DRD and MCID:
Absorbed dose profiles were taken at different positions in the models/phantoms. In the case of SPECT_1, SPECT_2 and PET_1, profiles were considered both crossing the hot spheres and the background, the last having a higher statistical noise. In the case of PET_2, three profiles were taken crossing the water, air/lung and bone region, respectively. The profiles were initially taken on the whole image size (128 points for SPECT images, 256 points for PET images), but the points falling outside the model/phantom were then disregarded since there was no activity there. The number of points falling inside the model/phantom and considered for the comparison, N, varied for the different cases and ranged between 40 and 80. For a given profile, the difference between the results yielded by two codes, namely code 1 and code 2, was first calculated for each of the N points as Dpoint = 100 · (code 2 – code 1)/code 1%. Then, as a single and representative parameter, Dprofile was calculated by averaging the absolute values of the N values of Dpoint.
Absorbed dose maps ratio (R) was calculated at the voxel level (FLUKA/VKC, FLUKA/3DRD, FLUKA/MCID). For each voxel of an image, an R value was obtained as the ratio between the two absorbed dose values calculated by the two different codes. Then, representative volumes of interest (VOIs) were identified on each image and the average R value among all the voxels inside each VOI (Rave) was calculated, together with the standard deviation (SD) and the range of variation (Rmin, Rmax). Thus, a different set of values (Rave, SD, Rmin, Rmax) was obtained for each VOI. In the case of SPECT models, cylindrical VOIs having the same axis as the cylinder and different radii, ranging from 3 to 9 cm, were taken into account. In the case of the PET_1 phantom, spherical VOIs placed inside the hot spheres or in the background were considered. In the case of the PET_2 phantom, one spherical VOI was drawn inside each insert (water, air/lung, bone).
Integral absorbed dose–volume histograms (DVH) were evaluated inside the VOIs and visually compared.
3. Results
3.1. CT scanner response
Circular regions of interest (ROIs) were drawn on the CT images of the Catphan® 500 phantom inside each of the seven inserts. The average measured CT number inside each ROI was compared to the value calculated according to Schneider et al using the specific composition of each insert and the same parameters derived in their study (k1 = 1.24 × 10−3 and k2 = 3.06 × 10−5). The data are reported in table 1. The relation between measured (#CTmeas) and calculated (#CTcalc) values is the following: (#CTcalc) = 1.02 × (#CTmeas) − 3.2 with a linear correlation coefficient R2 = 0.9998. In Schneider's study it was (#CTcalc) = 0.98 × (#CTmeas) + 2.6, with R2 = 0.9979.
Table 1.
Comparison between measured and calculated (Schneider method) CT numbers for the different materials in the Catphan® 500 phantom.
| Material | # CT measured | # CT calculated |
|---|---|---|
| Air | −971.85 | −1000.0 |
| PMP | −181.59 | −186.1 |
| LDPE | −93.86 | −102.1 |
| Polystryrene | −38.25 | −24.3 |
| Acrilyc | 119 | 118.3 |
| Delrin | 338.29 | 340.3 |
| Teflon | 928.4 | 937.4 |
3.2. First step: DMC simulation in a homogeneous water medium
3.2.1. FLUKA DMC simulation versus VKC
The FLUKA average statistical uncertainty inside each VOI (obtained by first evaluating the statistical uncertainty at the voxel level and secondly by averaging over all the voxels included in a VOI) was approximately the same—around 2%—for all the VOIs in all the models and phantoms.
The value of Dprofile (FLUKA DMC versus VKC) was the same whatever the model or the phantom (SPECT_1, SPECT_2, PET_1) and whatever the profile position (as reported in section 2.6, different profiles were considered for each model/phantom, taken at different positions). The average values among all the values of Dprofile for all the models and phantoms is reported in table 2.
Table 2.
Results from comparison between FLUKA DMC simulation in water and VKC. For Dprofile calculation, code 1 is represented by VKC and code 2 is represented by FLUKA.
| Profile comparison (all the models/phantoms) |
R inside the VOIs (all the models/phantoms) |
|
|---|---|---|
| Dprofile ± SD | Rave ± SD | [Rmin, Rmax] |
| (1.5 ± 1.1)% | 1.00 ± 0.02 | [0.82, 1.22] |
Rave did neither vary among the models/phantoms nor among the different VOIs inside each model/phantom. Thus, in table 2 the average values of Rave, SD, Rmin and Rmax among all the VOIs in the two SPECT models and in the PET phantom are reported.
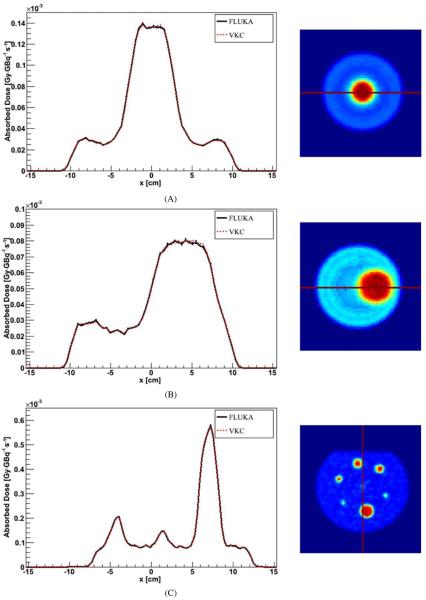
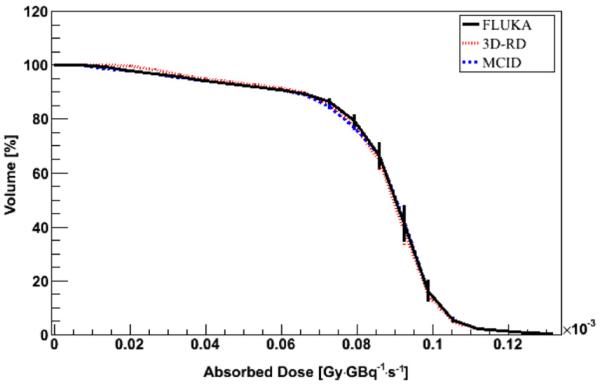
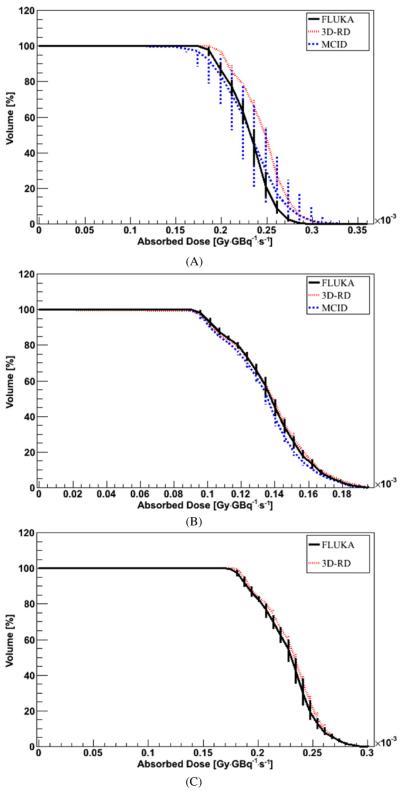
In figure 1, examples of profiles are shown. An example of integral DVHs is reported in figure 2 for the 9 cm radius VOI inside the SPECT_1 model.
Figure 1.
Profile comparison between FLUKA DMC simulation in water and VKC for the (A) SPECT_1 model, (B) SPECT_2 model and (C) PET_1 phantom. Error bars are not visible because they are fully included in the lines.
Figure 2.
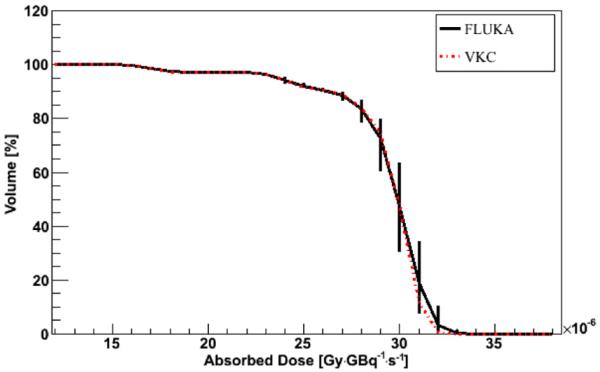
DVH comparison between FLUKA DMC simulation in water and VKC for a 9 radius cylindrical VOI inside the SPECT_1 model. Error bars represent 1 sigma uncertainty; when not visible, they are fully included in the lines.
3.2.2. FLUKA versus 3D-RD and MCID
The average values of the point-by-point difference between all the profiles considered (taken at different positions in the phantom) are reported in table 3. The values of Rave, SD, Rmin and Rmax are also reported in table 3, considering the same spherical VOIs as in section 3.2.1.
Table 3.
Results from comparison between FLUKA, 3D-RD and MCID DMC simulation in water. For Dprofile calculation, code 1 is represented by either 3D-RD or MCID and code 2 is represented by FLUKA.
| Profile comparison (all the profiles) |
R inside the VOIs (all the profiles) |
||
|---|---|---|---|
| Dprofile ± SD | Rave ± SD | [Rmin, Rmax] | |
| FLUKA versus 3D-RD | (3.0 ± 2.4)% | 1.01 ± 0.06 | [0.9, 1.6] |
| FLUKA versus MCID | (2.6 ± 2.1)% | 1.01 ± 0.07 | [0.8, 1.5] |
FLUKA average statistical uncertainty within the VOIs was 2%, ranging from 0.3% to 4% both in the background and in the hot sphere VOI. Only 3% of the whole phantom voxels, exclusively located on the sphere edge, had a statistical uncertainty higher than 4% up to a maximum of 20%. MCID and 3D-RD average statistical uncertainty, instead, ranged respectively from 0.6% to 2% and from 0.01% to 8% in the background and in the hot sphere VOIs.
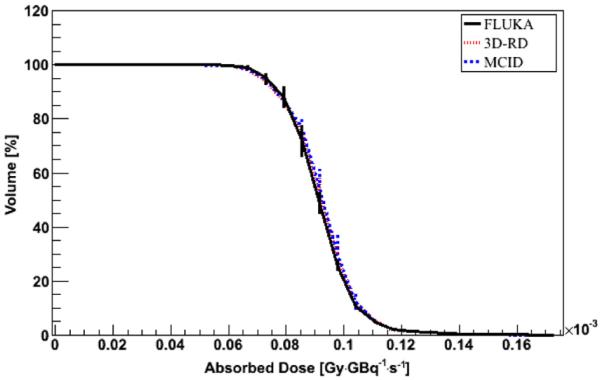
An example of FLUKA, 3D-RD and MCID profile comparison is reported in figure 3, whereas an example of DVH is reported in figure 4 for a VOI inside a hot sphere.
Figure 3.
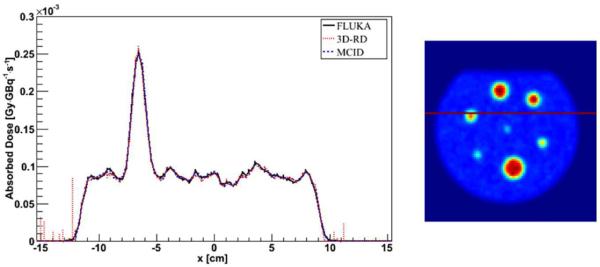
Profile comparison between FLUKA, 3D-RD and MCID DMC simulation in water (PET_1 phantom). Error bars are not visible because they are fully included in the lines, except for the region outside the phantom (at the profile edges) exhibiting low statistic.
Figure 4.
DVH comparison between FLUKA, 3D-RD and MCID DMC simulation in water for a VOI including a hot sphere in the PET_1 phantom. Error bars represent 1 sigma uncertainty; when not visible, they are fully included in the lines.
3.3. Second step: DMC simulation with voxelized CT-based density map
3.3.1. Water phantom
The average values of the point-by-point difference between all the profiles considered (at different positions in the phantom) are reported in table 4, together with the values of Rave, SD, Rmin and Rmax for the same spherical VOIs as in section 3.2.1 and 3.2.2.
Table 4.
Results from comparison between FLUKA, 3D-RD and MCID DMC simulation with a CT-based density map—homogeneous water phantom. For Dprofile calculation, code 1 is represented by either 3D-RD or MCID and code 2 is represented by FLUKA.
| Profile comparison (all the profiles) |
R inside the VOIs (all the profiles) |
||
|---|---|---|---|
| Dprofile ± SD | Rave ± SD | [Rmin, Rmax] | |
| FLUKA versus 3D-RD | (3 ± 2)% | 0.99 ± 0.04 | [0.9, 1.2] |
| FLUKA versus MCID | (3 ± 2)% | 0.98 ± 0.04 | [0.8, 1.2] |
Similarly to the homogeneous water case, the average statistical uncertainty affecting FLUKA results within the VOIs was 2%, ranging from 0.3% to 4%. Only 3% of the whole phantom voxels, exclusively located on the sphere edge, had a statistical uncertainty higher than 4%. MCID and 3D-RD average statistical uncertainty ranged respectively from 0.7% to 2.6% and from 0.01% to 8% in the background and in the hot sphere VOI.
An example of FLUKA, 3D-RD and MCID comparison is reported in figure 5 for the same profile as in figure 3. The DVH for the same VOI in figure 4 is reported in figure 6.
Figure 5.
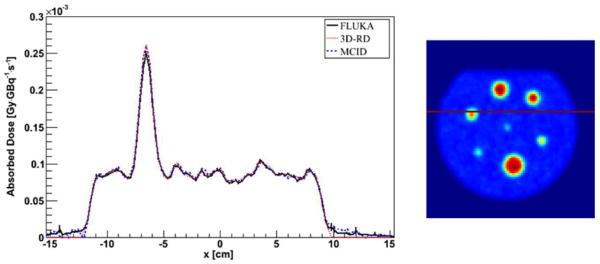
Profile comparison between FLUKA, 3D-RD and MCID DMC simulation with a CT-based density map—homogeneous water phantom. Error bars are not visible because they are fully included in the lines.
Figure 6.
DVH comparison between FLUKA, 3D-RD and MCID DMC simulation with a CT-based density map for a VOI including a hot sphere in the PET_1 phantom. Error bars represent 1 sigma uncertainty; when not visible, they are fully included in the lines.
3.3.2. Water phantom with air/lung and bone inserts
The average values of the point-by-point difference among the profiles, and the Rave, SD, Rmin and Rmax values are reported in table 5. Results are reported for the three codes using the air–water–bone segmentation (separately for water, air and bone) and the lung–water–bone segmentation (only for the lung insert, the values for water and bone being the same as for air–water–bone segmentation). Additionally, FLUKA and 3D-RD comparison using the Schneider segmentation is also reported (separately for water, air and bone).
Table 5.
Comparison between FLUKA, 3D-RD and MCID DMC simulation with a CT-based density map—water phantom with air, `lung' and bone inserts. For Dprofile calculation, code 1 is represented by either 3D-RD or MCID and code 2 is represented by FLUKA.
| Profile comparison |
R inside the VOIs |
|||
|---|---|---|---|---|
| Dprofile ± SD | Rave ± SD | [Rmin, Rmax] | ||
| FLUKA versus 3D-RD | ||||
| Air–water–bone segmentation | Water | (2 ± 1)% | 1.02 ± 0.02 | [1.0,1.1] |
| Air | (4 ± 3.5)% | 0.94 ± 0.03 | [0.8, 1.0] | |
| Bone | (4 ± 3.5)% | 1.04 ± 0.11 | [0.8, 1.5] | |
| Lung–water–bone segmentation | Lung | (3 ± 2)% | 0.99 ± 0.03 | [0.9, 1.1] |
| FLUKA versus MCID | ||||
| Air–water–bone segmentation | Water | (2 ± 1)% | 1.01 ± 0.05 | [0.9, 1.2] |
| Air | (5 ± 4.5)% | 1.00 ± 0.12 | [0.7, 1.7] | |
| Bone | (3 ± 2.5)% | 1.01 ± 0.24 | [0.4, 1.9] | |
| Lung–water–bone segmentation | Lung | (2 ± 1.5)% | 1.02 ± 0.03 | [1.0,1.1] |
| FLUKA versus 3D-RD | ||||
| Schneider segmentation | Water | (2 ± 1)% | 1.03 ± 0.02 | [1.0,1.1] |
| Air | (3 ± 2)% | 0.99 ± 0.03 | [0.9, 1.4] | |
| Bone | (4 ± 3.5)% | 1.03 ± 0.10 | [0.8, 1.5] | |
The average statistical uncertainty affecting FLUKA results was 1.2% (ranging from 0.9% to 1.6%) within the water VOI, 2.3% (ranging from 1.8% to 3.5%) in the air VOI and 7% (ranging from 5% to 10%) in the bone VOI when using the air–water–bone segmentation, and 2% (ranging from 1% to 4%) in the lung VOI when using the lung–water–bone segmentation. The higher statistical uncertainty in the air/lung and bone inserts is due to the fact that such inserts do not contain activity; thus, the absorbed dose is lower than in water being due only to the contribution of the activity in the surrounding water.
The average statistical uncertainty affecting MCID results was 1.3% (ranging from 1.2% to 1.5%) within the water VOI, 9% (ranging from 4% to 38%) in the air VOI and 7% (ranging from 5% to 9%) in the bone VOI when using the air–water–bone segmentation, and 1.8% (ranging from 1.4% to 2.2%) in the lung VOI when using the lung–water–bone segmentation. Finally, the average statistical uncertainty affecting 3D-RD results was 1% (ranging from 0.1% to 4%) within the water VOI, 2% (ranging from 0.1% to 7%) in the air VOI and 5% (ranging from 0.1% to 20%) in the bone VOI when using the air–water–bone segmentation, and 1% (ranging from 0.1% to 6%) in the lung VOI when using the lung–water–bone segmentation.
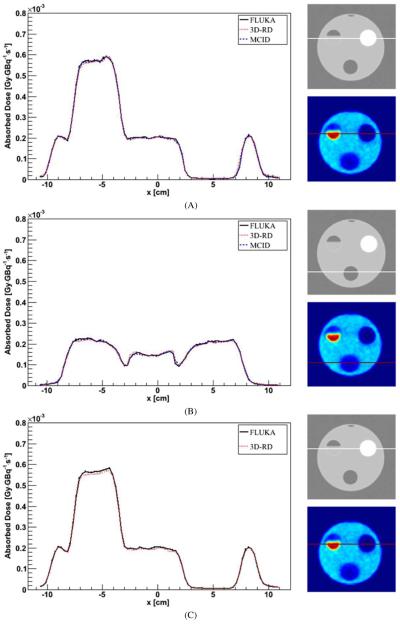
In figure 7, the profile crossing the bone insert in the case of air–water–bone segmentation (A) and the profile crossing the lung insert in case of lung–water–bone segmentation (B) are presented. The profile crossing the bone insert in the case of Schneider segmentation is also reported in figure 7(C).
Figure 7.
Profile comparison for DMC simulation with a CT-based density map and air–water–bone segmentation (A), lung–water–bone segmentation (B) and Schneider segmentation (C). The profile crosses the bone insert (A), (B) or the lung insert (B). Error bars are not visible because they are fully included in the lines.
In figure 8, the air DVH in case of air—water–bone segmentation (A) and the lung DVH in case of lung–water–bone segmentation (B) are presented. The air DVH in case of Schneider segmentation is also reported in figure 8(C).
Figure 8.
DVH comparison for DMC simulation with a CT-based density map and air–water–bone segmentation (A), lung–water–bone segmentation (B) and Schneider segmentation (C). The VOI is included in the air insert (A), (C) or in the `lung' insert (B). Error bars, when not visible, are fully included in the lines. Error bars represent 1 sigma uncertainty; when not visible, they are fully included in the lines.
4. Discussion
The therapeutic use of radiopharmaceuticals is gaining increasing importance, with the constant development of new molecules and new strategies for injection.
An accurate, patient-specific absorbed dose calculation is fundamental for the treatment optimization and for a complete understanding of the efficacy and the possible side effects.
The final accuracy of an absorbed dose calculation based on nuclear medicine images is firstly affected by the image quality and to what extent the image represents the real activity distribution inside the patient. The properties of the imaging device, the acquisition procedure and the post-processing sophistication all play a role in this sense.
Then, the absorbed dose result is also influenced by the precision of the individual biokinetic assessment. It was evidenced that the biological processes exhibit a first-order kinetic, which can be described as a sum of exponential decaying curves (Glatting et al 2007), generally from 1 to 3. Three measurements for each kinetic phase are needed to best depict the time-activity wash-out (Lassmann et al 2011); thus, the choice of the number of measurements, and their timing, importantly affect the result. For example, in peptide receptor radionuclide therapy with 90Y and 177Lu it was shown that when data gathering approximately reaches two radionuclide effective half-lives, the impact of the time–activity curve fitting on the absorbed dose estimate is lower than 10%. Conversely, when data points are too few and are not properly spaced, the estimation can easily fail by 20%–25% with exponential fittings, and even more than 50% with trapezoidal integration methods assuming physical decay after the last point (Guerriero et al 2013).
The images and the biokinetic parameters are the input data for the calculation tools, whose features ultimately affect the accuracy of the absorbed dose estimates: the method applied (for example, 2D versus 3D dosimetry), the robustness of the physical models used for the calculation, the approximations and the assumptions it relies on.
The 3D dosimetry based on DMC simulation is in principle the most accurate method for calculation. As reported in the introduction, many different tools were created to implement the DMC methodology. Considering their home-made development, they were mainly used by the developing centres, or shared within specific collaborations among institutions. The proliferation of new tools was ultimately positive, offering the possibility of inter-check comparisons; however, a more widespread diffusion of the already existing tools could also be useful, since the home-made development is very demanding and often goes beyond the possibilities of the physicists deeply involved in the hospital routine. Moreover, the long time required for the simulation, one of the major drawbacks for the systematic implementation of DMC simulation in clinical dosimetry, is probably not going to be an issue in the future, thanks to the rapid improvement of the modern computer processing power.
This study aims to test the routines specifically developed to perform patient-specific, image-based 3D dosimetry using the FLUKA MC code, by the comparison with analogous tools based on different MC codes.
The reliability of the FLUKA algorithm for electron transport in the energy range typical of nuclear medicine was verified by comparison with experimental data (Ferrari et al 1992, Aarnio et al 1994, Fassò et al 1997, 2001, Böhlen et al 2012). In addition, FLUKA dose point kernels were calculated in water and bone tissue for both monoenergetic electrons and beta emitting isotopes, and compared to those obtained with other MC codes commonly used for nuclear medicine dosimetry (Botta et al 2011). This latest study showed that the differences between the simulation algorithms of the different codes are not expected to have an impact when performing internal dosimetry at the voxel level.
The first step aimed to test the routine for handling PET and SPECT images only. Thus, the CT-based density map was temporarily disregarded and homogeneous water medium was assumed.
The results reported in section 3.2.1 show a perfect agreement, within the statistical uncertainty, between FLUKA simulation in homogeneous water and VKC in the same environment (table 2). Considering that the consistency of VKC results had been previously verified (Pacilio et al 2012), such agreement proves that the routine developed to handle the PET and SPECT images is working properly.
As a further confirmation, in section 3.2.2 these same FLUKA results have been compared with the analogous data obtained with 3D-RD and MCID, and even in this case the agreement is within the statistical uncertainty. With the same number of simulated particles, the accordance between FLUKA and 3D-RD or MCID (table 3) is slightly worse than that between FLUKA and VKC (table 2), probably due to the small differences between the simulation algorithms used by the three codes (FLUKA, EGSnrc, MCNP5) in homogeneous water. In fact, the differences in table 3 are similar to those commonly observed when comparing different simulation algorithms (Botta et al 2011, Uusijarvi et al 2009). When comparing FLUKA DMC and VKC, instead, no differences regarding the simulation algorithm come into play since the voxel kernels for VKC were calculated with FLUKA and with the same simulation parameters as for the DMC simulation.
In the second step (section 3.3), the CT-based density map was added, to test whether the two routines—the one handling the PET-SPECT images and the one handling the CT images—were properly integrated together in the simulation workflow.
Firstly, a homogeneous water phantom filled with activity was considered (section 3.3.1). As compared to the previous case (section 3.2.2), the only difference is that each group is adopting his own method to convert the CT number into density and tissue composition, whereas previously a perfectly homogeneous medium was assumed by all the codes. In spite of this, the three codes again agree within the statistical uncertainty: by comparing tables 4 and 3 it is evident that the same agreement is obtained when performing simulation in homogeneous water and when introducing the CT.
An analogous, further comparison was also performed with a non-homogeneous phantom (section 3.3.2) to get closer to the clinical application of the DMC simulation, which mainly regards the dosimetry in presence of non-uniform tissues. The VKC method, in fact, is more than adequate for homogeneous, water-equivalent tissues.
When all the codes implement the same air–water–bone or lung–water–bone segmentations, FLUKA agrees with both 3D-RD and MCID within the statistical uncertainty in all the materials. Looking at the absorbed dose profiles, the results obtained in all the inserts of the PET_2 phantom (air, water, bone) are comparable to those obtained in the water regions in the PET _1 phantom (table 5 versus table 4). Slightly higher discrepancies among the codes were observed in the air and bone inserts with respect to water (3–5% versus 2%) due to the lower statistic, but in any case the agreement was within the statistical uncertainty.
As expectable, Rave in water is basically the same for the PET_2 phantom as for the PET_1 phantom. A slight improvement is actually observed in the case of the PET_2 phantom, probably due to the fact that all the codes used an identical segmentation, whereas there were slight differences among the segmentations used by each code for the PET_1 simulation.
Rave values in air, bone and lung also indicate a similar agreement as for water (the SD being higher but coherent with the corresponding statistical uncertainties), except for the comparison between FLUKA and 3D-RD in air, with Rave = 0.94 (table 5 and figure 8(A)). However, when adopting the Schneider segmentation, the agreement between FLUKA and 3DRD in air is good even in air (Rave = 0.99 ± 0.03, table 5, figure 8(C)). Thus, such discrepancy is not ascribable to the FLUKA routine, but probably to some difference between the tools which becomes evident with the air–water–bone segmentation and not with the Schneider segmentation. The main difference between the two segmentations in the air region is the material density, 0.0013 g cm−3 for the air–water–bone segmentation and 0.027 g cm−3 in the case of Schneider segmentation.
All in all, these results adequately prove that the CT data enter properly in the simulation workflow.
In a future study, it will be also interesting to compare the different tools on patient images, each tool implementing its own segmentation, in order to quantify the impact of the segmentation on the absorbed dose in different districts.
Further studies are also foreseen in order to optimize FLUKA simulation parameters, minimizing the simulation duration without losing accuracy. In particular, the threshold for particle absorption can be easily increased to values higher than 1 keV in consideration of the fact that the voxel side is typically of the order of a few millimetres, more than three orders of magnitude larger than the range of a 1 keV electron in water or bone, and two orders of magnitudes in the case of air. The 1 keV value was adopted in this study just for comparison purpose with the other codes. Also, the necessity to switch from the default multiple scattering to a single scattering algorithm, limited to those cases where the Molière model is no longer reliable, could be investigated. Along with this, a user friendly tool that can be easily shared and used by medical physicists working in the clinic is under development.
To conclude, this study confirmed that the routines developed to perform DMC simulation on PET-CT and SPECT-CT images with FLUKA work properly.
With these tools it will be possible to investigate the adequacy of DMC calculation at the voxel level in relation to the accuracy of the PET and SPECT images and to the ability to assess activity and cumulated activity at the voxel level.
As a further step, it will be possible to use them for personalized dosimetry on patient images.
5. Conclusion
Specific routines were developed in the FLUKA environment to perform patient-specific 3D dosimetry through DMC simulation on PET-CT and SPECT-CT images. FLUKA results were in good agreement with those obtained with other tools developed to perform 3D-absorbed dose calculation as well, both in the assumption of homogeneous tissue and using the CT-based density map. The absorbed dose map correspondence was verified at the voxel level and the average discrepancy was always lower than 6%, an acceptable value considering both the statistical uncertainty and the fact that a 2–3% difference was expected due to the differences among the simulation algorithms. The time needed for simulation appeared moderate, and reliable results can be quite easily achievable, especially with the increasing availability of powerful computation tools. The FLUKA routines here developed are ready to be used for personalized dosimetry.
Footnotes
Based on work presented at the Third European Workshop on Monte Carlo Treatment Planning (Seville, 15–18 May 2012).
References
- Aarnio PA, Fassò A, Ferrari A, Moehring JH, Ranft J, Sala PR, Stevenson GR, Zazula JM. Electron-photon transport: Always so good as we think? Experience with FLUKA. In: Dragovitsch P, Linn SL, Burbank M, editors. Proc. MC93 Int. Conf. on Monte-Carlo Simulation in High Energy and Nuclear Physics (Tallahassee, FL, 22–26 February 1993); Singapore: World Scientific; 1994. pp. 100–10. [Google Scholar]
- Akkurt H, Eckerman KF, Wagner JC, Sherbini S. PIMAL: computational phantom with moving arms and legs. Trans. Am. Nucl. Soc. 2007;96:396–7. [Google Scholar]
- Battistoni G, Muraro S, Sala PR, Cerutti F, Ferrari A, Roesler S, Fassò A, Ranft J. The FLUKA code: description and benchmarking. AIP Conf. Proc. 2007;896:31–49. [Google Scholar]
- Bethe HA. Moliere's theory of multiple scattering. Phys. Rev. 1953;89:1256–66. [Google Scholar]
- Böhlen TT, Ferrari A, Patera V, Sala PR. Describing Compton scattering and two-quanta positron annihilation based on Compton profiles: two models suited for the Monte Carlo method. J. Instrum. 2012;7:07018–30. [Google Scholar]
- Bolch WE, Bouchet LG, Robertson JS, Wessels BW, Siegel JA, Howell RW, Erdi AK, Aydogan B, Costes S, Watson EE. MIRD Pamphlet No. 17: the dosimetry of nonuniform activity distributions—radionuclide S values at the voxel level. J. Nucl. Med. 1999;40:11S–36S. [PubMed] [Google Scholar]
- Bolch WE, Eckerman KF, Sgouros G, Thomas SR. MIRD Pamphlet No. 21: a generalized schema for radiopharmaceutical dosimetry—standardization of nomenclature. J. Nucl. Med. 2009;50:477–84. doi: 10.2967/jnumed.108.056036. [DOI] [PubMed] [Google Scholar]
- Botta F, et al. Calculation of electron and isotopes dose point kernels with FLUKA Monte Carlo code for dosimetry in nuclear medicine therapy. Med. Phys. 2011;38:3944–54. doi: 10.1118/1.3586038. [DOI] [PubMed] [Google Scholar]
- Chiavassa S, Bardiès M, Guiraud-Vitaux F, Bruel D, Jourdain JR, Franck D, Aubineau-Laniècel I. OEDIPE: a personalized dosimetric tool associating voxel-based models with MCNPX. Cancer Biother. Radiopharm. 2005;20:325–32. doi: 10.1089/cbr.2005.20.325. [DOI] [PubMed] [Google Scholar]
- Dieudonné A, Hobbs R, Bolch W, Sgouros G, Gardin I. Fine resolution voxel S-values for constructing absorbed dose distributions at variable voxel size. J. Nucl. Med. 2010;51:1600–7. doi: 10.2967/jnumed.110.077149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckerman KF, Endo A. MIRD: Radionuclide Data and Decay Schemes. 1st edn Society of Nuclear Medicine; Reston, VA: 2008. [Google Scholar]
- Fassò A, Ferrari A, Ranft J, Sala PR. New developments in FLUKA modelling of hadronic and EM interactions. In: Hirayama H, editor. Proceedings of the 3rd Workshop on `Simulating Accelerator Radiation Environments, SARE-3 (KEK-Tsukuba, May 7–9 1997); 1997. pp. 32–43. KEK Report Proceedings. [Google Scholar]
- Fassò A, Ferrari A, Sala PR. Electron-photon transport in FLUKA: status. In: Kling A, Barao F, Nakagawa M, Tavora L, Vazeds P, editors. Proc. Monte Carlo 2000 Conf. (Lisbon, October 23–26 2000); Berlin: Springer; 2001. pp. 159–64. [Google Scholar]
- Ferrari A, Sala PR, Fassò A, Ranft J. SLAC Report. 2005. FLUKA: a multi-particle transport code. CERN-2005-10, INFN/TC_05/11, SLAC-R-773. [Google Scholar]
- Ferrari A, Sala PR, Guaraldi R, Padoani F. An improved multiple scattering model for charged particle transport. Nucl. Instrum. Methods Phys. Res. 1992;B 71:412–26. [Google Scholar]
- Furhang EE, Chui CS, Kolbert KS, Larson SM, Sgouros G. Implementation of a Monte Carlo dosimetry method for patient-specific internal emitter therapy. Med. Phys. 1997;24:1163–72. doi: 10.1118/1.598018. [DOI] [PubMed] [Google Scholar]
- Furhang EE, Chui CS, Sgouros G. A Monte Carlo approach to patient-specific dosimetry. Med. Phys. 1996;23:1523–29. doi: 10.1118/1.597882. [DOI] [PubMed] [Google Scholar]
- Glatting G, Kletting P, Reske SN, Hohl K, Ring C. Choosing the optimal fit function: comparison of the Akaike information criterion and the F-test. Med. Phys. 2007;34:4285–92. doi: 10.1118/1.2794176. [DOI] [PubMed] [Google Scholar]
- Guerriero F, et al. Kidney dosimetry in 177Lu and 90Y peptide receptor radionuclide therapy: influence of image timing, time-activity integration method, and risk factors. Biomed. Res. Int. 2013;2013:935351. doi: 10.1155/2013/935351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hobbs RF, Wahl RL, Lodge MA, Javadi MS, Cho S, Chien D, Ewertz ME, Esaias CE, Ladenson PW, Sgouros G. 124I PET-Based 3D-RD dosimetry for pediatric thyroid cancer patient: case study for real-time patient-specific dosimetry. J. Nucl. Med. 2009;50:1844–7. doi: 10.2967/jnumed.109.066738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ICRU . ICRU Report. Vol. 44. ICRU; Bethesda, MD: 1989. Tissue substitutes in radiation dosimetry and measurement. [Google Scholar]
- Koivunoro H, Siiskonen T, Kotiluoto P, Auterinen I, Hippelainen E, Savolainen S. Accuracy of the electron transport in MCNP5 and its suitability for ionization chamber response simulation: a comparison with the EGSnrc and PENELOPE codes. Med. Phys. 2012;39:1335–44. doi: 10.1118/1.3685446. [DOI] [PubMed] [Google Scholar]
- Kost SD, Zhou S, Stabin MG. Patient-individualized dosimetry via semi-automated CT segmentation and voxel-based Monte Carlo transport methods. J. Nucl. Med. 2011;52(Suppl. 1):1460. available at http://jnumedmtg.snmjournals.org/cgi/content/meeting_abstract/52/1_MeetingAbstracts/1460. [Google Scholar]
- Lassmann M, Chiesa C, Flux G, Bardiès M. EANM Dosimetry Committee guidance document: good practice of clinical dosimetry reporting. Eur. J. Nucl. Med. Mol. Imaging. 2011;38:192–200. doi: 10.1007/s00259-010-1549-3. [DOI] [PubMed] [Google Scholar]
- Liu X, Ljungberg M, Strand SE. DOSIMG: a 3D voxel-based Monte Carlo program for absorbed dose calculations. J. Nucl. Med. 2001;42:662–9. available at http://jnm.snmjournals.org/content/42/4/662.abstract. [Google Scholar]
- Ljungberg M, Strand SE. A Monte Carlo program for the simulation of scintillation camera characteristics. Comput. Methods Programs Biomed. 1989;29:257–72. doi: 10.1016/0169-2607(89)90111-9. [DOI] [PubMed] [Google Scholar]
- Marcatili S, Pettinato C, Daniels S, Lewis DG, Edwards P, Fanti S, Spezi E. Development and validation of RAYDOSE: a Geant4-based application for molecular radiotherapy. Phys. Med. Biol. 2013;58:2491–508. doi: 10.1088/0031-9155/58/8/2491. [DOI] [PubMed] [Google Scholar]
- Mc Conn RJ, Jr, Gesh CJ, Pagh RT, Rucker RA, Williams RA., III . PIET-43741-TM-963 PNNL-15870 Revision 1. U.S. Department of Homeland Security, U.S. Customs and Border Protection and Domestic Nuclear Detection Office under U.S. Department of Energy Contract DE-AC05–76RL01830; 2011. Radiation Portal Monitor Project. Compendium of Material Composition Data for Radiation Transport Modeling. [Google Scholar]
- Moliere GZ. Theorie der Streuung schneller geladener Teilchen II - Mehrfach und Vielfachstreuung. Z. Naturforsch. 1948;3a:78–97. [Google Scholar]
- Moliere GZ. Theorie der Streuung schneller geladener Teilchen IIIc - Die Vielfachstreuung von Bahnspuren unter Beruecksichtigung der statistischen Kopplung. Z. Naturforsch. 1955;10a:177–211. [Google Scholar]
- Pacilio M, Torres Aroche LA, Botta F, Di Dia A, Lanconelli N, Coca Pérez M A, Basile C, Cremonesi M. 3D-dosimetry inter-comparison in clinical settings for cross-validation of two software implementing the MIRD formalism at the voxel level. Eur. J. Nucl. Med. Mol. Imaging. 2012;39(suppl 2):P0067. [Google Scholar]
- Parodi K, Ferrari A, Sommerer F, Paganetti H. Clinical CT-based calculations of dose and positron emitter distributions in proton therapy using the FLUKA Monte Carlo code. Phys. Med. Biol. 2007;52:3369–87. doi: 10.1088/0031-9155/52/12/004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prideaux A, Song H, Hobbs R, He B, Frey E, Ladenson P, Wahl R, Sgouros G. Three-dimensional radiobiologic dosimetry: application of radiobiologic modeling to patient-specific 3-dimensional imaging-based internal dosimetry. J. Nucl. Med. 2007;48:1008–16. doi: 10.2967/jnumed.106.038000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider W, Bortfeld T, Schlegel W. Correlation between CT numbers and tissue parameters needed for Monte Carlo simulations of clinical dose distributions. Phys. Med. Biol. 2000;45:459–78. doi: 10.1088/0031-9155/45/2/314. [DOI] [PubMed] [Google Scholar]
- Sgouros G, Kolbert K. The three-dimensional internal dosimetry software package, 3D-ID. In: Zaidi H, Sgouros G, editors. Therapeutic Applications of Monte Carlo Calculations in Nuclear Medicine. Institute of Physics; Philadelphia, PA, USA: 2002. pp. 249–61. [Google Scholar]
- Uusijarvi H, Chouin N, Bernhardt P, Ferrer L, Bardiès M, Forssell-Aronsson E. Comparison of electron Dose Point Kernels in water generated by the Monte Carlo codes PENELOPE, GEANT4, MCNPX and ETRAN. Cancer Biother. Radiopharm. 2009;24:461–7. doi: 10.1089/cbr.2008.0573. [DOI] [PubMed] [Google Scholar]
- Vergara Gil A, Coca Pérez M A, Torres Aroche LA, Pacilio M, Botta F, Cremonesi M. MCID: a personalized dosimetric tool associating voxel-based models with MCNP5. Proc. IAEA Int. Conf. on Radiation Protection in Medicine, Setting the Scene for the Next Decade (Bonn, 3–7 Dec.).2012. [Google Scholar]
- Wilderman SJ, Dewaraja YK. Method for fast CT/SPECT-based 3D Monte Carlo absorbed dose computations in internal emitter therapy. IEEE Trans. Nucl. Sci. 2007;54:146–52. doi: 10.1109/TNS.2006.889164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- X-5 Monte Carlo Team . MCNP - a general Monte Carlo N-particle transport code. version 5. I. Los Alamos National Laboratory; Los Alamos, NM: 2008a. overview and theory Report No: LA-UR-03-1987. [Google Scholar]
- X-5 Monte Carlo Team . MCNP - a general Monte Carlo N-particle transport code. version 5. II. Los Alamos National Laboratory; Los Alamos, NM: 2008b. user guide Report No: LA-CP-03-0245. [Google Scholar]
- Yoriyaz H, Stabin MG, Dos Santos A. Monte Carlo MCNP-4B-based absorbed dose distribution estimates for patient-specific dosimetry. J. Nucl. Med. 2001;42:662–9. [PubMed] [Google Scholar]