Monte Carlo-based 3-dimensional dosimetry of salivary glands in radioiodine treatment of differentiated thyroid cancer estimated using ¹²⁴I PET

Abstract

Aim

Salivary gland toxicity is of concern in radioiodine treatment of thyroid cancer. Toxicity is often observed while the estimated radiation absorbed dose (AD) values are below expected toxicity thresholds. Monte Carlo-based voxelized 3-dimensional radiobiological dosimetry (3D-RD) calculations of the salivary glands from eight metastatic thyroid cancer patients treated with ¹³¹I are presented with the objective of resolving this discrepancy.

Methods

GEANT4 Monte Carlo simulations were performed for ¹³¹I, based on pretherapeutic ¹²⁴I PET/CT imaging corrected for partial volume effect, and the results scaled to the therapeutic administered activities. For patients with external regions of high uptake proximal to the salivary glands, such as thyroid remnants or lymph node metastases, separate simulations were run to quantify the AD contributions from both (A) the salivary glands themselves, and (B) the external proximal region of high uptake (present for five patients). The contribution from the whole body outside the field of view was also estimated using modeling. Voxelized and average ADs and biological effective doses (BEDs) were calculated.

Results

The estimated average therapeutic ADs were 2.26 Gy considering all contributions and 1.94 Gy from the self-dose component only. The average contribution from the external region of high uptake was 0.54 Gy. This difference was more pronounced for the submandibular glands (2.64 versus 2.10 Gy) compared to the parotid glands (1.88 Gy versus 1.78 Gy). The BED values were on average only 6.6 % higher than (2.41 Gy) the ADs.

Conclusion

The external sources of activity contribute significantly to the salivary gland AD, however neither this contribution, nor the radiobiological effect quantified by the BED are in themselves sufficient to explain the clinically observed toxicity.

Radiopharmaceutical therapy using ¹³¹I is the treatment of choice for differentiated thyroid carcinoma of papillary and follicular origin,¹ since the ¹³¹I naturally targets the thyroid tumors and thyroid remnants through the sodium-iodine symporter mechanism.² However, radioiodine is also concentrated in the parotid and submandibular salivary glands, although not to any noticeable extent in the sublingual salivary glands.³ Radiation damage to the salivary parenchyma as a result of ¹³¹I radiation has been reported, consequently resulting in, inter alia, sialadenitis and xerostomia.^4-8 These conditions in turn can induce dysphagia, infectious diseases of the oral and pharyngeal mucosa, dental and periodontal diseases. Radiation induced salivary gland toxicity is a serious issue that affects the patients’ health-related quality of life significantly.^8-10

Normal organ toxicity from radiopharmaceutical therapy has been traditionally correlated with absorbed dose, most often in the form of maximum tolerated dose. Over the past decade, the importance of the biologic effective dose (BED)¹¹ in studies of normal organ toxicity has been demonstrated by the BED-response relationship, established in the context of renal toxicity from radiopeptide therapy.^12,13 However, to date, no correlation between any dosimetric quantity and clinically observed toxicity has been established for the salivary gland toxicity resulting from ¹³¹I therapy for thyroid cancer. In particular, a study by Jentzen et al.¹⁴ using ¹³¹I, planar gamma camera imaging and volume estimations primarily from ultrasonography gave absorbed dose values 5-10 times too low to satisfactorily explain the observed glandular radiation damages in radioiodine therapy. The dosimetry was based on standard MIRD methodology¹⁵ of absorbed fractions, and therefore, assumed homogenous distribution of activity in the salivary glands.

Positron emission tomography (PET) with ¹²⁴I-labeled radiopharmaceuticals has been established as a more accurate quantitative imaging tool than gamma camera-based imaging technologies,^16-18 as long as the partial volume effect (PVE) can be accounted for.^19-21 Specifically, ¹²⁴I has been used successfully as a tracer for ¹³¹I in pretherapy lesion or organ dosimetry in estimating the absorbed dose in radioiodine therapy.^22-24 Therefore, an ¹²⁴I PET and PET/CT-based salivary gland dosimetry study was subsequently undertaken by Jentzen et al.²⁵ with the goal of reconciling dosimetry and observed clinical toxicities using total salivary gland activity determined from the 3-D PET images and an absorbed fraction methodology assuming homogenous activity concentration with the volumes determined from contours drawn on CT. However, that study also calculated low absorbed dose results comparable to those from previous study,¹⁴ and the discrepancy between absorbed and observed toxicity remained unresolved. In this retrospective study, we performed salivary gland dosimetry using personalized Monte Carlo-based 3-dimensional radiobiological dosimetry (3D-RD) on a similar patient data set as for the ¹²⁴I study,²⁵ with the idea that 1) external factors such as thyroid remnants and lymph node metastases with high uptake proximal to the salivary glands may contribute significantly to the absorbed-dose of the salivary glands; 2) the BED may correlate better with toxicity; or 3) voxelized results may lead to identification of localization of the absorbed-dose.

Materials and methods

Patient data

The patient data were provided by the University of Duisburg-Essen (UDE) and have been described in the previous study.²⁵ Five patients in the present study were taken directly from the previous study while three others were added from a larger data set of patients who underwent an identical procedure.²⁶ Patients were selected whose individual gland dosimetry was immediately available for comparison, as opposed to those whose data had been averaged over both parotid and both submandibular glands, respectively. The patient profiles are shown in Table I. In short, serial ¹²⁴I PET images were acquired at seven time points (0.5, 1, 2, 4, 24, 48 and 72 or 96 h) after administration of the tracer ¹²⁴I activity. Images were acquired at the UDE on an ECAT EXACT HR+ PET scanner (CTI/Siemens; Erlangen, Germany). In addition, a ¹²⁴I PET/CT image (BIOGRAPH EMOTION DUO; Siemens Medical Solution, Hoffman Estates; IL, USA) was acquired after about 26 h.

Table I.

Patient clinical data with pretherapeutic (Dx) ¹²⁴I and therapeutic (Tx) ¹³¹I administrated activities (AA).

Patient	Group	Sex	Age (y)	Height (cm)	Mass (kg)	124I Dx AA (MBq)	131I Tx AA (GBq)
1	A	F	66	156	74	24.0	3.0
2	A	F	31	168	54	24.1	10.0
3	A	F	73	155	88	24.7	3.0
4	B	F	35	163	85	24.3	10.0
5	B	M	67	176	95	24.4	10.0
6	B	F	71	158	60	24.0	10.0
7	B	M	60	178	87	24.0	3.0
8	B	F	31	175	124	24.0	3.0

3D-RD input

The 3D-RD methodology has been previously described elsewhere.^24-27 The CT images provided the density maps for the dose calculation in the Monte Carlo simulation. The seven PET emission images were coregistered to each other using a mutual information-based algorithm and a HERMES software station (HERMES Medical Solutions; Stockholm, Sweden). For low activity maps with single points of high activity, logarithmic maps of the activity were made and used as a bridge for registration. The CT was registered using the same transformation parameters as for the associated PET. The salivary gland volumes of interest (VOIs) (right parotid [RP], right submandibular [RS], left parotid [LP], and left submandibular [LS]) were delineated on the fused 4 h PET/CT images. First, a threshold on the 4 h activity image equal to 25% of the maximum salivary gland activity was set, then the VOIs were adjusted manually using the registered CT image, when the mismatch was obvious and dental artifacts were not present. The threshold value of 25% was determined as the value that defined functional salivary glands volumes that best approximated the anatomical salivary gland volumes in the glands that were not compromised by dental artifacts on the CT image.

Recovery coefficient calculation

In order to correct for PVE using recovery coefficients (RCs) for the functionally defined volumes, PET/CT phantom data provided by UDE were used.²⁵ The phantom data consisted of PET images of 6 spheres, ranging in size from 4.8 to 18.5 mm in radius (Table II) filled with ¹²⁴I at known activity concentration, C₀=43.1 kBq/mL, no radioactivity in the phantom cavity was present. Both the phantom and patient PET images were reconstructed with an iterative attenuation-weighted ordered subsets expectation maximization algorithm (4 iterations, 16 subsets) followed by post-filtering with a 5-mm 3D Gaussian kernel.²⁵ The data file was converted to numeric data in a 128×128×128 matrix of 1.7×1.7×1.7 mm³ sized voxels (interpolated from the original voxel size of 1.7×1.7×2.4 mm³ in order to facilitate radial distribution analysis).

Table II.

—Functional fit parameters for the six spheres and the corresponding squared correlation coefficients (r²).

Sphere	R (mm)	c0 (kBq/mL)	r0 (mm)	q (mm)	r 2
1	18.5	40.6	17.7	4.84	0.99
2	14.0	39.3	13.1	4.67	0.99
3	11.1	38.7	10.0	4.63	0.98
4	8.5	38.5	7.13	4.82	0.97
5	6.1	36.2	5.06	4.68	0.91
6	4.8	34.1	2.53	4.53	0.78

The RCs were then calculated by:

1. plotting the voxel imaged activity concentration, in each sextant as a function of voxel radial position, and fitting the data with the following function:

   $$c_i\left(r\right)=\frac{c_0}{2}\mathit{erf}c\left(\frac{r_i-r_0}{\theta }\right)qq$$ (1)

   where c_i is the measured activity concentration of the i^th voxel r_i is the voxel’s radial position (distance to the center of the sphere); while c₀ (maximum measured activity concentration), θ, and r₀ (fitted radius) are parameters and erfc is the complementary error function.
2. Integrating equation (1) in spherical coordinates to obtain total measured activity, a, as a function of radial distance:

   $$a\left(r\right)=4\pi \underset{0}{\overset{r}{\int }}c\left(r^{\prime }\right)r^{\prime 2}{\mathit{dr}}^{\prime }$$ (2)

This was normalized against the total theoretical activity, A, in the sphere given by equation:

$$a\left(\infty \right)=A=C_0\frac{4}{3}\pi R^3$$ (3)

where C₀ is the known true activity concentration, and R is the sphere’s inner radius. The RCs may consequently be obtained by the ratio of imaged activity within the sphere, i.e., the integral a(r) calculated to the measured radius, R_m, of the sphere, to the true activity:

$$\mathit{RC}=\frac{a\left(R_m\right)}{A}=\frac{4\pi \underset{0}{\overset{R_m}{\int }}c\left(r\right)r^2\mathit{dr}}{C_0\frac{4}{3}\pi R^3}$$ (4)

For the spheres themselves or for any anatomically defined (known radius) volume, the value for R_m to be used in equation (4) would be the true radius, R; however, since the salivary glands are defined functionally with a 25 % threshold, in order to be applicable the RCs must be similarly defined; therefore, the R_m values used were the sphere radii defined with a 25 % threshold.

3. Fitting a function of the form RC(V_f) = a ln(V_f)+b, which gives the RC as a function of functionally defined sphere volume, V_f. The parameters a and b are fitting parameters. From this fit, the RC values of the salivary glands were obtained using the (functionally) measured volumes.

3D-RD simulation

3D-RD simulation on the Electron Gamma Shower (EGS) Monte Carlo (EGS4 DOSXYZnrc) was run for all time points using the imaged activity and attenuation density maps calculated from the CT. Details of the 3D-RD software package have been described elsewhere (24, 27); briefly:

1. the volumes of the salivary glands were delineated functionally (and anatomically, when possible, see prior description) on the fused PET/CT images and the activities inside the salivary gland VOIs were corrected for PVE using RCs obtained from the fit to the phantom data. By rearranging equation (4), the true activity of the salivary glands was obtained by dividing the measured activity by the RC. The activity outside of the salivary glands was not adjusted;

2. using the high energy physics-based EGSnrc Monte Carlo software, ten million events were run each for the β- and photon components of the ¹³¹I decay spectra, for each time point. Spectra probability distributions were obtained from the updated MIRD Radionuclide Data and Decay Scheme (28). For patients with large external sources of uptake near to the salivary glands, in order to evaluate the dose contribution from those external sources, two different simulation sets were created by dividing the activity in the PET images into (A) activity in the salivary glands and the surrounding background (head and lower part of the body), and (B) the region of high uptake found in the neck below the salivary glands (thyroid remnants and lymph node metastases);

3. the energy deposition distribution from the contributing components from Monte Carlo were weighted for probability and imaged activity (the ¹³¹I activity corrected for differing half-life, 8.02 days vs. 4.18 days, and adjusted to the therapeutic administered activity), then converted to absorbed dose rate for each voxel or each salivary gland as a whole;

4. the salivary gland mean absorbed dose and BED were calculated, for a hybrid trapezoid/piece-wise exponential decay fit to the dose rate time points. The area under the curve fit yielded the absorbed dose. The absorbed dose and BED were also calculated for each voxel in the salivary glands from similar fits. Additionally, the absorbed dose from the head and salivary gland activities, D_self, and the absorbed dose from external region of high uptake, D_ext, were calculated separately.

A piece-wise fit was deemed most accurate, rather than any functional fit, due to large fluctuations in dose rate for the first four time points and for the variability from patient to patient. The first four time points are fit with straight lines (or trapezoids, which is the shape under the curve for each segment of the fit) while the succeeding points were joined by simple exponential fits. The tail was either the continuation of the fit between the last two points, or in the case of a non-physical decay value, physical decay from the last time point.

The BED ^{11, 29} is defined as:

$$\mathit{BED}=D\left(1+\frac{G\left(\infty \right)}{\alpha ∕\beta }\cdot D\right)$$ (5)

where α and β are the linear-quadratic radiobiological parameters (30), D is the absorbed dose, and G(T) is the Lea-Catcheside factor:^{31, 32}

$$G\left(T\right)=\frac{2}{D^2}\cdot \underset{0}{\overset{T}{\int }}\stackrel{.}{D}\left(t\right)\mathit{dt}\underset{0}{\overset{t}{\int }}\stackrel{.}{D}\left(w\right)\cdot e^{-\mu (t-w)}\mathit{dw}$$ (6)

w and t are integration variables, while μ is the repair rate for DNA damage, assuming exponential repair. For a piece-wise defined function an analytical formula cannot be established for the BED as it is time-dependent and depends on full knowledge of the dose rate function from time 0 to the desired time point; however the BED can be calculated numerically.³³ The value used for the parameter α/β was 4.5 Gy (α=0.053 Gy⁻¹, β=0.0118 Gy⁻²),³⁴ while the value used for μ was taken to be 0.46 h⁻¹, typical of normal tissue.³⁵

The organ dose per administrated activity (ODpA),²⁵ as its name implies, is simply the absorbed dose, D, divided by the initial administered activity, A₀:

$$\mathit{ODpA}=\frac{D}{A_0}$$ (7)

Long range (rest of body) external absorbed dose contributions

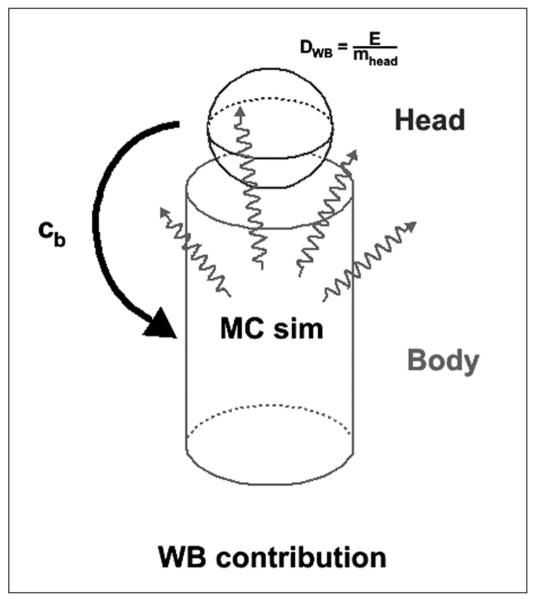
Since the field of view of the images extends only to the head and neck, a simplified geometrical model of the body was created to estimate the dose to the salivary glands from the background activity in the whole body. The applied model is illustrated in Figure 1. A cylinder representing the body was created in GEANT4,^{36, 37} surmounted by a sphere representing the head. The time-integrated activity in the cylinder was calculated assuming the same activity concentration as in the head: for each time point the activity from the salivary VOIs and the region of high uptake in the neck (when applicable) were excluded and the background activity concentration, c_b, was calculated. The time-integrated activity concentration for each patient was then obtained by integrating the resulting activity concentration values in a manner analogous to the VOI dose integration (i.e., hybrid trapezoid-exponential fitting). The dimensions of the cylinder were obtained from the patient data in Table I, modified by subtracting the mass and height of the head/neck region seen within the detector field of view, i.e: the height of the cylinder was the height of the patient minus the imaged head and neck height, while the diameter of the cylinder was obtained by assuming a 1.04 g/cm³ body density and a cylinder mass equal to the body mass minus the imaged head and neck mass. The time-integrated activity was then scaled to the cylinder (body) mass, placed in the cylinder and simulated for decay; the energy deposited in the sphere (head) was then collected and converted to absorbed dose.

Figure 1.

Schematic model of the rest-of-body (ROB) contribution to the salivary gland absorbed dose. The background activity concentrations (c_b) are taken from the head (minus VOIs and regions of high uptake) with a mass of m_head and simulated in the rest of body (cylinder). The energy E is collected in the head (sphere) and converted to dose D_WB.

Results

Phantom data

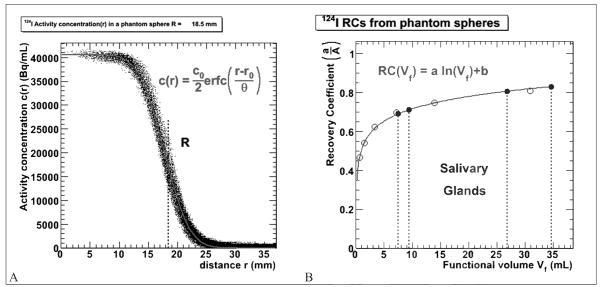
Figure 2A shows the plot of imaged activity concentration vs radius for each voxel for the largest sphere of the phantom (R_sph=18.5 mm) fit with Equation (1). The parameters for the functional fits using Equation (1) are given in Table II along with the squared correlation coefficients (r²). The fraction of measured activity, a/A, was obtained for six different sphere sizes and plotted as a function of functional volume for a threshold of 25%. The data were fit with a logarithmic function to obtain a RC curve as a function of functional volume (Figure 2B).

Figure 2.

A) imaged activity concentration plotted as a function of radius for the largest phantom sphere. The red solid line shows the complementary error function fit to the data and the dotted line shows the physical radius R; B) fraction of activity (RC) measured as a function of the functional volume for a 25% threshold of the maximum activity concentration (empty circles). The blue circles show the salivary gland volume correction values. The red solid line shows the functional fit to the phantom data and the four dotted lines represent the volumes of the salivary glands for patient 1.

Patient data

The results from the GEANT4 modeling show only very low contributions to the salivary gland absorbed dose from the modeled (Figure 1) background activity in the rest of body. The average value was 4.5 mGy, and therefore did not contribute to the total absorbed dose within the three significant figures. The absorbed dose contributions from the different sources, D_self and D_ext, were calculated separately for patients 4-8. The individual time point total dose rates, dD_SG/dt were set equal to dD_self/dt + dD_ext/dt. However, due to the complexity of the functional fit to the dose rates the integrals are not consistent, i.e.: D_SG is not necessarily equal to D_self + D_ext. Patients 1-3 had no external region of high uptake.

The total absorbed dose and the BEDs for all salivary glands were calculated from the hybrid trapezoid-partial exponential fit to the dose rates and the results are given in Table III. Because of the functional fluctuations in radioiodine uptake within the first four hours, no functional form to the early time points could be modeled with any real pretense at accuracy; nevertheless the functional fluctuations reflect real biological uptake and cannot simply be smoothed away with a single exponential function. An example of these results from Patient 1 is shown in Figure 3A. A similar example for a salivary gland with absorbed dose from the two different components is shown in Figure 3B.

Table III.

—Dosimetry results for the salivary glands. The “vox” subscript indicates the voxel-averages values. The mean (M) and standard deviation (SD) values for each category are given at the bottom of the table, where “SM” indicates all submandibular glands and “P” indicates all parotid glands.

Salivary Gland	Dselt (Gy)	Dext (Gy)	D (Gy)	BED (Gy)	Dvox (Gy)	BEDvox (Gy)
RP 1	0.99	-	0.99	1.03	0.99	1.02
LP 1	0.99	-	0.99	1.03	1.07	1.11
RSM 1	1.87	-	1.87	2.01	1.82	1.92
LSM 1	1.31	-	1.31	1.37	1.26	1.3
RP 2	2.31	-	2.31	2.48	2.31	2.53
LP 2	2.49	-	2.49	2.69	2.5	2.77
RSM 2	2.4	-	2.4	2.61	2.35	2.58
LSM 2	2.03	-	2.03	2.18	2.04	2.22
RP 3	1.41	-	1.41	1.47	1.44	1.49
LP 3	0.66	-	0.66	0.68	0.72	0.73
RSM 3	1.57	-	1.57	1.63	1.63	1.68
LSM 3	1.35	-	1.35	1.39	1.44	1.48
RP 4	2.05	0.24	2.5	2.55	2.26	2.34
LP 4	1.46	0.17	1.64	1.71	1.85	1.94
RSM 4	3.55	1.5	4.75	4.83	4.4	4.49
LSM 4	2.67	0.93	4.19	4.24	3.53	3.59
RP 5	3.21	0.16	3.32	3.6	3.58	3.97
LP 5	3.6	0.17	3.68	4.07	3.79	4.32
RSM 5	2.97	0.99	3.53	3.73	4.02	4.27
LSM 5	3.22	0.94	3.65	3.94	3.92	4.27
RP 6	3.13	0.23	3.29	3.86	3.35	4.05
LP 6	3.9	0.22	4.14	4.89	3.34	3.98
RSM 6	3.3	1.34	4.6	5.09	4.73	5.29
LSM 6	3.47	1.56	5.07	5.36	4.79	5.14
RP 7	0.75	0.02	0.77	0.79	0.81	0.83
LP 7	0.61	0.2	0.64	0.65	0.68	0.69
RSM 7	0.69	0.11	0.77	0.78	0.86	0.88
LSM 7	0.99	0.11	1.13	1.14	1.02	1.03
RP 8	0.36	0.16	0.55	0.56	0.68	0.69
LP 8	0.54	0.16	0.75	0.76	0.89	0.91
RSM 8	1.11	0.82	2.05	2.08	2.4	2.43
LSM 8	1.17	0.77	1.93	1.95	2.24	2.27
M (P)	1.78	0.17	1.88	2.05	1.89	2.09
SD (P)	1.19	0.06	1.23	1.43	1.14	1.36
M (SM)	2.10	0.91	2.64	2.77	2.65	2.80
SD (SM)	0.98	0.50	1.43	1.52	1.36	1.49
M (Tot)	1.94	0.54	2.26	2.41	2.27	2.44
SD (Tot)	1.09	0.51	1.36	1.50	1.30	1.45

Figure 3.

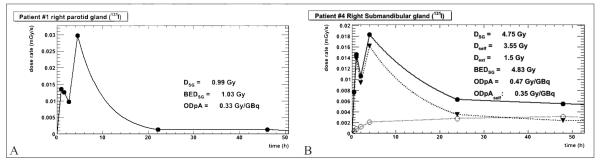
A) dose rate plot for the therapeutic ¹³¹I in the right parotid gland of patient 1. The circles are the overall dose rate values in the VOI. The solid line shows the hybrid trapezoid-exponential fit to the data; B) similar plot for the right submandibular gland of patient 4. The activity is divided into the two contributing compartments and D_ext (empty circles), D_self (triangles) and D_SG (full circles) are calculated by integration separately. Hence, the sum of the two contributions is not always equal to the whole.

The same integration was performed on each voxel in the VOIs. The results were plotted in dose volume histograms (DVHs) as shown in Figure 4 for the same example salivary gland as in Figure 3A. The mean voxel absorbed dose and BED are shown in Table III. Voxelized results enabled better visualization: coronal slices of selected results are presented in Figure 5; Figure 5A shows the absorbed dose distribution for patient 1, while Figure 5B shows D_ext for patient 4. In this patient the non-uniform spatial dose distribution in the submandibular salivary glands reflects the dose contribution from the high and persistent activity concentration in the external source of uptake (possibly thyroid remnant or lymphnode).

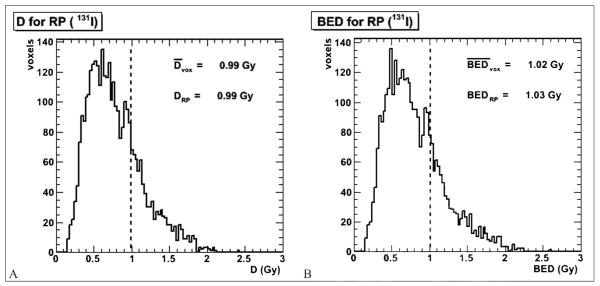
Figure 4.

Absorbed dose (A) and BED (B) DVHs for patient 1. The dotted line represents the average voxel absorbed dose (or BED). The “RP” suffix designates the value representing the overall (i.e., not voxel-averaged) salivary gland (right parotid) dose from Figure 3A, given for comparison.

Figure 5.

Selected coronal slices of absorbed dose maps. A) The dose map for patient 1; B) the D_ext dose map for patient 4. The scales are in gray.

External contributions

The average D_ext contribution to the salivary gland dose was 0.54 Gy, a non-negligible effect considering the scale of values under consideration. In particular, the submandibular glands, closer to the external uptake region, received on average 0.91 Gy of additional absorbed dose compared to the 0.17 Gy on average absorbed by the parotid glands. This contribution is provided on a gland by gland basis for patients in Table III. In particular, the much larger contribution to the submandibular glands absorbed dose is apparent.

Comparison to absorbed fraction method

In a standard approach as was the case for the UDE absorbed fraction method, the volumes have been drawn directly on CT from anatomy.²⁵ The functionally (and to a lesser extent, anatomically) defined volumes drawn at Johns Hopkins are compared to the UDE volumes in Table IV. The average volumes were 34.3 mL and 15.0 mL for the parietal and submandibular glands, respectively, using anatomical drawing 25 and 32.9 mL and 13.2 mL, respectively for the hybrid PET/CT defined volumes.

Table IV.

—Methodological comparison for the salivary glands. For the volumes and ODpA, the “UDE” subscript designates the absorbedfraction method, while “3DRD” is for the 3D-RD calculation. For the 3D-RD values, only the self component was taken into consideration in the values reported in this table, in order to better compare methodologies. The mean (M) and standard deviation (SD) values for each category are given at the bottom of the table.

Salivary Gland	VolUDE (mL)	vol3DRD (mL)	ODpAUDE (Gy/GBq)	ODpA3DRD (Gy/GBq)
RP 1	26.1	26.4	0.41	0.33
LP 1	28.7	30.7	0.36	0.33
RSM 1	15.4	17.7	0.61	0.62
LSM 1	16.4	14.9	0.48	0.44
RP 2	27.5	26.3	0.21	0.23
LP 2	26.5	25.2	0.25	0.25
RSM 2	13.7	16.7	0.22	0.24
LSM 2	13.3	12.1	0.22	0.20
RP 3	31.0	24.1	0.28	0.47
LP 3	27.6	23.2	0.30	0.22
RSM 3	11.9	8.5	0.24	0.52
LSM 3	12.0	6.4	0.23	0.45
RP 4	44.1	36.9	0.34	0.21
LP 4	50.4	34.4	0.34	0.15
RSM 4	19.3	12.3	0.28	0.35
LSM 4	18.4	10.7	0.30	0.27
RP 5	38.9	52.1	0.61	0.32
LP 5	35.9	48.7	0.31	0.36
RSM 5	16.2	18.0	0.59	0.30
LSM 5	16.0	15.5	0.47	0.32
RP 6	23.2	29.3	0.23	0.31
LP 6	22.2	22.9	0.24	0.39
RSM 6	10.7	11.5	0.24	0.33
LSM 6	9.7	13.8	0.24	0.35
RP 7	51.1	26.7	0.26	0.25
LP 7	47.8	42.2	0.27	0.21
RSM 7	16.7	15.5	0.25	0.23
LSM 7	13.8	12.8	0.25	0.33
RP 8	48.1	56.7	0.17	0.08
LP 8	53.5	54.0	0.22	0.09
RSM 8	18.2	12.4	0.33	0.21
LSM 8	17.6	12.5	0.29	0.25
M (P)	34.3	32.9	0.28	0.25
SD (P)	11.1	11.9	0.10	0.11
M (SM)	15.0	13.2	0.33	0.34
SD (SM)	2.9	3.2	0.13	0.12
M (Tot)	25.7	24.1	0.31	0.30
SD (Tot)	13.5	14.0	0.12	0.12

The average organ dose per administered activity (ODpA) values were 0.28 Gy/GBq and 0.33 Gy/GBq for the parotid and submandibular glands using the absorbed fraction method ²⁵ and 0.25 Gy/GBq and 0.34 Gy/GBq, respectively for the 3D-RD method. The volume and ODpA values obtained with the two methods are compared, gland to gland, in Table IV (3D-RD ODpA values are only those calculated using D_self, in order to provide a better direct comparison between the methodologies).

With the 3D-RD calculation, a relatively smaller volume and a relatively larger ODpA for the submandibular glands was observed. Since the two quantities are related to each other (D ~ 1/m, where m is mass), it was reasonable to assume a correlation. The difference in volume (Delta V) estimation between the two methods for each gland was plotted versus the difference in ODpA (Delta ODpA) as shown in Figure 6. The results were fit to a linear model for the submandibular and parotid glands independently. However, from Figure 6, the slope of the linear fit is actually positive rather than negative for the submandibular glands, and neither the parotid, nor the submandibular fits are significant with respect to their squared correlation coefficients (r²=0.08 for the parotid glands and r²=0.28 for the submandibular glands). Therefore, there appears to be no relation in evidence for a simple cause-effect relationship between the difference in volume and the difference in ODpA between the two methodologies.

Figure 6.

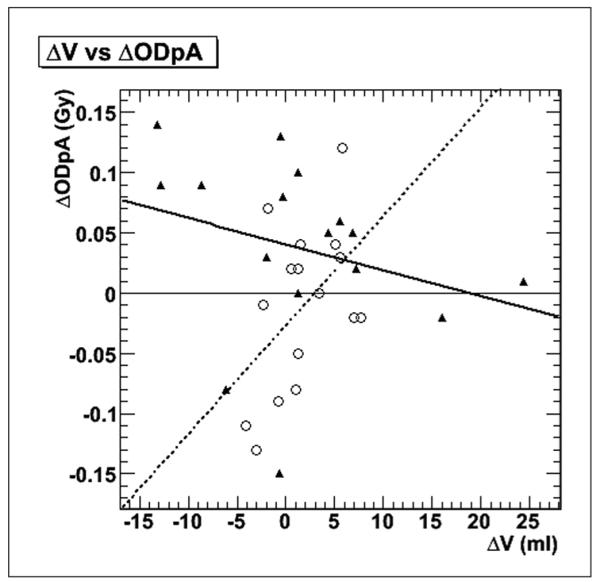
Gland-by-gland comparison of volume difference versus ODpA difference between methods. The white circles and dotted line are for the submandibular gland results, while the black triangles and solid line represent the parotid gland data and fit.

Radiobiology

The relatively low absorbed dose values meant that the BED values were only slightly larger on average, 2.41 Gy BED per salivary gland vs. 2.26 Gy absorbed dose. In particular, the contribution from the neck-high uptake region, D_ext, was absorbed BED effect over a prolonged period of time, with a low dose rate, and therefore the BED “effect”, or difference, between the BED and absorbed dose is not enhanced by the addition of D_ext. This is illustrated in Figure 7, where the quadratic nature of BED is made evident by plotting the square root of the difference between the BED and the absorbed dose components. For the self-dose component, D_self, a stronger correlation for the linear fit is obtained (r²=0.80), than for the external component D_ext (r²=0.61).

Figure 7.

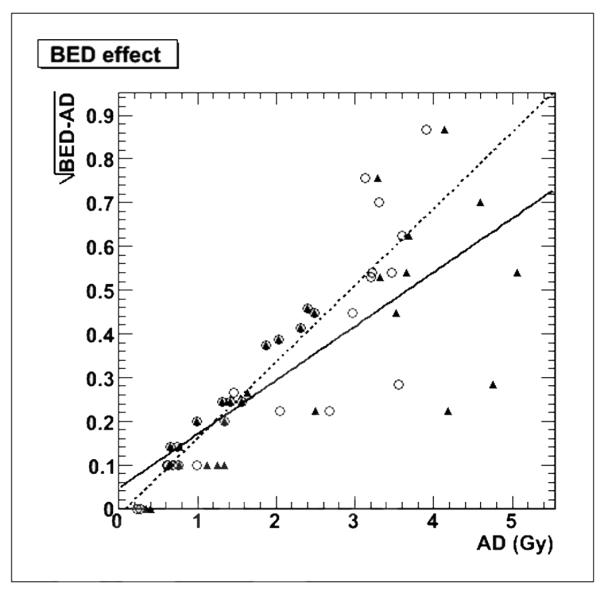
Measure of the BED effect by plotting the square root of the BED - absorbed dose difference as a function of D_self (white circles and dotted line) and the total absorbed dose including D_ext (black triangles and solid line). The overlapping triangles and circles exist for the three patients with no calculated D_ext.

Furthermore, the voxel average absorbed dose and BED values are not necessarily identical to the values calculated as a whole, which is not surprising considering the non-linear nature of the dose rate plots (Figure 3) For the same reason, the sum of D_ext and D_self are not necessarily equal to D_tot, calculated separately.

Discussion

RCs

The RCs were established from phantom data with spheres containing uniform activity concentrations. Activity inhomogeneities, as well as the size and shape of the VOI, could potentially affect the real VOI RCs. This is true for our method, but is also the constraint for all PVE correction methodologies, which assume spherical shape, homogenous activity distribution and a minimal size of the volume of interest. A constraint that was not factored in, which is included in most of the PVE correction methods, was the background contribution, or the spill-in effect of background activity. The assumption was that though this might be a factor in the precision of the RCs (20), the uncertainty due to the heterogeneity of the uptake was a much greater factor, therefore the spill-in effect was not of prime concern. Another concern is that in correcting the activity values within the VOIs without relocating the activity from outside the VOIs, there is still an artificial excess of activity remaining on the perimeter which contribute a small amount of absorbed dose to the VOIs. Thus the RC method used here could potentially slightly overestimate the dose to the VOIs. Here again, methodologies exist that relocate the activity, but still under the assumption of spherical shape, homogenous activity distribution and a minimal size of the volume of interest.³⁸

Methodological considerations for comparison

The UDE methodology has been described previously; briefly as a reminder and to better situate the result comparison, it consisted of: 1) approximating the gland geometry as spheres; 2) fitting the time activity curves to the entire salivary glands with trapezoids with a truncation at 96 h to obtain time-integrated activity; and 3) estimating the mean absorbed dose from time-integrated activity and salivary gland volume using empirically established formulas for both the beta and gamma contributions. A correction for partial volume effects (PVE) was also applied, using the isovolume.

The values from the absorbed fraction method, including beta and gamma contributions, were calculated by the UDE, and are referred to as ODpA_UDE.²⁵ The overall fluctuations can be attributed to differences in methodology, such as: 1) the use of trapezoids rather than exponential pieces between the 4 h and 24 h time points; 2) truncation at 96 h; and 3) differently drawn contours, but also to differences in implementation, such as coregistration. For the 3D-RD calculation, the emission images were registered to each other, the CT was registered using the same transformation parameters as for the associated PET. The coregistration of activity was deemed preferable for accurate dosimetry, considering the low resolution of the attenuation maps, particularly if voxelized data need to be examined. The absorbed fraction method registered each activity time point individually to the CT using the PET transmission images as a bridge to co-register PET emission and CT images, and subsequently, performing a manual fine tuning coregistration of the emission and CT images to ensure optimal spatial alignment.^{25, 39} However, to first order, in spite of the multiple minor differences in methodology the agreement between results is quite good (Table IV), which certainly confirms the order of magnitude of the calculated absorbed dose values and hence the discrepancy between expected and observed toxicity.

External activity contributions

The greater absorbed dose values in the submandibular glands can be partly attributed to the proximity of regions of mainly high prolonged thyroidal or nodal activity uptake. The external dose contribution, D_ext, to these glands takes on a different aspect as evidenced by comparing Figure 5B with Figure 5A. Figure 5A, for a patient with no large proximal source of dose contribution, shows a typical absorbed dose pattern very similar to the inhomogenous activity uptake, while in Figure 5B, the external dose contribution, D_ext, shows a higher dose in the inferior voxels of the glands, those closest to the high uptake tumor. Moreover, Figure 3B shows that the temporal variation of D_ext also differs from D_self: the regions of high uptake have much longer half-lives, which maintains a more consistent dose rate out to much later times.

This illustrates one of the advantages of the 3D-RD method which takes into account dose contributions in the vicinity of the target, but not explicitly within the target VOI. It also justifies the longer time scale used for dose integration, since if tumors or nodes with uptake proximal to the salivary glands are present their uptake and clearance will tend to take place over a longer time scale.²⁴

Although the modeled contribution from the rest of body background activity did not result in any significant contribution to the salivary gland absorbed dose, these calculations were only for estimated rest-of-body activity levels which are relatively low and which have a short half-life. For regions of higher uptake outside of the field of view, such as large tumors, thyroid remnants, or extensive lung metastases, it is possible that there may indeed be a non-negligible contribution to the salivary gland dose, although it is highly unlikely to be a major contributor.

In sum, the additional methodologies employed here did not raise the AD values to the expected values commensurate with salivary gland toxicity and still remain about 5-10 times lower than expected. This discrepancy has previously been detailed by Jentzen et al.¹⁴ who quantified the discrepancy by comparing absorbed fraction-based results with the results from external beam therapy, where an absorbed dose value of 60 Gy is associated with a complete loss of salivary gland function.^{40, 41}

Voxelization

The voxelized results must be examined with a number of caveats. First, PVE corrections only make sense at the gland level. At the voxel level, there exists not only an overall correction factor but also a redistribution of activity (and consequently dose, though not in identical manner). The PVE issue is further complicated with the addition of the external source. For certain patients (patient 4 in particular), the source was nearly adjacent to the salivary glands, resulting in spill-out from the tumor localized in the salivary glands at later time points and considered as D_self, as well as spill-out from the salivary glands considered as contributing to D_ext.

In general, voxelized results contain an element of uncertainty, given that the registration over time is not accurate at the level of the voxel, and the resolution of activity is only on the scale of the voxel dimensions. However, while individual voxel results are questionable, taken as a whole they may provide valuable insight into the dosimetry of the VOI.

Conclusions

The purpose of this work was to examine the possible source of discrepancies between observed clinical toxicity and calculated dosimetry. The 3D-RD methodology accounts for dose contributions from external sources, which may contribute long-lived components to the absorbed dose and BED and should not be neglected. However, neither the use of the BED nor the external sources of absorbed dose were sufficient to explain the observed salivary glands toxicity, although the addition of D_ext did increase the total absorbed dose significantly. The issue of potential localized hot spots of activity within the salivary glands has not been adequately addressed by this study and requires further investigation. Further studies could also involve micro-dosimetry and modeling of the epithelium of the intralobular ducts ^42-45 to ascertain the absorbed dose (and BEDs) at smaller scales.