Estimating the Repeat Structure and Length of DNA Sequences Using ℓ-Tuples

Abstract

In shotgun sequencing projects, the genome or BAC length is not always known. We approach estimating genome length by first estimating the repeat structure of the genome or BAC, sometimes of interest in its own right, on the basis of a set of random reads from a genome project. Moreover, we can find the consensus for repeat families before assembly. Our methods are based on the ℓ-tuple content of the reads.

Whole-genome shotgun sequencing began in 1995 with the TIGR publication of the 1.83-Mb sequence of Haemophilus influenzae (Fleischmann et al. 1995). This approach has become increasingly common for genomes of various sizes, and shotgun sequencing of BAC clones is now routine. In many cases, the genome sizes are not known precisely, and in the case of BAC sequencing, the clone size can vary greatly.

In the process of shotgun sequence assembly, reads of length ∼600 bp are sampled randomly from a DNA clone library. In traditional sequencing, using the sequences of those reads, pairwise overlaps are calculated, and then read layout is determined, and finally, the consensus sequence is deduced. This yields an estimate of the original DNA sequence. In 1988, Lander and Waterman (Lander and Waterman 1988; Waterman 1995) described the statistical issues of this process. They model the left (right) ends of reads as a Poisson process, and give formulas for the expected properties of the project. In 1995, Idury and Waterman (Idury and Waterman 1995) proposed a new algorithm for shotgun sequencing. By combining the shotgun sequencing data with the algorithmic ideas from sequencing by hybridization, their algorithm gave an entirely new approach to assembly using ℓ-tuples from the reads. Later, Pevzner et al. (2001) proposed methods for read error correction and carried on that set of ideas.

In this study, we try to solve the following problem. Assume N reads are drawn randomly from the clone library for an unknown DNA sequence. For simplicity, assume all reads are L base-pairs long. Furthermore, assume the unknown coverage is at least 2×, that is,

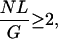in which G is the length of the DNA. Under those assumptions, can we estimate G? Moreover, can we tell how many families of repeats there are in the sequence? Also, what fraction does each family of repeats account for in the overall sequence? Here, a family of repeats means a set of highly similar substrings occurring at different locations in the sequence. Of course, the frequency of similar substrings is very different for different families, as are the lengths.

To understand the problem better, here is an example. Assume 1% of the genome is composed of substrings that are repeated 10 times, 2% that are repeated 12 times, 7% that are repeated 40 times, and 90% of the genome is unique sequence. The genome is 5-Mb long. Then, can we give an approximate estimate of those numbers given a set of reads that cover the genome at least 2×?

In the following, we use ℓ-tuples from reads for the purpose of estimating the length and the repeat structure of the DNA being sequenced. Moreover, we will give the consensus for each repeat family. Our method has other applications. It can be used to mask out the reads sampled from repeat regions of the genome before assembling reads sampled from unique regions, even without any prior information about the repeats in the genome. In addition, by using the advanced algorithm, we can provide useful information for assemblers. Furthermore, the advanced algorithm is useful to find the biologically meaningful repeats in a genome.

RESULTS

Assuming that the left ends of reads consist of a Poisson process, we have shown the occurrence numbers of ℓ-tuples form mixture Poisson samples by choosing ℓ properly (see Methods section). Using the EM algorithm (Mclachlan et al. 1997, Lange 1998) to decompose those mixture Poisson samples, the basic algorithm can find the coverage of the reads and the repeat structure of the genome. Moreover, we have the advanced algorithm to find the consensus of repeats in the genome on the basis of a set of random reads. In the following, we will show the results on simulated data first, then consider the result on 1674 real reads from a BAC, H_NH0140H23.

Positions of Repeats in the Sequence

To test the fact that the result of the basic algorithm has no relation to the positions of repeats, given that reads are randomly chosen from the genome, we generate the starting positions of repeats in the original sequence in two ways. One is to generate the starting positions of repeats randomly. The other is to let repeats appear in tandem. In both cases, the algorithm gives good results. Next, we illustrate this with two examples.

Example 1

The genome length is 100 kb, each read is 500-bp long, and the coverage is 3×. There are two families of repeats. One is 2-kb long with 15 copies, whereas the other is 2-kb long with 7 copies (i.e., ĉ₁ = 21 and ĉ₂ = 45). Repeats appear randomly in the original sequence. Our result is as follows. The estimated genome length is 98,371 bp. The estimated coverage is 3.05×. The unique sequence accounts for 56.8% of the genome. There are two families of repeats, one of which has 7 copies and accounts for 13.1% of the sequence, whereas the other has 15 copies and accounts for 30.1% of the sequence (i.e., ĉ₁ = 20.34 and ĉ₂ = 43.92).

Example 2

The genome length is 100 kb, each read is 500-bp long, and the coverage is 3×. There are two families of repeats. One is 2-kb long with 15 copies, whereas the other is 2-kb long with 7 copies (i.e., ĉ₁ = 21 and ĉ₂ = 45). Repeats appear in tandem in the original sequence. Our result is as follows. The estimated genome length is 97,087 bp. The estimated coverage is 3.09×. The unique sequence accounts for 47.5% of the genome. There are 2 families of repeats, one of which has 7 copies and accounts for 17.2% of the sequence, whereas the other has 13 copies and accounts for 35.3% of the sequence (i.e., ĉ₁ = 20.6 and ĉ₂ = 39.24).

The above examples show that the estimates have no relation to the distribution of the positions of repeats in the original sequence. This results from the fact that the positions of left ends of reads are random in the sequence. No matter where the repeats appear, they have the same chance to be covered by reads.

The Number of Independent ℓ-Tuple Observations Has Great Effects

In general, if we have enough reads, we always can separate two families of substrings efficiently, no matter how similar they are. Following are two examples, each with 3× coverage, that challenge the method. In Example 3, we cannot distinguish the two families of tuples very well, but in Example 4, we can. Note that the genome size in Example 4 is 10× as long as that in Example 3. That is, we have more independent ℓ-tuple observations for the repeat families in Example 4. In fact, simulation shows that we cannot separate the observations by the basic algorithm if half of the observations are from Poisson variable with intensity 2 and the other half from Poisson variable with intensity 4, even when the number of observations is 800, and those observations are independent with each other. However, we can do so when we have 8000 independent observations. That is, we may not be able to distinguish the two sequence families, of which one has two copies and another is unique, when the coverage is 2× and the DNA is about 800-bp long. But, we can do so when we have longer DNA sequence with the same percent unique and repeated sequences.

Example 3

The genome length is 80 kb, each read is 500-bp long, and the coverage is 3×. There are two families of repeats. One is 6-kb long with 2 copies, whereas the other is 1-kb long with 12 copies. Repeats appear in tandem in the original sequence. In more than 95% of the simulations, we obtain the following results: The estimated genome length is 73,104 bp; the estimated coverage is 3.283×; the unique sequence accounts for 82.7% of the genome. There is only one family of repeats, which has 12 copies and accounts for 17.3% of the sequence. For the remainder of the simulations, we may get similar fractions and copy numbers as those in Example 4.

Example 4

The genome length is 800 kb, each read is 500-bp long, and the coverage is 3×. There are two families of repeats. One is 60-kb long with 2 copies, whereas the other is 10-kb long with 12 copies. Repeats appear in tandem in the original sequence. Our result is as follows: the estimated genome length is 782,789 bp; the estimated coverage is 3.067×; the unique sequence accounts for 70.7% of the genome. There are two repeat families, one of which has 2 copies and accounts for 14.2% of the sequence, whereas the other has 12 copies and accounts for 15.1% of the sequence.

Another way to increase the number of independent ℓ-tuples is to increase the coverage. For the sequence in Example 3, if we let coverage be 10× instead of 3×, we obtain the following results: The estimated genome length is 79,289 bp; the estimated coverage is 9.928×; the unique sequence accounts for 57.3% of the genome. There are two repeat families, one of which has 2 copies and accounts for 27% of the sequence, whereas the other has 12 copies and accounts for 15.7% of the sequence. Note that a large set of observations for the unique tuples has been considered as those for the first repeat family. No matter how much we increase the coverage, this will not change much, due to the fact that the substrings from the first repeat family are repeated only twice.

In summary, the more independent ℓ-tuples there are, the better our estimate for the coverage should be. But how can we know whether the number of independent ℓ-tuples is large enough? In general, if we have a set of samples and we find that the group i for i = 1, 2,..., groupNum are distributed very sparsely, no matter what number we choose as the tuple length, we should infer that either our samples are somehow biased or our sample size is too small.

Different Nucleotide Distributions

Our method is based on the random locations of reads along the sequence. In other words, the left ends of reads are uniformly distributed along the sequence. Therefore, our result really has no relation to the distribution of the nucleotides in the sequence. Following are two examples in which the DNA sequence is 80 kb, each read is 500-bp long, and the coverage is 3×. There are two repeat families, one is 800-bp long and has 5 copies, whereas the other is 800-bp long and has 15 copies. In the first example, the distribution of nucleotides is Pr(A) = Pr(G) = Pr(C) = Pr(T) = 0.25. In the second example, Pr(A) = 0.10, Pr(C) = 0.15, Pr(G) = 0.2, Pr(T) = 0.55. The results for both examples are the same, because the positions of the repeats are the same in the sequence. The result is as follows: The estimated coverage is 3.004×, the estimated length of the sequence is 79,886, and there is an estimated 79.4% unique sequence. There are two repeat families: One has 5 copies and accounts for 4.7% of the sequence, the other has 16 copies and accounts for 15.9% of the sequence.

Real Experiments

In practice, there are some errors in reads. Will that restrict the applications of the basic algorithm? Fortunately, Pevzner et al. (2001) introduced a method to do the error correction for us; therefore, we use the basic algorithm on the reads after error correction.

The data is as follows: The original sequence is the consensus of the insert of a BAC, H_NH0140H23, with 103,432 bp. After error correction, we have 1674 reads that share >90% similarity to the consensus. Actually, we have 3328 corrected reads, but we can find only 1674 reads sharing >89% similarity to somewhere in the consensus. We doubt that there are some reads from other BACs. On the other hand, the consensus provided at NCBI is said to be expected longer or shorter. Following is the summary statistics of those reads. Minimal read length is 101 bp; maximal read length is 777 bp; mean of read length is 507 bp; median of read length is 553 bp, and standard deviation is 148 bp.

Those 1674 reads cover the consensus ∼8.27 times on average. There are 1465 reads occurring exactly in the consensus of the BAC, and 209 reads sharing >90% similarity to some substrings of the BAC.

In Table 1, numbers in the second column are the results from using basic algorithm on 609 real reads, which are randomly chosen from the 1674 real reads (see Supplemental Material, available online at www.genome.org). For the third column, we randomly chose 1674 positions in the consensus as the starting positions of reads and make those simulated reads have the same length distribution and the same rate of error bases, and then calculate the numbers using the basic algorithm. (We use 12-tuples in the basic algorithm.) For the fourth column, we counted 12-tuples in the consensus and found 50% 12-tuples are unique, 14% occurred twice, 21% occurred three times in the consensus. For the fifth column, we found repeat sequences by using the REPuter (Kurtz et al. 2001).

Table 1.

The Efficiency of the Basic Algorithm for the Repeat Structure

Substring family	Real reads	Simulated reads	Count 12-mer with errors	REPuter
unique	66.1%	47.8%	50%	69.33%
repeated twice	16.46%	11.99%	14%	14.78%
repeated 3 times	0%	22.11%	21%	15.89%
repeated 4 times	14.25%	4.24%	4%	0
repeated 5 times	0%	4.39%	3%	0
the rest	3.19%	9.47%	8%	0

There are many factors making the estimation on the basis of the real reads a little bit different from others. The most critical one is that the reads are too far away from random. Even the 609 real reads are not so random, as the Kolmogorov-Smirnov Goodness-of-Fit (Stevens 1986) Test gives the P-value 0.337. Moreover, we know there are totally 10,185 bp in 12 intervals without any read covered, the longest of which is 4757 bp, even in original 1674 real reads.

In summary, the basic algorithm can tell us the basic repeat structure of the genome. Moreover, the estimated genome size is 103,696 bp and the estimated coverage is 2.945×, which are close to the corresponding real values 103,432 bp and 3.018×, given the fact that the reads are not uniformly distributed in the BAC.

Finding the Consensus for Repeats

The repeat structure given by the basic algorithm is the description of the genome by using the occurrence numbers of ℓ-tuples. Sometimes it is more biologically meaningful to show what the repeat sequences are. In the following, we try to find the repeat sequences from the reads in a very simple way. We use the advanced algorithm, which is based on two simple observations.

1. For a repeat family, there are at least a few ℓ-tuples appearing an unusual number of times in reads. Otherwise, the fraction of this repeat family can be neglected, due to its low-copy number and short length.

2. If there are no errors in the reads, we can separate reads covering different copies of a repeat family into different groups by starting from one read and extending it when there are more than a predefined number of reads with their prefixes exactly the same as the suffix of the read we are considering.

After calculating the coverage from reads, we can find very long suspect regions for repeats on the basis of observation 1, and the second observation can help us extend the repeats from the suspect regions and obtain different instances of each repeat family, and thus obtain the consensus of the repeat family. After we obtain the consensus for each repeat family, we have two ways to estimate the copy number for each repeat family. The first is to calculate the sum of the length of reads similar to each consensus and then divide it by the estimated coverage. The second way consists of two steps. First, for a given consensus, find left reads whose suffixes are similar to the prefix of the consensus. Similarly, find the middle reads that are similar to some substring in the middle of the consensus, and the right reads whose prefixes are similar to the suffix of the consensus. Second, use those reads to build a graph, in which a vertex is a read and there is a directed edge from vertex i to vertex j; if the suffix of read i is the same as the prefix of the read j and the overlap is larger than a statistically given threshold, then find all paths starting from a left read and ending at a right read.

The advanced algorithm has two advantages compared with the Euler assembler. First, from the beginning we are focused on some special regions that are parts of the repeats. Therefore, we have minimized our difficulties by minimizing the size of the problem. Second, when we consider a repeat family, there is no need to resolve the repeat graph. We are trying to find at least two different paths that (partially) represent two instances of the repeat family. From those paths, we can estimate the consensus, and then the copy number of the repeat family, by using the coverage and then all other paths sometimes. However, the Euler assembler must locate all four paths if there are four. Sometimes it must fail to do this.

We tested our algorithm on simulated data first. Our simulation parameters are as follows: the genome length is 80 kb, each read is 500-bp long, and the coverage is 3×. There are two families of repeats. One is 700-bp long with 27 copies, whereas the other is 300-bp long with 53 copies. In the genome sequence, any two copies of the repeat is at least 100-bp apart. Then, we use our advanced algorithm and obtain the following result. The estimated genome length is 81,561 bp. The estimated coverage is 2.94×. There are two repeat families, one of which is 704-bp long with 28 copies and the other is 305-bp long with 49 copies.

Next, we use REPuter (Kurtz et al. 2001) to find repeat sequences and their positions in the consensus of the BAC, H_NH0140H23. We found the seven repeat families (see Supplemental Material).

Next, we use the 1674 reads directly to find the consensuses. We can only find the seventh repeat family, as other repeat regions are poorly covered or not covered at all. Note that we can find coverage, genome length, and sometimes even repeat structure very precisely, even when there are some regions uncovered by any read by using the basic algorithm, due to the Poisson process property, as is shown above. However, the advanced algorithm really depends on the good random locations of reads and the good coverage of the genome. Therefore, it is still a naive idea that may be used to provide useful information in the process of assembly.

On the other hand, however, the advanced algorithm is so powerful that it can be used to find the biological repeat structure of a genome when the genome sequence is given. To our knowledge, REPuter cannot find repeats in a genome by inputting phrases such as “finding repeats sharing 90% similarity” because of the suffix tree structure, whereas the advanced algorithm can be implemented in this way naturally. With the genome sequence given, we can generate reads uniformly across the genome with some coverage, for instance, 3×. Then, we can use the advanced algorithm. Because the algorithm is based on ℓ-tuples, it has linear time complexity. Our preliminary test shows that we can find more consensuses than REPuter, which are biologically more meaningful (X. Li and M.S. Waterman, unpubl.).

METHODS

Mixture Poisson Samples

Let us consider a given DNA sequence. If we can choose ℓ, such that almost all ℓ-tuples appear only once in the sequence if they appear at all, then, by counting how many different ℓ-tuples there are in the reads, we can have a good estimate of the length of the sequence. This is by assuming that the sequence is random with letters generated independently. However, there may be many repeats in the sequence (Primrose 1998), such that many ℓ-tuples appear twice or more in it, even if ℓ is quite large. In this case, the number of different ℓ-tuples in the reads should be much smaller than the number of nucleotides in the sequence. However, if we know how many times each ℓ-tuple is repeated, and what fraction of the sequence it accounts for, we can estimate the sequence length. That is, we may have to estimate the repeat structure and coverage in order to estimate the sequence length.

Note that there is a confounding between genome duplication and coverage. A 3× coverage of a duplicated genome would, by our methods, be estimated at 6× coverage of half of the duplicated genome. But in practice this seldom occurs, and there are some unique substrings in the genome in most cases.

Recall that we obtain the number of a tuple's occurrence from N reads instead of the original sequence for an ℓ-tuple appearing in the sequence. Because the reads are chosen randomly from clone libraries, their positions in the original sequence are random, as is the number of occurrences of any ℓ-tuple in the sequence. Let us consider the distributions of those random variables first.

Here is our formulation of the problem. Assume we know the coverage,

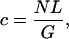of the genome by those N reads. Also assume that an ℓ-tuple in the sequence cannot appear twice or more in any read, that is, any two copies of an ℓ-tuple are at least L base-pairs apart in the original sequence. For a given ℓ-tuple, for instance, w, that appears in the sequence n(w) times, how many times will it appear in N reads?

Assume x_i(w) is the number of reads that cover the i-th copy of w, in which i is from 1 to n(w). Then, w appears x_n(w)(w) times in the reads. Please note that x_i(w), i = 1,..., n(w), are i.i.d. They are independent, due to the assumption that a read cannot cover two adjacent copies of w. The fact that they have identical distributions follows from the homogenity of the Poisson process5. Assume the parameter of the Poisson process is λ, in which

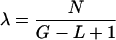(Lander et al. 1988). Obviously, the distribution of x₁(w) is Poisson with parameter λ(L - ℓ + 1). Due to the additivity of Poisson process, the distribution of x(w) is Poisson with parameter n(w)λ(L - ℓ + 1).

Unfortunately, for any given ℓ-tuple w in the sequence, what we have is not a multiset of {x_i(w)│i = 1,..., n(w)}, but x(w), the sum of the elements in the multiset. That is, there is only one observation for w. Clearly, we cannot get good estimates for n(w) and λ by using only x(w). Fortunately, there may be many ℓles appearing n(w) times in the sequence, for some n(w). For example, there are many unique tuples in the original sequence, that is, there are always many ℓ-tuples for n(w) = 1. Therefore, we can use all observations from those ℓ-tuples, that appear approximately n = n(w) times in the original sequence, as samples of w. We will refer to these tuples as those of family n. Recall that the number of occurrences of those ℓ-tuples may not be independent, although they have the same distribution. Assume w₁, w₂,..., w_m are those ℓ-tuples appearing n(w) times in the original sequence. At first glance, it appears incorrect to use

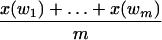as an approximation to n(w)λ(L - ℓ + 1). But, as the length of reads is fixed and very small compared with that of the sequence, and any of those random variables is dependent on at most L - ℓ + 1 of others, we know

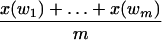will approach n(w)λ(L - ℓ + 1). When m is large, we can use the former to approximate the latter.

Therefore, if we assume there are k families of tuples in the original sequence, the number of occurrences of any tuple in the reads from the i-th family is a Poisson random variable with parameter a_ic̄, in which c̄ = λ(L - ℓ + 1) is the coverage and a_i is an unknown integer. Moreover, we assume the different tuples in the i-th family account for α_i × 100% of all different tuples in the original sequence. Then, we can rephrase our problem in a more mathematical way; if we have a set of samples from a mixed Poisson distribution, and some of the samples are dependent, can we estimate a_i, α_i, and c̄ for i = 1, 2,..., k?

The above problem is well known as the mixed-proportion problem in statistics (Mclachlan et al. 1997) when the samples are independent. For the mixed-Poisson proportion problem, it is very easy to get the following formulas (Lange 1998):

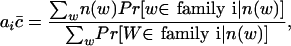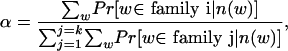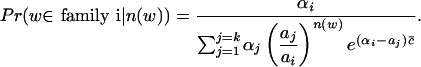Note that there are two conditions that our problem does not satisfy. The first is that we have no data for w with n(w) = 0 in order to use the formulas. That is, we do not know group 0 if we assume there are group i tuples in the sequence, which appear i times in the reads, for i = 0,..., groupNum6. But, we can use the following formulas to estimate group 0.

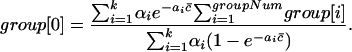The second condition not satisfied is that our samples are not independent. Fortunately, any one of them is dependent on at most L - ℓ + 1 others. Because the size of samples in each family is much larger than L - ℓ + 1 (otherwise, we are not interested in such repeat families), we can use the above recursive formulas. Moreover, we will use the following formulas to calculate the length of the sequence and the percentage of each family of substrings. The length of the sequence in our problem is calculated by the last formula below.

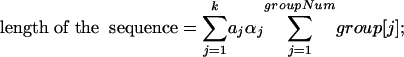or

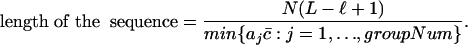Basic Algorithm

1. Set a large number for k and a proper number for ℓ;

2. Calculate group j, for j = 1, 2,..., groupNum;

3. Set an initial value for c̄, a_i and α_i, respectively for i = 1, 2,..., k. Set d to be 1.

4. While (d > 1 × 10^-3)

   1. Calculate group 0;
   2. Calculate the new values for c, a_i, and α_i, respectively for i = 1, 2,..., k;
   3. Calculate d, which is the sum of the square of the distance between new c̄, a_i, and α_i and corresponding old ones for i = 1, 2,..., k.

5. Calculate the percentage of each family of substrings from c̄, a_i, and α_i for i = 1, 2,..., k; and calculate the length of the sequence.

How to Choose ℓ and k

As we stated above, we should let ℓ be large enough such that many ℓ-tuples in the original sequence are unique tuples. That is, when the DNA is G-base pairs long, ℓ should satisfy 4^ℓ > G if the sequence is generated from a uniform i.i.d. mechanism. If the sequence is from a nonuniform i.i.d. mechanism, we should let

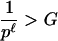in which p is the probability that the most frequent nucleotide will appear at a given position.

On the other hand, we cannot let ℓ be too large. For instance, if we let ℓ = L, then there are N tuples in all. And each ℓ-tuple appears once in the reads in general. Then, our estimation of c̄ is 1. That is not what we want and is incorrect. Moreover, in some sense, the larger that ℓ is, the fewer the number of samples, and the less accurately we can estimate c̄, a_i, and α_i for i = 1, 2,..., k. Therefore, ℓ must be large, but not too large.

How large should ℓ be? Let us consider a given DNA sequence. Assume there are n_i tuples appearing i times in the sequence, for i = 1, 2,..., k. Recall we used

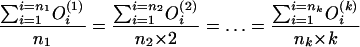to approximate c̄ in the above algorithm, in which 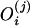is the number of occurrences of the i-th tuples that appear j times in the sequence. By summing up the above denominators and nominators, we actually use

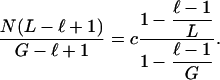1

to approximate c̄. That is, the theoretical c̄ satisfies the following formula:

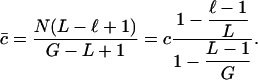2

When L ≪ G, our calculation is almost the same as the theoretical one. Because we do not know G, we prefer to use the calculated c̄ to approximate c. Under such considerations, we should let ℓ be as small as possible.

Table 2 gives an example showing how ℓ affects our estimation. In this example, the original sequence is 80 kb, 55% of which are unique ℓ-tuples. There are two kinds of repeats. One is 6-kb long, repeated 4 times; the other is 1-kb long, repeated 12 times. From the above analysis, we know it is better to choose ℓ to be 11 or 12, and this agrees with the experimental results. Moreover, from the above formula, we know that the estimations for coverage become less accurate when ℓ increases to some degree. Similar phenomena occur in column c₁, c₂, and c₃.

Table 2.

The Effect of Tuple Length

ℓ	G/4ℓ	ĉ1	% Unique	ĉ2	% Repeat1	ĉ3	% Repeat2	Ĝ
9	3.1e-001	3.14	49	12.17	34	38.97	17	76433
10	7.6e-002	3.03	52	12.08	31	38.65	17	79207
11	1.9e-002	3.00	53	12.07	31	38.49	16	79980
12	4.8e-003	2.99	53	12.04	31	38.36	16	80268
13	1.2e-003	2.98	53	12.02	31	38.29	16	80537
14	3.0e-004	2.97	53	11.99	31	38.22	16	80808
15	7.5e-005	2.97	53	11.97	31	38.14	16	80808
16	1.9e-005	2.96	53	11.94	31	38.06	16	81081
17	4.7e-006	2.96	53	11.91	31	37.98	16	81081
18	1.2e-006	2.96	53	11.89	31	37.90	16	81081
19	2.9e-007	2.95	53	11.86	31	37.82	16	81356
20	7.3e-008	2.95	53	11.84	31	37.74	16	81356
21	1.8e-008	2.94	53	11.81	31	37.66	16	81633
22	4.5e-009	2.94	53	11.79	31	37.58	16	81633
23	1.1e-009	2.93	53	11.76	31	37.50	16	81911
24	2.8e-010	2.93	53	11.73	31	37.42	16	81911

ĉ₁, ĉ₂ and ĉ₃ are estimates of the average number of occurrences (in the reads) of the first, second, and third family of tuples, respectively. Here, the first family of tuples are unique ones. The numbers under the column named unique, repeat1, and repeat2 are the percentages of sequences that belong to the unique part, the first repeat family, and the second repeat family, respectively

Next, let us look at how to choose k. At first glance, choosing k seems difficult. However, the fact is that we only need to choose a large number for k. Table 3 shows the result of using different k for the above setup.

Table 3.

The Effect of the Number of Families

k	ĉ1	% (1)	ĉ2	% (2)	ĉ3	% (3)	ĉ4	% (4)	ĉ5	% (5)	Ĝ
1	4.81	100									48684
2	3.07	56	16.84	44							78175
3	2.98	53	12.02	31	38.29	16					80537
4	2.98	51	2.98	2	12.02	31	38.29	16			80537
5	2.98	51	2.98	2	12.02	23	12.02	8	38.29	16	80537

The numbers under ĉ₁, ĉ₂, ĉ₃, ĉ₄, and ĉ₅ are the average number of occurrences (in the reads) of the first, second, third, fourth and fifth family of tuples, respectively. The numbers under (1), (2), (3), (4) and (5) are the percentages of ℓ-tuples from the first, second, third, fourth, and fifth family of tuples, respectively. Ĝ is the estimated genome length. In all experiments, ℓ = 11

If we increase the number of families, we will get similar results. That is, after arriving at the correct number of families, we will divide some into subfamilies with almost the same coverage. Moreover, the sum of the percentages that those subfamilies account for is the percentage for which the original family accounts. Therefore, by increasing k one by one from 1 and running our algorithm for each k, we discover how many repeat families we should choose.

Advanced Algorithm

1. Choose k and ℓ as we did in the basic algorithm;

2. Define suspect regions in each read according to the frequency of tuples in the region and the length of the region;

3. While (there is a suspect region in any read),

   1. Select the longest suspect region and collect all the reads that contain at least one tuple in the suspect region;
   2. Do an Eulerian tour by using those reads and output the possible paths;
   3. If (the number of paths is larger than 2)
      1. Choose the best path from those paths by finding the one with maximal sum of the similarity scores of pairwise alignments of it and all chosen reads;
      2. Find pairwise alignment between other paths and the best path;
      3. Get the multiple alignment and output the core consensus;
      4. Extend the core consensus as long as possible;
      5. Compare reads with the consensus and redefine the suspect regions;
      6. Compute the copy number for the current repeat;
   4. Delete the current suspect regions that are similar to the current repeats;

4. Define the unique part in each read by comparing with all consensuses;

5. Use basic algorithm to find the coverage from the unique part;

6. Calculate the length of the genome.

Note that the alignments in the algorithm are banded alignments, because we know the starting position of the alignments. Therefore, the alignments can be done in linear time. Finding Eulerian tours is also a linear algorithm, in which we walk from read to read on the basis of the sharing of tuples. So, the advanced algorithm is very fast.

DISCUSSION

There are many factors affecting our estimates, of which the random locations of reads is the most important one. If they are too biased, we cannot achieve much. To get good estimates given a set of samples, we prefer to use the data many times, and each time we randomly choose a fixed fraction of samples. If the original samples are too biased, the results will have larger variance. If they are not biased, by summarizing those experiment results, we can get better results.

Beside the randomness of the samples, the initial values of our parameters have some effects. In general, we should let our initial coverage be larger than 1×. Otherwise, the estimated group 0 is so bad that it affects the following estimates, and the coverage, in general, will converge to an incorrect value. Therefore, our principle to set initial values is to begin with large initial coverage. As to the initial values of the number of occurrence of those tuples, we only need to use different numbers. In general, if we can try different starting points for the data and get consistent results, we are finished.

Although Pevzner et al. (2001) can remove many errors in reads, there are still some errors remaining. The largest error rate the basic algorithm can use is 0.0075. That is, if there are >7.5% errors per nucleotide in the reads, we cannot get good estimations.

Serious readers may find that we have not talked much about the repeats that appear many times in the genome, such as ALU in the human genome. We can use the algorithm in those cases as well. We suggest dealing with this case as follows. First, we use group i for i = 1, 2,..., M to estimate the coverage first, in which M is specified in advance. For example, M is <300. Then, we can estimate the copy numbers of tuples for frequently duplicated repeats by using the occurrence numbers of those tuples and the estimated coverage.

As for the advanced algorithm, it can always help to find the consensus for each repeat family, given that the genome or BAC is uniformly covered. Although in practice uniform coverage is seldom true, the advanced algorithm can give many repeat substrings. Sometimes it may give portions of a consensus sequence instead of the whole. However, all of this information will help our assembly. First, the advanced algorithm can be used as the repeat masker very efficiently. When we finished this work, we noticed that RePs (Wang et al. 2002) used a naive idea of the advanced algorithm to mask repeats. They count the occurrence numbers of each 20-mer in the reads. If the occurrence number of a 20-mer is larger than some threshold, they consider this 20-mer as the one from a repeat region. By the advanced algorithm, we can obtain the threshold in a more reasonable way. Second, the advanced algorithm is designed to find the consensus instead of assembling reads. It will benefit the assemblers if it is properly implanted into them. Moreover, preliminary tests show the idea that the advanced algorithm can be used to find the repeats in a given genome sequence. Further efforts will be spent to implement this to get the biologically more meaningful repeats.

There is much information we have not used in our simple setup. Our goal is to obtain as much information as possible before assembly. In the near future, we hope this idea can be incorporated into current assemblers.