Dragon Gene Start Finder: An Advanced System for Finding Approximate Locations of the Start of Gene Transcriptional Units

Abstract

We present an advanced system for recognition of gene starts in mammalian genomes. The system makes predictions of gene start location by combining information about CpG islands, transcription start sites (TSSs), and signals downstream of the predicted TSSs. The system aims at predicting a region that contains the gene start or is in its proximity. Evaluation on human chromosomes 4, 21, and 22 resulted in Se of over 65% and in a ppv of ∼78%. The system makes on average one prediction per 177,000 nucleotides on the human genome, as judged by the results on chromosome 21. Comparison of abilities to predict TSS with the two other systems on human chromosomes 4, 21, and 22 reveals that our system has superior accuracy and overall provides the most confident predictions.

As indicated by Fickett and Hatzigeorgiou (1997) and Pedersen et al. (1999), recognition of eukaryotic promoters remains a difficult problem. Numerous systems for promoter prediction have been developed (for reviews, see Fickett and Hatizigeorgiou 1997; Prestridge 2000), but the general conclusion is that the level of false positive (FP) predictions appears to be unacceptably high. The first breakthrough from such inferior performance was developed by the PromoterInspector program (Scherf et al. 2000), which reduced FP predictions to an acceptable level, while maintaining relatively high sensitivity (Se). The initially reported performance of PromoterInspector (Scherf et al. 2000, 2001) implied Se = ∼0.43 and a positive predictive value (ppv) of ∼0.43. However, in later research (Down and Hubbard 2002), it became apparent that PromoterInspector had in fact better overall performance, at least as measured on human chromosome 22. Also, Werner (2002) suggests that PromoterInspector has Se > 0.5 and ppv > 0.85. These last claims require proper validation, but we can conclude that PromoterInspector represented a breakthrough in promoter prediction.

After the appearance of PromoterInspector, several systems for promoter predictions were developed (Ioshikhes and Zhang 2000; Davuluri et al. 2001; Hannenhalli and Levy 2001; Bajic et al. 2002a,b, 2003; Down and Hubbard 2002; Ponger and Mouchiroud 2002) that resulted in an acceptably low level of FP predictions. These systems are based on different principles and do not share the same design goals. Some are aimed at recognizing the actual transcription start site (TSS), such as Dragon Promoter Finder (Dragon PF; Bajic et al 2002a,b, 2003) and Eponine (Down and Hubbard 2002). Others make predictions of a region that should be in proximity with the TSS, such as CpG-Promoter (Ioshikhes and Zhang 2000), the system of Hannenhalli and Levy (2001), and CpGProD (Ponger and Mouchiroud 2002). The third group of systems provides more comprehensive information about the promoters and first exons, such as FirstEF (Davuluri et al. 2001). All of these systems, with the exception of CpG-Promoter, have been compared with PromoterInspector in one way or another, and all reported better overall performance on the data sets that they used.

In the human genome, many genes were recognized and validated successfully (Lander et al. 2001; Venter et al. 2001) by using the so-called CpG islands as gene markers. CpG islands are unmethylated segments of DNA longer than 200 bp, with a G + C content of at least 50%, and the number of CpG dinucleotides being at least 60% of what could be expected from the G + C content of the segment (Bird et al 1986; Gardiner-Garden and Frommer 1987; Larsen et al. 1992; Cross and Bird 1995). CpG islands are found around gene starts in approximately half of mammalian promoters (Larsen et al. 1992; Cross and Bird 1995) and are estimated to be associated with ∼60% of human promoters (Cross et al. 1999). For this reason, Pedersen et al. (1999) suggested that CpG islands could represent a good global signal to locate promoters across genomes. At least in mammalian genomes, CpG islands are a good indicator of gene presence. Programs such as CpG-Promoter, the system of Hannenhalli and Levy 2001, CpGProD, and FirstEF explicitly use information on CpG islands in their promoter-finding algorithms, although the type of information varies from program to program.

Here we introduce a new system, Dragon Gene Start Finder (Dragon GSF), for predictions of promoters in mammalian genomes. This system uses information about the CpG islands, predicted TSS locations, and information about a region downstream of the predicted TSSs. This information is processed to infer promoter presence, give an estimate of the region expected to contain the TSS and to overlap with the first exon, and give an estimate of the gene start. This system is rigorously tested on genomic sequences of human chromosomes 4, 21, and 22. The system is compared in its ability to predict TSS locations with other systems that provide strand-specific prediction of TSSs, such as Eponine and FirstEF. In these tests, our system exhibited superior accuracy. Its overall performance appears to be, at the moment of this writing, the best of the currently available systems for gene start predictions. We estimate that the Se with respect to all promoters in the human genome is ∼0.65, with a ppv of ∼0.78, and the frequency of strand-specific predictions that our system makes is approximately one per 177,000 nt.

RESULTS

We analyzed the performance of Dragon GSF on three human chromosomes. No sequences from these chromosomes were used in the training and tuning of our system. We selected chromosomes 4, 21, and 22 for the analysis because of their different G + C contents in order to better understand the behavior of our system and the other systems when the G + C content varies. To obtain information about the relative performance of Dragon GSF, we compared it with the other two systems, FirstEF and Eponine.

The main results are summarized in Tables 1, 2, 3, 4, 5, 6, 7. Results are given with respect to several criteria related to the maximum allowed distance between the predicted TSS and the real TSS. In these experiments, Dragon GSF, FirstEF, and Eponine have been used with their default parameter settings (see Methods).

Table 1.

Results on Chromosome 4 With TSSs Determined Based on Mapped Full-Length cDNA Sequences From DBTSS (Sugano Laboratory)

	TP	FP	Total # of TSSs	Total # of predictions	Se	ppv	ASM	CC
Dragon GSF	179	55	304	1349	0.5888	0.7650	1.6364	0.6711
FirstEF	220	169	304	3620	0.7237	0.5656	3.4545	0.6398
FirstEF (CpG+)	217	110	304	2509	0.7138	0.6636	1.9091	0.6883
Eponine	120	36	304	2296	0.3947	0.7692	3.0000	0.5510

The maximum allowed distance between the predicted TSS and real TSS is 2000 nt

Table 2.

Results on Chromosome 21 With TSSs Determined Based on Mapped Full-Length cDNA Sequences From DBTSS (Sugano Laboratory)

	TP	FP	Total # of TSSs	Total # of predictions	Se	ppv	ASM	CC
Dragon GSF	62	17	89	383	0.6966	0.7848	1.2727	0.7394
FirstEF	74	108	89	1236	0.8315	0.4066	3.7273	0.5814
FirstEF (CpG+)	69	58	89	746	0.7753	0.5433	2.6364	0.6490
Eponine	46	16	89	816	0.5169	0.7419	2.3636	0.6193

The maximum allowed distance between the predicted TSS and real TSS is 2000 nt

Table 3.

Results on Chromosome 22 With TSSs Determined Based on Mapped Full-Length cDNA Sequences From DBTSS (Sugano Laboratory)

	TP	FP	Total # of TSSs	Total # of predictions	Se	ppv	ASM	CC
Dragon GSF	134	35	183	898	0.7322	0.7929	1.2727	0.7620
FirstEF	159	199	183	2595	0.8689	0.4441	3.3636	0.6212
FirstEF (CpG+)	153	74	183	1428	0.8361	0.6740	2.1818	0.7507
Eponine	84	31	183	2066	0.4590	0.7304	3.1818	0.5790

The maximum allowed distance between the predicted TSS and real TSS is 2000 nt

Table 4.

Overall Performance on Chromosomes 4, 21, and 22 with TSSs Determined Based on Mapped Full-Length cDNA Sequences From DBTSS (Sugano Laboratory)

	TP	FP	Total # of TSSs	Total # of predictions	Se	ppv	ASM	CC
Dragon GSF	375	107	576	2627	0.6510	0.7780	1.2727	0.7117
FirstEF	453	476	576	7451	0.7865	0.4876	3.4545	0.6193
FirstEF (CpG+)	439	242	576	4683	0.7622	0.6446	2.1818	0.7009
Eponine	250	83	576	5178	0.4340	0.7508	3.0909	0.5708

The maximum allowed distance between the predicted TSS and real TSS is 2000 nt

Table 5.

Results on Chromosome 22 Based on the Annotation and Sequence Used by Collins et al. (2003)

	TP	FP	Total # of TSSs	Total # of predictions	Se	ppv	ASM	CC
Dragon GSF	269	69	393	898	0.6845	0.7959	1.1818	0.7381
FirstEF	331	501	393	2595	0.8422	0.3978	3.6364	0.5789
FirstEF (CpG+)	310	185	393	1428	0.7888	0.6263	2.1818	0.7028
Eponine	199	79	393	2066	0.5064	0.7158	3.0000	0.6021

The maximum allowed distance between the predicted TSS and real TSS is 2000 nt

Table 6.

Overall Performance on Chromosomes 4, 21, and 22 with TSSs Determined Based on Mapped Full-Length cDNA Sequences from DBTSS (Sugano Laboratory) and the Counting Criterion From Fickett and Hatzigeorgiou (1997)

	TP	FP	Total # of TSSs	Total # of predictions	Se	ppv	ASM	CC
Dragon GSF	162	213	576	2627	0.2812	0.4320	2.0000	0.3486
FirstEF	166	718	576	7451	0.2881	0.1877	3.7273	0.2326
FirstEF (CpG+)	162	477	576	4683	0.2812	0.2535	2.9091	0.2670
Eponine	156	160	576	5178	0.2708	0.4936	1.3636	0.3657

According to the criterion of Fickett and Hatzigeorgiou (1997), a known gene is counted as a TP prediction if in the region [-200,+100] relative to the real TSS there were predicted TSSs. All other predictions falling into the region [+101, EndOfGene] relative to the real TSS for the known gene are counted as FP predictions

Table 7.

Overall Performance on Chromosomes 4, 21, and 22 with TSSs Determined Based on Mapped Full-Length cDNA Sequences From DBTSS (Sugano Laboratory)

	TP	FP	Total # of TSSs	Total # of predictions	Se	ppv	ASM	CC
Dragon GSF	228	175	576	2627	0.3958	0.5657	1.4545	0.4732
FirstEF	270	619	576	7451	0.4687	0.3037	3.7273	0.3773
FirstEF (CpG+)	264	380	576	4683	0.4583	0.4099	2.8182	0.4335
Eponine	186	130	576	5178	0.3229	0.5886	2.0000	0.4360

The maximum allowed distance between the predicted TSS and real TSS is 250 nt

Annotation related to the tables is as follows:

“Total # of TSSs” represents the total number of TSSs used for the reference analysis; “Total # of predictions” represents the total number of predictions in the two-strand search and with strand-specific counting of predictions.

In these tables, the performance of FirstEF is given in two ways: (1) as the overall performance when all classes of predictions are taken into account, and (2) as the performance achieved when only promoters of the CpG island-related first exons are considered.

The average score measure (ASM) is from Bajic (2000), where it has been introduced to deal with the problem of comparing programs that produce different Se and ppv scores. In all tables we also present the correlation coefficient (CC) scores, because this measure is traditionally used in bioinformatics, with the proviso that it is not the most appropriate measure for ranking the predictor programs. In interpreting the ASM measure, the smaller the ASM, the better the overall relative performance of the program.

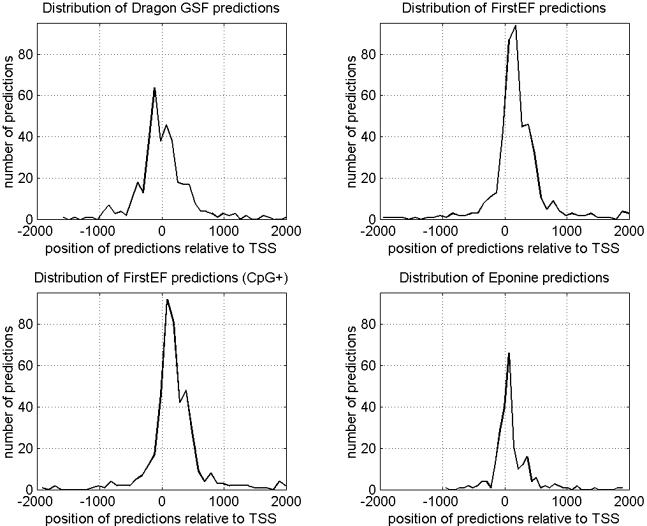
For a more complete picture about the abilities of Dragon GSF, we present in Figure 1 the distribution of predictions from all three programs in the interval [-2000,+2000] relative to the start of gene transcripts determined based on DBTSS data. The calculated values are taken in bins of 100 nt in length. The frequency of predictions for Dragon GSF, with the default setting based on chromosome 21 results, is one prediction in strand-specific manner per 177,000 nt. The average length of the predicted interval that Dragon GSF produces is 1112.6 nt, 1169.8 nt, and 1032.1 nt, for chromosomes 4, 21, and 22, respectively. This amounts to coverage of 0.4%, 0.66%, and 1.34% of the genomic sequences by the predicted regions for chromosomes 4, 21, and 22, respectively. The coverage of genomic sequences for all three chromosomes taken together is 0.56%. Finally, Dragon GSF makes 36,080 predictions on the whole human genome (build 31).

Figure 1.

Distributions of predictions for Dragon GSF, FirstEF, FirstEF in which only predictions classified by the program as CpG island-related are counted, and Eponine in the region [-2000,+2000] relative to the 576 TSS locations on chromosomes 4, 21, and 22, determined based on mapped full-length cDNA sequences from DBTSS (Sugano Laboratory). Bins of length of 100 nt were used to calculate the values presented on these graphs.

DISCUSSION

The algorithm of Dragon GSF (see Methods) combines different information in order to predict gene starts. In this process it uses prediction of CpG islands as one of the global signals that is frequently found around gene starts (Pedersen et al. 1999). However, because the computational determination of CpG islands results in relatively many predictions, additional signals are required to properly assess the presence of a gene start. Our system uses the potential predictions of TSS by Dragon PF v.1.3 (Bajic et al. 2003), as well as an additional signal obtained from the region [+1,+460] downstream of the predicted TSS location (see Methods). For every predicted CpG island, an artificial neural network (ANN) will evaluate all combinations of this CpG island and the predicted TSSs within the range [-3700,+3700] relative to the midpoint of the CpG island, together with the additional signals. The best scoring combination with the score above threshold will be selected as the winning one. Thus, there is no guarantee that the ANN that combines these signals will select the TSS that is closest to the real TSS location.

Because of its nature, the algorithm of Dragon GSF is suitable for the analysis and discovery of promoters of those genes that are associated with CpG islands.

The average G + C content of the human genome is ∼42%. Chromosome 22 was selected as being well annotated and representing one of the most GC-rich human chromosomes (G + C content of ∼48%). Chromosome 21 was selected because it has a G + C content of 41%, which approximates the average for the human genome. Finally, chromosome 4 was selected as it is the most GC-poor human chromosome (G + C content of ∼38%). As can be observed from the results on all three evaluated chromosomes, all three systems make predictions even on the GC-poor chromosome 4. This makes sense because the G + C content is not uniformly distributed over the chromosomes and the CpG island density varies according to the isochores' G + C content (Ponger et al. 2001). However, the resulting performance of all systems generally degrades with the lowering of the G + C content of the analyzed sequences. The most significant reduction is in Se for all three systems (viewed as the differences between the results on chromosomes 4 and 22), but the behavior of the systems is different. For example, based on TSS mapping relative to the full-length cDNA sequences from DBTSS (Tables 1, 2, 3) Eponine's ppv increases as the G + C content decreases, and its Se is higher on chromosome 21 than on chromosome 22, which is more GC rich. FirstEF achieves higher ppv on chromosome 4 than on chromosome 21 (Tables 1, 2), and its Se gradually decreases with the reduction of the G + C content. For Dragon GSF, ppv reduces with the decrease of the G + C content, but remains relatively high (see Table 4 for the summary results). Eponine has good performance in terms of the number of FP predictions; however, in the strand-specific predictions, its Se is below 44% (Table 4).

The results for the FirstEF do not match fully the originally reported ones (Davuluri et al. 2001). The original results were given for the recognition of the first exons. Here, we evaluated only the ability of the programs to correctly predict TSS, whereas the other program features were not considered. This partly explains the discrepancy of the results for FirstEF. Also, one of the reasons for the different results is that we performed an analysis on whole chromosomes, thus reducing a potential bias that always occurs when sets of specific isolated sequences are used in evaluations. In the original report (Davuluri et al. 2001) a nongenomic analysis was adopted with very specific construction of the test sets. We consider the region [-2000,+2000] relative to the mapped gene start/TSS of the known genes as a reasonable approximation of the TSS location. Although there is no guarantee that all mapped gene starts are absolutely correct, the selected regions are relatively broad to accommodate most gene starts even in cases of possibly incorrect annotation. The interval [-2000,+2000] relative to the annotated gene start was already used by Down and Hubbard (2002) in evaluation of promoter prediction performance of several programs. Moreover, to provide information about the positional accuracy of all tested programs, we present in Figure 1 distributions of predictions in the interval [-2000,+2000] relative to the mapped 576 TSSs of known genes on chromosomes 4, 21, and 22. We also present the summary results relative to these TSSs, using different distance criteria between the predicted TSS and real TSS. We used the criterion from Fickett and Hatzigeorgiou (1997), in which the true positive (TP) hits were counted only if the predicted TSS falls in the region [-200,+100] relative to the real TSS (Table 6). In Table 7, we also used the region [-250,+250] relative to the real TSS for counting TP predictions. In our opinion, these results convincingly show (based on ASM and CC measures) that the overall performance of Dragon GSF is better than those of the other two compared programs.

The first impression is that performances of all evaluated systems are far from being satisfactory and there is still a lot of room for improvement. The Dragon GSF system detects promoters associated with the CpG islands quite well, while making a relatively small number of predictions. If we consider the density of our system's predictions, we get on average in the strand-specific counting one prediction per >177,000 nt based on the chromosome 21 results. We use these as the reference because the G + C content of chromosome 21 is about average for the human genome. The results on chromosomes 4 and 22 are less typical because these chromosomes are extremes for the human genome regarding the G + C content. In the same manner, frequency of predictions of FirstEF is 55,000 nt if all classes of its predictions are considered. If we consider only those predictions of FirstEF that are denoted as CpG island related, then FirstEF makes one prediction per 91,000 nt. Eponine makes one prediction per 83,000 nt, but many of its predictions could be clustered, and the frequency of such clusters is much smaller.

We did not make direct comparisons with the programs that cannot provide strand-specific predictions of TSSs. This excluded many good programs such as PromoterInspector, CpGProD, CpG-Promoter, and the system of Hannenhalli and Levy. PromoterInspector system is a commercial system with very limited Web access. CpGProD reported better performance than CpG-promoter and PromoterInspector. However, CpGProD's performance does not match the performance of our system and it does not provide strand-specific predictions, although it makes inaccurate assessment of the strand where the gene should be. The system of Hannenhalli and Levy is not publicly available, but they reported a performance similar to PromoterInspector.

The advantages of the Dragon GSF system are the sparseness of predictions, very high ppv, relatively high Se, good localization of the predicted TSSs within 2000 nt, a relative independence on the G + C content down to certain limits (as can be seen from Tables 2 and 3), and strand-specific predictions.

Disadvantages, however, are the dependence on the presence of the CpG islands of specific characteristics, which also limits the upper bound on Se that can be achieved by this system. Also, TSS predictions could be more accurate if there was a way to select the prediction closest to the actual TSS and use it within the combination algorithm.

METHODS

The chromosome 22 sequence and annotation data are based on Collins et al. (2003) and were obtained from the world wide Web at http://www.sanger.ac.uk/HGP/Chr22/. The sequences and annotation data of chromosomes 21 and 4 were downloaded from NCBI GenBank (http://www.ncbi.nlm.nih.gov/). The update dates for the two chromosomes were 7 February 2002 and 1 August 2002, respectively. The total length of chromosomes 4, 21, and 22 used in the analysis is 188,018,198 bp, 33,981,048 bp, and 34,748,585 bp, respectively.

Using program FIE v1.1 (Chong et al. 2002), we extracted 6612 sequences from the human genome covering the region [-5000,+5000] relative to the start of exon 1. From this set, we eliminated sequences that belong to chromosomes 4, 21, and 22. This resulted in 6114 remaining sequences. For the generation of matrix D (see following), we randomly selected 2000 sequences from this set. We used the remaining 4114 sequences to tune our program.

Reference TSS Locations

We used data from DBTSS (http://dbtss.hgc.jp/samp_home.html) mapped on genomic contig, kindly provided by Yutaka Suzuki from Sugano Laboratory (http://www.hgc.ims.u-tokyo.ac.jp/labo.html). These mappings are based on the use of full-length cDNA sequences (Maruyama and Sugano 1994; Suzuki et al. 1997, 2001, 2002) and contain much more accurate estimates of TSS locations than provided by most of the current annotation. Although one may argue that the coverage and the selection of these data may be biased, they still represent a very significant collection of estimated TSSs derived from experimentally obtained transcripts (see results in Tables 1, 2, 3, 4, 6, 7) from chromosomes not used in training or tuning of our system. For the sake of completeness, we also present the results on chromosome 22 with the latest annotation based on Collins et al. (2003; Table 5).

How the Hits Are Counted

Hits (predictions) are counted as strand specific. For Dragon GSF we used the predictions of the gene start (the position denoted by identifier “GS” in the report file) as the TSS prediction. For FirstEF we used the position of the TSS as determined by the point 500 nt downstream of the first nucleotide of the promoter region predicted by FirstEF, which is in accordance with the explanation provided in the original publication on FirstEF. When FirstEF makes cluster predictions, we used only the highest ranked prediction as correct. For Eponine, we used all predictions as reported.

No predictions were merged. The algorithm of FirstEF already makes some clustering of its predictions. Eponine predictions could be easily clustered, but it is not clear how big the gap should be, and what should be considered as the predicted TSS after the clustering. Thus we did not cluster predictions of Eponine.

All hits that fell in the region [-2000,+2000] around the mapped TSS/Gene start were counted as correct, and all respective genes represented TP. All known genes missed in this way were counted as false negative. All hits that fell on the annotated part of the gene on the region [+2001,EndOfTheGene] were counted as FP hits. Other hits were not considered in counting TP and FP. On all three chromosomes, only the known genes were considered based on the official annotations. For chromosome 22, the annotation used was from Collins et al. (2003), whereas for chromosomes 21 and 4, it was from NCBI GenBank. The annotation was used to associate mapped TSS locations to the known genes. In Tables 6, 7 instead of the [-2000,+2000] region for determining TP predictions, we used other, far more stringent criteria, with the [-200,+100] region and [-250,+250] region, where the FP predictions were counted if they fell on the regions [+101,EndOfTheGene] and [+251,EndOfTheGene], respectively.

Measures of Success

In order to objectively compare results of predictions, we need to use some measures that express predictor's performance. We use the following measures: Se, ppv, CC, and ASM. Explanation of these measures is as follows:

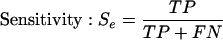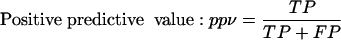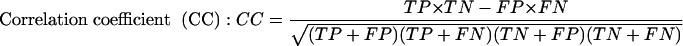ASM is introduced in Bajic (2000) to enable meaningful comparison of predictors that achieve different Se and ppv scores. ASM is the averaged rank position measure obtained by computing 11 different prediction measures, ranking the compared programs based on these measures, and averaging the rankings. It represents the relative performance of compared prediction programs in a more balanced manner than can be obtained by using any individual comparison measure, including the popular CC. For example, CC does not take into account the total number of predictions that predictor programs make in achieving a specific performance.

Algorithm and Training of Dragon GSF

Dragon GSF estimates the presence of the CpG islands based on the following criteria: CpG score ≥0.6, G+C content ≥0.5, CpG island length ≥500. The system also uses predictions made by the Dragon PF ver.1.3 system. All predicted TSS locations in the segment [-3700,+3700] relative to the midpoint of the predicted CpG island are evaluated by an ANN, which uses several signals as inputs: (1) distance of the predicted TSS from the middle point of the predicted CpG island, (2) G + C score of the CpG island, (3) CpG score of the CpG island, (4) #C/length, and (5) the total sum of scores obtained by a differential pentamer matrix D in the region 460 nt downstream of the predicted TSS (see explanation following). Here, #C is the number of C nucleotides and length is the length of the predicted CpG island. Based on these input data, ANN predicts whether the combination of the CpG island and the predicted TSS indicates the presence of gene starts. When the combination is identified, then the boundaries for the predicted region are given by the formula obtained empirically from the training data:

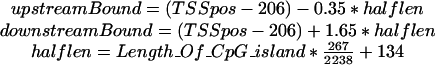where TSSpos is the position of TSS as predicted by Dragon PF v.1.3. Note that there is no guarantee that the algorithm for combining the CpG islands and the TSS predictions will identify the TSS predictions that are closest to the real TSS locations. The algorithm will only select the one of possibly many predicted TSS locations in the region [-3700,+3700] relative to the midpoint of the CpG island, such that, jointly with the other input data, the ANN system produces the highest score above the selected threshold. This produces a statistical bias in the selected TSS locations of ∼206 nt downstream of where they really should be. For this reason, the positions of such selected TSSs are corrected by 206 nt upstream of the TSS locations given by Dragon PF. This is implemented in the algorithm and such a corrected TSS position is denoted as the gene start with the “GS” identifier in the report file. One can consider these predictions as being predictions of a new TSS predictor.

The differential position weight matrix D of pentamers is obtained by using 2000 human genes. From these sequences, we extracted segments in the range [-50,-1] and [+1,+50] relative to the central point (position +1) of the annotated first exons. From sequences corresponding to [-50,-1] segments, we constructed a position weight matrix P1 of overlapping pentamers, as explained in Bajic et al. (2002b). Analogously, we generated matrix P2 by using the sequences corresponding to the segments [+1,+50]. Then we formed the matrix D = P1–P2, which is used to calculate the score for any sequence by matching the input sequence to the coefficients of D and summing these coefficients analogously to the algorithm in Bajic et al. (2002b). This is used to generate the additional signal to accompany predicted TSS locations. This signal is the sum of scores obtained from sliding a window of length 50 nt one nucleotide ahead along the segment [+1,+460] relative to the TSS location predicted by Dragon PF and matching the window content with matrix D.

Before the data are processed by ANN, they have to be normalized. Normalization involved conversion of training data to zero mean with a standard deviation of one and the principal component transformation (Bishop 1995). These were applied to the training data and the resulting parameters were then used for the transformation of the test data. These parameters are made part of the data used by the algorithm. The ANN used is a feed-forward four-layer network (input layer, two hidden layers, and output layer) with “logsig” transfer functions (Bishop 1995) of neurons in the hidden layers and the output layer. It has 10 neurons in the first hidden layer, 15 neurons in the second hidden layer, and 1 neuron in the output layer. It is trained by the optimized back-propagation algorithm (Sha and Bajic 2002) with additional weight decays. In total, 1000 training epochs have been used. Let X_i = [x₁, x₂,..., x_k] represent a normalized input vector (sample) for the ANN system. Before each presentation of the new training sample X_j, sample X_j was subjected to random alteration of its coordinate values so that the altered sample became X_ja = X_j + ΔX_j. Then the randomly altered sample X_ja and the original sample X_j were presented to the system, first X_ja, then X_j. Random variation of the training samples was made with <5% change of the absolute numeric values of the training sample coordinates. The training goal was to distinguish which combinations of the CpG island parameters, D matrix score, and distances of the DPF predictions from the midpoint of the CpG island are the correct ones for gene start predictions. Combinations that had TSS prediction closest to the actual gene start were considered the positive samples. All other samples were considered the negative samples.

Programs Used for the Comparison Analysis

Dragon GSF has been used with its default setting (the threshold of 0.994). FirstEF program has been used as the download version with its default parameters (Davuluri et al. 2001): cutoff value for the first-exon a-posteriori probability of 0.5, cutoff value for the promoter a-posteriori probability of 0.4, and cutoff value of the splice-donor a-posteriori probability of 0.4. Eponine has also been used as the download version with the default threshold of 0.999 as suggested in Down and Hubbard (2002).

Conclusions

We have presented a system for locating the region where the gene start is in genomic large-scale analyses. The system is applicable to genomes of those species that are characterized by the presence of CpG islands around gene starts. The high accuracy of the system and sparseness of its predictions makes it convenient for an ab initio identification of gene starts and a useful complement to the existing gene-finding tools (see Stormo 2000). The system is free for academic and nonprofit institutions and can be accessed at http://sdmc.lit.org.sg/promoter/dragonGSF1_0/genestart.htm.