Automated Detection of Informative Combined Effects in Genetic Association Studies of Complex Traits

Abstract

There is a growing body of evidence suggesting that the relationships between gene variability and common disease are more complex than initially thought and require the exploration of the whole polymorphism of candidate genes as well as several genes belonging to biological pathways. When the number of polymorphisms is relatively large and the structure of the relationships among them complex, the use of data mining tools to extract the relevant information is a necessity. Here, we propose an automated method for the detection of informative combined effects (DICE) among several polymorphisms (and nongenetic covariates) within the framework of association studies. The algorithm combines the advantages of the regressive approaches with those of data exploration tools. Importantly, DICE considers the problem of interaction between polymorphisms as an effect of interest and not as a nuisance effect. We illustrate the method with three applications on the relationship between (1) the P-selectin gene and myocardial infarction, (2) the cholesteryl ester transfer protein gene and plasma high-density-lipoprotein cholesterol concentration, and (3) genes of the renin-angiotensin-aldosterone system and myocardial infarction. The applications demonstrated that the method was able to recover results already found using other approaches, but in addition detected biologically sensible effects not previously described.

Unlike Mendelian disease, the genetic deciphering of which has known an extraordinary success in the past decades, advances in the genetics of complex diseases have been much more tenuous, and strategies aimed at identifying genes underlying these diseases must be reconsidered (Botstein and Risch 2003). Approaching complex diseases by studying one or a few genetic polymorphisms has shown its limitations. It is now increasingly recognized that understanding the genetic basis of complex phenotypes requires not only the investigation of all polymorphisms located in functional regions of candidate genes (Corbex et al. 2000; Stengard et al. 2002; Tregouet et al. 2002), but also the integration of information about the network of genes involved in biological systems of major physiological importance, such as lipid metabolism, cellular adhesion, inflammation, etc. “Systems biology”, aimed at describing the structure, function, and control of biological processes in health and disease, is emerging as one of the major challenges of the post-genome era (Stoll et al. 2001; Patterson and Aebersold 2003). From a genetics perspective, this approach implies characterizing the different genes involved in biological pathways, their functional polymorphisms, and their interactions with other genes and/or environmental factors.

This multidimensional approach requires the development of statistical methods able to handle multiple variable loci, possibly in several genes, and the detection, among all measured polymorphisms, of those which, alone or in combination, may influence the phenotype. Indeed, there is increasing evidence that even in the absence of significant marginal effects, polymorphisms may exhibit epistatic effects on complex traits that are detectable only by a multilocus approach (Templeton 2000).

Neural networks have been recently proposed for investigating the relationship between complex phenotypes and multilocus genotypes (Curtis et al. 2001; Sherriff and Ott 2001). These methods, aimed at revealing hidden patterns of relationships between variables, are theoretically well suited for analyzing data with high-order interactions. However, the results of these methods, expressed as weights associated with predictors, are difficult to interpret and do not clearly identify the interacting predictors. Moreover, the results are sensitive to small changes in the data and depend on various tuning parameters such as the number of hidden units and hidden layers.

Recursive partitioning methods, that is, classification and regression trees (Breiman et al. 1984), were recently introduced to genetics (Zhang and Bonney 2000; Czika et al. 2001; Province et al. 2001). The principle of this approach is to split the sample in successive nodes based on genotype dichotomies that maximize a split function depending on the nature of the response. However, the partitioning aspect often leads to high-order partial interactions that concern very few individuals and are difficult to interpret. Moreover, these methods are not well adapted to the detection of main effects which are no longer identifiable after several dichotomies. Additionally, results appear quite dependent on the choice of the division variables, and their threshold values are often unstable (Dannegger 2000).

A combinatorial partitioning method (CPM) was recently developed to identify multilocus genotypic partitions that predict quantitative trait variation (Nelson et al. 2001). From a set of polymorphisms, the method identifies the partitions of two-locus genotypes which are the most predictive in terms of explained phenotypic variability. As for tree-based methods, the partitions are generally suggestive of interactions between polymorphisms, but these interactions are not easily interpretable. Moreover, the capacity of the method to detect additive effects of polymorphisms is unclear, and adjustment on covariates must be done prior to analysis. One current limitation of the method is that it is restricted to two-locus partitions, and extension to partitions of higher dimension may rapidly become prohibitive in terms of the number of possible partitions to be examined.

Inspired by the CPM for quantitative traits, a multifactor-dimensionality reduction (MDR) method was proposed for exploring high-order interactions between polymorphisms in the framework of case/control studies (Ritchie et al. 2001, 2003). The principle of the MDR method is to reduce the genotype predictors from n dimensions to one, by pooling genotypes into two groups at high risk and low risk, respectively. Among all possible combinations, the method selects the partition that maximizes the cases:controls ratio of the high-risk group. The MDR method is not limited to two-locus combinations as is the CPM; however, as for the CPM, results can be difficult to interpret. Further limitations of the MDR method are that it is currently limited to balanced case/control studies, and it is not possible to adjust for covariates.

A stepwise regression procedure was proposed for evaluating the contribution of several polymorphisms within a small genetic region in a case/control framework (Cordell and Clayton 2002). This classical parametric approach has the advantage that results are more easily interpretable than those of nonparametric approaches. However, although interaction terms were potentially included in the series of fitted models, the proposed strategy of hypothesis testing was primarily aimed at detecting main effects of polymorphisms. More generally, automated selection procedures are—in their classical use proposed by standard statistical software—ill-adapted for the systematic investigation of interactions. Forward and stepwise procedures select only interactions composed by predictors already selected at previous steps, whereas the backward procedure, starting with a model including main effects and interactions of different orders, is very quickly limited by convergence problems.

In this report, we propose a fully automated method for exploring the effects of several polymorphisms (and other nongenetic covariates) in the framework of association studies involving any kind of phenotype (quantitative, binary, or censored). This method, called DICE (Detection of Informative Combined Effects), combines the advantages of the regressive approaches in terms of modeling and interpretation of effects, with those of data exploration tools. Importantly, the approach considers the problem of interaction between polymorphisms as an effect of interest and not as a nuisance effect. It is therefore well suited to the exploration of the spectrum of polymorphisms within candidate genes and more generally, within biological systems. The forward selection approach is based on the principle of parsimony, the principle of marginality, and the information theory paradigm. The algorithm compares at each step a wide variety of models and chooses the one(s) that provide(s) the best approximation to the data, while having the least number of parameters. To avoid difficulties related to the null-hypothesis testing theory (Goodman 1993; Royall 1997), such as the choice of a significance level (especially for nonindependent tests), the selection for the “best” approximating model(s) is based on an information criterion (IC) to be minimized. The algorithm identifies a subset of polymorphisms that are, either individually or in combination, associated with the phenotype.

The method was applied to several real data samples, and the results are available at our Web site GeneCanvas (http://genecanvas.idf.inserm.fr/). Here, we detail the results of three applications. The first one concerns the relationship between polymorphisms of the P-selectin (SELP) gene and a binary phenotype, myocardial infarction (MI). The second application investigates the association between polymorphisms of the cholesteryl ester transfer protein (CETP) gene and a quantitative trait, plasma high-density lipoprotein (HDL)-cholesterol concentration, while taking into account alcohol consumption. The third application investigates the association between polymorphisms of several genes belonging to the renin-angiotensin-aldosterone (RAA) system and MI. We show that the proposed method recovers results already found using other techniques, but can also detect effects not previously described and that will deserve further detailed investigation. In addition, we present the results obtained in a preliminary stability study of the set of effects identified in the SELP gene application.

METHODS

The relationship between the phenotype and the covariates, which can be genotypes as well as nongenetic variables, is modeled using a logistic (binary outcome), linear (quantitative trait), or Cox (censored response) regression model. The algorithm explores by a forward procedure a set of competing models for which an IC is derived. Based on certain modalities developed below, this exploration leads to the selection of a best approximating model (or models). The model space is explored in a systematic way, and the best model(s) can include main effects and interactions of different orders.

Exploration Phase of the Algorithm

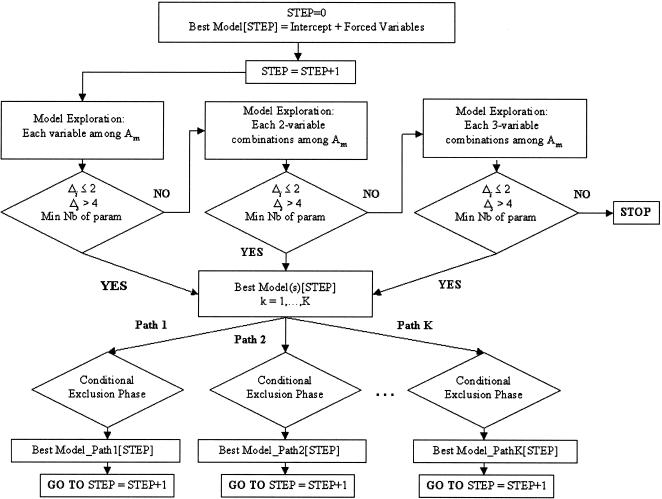
In what follows, we assume that all covariates are genetic polymorphisms, for ease of presentation. At step 0, the DICE algorithm calculates the IC value associated with the model including the intercept and possibly variables forced into the model, such as stratification variables (model 0). At step 1, DICE calculates the IC values for all competing models obtained by the individual addition of each polymorphism to model 0. At this step, the main effects of polymorphisms, as well as their interactions with each variable imposed in model 0, are considered. If a certain composite condition, which will be developed in a following section, is verified for one of these models, DICE keeps in memory the model and continues to step 2. If the composite condition is not satisfied, DICE explores all two-marker combinations, by comparing all models obtained from model 0 to which are added any pair of markers, either additively or interactively, and possibly interacting with the variables of model 0. If the composite condition is still not satisfied, DICE continues to explore in the same way all three-marker combinations. If, at the end of the exploration of three-marker combinations, the composite condition has not been satisfied, DICE stops. In this case, the algorithm has detected no one-, two- or three-locus combination associated with the phenotype. Higher than three-locus combinations were not explored in the current applications, because this would require very large sample sizes, but extension of the method is straightforward.

If the composite condition has been satisfied at step 1, the algorithm goes to step 2 and replaces model 0 with the model retained at step 1. The procedure continues iteratively until there is no more improvement of the IC value.

Information Criterion (IC)

The implemented IC is the AIC_c (Hurvich and Tsai 1989) corresponding to Akaike's information criterion (AIC; Akaike 1974) corrected for the second-order bias in the case of finite sample size. The formula is:

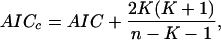where AIC = -2log_e[ℓ(θ̂/data)]+2K corresponds to an estimator of the expected relative Kullback-Leibler (K-L) distance. The term log_e[ℓ(θ̂)/data)] yields the value of the maximized log-likelihood over the unknown parameters (θ̂), given the data and the model, leading to the estimated parameters (θ̂). K is the number of parameters estimated in that approximating model, and n is the total sample size. The first term in AIC is a lack of fit component which decreases as more parameters are fitted in the model; the second term increases as a penalty for adding extra parameters. Thus, AIC forces a trade-off between bias and variance as the number of parameters is increased.

Evaluation of the Composite Condition

The general goal of the algorithm is to detect the most parsimonious and informative model that minimizes the IC within each step, and between the various steps explored. Because the AIC_c is on a relative scale, it was proposed to rescale AIC_c values such that the model with the minimum AIC_c has a value of 0(Burnham and Anderson 2002), that is:

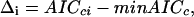where AIC_ci is the IC corresponding to candidate model i, and minAIC_c is the minimum AIC_c value within the considered step, among the set of competing models noted {g_i(data/θ),i=1,..., R}. If we note f, the full reality, with infinite number of parameters, such differences estimate the relative expected K-L differences between f and g_i(data/θ):

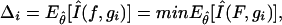where E_^θ [Î(f,g_i)] is the expected estimated K-L distance between f and g_i(data/θ), and min is over the set of models explored.

Following a simple heuristic rule derived by extensive Monte Carlo simulation (Burnham and Anderson 2002), a model having a Δ_i ≤ 2 has a substantial level of empirical support and can be considered equivalent to the minAIC_c model, whereas a model with Δ_i ≥ 4 is implausible as the actual K-L best model and can be considered different from the minAIC_c model. At each step, the algorithm calculates the Δ_i for each model, and among the models having a Δ_i ≤ 2, the algorithm selects the one(s) presenting a `substantial' decrease of AIC<sub>c</sub> relative to the previous step. The definition of a `substantial' decrease is arbitrary and depends on the stringency criteria imposed for model selection. Following the guideline values described above, adapted here to the inter-step minimization of the IC criterion, a difference was considered substantial if:

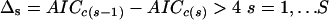where S is the total number of steps explored.

It may happen that several models fulfill the composite condition, that is Δ_i ≤ 2 and Δ_s > 4. Among these models, the algorithm selects the one(s) having the least number of parameters (principle of parsimony). When several models are selected at a given step (due to satisfying both the composite condition and the same number of parameters), DICE then evolves in parallel from the various best models identified. This parallel exploration of `tie models' is a way to accommodate the possible ambivalence of the data.

Conditional Exclusion Phase

The procedure described above would not be globally optimal if only a forward, sequential exploration was performed without re-evaluating at the end of each step the terms included at the previous steps. To overcome this problem, a conditional exclusion phase was incorporated after the inclusion phase. This phase is derived from the sequential floating forward search (SFFS) algorithm, extended here not only to main effects, as originally described (Pudil et al. 1994), but also to interaction terms. After the selection of the best model at step s, DICE fits all models that differ from the current model by dropping a single term, while maintaining the principle of marginality; that is, whenever an interaction is present in a model, all marginal main effects and interactions of lower orders must also be present (Fox 1997). Among all the reduced models j (j=1,..., J) thus obtained, the algorithm keeps the one with the lowest AIC_cj value, provided it is not different from that of the current model (Δ_j ≤ 2) and the inter-step difference remains substantial (Δ_s > 4). Figure 1 presents a summary of the algorithm.

Figure 1.

Diagram summarizing the steps of the DICE algorithm. A_m is the set of remaining variables not included in the model[STEP-1] (at STEP=1, A_m is the total number of variables explored). Several models can be identified at each step, leading the algorithm to evolve in parallel the tie models (Paths 1,...,K).

Coding of Genotypes

In the most general form specifying no particular model of inheritance, genotypes at each locus are coded as dummy variables ([m-1] independent variables in the case of m genotypes). However, with this general coding scheme, results can be difficult to interpret in particular when the dimensionality of the best model is relatively high. Moreover, the problem of sparse cells frequently arises. For these reasons, we propose to run the algorithm with different coding schemes corresponding to specific genetic models and to retain for further evaluation the polymorphisms selected in at least one of the configurations.

Algorithm Implementation

DICE was implemented in the R language for the present applications. We used the generalized linear model function for the regression modeling, with a Gaussian error distribution for a continuous outcome and a binomial error distribution for a binary response. The iteratively reweighed least squares algorithm was used to fit the models. The convergence criterion value for maximizing the likelihood was fixed to 1e-08, corresponding to the default option of most statistical packages. We are currently developing an optimized version of the algorithm in the C language, which will be more efficient to accommodate a large number of variables. This program will be made available at our Web site.

RESULTS

SELP Gene Polymorphisms and Myocardial Infarction

P-selectin is a cellular adhesion molecule which plays a major role in the recruitment of inflammatory cells from the circulation and their transendothelial migration, the critical initial step of atherosclerosis (Price and Loscalzo 1999). A molecular screening of the SELP gene had previously led to the identification of several polymorphisms (Herrmann et al. 1998). We applied our method to re-analyze the association between these polymorphisms and MI, using the same data set as the one previously used for a haplotype analysis in the Etude Cas-Témoin de l'Infarctus du Myocarde (ECTIM; Tregouet et al. 2002). The study sample included 551 MI cases and 596 control subjects, and full genotypic information was available for these samples.

Five polymorphisms were identified in the 5′ region (C-2123G, A-1969G, T-1817C, C-1576G, and -485I/D) and eight in the coding region (P98P, S290N, C557C, N562D, N563N, V599L, T715P, and T741T; see our Web site for the description of polymorphisms, their allele frequencies, and the pairwise linkage disequilibrium [LD] coefficients). Due to their low allele frequency (<1%), the C-1576G and P98P polymorphisms were not included in analysis. In addition, because the C557C, N563N, and V599L polymorphisms were completely concordant, only the V599L, which had the less missing data, was selected, leaving nine polymorphisms for the analysis.

Two different coding schemes for the genotypes were used. The first one, referred to as `dominant', opposed frequent homozygotes to others (genotype coded as a dichotomous variable 0, 1), whereas the second, referred to as `codominant', assumed for each marker an additive allele effect on a logistic scale (genotype coded as an ordinal variable 0, 1, 2). Because the country of origin (Northern Ireland/France) was a stratification variable of the study, this variable was forced in model 0. Table 1 presents the detailed results obtained with the codominant coding scheme. For each step, the four best models are reported. Figure 2 summarizes the results obtained with this coding scheme.

Table 1.

Application of DICE to the Association Between Myocardial Infarction and Nine Polymorphisms of the SELP Gene, Using a Codominant Coding Scheme

	Modela	AICci	Δib	#parc	Δsd
Step 0	y = intercept + country	1590.07	0.00	2	—
Step 1	T715P	1582.73	0.00	3	7.35
	country*T715P	1584.16	1.44	4	5.91
	country*T-1817C	1589.49	6.76	4	0.58
	T741T	1589.98	7.25	3	0.10
Step 2	T715P*T741T	1577.34	0.00	5	5.39
	T715P*N562D	1580.28	2.94	5	2.45
	T715P*V599L	1580.41	3.07	5	2.32
	country*N562D	1580.54	3.20	5	2.19
Step 3e	country*N562D	1576.27	0.00	7	1.07
	N562D	1576.35	0.08	6	0.99
	T741T*T-1817C	1577.34	1.06	7	0.00
	T715P*N562D	1577.42	1.14	7	-0.07
Step 3bisf	S290N *N562Dg	1570.84	0.00	8	6.50
	country*S290N*N562D	1572.13	1.29	11	5.21
	T-1817C*N562Dg	1572.52	1.68	8	4.82
	T741T*S290N*N562D	1573.39	2.55	11	3.95
Step 4/path1	S290N*N562D*V599L	1563.42	0.00	12	7.42
	T-1817C	1571.20	7.78	9	-0.36
	country*T-1817C	1571.32	7.90	10	-0.48
	N562D*-485I/D	1571.85	8.42	10	-1.01
Step 4/path2e	N562D*A-1969G	1572.80	0.00	10	-0.27
	N562D*S290N	1573.11	0.31	10	-0.59
	N562D*-485I/D	1573.50	0.70	10	-0.98
	-485I/D	1573.58	0.78	9	-1.06
Step 4bis/path2f	S290N*N562D*V599L	1566.15	0.00	14	6.37
	country*C-2123G*S290N	1573.84	7.69	14	-1.32
	N562D*-485I/D+N562D*S290N	1574.07	7.92	12	-1.55
	country*C-2123G+country*S290N	1574.18	8.03	12	-1.65
	Conditional exclusion: deletion of T-1817C*N562D and T-1817C
	Stop for both paths
Final model in both paths: y = country + T715P*T741T + S290N*N562D*V599L

n = 1147. Each model represents an update of the best approximating model identified at the previous step. The four best models within each step are shown. In bold are the best model(s) retained at each step

^aSymbols are as follows: y is the outcome, “+” means addition of term(s), “^*” means interaction (implying that all the terms of lower order are included in the model according to the principle of marginality)

^bΔ_i = AIC_ci - minAIC_c

^cNumber of parameters in the model

^dΔ_s = minAIC_c(s-l) - minAIC_c(s)

^eNc model satisfying the composite condition

^fCombinations of two markers

^gTie models

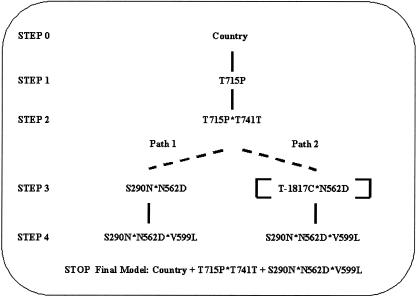
Figure 2.

Summary of the results obtained in the application of DICE to the association between myocardial infarction and nine polymorphisms of the SELP gene, using a codominant coding scheme (n = 1147). Dashed lines represent tie models. The terms deleted after the conditional exclusion phase are shown in brackets.

At steps 1 and 2, a unique best model was identified, which is indicated in bold. At step 3, no model met the composite condition (Δ_i ≤ 2 and Δ_s > 4) when including each marker individually in the model selected at step 2. The algorithm then considered all pairs of markers (step 3^bis). Two tie models were identified, including S290N^*N562D and T-1817C^*N562D, respectively. Note that S290N and T-1817C are in strong LD (D′ = +0.96) and have allele frequencies of the same order of magnitude, explaining why the two models were nearly equivalent. In parallel, the algorithm then considered the two resulting paths, noted path 1 and path 2, respectively. At step 4/path 1, the model including a three-locus combination: S290N^*N562D^*V599L was identified. At step 4/path 2, none of the models explored with the five remaining markers individually met the composite condition, and thus the algorithm continued to explore all remaining pairs of markers. Interestingly, the same three-locus combination as in path 1 was identified. Furthermore, after application of the conditional exclusion phase at the end of this step, the T-1817C main effect and the T-1817C^*N562D interaction term were removed. The final models obtained at the end of both paths were then the same and included: country, T715P^*T741T, and S290N^*N562D^*V599L (as well as all the lower-order interaction terms).

Detailed results of the exploration with the dominant coding scheme are available at our Web site. Briefly, the dominant coding scheme led to the same models as the codominant scheme for the first two steps. At step 3, a final unique best model was identified including the interaction S290N^*N562D. Actually, the model including the three-locus combination S290N^*N562D^*V599L had the minAIC_c at step 4, but was not retained due to a Δ_s of 2.63. Results are then fairly consistent irrespective of the coding scheme used.

CETP Gene Polymorphisms and HDL-Cholesterol Levels

CETP is a key enzyme in reverse cholesterol transport and HDL metabolism (Tall 1993). For this reason, the CETP gene is a candidate gene for coronary heart disease. A molecular screening of the gene led to the identification of several polymorphisms which were further investigated in the ECTIM study in relation to MI and HDL-cholesterol, taking into account alcohol consumption, which is known to influence HDL-cholesterol levels (Fumeron et al. 1995; Corbex et al. 2000). In the present application, we re-analyzed the association between HDL-cholesterol levels (continuous variable) and CETP polymorphisms in the sample of control subjects of the ECTIM study (n=671), including alcohol consumption as an environmental variable. Alcohol consumption was stratified in five classes and considered an ordinal variable, as in our previous analysis (Fumeron et al. 1995).

Ten polymorphisms had been previously identified (see our Web site for detailed information). Because three groups of polymorphisms were almost completely concordant (G+279/in1A and C+8/in7T, A373P and R451Q, I405V and G+524T), we excluded the marker of each pair having the most missing data, that is, G+279/in1A, A373P and I405V, respectively. Variables considered for exploration were therefore the seven remaining polymorphisms and alcohol consumption. All models were systematically adjusted for age and center of recruitment. Table 2 and Figure 3 show the results of the exploration using the dominant coding scheme. Results obtained with the codominant coding scheme are available at our Web site.

Table 2.

Application of DICE to the Association Between HDL-Cholesterol Levels and Seven Polymorphisms of the CETP Gene, Using a Dominant Coding Scheme

	Modela	AICci	Δib	#parc	Δsd
Step 0	y = intercept + center + age	-657.68	0.00	5	—
Step 1	center*alcohol	-679.57	0.00	9	21.90
	alcohol	-678.61	0.97	6	20.93
	age*alcohol	-678.22	1.36	7	20.54
	C+8/in7T	-661.66	17.91	6	3.98
Step 2	alcohol*C-629Ag	-688.66	0.00	8	10.05
	alcohol*C+8/in7Tg	-687.94	0.72	8	9.33
	C+8/in7T	-682.69	5.97	7	4.08
	age*C+8/in7T	-680.99	7.67	8	2.38
	STOP for both paths
Final model path1: y = center + age + alcohol*C-629A or Final model path2: y = center + age + alcohol*C+8/in7T

n = 671. See footnotes of Table 1

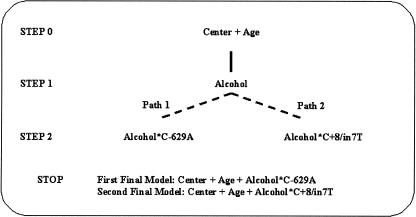
Figure 3.

Summary of the results obtained in the application of DICE to the association between HDL-cholesterol and seven polymorphisms of the CETP gene, using a dominant coding scheme (n = 671). Dashed lines represent tie models.

At step 1, based on the principle of parsimony, DICE selected the model including alcohol consumption as the main effect. At step 2, two tie models were selected, having the same number of parameters and both satisfying the composite condition: (1) an interaction between alcohol and the C-629A polymorphism, and (2) an interaction between alcohol and the C+8/in7T polymorphism. Note that these two polymorphisms are in strong LD (D′ = +0.95) and have similar allele frequencies. The algorithm stopped at the following step for both paths evolving in parallel. With the codominant coding scheme, after inclusion of alcohol consumption at step 1, the interaction between alcohol and the C+8/in7T marker was selected.

Renin-Angiotensin-Aldosterone System Gene Polymorphisms and Myocardial Infarction

The RAA system plays a critical role in the maintenance of cardiovascular homeostasis. Polymorphisms of the main genes of the RAA system—namely, angiotensin-converting enzyme (ACE), angiotensinogen (AGT), angiotensin II receptor type 1 (AGTR1), and aldosterone synthase (CYP11B2)—were investigated in the ECTIM study in relation to MI (Cambien et al. 1992; Tiret et al. 1994, 1995; Poirier et al. 1998; Pojoga et al. 1998). In the present application, we analyzed the association between MI and the overall set of polymorphisms of the RAA system previously investigated.

Nine polymorphisms were considered: the I/D polymorphism in the ACE gene, the M235T and T174M polymorphisms in the AGT gene, the T-810A, C-521T, T+55/ex4C, L191L, and A+39C polymorphisms in the AGTR1 gene (after exclusion of redundant polymorphisms), and the T-344C polymorphism in the CYP11B2 gene (see our Web site for details). All models were adjusted on country of origin. Table 3 shows the results using the codominant coding scheme. Results obtained with the dominant coding scheme are available at our Web site.

Table 3.

Application of DICE to the Association Between Myocardial Infarction and Nine Polymorphisms of the RAA System, Using a Codominant Coding Scheme

	Modela	AICci	Δib	#parc	Δsd
Step 0	y = intercept + country	1561.28	—	2	—
Step 1e	ACE I/D	1558.93	0.00	3	2.35
	AGTR1/T-810A	1559.87	0.94	3	1.41
	AGTR1/A+39C	1560.51	1.57	3	0.78
Step 1bis f	ACE I/D*AGTR1/A+39C	1553.67	0.00	5	7.61
	ACE I/D + AGTR1/T-810A	1556.90	3.23	4	4.38
	ACE I/D*AGT/M235T	1556.92	3.24	5	4.37
	STOP
	Final model: y = country + ACE I/D*AGTR1/A+39C

n = 1133. See footnotes of Table 1

At step 1, considering the individual addition of each polymorphism and their possible interaction with country, the composite condition was not verified for any of the candidate models. DICE then considered all two-locus combinations (Step 1^bis) and selected the model including the interaction between ACEI/D and AGTR1/A+39C previously described (Tiret et al. 1994). The algorithm stopped at the following step. The same result was obtained with the alternative coding scheme.

Preliminary Study of Stability

It is well known that the choice of variables (and their associated effects) for inclusion in a regression model varies across repeated samples. This model selection uncertainty is explained by the interrelationship and partial redundancy among the explanatory variables (Draper 1995). This is particularly true for genetic polymorphisms which are in strong LD.

To evaluate the stability of the effects identified by the proposed algorithm, we performed a preliminary stability study by the bootstrap method (Efron and Gong 1983) on the SELP data set. In line with the exploratory nature of the proposed approach, stability refers here to the selection of effects (main effects or interactions) and not to the prediction capabilities of the models, as it is generally done in a context of variable selection for prediction (Altman and Andersen 1989; Sauerbrei and Schumacher 1992). One hundred bootstrap samples were generated from the original SELP data set and analyzed successively with both coding schemes. For each bootstrap replicate, we counted the number of occurrences of main effects and interactions which were selected by the algorithm. When an interaction was selected at a given step, we counted only this term and not the marginal effects and interactions of lower order introduced to respect the principle of marginality.

Table 4 presents the results of the stability study with the codominant coding scheme, with effects being ranked by frequency of inclusion over the 100 replicates. The main effect of the T715P polymorphism was detected in 61% of replicates and was the first effect selected in 54% of them. Frequency of inclusion of other main effects varied from 1% to 18%, far behind the T715P. Concerning the first-order interactions, the two highest frequencies of inclusion (46% and 44%, respectively) corresponded to the interactions detected in the original data set. The interaction between country and T-1817C had the third highest frequency (19%). The most frequent selected effect among second-order interactions (52%) was the one identified in the original data set. Analogous results were obtained with the dominant coding scheme and are available at our Web site.

Table 4.

Selection Frequency of Main Effects and Interactions by DICE on 100 Bootstrap Replicates of the SELP Dataset Using the Codominant Coding Scheme

Main effect	Selection frequency	First-order interaction	Selection frequency	Second-order interaction	Selection frequency
T715P	61	T715P*T741T	46	S290N*N562D*V599L	52
N562D	18	S290N*N562D	44	S290N*N562D*C-2123G	13
T741T	6	country*T-1817C	19	S290N*N562D*T741T	10
T-1817C	4	V599L*T715P	16	S290N*N562D*-485I/D	6
-485I/D	4	N562D*-485I/D	15	N562D*T-1817C*T741T	5
A-1969G	3	country*N562D	15	N562D*C-2123G*V599L	5
V599L	2	N562D*T-1817C	13	S290N*N562D*A-1969G	4
S290N	1	country*T715P	11	N562D*V599L*A-1969G	4
C-2123G	1	country*C-2123G	11	N562D*V599L*C-2123G	4
		N562D*T715P	10	country*S290N*N562D	4

n = 1147. The first 10 ranked interactions are shown. In bold are the effects selected in the original dataset

DISCUSSION

The concomitant availability of an increasing amount of genetic data, large study samples, and computer power offers a new opportunity to assess multilocus associations in a more systematic fashion than ever before and to build models that may reveal hidden association structure. Different methods, reviewed above in the introductory text, have been proposed for the identification of multilocus combinations associated with disease risk or quantitative traits in association studies. Each method has advantages and drawbacks. However, as stressed in a recent editorial (Spence et al. 2003), there is no “sole true path”, especially in the domain of complex traits, rather, several complementary approaches which might cast different lights on the problem under study. Overall, in the domain of data mining, it is the replication of results which constitutes the most important step.

The method proposed here combines the advantages of exploration tools with those of the regressive approach, such as easily interpretable modeling and the possibility of incorporating adjustment covariates, while trying to overcome some methodological difficulties of parametric methods related to hypothesis testing. Among other problems of the classical parametric selection procedures are those of multiple testing correction and the asymptotic distribution, under the null hypothesis, of the tests performed for each variable (Derksen and Keselman 1992). Because the choice of models in DICE is based on an IC, it circumvents problems related to the null-hypothesis testing theory (Johnson 1999). The method respects the particularity of genetic data by allowing the detection of interactions between markers in the absence of marginal effect. By alternating exploration and conditional exclusion phases, it can identify complex relationships between variables that may be missed using other techniques.

The algorithm is fully automated, making the tool easy to use without any a priori hypothesis. It could be used in different situations, such as the exploration of several polymorphisms within a gene, as we did in the SELP and the CETP applications, or the investigation of several genes belonging to a common biological system, as we did with the RAA system. We note that the main purpose of the method is not to provide estimates of parameters and of their variances, nor to make inferences about the sampled population, but to identify a subset of variables and effects that would deserve further detailed analysis using other complementary methods, such as haplotype analysis or multivariate analysis, or would require further investigation in replication studies. This is a data mining method useful as an exploratory tool for data reduction and variable detection.

Several aspects of the method deserve discussion. We based the model selection procedure on information theory and not on the classical hypothesis testing theory for several reasons. First, in a context of data mining and hypothesis generation, the use of the null-hypothesis testing theory seemed conceptually counterintuitive (there is no real null-hypothesis to test), generating practical difficulties related to multiple testing as mentioned above. Second, when many models are considered, it may happen that several of them fit the data almost equally well. By selecting a single model, the null-hypothesis testing theory ignores model uncertainty and potential ambivalence of the data. Furthermore, one particularity of genetic data is the correlation between genetic polymorphisms, through LD, that can lead to collinearity. Multicollinearity does not affect, in general, the overall fit of the model, (i.e., the likelihood) nor does it tend to bias the estimates, but regression coefficients will tend to have inflated sampling variances, leading to incorrect statistical tests (Neter et al. 1996). Finally, the IC, unlike the likelihood ratio test, allows the comparison of non-nested models. Among the numerous IC proposed in the literature, we chose the AIC_c (Hurvich and Tsai 1989) because it integrates the popular AIC and a correction for finite sample size, is easy to implement, and has operational properties that have been extensively evaluated (Burnham and Anderson 2002).

Another technical aspect of the algorithm concerns the thresholds adopted for the Δ_i and Δ_s parameters. The first threshold (Δ_i ≤ 2) is aimed at identifying models that could be considered as almost equivalent in terms of IC, while the second threshold (Δ_s > 4) is aimed at selecting a model which substantially improved the likelihood between steps. However, these guideline values must be considered as tuning parameters that can be modified to make the model selection more or less stringent according to the objective to be achieved.

Another important aspect of the algorithm is the principle of parsimony on which the model selection procedure is based. This principle, widely used in statistics, states that among two equivalent models in terms of IC, the one with the fewest parameters is to be preferred (Forster 2001). Different situations leading to `equivalent' models exist. One situation, which we actually encountered in our applications, is the case where an interaction term slightly improves the likelihood (Δ_i ≤ 2) but with a penalty of one extra-parameter. In that case, the principle of parsimony seems quite reasonable. Another situation, however, is the case where two different models, including completely different sets (and numbers) of markers, would have nearly the same AIC_c. In this case, the principle of parsimony might be questioned and one might consider the possibility of letting the tie models evolve in parallel. The practical consequences of relaxing the principle of parsimony will have to be further assessed. In order not to overload the algorithm with too many tie models, one may wish to discard, prior to analysis, the polymorphisms which are in nearly complete association.

Finally, DICE, as other combinatorial methods (Nelson et al. 2001; Ritchie et al. 2001), can be computationally intensive when a large number of polymorphisms needs to be evaluated. The exploration of biological systems involving hundreds of polymorphisms will require robust machine-learning algorithms, because all possible multilocus combinations (and potential environmental factors) cannot be exhaustively searched. Further research is needed to optimize the selection procedure of polymorphisms in the context of large-scale explorations.

The three applications described here showed that the algorithm was able to recover the polymorphisms that were previously identified by haplotype analysis (Tregouet et al. 2002) or multivariate regression analysis (Tiret et al. 1994; Corbex et al. 2000). Furthermore, it identified other polymorphisms that might be of interest, such as the V599L and the T741T polymorphisms of the SELP gene which were not detected by haplotype analysis. Applications of the algorithm to other genes are available at our Web site. Importantly, these applications suggested that the algorithm had no tendency towards overfitting, since for several genes, no effect of any polymorphism was detected. In the application to the RAA system, only the interaction previously described (Tiret et al. 1994) was identified and no other multilocus effect was detected, despite the fact that four different genes of the system were analyzed. Finally, in the preliminary stability study, the most frequently selected effects were those identified in the original data set. A simulation study is ongoing for investigating the properties of the algorithm in different data configurations in terms of stability of the results obtained, false negative and false detection rates.

Another important issue requiring further research is the handling of missing data, because this becomes a critical problem as the number of investigated polymorphisms increases. Variants of AIC have been proposed for model selection in the presence of incomplete data (Cavanaugh and Shumway 1998), which will have to be further explored. Another further development concerns the possibility of considering a hierarchical strategy of analysis when there is a mixture of intra-gene polymorphisms and polymorphisms belonging to different genes.