Skip to main content
PMC home page
Genome Research logoLink to Genome Research
letter
. 2003 Dec;13(12):2594–2601. doi: 10.1101/gr.1317703

Nucleotide Frequency Variation Across Human Genes

Elizabeth Louie 1, Jurg Ott 1, Jacek Majewski 1,1
PMCID: PMC403801  PMID: 14613976

Abstract

The frequencies of individual nucleotides exhibit significant fluctuations across eukaryotic genes. In this paper, we investigate nucleotide variation across an averaged representation of all known human genes. Such a representation allows us to average out random fluctuations that constitute noise and uncover remarkable systematic trends in nucleotide distributions, particularly near boundaries between genetic elements—the promoter, exons, and introns. We propose that such variations result from differential mutational pressures and from the presence of specific regulatory motifs, such as transcription and splicing factor binding sites. Specifically, we observe significant GC and TA biases (excess of G over C and T over A) in noncoding regions of genes. Such biases are most probably caused by transcription-coupled mismatch repair, an effect that has recently been detected in mammalian genes. Subsequently, we examine the distribution of all hexanucleotides and identify motifs that are overrepresented within regulatory regions. By clustering and aligning such sequences, we recognize families of putative regulatory elements involved in exonic and intronic splicing control, and 3′ mRNA processing. Some of our motifs have been identified in prior theoretical and experimental studies, thus validating our approach, but we detect several novel sequences that we propose as candidates for future functional assays and mutation screens for genetic disorders.

Eukaryotic genomes exhibit marked within-genome variations in the distributions of characteristic features such as density of genes, repetitive elements, recombination rates, and nucleotide content. The subject of this study, nucleotide composition, is known to vary within genomes at various levels of complexity. In warm-blooded vertebrates, isochores, extended chromosomal domains, which can be several megabases in length, are characteristically identified with elevated or decreased G + C content (Bernardi et al. 1985). Genes are preferentially located along GC-rich isochores (Mouchiroud et al. 1991).

At a finer scale, nucleotide content also varies within genes. Different parts of a gene (i.e., promoter, exon, intron, UTRs) have specific functional requirements. Most gene promoters contain elements such as the TATA box, the CAAT box, transcription factor binding sites, and CpG islands (Cross and Bird 1995; Takai and Jones 2002), characterized by high densities of the normally underrepresented CG dinucleotide. In expressed genes, promoters are unmethylated, which prevents mutational decay of cytosines and results in an increased GC level. Many common GC-rich regulatory elements are contained in the promoter region (Gardiner-Garden and Frommer 1987; Segal et al. 1999), further contributing to the specific nucleotide content of the promoter.

Exons, the protein-coding elements, have particular preferences regarding codon usage. They also need to be spliced, and therefore require splicing control elements (SCE), which will influence nucleotide content. A common exonic SCE is a GAA-containing motif (Ramchatesingh et al. 1995). Introns, although they have far fewer functional constraints than exons, must still contain intronic SCEs, which impose some conditions on their nucleotide content. For example, a GGG triplet is known to act as a common intronic splicing enhancer (McCullough and Berget 1997).

Finally, posttranscriptional 3′ pre-mRNA processing depends on certain enhancer motifs, such as the TG-rich or T-rich element, commonly present downstream of the poly(A) signal (Graber et al. 1999). Although the process is still poorly understood, the existence of additional upstream and downstream elements is also suspected (Colgan and Manley 1997; Moreira et al. 1998; Natalizio et al. 2002). The 3′-UTR is also known to contain binding sites for proteins involved in translation regulation and mRNA stability (Grzybowska et al. 2001).

Because of the above considerations, different parts of the gene are likely to possess characteristic nucleotide contents. Moreover, because regulatory elements are expected to be predominantly located at the boundaries of genetic regions (e.g., exon–intron boundaries or close to the transcription start and end positions), we should expect significant nucleotide variations within specific sections of genes.

Using the complete human genome sequence and its annotation (Lander et al. 2001; Kent et al. 2002), we look at nucleotide distribution across all human genes. Following Majewski and Ott (2002), we construct a model gene, which represents important characteristic genetic regions and contains information on nucleotide content averaged from all known human genes. First, we study the distribution of single nucleotides across the model gene and find drastic differences in position-specific nucleotide content, particularly near the boundaries of genetic elements. We postulate that the variations in nucleotide frequencies are largely caused by two factors: mutational pressures and the underlying distribution of common regulatory elements. Hence, we determine the frequencies of hexamer motifs within the model gene. By investigating the distribution of overrepresented motifs in candidate regulatory regions, we infer their functions as likely regulatory elements. We then use a method adapted from Fairbrother et al. (2002), to classify the elements into families and determine their characteristic sequences.

RESULTS

Single-Nucleotide Distribution

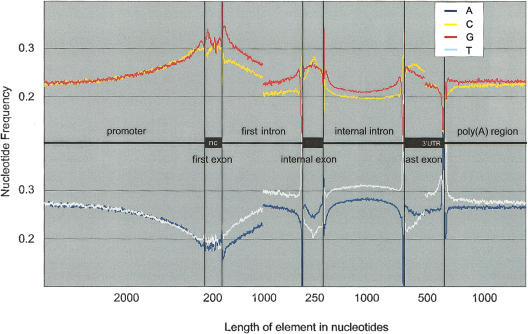
The distribution of single nucleotides in the model gene is shown in Figure 1. Note that all measures are taken on the sense strand. As expected, in the promoter region, there is an increase in C+G content and a decrease in A+T content. It has been shown earlier (Cross and Bird 1995; Majewski and Ott 2002), that this trend is mostly due to the presence of excess CpG dinucleotides, most likely associated with lack of methylation. The elevated C+G content generally continues within the first exons, and the first part (∼500 bp) of first introns. This is consistent with methylation patterns observed in empirical studies (Tomatsu et al. 2002).

Figure 1.

Figure 1

Open in a new tab

Single nucleotide frequency distribution in human genes. Note the fluctuations of nucleotide frequencies in the proximity of boundaries, such as splice sites, transcription initiation, and polyadenylation site. Such variations are probably caused by the presence of regulatory elements within those regions. Also note the GC and TA biases (skews) in all noncoding, transcribed portions of the genes. The biases reflect the mutation asymmetry on the sense and antisense strands, possibly caused by the action of transcription-coupled DNA repair.

Coding exons also have a generally elevated C+G content, but this is most likely caused by constraints imposed by the protein-coding function. However, the individual nucleotide content is not constant across exons. Exon edges are relatively A+T-rich, whereas the interiors are more C+G-rich. Also note that the GC bias (measured as G-'C) differs between the edges and the interior of exons. Particularly, near the 5′ exon edge of fully coding interior exons, the bias changes from positive (G-rich) to negative (C-rich). The variations within exons are likely to be caused at least in part by exonic regulatory elements.

The variation within introns is even more interesting. We have already noted the special characteristics of first introns. In the remaining introns, individual nucleotide frequencies are quite uniform, except for the first and last 150 bp. The 3′ intron ends are known to contain polypyrimidine tracts (PPT) and branch sites. This results in elevated C and T content within the last 40 nucleotides. Otherwise, both intron ends appear more or less symmetrical. The ends are C- and G-rich, resulting at least partly from the excess of GGG (involved in splicing regulation) and CCC (putative splicing regulatory element) trinucleotides (see Discussion).

Another notable feature of introns is an evident GC and TA bias—an excess of G over C and T over A. This bias persists in all noncoding, transcribed portions of genes. It is most likely caused by the action of the transcription-coupled DNA repair system (Green et al. 2003; see Discussion). The bias is detectable as far as 1000 bp past the end of transcription. This can be explained by the fact that transcription typically proceeds past the poly(A) signal and the pre-mRNA is then cleaved at the signal sequence before the addition of the poly(A) tail (Dye and Proudfoot 2001).

Finally, regions in the proximity of the polyadenylation site are A + T-rich and C + G-poor. This is most likely because of the presence of sequences necessary for the recognition of the poly(A) signal and final processing of the mRNA, as well as stability and translation control elements upstream of the poly(A) site.

Overrepresented Motifs

We postulate that the above variations are caused at least partly by differences in distribution of regulatory motifs that are specific to each region. Hence, we use the method described by Majewski and Ott (2002), where we compare the occurrence of a motif in a functional segment of a gene with the frequency of occurrence of the motif in likely nonfunctional sequences that do not lie within any known genes. The intergenic sequences serve as a control, and a statistically significant overrepresentation of a motif within a gene suggests functional significance (see Methods).

From variations of nucleotide frequencies in Figure 1, we selected regions of potential regulatory interest. These include noncoding internal exon ends (bases 5 to 55 and -55 to -5), intron ends (bases 5 to 55 and -95 to -45, excluding the PPT and branch site), 3′ processing (bases -55 to -5 of the last 3′-UTRs and bases 5 to 55 of the polyadenylation region). Note that the negative numbers refer to measurements from the 3′-ends of the respective elements. We analyzed a total of 2397 unique exons, 81,945 introns, and 13,054 polyadenylation regions. Within those regions, we measured the ratio R = O/E, where the observed count O is determined from the raw data, and the expected number E is calculated from local nucleotide frequencies, corrected for genome-wide biases, under the hypothesis of regulatory neutrality.

It is important to investigate only noncoding sequences, because motif frequencies within coding regions are governed by different sets of constraints, imposed by protein-coding functions, and should not be directly compared to noncoding sequences. Hence, we do not include coding exons in this part of the study. In addition, even though it would be interesting to extend our method to regions most likely to be involved in transcription control—the promoter, first exon, and first intron— those regions are known to be usually unmethylated, and they contain a large excess of all motifs containing the CpG dinucleotide. This excess may not necessarily be due to functional constraints, but could be a simple result of lack of methylation. Thus, at this point we choose not to investigate putative transcription regulatory motifs, and concentrate on noncoding, methylated regions of genes.

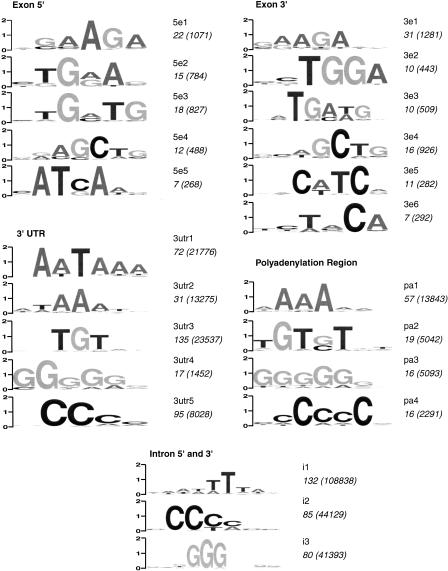
We have previously looked in detail at two particular motifs, CpG and GGG. Now we extend the analysis to all hexamers. We used a method derived from Fairbrother et al. (2002) to align and cluster all overrepresented motifs and determine consensus sequences representative of each family of putative regulatory elements. Figure 2 shows the results of the clustering analysis of all motifs that were significantly overrepresented in the above regions. Below we describe their potential roles as regulatory elements.

Figure 2.

Figure 2

Open in a new tab

Overrepresented motifs, corresponding to putative regulatory elements in human genes. Each sequence logo represents the consensus sequence of a family of regulatory elements determined by clustering and alignment of sequences within various regulatory regions. The vertical scale (bits) corresponds to the information content and degree of conservation. The name of each family appears to the right of the pictogram (e.g., 5e1 is the first exonic family in the 5′ exonic region). The number of distinct, overrepresented hexamer sequences contributing to the consensus alignment is shown under the name. The total number of such motifs within the human genes tested is shown in parentheses. Note that the total number of motifs includes overlapping sequences and is not equal to the number of regulatory elements present in the genome. It may be interpreted, however, as the relative importance of each family of putative regulatory elements.

Exonic SCEs

Our analysis uncovered five families of exonic splicing regulators at the 5′ regions of exons, and six families in the 3′ regions. The most overrepresented and abundant motif, at both exon ends, is the GAA-containing motif (5e1 and 3e1), with a GAAGAA consensus sequence. This motif is known to be a functional splicing enhancer (Ramchatesingh et al. 1995) and was also the top candidate in the computational approach of Fairbrother et al. (2002). Several of the motifs resemble known exonic splicing enhancers (see Discussion).

Intronic SCEs

Whereas putative exonic regulatory elements seem to cluster into families with rather distinct consensus sequences, intronic SCEs form clusters that are characterized by their nucleotide composition, rather than a particular DNA sequence. We recognize three families that are overrepresented at both intron edges: (1) G-rich sequences, containing a strong central GGG motif, known to be a functional intronic splicing enhancer (McCullough and Berget 1997); (2) C-rich sequences; and (3) AT-rich sequences. All three families are overrepresented at the 5′-ends of introns, and the 3′-ends (upstream of the PPT tract), but not in the interiors of introns. An excess of G-rich and C-rich sequence types is observed in all types of introns: low GC, mid-range GC, and high GC, as well as short (<200 bp) and long (>1000 bp) introns within each GC range. The AT-rich sequences are present in all introns, except for the short, GC-rich subset.

3′ mRNA Processing

Within the 3′-UTR, the two most abundant elements (3utr1 and 3utr2) represent the polyadenylation signal with a known consensus sequence AATAA. We also recognize a TGT-containing family, along with G-rich and C-rich sequences.

Within the polyadenylation region itself, we find four motifs: A-rich (this may be an artifact of mRNA amplification methods, see Discussion), C-rich, G-rich, and TGT elements. The last family constitutes a well-known downstream positioning element (Colgan and Manley 1997).

DISCUSSION

GC and AT Bias

One of the first discovered sets of rules governing the DNA content, known as Chargaff's rules or parity rules, postulate that over a large enough region, two DNA strands should be symmetrical in their nucleotide content (parity rule 2), that is, on each strand the frequencies of respective nucleotides obey the following equalities: C=G and A=T (Chargaff 1951; Forsdyke and Mortimer 2000; Baisnee et al. 2002). This rule may be violated in the presence of an asymmetry in mutation rates between the two strands (Francino and Ochman 1997). Such asymmetry does, indeed, occur, during the processes of replication and transcription. In bacteria and viruses that possess a single origin of replication, the leading strand is distinct from the lagging strand, resulting in a GC bias throughout the chromosome (Lobry 1996; Kano-Sueoka et al. 1999). Also, in bacteria it has been suggested and demonstrated (Beletskii and Bhagwat 1996; Francino and Ochman 2001) that during the transcription process, the untranscribed, single-stranded DNA becomes susceptible to mutation of cytosines into thymines by the process of deamination. Furthermore, repair of mutations on the untranscribed (also known as the sense, or plus) strand is thought to be less efficient than on the transcribed (antisense or minus) strand (Francino and Ochman 1997). Both processes may result in a GC bias (excess of G over C), in transcribed regions.

However, in eukaryotes, where multiple origins of replication exist, no systematic replication biases have been observed (there may exist localized effects near known replication origins; Francino and Ochman 2000). Similarly, because transcription is a local phenomenon, and genes can be coded on either DNA strand, the long-range effects of transcription-associated mutation/repair have not previously been analyzed in eukaryotes. It has been noted (e.g., Mrazek and Kypr 1994), that there exists an excess of T over A in eukaryotic introns, but such studies are usually carried out in the context of investigating codon bias and refrain from discussing the biases existing in noncoding sequences.

Transcription-associated effects are likely to be small and, because of stochastic variations, difficult to observe in single genes. Studies relying on a sliding window approach (e.g., Shioiri and Takahata 2001) fail to detect such minor fluctuations in nucleotide biases. In addition, transcription-associated effects are only going to be observable in a subset of genes—those expressed in the germ line—because only mutations occurring in the germ line are heritable. Our approach of averaging the entire gene complement within the genome allows us to average out the chance variations and observe the general effect of transcription on nucleotide content. Here, we show that all noncoding, transcribed regions (UTRs, introns) show systematic GC and TA biases. The biases are not observed prior to the transcription start (promoter region) but persist at least 1000 bp beyond the transcription poly(A) site. The maintenance of the transcription-related nucleotide biases beyond the end of transcribed regions sites may be puzzling at first sight. However, the “transcription end points” described in genomic databases are determined by the 3′-ends of the available mRNAs. In reality, it is known that transcription typically proceeds past the poly(A) signal, and that further cleavage of the RNA molecule is required before addition of the poly(A) tail and production of the mature mRNA (Dye and Proudfoot 2001). In some cases, the site of transcription termination may be as far as 2 kb beyond the polyadenylation signal. The persistence of the GC and TA biases shows that the above observation is true in general, and that in a significant number of genes, transcription proceeds at least 1 kb past the poly(A) site.

Concurrently with our observation of GC and TA biases in noncoding regions of human genes, Green et al. (2003) have published a comparative analysis of orthologous genomic regions of mammals, resulting in estimates of specific mutation rates occurring on complementary strands of DNA. This recent work sheds new light on the origins of compositional asymmetry in transcribed regions of mammalian genomes. The authors show that rates of complementary substitutions differ in transcribed sequences, and that this difference is expected to result in an excess of G+T over A+C on the coding strands of genes. In addition, their work strongly implies that the asymmetry in mutation rates is not the effect of increased deamination of cytosine (shown to occur in bacteria) but, rather, may be a byproduct of the mammalian transcription-coupled repair system.

Nucleotide Variation and Overrepresented Motifs

We hypothesize that at least a portion of the variation in single-nucleotide density across genes is caused by the presence of regulatory elements such as transcription regulators, splicing regulators, and motifs necessary for the termination of transcription and posttranscriptional processing of the 3′-end of the mRNA.

Our approach is suitable for detection of motifs involved in splicing regulation and 3′ mRNA processing. First, we investigated exonic splicing regulators. A similar analysis has been recently carried out by Fairbrother et al. (2002), but using a different set of criteria to detect overrepresented motifs. We expected that the result of our analyses should coincide, at least partially. In fact, two of our most overrepresented sequences, the GAA-containing motif (5e1, 3e1) and the GGA-containing motif (5e2, 3e2), were also the most prominent sequences in the Fairbrother et al. (2002) study and were experimentally shown to act as exonic splicing enhancers (Ramchatesingh et al. 1995; Fairbrother et al. 2002). We find this to be a validation of our approach. Two other motifs in our study, 5e5 and 3e5 (CATCA), were also highly similar to a sequence (5B/3A) implicated and later experimentally validated by Fairbrother et al. (2002), and are similar to the sequence WCATCGAYY, shown to bind the SRp20 protein in SELEX studies (Tacke et al. 1997). Two additional motifs, 5e4 and 3e4 (AGCTG), are similar to the TGCNGYY binding site of the SC35 protein, determined in functional SELEX studies (Schaal and Maniatis 1999), and the SRp40 binding site (Tacke et al. 1997). Finally, the TGATGA motif (5e3 and 3e3) is found in the human HPRT exon 3 enhancer (Steingrimsdottir et al. 1992).

It is worth noting that our most common exonic SCE candidates are G- and A-rich. In Figure 1, we see that exon edges exhibit an increase in the frequency of G relative to C, and A relative to T. This agrees well with our hypothesis that the variation in nucleotide frequencies across exons, introns, and other genetic elements is due to the variation in distribution of regulatory elements, particularly due to their increased density in the vicinity of genetic boundaries.

In an earlier study of intronic SCEs, we have previously shown (Majewski and Ott 2002) that the GGG trinucleotide is overrepresented in the proximity of both intron edges. The GGG motif has been empirically determined to act as an intronic splicing enhancer (McCullough and Berget 1997). In this study, we extend the earlier results to detect other putative intronic SCEs. As expected, we identify the GGG-containing element (i3), which using the present method we can define as a GGG triplet in a G-rich context. This is not surprising, because splicing efficiency has been shown to increase with the number of GGG triplets present (McCullough and Berget 1997). Hence, the G-rich context is probably the result of several GGG triplets present in close proximity.

The second putative intronic SCE identified in this study is a C-rich sequence (i2). This motif is present in excess near both 5′ and 3′ intron edges. We have previously suggested that the CCC triplet may be involved in the splicing process (Majewski and Ott 2002), but this hypothesis has not so far been confirmed experimentally. Note that the CCC and GGG triplets are not simply complementary motifs on complementary strands, because all nucleotide counts are determined on the sense strand. Neither the GGG nor the CCC motif is significantly overrepresented in the interior of introns, indicating that their excess is not a result of transcription-related effects—such as transcription-coupled DNA repair—again, implying functional importance.

We also find that intron edges contain an excess of AT-rich elements (i1). We have previously suggested that AT-rich elements may be involved in splicing control (Majewski and Ott 2002); however, we used a very different approach based on identifying simple repeats and low-complexity regions using RepeatMasker. Here, we confirm and extend the earlier result using a new method. Although AT-rich sequences have not been considered as SCEs in mammals, they have been shown to act as intronic splicing enhancers in plants (McCullough and Schuler 1997).

Once again, we note that intron edges are relatively G-, C-, and T-rich, while being A-poor. This is probably the effect of an increased density of intronic SCEs, which are predominantly G-, C-, and T-rich sequences (Fig. 2). It is also important to point out that the variations in nucleotide densities are not simply the result of short introns being, in general, GC-rich relative to longer introns (Lander et al. 2001). In our combined analysis, both short and long introns contribute to the calculation of nucleotide frequencies near the edges, whereas only longer introns (GC-poor) contribute to the numbers further away from the edges. This fact may be used to explain the variation in individual nucleotide frequencies. However, we find that similar, although less pronounced, variations are observed even when only long introns (>1000 bp) are considered in the analysis (data not shown). Hence, we suggest the possibility that short introns may be GC-rich not exclusively because they are situated in GC-rich isochores, but also because they contain a high proportion of SCEs, which are predominantly GC-rich.

3′-UTRs contain binding sites for various regulatory proteins, such as the PUF or CPEB binding sites (Grzybowska et al. 2001; Wickens et al. 2002), as well as elements necessary for final processing of pre-mRNA, recognition of the poly(A) site, and the subsequent addition of the poly(A) tail (Dichtl and Keller 2001). The poly(A) processing signal, also known as the positioning element (Graber et al. 1999, 2002), has a well-known canonical consensus sequence AATAAA. Cleavage and addition of the poly(A) tail occurs at a consensus CA dinucleotide (but other motifs are often recognized) immediately downstream of the signal sequence. However, because such elements are abundant in the genome, it is well known that additional regulatory elements need to be recognized to properly process the 3′-end of premRNA (Graber et al. 1999; Dichtl and Keller 2001). In yeast, there are both upstream and downstream sequences that are known to enhance processing efficiency (Graber et al. 2002). In mammals, our understanding of 3′-end processing motifs is poorer, but there is at least one known sequence, the T-rich or TG-rich downstream element (McLauchlan et al. 1985), that is required for the recognition of the poly(A) signal. Several statistical approaches to further define the poly(A) signals exist, but most of them are based on position-specific nucleotide weight matrices (Tabaska and Zhang 1999), which are not optimal for recognizing specific elements that may be present at various distances from the signal sequence.

Within the 3′-UTR, our analysis correctly identifies the poly(A) signal sequence (3utr1, 3utr2). However, our most abundant family of motifs is the TGT-containing element (3utr3), which is usually present slightly upstream of the poly(A) signal. This element is similar to the TGT-containing binding site of the PUF family of mRNA-binding regulatory proteins (Zamore et al. 1999). It is also similar to the upstream sequence element (USE) implicated in two isolated 3′ mRNA processing studies in yeast (Moreira et al. 1998; Natalizio et al. 2002). Because such elements are both overrepresented and frequent (>20,000 detected in our sample), we propose that they constitute a general class of USEs, similar to those present in yeast and plants (Graber et al. 1999). It will be interesting to determine whether TGT-containing elements are mostly responsible for poly(A)-site selection, or regulatory functions related to PUF proteins.

On both sides of the poly(A) addition site, we find an excess of G-rich elements (upstream 3utr4 and downstream pa3) and C-rich elements (upstream 3utr5 and downstream t4). Interestingly, the excess of C-rich and G-rich sequences in both intronic and 3′ mRNA regulatory regions may be explained by the observation that the polyadenylation machinery may use splicing factors and associated sequence elements (Colgan and Manley 1997).

Finally, downstream of the poly(A) site we identify the known TG-rich downstream element (McLauchlan et al. 1985), which we find to have a TGTGTGT consensus sequence (pa2). We also find a very significant excess of A-rich sequences (pa1). However, it is likely that the overrepresentation of long A-runs is an artifact related to amplification of ESTs and database annotation (Beaudoing and Gautheret 2001). Internal priming from A-rich sequences sometimes results in recovery of mRNAs that are incomplete at the 3′-end, and the sequences that were used for priming are subsequently overrepresented in the region immediately downstream of the falsely annotated poly(A) signal.

In summary, we have analyzed the spatial distribution— with respect to the boundaries of genetic elements—of single nucleotides in human genes. We found strong GC and TA biases in all noncoding sequences, an effect of transcription-associated, strand-specific asymmetry of mutation rates. In addition, we found the nucleotide distribution to vary across genes and, in particular, in the proximity of the boundaries, such as the transcription start, splice sites, and the poly(A) signal. We postulate that the variation is the result of the presence of regulatory elements, such as transcription factor binding sites and splicing factor binding sites. Using a method based on identifying overrepresented hexamer motifs, followed by clustering and alignment of the selected sequences, we discovered several families of putative regulatory elements. Some of our candidates have already been identified in prior computational and experimental screens. The others are likely to constitute novel regulatory motifs that should be considered for empirical validation.

METHODS

Database

We used the November 2002 human genome annotation of the University of California, Santa Cruz human genome browser (Lander et al. 2001; Kent et al. 2002; http://genome.cse.ucsc.edu). To avoid interspersed repeats that have not yet reached equilibrium with the rest of the genome, we used RepeatMasker (A.F.A. Smit, unpubl.; http://ftp.genome.washington.edu/RM/RepeatMasker.html) to mask all interspersed repeats (but not simple repeats and low complexity regions.) We used only genes with putatively complete coding sequences, beginning with an ATG start codon and ending with a stop codon, from the known human gene annotation (RefSeq). We found that ∼15% of the genes in the database did not translate into the corresponding proteins. This is most likely because of inefficiency of BLAT as a tool for precise mapping of mRNA to genomic sequence. If possible, we corrected the gene annotation to force the correct translation. Otherwise, we discarded the genes containing errors.

All of the analyses presented here were carried out on the entire RefSeq gene annotation. To exclude the possibility of isochore-specific effects, we also repeated the analyses on three subsets of the gene complement: GC-rich (>46% G+C), GC-average (42%–46%), and GC-poor (<42%). The GC context of each gene was calculated as the average GC content of the 50-kb region ending 500 bp upstream of the transcription start, and the 50-kb region beginning at 500 bp past the poly(A) site of the gene. In addition, to investigate differences between introns of different lengths, within each GC range we also subdivided introns into short (<200 bp) and long (>1000 bp). The nucleotide variations, as well as families of putative regulatory elements, did not visibly differ across GC subsets. Thus, we present the results of the combined analyses.

Model Gene Analysis

The model gene is a composite of all known human genes (a total of 14,534 genes). The gene consists of a 2-kb promoter region, a first 200-bp noncoding exon, a 1-kb first intron, one 250-bp internal coding exon (representative of all coding exons), one 1-kb internal intron (representative of all internal introns), and a 500-bp terminal exon [irrespective of coding classification, including the poly(A) signal], followed by a 1000-bp polyadenylation region. Single-exon genes were excluded from the analysis. Although this is not the most general representation of a human gene, it is suitable for illustrating the properties of elements that frequently harbor regulatory regions: promoter, splice sites, and 3′ processing. We determined nucleotide contents (C, G, A, T) of all the elements and averaged them to obtain a value representative of a typical gene. For introns, the values are calculated for positions 1 to 500 bp from the 5′-end and -1 to -500 bp from the 3′-end (or 1 to n/2 and -1 to -n/2 for introns of length n, shorter than 1000 bp). The procedure is similar for exons, but for positions 1 to 125 and -1 to -125 (or 1 to n/2 and -1 to -n/2 for shorter exons). Because many introns and some exons are longer than the above limits, the curves for some of the nucleotide contents are discontinuous at the midpoint of the genetic elements. The observed genome-wide average values were calculated as follows: The content of the nucleotide X at position i within a particular genetic element is given by the total number of nucleotides X at positions i within the entire genome, divided by the total number of elements containing the position i, that is, being at least 2i in length. A similar approach was used for polynucleotide content, but using a sliding window of the size of the polynucleotide, beginning at position i.

To calculate the expected frequencies for polynucleotide motifs, we used local single-nucleotide content as calculated above, corrected for the genome-wide biases in the neutral (i.e., nonfunctional) occurrence of the motifs. Most biases in neutral noncoding sequences stem from mutational pressures. For example, the underrepresentation of the CpG dinucleotide results from hypermutation of the methylated cytosine. The general overrepresentation of repetitive motifs (e.g., single-nucleotide runs, or tandem repeats) results from polymerase stutter during replication (Burge et al. 1992). To determine these systematic average biases, we determined individual nucleotide and motif frequencies in noncoding (according to the present annotation) regions found at a distance 5–20 kb from known genes. For each gene, to identify a corresponding nonfunctional sequence, we sequentially searched the upstream and downstream genomic regions for 1000-bp segments that were within 5–20 kb from the gene of interest, and at least 5 kb away from any other gene. This search method resulted in a >99% success rate of finding a noncoding sequence matched with each gene.

Consider, in a neutral control sequence, the expected frequency (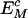Inline graphic) of a motif M of length L bases, to be equal to the product of the frequencies of individual component bases, the total number of motifs present (Nc), and a correction factor (CM). The correction factor represents the functionally neutral bias in motif representation. Thus

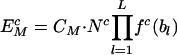graphic file with name M2.gif 1

where fc(bl) are the frequencies of individual bases. The correction factors are then calculated by setting 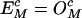Inline graphic in the neutral sequence set. Hence,

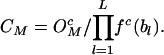graphic file with name M4.gif

After determining each correction factor from neutral sequences, the expected motif frequencies in potentially functional regions (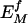Inline graphic, where the superscript f indicates functional, as opposed to control sequence) are then calculated according to equation 1, but using locally determined nucleotide frequencies ff (bl) and total motif count (Nf). Thus, the ratio of observed to expected counts

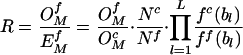graphic file with name M6.gif 2

The first factor in equation 2 may be viewed as a comparison of observed counts between the functional region and the control region, the second factor corrects for the differences in sizes of the two regions, whereas the third factor corrects for possible differences in individual nucleotide frequencies. Alternatively, equation 2 can also be viewed as R = Rf / Rc, where Rf is the ratio of observed to expected (based on the M0 Markov model) word frequencies in the functional region, and Rc is the corresponding ratio in the control region. Thus, our method compares the distribution of a motif within a candidate regulatory region to its expected distribution in a neutral sequence; it rejects motifs that are abundant throughout the genome simply because of mutational pressures. One potential drawback of our approach is that it does not account for differences in mutational rates in transcribed and untranscribed regions that we have described during this investigation.

It had been noted that the representation ratio (R) of the type calculated above does not adequately reflect the effect of self-overlapping motifs (Leung et al. 1996) and that normalized z-scores (Prum et al. 1995; Schbath 2000) should be the preferred statistic. However Leung et al. (1996) also show that R and z-scores are highly correlated (Spearmann r = 0.99 for words up to five letters in viral sequences). This correlation should be even more pronounced in larger sets of sequence, such as the one considered in our study. Because the variance of the expected motif count (and hence the z-score) in equation 2 is difficult to derive, we use the ratio R as the measure of overrepresentation and putative regulatory importance of candidate motifs. The significance of the deviation R > 1 can be assessed using a simple χ2 test, where 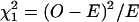Inline graphic, where the expected count is defined in equation 2. A Bonferroni correction was applied by multiplying the resulting P values by 4N, where N is the number of nucleotides in the motif. Note that the Bonferroni correction is conservative, because of the nonindependence of occurrence of overlapping motifs.

Candidate Regulatory Motifs

We searched for putative regulatory motifs in the following gene regions: (1) Noncoding exons (exonic splicing regulators). We excluded first exons to avoid unmethylated, CpG rich regions. (2) Introns (intronic splicing regulators). Once again, we excluded first introns to avoid unmethylated sequences. (3) 3′-UTR (3′ mRNA processing, translation control). (4) Sequence immediately following the poly(A) signal (3′ mRNA processing). Within each region of interest, we excluded the first five bases immediately adjacent to the region boundary, to avoid consensus sequences [such as the splice donor and acceptor sites, poly(A) site, etc.] that are known to be essential to determine the boundary. We then determined the relative overrepresentation (R) and the associated χ2 values for all motifs within the adjacent 50-nt interval.

Because the number of overrepresented sequences within each region may be large, we used a method based on Fairbrother et al. (2002) to cluster sequences according to their similarity. This allowed us to determine consensus sequences representative of each family of putative regulatory sequences. First, the sequences were pairwise-aligned using CLUSTALW (Thompson et al. 1994) with default settings, and a distance matrix was constructed by assessing a distance of +1 for each mismatch and +1 for each shift. The sequences were then clustered using the UPGMA algorithm implemented in the PHYLIP package (Felsenstein 1989). Following Fairbrother et al. (2002), clusters were defined using an arbitrary dissimilarity cutoff, ensuring maximum stability of the clusters. To concentrate on the most significant families of general regulatory elements, only clusters containing four or more hexamers were used in further analysis. Within each cluster, sequences were then aligned using the multiple alignment algorithm in CLUSTALW. After alignment, the actual counts and extended nucleotide contexts of each hexamer were obtained from the human genomic sequence. The resulting consensus alignment for each putative family of regulatory elements was subsequently represented as a sequence logo (Schneider and Stephens 1990; http://weblogo.berkeley.edu/). The strength of the consensus at each position also allows us to determine whether a candidate motif is important in itself, is a part of a longer regulatory sequence, or contains a shorter motif.

Acknowledgments

This work was supported by grant HG00008 from the National Human Genome Research Institute. We thank Phil Green and an anonymous reviewer for helpful comments on the manuscript.

The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.

Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.1317703. Article published online before print in November 2003.

References

  1. Baisnee, P.F., Hampson, S., and Baldi, P. 2002. Why are complementary DNA strands symmetric? Bioinformatics 18: 1021-1033. [DOI] [PubMed] [Google Scholar]
  2. Beaudoing, E. and Gautheret, D. 2001. Identification of alternate polyadenylation sites and analysis of their tissue distribution using EST data. Genome Res. 11: 1520-1526. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Beletskii, A. and Bhagwat, A.S. 1996. Transcription-induced mutations: Increase in C to T mutations in the nontranscribed strand during transcription in Escherichia coli. Proc. Natl. Acad. Sci. 93: 13919-13924. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bernardi, G., Olofsson, B., Filipski, J., Zerial, M., Salinas, J., Cuny, G., Meunier-Rotival, M., and Rodier, F. 1985. The mosaic genome of warm-blooded vertebrates. Science 228: 953-958. [DOI] [PubMed] [Google Scholar]
  5. Burge, C., Campbell, A.M., and Karlin, S. 1992. Over- and under-representation of short oligonucleotides in DNA sequences. Proc. Natl. Acad. Sci. 89: 1358-1362. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Chargaff, E. 1951. Structure and function of nucleic acids as cell constituents. Fed. Proc. 10: 654-659. [PubMed] [Google Scholar]
  7. Colgan, D.F. and Manley, J.L. 1997. Mechanism and regulation of mRNA polyadenylation. Genes & Dev. 11: 2755-2766. [DOI] [PubMed] [Google Scholar]
  8. Cross, S.H. and Bird, A.P. 1995. CpG islands and genes. Curr. Opin. Genet. Dev. 5: 309-314. [DOI] [PubMed] [Google Scholar]
  9. Dichtl, B. and Keller, W. 2001. Recognition of polyadenylation sites in yeast pre-mRNAs by cleavage and polyadenylation factor. EMBO J. 20: 3197-3209. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Dye, M.J. and Proudfoot, N.J. 2001. Multiple transcript cleavage precedes polymerase release in termination by RNA polymerase II. Cell 105: 669-681. [DOI] [PubMed] [Google Scholar]
  11. Fairbrother, W.G., Yeh, R.F., Sharp, P.A., and Burge, C.B. 2002. Predictive identification of exonic splicing enhancers in human genes. Science 297: 1007-1013. [DOI] [PubMed] [Google Scholar]
  12. Felsenstein, J. 1989. PHYLIP—Phylogeny Inference Package (Version 3.2). Cladistics 5: 164-166. [Google Scholar]
  13. Forsdyke, D.R. and Mortimer, J.R. 2000. Chargaff's legacy. Gene 261: 127-137. [DOI] [PubMed] [Google Scholar]
  14. Francino, M.P. and Ochman, H. 1997. Strand asymmetries in DNA evolution. Trends Genet. 13: 240-245. [DOI] [PubMed] [Google Scholar]
  15. Francino, M.P. and Ochman, H. 2000. Strand symmetry around the β-globin origin of replication in primates. Mol. Biol. Evol. 17: 416-422. [DOI] [PubMed] [Google Scholar]
  16. Francino, M.P. and Ochman, H. 2001. Deamination as the basis of strand-asymmetric evolution in transcribed Escherichia coli sequences. Mol. Biol. Evol. 18: 1147-1150. [DOI] [PubMed] [Google Scholar]
  17. Gardiner-Garden, M. and Frommer, M. 1987. CpG islands in vertebrate genomes. J. Mol. Biol. 196: 261-282. [DOI] [PubMed] [Google Scholar]
  18. Graber, J.H., Cantor, C.R., Mohr, S.C., and Smith, T.F. 1999. In silico detection of control signals: mRNA 3′-end-processing sequences in diverse species. Proc. Natl. Acad. Sci. 96: 14055-14060. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Graber, J.H., McAllister, G.D., and Smith, T.F. 2002. Probabilistic prediction of Saccharomyces cerevisiae mRNA 3′-processing sites. Nucleic Acids Res. 30: 1851-1858. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Green, P., Ewing, B., Miller, W., Thomas, P.J., and Green, E.D. 2003. Transcription-associated mutational asymmetry in mammalian evolution. Nat. Genet. 33: 514-517. [DOI] [PubMed] [Google Scholar]
  21. Grzybowska, E.A., Wilczynska, A., and Siedlecki, J.A. 2001. Regulatory functions of 3′UTRs. Biochem. Biophys. Res. Commun. 288: 291-295. [DOI] [PubMed] [Google Scholar]
  22. Kano-Sueoka, T., Lobry, J.R., and Sueoka, N. 1999. Intra-strand biases in bacteriophage T4 genome. Gene 238: 59-64. [DOI] [PubMed] [Google Scholar]
  23. Kent, W.J., Sugnet, C.W., Furey, T.S., Roskin, K.M., Pringle, T.H., Zahler, A.M., and Haussler, A.D. 2002. The Human Genome Browser at UCSC. Genome Res. 12: 996-1006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Lander, E.S., Linton, L.M., Birren, B., Nusbaum, C., Zody, M.C., Baldwin, J., Devon, K., Dewar, K., Doyle, M., FitzHugh, W., et al. 2001. Initial sequencing and analysis of the human genome. Nature 409: 860-921. [DOI] [PubMed] [Google Scholar]
  25. Leung, M.Y., Marsh, G.M., and Speed, T.P. 1996. Over- and underrepresentation of short DNA words in herpesvirus genomes. J. Comput. Biol. 3: 345-360. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Lobry, J.R. 1996. Asymmetric substitution patterns in the two DNA strands of bacteria. Mol. Biol. Evol. 13: 660-665. [DOI] [PubMed] [Google Scholar]
  27. Majewski, J. and Ott, J. 2002. Distribution and characterization of regulatory elements in the human genome. Genome Res. 12: 1827-1836. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. McCullough, A.J. and Berget, S.M. 1997. G triplets located throughout a class of small vertebrate introns enforce intron borders and regulate splice site selection. Mol. Cell. Biol. 17: 4562-4571. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. McCullough, A.J. and Schuler, M.A. 1997. Intronic and exonic sequences modulate 5′ splice site selection in plant nuclei. Nucleic Acids Res. 25: 1071-1077. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. McLauchlan, J., Gaffney, D., Whitton, J.L., and Clements, J.B. 1985. The consensus sequence YGTGTTYY located downstream from the AATAAA signal is required for efficient formation of mRNA 3′ termini. Nucleic Acids Res. 13: 1347-1368. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Moreira, A., Takagaki, Y., Brackenridge, S., Wollerton, M., Manley, J.L., and Proudfoot, N.J. 1998. The upstream sequence element of the C2 complement poly(A) signal activates mRNA 3′ end formation by two distinct mechanisms. Genes &Dev. 12: 2522-2534. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Mouchiroud, D., D'Onofrio, G., Aissani, B., Macaya, G., Gautier, C., and Bernardi, G. 1991. The distribution of genes in the human genome. Gene 100: 181-187. [DOI] [PubMed] [Google Scholar]
  33. Mrazek, J. and Kypr, J. 1994. Biased distribution of adenine and thymine in gene nucleotide sequences. J. Mol. Evol. 39: 439-447. [DOI] [PubMed] [Google Scholar]
  34. Natalizio, B.J., Muniz, L.C., Arhin, G.K., Wilusz, J., and Lutz, C.S. 2002. Upstream elements present in the 3′-untranslated region of collagen genes influence the processing efficiency of overlapping polyadenylation signals. J. Biol. Chem. 277: 42733-42740. [DOI] [PubMed] [Google Scholar]
  35. Prum, B., Rodolphe, F., and de Turckheim, E. 1995. Finding words with unexpected frequencies in deoxyribonucleic acid sequences. J. R. Statist. Soc. B 57: 205-220. [Google Scholar]
  36. Ramchatesingh, J., Zahler, A.M., Neugebauer, K.M., Roth, M.B., and Cooper, T.A. 1995. A subset of SR proteins activates splicing of the cardiac troponin T alternative exon by direct interactions with an exonic enhancer. Mol. Cell. Biol. 15: 4898-4907. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Schaal, T.D. and Maniatis, T. 1999. Selection and characterization of pre-mRNA splicing enhancers: Identification of novel SR protein-specific enhancer sequences. Mol. Cell. Biol. 19: 1705-1719. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Schbath, S. 2000. An overview on the distribution of word counts in Markov chains. J. Comput. Biol. 7: 193-201. [DOI] [PubMed] [Google Scholar]
  39. Schneider, T.D. and Stephens, R.M. 1990. Sequence logos: A new way to display consensus sequences. Nucleic Acids Res. 18: 6097-6100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Segal, J.A., Barnett, J.L., and Crawford, D.L. 1999. Functional analyses of natural variation in Sp1 binding sites of a TATA-less promoter. J. Mol. Evol. 49: 736-749. [DOI] [PubMed] [Google Scholar]
  41. Shioiri, C. and Takahata, N. 2001. Skew of mononucleotide frequencies, relative abundance of dinucleotides, and DNA strand asymmetry. J. Mol. Evol. 53: 364-376. [DOI] [PubMed] [Google Scholar]
  42. Steingrimsdottir, H., Rowley, G., Dorado, G., Cole, J., and Lehmann, A.R. 1992. Mutations which alter splicing in the human hypoxanthine-guanine phosphoribosyltransferase gene. Nucleic Acids Res. 20: 1201-1208. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Tabaska, J.E. and Zhang, M.Q. 1999. Detection of polyadenylation signals in human DNA sequences. Gene 231: 77-86. [DOI] [PubMed] [Google Scholar]
  44. Tacke, R., Chen, Y., and Manley, J.L. 1997. Sequence-specific RNA binding by an SR protein requires RS domain phosphorylation: Creation of an SRp40-specific splicing enhancer. Proc. Natl. Acad. Sci. 94: 1148-1153. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Takai, D. and Jones, P.A. 2002. Comprehensive analysis of CpG islands in human Chromosomes 21 and 22. Proc. Natl. Acad. Sci. 99: 3740-3745. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Thompson, J.D., Higgins, D.G., and Gibson, T.J. 1994. CLUSTAL W: Improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res. 22: 4673-4680. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Tomatsu, S., Orii, K.O., Islam, M.R., Shah, G.N., Grubb, J.H., Sukegawa, K., Suzuki, Y., Orii, T., Kondo, N., and Sly, W.S. 2002. Methylation patterns of the human β-glucuronidase gene locus: Boundaries of methylation and general implications for frequent point mutations at CpG dinucleotides. Genomics 79: 363-375. [DOI] [PubMed] [Google Scholar]
  48. Wickens, M., Bernstein, D.S., Kimble, J., and Parker, R. 2002. A PUF family portrait: 3′UTR regulation as a way of life. Trends Genet. 18: 150-157. [DOI] [PubMed] [Google Scholar]
  49. Zamore, P.D., Bartel, D.P., Lehmann, R., and Williamson, J.R. 1999. The PUMILIO–RNA interaction: A single RNA-binding domain monomer recognizes a bipartite target sequence. Biochemistry 38: 596-604. [DOI] [PubMed] [Google Scholar]

WEB SITE REFERENCES

  1. http://ftp.genome.washington.edu/RM/RepeatMasker.html; RepeatMasker.
  2. http://genome.cse.ucsc.edu; Santa Cruz human genome browser.
  3. http://weblogo.berkeley.edu/; Schneider and Stephens sequence logo.

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES