IMPACT OF VENTILATION FREQUENCY AND PARENCHYMAL STIFFNESS ON FLOW AND PRESSURE DISTRIBUTION IN A CANINE LUNG MODEL

Abstract

To determine the impact of ventilation frequency, lung volume, and parenchymal stiffness on ventilation distribution, we developed an anatomically-based computational model of the canine lung. Each lobe of the model consists of an asymmetric branching airway network subtended by terminal, viscoelastic acinar units. The model allows for empiric dependencies of airway segment dimensions and parenchymal stiffness on transpulmonary pressure. We simulated the effects of lung volume and parenchymal recoil on global lung impedance and ventilation distribution from 0.1 to 100 Hz, with mean transpulmonary pressures from 5 to 25 cmH₂O. With increasing lung volume, the distribution of acinar flows narrowed and became more synchronous for frequencies below resonance. At higher frequencies, large variations in acinar flow were observed. Maximum acinar flow occurred at first antiresonance frequency, where lung impedance achieved a local maximum. The distribution of acinar pressures became very heterogeneous and amplified relative to tracheal pressure at the resonant frequency. These data demonstrate the important interaction between frequency and lung tissue stiffness on the distribution of acinar flows and pressures. These simulations provide useful information for the optimization of frequency, lung volume, and mean airway pressure during conventional ventilation or high frequency oscillation (HFOV). Moreover our model indicates that an optimal HFOV bandwidth exists between the resonant and antiresonant frequencies, for which interregional gas mixing is maximized.

INTRODUCTION

The distributions of regional flow and pressure within the mammalian lung depend on impedances of the airways and parenchymal tissues, as well as the ventilatory parameters such as frequency, tidal excursions, and lung volume^2,9. In a recent study, we developed a computational lung model based on an asymmetric, binary tree data structure⁹. This model, consisting of over 450,000 discrete compartments for gas transport, allowed for a quantitative and computationally-efficient determination of ventilation distribution in healthy and injured canine lungs. These distributions were simulated over frequencies encompassing physiologic breathing, conventional ventilation, as well as high frequency oscillatory ventilation (HFOV). These simulations were also consistent with experimental data from alveolar capsule studies, which demonstrated that pressure transmission to the lung periphery is strongly dependent on ventilation frequency and parallel time constant heterogeneity^1–3,12. Similar to previous modeling studies of ventilation distribution^{6,13,18,33,34}, we assumed a linear and stationary representation of the mammalian lung, consisting of a branching network devoid of explicit anatomic detail. In addition, our simulations consisted of sinusoidal flow perturbations applied only at functional residual capacity (FRC), and did not account for variations in airway size or parenchymal stiffness with lung volume.

Due to their compliance, airway segments are known to vary their dimensions with transmural pressure³⁶. This results in alterations in anatomic dead space and effective airway impedance. In addition, parenchymal stiffness and viscoelasticity are complicated nonlinear functions of lung volume or distending pressure^15,20,28,30. Parenchymal recoil is known to increase with lung volume, due to increases in alveolar surface tension and progressive recruitment of collagen fibers in the connective tissue matrix^4,20. Such dependences on volume will affect regional and global impedances to flow within the lung, as well as the distribution of oscillatory flow and pressure throughout the periphery.

The goal of the current study was to enhance our existing computational model with volume-dependent mechanical properties of the airway tree and parenchymal tissues. Specifically we allowed airway segment lengths and diameters, as well as parenchymal viscoelasticity, to be empirically-dependent on distending transmural and transpulmonary pressures^20,36. We also incorporated into our model a more realistic representation of the central airway tree, consistent with actual canine bronchial anatomy⁴¹. We hypothesized that the inclusion of volume-dependent airway and tissue properties would have considerable influence on global mechanics, as well as regional flow and pressure distributions throughout the lung. With this model, we simulated the distribution of oscillatory flows and pressures over frequencies from 0.1 to 100 Hz and mean transpulmonary pressures of 5 to 25 cmH₂O. We expect that these simulations will allow for a more thorough understanding of the effects of frequency, lung volume, and parenchymal stiffness on global mechanical impedance and ventilation distribution throughout the lung.

METHODS

Model Structure

The central airway geometry of our model is based on the study of Woldehiwot and Horsfield⁴¹, consisting of nine distinct anatomic lobes. Each central bronchus is assigned to one of 47 specified order numbers (m), based on diameter indices detailed in the previous airway cast study of Horsfield et al.¹⁶. The detailed arrangement of the bronchial anatomy, with corresponding assigned orders, is shown in Figure 1-A. The terminal portions of this central airway tree are subtended by nine self-consistent binary tree structures. Asymmetry in each of these subtrees is accounted for by a recursion index, which is defined as the difference between orders of two sibling branches¹⁶. Figure 1-B shows an extension of the right diaphragmatic bronchus of the central airway tree, which begins with order number 44. The total number of airway segments in the complete model is 386,978, which includes 193,489 terminal branches.

Figure 1.

(A) Central airway tree used for canine lung model, as reported by Woldehiwot and Horsfield⁴¹. Numbers in the parentheses are the assigned order numbers for each airway segment. There are 47 distinct orders for this model, as reported by Horsfield et al.¹⁶. T: trachea; RM1: right main bronchus; RA: right apical bronchus; RC: right cardiac bronchus; RD: right diaphragmatic bronchus; RI: right intermediate bronchus; R1D: first branch of right diaphragmatic bronchus; LM1: left main bronchus; LA1: left apical bronchus; LA2: continuation of left apical bronchus; LC: left cardiac bronchus; LD1: left diaphragmatic bronchus; RM2, RM3: continuations of right main bronchus; LD2: continuation of left diaphragmatic bronchus. (B) Portion of the self-consistent airway tree subtending right diaphragmatic bronchus, with root assigned to order 44.

Each airway segment of order m in the model was assumed to be a simple distensible cylinder, with wall thickness h_m, length l_m, and internal radius r_m. Each l_m and r_m were dependent on transmural pressure (or mean transpulmonary pressure P̄_tp) according to the empiric relationship of Thorpe and Bates ³⁶:

$$l_m=l_{m,\mathit{TLC}}\left[{\beta }_m+(1-{\beta }_m){\left(\frac{{\overline{P}}_{tp}}{{\overline{P}}_{\mathit{TLC}}}\right)}^{1/3}\right]$$ (1)

$$r_m=r_{m,\mathit{TLC}}\left[{\beta }_m+(1-{\beta }_m){\left(\frac{{\overline{P}}_{tp}}{{\overline{P}}_{\mathit{TLC}}}\right)}^{1/3}\right]$$ (2)

where l_m,TLC and r_m,TLC denote the length and radius, respectively, of a m^th-ordered airway segment at total lung capacity (TLC). P̄_TLC is the mean transpulmonary pressure at TLC (assumed to be 25 cmH₂O), and β_m is a constant for each airway order given by³⁶:

$${\beta }_m=0.2+0.011m$$ (3)

The relationship between the pressure across and flow through each cylindrical segment is represented by a longitudinal impedance that accounts for viscous and inertial losses³⁷:

$$Z_{\mathit{seg},m}=\left(\frac{j\omega {\rho }_{\mathit{air}}{l}_m}{\pi r_m^2}\right){\left[1-\frac{2J_1\left({\alpha }_m\sqrt{-j}\right)}{{\alpha }_m\sqrt{-j}{J}_0\left({\alpha }_m\sqrt{-j}\right)}\right]}^{-1}$$ (4)

where j is the unit imaginary number, ω is the angular frequency, ρ_air is the saturated air density at 37 C (1.0855×10⁻⁴ cmH₂O s² dm⁻²), J₀ and J₁ are the complex Bessel functions of orders 0 and 1, respectively, and α_m is the so-called Womersley parameter⁴², given by:

$${\alpha }_m=r_m\sqrt{\frac{\omega {\rho }_{\mathit{air}}}{{\mu }_{\mathit{air}}}}$$ (5)

with μ_air being the viscosity of air (1.863 × 10⁻⁷ cmH₂O s). The longitudinal impedance Z_seg,m was partitioned into two equal halves by a shunt impedance corresponding to isothermal gas compression and viscoelastic wall distention⁹. The wall thickness for each segment varied with r_m according to⁴⁰:

$$h_m=\sqrt{r_m^2+\frac{A_m}{\pi }}-r_m$$ (6)

where A_m is the cross sectional area of the airway wall. The viscoelastic wall properties were assumed to arise from the distribution of soft tissue and cartilaginous component as previously described^14,19.

Each of the 193,489 terminal bronchioles in the model was subtended by a discrete acinar unit with index n. Each acinus consisted of a gas compression compliance (C_g,n), a tissue inertial element (I_ti,n), and viscoelastic constant-phase tissue impedance with parameters for tissue hysteresivity (η) and tissue elastance (H_n), all arranged to yield an effective acinar impedance (Z_acn,n):

$$Z_{\mathit{acn},n}={\left[j\omega C_{g,n}+\frac{{\omega }^{\alpha }}{j{\omega }^{\alpha +1}{I}_{ti,n}+(\eta -j)H_n}\right]}^{-1}$$ (7)

where α = (2/π) tan⁻¹ (1/η). We assumed that both η and H_n varied with P̄_tp according to the quadratic functions:

$$\eta =0.2832-0.0248{\overline{P}}_{tp}+0.0008{\overline{P}}_{tp}^2$$ (8)

$$H_n=2.223-0.066{\overline{P}}_{tp}+0.017{\overline{P}}_{tp}^2$$ (9)

where H_n is expressed in units of cmH₂O μL⁻¹. The coefficients of Equations 8 and 9 were estimated from our recently reported data of canine parenchymal viscoelasticity²⁰, using multiple linear regression (Figure 2). Thus according to Equations 8 and 9, the model predicts effective acinar tissue resistance to be (ηH_n)/ω^α, which will also increase with P̄_tp²⁰. The isothermal acinar gas compression compliance was also assumed to vary as a function of P̄_tp according to:

$$C_{g,n}=\frac{{\overline{V}}_{\mathit{acn},n}}{P_0-P_{H_{2}O}}$$ (10)

where P₀ is the atmospheric pressure at sea level (1033 cm H₂O), P_H2O is partial pressure of water vapor in saturated air at 37°C (64 cmH₂O), and V̄_acn,n denotes the mean acinar volume at the specified P̄_tp given by:

$${\overline{V}}_{\mathit{acn},n}=\frac{V_{\mathit{FRC}}}{N}+\underset{5}{\overset{{\overline{P}}_{tp}}{\int }}\frac{d\overline{P}}{H_n(P)}$$ (11)

Figure 2.

Relationship of H_n and η with distending pressure (P̄_tp), based on the data of Kaczka and Smallwood²⁰. Symbols are data averaged from 12 dogs, with error bars denoting standard errors of the mean. Solid lines denote quadratic fits to the experimental data as given by Equations 8 and 9.

The V_FRC denotes functional residual capacity for the entire canine lung (assumed to be 1.316 L in a 25 kg dog at P̄_tp = 5 cmH₂O)²⁹. We assumed a total parenchymal tissue inertance (I_ti) of 0.005 cmH₂Os²L⁻¹, according to values reported by Jackson and Lutchen¹⁷. This I_ti was evenly distributed across all acini as I _ti,n = I_ti × N.

Simulations

The complete model was stored explicitly in computer memory as a binary tree data structure⁹, which allowed for easy access to the airway segment dimensions and local impedances at every node. Anatomic dead space was determined by cumulative addition of all cylindrical airway segment volumes at distending pressures P̄_tp of 5, 10, 15, 20, and 25 cmH₂O. Total gas volume in the model at each P̄_tp was determined as the sum of the anatomic dead space to the sum of all acinar gas volumes, as computed according to Equation 11. The 193,489 pathlengths from trachea to each acinus were also determined for each P̄_tp by summation of airway segment lengths, and their corresponding distributions were examined using histograms with bin sizes of 0.15 cm. Mechanical impedance looking into each node of the tree was computed using our previously published recursive algorithm¹⁹, which employs complex summation of all airway, gas compressive, and parenchymal tissue impedances in the appropriate serial and parallel fashion. Total lung impedance (Z_L) was determined as the impedance looking into the trachea of the model, and was simulated for frequencies of 0.1, 1, 4, 7, 10, 20, 30, 40, 50, 60, 70, 80, and 100 Hz. Resonant frequency (f_r) at each P̄_tp was defined as the frequency at which lung reactance was zero. The antiresonant frequency (f_ar) was defined as the frequency above f_r for which the impedance magnitude achieved a local maximum. Linear interpolations between two adjacent frequencies were performed to estimate the locations of f_r and f_ar.

Although it is established that diffusion dominates molecular transport and gas exchange at the acinar level⁸, we assumed that the primary mechanism for bulk motion of gas from trachea to acinus is via advection. Oscillatory flow and pressure distributions throughout the entire tree were simulated for discrete, sinusoidal tracheal flows (V̇_tr) at the same frequencies and P̄_tp, using a recursive flow divider algorithm with a preorder tree traversal sequence⁹. All impedance values, flows, and pressures within the tree were complex values with both real and imaginary components, or equivalently, magnitudes and phases. To quantify the total flow lost to gas compression and airway wall distention as functions of frequency and P̄_tp, the flow at every node in the tree was partitioned, summed, and normalized by the corresponding V̄_tr to yield the net parenchymal flow, net gas compression flow, and net airway wall distention flow as previously described⁹. This allowed us to determine the actual portion of advective flow delivered to the parenchymal tissues. We confirmed that the total flow mass was conserved in the model simulations, as the complex summation of all of these flow components was exactly equivalent to V̇_tr, in terms of both magnitude and phase.

To quantify the distribution of ventilation, we examined histograms of acinar flows and pressures at each frequency and P̄_tp⁹. For these simulations, the term heterogeneity refers to the width of the amplitude distributions for flow or pressure, while asynchrony refers to the width of the corresponding phase distributions. Each acinar flow amplitude |V̇_acn,n| was normalized relative to what its value would be assuming that tracheal flow was equally distributed to all acini in a perfectly symmetric, homogeneous lung with rigid airway walls and no gas compression, independent of lung volume^9,13:

$$\frac{\left|{\stackrel{.}{V}}_{\mathit{acn},n}\right|}{\left|{\stackrel{.}{V}}_{tr}\right|/N}$$ (12)

Acinar pressure amplitudes were normalized relative to the tracheal pressure amplitude. The phases of the flows and pressures were normalized relative to the corresponding tracheal phase, constrained to be within ±180. Bin sizes for the normalized flow and pressure amplitudes were 0.025 and 0.005, respectively, and 1 for the phases. The algorithms were written and executed using MATLAB v7.0 (The Mathworks, Natick, MA). Total computation time for one simulation at a specified frequency and P̄_tp was approximately 18 minutes on a Dell Optiplex 980 desktop computer with an Intel® Core^™ i7 CPU 860 operating at 2.80 GHz with 3.42 GB RAM.

RESULTS

Figure 3-A shows the total anatomic dead space volume of the model as a function of distending pressure. Dead space demonstrated a near-linear dependence on P̄_tp, with values consistent with previous estimates for a dog of this size³⁸. Total gas volume in the model demonstrated a curvilinear relationship with P̄_tp as shown in Figure 3-B, consistent with nonlinear parenchymal stiffening of the acini (Figure 2). The distribution of pathlengths from trachea to each acinus at each P̄_tp in the model is shown in Figure 4. These distributions were largely unimodal, and demonstrated a rightward shift with increasing P̄_tp.

Figure 3.

(A) Anatomic dead space volume of the model as a function of mean distending pressure; (B) Total gas volume in the model as a function of distending pressure.

Figure 4.

Distribution of pathlengths from trachea to acini at mean distending pressures of 5, 10, 15, 20, and 25 cm H₂O. Each distribution consists of 193,489 pathlengths, with bin sizes of 0.15 cm.

Figure 5 shows the total lung impedance (Z_L) looking into the trachea versus frequency at all P̄_tp. The Z_L is expressed in terms of magnitude (|Z_L|), phase (Z_L), resistance (R_L), and reactance (X_L). Table 1 lists the values f_r and f_ar estimated from these Z_L at each P̄_tp. The |Z_L| demonstrated substantial positive dependence on P̄_tp for frequencies less than f_r. At all values of P̄_tp, |Z_L| decreased with increasing frequency, achieving a minimum at f_r. For frequencies between f_r and f_ar, |Z_L| decreased with increasing P̄_tp. Above f_ar, |Z_L| gradually converged to a line at all P̄_tp. Oscillatory pressure at the trachea was observed to lag flow below f_r, as indicated by negative values of Z_L at all P̄_tp. The Z_L crossed zero at f_r, and became positive at higher frequencies, indicating that oscillatory pressure led flow. Below f_r, R_L demonstrated a negative dependence on frequency at all P̄_tp. However, R_L increased above f_r, achieving a local maximum near the corresponding f_ar. R_L demonstrated a variable response to P̄_tp, with mainly a positive dependence below f_r, but negative dependence above f_ar. The X_L increased with frequency and decreased with P̄_tp for frequencies smaller than f_ar. A maximum value of X_L at each P̄_tp was also observed at frequencies lower than f_ar (Figure 6-D, inset).

Figure 5.

Total lung impedance Z_L looking into the trachea versus frequency at mean distending pressures of 5, 10, 15, 20, and 25 cm H₂O. Impedance is expressed as (A) magnitude; (B) phase; (C) resistance; and (D) reactance. Inverted triangles (▼) denote resonant frequency (f_r), while upright triangles (▲) denote anti-resonant frequency (f_ar).

Table 1.

Resonant and anti-resonant frequencies estimated from Z_L for mean distending pressure of 5 to 25 cmH₂O.

P̄tp (cm H2O)	Resonant Frequency (Hz)	Antiresonant Frequency (Hz)
5	5.25	43
10	5.89	35
15	7.19	31
20	8.82	30
25	10.75	33

Figure 6.

Summary of total tracheal flow partitioned into net parenchymal tissue flow, net gas compression flow, and airway wall shunting flow versus frequency for five different distending pressures. Inverted triangles (▼) denote resonant frequency (f_r), while upright triangles (▲) denote anti-resonant frequency (f_ar). Net flow magnitudes and phases are normalized relative to tracheal flow.

Figure 6 summarizes the effects of frequency and P̄_tp on the net acinar flow, net gas compression flow, net wall distension flow. At low P̄_tp and low frequencies, normalized acinar flow magnitude was close to unity, indicating minimal losses due to gas compression or airway wall distension. However at high P̄_tp and high frequencies this ratio became substantially less than unity, consistent with the corresponding increases in flow loss due to gas compression and wall distension. These simulations also demonstrated that normalized acinar flow decreased with increasing P̄_tp for frequencies less than 10 Hz. Acinar flow amplification occurred at frequencies higher than f_r, achieving maximum values close to f_ar at all P̄_tp. The largest flow amplification occurred at the lowest P̄_tp of 5 cm H₂O. Gas compressive and airway wall losses also increased with P̄_tp for frequencies less than f_r. Both of these flow losses achieved minima for frequencies slightly greater than f_r, then increased to a maximum near f_ar. For frequencies above f_ar, gas compressive losses were larger at lower P̄_tp. The magnitude of losses due to gas compression were comparable to losses due to airway wall distention, although the latter were consistently larger at each P̄_tp for frequencies less than f_r. The maximum flow loss due to airway wall distension appeared near f_ar. At all P̄_tp, net acinar flow lagged tracheal flow for frequencies above 20 Hz, approaching 180° near 100 Hz. Net gas compressive and wall distension flows generally led tracheal flow between 10 to 100 Hz. Both of these flow losses became out-of-phase with tracheal flow for frequencies above f_r, with the greatest differences occurring at lower P̄_tp. These phase angles led tracheal flow, with increasingly out-of-phase behavior above f_r. However they slightly lagged the tracheal flow at higher frequencies. Increased out-of-phase behavior of the wall distension flow was observed between f_r and f_ar at lower P̄_tp.

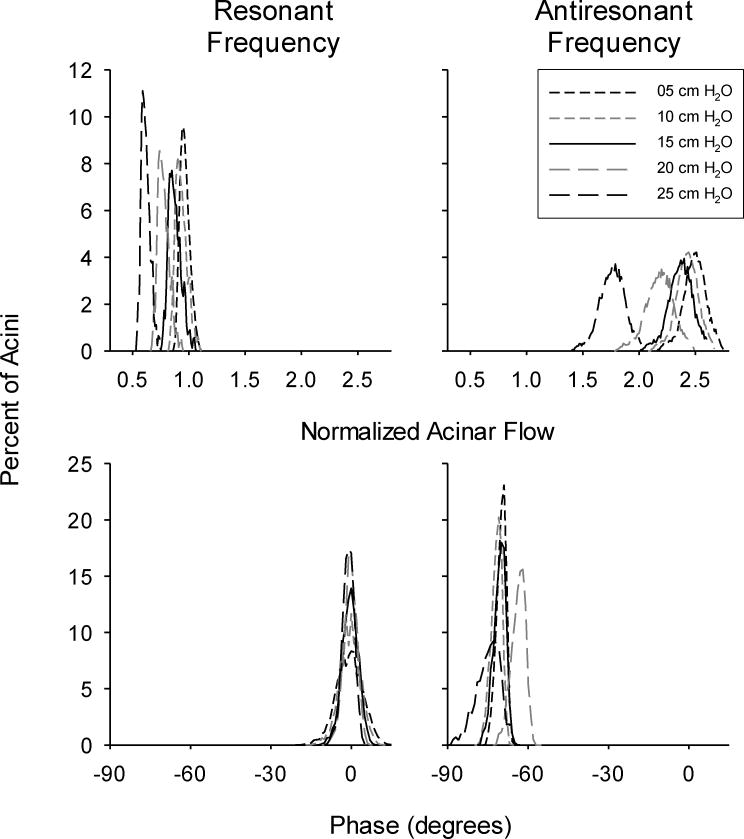
Figure 7 shows representative amplitude and phase distributions for the normalized acinar flows for all P̄_tp at f_r and f_ar. These distributions followed a Gaussian-like pattern. In general, the amplitude distributions widened with increasing frequency, and were shifted to the left with increasing P̄_tp. This is consistent with decreased ventilation to the acini, as greater portions of the tracheal flow will be shunted into gas compression and airway wall distention. Amplification of acinar flows relative to the normalized tracheal flow was observed at f_ar. At f_r acinar flows were generally in-phase with tracheal flow, although there was a tendency toward less asynchrony with decreasing P̄_tp. This was indicated by a narrowing of the corresponding phase distributions. At f_ar, acinar flows lagged tracheal flow, and asynchrony generally increased with P̄_tp.

Figure 7.

Representative histograms of acinar flow distributions at resonant (f_r) and antiresonant (f_ar) frequencies. Data are shown for mean distending pressures of 5, 10, 15, 20, and 25 cmH₂O. Magnitudes (left panels) are normalized relative to what the theoretical flow distribution would be in an entirely homogeneous lung with symmetric branching and rigid airway walls (Equation 12). Phases (right panels) are expressed relative to tracheal flow.

Figure 8 summarizes the normalized acinar flow amplitudes and phases for all P̄_tp and frequencies. These flows are presented as averaged values for all acini in the model (left panels), as well as standard deviations (right panels). The averaged flow amplitudes tended to decrease with increasing P̄_tp regardless of frequency. At all P̄_tp, averaged flow amplitudes achieved relative maxima at f_ar, with the greatest amplification occurring for P̄_tp = 5 cm H₂O. The standard deviations of these flow amplitudes were generally greatest between f_r and f_ar. Averaged acinar flows were generally in-phase with tracheal flow for frequencies less than 20 Hz, although these flows progressively lagged tracheal flow with increasing frequency. Moderate asynchrony in flow phase was observed between f_r and f_ar, as indicated by their corresponding standard deviations. Large asynchrony was observed above f_ar at all P̄_tp, as frequency approached 100 Hz.

Figure 8.

Averaged acinar flow (A) magnitudes and (B) phases, along with standard deviations of acinar flow (C) magnitudes and (D) phases. Data are shown for mean distending pressures of 5, 10, 15, 20, and 25 cmH₂O. Magnitudes are normalized relative to what the theoretical flow distribution would be in an entirely homogeneous lung with symmetric branching and rigid airway walls^9,13. Phases are expressed relative to tracheal flow. Inverted triangles (▼) denote resonant frequency (f_r), while upright triangles (▲) denote anti-resonant frequency (f_ar).

Representative distributions of normalized acinar pressures at f_r and f_ar are shown in Figure 9. Amplification of acinar pressures relative to tracheal pressure occurred at f_r. This oscillatory pressure amplification increased with increasing P̄_tp. At f_ar acinar pressures became attenuated relative to tracheal pressure, as well as more homogeneous as indicated by narrowing of their distribution widths. Acinar pressures also lagged tracheal pressure at f_r, and became less asynchronous with increasing P̄_tp. However at f_ar, acinar pressure asynchrony increased with increasing P̄_tp.

Figure 9.

Representative histograms of acinar pressure distributions at the resonant (f_r) and antiresonant (f_ar) frequencies. Data are shown for mean distending pressures of 5, 10, 15, 20, and 25 cmH₂O. Pressure magnitudes (left panels) and phases (right panels) are normalized relative to corresponding tracheal pressure.

Figure 10 summarizes the normalized acinar pressure amplitudes and phases for all P̄_tp and frequencies. Substantial pressure amplification was observed at frequencies greater than 1 Hz, with maxima occurring at f_r for each P̄_tp. Average acinar pressures generally lagged tracheal pressure, as indicated by negative phase angles for frequencies above 1 Hz. The greatest heterogeneity in acinar pressure occurred at f_r, as shown by the standard deviations of oscillatory pressure amplitudes. Acinar pressure asynchrony followed a very similar trend to that of the acinar flow.

Figure 10.

Averaged acinar pressure (A) magnitudes and (B) phases, along with standard deviations of acinar pressure (C) magnitudes and (D) phases. Data are shown for mean distending pressures of 5, 10, 15, 20, and 25 cmH₂O. Pressure amplitudes and phases are normalized relative to tracheal pressure. Inverted triangles (▼) denote resonant frequency (f_r), while upright triangles (▲) denote anti-resonant frequency (f_ar).

DISCUSSION

The design of optimal ventilation modalities for supportive therapy in acute and chronic lung diseases requires a thorough understanding of gas transport at the acinar level. Heterogeneity in peripheral flows and pressures may result in substantial over- or under-ventilation of lung regions, resulting in impaired gas exchange⁹. Since it is not possible to directly measure the flows and pressures within a representative number of acini in large mammals in vivo, we relied on a computational model of the canine lung to explore the effects of frequency and distending pressure on global mechanical properties and advective acinar ventilation distribution. We combined a realistic arrangement of canine central bronchi as determined by the cast study of Woldehiwot and Horsfield⁴¹, with subtending self-consistent airway tree structures¹⁶ to develop a model with more anatomic detail compared to previous modeling studies of ventilation distribution^9,13,18. Airway segment dimensions in our model varied according to the cube root of transmural pressure³⁶, affecting dead space volume, longitudinal airway segment impedances, and the distribution of pathlengths from trachea to acini. We also incorporated empiric dependencies of airway wall and parenchymal viscoelasticity on distending pressure, allowing for detailed predictions of local and global mechanical behavior, as well as the distribution of peripheral oscillatory flows and pressures over frequency ranges encompassing conventional ventilation and high frequency oscillation.

Global Mechanics

Global mechanical properties of the model were assessed according to its static pressure-volume characteristics (Figure 3), as well as its mechanical impedance to oscillatory flow at the trachea (Figure 5). The curvilinear relationship between total lung volume and distending pressure are consistent with parenchymal strain-stiffening and increases in alveolar surface tension, as predicted by increases in acinar tissue elastance with P̄_tp (Figure 2). Dynamic lung impedance, as a complex quantity, may be expressed in Cartesian coordinates, corresponding to energy dissipation (resistance, R_L) and energy storage (reactance, X_L). Impedance may alternatively be expressed in polar coordinates, with magnitude and phase components. Below 1 Hz where parenchymal viscoelasticity dominates mechanical behavior²⁰, increases in distending pressure resulted in increases in R_L and decreases in X_L. This is consistent with increases lung tissue resistance and elastance, respectively, as predicted by Equations 7 to 9. At higher frequencies where airway properties dominate mechanical behavior, R_L decreases with increases in P̄_tp, consistent with decreases in airway resistance due to increasing airway segment diameters (Equation 2).

We defined the resonant (f_r) and antiresonant (f_ar) frequencies for our model according to the local minimum and maximum of impedance magnitude¹⁷. In the nomenclature of other studies, f_r and f_ar may refer to the minimum and maximum, respectively, of lung resistance ^17,35. At the resonant frequency, the phase and reactance of lung impedance is zero, as the kinetic energy associated with gas acceleration in airways is transferred to the potential energy stored in the elastic recoil of the parenchyma, and vice-versa¹⁷. Thus at f_r, the lungs appear to offer a purely resistive pathway to oscillatory flow at the trachea²⁷. The resonant frequency can be approximated as:

$$f_r=\frac{\sqrt{E_L/I_L}}{2\pi }$$ (13)

where E_L and I_L denote the effective lung elastance and inertance, respectively²⁷. Thus our model predicts that f_r increases with distending pressure (Table 1), as parenchymal stiffness increases according to Equation 9. Moreover I_L, which is dominated by acceleration of gas in the central airways for frequencies close to f_r, decreases as airway segment radii increase with lung volume. While our simulations predict that lung resistance approaches a local minimum near f_r, the minimum resistance appeared at slightly higher frequency where the phase angle was not zero.

Our simulations also demonstrate that the frequency for which resistance is maximum may be slightly higher than f_ar, consistent with experimental results in rats³⁵. Our model predicts that f_ar ranges from 32 to 46 Hz for a 25 kg dog. Lutchen and Jackson estimated f_ar to be 97 ± 13 Hz in six mixed breed dogs weighing between 15 to 25 kg¹⁷. This discrepancy may be due to the different sizes of their canine lungs compared to our model, as smaller lungs will have relatively higher elastance. They postulated that in dogs, f_ar arises from the harmonic oscillation of gas compression with tissue inertia, both of which are independent of gas density. Similarly, Thamrin et al.³⁵ demonstrated that f_ar in rats was independent of inhaled gas density, but decreased with lung volume. Since the only density dependent element in our model was the longitudinal airway segment impedance (Equation 4), our simulations are consistent with f_ar arising from oscillations between inertial and elastic elements which are independent of gas density. Nonetheless these elements may be dependent on distending pressure, as our results also demonstrate that f_ar decreases with increasing P̄_tp (Table 1). Such behavior is also consistent with experimental data³⁵.

Pressure and Flow Distribution

Previous experimental studies have demonstrated that the amplitude of oscillatory pressures in the alveoli can exceed tracheal pressure at frequencies near f_r^1–3,12. In a study using alveolar capsules in excised canine lungs, Fredberg et al.¹² relied on a four element model to explain regional variations in alveolar oscillatory pressures at different lung volumes. This model demonstrated that f_r was inversely related to airway inertia and tissue compliance, with greater alveolar pressure amplification occurring at higher lung volumes. Moreover the magnitude of alveolar pressure at f_r was roughly proportional to the square-root of the product of airway inertia and tissue elastance, but inversely proportional to total lung resistance^3,12. Such behavior arises from the fact that alveolar gas is mechanically in series between the accelerating column of gas in the airways and the elastic parenchymal tissues. However this simple lumped-element model did not account for effects of airway tree asymmetry, gas compression in the airways and parenchyma, or airway wall distension.

Our more complex computational model also predicts that maximum oscillatory acinar pressure amplitudes occur at f_r, consistent with a minimum in impedance magnitude. This is to be expected, since for frequencies less than f_r and distending pressures less than 15 cmH₂O, the magnitude of flow losses due to airway wall distension or gas compression within the airways and parenchyma amounts to less than 10% of the tracheal flow magnitude (Figure 6). Thus predictions of alveolar pressure based on a simplified four element model are reasonably accurate. Even at higher distending pressures, where these flow losses may become a sizeable portion of the tracheal flow, acinar pressure amplification predicted from our model follows a similar trend to that of a four element model¹². However our model predicts that the greatest heterogeneity in acinar pressures occurs at f_r. For frequencies close to f_r, we observed that acinar pressure heterogeneity generally increases with P̄_tp. However for frequencies above f_ar, heterogeneity generally decreases with P̄_tp (Figure 10-C, inset), an observation also made by Fredberg et al. using alveolar capsules in dogs¹². Such similarities between their data and our model predictions are remarkable, given that capsular pressure measurements within a limited number of surface alveoli may not be appropriately representative of the entire population of acini¹².

Our model also predicts that the maximum average acinar flow amplitude occurs at f_ar, where impedance magnitude and reactance (due to gas acceleration) are maximum. This flow amplification generally decreased with increasing P̄_tp, consistent with increasing flow losses due to gas compression and airway wall distention. This phenomenon is characteristic of inertial-elastic systems⁷. Acinar flows also demonstrated minimal phase lag (Figure 8-B) and asynchrony (Figure 8-D) compared to tracheal flow for frequencies less than f_r. This is to be expected, since the distribution of ventilation in the lung is dominated by regional elastances for frequencies surrounding physiologic breathing⁹, and our simulations were performed assuming an entirely homogenous population of H_n values for a given P̄_tp. The greatest heterogeneity in acinar flow occurred for frequencies between f_r and f_ar (Figure 8-C). Moderate increases in asynchrony were also observed between f_r and f_ar, with considerable increases observed above f_ar (Figure 8-D). Such heterogeneity and asynchrony are consistent with variations in the pathlengths from trachea to acini (Figure 4), as ventilation distribution will be determined by regional resistive-elastic time constants at higher frequencies, regional resistive-inertial time constants near f_r, and the distribution of mechanical inertances above f_r^2,23.

These simulations thus have important clinical implications for optimizing ventilator settings during high frequency oscillatory ventilation (HFOV). This ventilator modality has been gaining considerable interest for the supportive treatment of acute lung injury (ALI)¹⁰, since it applies tidal volumes smaller than the anatomic dead space to minimize parenchymal overdistention, and adjusts mean distending pressures to maintain lung recruitment. While the mechanisms of gas exchange during HFOV are quite different compared to conventional mechanical ventilation³⁹, it nonetheless has the potential to minimize the two pathophysiologic processes associated with ventilator-induced lung injury (VILI); namely, volumtrauma (i.e., overdistention) and atelectrauma (i.e., cyclic recruitment and derecruitment).

Two recent clinical trials have demonstrated that the use of HFOV in ALI yields mortality outcomes that are no better (or even worse) than conventional mechanical ventilation^11,43. This may be the result of the specific HFOV protocols used in these studies²⁶, as well as an incomplete understanding of the important interaction between oscillatory frequency and mean airway pressure. For example, amplification of delivered volume during HFOV has been demonstrated in dogs and various in vitro preparations^7,31, similar to our model predictions. This may be beneficial in the injured lung, as it would allow for the delivery of smaller tidal volumes at the airway opening as compared to conventional ventilation strategies. However to the extent that parenchymal overdistention is an important contributor to VILI, our simulations indicate that caution should be exercised when oscillatory frequencies are adjusted above f_r. Our data also demonstrate that ventilation asynchrony increases above f_r, which may be desirable if pendelluft and intraregional gas mixing are important mechanisms for gas exchange during HFOV^8,24. Our present model suggests that an ‘optimal’ HFOV bandwidth may exist between f_r and f_ar, although the exact locations of the frequencies may vary from subject-to-subject or with disease conditions⁹. Indeed, our previous simulation of ventilation distribution suggests that ALI makes the distribution of flow amplitudes to the lung periphery more heterogeneous, although such pathology may also decrease ventilation asynchrony⁹.

Model Limitations

Several limitations of our model should be noted. First, our simulations were limited to sinusoidal volume perturbations with linear behavior of a lung occurring within a breath. Intratidal nonlinearity (as may occur during large volume excursions) may require within-breath variations in both airway caliber and parenchymal stiffness. Moreover turbulent airflow, as well as additional pressure losses at bifurcations in the airway tree, will also enhance nonlinear resistive behavior ²¹. Our model also does not account for variations in branching angles of the airways, which may become an important determinant of flow distribution during HFOV, as gas will tend to travel along the straightest pathway toward the acini^2,22. Incorporation of additional parameters in the model might also be necessary in presence of airway closure, gravitational dependence of regional elastances, time-dependent recruitment/derecruitment, or the influence of chest wall elasticity on gas transport^5,20,32. While our existing data structure is theoretically capable of simulating all these conditions, we optimized the computational burden to characterize the most relevant parameters for a healthy lung. We also did not account for the impedance of the collateral channels between adjacent acini, which in dogs are thought to provide additional pathways to homogenize ventilation distribution²⁵.

Perhaps most importantly, our model allows for simulation of advective acinar flow distribution only. It does not take into account diffusive mechanisms that may dominate gas transport and exchange at the alveolar level⁸. That is, we accounted only for the bulk motion of gas transport as the acini expand and deflate. In reality, acinar flow velocities during ventilation or oscillation are so slow that convective gas mixing is minimized, and O₂ and CO₂ diffuse according to their respective concentration gradients. Thus it is unclear how the acinar flow amplification and attenuation we observed at various frequencies may influence O₂ uptake or CO₂ elimination in the presence of diffusion. Future simulations, incorporating pulmonary blood flow for various ventilation-perfusion distributions, will allow some insight into how advective and diffusive processes interact to influence gas exchange.

CONCLUSIONS

In summary, we have developed an anatomically-based computational model of the canine lung to explore the effects of ventilation frequency and parenchymal stiffness on advective ventilation distribution. Our simulations predict that the resonant frequency increases with lung volume due to increasing parenchymal stiffness, while the antiresonant frequency decreases due to increasing gas volume. The distribution of acinar pressures is heterogeneous and amplified relative to tracheal pressure at resonant frequency. With increasing lung volume and tissue stiffness, the distribution of acinar flow narrows and becomes more synchronous for frequencies below resonance. At higher frequencies, large interregional variations in acinar flow are observed, with maximum acinar flow occurring at the antiresonant frequency. These data demonstrate the important interaction between frequency and parenchymal stiffness during ventilation in an asymmetrically-branching airway tree, as well as their combined influence on the distribution of acinar flows and pressures. These simulations may provide insight into physical phenomena associated with mechanical ventilation over a wide range of frequencies and lung volumes, and may provide useful information for the optimization of frequency, lung volume, or mean airway pressure during conventional mechanical ventilation or high frequency oscillatory ventilation.