λ-prophage induction modeled as a cooperative failure mode of lytic repression

Abstract

We analyze a system-level model for lytic repression of λ-phage in E. coli using reliability theory, showing that the repressor circuit comprises 4 redundant components whose failure mode is prophage induction. Our model reflects the specific biochemical mechanisms involved in regulation, including long-range cooperative binding, and its detailed predictions for prophage induction in E. coli under ultra-violet radiation are in good agreement with experimental data.

Viruses were one of the first biological systems to attract the attention of physicists[1]. Despite their apparent simplicity, it has become increasingly clear[2, 3] that they provide a window into the full systems complexity of the cell[4], as well as representing a major evolutionary[5] and ecological force[6] affecting all three domains of life. The viruses that infect bacteria are known as bacteriophages (or phages). When some phages infect a bacterial cell, there can be two possible outcomes or pathways[4]. In the lytic pathway, the phage hijacks the cell's machinery to replicate itself many times, and to release the replicates by breaking open or lysing the cell. In the lysogenic pathway, the phage integrates its genome into that of the host microbe, becoming a prophage, but otherwise does not damage the cell. This lysogenic state is very stable[7]; however, an insult to the cell through, for example, starvation or exposure to ultra-violet (UV) radiation[8] can trigger a process known as prophage induction[9]: the prophage is excised from the cell's genome, and viral replication occurs leading to cell lysis. The most well-studied lysogenic system is the bacteriophage λ, or λ-phage, which infects Escherichia coli. Understanding the lysis-lysogeny system in detail is important, because this system is one of the simplest examples of a gene regulatory network[10]—a pervasive and fundamental form of biological organization and function, whose principles are still being elucidated. Although there has been considerable interest recently in the role of stochasticity[11] in the switching behavior between lytic and lysogenic states as part of the phage life-cycle[12, 13, 14, 15, 16], here we focus on UV prophage induction, where a different mechanism is involved.

UV prophage induction experiments exhibit threshold behavior[17], in which the fraction of induced lysogens, (i.e., prophage containing cells) rapidly increases as a function of UV dose. Under typical laboratory growth conditions, the fraction of induced lysogens versus the UV dosage obeys a power law with a power very close to 4[17]. Power law behaviors of this type can arise in several ways: (i) as an event caused by 4 independent hits on a “target” (target theory[18]); or (ii) a chemical equilibrium reaction involving a substrate bound to 4 chemical species, and quantified by the empirical Hill equation for chemical kinetics[19, 20]. Target theory and chemical kinetics could provide a way of understanding how UV dose curves can yield an exponent of 4, but have little connection to the biochemical regulatory mechanisms of λ-phage lytic repression[9, 21]. An alternative perspective is to view UV induction in the framework of the standard stochastic model of lytic repression[13, 14] with adjusted rate constants. While these models are informed by the biochemistry, the mapping to UV prophage induction remains dependent on unknown parameters.

In this Letter, we show how the emerging understanding of the role of DNA loops and long-range cooperative binding[22, 23] in the biochemical picture of lytic repression can account quantitatively for the phenomenology of prophage induction. Our approach is to abstract the biochemistry into a systems-level description, in which the lytic repressor circuit is represented as a device comprised of a number of redundant elements and one failure mode, lysis. This allows us to draw connections between the biochemical regulatory mechanism and reliability theory[24, 25, 26] and also predict the characteristic power law for UV prophage induction.

Biochemistry of lytic repression

Fig. 1 illustrates a widely accepted model of the lytic repressor switch in λ-phage (for a review see [4]). The lytic repressor molecule CI dimerises and binds to specific DNA sites in the O_L and O_R control boxes, O_L1 and O_L2, blocking expression of genes under the control of the P_L promoter. In the O_R control box, O_R1 and O_R2 regulate P_R. Since only free O_R1 and O_R2 sites allow the expression of P_R controlled genes, CI binding at either the O_R1 or O_R2 suffice for repression of P_R. Fig. 2 sketches the relationship between these 2 O_R sites and P_R expression. The same applies to the role of O_L1 and O_L2 in suppressing P_L. Also, as drawn in Fig. 2, expression of genes under the control of both P_L and P_R promoters lead to lytic development of the prophage[30]. Derepression of all of the 4 binding sites results in lysis while bound CI dimers at any site block the lytic pathway. In UV induction, RecA-mediated autocleavage of CI monomers deprives the binding sites of available CI dimers. RecA-mediated autocleavage can happen once RecA is activated as part of the host SOS response to DNA damage[31].

Fig. 1.

Schematic diagram of the λ-phage lytic repression system. Attachment of RNA polymerase to promoter regions, indicated here by arrows, lead to gene expression. P_R and P_L lead to expression of genes in the lytic pathway. However, CI dimer binding at O_R1 or O_R2 blocks transcription of P_R while CI binding at O_L1 and O_L2 block transcription of P_L. O_R3 likewise regulates the transcription of genes by the promoter region P_RM while CI bound to O_R2 promotes transcription of genes from P_RM. Dimers of CI are capable of forming stable quadramers when attached to adjacent sites such as at O_R1 and O_R2[12, 13] (modeled by [27]). Furthermore, O_R1-O_R2 and O_L1-O_L2 quadramers can form a stable octamer in a long range interaction typically spanning 2.4 kb, but up to 3.8 kb[28, 29].

Fig. 2.

λ-phage lytic repression regulatory circuit. CI bound to O_R1 or O_R2 blocks expression of lytic genes under the control of P_R. CI bound to O_L1 or O_L2 blocks expression of lytic genes under the control of P_L. Since both sets of genes under the control of P_R and P_L are required, blocking expression of either effectively represses lysis. Thus, each of the 4 CI bound components blocks lysis when intact. These can be seen as redundant elements that perform the same task.

Abstraction of the lytic repression circuit

Prophage induction can be understood as the failure of the lytic repression circuit, which consists of 4 redundant components that each prevent lysis. Each has a failure rate μ_i (i = 1…4) per UV dose x and a corresponding survival probability p_i = exp(−μ_ix). Fig. 2 diagrams the relevant aspects of the λ-phage lytic repressor regulatory system. Each component consists of a lytic repressor CI dimer bound to one of 4 specific DNA sites, i.e., either O_R1, O_R2, O_L1, or O_L2. Each site regulates the expression of genes essential to the lytic pathway by its influence on either the promoter P_R, by O_R1 and O_R2, or P_L, by O_L1 and O_L2. Thus, these 4 components have redundant functionality, i.e., repressing lysis. Since suppression of genes under the control of either promoter keeps lysis in check, only damage to the final component results in lysis.

Reliability theory of the repressor circuit

To understand the failure rate of the system, i.e., the fraction of cells lysed, note that the probability of failure, for UV dose x, is 1 − p_i for each of the 4 redundant components (the 4 CI dimers bound to O_R1, O_R2, O_L1, and O_L2) in the lytic repression system (see Fig. 2). In general, the probability of failure as a function of total UV dose, F, for a system of n redundant components is

$$F=\mathbf{\prod }_{i=1}^n(1-p_i).$$ (1)

We model the effects of radiation on the failure rate of the lytic repression system, by assuming that near the threshold x_c, p_i = exp[−μ_i(x − x_c) + O((x − x_c)²)].

By taking measurements of the fraction of failed systems and Eq. 1, the number of redundant elements in the system can be deduced. The fraction of failed units is then given by

$$F(x)=\mathbf{\prod }_{i=1}^n(1-exp[-{\mu }_{i}x])\approx {(\mu x)}^n(\mu x\ll 1)$$ (2)

where $\mu ={({\mathbf{\prod }}_{i=1}^n{\mu }_i)}^{1/n}$ is an effective failure rate. The UV prophage induction curve describes the fraction of cells lysed as a function of UV dose x and is predicted to follow Eq. 2 with n = 4. In other words, the fraction of cells lysed can be computed from the effective failure rate μ for the 4 CI dimer bindings at O_R1, O_R2, O_L1, and O_L2. The effective rate of failure μ varies between different experimental systems and depends on a number of parameters. For example, different E. coli hosts may exhibit varying levels of RecA activity[31, 32]. Alternatively, mutant cI alleles may offer operator site binding affinities[33]. Below, we test Eq. 2 against data from experiments on radiative induced lysis, and extract μ.

Experimental tests

In order to measure the fraction of lysogens induced as a function of UV dose, we followed standard protocols[34]. Briefly, exponentially growing lysogenic cells were harvested and resuspended in buffer. The cells were then irradiated by a germicidal UV lamp in dim ambient light for a range of doses at ∼ 1 J/m²/s. After irradiation, aliquots were diluted into growth medium, shaken for 2 h at 37C in the dark, treated with CHCl₃ and titered for plaque forming units.

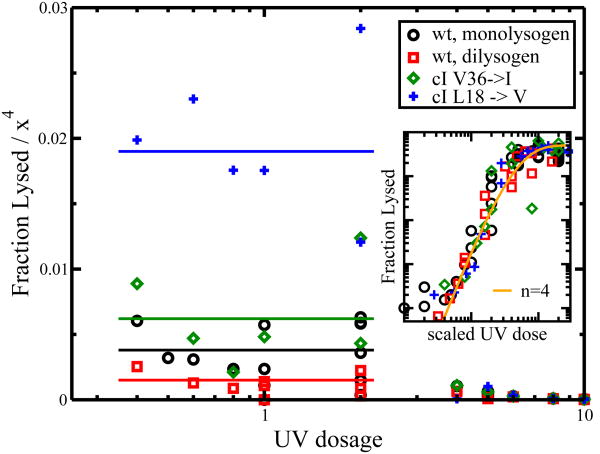
In our abstraction of the lytic repression system, we noted four redundant components, as shown in Fig. 2. Since this implies n = 4, we can test the applicability of Eq. 2 to our experimental results by plotting F/(x⁴) against UV dose x, as shown in Fig. 3.

Fig. 3.

The UV prophage induction curve. F/(x⁴) versus UV dosage x. The data is taken from different λ strains. Wild-type prophages were integrated as monolysogens and dilysogens with one or two inserted λ genomes, respectively. All 4 induction curves scale approximately as a power of 4 for small UV doses (0.2-2 J/m²). (Inset) Log-log plot of the same data. Curves are right- and left-shifted so that they overlay each other. The line represents Eq. 1 for n = 4.

In Fig. 3, the effective rate of failure μ manifests itself as a horizontal line. As shown in Fig. 3, experimental data agrees with Eq. 2 for a certain range of UV dosage. Disagreement between theory and experiment occurs at both low and high UV dosage. The breakdown in both these regimes is readily interpreted. For extremely low dosage (near zero), spontaneous lysis events not induced by UV irradiation become the strongest contributing factor to the failure rate. These failures come from other events, such as spontaneous RecA activity[9] and mutations to λ-phage[7]. At high radiation doses (not plotted, see [17]), the fraction of lysis does not saturate at one and instead begins falling with respect to UV dose. Here, damage to the lytic pathway likely results in the inability of a cell to lyse, either because key components of the lytic pathway or host metabolism have been crucially damaged. In other words, this drop is not the effect of a lower failure rate of lytic repression, but a reflection of the high failure rate of other cellular systems upon which lysis relies. In these cases, failure of lytic repression cannot be detected by cell lysis since the lytic response has been disabled.

Discussion

Our model postulates that induction, or a failure event, is dominated primarily by CI dimer dissociation. Though many factors, such as DNA damage and RecA activity [35], contribute in principle to the failure of lytic repression, near the threshold of prophage induction, only the most rapidly-varying parameter is important. The rapidly-varying CI-dimer operator site bindings about the threshold point for lytic induction x_c justifies the approximation made in Eq. 2 allowing us to observe the predicted n = 4 power law.

In contrast, chemical kinetic models assume that since the timescale of CI dimer dissociation (∼ 30 sec[33]) falls an order of magnitude below the time required for lysis (∼ 30 min), the CI bindings can be regarded as being adiabatically slaved to CI monomer concentration[13, 14], and thus not a determining factor in the switch. The prophage induction curve and its power law behavior then arise from the behavior of the CI monomer depletion. However, as can be seen from the data presented in Fig. 3, the power law dependence n = 4 is robust, and not sensitive to the different strains or experimental conditions. In our model, the power n reflects the number of redundant elements—not the properties of the individual components—and so is robust. This can be directly tested by manipulating the number of redundant operator sites and measuring the resultant power law dependence. Ref. [20] measured P_R expression as a function of CI concentration. As shown in Fig. 1 P_R expression is regulated by 2 bound operator sites, so we predict that P_R expression should be described by a kinetic curve with an n = 2 power law dependence, as has been previously noted[36]. The kinetic data of ref. [20] are indeed consistent with the prediction we have made here, based on our system-level abstraction of the underlying biology. This finding supports our view that the threshold behavior of prophage induction is determined by CI, and not by other steps in the repressor circuit. To establish this more conclusively, it would be necessary to check that P_L expression also exhibits the predicted n = 2 power law behavior.

Our model implies that the repressor sites are the key to stabilizing the lysogenic state while the presence of Cro does not play a role in the switching[37, 38] except to enforce commitment to the developmental transition[39]. Once the switch has been activated, it cannot be reversed, due to the role of Cro. Our model also suggests a mechanism for abortive induction events that are sometimes observed[9]. In our model these arise when unblocked P_L transcribes the genes required for excision (see [4]) while P_R remains blocked.

As shown by Fig. 3, different conditions lead to different values for μ. We can use reliability theory to anticipate the trends in variation of μ between 2 similar experiments. The rate of component failure depends on a number of variables including RecA activity, CI concentration, binding strength of repressor sites, and stability of CI to autocleavage. Here, damage to redundant components corresponds to the dissociation of CI dimers from O_L1/2 and O_R1/2 sites (see Fig. 2).

Table I lists theoretical predictions for the variation in the failure rate of the lytic repressor or inducability arising from possible laboratory manipulations of the rate of failure μ. As expected, increasing RecA or rate of CI autocleavage leads to increased failure rates while an increased number of CI dimers slows down the rate of failure. Increasing operator site binding strengths through cooperative binding or operator site mutations lowers the rate of failure. In summary, weakening the CI operator site bindings results in an increased failure rate for the lytic repressor, while increasing the probability of those binding events will have the opposite effect.

Table I.

List of predicted and observed changes in inducibility tabulated according to mutation, either in λ or the E. coli host. ↑ indicates that the change results an increase in μ, while ↓ indicates a decrease. Predictions based on reliability theory match with currently available data.

Strain	Phenotype	Theory	Data	Ref.
λ cI inds-1	faster CI cleavage	↑	↑	[32]
lexA51 recA441	increased RecA activity	↑	↑	[32]
λ cI ind543	stronger CI dimerization	↓	↓	[32]
λ cI Y210→N	disrupts CI dimer-dimer cooperative binding	↓	↓	[40]
OR2*	weaker OR2-CI binding	↑	↑	[20]a

^aMeasured P_R expression