Coordination of bacterial proteome with metabolism by cAMP signalling

Abstract

Cyclic AMP (cAMP) dependent catabolite repression effect in E. coli is among the most intensely studied regulatory processes in biology. However, the physiological function(s) of cAMP signalling and its molecular triggers remain elusive. Here we use a quantitative physiological approach to show that cAMP signalling tightly coordinates the cell’s protein expression program with its metabolic needs during exponential cell growth: The expression of carbon catabolic genes increased linearly with decreasing growth rates upon limitation of carbon influx, but decreased linearly with decreasing growth rate upon limitation of nitrogen or sulfur influx. In contrast, the expression of biosynthetic genes exhibited the opposite linear growth-rate dependence as the catabolic genes. A coarse-grained mathematical model provides a quantitative framework for understanding and predicting gene expression responses to catabolic and anabolic limitations. A scheme of integral feedback control featuring the inhibition of cAMP signalling by metabolic precursors is proposed and validated. These results reveal a key physiological role of cAMP-dependent catabolite repression: to ensure that proteomic resources are spent on distinct metabolic sectors as needed in different nutrient environments. Our finding underscores the power of quantitative physiology in unravelling the underlying functions of complex molecular signalling networks.

Biological organisms employ a myriad of signalling pathways to monitor the environment and adjust their genetic programs in accordance with environmental changes^1–4. Understanding how the signalling systems perceive the environment and orchestrate the downstream genetic changes is a grand challenge of systems biology^5–8. One of the earliest signalling systems ever discovered in modern biology is the cyclic AMP (cAMP) dependent pathway in E. coli^9,10. This system is known to mediate carbon catabolite repression (CCR)¹¹, a ubiquitous phenomenon among microorganisms whereby the synthesis of catabolic proteins is inhibited when growing on glucose or other rapidly metabolizable sugars^12,13. In E. coli, it was long established that the uptake of glucose inhibited the synthesis of cAMP¹⁰, which is required for the expression of many catabolic genes through its activation of the pleiotropic regulator Crp (the cAMP receptor protein)¹⁴.

Despite extensive studies on this cAMP signalling pathway, a number of basic issues remain unanswered even for this classic system: Although the inhibitory effect of glucose uptake on cAMP synthesis via the phosphotransferase system (PTS) is well established^15,16 (Fig. S1), the growth of E. coli cells on various PTS-independent sugars also exhibited reduced cAMP levels^17–19. Moreover, limitation of nitrogen, phosphorous, and other elements also led to much reduced cAMP levels^20–22. Elucidating the physiological signal(s) that triggered cAMP signalling in those conditions was in fact the pursuit of Monod’s last paper²³, but these signal(s) remain mysterious today. Also, it is unclear to what extent cAMP signalling is intended for implementing CCR²⁴, as hierarchical carbon usage²⁵, a behavior widely associated with CCR¹⁶, was shown to be independent of cAMP in several studies^26,27. Thus, the true physiological function of cAMP signalling in E. coli remains open nearly 50 years after its discovery. In this study, we describe a top-down approach which first addresses quantitatively the physiological function of cAMP signalling – not for CCR per se as we will show, but for the coordination of metabolism with proteomic resource allocation. This knowledge is then used as a guide to reveal the signalling strategy and mechanism by which E. coli cells use to trigger cAMP signalling.

Catabolic genes exhibit linear response

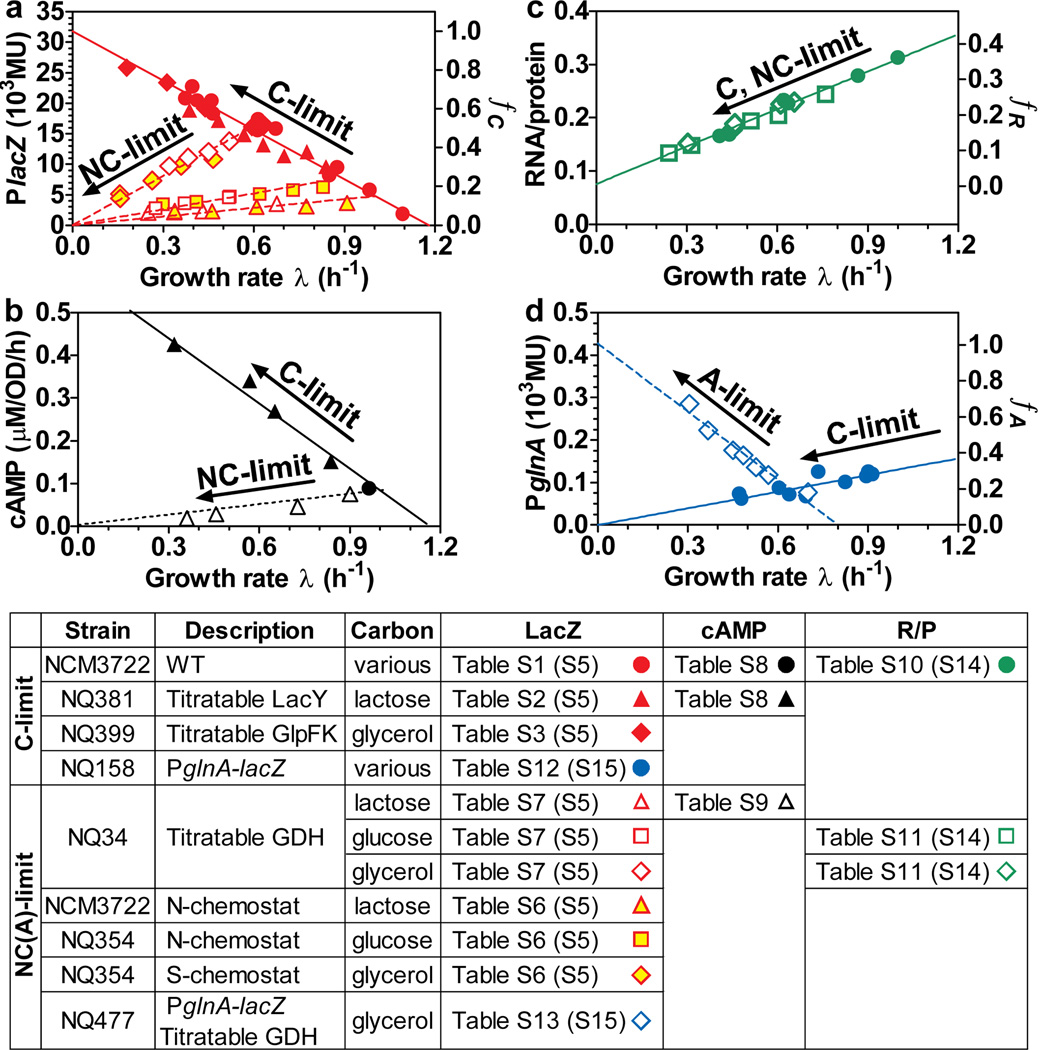
To characterize the physiological consequences of cAMP-dependent signalling, we used the well-studied lac system of E. coli, one of the many catabolic operons activated by the Crp-cAMP complex^14,28. Wild-type E. coli K-12 cells were grown in minimal medium batch culture with saturating amount of one of many carbon sources, with the Lac repressor (LacI) deactivated by the inducer IPTG. As such, the native LacZ expression indicated the degree of cAMP signalling²⁹. Table S1 lists the LacZ expression level (L) together with the growth rate (λ) for cells growing in each medium. A scatter plot of the data exhibits a striking linear relation (solid circles in Fig. 1a). The same relation is obtained by limiting the carbon influx: by titrating the lactose permease for cells growing on lactose (Table S2, solid triangles in Fig. 1a), or titrating the glycerol uptake system for cells growing on glycerol (Table S3, solid diamonds in Fig. 1a); see Figs. S2, S3 and Table S4 for strain details. The red solid line is the best-fit of all data to the form

$$L=L_{\text{max}}·(1-\lambda /{\lambda }_C),$$ [1]

referred to below as the “C-line”; see Table S5 for fitted values of the x-intercept λ_C and y-intercept L_max. Similar linear relations are seen (Fig. S4) for lac in various other strains of E. coli characterized here and previously^20,30,31, and for different catabolic promoters (solid symbols in Fig. S5).

Figure 1. Catabolic and biosynthetic gene expression under nutrient limitations.

For clarity, growth conditions and depository of data are summarized in the legend table. Parenthesis indicates the supp. tables containing the parameters of the best-fit lines. (a) Correlation of PlacZ expression with the growth rate under C-limitations (solid symbols) and NC-limitations (open symbols). The left y-axis shows LacZ expression per OD₆₀₀ (Miller Unit or MU), which is proportional to per total protein; see Supp. Methods and Fig. S14. The right y-axis shows the equivalence in normalized fractions f_C (Supp. Note 3). (b) Internal cAMP level as indicated by the cAMP excretion rate (Fig. S11) for cells grown under C- and NC- limitations (filled and open symbols, respectively). (c) RNA/protein ratio for both C- and NC- limited growth (filled and open symbols, respectively). The right y-axis shows the equivalence in normalized fractions f_R (Supp. Note 3). (d) PglnA-lacZ expression under C- and A-limited growth (filled and open symbols, respectively). The right y-axis shows the equivalence in normalized fractions f_A (Supp. Note 3).

Above data suggest that the C-line is a common response pattern exhibited by the catabolic genes – a gradual increase upon reduction in carbon influx or for less rapidly metabolized carbon compounds. We refer to such carbon-dependent mode of growth limitation as “C-limitation”. To show that the C-line is a response specific to changes in carbon catabolism rather than to general growth parameters^32,33, we modulated cell growth by various non-carbon (NC) modes of growth limitation, including continuous culture with ammonium- or sulfate- limitation (Table S6), and batch culture using a titratable nitrogen uptake system (Table S7). The latter system bypasses the highly regulated nitrogen response system³⁴, creating a situation in which the formation of amino acids from their respective carbon can be directly titrated by the expression of Glutamate Dehydrogenase (GDH); see Fig. S6. PlacZ expressions obtained for these modes of NC-limited growth are plotted against the growth rates in Figs. 1a, S7 for several exemplary carbon sources (open symbols). In each case, a positive linear relationship was observed (dashed lines). Similar relations are seen for several other catabolic promoters (open symbols in Fig. S5de). We refer to these positive linear relations as the “NC-lines”. Both C- and NC- lines also described the expression of a PlacZ-gfp fusion reporter in wild-type cells grown in microfluidic devices with rapid medium exchange³⁵ to maintain low nutrient levels and remove excretion products (Fig. S8).

We next examined the dependence of the C- and NC- lines on Crp-cAMP mediated activation. Upon replacing the lacZ promoter by the lacUV5 promoter whose independence of Crp-cAMP is well established³⁶, LacZ expression in these strains exhibited little growth-rate dependence under both C- and NC- limited growth (Fig. S9). Additionally, we characterized the expression of a synthetic lac promoter with the Crp site scrambled, and found only a weak growth-rate dependence, resembling that previously reported for constitutive gene expression³³, under both C- and NC- limitations (Fig. S10). Thus both the C- and NC- lines rely completely on Crp-cAMP mediated gene regulation.

We also characterized the cAMP excretion rate (Fig. S11), taken to reflect the internal cAMP concentration¹⁷. It is seen to correlate well with PlacZ expression in the respective medium for both C- and NC- limited growth (Fig. S12, Tables S8–S9). Moreover, scatter plot of cAMP excretion rates against the corresponding growth rates (Fig. 1b) resembles the C- and NC- lines of PlacZ (Fig. 1a). Together, these data strongly indicate that the C- and NC- lines are two sides of the same coin, both regulated by Crp-cAMP primarily through cAMP signalling.

Opposing linear response by anabolic genes

To understand the linearity of catabolic gene expression with the growth rate, we recall a linear relation between the cellular ribosome content and the growth rate for exponentially growing bacteria^33,37,38. This relation (a bacterial growth law), which arises due to the allocation of ribosomes as a key growth-limiting resource^33,38, is verified for our strains by characterizing the RNA/protein ratio (r) under both C- and NC- limited growth (Tables S10, S11, Fig. 1c). The striking contrast between the linear increase in catabolic gene expression (solid red symbols in Fig. 1a) and the concomitant linear decrease in the ribosome content (Fig. 1c) upon C-limitation (solid green symbols in Fig. 1c) suggests that these phenomena might share a common origin.

This line of qualitative reasoning predicts that upon NC-limitation where the expression levels of catabolic and ribosomal genes both decrease linearly as fractions of total protein (open symbols in Figs. 1a, 1c), the expression of other genes (e.g., biosynthetic genes) should increase linearly with the growth rate. We tested this prediction by characterizing the expression of glnA, which encodes the major ammonia assimilating protein Glutamine Synthetase³⁴ using the titratable GDH system under a fixed carbon source (glycerol). As expected, the expression level of the chromosomal PglnA-lacZ fusion reporter (open blue diamonds in Fig. 1d, denoted as G) exhibited a negative linear correlation with growth rate; similar behaviors were seen for the expression of several other genes in amino acid synthesis pathways (Fig. S13). These responses suggest a general amino acid limitation imposed by the titratable GDH system (Fig. S6), referred to henceforth as “A-limitation” and the resulting response as the “A-line” (dashed blue line in Fig. 1d). The latter is described mathematically by

$$G=G_{\text{max}}·(1-\lambda /{\lambda }_A),$$ [2]

with an x-intercept λ_A and an y-intercept G_max (Table S15). Interestingly, PglnA-lacZ also exhibited positive linear correlation with the growth rate in C-limited growth (solid blue line in Fig. 1d). Thus E. coli perceives carbon limitation as a nitrogen excess, a feature reported qualitatively long ago in Klebsiella³⁹.

Quantifying the proteome fractions

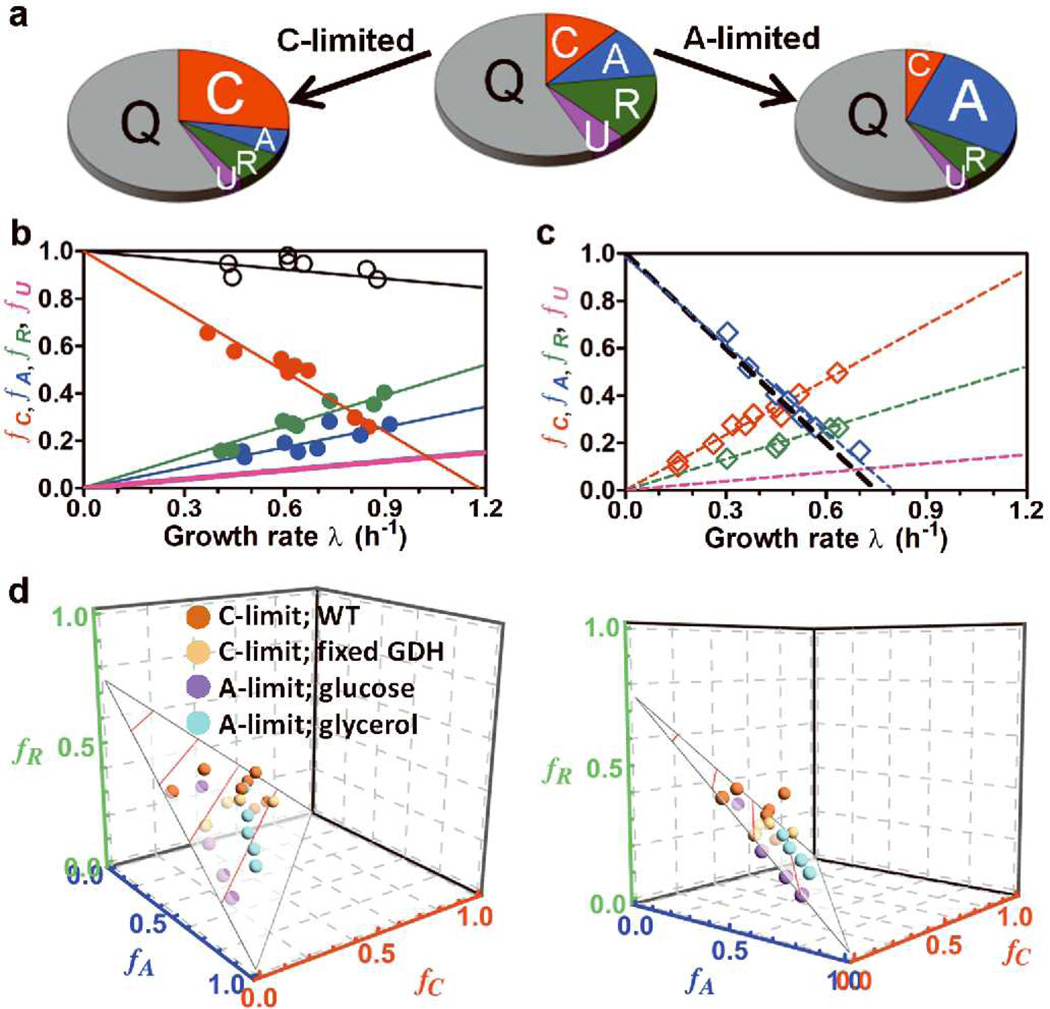
To see whether the response of the catabolic genes can be quantitatively accounted for by changes in the biosynthetic genes and the ribosome content, we apply and extend a mathematical model of proteome partition introduced recently^33,40 to relate various growth laws to the global regulation of gene expression. As illustrated in Fig. 2a and explained in detail in Supp. Note 1, we hypothesize that the proteome is comprised of several major “sectors”, i.e., groups of genes whose expression share similar growth rate dependences upon various modes of growth limitation. These include a catabolic sector (C) of mass fraction ϕ_C that increases specifically in response to C-limitation as exemplified by lacZ (Fig.1a, S5), an anabolic sector (A) of mass fraction ϕ_A that increases specifically in response to A-limitation as exemplified by glnA (Fig. 1d, S13), and a ribosomal sector (R) of mass fraction ϕ_R that increases specifically in response to translational inhibition (Fig. S15). To account for additional sectors which have not been specifically targeted by the various modes of growth limitation applied in this study, we propose an uninduced sector (U) of mass fraction ϕ_U which generally decreases with decreasing growth rate. Examples of the latter might include enzymes for sulfur assimilation and nucleotide synthesis (Fig. S16).

Figure 2. Proteome fractions and the partition model.

(a) Illustration of the proteome partition model: Upon C-limitation, the C-sector increases and the A-, R-, U- sectors decrease, while upon A-limitation, the A-sector increases and the C-, R-, U- sectors decrease ; see Supp. Note 1. (b) Normalized responses (f_C, f_A, f_R) indicated by the C-, A-, R- sector reporters upon C-limitation (solid red, green, blue circles respectively from Figs. 1a, 1c, 1d). The black circles show the sum f_C + f_A + f_R at each growth rate; they decrease linearly with the growth rate (black line). The purple line is the predicted U-sector fraction f_U based on Eq. [3]. (c) f_C, f_A, f_R upon A-limitation with glycerol as the carbon source (open red, green, blue diamonds respectively from Figs. 1a, 1c, 1d). Taking f_U (purple line) to be the same as that in panel b (f_U = 0.3· f_R), Eq. [3] predicts f_A to follow the black line, and blue line shows the best fit. (d) f_C, f_A, f_R for the four sets of C- and A- limited growth conditions characterized (panels b, c and Figs. S19, S20) are plotted in a 3D plot. (Unavailable data for f_R, f_A are generated from the straight line fit.) Two views are shown. The data are seen to fall on the predicted surface (Eq. [3] with f_U = 0.3· f_R).

As exhibited by the various reporters, we expect each of the above proteome sector j to contain a growth-rate dependent part Δϕ_j (λ) and a growth-rate independent offset ϕ_j,0, with ϕ_j (λ) = ϕ_j,0 + Δϕ_j (λ); see Fig. S17. Additionally, there may exist a growth-rate independent sector (I) of mass fraction ϕ_I. Together, the growth-rate independent components can be lumped into an effective sector (Q) of mass fraction ϕ_Q = ϕ_I + ∑_j ϕ_j,0 as suggested from previous study³³, providing a cap ϕ_max = 1−ϕ_Q on how large the specific responses of each sector can increase to, i.e., ∑_j Δϕ_j (λ) = ϕ_max. We estimated ϕ_max ≈ 43% using protein overexpression data (Fig. S18, Supp Note 2).

The constraint that the Δϕ_js add up to a constant (ϕ_max) imposes quantitative relations between the responses of the various sectors upon different modes of growth limitation. This constraint is most simply expressed (Supp. Note 3) in terms of a normalized fraction, f_j (λ) = Δϕ_j (λ) / ϕ_max (see Eq. [S21]) for each sector j, as

$$f_C(\lambda )+f_A(\lambda )+f_R(\lambda )+f_U(\lambda )=1.$$ [3]

Assuming that changes in the expression levels of PlacZ and PglnA report changes in the C- and A- sectors respectively, i.e., ΔL ∝ Δϕ_C (λ) and ΔG ∝ Δϕ_A (λ), the normalized proteome sectors f_C (λ) and f_A (λ) can be estimated from the reporter expression levels using our model (Fig. S17). The results are indicated on the right vertical scales in Figs. 1a, 1d. Similarly, f_R (λ) can be obtained from the RNA/protein ratio r(λ) (right vertical scale of Fig. 1c and S15a). The values of these normalized fractions under C-limited growth are plotted together as colored circles in Fig. 2b, and their best linear fits are shown as lines of corresponding colors. Since f_C (λ) + f_A (λ) + f_R (λ) < 1 (black open circles and line), we deduce from Eq. [3] the existence of an uninduced sector U whose abundance, f_U (λ), is shown by the purple line: It is approximately 30% of the R-sector (green line).

Tight coordination of proteome sectors

The constraint Eq. [3] suggests that the growth-rate dependences of the C- and A- sectors are simply related, given that f_R (λ) follows the growth law (Fig. 1c) and f_U ≈ 0.3· f_R. Applying this to A-limited growth, we can use the observed expression of PlacZ under A-limitation (Fig. 1a) to predict PglnA expression under A-limitation; the result is in good agreement with the best-fit as shown in Fig. 2c (black line), with glycerol as the carbon source. This is repeated for A-limitation on glucose, where we expect the smaller C-sector for glucose to lead to an expanded A-sector, and hence an increased intercept λ_A for PglnA. This prediction is verified in Fig. S19, with the data quantitatively accounted for by the predicted A-line (black line). Similarly, the value of the intercept λ_C for PlacZ under C-limitation with a fixed degree of A-limitation is reduced to the expected range (Fig. S20). See Fig. S21 and Table S16 for the direct comparison of the predicted and best-fit values of λ_C, λ_A. As one additional test of this picture, we applied sub-lethal amounts of antibiotics to probe the effect of translational limitation on the various proteome sectors (Fig. S22). While the R-sector increased linearly with decreasing growth rate³³, PlacZ and PglnA expressions both decreased linearly with decreasing growth rate as predicted, again in a manner that conforms quantitatively to the constraint Eq. [3].

These datasets (Figs. 2b, 2c, S19, S20) can also be displayed simultaneously on 3D plot (Fig. 2d); the data are seen to lie close to a plane, defined by Eq. [3] with f_U ≈ 0.3· f_R. This is an example of the Pareto surface⁴¹, which results generally from trade-off between competing objectives that cannot be simultaneously optimized. The linear dependences of these fractions on the growth rate further suggest that they arise from protein synthesis being the common bottleneck of cell growth. For example, catabolic proteins are needed to increase carbon influx while ribosomal and anabolic proteins are needed to increase biosynthesis, all of which depend on translation by ribosomes (Supp Note 4). This logic leads to an important physiological rationale for the pleiotropic regulation of catabolic genes by Crp-cAMP: Given rapidly metabolizable carbons, cells reduce catabolic gene expression to increase the expression of ribosomal and anabolic genes for rapid cell growth.

Metabolic-proteome coordination: strategy

The opposing behaviors exhibited by the C- and A- sectors upon different modes of growth limitation (Figs. 1 and 2) point strongly to the existence of control system(s). Fig. 3a describes a simple regulatory scheme wherein a single signal can sense and eliminate imbalance between metabolic activities on the carbon and nitrogen side. In this coarse-grained scheme, the external carbon source is converted to the pool of carbon precursors (K), e.g, α-ketoacids, which subsequently combine with ammonium to form amino acids (a) via trans-amination reactions (Fig. S6). If the carbon influx (J_C) exceeds the nitrogen influx (J_N), then precursors (K) will accumulate^42–44. A signal from K to inhibit Crp-cAMP activity (dotted red line in Fig. 3a) can account for the observed responses by the catabolic genes (Figs. 1a, S5), both for increases in J_C (relief of C-limitation) and decreases in J_N (A-limitation). An opposite signal from K could underlie changes in the A-sector (dashed blue arrow). Detailed mathematical analysis (Supp. Note 5) shows how such a feedback loop (known as “integral feedback”^35,45 since K is the time-integral of the flux difference between J_C and J_N being regulated), together with global constraints provided by proteome partition, can generate the C- and A- lines generically, independent of the detailed forms of the regulatory functions.

Figure 3. Transient repression by metabolic precursors.

(a) A coarse-grained view of metabolism, focusing on the biosynthesis of amino acids from the carbon and nitrogen influxes (J_C and J_N respectively). Carbon precursors such as α-ketoacids (K) sense the difference between J_C and J_N. An integral feedback scheme employing the regulation of catabolic and anabolic enzymes (ϕ_C and ϕ_N respectively) by K can coordinate these metabolic sectors in a parameter-free manner; see Supp. Note 5 for details. (b) PlacZ-lacZ expression was characterized for wild-type NCM3722 cells grown exponentially in various carbon sources and with 1 mM IPTG to deactivate LacI. At time zero, 20 mM oaa was added; a transient repression period of ~30 min is shaded in grey. PlacUV5-lacZ expression in strain NQ1053 was characterized in a same way (black squares; right y-axis). (c) LacZ expression levels before and during the repression period (Figs. 3b, S23–S27) are summarized by the open and grey bars. Striped bars show the results of PlacUV5-lacZ. (d) cAMP concentrations in the medium were monitored for wild-type cells grown in glycerol and the two PTS-deletion strains, NQ721 (Δpts) and NQ506 (Δ5EI Δpts), grown in lactose. 20 mM oaa was added at time zero. (e) Relative cAMP excretion rates were quantified before and during the repression period; see Supp. Method. In (c) and (e), data were expressed as mean ± s.e.m (n ≥ 3).

The proposed integral feedback strategy can be tested by adding a precursor to an exponentially growing culture. If the uptake of precursor significantly exceeds its metabolic turnover, then the transient build-up of the precursor should reduce the internal cAMP level and the expression of catabolic genes, until a later time when metabolic fluxes are reequilibriated. We first tested oxaloacetate (oaa), a major metabolic precursor (an α-ketoacid) which is co-utilized with other carbons by wild-type cells to give faster steady-state growth (Table S17). The addition of oaa to cells growing exponentially in glycerol, glucose, or lactose strongly inhibited PlacZ expression (with LacI deactivated) for up to 30 minutes (Fig. 3bc, Fig. S23). This transient effect was Crp-cAMP dependent since no effect was observed for PlacUV5 (Fig. 3bc) and another Crp-independent promoter (Fig. S23f). The inhibitory effect is most likely exerted on cAMP synthesis, since the excretion of cAMP which reflects the internal cAMP level¹⁷ was also inhibited over the same period upon oaa addition (Fig. 3de). Thus, oaa is a candidate precursor implementing the feedback inhibition depicted in the dotted red line of Fig. 3a.

Strong to moderate repressive effects were also observed following the addition of α-ketoglutarate (akg) (Figs. 3c, S24, S25) and pyruvate (pyr) (Fig. 3c, S26), both of which are α-ketoacids. In contrast, the addition of succinate (succ), which is a dicarboxylic acid like oaa and akg but is not an α-ketoacid, leads to only minor repression (Fig. 3c, Fig. S27). While our study does not rule out other possible causes of transient repression⁴⁶, the inhibitory effects produced by the α-ketoacids are much stronger than those by glucose and the nonhydrolyzable compound TMG investigated previously⁴⁷; see Fig. S28. Finally, α-ketoacid addition also caused transient increase in the expression of the anabolic gene glnA (Fig. S29ab). This regulatory effect is independent of cAMP (Fig. S29cde), and is captured by the dashed blue arrow in Fig. 3a.

Metabolic-proteome coordination: mechanism

The cAMP signalling pathway linking metabolism to catabolic gene expression is commonly thought to comprise of the PTS proteins^15,16 (Fig. S1). Recently, akg was reported to interact directly with EI of the PTS proteins⁴³, making PTS proteins likely candidates for implementing the proposed feedback by precursors (dotted red line in Fig. 3a). However, strong transient repression was still observed upon the addition of α-ketoacids in strains with deletion of various PTS proteins, including one with the 3 major PTS proteins deleted (Δpts) and another with additionally all 5 EI proteins deleted (Δ5EI Δpts); see Figs. 4ab, S30, S31. This transient effect was still accompanied by similar fold of reduction in cAMP excretion in vivo (Fig. 3de), and the PTS mutants in steady state still exhibited C-lines for C-limited growth (Fig. 4c). The C-lines of the PTS mutants (dashed lines) exhibited similar x-intercept (λ_C) as the wild-type (red line), indicating that while PTS proteins do affect the degree of Crp-cAMP mediated regulation of catabolic gene expression as is long known¹⁵, they are not necessary for the existence of this response (i.e., the occurrence of the C-line).

Figure 4. Mechanism of cAMP-dependent signalling.

(a) oaa transiently repressed PlacZ-lacZ expression in PTS-deleted cells, NQ721 (Δpts) and NQ506 (Δ5EI Δpts), grown exponentially in lactose. 20 mM oaa was supplied at time zero. The response of WT cells to oaa in Fig. 3b (red triangles) was plotted for comparison. (b) The magnitudes of transient repression by oaa and akg were quantified as in Fig. 3c, based on the data in Figs. 4a, S30, S31. (c) Steady state PlacZ-lacZ expression in PTS mutants under various modes of C-limitations; see Table S18 for data and conditions. Dashed lines show the best linear fit (Table S19). The C-line of Fig. 1a is shown in red for reference. (d) in vitro AC activities in strains NQ385 (pts⁺), NQ976 (Δpts) and NQ977 (Δ5EI Δpts) were assayed with or without 10 mM of various candidate inhibitors; see Supp. Methods for details. These strains are also deleted of the cAMP phosphodiesterase which is not primary to signalling in cAMP-dependent CCR; see Fig. S33. In (b) and (d), data were expressed as mean ± s.e.m (n ≥ 3).

Next we investigated directly the inhibitory effect of various candidate metabolites on cAMP synthesis, by in vitro assays with permeabilized cells (Ref. 48 and Supp. Methods). The rate of cAMP synthesis by Adenylate Cyclase (AC) was significantly reduced by several α-ketoacids but not by succ, in either PTS⁺ or PTS⁻ background (Figs. 4d, S32). Thus, the simplest regulatory route consistent with all data is to have precursors such as oaa inhibiting cAMP synthesis by AC (Fig. S34), either directly or through the help of a mediator protein. Simple inhibition kinetics was found for oaa, with half-inhibition concentrations in the sub-mM range (Fig. S35).

Discussion

cAMP-mediated CCR is one of the most intensely studied regulatory systems in biology. Results described here suggest that the physiological function of cAMP signalling is not centered on carbon metabolism per se as commonly thought; rather this pathway orchestrates the allocation of proteomic resources (Fig. 2a) in response to different metabolic demands in different nutrient environments. This global regulatory process is directed by an integral feedback system (Fig. 3a), driven by cAMP signals modulated by metabolic precursors such as several α-ketoacids. These precursors can be identified as the “catabolites”, the accumulation of which was proposed to induce CCR over 50 years ago¹¹.

The complexity of molecular interactions underlying this signalling system made it difficult to elucidate its physiological function in a bottom-up approach despite the wealth of molecular data known for this classic system. However, the top-down physiological approach described here was able to reveal simple quantitative relations between gene expression and growth rates; these relations provided key insight on the physiological function of cAMP signalling, leading to the elucidation of molecular strategy and implementation. The effectiveness of this approach provides a conceptual framework to pursue the use of quantitative physiological approaches to elucidate other complex signalling networks.

Methods summary

Material and method including strain construction, cell culture, LacZ activity assay, cAMP excretion rate assay, R/P ratio assay, in vitro AC activity assay, and theoretical analysis are provided in detail in Supplementary Information.