Visual crowding cannot be wholly explained by feature pooling

Abstract

Visual perception is dramatically impaired when a peripheral target is embedded within clutter, a phenomenon known as visual crowding. Despite decades of study, the mechanisms underlying crowding remain a matter of debate. Feature pooling models assert that crowding results from a compulsory pooling (e.g., averaging) of target and distractor features. This view has been extraordinarily influential in recent years, so much so that crowding is typically regarded as synonymous with pooling. However, many demonstrations of feature pooling can also be accommodated by a probabilistic substitution model where observers occasionally report a distractor as the target. Here, we directly compared pooling and substitution using an analytical approach sensitive to both alternatives. In four experiments, we asked observers to report the precise orientation of a target stimulus flanked by two irrelevant distractors. In all cases, the observed data were well-described by a quantitative model that assumes probabilistic substitution, and poorly described by a quantitative model that assumes that targets and distractors are averaged. These results challenge the widely-held assumption that crowding can be wholly explained by compulsory pooling.

Objects in the periphery of a scene are more difficult to identify when presented amid clutter. This phenomenon is known as visual crowding, and it is thought to impose fundamental constraints on reading (e.g., Pelli et al., 2007; Chung, 2002; Levi, Song, & Pelli, 2007) and object recognition (e.g., Levi, 2008; Whitney & Levi, 2011; Pelli, 2008; Pelli & Tillman, 2008). Moreover, mounting evidence suggests that crowding is amplified in a number of developmental and psychiatric disorders, including ADHD (Stevens et al., 2012) and Dyslexia (Moores, Cassim, & Talcott, 2011; Spinelli et al., 2002). Thus, there is a strong motivation to understand the basic factors that mediate this phenomenon.

Explanations of crowding typically invoke one of two broad theoretical models. On the one hand, pooling models assert that crowding results from a compulsory integration of information across stimuli (e.g., Parkes et al., 2001; Greenwood, Bex, & Dakin, 2009; 2010). Although this integration preserves the ensemble statistics of a display (e.g., mean size or orientation), it prohibits access to the individual stimuli from which these statistics are derived. In an influential paper, Parkes et al. (2001) asked observers to report the tilt (clockwise or counterclockwise from horizontal) of a target Gabor embedded within an array of horizontal distractors. On each trial, a variable number of the distractors were tilted in the same direction (and by the same magnitude) as the target. Tilt thresholds (i.e., the minimum target tilt needed for observers to perform the task with criterion accuracy) were found to decrease monotonically as the number of tilted distractors increased, and these data were well-approximated by a quantitative model which assumes that target and distractor tilts were averaged at an early stage of visual processing (e.g., prior to the point where the orientation of any one stimulus could be accessed and reported). In a second experiment, Parkes et al. asked observers to report the configuration of three tilted patches (e.g., horizontal or vertical) presented among horizontal distractors. Performance on this task was at chance, indicating that even though the number of tilted distractors in the display had a substantial effect on tilt thresholds, observers could not access or report the tilt(s) of individual items.

In a third experiment, Parkes et al. asked observers to report the tilt of a target patch embedded within an array of horizontally tilted, similarly tilted (i.e., same direction as the target), or dissimilarly tilted (i.e., different direction from the target) distractors. As before, embedding a target within in array of similarly tilted distractors reduced tilt thresholds (relative to displays containing horizontally tilted distractors). However, performance was drastically reduced for displays where distractors were tilted opposite the target. Specifically, it was no longer possible to estimate tilt thresholds for either of the observers who participated in this experiment. A simple pooling model provides a straightforward explanation of this result: if orientation signals are averaged at an early stage of visual processing, then presenting a target among similarly tilted distractors should facilitate observers’ performance relative to a condition where the target is presented among horizontal distractors. Conversely, presenting the target among dissimilarly tuned distractors should yield a percept of horizontal or opposite tilt, leading to an increased number of incorrect responses.

Pooling models have enjoyed widespread popularity in recent years, so much so that the term “pooling” has become nearly synonymous with crowding. However, an important alternative view asserts that crowding stems from the spatial uncertainty inherent in peripheral vision. Unlike pooling models, these so-called “substitution“ models assume that observers can access the individual feature values from the items within a display, but are incapable of differentiating these feature values across space. Our view is that substitution errors are capable of describing many (if not all) findings that appear to support compulsory feature pooling. Consider the study by Parkes et al. (2001), where tilt thresholds were found to decrease as the number of tilted distractors increased. These findings are consistent with feature pooling, but they can also be accommodated by a substitution model. For example, assume that the observer substitutes a distractor for a target on some proportion of trials, and assume further that each distractor in a given display is equally likely to be substituted for the target. Under these conditions, increasing the number of tilted patches will naturally increase the likelihood that one tilted patch will be substituted for the identically tilted target, and tilt discrimination performance should be largely unaffected. Conversely, decreasing the number of tilted patches in the display will increase the likelihood that a horizontal distractor will be substituted for the tilted target, forcing the observer to guess and leading to an increase in tilt thresholds¹. This could also explain why performance was impaired when targets were embedded within arrays of oppositely tilted distractors - if a clockwise distractor is substituted for a counterclockwise target, the observer will incorrectly report that the target is tilted clockwise. If substitutions are probabilistic (i.e., they occur on some trials but not others) then observers’ performance could fall to near-chance levels and make the estimation of tilt thresholds virtually impossible.

More recently, Greenwood and colleagues (Greenwood et al., 2009) reported that pooling can also explain crowding for “letter-like” stimuli. In this study, observers were required to report the position of the horizontal stroke of a cross-like stimulus that was flanked by two similar distractors. Results suggested that observers’ estimates of stroke position were systematically biased by the position of the distractors’ strokes. Specifically, observers tended to report that the target stroke was located midway between its actual position and the position of the flanker strokes. This result is consistent with a model of crowding in which the visual system averages target and distractor positions. However, this result may reflect the interaction of two response biases rather than positional averaging per se. For example, observers responses were systematically repulsed away from the stimulus midpoint (i.e., observers rarely reported the target as a “+”). We suspect that observers had a similar disinclination to report extreme position values (i.e., it is unlikely that observers would report the target as a “T”), though the latter possibility cannot be directly inferred from the available data. However, these biases could impose artificial constraints on the range of possible responses, and may have led to an apparent “averaging” where none exists.

Although probabilistic substitution provides a viable alternative explanation of apparent feature pooling in crowded displays, there are important limitations in the evidence supporting it. Specifically, virtually all studies favoring substitution have employed categorical stimuli (e.g., letters or numbers; Wolford, 1975; Strasburger, 2005; though see Gheri & Baldassi, 2008 for a notable exception) that preclude the report of an averaged percept. For example, observers performing a letter report task cannot report that the target “looks like the average of an ‘E’ and a ‘B’”. In the current study, we attempted to overcome this limitation by using a task and analytical procedure that could provide direct evidence for both pooling and substitution. Specifically, we asked observers to report the orientation of a “clock-face” stimulus (see Figure 1) that appeared alone or was flanked by two irrelevant distractors. We then examined how observers’ report errors (i.e., the angular difference between the reported and actual target orientations on a given trial) were influenced by the introduction of distractors. If crowding results from a compulsory pooling of target and distractor features at a relatively early stage of visual processing, then one would expect observers’ report errors to be biased towards the average orientation of items in the display (as in Parkes et al., 2001). Alternately, if crowding results from a probabilistic substitution of target and distractor features, then one would expect observers’ report errors to take the form of a bimodal distribution, with one peak centered over the target's orientation and a second peak over the distractors’ orientation.

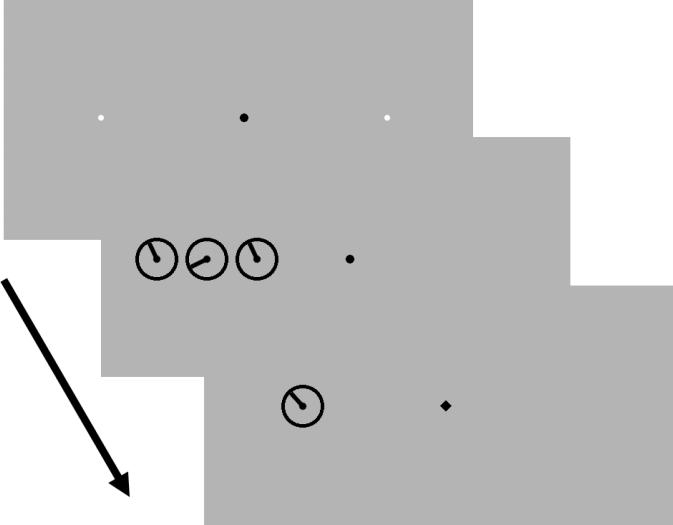
Figure 1. Behavioral Task.

Trials began with a fixation array (upper panel) 500 ms. The small white dots to the left and right of fixation denoted where a target could appear. The target array (middle panels) was then presented for 75 ms. Observers were instructed to discriminate the orientation of the clock-face appearing over the placeholder. On 50% of trials, only the target was presented (“uncrowded” trials, not shown). On the remaining 50% of trials the target was flanked by two distractors. When present, these distractors were rotated ±60, 90, or 120°. At the end of each trial a randomly oriented probe was rendered at the same location as the target (bottom panel); observers adjusted the orientation of this stimulus until it matched their percept of the target's orientation.

Experiment 1

In Experiment 1, observers were asked to report the orientation of a “clock-face” stimulus presented in the periphery of a display (Figure. 1). On 50% of trials, only the target was presented (uncrowded trials). On the remaining 50% of trials, the target was flanked by two irrelevant distractors (crowded trials). When present, the distractors were rotated ±60, 90, or 120° relative to the target. For each experimental condition, we modeled observers’ report errors (i.e., the angular distance between the reported and actual target orientations) with quantitative functions derived from the assumptions of a pooling model and a substitution model. We then compared these models to determine which provided a better description of the observed data (see Data Analysis and Model Fitting).

Method

Observers

Eighteen undergraduate students from the University of Oregon participated in a single 1.5 hour testing session in exchange for course credit. All observers reported normal or corrected-to-normal visual acuity, and all gave written and oral informed consent. All experimental procedures were approved by the local institutional review board.

Stimuli and Apparatus

Stimuli were generated in Matlab using Psychophysics toolbox software (Brainard, 1997; Pelli, 1997) and rendered on an 18-inch CRT monitor cycling at 120 Hz. All stimuli were black and rendered on a medium-grey background (60.2 cd/m²). Participants were seated approximately 60 cm from the display, though head position was unconstrained. From this distance, clock-face stimuli subtended 2.67° in diameter and were centered ±9.23° from fixation along the horizontal meridian. The center-to-center distance between stimuli was fixed at 3.33°.

Design and Procedure

A representative trial is depicted in Figure 1. Each trial began with the presentation of a fixation array containing a central black dot (subtending 0.25°) flanked by two small white placeholders (0.18°) at ±9.23° eccentricity along the horizontal meridian. After 500 ms, a target array was presented for 75 ms. On 50% of trials, a single, randomly oriented clock face stimulus (the target) appeared over one of the two placeholders (uncrowded trials; not shown). On the remaining 50% of trials, the target was flanked by two distractors (crowded trials; Figure 1). Crowded and uncrowded trials were fully mixed within blocks. When present, the distractors were rotated ±60, 90, or 120° relative to the target (both distractors had the same orientation on a given trial). Observers were explicitly instructed to ignore the distractors and focus on reporting the target that appeared over one of the two placeholders. After a 250 ms blank interval, a randomly oriented probe was rendered at the same spatial location as the target; observers rotated this probe using the arrow keys on a standard US keyboard until it matched their percept of the target's orientation, and entered their final response by pressing the spacebar. Observers were instructed to respond as precisely as possible, and no response deadline was imposed. A new trial began 250 ms after their response. Each observer completed 15 blocks of 72 trials, for a total of 1080 trials.

Data Analysis and Model Fitting

For each experimental condition, we fit observers’ report errors (at the group and individual level) with quantitative functions that capture key predictions of pooling and substitution models. During uncrowded trials, we assume that the observer encodes a representation of the target's orientation with variability σ. Thus, the probability of observing a response × (where –π ≤ × ≤ π) is given by a von Mises distribution (the circular analog of a standard Gaussian) with mean μ (uniquely determined by the perceived target orientation, θ) and concentration k (uniquely determined by σ and corresponding to the precision of the observer's representation²):

$$p(x\mid \theta ,\sigma )=\frac{e^{k\cos (x-\mu )}}{2\pi I_0\left(k\right)}$$ (Eq. 1)

where I₀ is the modified Bessel function of the first kind of order 0. In the absence of any systematic perceptual biases (i.e., if θ is a reliable estimator of the target's orientation), then estimates of μ should take values near the target's orientation and observers’ performance should be limited solely by noise (σ).

The same model can be used to approximate observers’ performance on crowded trials given a pooling model like the one described by Parkes et al. (2001). Consider a scenario where a 0° target is flanked by two distractors rotated by 60° (relative to the target). If these values are averaged prior to reaching awareness, then one would expect the observer's percept, θ, to resemble the mean of these orientations: (60°+60°+0°)/3 = 40°, and estimates of μ should be near this value³. Of course, more complex pooling models are plausible (see, e.g., Freeman et al., 2012). For example, one possibility is that pooling occurs on only a subset of trials. Alternately, pooling might reflect a nonlinear combination of target and distractor features (e.g., perhaps targets are “weighted” more heavily than distractors). However, we note that Parkes et al. (2001) and others have reported that a linear averaging model was sufficient to account for crowding-related changes in tilt thresholds. Nevertheless, in the present context any pooling model must predict the same basic outcome: observers’ orientation reports should be systematically biased away from the target and towards a distractor value. Thus, any bias in estimates of μ can be taken as evidence for pooling.

Alternately, crowding might reflect a substitution of target and distractor orientations. For example, on some trials the participant's report might be determined by the target's orientation, while on others it might be determined by a distractor orientation. To examine this possibility, we added a second von Mises distribution to Equation 2 (following an approach developed by Bays et al., 2009):

$$p(x\mid {\theta }_t,{\theta }_{nt},\sigma ,nt)=(1-d)\frac{e^{k\cos (x-{\mu }_t)}}{2\pi I_0\left(k\right)}+d\frac{e^{k\cos (x-{\mu }_{nt})}}{2\pi I_0\left(k\right)}$$ (Eq. 2)

Here, μ_t and μ_nt are the means of von Mises distributions (with concentration k) relative to the target and distractor orientations (respectively). nt (uniquely determined by estimator d) reflects the relative frequency of distractor reports and can take values from 0 to 1.

During pilot testing, we noticed that many observers’ response distributions for crowded and uncrowded contained small but significant numbers of high-magnitude errors (e.g., ≥ 140°). These reports likely reflect instances where the observed failed to encode the target (e.g., due to lapses in attention) and was forced to guess. Across many trials, these guesses will manifest as a uniform distribution across orientation space. To account for these responses, we added a uniform component to Eqs. 1 and 2. The pooling model then becomes:

$$p(x\mid {\theta }_t,{\theta }_{nt},\sigma ,nr)=(1-r)\frac{e^{k\cos (x-\mu )}}{2\pi I_0\left(k\right)}+\frac{r}{2\pi }$$ (Eq. 3)

and the substitution model:

$$p(x\mid {\theta }_t,{\theta }_{nt},\sigma ,nt,nr)=(1-d-r)\frac{e^{k\cos (x-{\mu }_t)}}{2\pi I_0\left(k\right)}+d\frac{e^{k\cos (x-{\mu }_{nt})}}{2\pi I_0\left(k\right)}+\frac{r}{2\pi }$$ (Eq. 4)

In both cases, nr is height of a uniform distribution (uniquely determined by estimator r) that spans orientation space, and it corresponds to the relative frequency of random orientation reports.

To distinguish between the pooling (Eqs. 1 and 3) and substitution (Eqs. 2 and 4) models, we used Bayesian Model Comparison (Wasserman, 2000; MacKay, 2003). This method returns the likelihood of a model given the data while correcting for model complexity (i.e., number of free parameters). Unlike traditional model comparison methods (e.g., adjusted r² and likelihood ratio tests), BMC does not rely on single-point estimates of model parameters. Instead, it integrates information over parameter space, and thus accounts for variations in a model's performance over a wide range of possible parameter values⁴. Briefly, each model described in Eqs. 1-4 yields a prediction for the probability of observing a given response error. Using this information, one can estimate the joint probability of the observed errors, averaged over the free parameters in a model – that is, the model's likelihood:

$$L\left(M\right)=p(D\mid M)=\int p(\Omega \mid M)p(D\mid \Omega )d\Omega =\int \prod _{i=1}^{N_{trials}}p(D_i\mid \Omega )p(\Omega \mid M)d\Omega$$ (Eq. 5)

where M is the model being scrutinized, Ω is a vector of model parameters, and D is the observed data. For simplicity, we set the prior over the j^th model parameter to be uniform over an interval R_j (intervals are listed in Table 1). Rearranging Eq. 5 for numerical convenience:

$$\log L\left(M\right)=L_{\max }\left(M\right)-\sum _{j=1}^{\dim \Omega }\log R_j+\log \int e^{\log L_{\max }\left(\Omega \right)-\log L_{\max }\left(M\right)d\Omega }$$ (Eq. 6)

Here, dim Ω is the number of free parameters in the model and L_max(M) is the maximized log likelihood of the model.

Table 1.

Range of parameter values used for Bayesian Model Comparison in Experiment 1A.

	μ t	μ d	k	nt	nr
Range	−180:180	0:180	0.1:50	0:0.5	0:0.5

Results

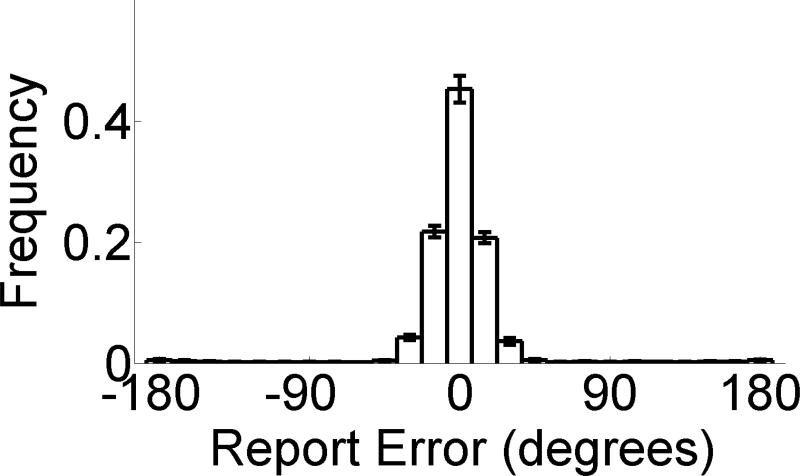
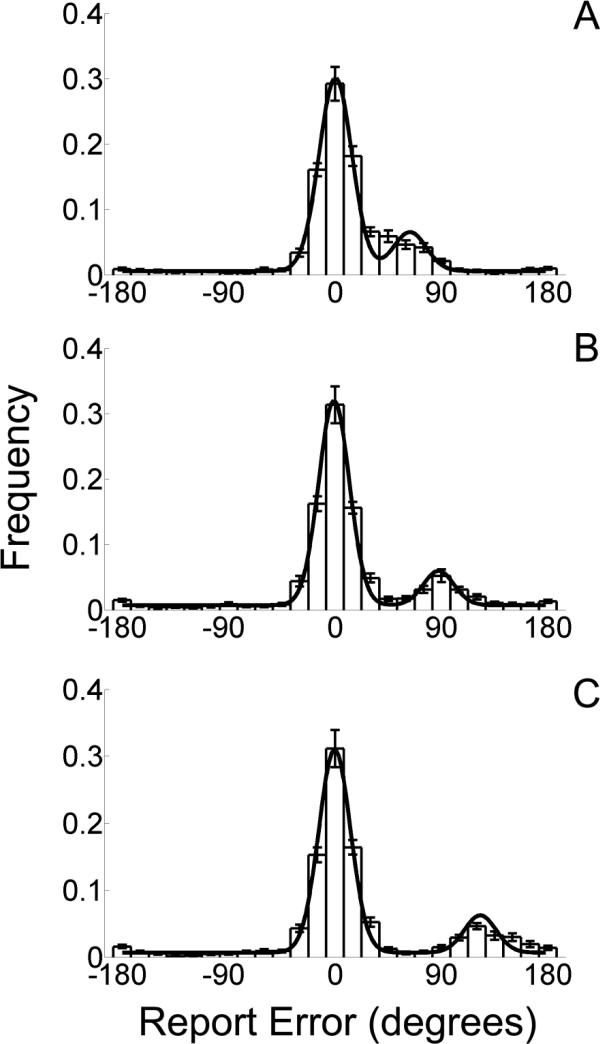
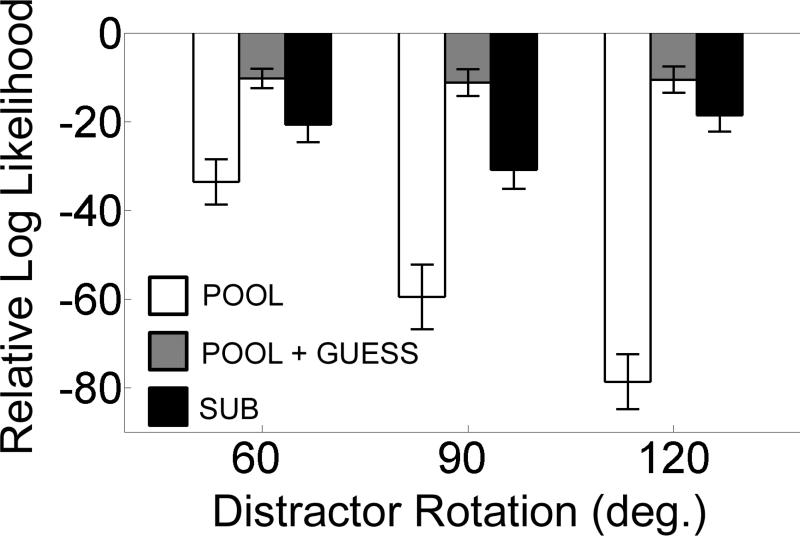
Figure 2 depicts the mean (±1 S.E.M.) distribution of report errors across observers during uncrowded trials. As expected, report errors were tightly distributed around the target orientation (i.e., 0° report error), with a small number of high-magnitude errors. Observed error distributions were well-approximated by the model described in Eq. 3 (mean r² = 0.99 ± 0.01), with roughly 5% of responses attributable to random guessing (see Table 2). Of greater interest were the error distributions observed on crowded trials. If crowding results from a compulsory integration of target and distractor features at a relatively early stage of visual processing (before features can be consciously accessed and reported), then one would expect distributions of report errors to be biased towards a distractor orientation (and thus, well-approximated by the pooling models described in Eqs. 1 and 3). However, the observed distributions (Figure 3) were clearly bimodal, with one peak centered over the target orientation (0° error) and a second, smaller peak centered near the distractor orientation. To characterize these distributions, the pooling and substitution models described in Equations 1-4 were fit to each observer's response error distribution using maximum likelihood estimation. Bayesian model comparison (see Figure 4) revealed that the log likelihood⁵ of the substitution model described in Eq. 4 (hereafter “SUB + GUESS) was 57.26 ± 7.57 and 10.66 ± 2.71 units larger for the pooling models described in Eqs. 1 and 3 (hereafter “POOL” and “POOL + GUESS”), and 23.39 ± 4.10 units larger than the substitution model described in Eq 2. (hereafter “SUB”). For exposition, that the SUB + GUESS model is 10.66 log likelihood units greater than the POOL + GUESS model indicates that the former model is e^10.66, or ~42,617 times more likely to have produced the data (compared to the POOL + GUESS model). At the individual subject level, the SUB + GUESS model outperformed the POOL + GUESS model for 17/18 (±60° rotations), 14/18 (±90°) and 15/18 (±120°) subjects. Classic model comparison statistics (e.g., adjusted r²) revealed a similar pattern. Specifically the SUB + GUESS model accounted for 0.95 ± 0.01, 0.94 ± 0.01, and 0.94 ± 0.01 of the variance in error distributions for ±60, 90, and 120° distractor rotations, respectively. Conversely, the POOL + GUESS model accounted for 0.34 ± 0.17, 0.88 ± 0.04, and 0.90 ± 0.03 of the observed variance. For the latter model, most high magnitude errors were absorbed by the nr parameter; there was little evidence for a large shift in μ_t towards distractor values (mean μ_t estimates = 7.28 ± 2.03, 1.75 ± 1.79, and 0.84 ± 0.41° for ±60, 90, and 120° distractor rotations, respectively). Together, these findings constitute strong evidence in favoring a substitution model.

Figure 2.

Distribution of mean (±1 S.E.M.) report errors during uncrowded trials in Experiment 1.

Table 2.

Mean (±1 S.E.M.) parameter estimates obtained from the SUB + GUESS model in Experiment 1.

	μ t	μ d	k	nt	nr
Uncrowded	−0.27 (0.28)	---	12.00 (0.48)	---	0.05 (0.02)
Crowded: ±60°	1.34 (0.59)	64.32 (6.38)	14.67 (0.72)	0.14 (0.02)	0.15 (0.02)
Crowded: ±90°	0.13 (0.40)	88.63 (2.39)	13.72 (0.71)	0.12 (0.02)	0.18 (0.02)
Crowded: ±120°	0.69 (0.42)	123.78 (2.35)	14.77 (0.94)	0.13 (0.02)	0.17 (0.02)

All values of μ_t μ_nt and k are in degrees.

Figure 3. Distributions of report errors observed during crowded trials of Experiment 1A.

Panels A, B, and C depict the mean (±1 S.E.M.) histogram (bin width = 14.4°) of report errors during trials where the distractors were rotated by ±60, 90, and 120°, respectively (data were pooled across clockwise and counterclockwise rotations). The best fitting substitution model (SUB+GUESS; see text) is overlaid.

Figure 4. Bayesian Model Comparison – Experiment 1.

Mean (±1 S.E.M.) log-likelihood values for the POOL (Eq. 1), POOL+GUESS (Eq. 3), and SUB (Eq. 2) models are plotted relative to the SUB+GUESS model. A negative log-likelihood value, x, means that the data are e^x times more likely under the SUB+GUESS model.

Mean (±S.E.M.) maximum likelihood estimates of μ, k, and nr (for uncrowded trials), as well as μ_t, μ_nt, k, nt, and nr (for crowded trials) obtained from the SUB + GUESS model are summarized in Table 1. Estimates of μ_t rarely deviated from 0 (the sole exception was during ±60° rotation trials; M = 1.34°; t(17) = 2.26, p = 0.03; two-tailed t-tests against distributions with μ = 0), and estimates of μ_nt were statistically indistinguishable from the “real” distractor orientations (i.e., ±60, 90, 120°), t(17) = 0.67, −0.57, and 1.61 for ±60, 90, and 120° trials, respectively; all p-values > 0.12. Within each condition, distractor reports accounted for 12-15% of trials, while random responses accounted for an additional 15-18%. Distractor reports were slightly more likely for ±60° distractor rotations (one-way repeated-measures analysis of variance, F(2,17) = 3.28, p = 0.04), consistent with the basic observation that crowding strength scales with stimulus similarity (Kooi, Toet, Tripathy, & Levi, 1994; Felisberti, Solomon, & Morgan, 2005; Scolari, Kohnen, Barton, & Awh, 2007; Poder, 2012).

Examination of Table 2 reveals other findings of interest. First, estimates of k were significantly larger during crowded relative to uncrowded trials; t(17) = 7.28, 3.82, and 4.80 for ±60, 90, and 120° distractor rotations, respectively, all ps < 0.05. In addition, estimates of nr were 10-12% higher for crowded relative to uncrowded trials; t(17) = 4.97, 7.11, and 6.32 for the ±60, 90, and 120° distractor rotations, respectively, all ps < 0.05. Thus, at least for the current task, crowding appears to have a deleterious (though modest) effect on the precision of orientation representations. In addition, it appears that crowding may result in a total loss of orientation information on a subset of trials. We suspect that similar effects are manifest in many extant investigations of crowding, but we know of no study that has documented or systematically examined this possibility.

Discussion

To summarize, the results of Experiment 1 are inconsistent with a simple pooling model where target and distractor orientations are averaged prior to reaching awareness. Conversely, they are easily accommodated by a probabilistic substitution model in which the observer occasionally mistakes a distractor orientation for the target. Critically, the current findings cannot be explained by tachistoscopic presentation times (e.g., 75 ms) or spatial uncertainty (e.g., the fact that observers had no way of knowing which side of the display would contain the target on a given trial) as prior work has found clear evidence for pooling under similar conditions (e.g., Parkes et al., 2001, where displays were randomly and unpredictably presented to the left or right of fixation for 100 ms).

One important difference between the current study and prior work is our use of (relatively) dissimilar targets and distractors. Accordingly, one might argue that our findings reflect some phenomenon (e.g., masking) that is distinct from crowding. However, we note that we are not the first to document strong “crowding” effects with dissimilar targets and flankers. In one high-profile example, He et al. (1996; see also Blake et al., 2006) documented strong crowding when a tilted target grating was flanked by orthogonally tilted gratings. In another high-profile example, Pelli et al. (2004) reported strong crowding effects when a target letter (e.g., “R”) was flanked by two very dissimilar letters (“S” and “Z”; see their Figure 1). Thus, the use of dissimilar targets and distractors does not preclude crowding.

Alternately, one could argue that our findings reflect a special form of crowding that manifests only when targets and flankers are very dissimilar. For example, perhaps pooling dominates when similarity is high, whereas substitution dominates when it is low. We are not aware of any data supporting this specific alternative, but there are a handful of studies suggesting that different forms of interference manifest when target-distractor similarity is high vs. low. In one example, Marsechal et al. (2010; see also Solomon et al., 2004; Poder, 2012) asked participants to report the tilt (clockwise or anticlockwise from horizontal) of a crowded grating. These authors reported that estimates of orientation bias (defined as the minimum target tilt needed for a target to be reported clockwise or anticlockwise of horizontal with equal frequency) were small and shared the same sign (i.e., clockwise vs. anticlockwise) of similarly tilted flankers (e.g., within 5 degrees of the target) at extreme eccentricities (10° from fixation). However, estimates of bias were larger and of the opposite sign for dissimilar flankers (greater than 10 degrees away from the target) at intermediate eccentricities (4° from fixation; see their Figure 2 on page 4). These results were interpreted as evidence for “small angle assimilation” and “repulsion”, respectively. However, we suspect that both effects can be accounted for by probabilistic substitution. Consider first the case of “small-angle assimilation”. Because participants in this study were limited to categorical judgments (i.e., clockwise vs. counterclockwise), this effect would be expected under both pooling and probabilistic substitution models. For example, participants may be more inclined to report a +5° target embedded within +10° flankers as “clockwise” either because they have averaged these orientations or because they have mistaken a flanker for the target. As for repulsion, the “bias” values reported by Mareschal et al. imply that that (for example) a target embedded within −22° flankers needs to be tilted about +10° clockwise in order to be reported as clockwise and anticlockwise with equal frequency. This result can be accommodated by substitution if one assumes that “crowding” becomes less potent as the dissimilarity between targets and distractors increases. In this framework, “bias” may simply reflect the amount of target-flanker dissimilarity needed for substitution errors to occur on ~50% of trials.

Finally, we would like to note that our use of dissimilar distractor orientations (relative to the target) was motivated by necessity. Specifically, it becomes virtually impossible to distinguish between the pooling and substitution models (Eq. 3 and Eq. 4, respectively) when target-distractor similarity is high (see Hanus & Vul, 2013, for a similar argument). To illustrate this, we simulated report errors from a substitution model (Eq. 4) for 20 synthetic observers (1000 trials per observer) over a wide range of target-distractor rotations (±10-90° in 10° increments). For each observer, values of μ_t, μ_nt, k, nt, and nd were obtained by sampling from normal distributions whose means equaled the mean parameter estimates (averaged across all distractor rotation magnitudes) given in Table 2. We then fit each hypothetical observer's report errors with the pooling and substitution models described in Eq. 3 and Eq. 4. For large target-distractor rotations (e.g., ≥ 50°), accurate parameter estimates for the substitution model (i.e., within a few percentage points of the “true” parameter values) could be obtained for the vast majority (N ≥ 18) of observers, and this model always outperformed the pooling model. Conversely, when target-distractor rotation was small (≤ 40°) we could not recover accurate parameter estimates for most observers, and the pooling model typically equaled or outperformed the substitution model⁶. Virtually identical results were obtained when we simulated an extremely large number of trials (e.g., 100,000) for each observer. The explanation for this result is straightforward: as the angular distance between the target and distractor orientations decreases, it became much more difficult to segregate response errors reflecting target reports from those reflecting distractor reports. In effect, report errors determined by the distractor(s) were “absorbed” by those determined by the target. Consequently, the observed data were almost always better described by a pooling model, even though they were generated using a substitution model! These simulations suggest that it is very difficult to tease apart pooling and substitution models as target-distractor similarity increases, particularly once similarity exceeds the observers’ acuity for the relevant stimuli.

Experiment 2

In Experiments 2 and 3, we systematically manipulated factors known to influence the severity of crowding: target-distractor similarity (e.g., Kooi et al., 1994; Scolari et al., 2007; Experiment 2) and the spatial distance between targets and distractors (e.g., Bouma, 1970; Experiment 3). In both cases, our primary question was whether parameter estimates for the SUB + GUESS model changed in a sensible manner with manipulations of crowding strength.

Method

Participants

Seventeen undergraduate students from the University of Oregon participated in a single 1.5 hour testing session in exchange for course credit. All observers reported normal or corrected-to-normal visual acuity, and all gave written and oral informed consent. Data from one observer could not be modeled due to a large number of high-magnitude errors; the data here reflect the remaining 16 observers.

Design and Procedure

The design of this experiment was identical to that of Experiment 1, with the exception that on 50% of distractor-present trials the target was rendered in red and the distractors in black (“popout” trials). On the remaining 50% of trials, both the target and distractors were black (“uniform” trials). When present, distractors were always rotated ±110° relative to the target.

Results

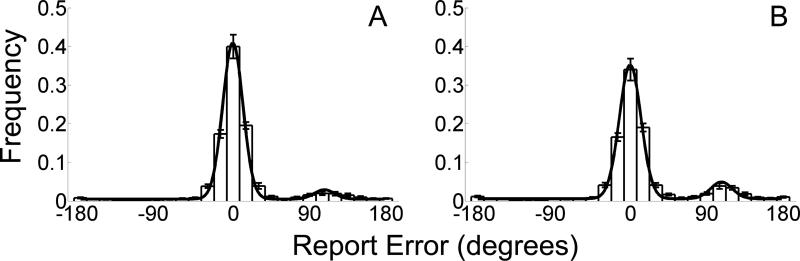
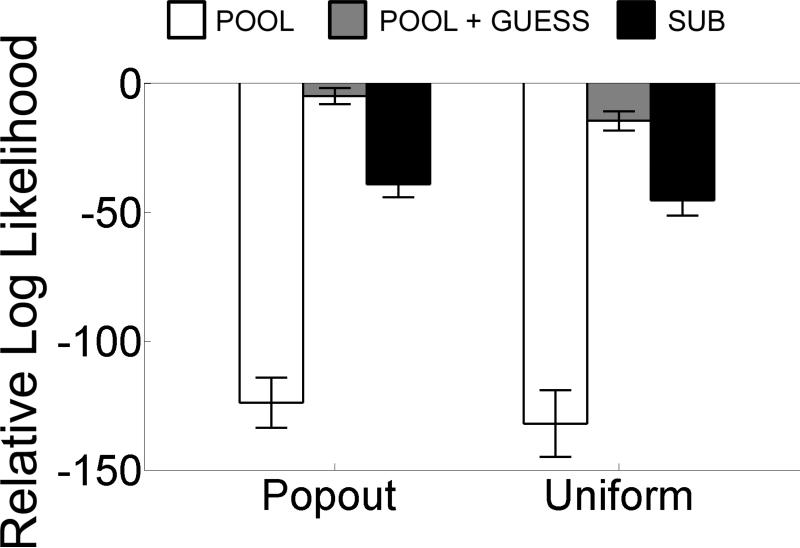
As in Experiment 1, Distributions of response errors observed during uniform and popout trials were bimodal, with one distribution centered over the target orientation and a second centered over the distractors’ orientation (Figure 5). For popout trials (i.e., when crowding strength should be low), Bayesian model comparison (Figure 6) revealed that the log likelihood of the SUB + GUESS model (Eq. 4) was 123.84 ± 9.76, and 4.97 ± 3.14, and 39.16 ± 5.02 units larger than the POOL, POOL + GUESS, and SUB models, respectively. During uniform trials (i.e., when crowding strength should be high), the log likelihood of the SUB + GUESS model exceeded the POOL, POOL + GUESS, and SUB models by 131.98 ± 12.90, 14.57 ± 3.66, and 45.46 ± 5.87 units. At the individual subject level, the SUB + GUESS model outperformed the POOL + GUESS model for 9/16 subjects during popout trials and 14/16 subjects during uniform trials. Estimates of nt were lower during popout relative to uniform trials (see Table 3; t(15) = 6.40, p < 0.01), while estimates of nr were marginally lower; t(15) = 1.69, p = 0.10. Estimates of μ_nt were statistically indistinguishable from the actual distractor orientations (i.e., ±110°); t(15) = 0.21 and 0.57, for popout and uniform trials, respectively, both ps > 0.50. Thus, the results of Experiment 2 are consistent with those observed in Experiment 1, and establish that the relative frequencies of distractor reports change in a sensible manner with a factor known to influence the severity of crowding.

Figure 5. Task performance in Experiment 2.

Panels A and B depict the mean (±1 S.E.M.) distribution of report errors across observers for popout (A) and uniform (B) trials. The best fitting SUB + GUESS model is overlaid (solid black line).

Figure 6. Bayesian Model Comparison – Experiment 2.

Mean (±1 S.E.M.) log-likelihood values for the POOL (Eq. 1), POOL+GUESS (Eq. 3), and SUB (Eq. 2) models are plotted relative to the SUB+GUESS model.

Table 3.

Mean (±1 S.E.M.) parameter estimates obtained in Experiment 2.

	μ t	μ d	kt	nt	nr
Uncrowded	−0.98 (0.36)	---	11.96 (0.73)	---	0.03 (0.01)
Popout	0.46 (0.28)	108.33 (7.67)	12.58 (0.70)	0.05 (0.01)	0.11 (0.02)
Uniform	0.63 (0.37)	108.14 (3.26)	13.53 (0.74)	0.09 (0.02)	0.13 (0.02)

Estimates have been collapsed and averaged across clockwise and counterclockwise distractor rotations. All values of μ and k are in degrees.

Experiment 3

The results of Experiments 1 and 2 are readily accommodated by a substitution model where observers occasionally substitute a distractor for the target. In Experiment 3, we asked whether our findings are idiosyncratically dependent on the use of yoked distractors. For example, the distractors in Experiments 1 and 2 always shared the same orientation. One possibility is that this configuration encouraged a Gestalt-like grouping of the distractors that discouraged pooling and/or encouraged target-distractor substitutions. To examine this possibility, distractors in Experiment 3 were randomly oriented with respect to the target (and each other). In addition, we took this opportunity to examine how substitution frequencies change with another well-known manipulating of crowding strength: target-distractor spacing (e.g., Whitney & Levi, 2011; Pelli, 2008; Bouma, 1970).

Method

Participants

Fifteen undergraduate students from the University of Oregon participated in a single 1.5 hour testing session in exchange for course credit. All observers reported normal or corrected-to-normal visual acuity, and all gave written and oral informed consent.

Design and Procedure

Experiment 3 was similar to Experiment 1A, with the following exceptions: First, on 50% of crowded trials, distractors were presented adjacent to the target (3.33° center-to-center distance; “near” trials), while on the remaining 50% of crowded trials distractors were presented at a much greater distance from the target (6.50° center-to-center distance; “far” trials). Second, all distractors were randomly oriented with respect to the target (and one another).

Modeling

Each crowded display contained two uniquely oriented distractors in addition to the target. If these orientation values are pooled prior to reaching awareness, then observers’ responses should be normally distributed around the mean orientation of each display and can be approximated by Eq. 1. If errors are instead determined by feature substitutions, then the probability of observing response x is:

$$p(x\mid \theta ,\sigma ,nt,nr)=(1-nt-nr)\frac{e^{k\cos (x-t)}}{2\pi I_0\left(k\right)}+nt\frac{1}{2}\sum _{i=1}^2\frac{e^{k\cos (x-nt)}}{2\pi I_0\left(k\right)}+\frac{nr}{2\pi }$$ (Eq. 7)

where t refers to the target orientation and d_i refers to the orientation of the ith distractor. For simplicity, we assumed that each distractor had an equal probability of being substituted for the target (subsequent analyses justified this assumption; see below).

Results and Discussion

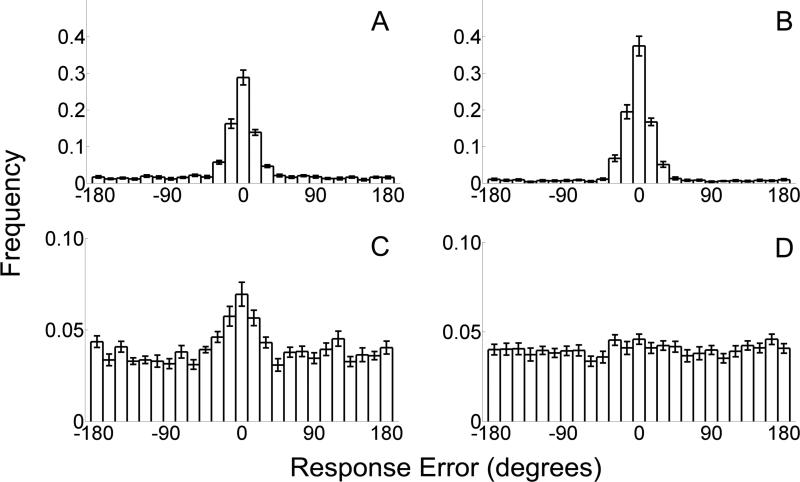
Distributions of report errors relative to the target orientation during near and far trials are shown in Figures 7A and 7B. Note that both distributions feature a prominent central tendency, along with a smaller uniform profile that spans orientation space. Since distractor orientations varied randomly with respect to the target (and each other) on each trial, the uniform profile in this distribution could reflect reports of distractor values. To examine this possibility, we generated distributions of response errors relative to the individual distractor orientations in each display (i.e., by defining response error as the difference between the reported orientation and a distractor's orientation)⁷; these are plotted for near and far trials in Figures 7C and 7D (respectively). Note that the distribution observed during near trials (Figure 7C) features a prominent central tendency, suggesting that observers did in fact report distractors on some proportion of trials. Estimates of k, nt, and nr for the near and far conditions are shown in Table 4. As expected, increasing the separation between the target and distractor substantially reduced the frequency of distractor (M = 0.17 and 0.04, for near and far trials, respectively, t(14) = 4.60, p < 0.001) and random orientation reports (M = 0.20 and 0.12 for near and far trials, respectively, t(14) = 5.78, p < 0.001). These findings demonstrate that substitution errors varied in an orderly fashion when we manipulated flanker distance (a factor known to modulate the strength of visual crowding). Moreover, they establish that the findings described in Experiments 1 and 2 are not idiosyncratic to the use of yoked distractors.

Figure 7. Task performance in Experiment 3.

Panels A and B depict the mean (±1 S.E.M.) histogram (bin width = 14.4°) of report errors across participants relative to the target orientation during near (A) and far (B) trials. Conversely, panels C and D plot errors relative to the flankers’ orientations on near (C) and far (D) trials. Note that the distribution of report errors during “near” trials (C) features a prominent central tendency. This indicates that observers did, in fact, report distractor values on a subset of trials.

Table 4.

Mean (±1 S.E.M.) parameter estimates obtained in Experiment 3.

	k	nt	nr
Uncrowded	11.88 (0.57)	---	0.04 (0.01)
Near	13.80 (0.64)	0.17 (0.03)	0.20 (0.03)
Far	13.60 (0.82)	0.05 (0.01)	0.12 (0.03)

Estimates have been collapsed and averaged across clockwise and counterclockwise distractor rotations. Values of μ and k are in degrees.

Experiment 4

How are targets and distractors substituted? One possibility is that observers encode one – and only one – stimulus from a crowded display (in this case, either the target or one of the two distractors; Freeman et al. 2012). Alternately, observers might enjoy access to information about all of the stimuli, but cannot determine what information goes where (e.g., Balas et al., 2009; Freeman et al., 2012). The goal of Experiment 4 was to distinguish between these two alternatives. The design of this Experiment was identical to Experiment 1, with the exception that observers were asked to report the average orientation of the three display elements (henceforth referred to as center and flanker items, respectively). If the simple substitution model is correct and only one item from the display is encoded on each trial, then observers’ report errors should be bimodally distributed around the center and flanker orientations and well-described by a substitution model (e.g., Eq. 4)⁸. Alternately, if observers enjoy access to all the items in the display and can average these values, then their report errors should be normally distributed around the mean orientation of the three items in the display and performance should be well-described by a pooling model (e.g., Eq. 3).

Methods

Participants

15 undergraduate students from the University of Oregon participated in Experiment 3. All observers reported normal or corrected-to-normal visual acuity, and all gave written and oral informed consent. Observers in each experiment were tested in a single 1.5 hour session in exchange for course credit.

Design and Procedure

Experiment 4 was similar to that of Experiment 1, with the exception that observers were now asked to report the average orientation of the center (formerly “target”) and flanking (formerly “distractor”) orientations. When present, flanker orientations were rotated ±60, 90, or 120° relative to the center orientation. Additionally, on 50% of trials the flankers were rendered adjacent to the center stimulus; on the remaining 50% of trials flankers were rendered at 6.67° eccentricity from the target (as in Experiment 3). This was done to examine whether estimates of mean orientation are unaffected by crowding strength, as has been reported earlier (e.g., Solomon, 2010). To characterize observers’ performance, data were fit with the pooling and substitution models described in Eqs. 3 and 4.

Results and Discussion

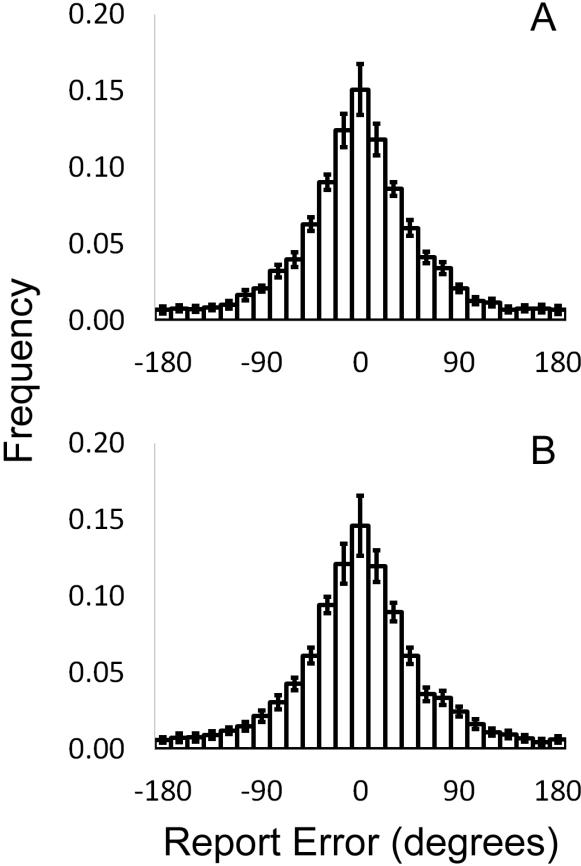
Mean distributions of report errors (relative to the mean orientation of the display) observed during near and far trials are shown in Figures 8A and 8B, respectively⁹. Data have been pooled and averaged across distractor rotation direction (i.e., clockwise and counterclockwise) and magnitude (i.e., 60, 90, 120°) as these factors had no effects on our findings. Here, the pooling and substitution models provided comparably good descriptions of the observed distributions, and parsimony favors the simpler of the two models (pooling). Mean (±1 S.E.M.) estimates of μ and k obtained from the pooling model are shown in Table 4. The estimated parameters were identical across all factors that we manipulated (i.e., distractor rotation magnitude and target-direction separation), t(14) = 0.84 and 1.11 for μ and k, respectively, both p-values > 0.25. This finding complements earlier work (e.g., Solomon, 2010) suggesting that large variations in crowding strength have no effect on an observer's ability to report mean orientation. More generally, the results of Experiment 4 provide further evidence favoring the view that observers have access to feature values from multiple items within a crowded display (see, e.g., Freeman et al., 2012).

Figure 8. Task Performance in Experiment 4.

Panels A and B depict the mean (±1 S.E.M.) histogram of report errors (bin width = 14.4°) relative to the mean orientation of the center and flanker items during near (A) and far (B) trials. Both distributions are unimodal, suggesting that observers could in fact access, compute, and report the mean orientation of each display. Moreover, this ability was unaffected by strong manipulations of crowding strength, replicating earlier findings (e.g., Solomon et al., 2010).

General Discussion

Here, we show that when observers are required to report the orientation of a crowded target, they report the target's orientation or the orientation of a nearby distractor (Experiments 1-3). The frequency of distractor reports changed in a sensible manner with well-established manipulations of crowding strength (Experiments 2 and 3), and are not idiosyncratic to the use of yoked distractors (Experiment 3). Moreover, when observers were required to report the average orientation of items in a display, strong manipulations of crowding strength had a negligible effect on performance (Experiment 4). Together, these results suggest that observers can access and report individual feature values from a crowded display, but cannot bind these values to the appropriate spatial locations. In this respect, they challenge the widely held assumption that visual crowding always reflects an averaging of target and distractor features (Parkes et al., 2001; Pelli et al., 2004; Greenwood et al., 2009; Greenwood et al., 2010; Balas et al., 2009).

Although our data favor a substitution model, we do not claim that feature pooling is impossible or unlikely under all experimental conditions. Specifically, we cannot exclude the possibility that substitution manifests primarily when target-distractor similarity is low (as in the current study), whereas feature pooling manifests when similarity is high (e.g., Cavanagh, 2001; Mareschal et al., 2010). That said, we believe that there is ample room for doubt on this point. First, we know of no evidence that supports this specific view (see Discussion, Experiment 1 for a detailed discussion of this point). Second, our simulations (Discussion, Experiment 1A) suggest that data consistent with feature pooling obtained under high target-distractor similarity might not be that diagnostic. Specifically, we were unable to recover parameter estimates for the substitution model (e.g., Eq. 4) when target-distractor similarity was high, presumably because report errors determined by the target and those determined by a distractor could no longer be segregated. Consequently, a simple pooling model (e.g., Eq. 3) almost always outperformed the substitution model, even though the data were synthesized while assuming the latter. Although some aspects of these simulations (e.g., the parameters of the mixture distributions from which data were drawn) were idiosyncratic to the current set of experiments, we suspect that the core result – namely, that it is difficult to distinguish between pooling and substitution when target-distractor similarity is high – generalizes to many other experiments (see Hanus & Vul, 2013, for a similar point).

We suspect that contributions from neuroscience will be instrumental in resolving this issue. For example, recent human neuroimaging studies have used encoding models to construct population-level orientation-selective response profiles within and across multiple regions of human visual cortex (e.g., V1-hV4; e.g., Brouwer & Heeger, 2011; Scolari, Byers, & Serences, 2012; Serences & Saproo, 2012). These profiles are sensitive to fine-grained perceptual and attentional manipulations (see, e.g., Scolari et al., 2012), and pilot data from our laboratory suggests that they may be influenced by crowding as well. One potentially informative study would be to examine how the population-level representation of a target orientation changes following the introduction of nearby distractors. This would be a useful complement to earlier work demonstrating that the responses of orientation-selective single units in cat (e.g., Gilbert & Wiesel, 1990; Dragoi, Sharma, & Sur, 2000) and macaque (e.g., Zisper, Lamme & Schiller, 1996) V1 are modulated by context. For example, one possibility is that these response profiles will “shift” towards the mean orientation of the target and distractor elements, consistent with a pooling of target and distractor features. Alternately, the profile might shift towards the identity of a distractor orientation, consistent with a substitution of the target with a distractor. We are currently investigating these possibilities.

Our core findings are reminiscent of an earlier study by Gheri and Baldassi (2008). These authors asked observers to report the specific tilt (direction and magnitude relative to vertical) of a Gabor stimulus embedded within an array of vertical distractors. These reports were bimodally distributed over moderate tilt magnitudes (i.e., observers seldom reported that the target was tilted by a very small or large amount) and well-approximated by a “signed-max” model similar to the one examined by Parkes et al. (2001). The current findings extend this work in three important ways: First, we provide an explicit quantitative measure of the relative proportion of trials for which observers’ orientation reports were determined by the properties of a distractor. The same measure also allows one to infer the acuity of observers’ orientation estimates. Second, we show that the relative frequencies of distractor reports change in an orderly way with manipulations of crowding strength. Third, we show that all findings generalize across large pools of observers (Gheri and Baldassi tested only three observers, one of whom was an author and a second of whom could not perform the task without substantial alterations to the stimulus display) and substantial variations in experimental conditions (e.g., stimulus classes).

The findings reported here suggest a number of novel hypotheses regarding factors that influence the severity of crowding. For example, because the substitution model emphasizes binding errors, it predicts that manipulations that facilitate binding, such as directing attention to a crowded stimulus (He, Cavanagh, & Intriligator, 1996; Intriligator & Cavanagh, 2001), will reduce the severity of crowding. Some recent evidence supports this view (Livine & Sagi, 2007; Sayim, Westheimer, & Herzog, 2010; 2011; Chakravarthi & Pelli, 2011; Yeotikar, Khuu, Asper, & Suttle, 2011). In one example (Sayim et al., 2010), observers were asked to discriminate the orientation of a vernier stimulus. On some trials this stimulus was flanked by two horizontal lines (line-only condition). On other trials, physically identical horizontal lines were rendered as part of a geometric shape (e.g., a rectangle; shape condition). Vernier discrimination thresholds were substantially lower in the shape condition relative to the line-only condition, suggesting that global contextual factors influence the severity of crowding. Presumably, these and other grouping strategies may reduce the severity of crowding by facilitating the individuation of target and distractor stimuli. If so, then this may explain recent findings where increasing the number of flankers surrounding a target was found to reduce the severity of crowding (Poder, 2006; Levi & Carney, 2009). Finally, one interesting question concerns whether feature values can be “substituted” to empty portions of visual space. If so, this could explain a recent finding in which oriented flankers were found to confer a perceptual orientation to a Gaussian noise patch (Greenwood et al., 2010).

To summarize, we have shown that when observers are required to report the orientation of a crowded target, they report the target's orientation or the orientation of a nearby distractor. This result is well-described by probabilistic substitution model where observers occasionally confuse a distractor for a target, and poorly described by a pooling model where information is integrated (e.g., averaged) across targets and distractors prior to reaching awareness. While we cannot claim that pooling is unlikely under all circumstances, our view is that the available evidence supporting pooling is relatively weak, and that many demonstrations of apparent pooling can also be explained by a probabilistic substitution of targets and distractors.

Table 5.

Mean (±1 S.E.M.) parameter estimates obtained in Experiment 4.

	μ	k	nr
Near	0.42 (1.80)	35.30 (2.47)	0.12 (0.03)
Far	1.16 (1.89)	40.33 (6.53)	0.10 (0.03)