Stoichiometries and affinities of interacting proteins from concentration series of solution scattering data: decomposition by least squares and quadratic optimization

A new method analyzes solution scattering data from equilibrium mixtures of interacting proteins, in order to determine both the association model and the individual scattering curves of the mixture components.

Abstract

In studying interacting proteins, complementary insights are provided by analyzing both the association model (the stoichiometry and affinity constants of the intermediate and final complexes) and the quaternary structure of the resulting complexes. Many current methods for analyzing protein interactions either give a binary answer to the question of association and no information about quaternary structure or at best provide only part of the complete picture. Presented here is a method to extract both types of information from X-ray or neutron scattering data for a series of equilibrium mixtures containing the initial components at different concentrations. The method determines the association pathway and constants, along with the scattering curves of the individual members of the mixture, so as to best explain the scattering data for the mixtures. The derived curves then enable reconstruction of the intermediate and final complexes. Using simulated solution scattering data for four hetero-oligomeric complexes with different structures, molecular weights and association models, it is demonstrated that this method accurately determines the simulated association model and scattering profiles for the initial components and complexes. Recognizing that experimental mixtures contain static contaminants and nonspecific complexes with the lowest affinities (inter-particle interference) as well as the desired specific complex(es), a new analytical method is also employed to extend this approach to evaluating the association models and scattering curves in the presence of static contaminants, testing both a nonparticipating monomer and a large homo-oligomeric aggregate. It is demonstrated that the method is robust to both random noise and systematic noise from such contaminants, and the treatment of nonspecific complexes is discussed. Finally, it is shown that this method is applicable over a large range of weak association constants typical of specific but transient protein–protein complexes.

1. Introduction  

Gaining a deeper understanding of the functions and mechanisms of protein–protein interactions requires extending the binary information (interaction or not) provided by high-throughput techniques and characterizing the stoichiometries, affinities and three-dimensional structures of protein complexes. However, experimental methods for the detailed study of protein complexes typically fall into two separate categories: some (e.g. X-ray crystallography and NMR spectroscopy) enable structure determination but do not readily reveal the association model, while others [e.g. H/D exchange (Codreanu et al., 2005 ▶), analytical ultracentrifugation (Lebowitz et al., 2002 ▶), titration calorimetry (Velazquez-Campoy et al., 2004 ▶) and composition gradient static light scattering (Attri & Minton, 2005 ▶; Kameyama & Minton, 2006 ▶)] enable characterization of the stoichiometry and strength of interaction but provide no or very limited structural information.

As we show here, small-angle scattering in solution (SAS) (Feigin & Svergun, 1987 ▶) provides an alternative experimental technique that can simultaneously provide both structural and association information for a complex. SAS has recently gained popularity in low-resolution structural studies of protein monomers and tight complexes (Svergun & Stuhrmann, 1991 ▶; Walther et al., 2000 ▶; Chacón et al., 1998 ▶; Svergun, 1999 ▶; Svergun et al., 2001 ▶), as it is applicable to proteins of practically any size under physiological conditions, while data can now be collected rapidly at new higher-flux X-ray or neutron sources. However, its applicability to the study of complexes has been limited owing to the requirement for a homogeneous and monodisperse sample, rendering SAS unsuitable for important, more weakly binding, transient but specific complexes (e.g. those associated with cellular signaling, which contain mixtures of the component monomers and intermediate and final complexes).

We recently described a method for the elucidation of weaker homo-oligomeric complexes from solution scattering data (Williamson et al., 2008 ▶), and subsequent reports of similar numerical approaches applied to experimental data (Bernadó et al., 2009 ▶) have demonstrated the value of such methods. However, these methods were only applied to homo-oligomers and were limited in their ability to handle systematic noise in the scattering data. Here, we extend our earlier method so as to characterize hetero-oligomeric complexes and we develop a new analytical approach to handle contaminants in the mixtures, thereby yielding a method with potential applicability to an even broader range of biological systems and experimental conditions.

An equilibrium mixture of protein components contains multiple different molecular species, including the initial components (often monomers), the desired higher-affinity complexes (both intermediate and final), nonspecific complexes of the lowest affinity (sometimes thought of as interparticle interference) and perhaps static contaminants. The method presented here focuses on the initial components and higher-affinity complexes, and includes an extension for particular static contaminants (such as a nonparticipating monomer or homo-oligomeric aggregate). The method determines the association model (stoichiometry and affinity constants) for the higher-affinity complexes from SAS data collected from a set of solutions containing the initial components in varying concentrations. In addition to the association model, this method accurately reconstructs the individual scattering curves of all the molecular species. These reconstructed curves can form the basis for low-resolution structural analysis of the intermediate and final complexes. While not addressed by the present method, the handling of interparticle interference is important, and interesting future work and possible ways to deal with the lowest-affinity non­specific complexes are discussed.

Scattering from such equilibrium mixtures can be approximated as a fractional mass-weighted linear combination of the ‘pure’ scattering from the initial components and specific complexes (an approximation that is most accurate under conditions when the lowest-affinity nonspecific complexes and contaminants make only a small contribution). First, low-rank approximation is employed to remove from the observed mixture data some of the experimental noise and contributions from minor species. A search is then carried out over possible association models (which define a set of expected fractional masses for all the species), establishing a least-squares problem for each. Solution of the least-squares problem yields reconstructions of the pure scattering curves. These hypothesized reconstructions are evaluated for consistency with the data and with the postulated association model, and the best model is selected. If no model is of sufficient quality, the search can be expanded to consider association models containing a static contaminant. We have investigated the situation where the contaminant is either a nonparticipating monomer or a homo-oligomeric aggregate of one of the initial components, since these represent the most important practical situations where the contaminants are less likely to be removed by biochemical means during preparation of the initial components. In these cases, the least-squares approach is no longer applicable, so, at the cost of computational time, a convex quadratic program is employed to compute scattering curves that are consistent with the data and which satisfy the additional constraints expected of physically realistic scattering curves.

We demonstrate the effectiveness of this method on simulations of four hetero-oligomeric complexes with different association pathways, association constants, molecular weights and three-dimensional structures. Our simulation studies further demonstrate the robustness of the method to both random noise and systematic noise due to contaminants. In all cases, it is possible to infer the correct association pathway and obtain association constants that are very close to those used in the simulation, as well as scattering curves that closely approximate those of the monomers and oligomers.

2. Methods  

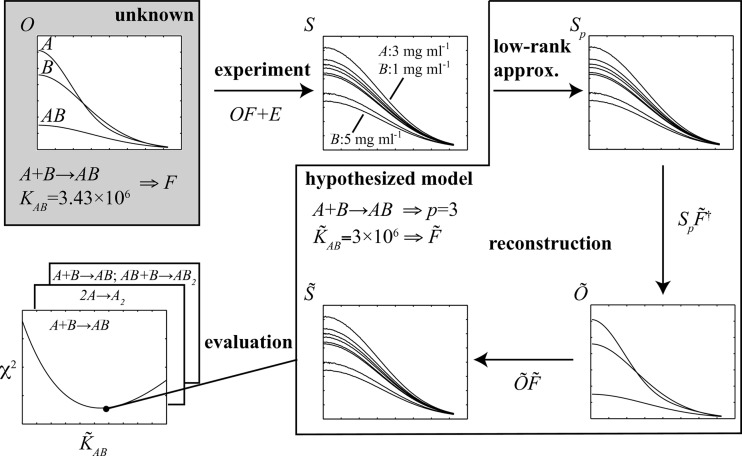
When several molecules are present in a solution, the observed scattering curve is the mass-fraction-weighted linear combination of the scattering intensities for the individual components. Starting with scattering intensities collected from the equilibrium mixtures of a series of different concentrations of the initial components, the goal is to infer the association model, along with the underlying scattering curves of the molecular species involved, including the initial components and intermediate and final complexes. Fig. 1 ▶ provides an overview of the present approach for an example in which the initial components A and B form an AB complex, with an association constant K _AB establishing the fractional amount of each of these forms at equilibrium. Each molecular species has an underlying scattering curve, but the association model and underlying scattering curves are unknown (gray shaded box in Fig. 1 ▶). At given initial concentrations of A and B, the scattering curve for the equilibrium mixture is the weighted sum of those for pure A, pure B and pure AB, weighted by the equilibrium fractional masses. The experimentally measured curve (normalized by the total mass concentration of the mixture) is then composed of this weighted sum, plus experimental error. A series of such curves is collected (or for the results presented here, simulated) over a range of initial concentrations of A and B. A search is then carried out over possible association models, considering alternative pathways and values for the corresponding association constants (here only K _AB). When considering a possible pathway, an associated number p of molecular species present is hypothesized, and thus a corresponding reduced set of scattering curves with random experimental noise partly removed can be extracted. When considering a set of association constants under this pathway, a set of fractional masses is hypothesized and these are used to reconstruct the underlying curves. To determine the best association model and reconstructed curves, first a broad coarse-grid search is performed over possible association constants, followed by a narrow fine-grid search, and each is scored for quality of fit to the observed data and agreement between the scattering curves and proposed stoichiometries of the complexes. Finally, the best pathway and constant are returned, along with the corresponding reconstructed curves.

Figure 1.

An overview of the present method for an example one-stage system. The association model and scattering curves of the various molecular species are unknown. Scattering curves are collected over a series of different initial concentrations of the components. Each observed scattering curve is a linear combination of the unknown curves of the different species, according to the association model and initial concentrations of the components, plus noise. A systematic search is carried out over possible association models; for each, a corresponding low-rank approximation is used to de-noise the data, and a least-squares formulation is employed to reconstruct the scattering curves of the different species. The agreement of the reconstructed curve of each model with the experimental data is evaluated and the best model selected. This ideal framework is then extended to account for the most problematic possible contaminants (non­participating monomers and homo-oligomeric aggregates have been tested) by including an additional unknown scattering curve and fractional mass, and solving a quadratic optimization problem for reconstruction.

More formally, the input scattering data are represented as an m × n matrix S, with n columns for n samples at different concentrations of the initial A and B components, each with m rows for the scattering intensities at a fixed set of m scattering angles. Each scattering curve normalized to the mass concentration (column in S) represents a linear combination of p curves (the initial components and intermediate and product oligomers, each at the standard mass concentration), weighted according to their equilibrium fractional masses. Collecting the curves into an m × p matrix O (one column per molecular species) and the fractional masses into a p × n matrix F (one row per set of initial monomer concentrations), and adding experimental noise E (one value per data point), we obtain

While S is the observed data, the values in the other matrices are unknown. The goal is to infer the association model, which determines F and the set of curves O. These in turn produce the observed matrix S.

We now detail each of the steps in the following subsections. The presentation is generalized from that of our previous homo-oligomeric study (Williamson et al., 2008 ▶) and refocused directly on solving the underlying least-squares problem. We initially assume that only the species in the modeled association are present in the various mixtures. We subsequently show how to modify the methods to handle potential situations where the presence of a contaminant that is a non­participating monomer or homo-oligomeric aggregate alters the ideal situation.

2.1. Low-rank approximation  

When considering an association pathway (recall that the search will be carried out over the possibilities), the number p of molecular species that are present at equilibrium is known. Since the relationship between their mass fractions (and hence between rows of F) is nonlinear, and since the number of concentrations is greater than the number of molecular species, a p-rank approximation S _p can be extracted. This low-rank approximation S _p is a ‘de-noised’ version of S (i.e. with E partially removed) containing the appropriate number p of curves with which to reconstruct the scattering curves according to the association model.

Singular value decomposition (SVD) is a popular technique for low-rank approximation and has been employed by us (Williamson et al., 2008 ▶) and others (Segel et al., 1998 ▶, 1999 ▶; Chen et al., 1996 ▶) in the analysis of scattering data. SVD computes the low-rank approximation with the smallest distance to the input matrix, as measured by the Frobenius norm of the matrix difference,

The SVD of the m × n matrix S is given by S = UΣV ^T, where m × m matrix U and n × n matrix V are orthogonal matrices whose column vectors are the left and right singular vectors, respectively, and m × n matrix Σ is a diagonal matrix whose elements are the singular values associated with the corresponding left/right singular vectors. The singular values are in order along the diagonal from largest to smallest, weighting the contributions from the most to the least important singular vectors. To compute the pth low-rank approximation, the smallest m − p singular values on the diagonal of Σ are replaced with zero to give Σ_p, and then S _p = UΣ_p V ^T is computed.

2.2. Reconstruction  

When considering a set of association constants for a pathway (recall that a grid search will be conducted over possible values for the association constants), standard association equilibria can be applied to compute the resulting equilibrium fractional mass of each of the p molecular species. These fractional masses are collected into a matrix 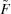(where the tilde indicates that it is a reconstruction of the ‘true’ unobserved matrix F). Combining this with the low-rank approximation S _p in a de-noised version of equation (1), the least-squares solution is computed in order to reconstruct the scattering curves of the various species:

where 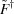denotes the Moore–Penrose pseudo-inverse. This formalization in terms of a p-rank approximation is a generalization of the approach given by Williamson et al. (2008 ▶), where using basis vectors from SVD was an explicit part of the equations. It clarifies the role of the decomposition and allows the use of alternative approximation approaches. It is also different from the approach of Bernadó et al. (2009 ▶), where a related approach employs principal component analysis to find the number of components in the solution.

If the least-squares solution has more than 10% negative intensity values or contains negative values in the small scattering angle range considered for Guinier analysis (Dervichian et al., 1952 ▶), it is considered to be nonphysical and the reconstruction is rejected without further analysis.

The solution is then used to compute 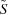, an approximation of the observed scattering curves of the equilibrium mixtures, by linearly combining the curves of the species involved at the appropriate fractional masses:

Thus, the low-rank approximation is used to reconstruct the scattering data so as to be consistent with the hypothesized association model.

2.3. Evaluation  

An association model is assessed in terms of how well the reconstructed scattering curves 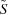match the experimental ones S. The two scoring approaches of our homo-oligomeric work (Williamson et al., 2008 ▶) are employed, customized for hetero-oligomers.

First, a χ² score quantifies the differences over the entire set of scattering curves, weighted by the estimated error σ(i, j) for each experimental data point:

The sum of the squared differences between points on the reconstructed and original curves is normalized by m(n − p) degrees of freedom to yield a χ² score. While there are mn data points, p of the n degrees of freedom are fixed by the low-rank approximation. In practice, this score is observed to be approximately 1 for the best fit to the data with Gaussian simulated noise.

Second, the mean-squared mass ratio difference (MSMRD) score calculates whether the zero-angle intensities match the stoichiometry of the hetero-oligomeric forms. The scattering intensity at zero angle, estimated by Guinier analysis (Dervichian et al., 1952 ▶), is proportional to the molecular weight. Thus, for example, one would expect I(0) for species AB, denoted I _AB(0), to equal I _A(0) + I _B(0), and thus I _AB(0)/[I _A(0) + I _B(0)] = 1. Thus, the MSMRD score computes the average, over the various hetero-oligomeric forms, of the deviations of such ratios from the ideal value of 1. Its expected value is thus zero. For a hetero-oligomer formed by A and B monomers, we compute the MSMRD as

where C is a set of (a, b) pairs indicating the various A _a B _b hetero-oligomeric forms and I _{Aa Bb}(0) represents their zero-angle intensity. For example, if the association model is A + B → AB, AB + B → AB ₂, then

These two scores are complementary. The χ² value is global, assessing the overall agreement between the reconstruction and the data. However, two related association pathways (with an appropriate choice of association constants) can generate similar solutions and similar χ² values. For example, this can happen with a one-stage association pathway A + B → AB and the extended two-stage association pathway A + B → AB, A + B → AB ₂, with similar association constants K _AB for both cases and a very weak K _AB2 for the second (see Results, §3). This is because equation (4) can give similar solutions for two different matrices F, as long as the column space spanned by the fractional matrix is the same. On the other hand, the MSMRD is very local, ignoring the agreement over most of the curve and focusing on the zero-angle intensity in order to assess the agreement between the independent (and not directly optimized) expected molecular weights and the stoichiometry. We have found that considering both χ² and the MSMRD improves the determination of the correct association model (see Results, §3).

2.4. Association model search  

We have discussed how to reconstruct and evaluate scattering curves for a given association model defined by a pathway and a corresponding set of association constants. In order to determine the best model, models for a set of plausible pathways are separately reconstructed and evaluated over a grid of possible association constants.

The pathways to be considered are chosen from the set of oligomers that could possibly be present in the equilibrium mixture. Although that set is potentially infinite, a most likely set of oligomers can be selected, for example, from an analysis of the zero-angle scattering or by the radii of gyration of the experimental scattering curves. Then all pathways that could form complexes with the allowed sets of subunits are considered. For example, if it is known that there are two monomers, A and B, and it has been determined that the final oligomer has at most three subunits, then the one-stage associations 2A → A ₂, 2B → B ₂ and A + B → AB would be evaluated, along with the two-stage associations that extend these to yield A ₂ B and AB ₂. Like other approaches, for example analytical ultracentrifugation, where postulated association models are fitted to the data, assumptions have to be made for the most likely models to be assessed.

Coarse- and fine-grid searches are performed over possible values for the association constants. Each association constant is an independent dimension in the grid. The results presented below use grids covering the range of plausible constants: 10⁻⁶ to 10²⁵ for a one-stage association and 10¹ to 10¹⁵ for a two-stage association. An initial coarse grid is searched at integer multiples of the powers of 10 (e.g. 1 × 10³, 2 × 10³, 3 × 10³,…, 9 × 10³, 1 × 10⁴, 2 × 10⁴,…). For each point (representing one or a pair of association constants), the curves are reconstructed and evaluated by χ² and MSMRD, as described above. The constants with the best scores establish a region for a fine-grid search, plus or minus one unit in each dimension, with a spacing of 1% of that of the coarse grid. Fine-grid searches are only performed for the models with the best χ² and MSMRD values from the coarse-grid search and for which the best coarse-grid association constants from the χ² and MSMRD scores are in sufficient agreement. Finally, the model with the best fine-grid χ² and MSMRD scores is selected, determining the corresponding pathway, association constants and reconstructed curves. In cases where the fine-grid search fails to yield an acceptable model, owing to either a high χ² for the best fine-grid point or a large disagreement between the best χ² and MSMRD fine-grid points, the methods in the next section can be employed to account for contaminants.

2.5. Accounting for contaminants  

An extension to the current methodology has been developed to deal with the case when the scattering data contain a substantial contaminant. Since contaminants that are unrelated to the initial components are generally readily purified out by current protein-separation methods, we seek to solve the biochemical situations that arise most frequently. Thus, our focus is on cases in which the contaminant is either a non­participating monomer or a large homo-oligomeric aggregate of one of the components.

Let us assume that the contaminant is a non­participating monomer or homo-oligomeric aggregate of A (the methodology works the same for any component and could be generalized to multiple such contaminants). Note that, in our approach, the contributions from all species in a polydisperse homo-oligomeric aggregate can be accounted for by one combined scattering curve and one total contaminant fraction. Let c be the unknown mass fraction of A that forms the contaminant. As part of the grid search, possible values for c will be considered along with those for the association constant(s). Given hypothesized values for c and the association constant(s), a fractional mass matrix 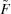must be built for each, now containing p + 1 rows, with the extra row for the contaminant. In constructing this matrix, let a _i be the initial amount of A in sample i. Then the amount of a _i still participating in the hypothesized association (rather than in the contaminant) is a _i(1 − c). The equilibrium concentrations, and thereby the masses of the other forms, are determined from the reduced A concentration and the initial concentrations of the other initial component(s).

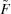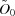Unfortunately, the extended matrix is no longer of full rank in the presence of contaminant, as the fractional mass vector for the contaminant is linearly dependent on A. This in turn implies that there is an infinite set of widely varying least-squares solutions satisfying . One of these, denoted , is the solution from equation (3), 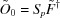. Using this 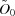to reconstruct 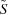, as in equation (4), gives 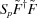, denoted 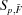. Each least-squares solution produces this same 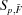and thus cannot be distinguished by comparison with the data S or the de-noised data S _p. This equivalence of solutions is due to the fact that the set of least-squares solutions is composed of the sum of 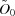with an infinite set of matrices of row vectors (that is, adjustments to the scattering curves) from the null space of 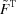. Post-multiplication by 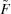then reduces the second matrix in this sum to zero, resulting in no change in .

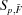In summary, there are an infinite number of reconstructions of the pure curves , but each produces the same reconstructed data 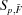. Since the reconstructed data are used to compute χ² [equation (5)], the best association model (best 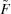) can be found via coarse- and fine-grid searches as before, with an additional dimension of the contaminant fraction in addition to the association constant(s). However, this approach does not produce correct reconstructed pure scattering curves and thus also does not give MSMRD values. Therefore, after identifying the best χ² point (or a set of feasible points for consideration), one must search over the space of satisfying to reconstruct and evaluate pure scattering curves and identify the best one.

A quadratic optimization framework has been developed that seeks a solution that not only explains the data (which all do equally) but also has properties desirable of physically realistic scattering curves. In particular, smoothness is established as the objective function and constraints are incorporated limiting the sub-optimality of χ², while the expected decaying exponential trend in the Guinier region of the scattering curves is also enforced, as well as the expected ratios of I(0) values (as also employed in the MSMRD score). Note that, if the contaminant only involves form A, for example, then the row for B in the fractional mass matrix is linearly independent of the contaminant and yields a unique least-squares solution (the same in for any 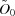). Thus, after computing 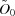, the row for initial component B is removed from 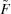and from 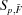(via its row in 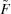and its column in 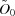). For simplicity, we continue to refer to and 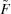without distinguishing the reduced-parameter versions.

We now outline the components of the quadratic program: the objective to optimize and the constraints to limit the considered solutions.

2.5.1. Objective: smoothness  

With the available freedom in , there are curves that use wildly fluctuating values to obtain good χ² scores upon post-multiplication by 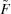. Since physical curves are expected to be relatively smooth, a discrete evaluation of smoothness is established as the objective function. A finite difference matrix D is constructed that, when multiplied by , approximates the second-order derivative at each point on the curve. The quadratic program then seeks to minimize the total of the squared differences, i.e. the square of the Frobenius norm of :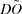

2.5.2. Constraint: χ² deviation  

A reconstruction is sought with the optimum χ² (as with all the , satisfying 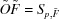), but since the data are noisy, one may sacrifice a little in the χ² score in order to ensure a feasible optimization problem and do better in terms of smoothness and other characteristics. Thus, a constraint is imposed that the reconstructed curves are no more than a tolerance ∊_fit away from the one that gives the lowest χ². This tolerance should be set fairly low to keep the identified curves near the optimum one; for the present results, a value of 10⁻³ is used. The constraint then requires

2.5.3. Constraint: non-negativity  

This requires that the scattering curves are non-negative,

2.5.4. Constraint: Guinier  

Scattering curves decay exponentially in the Guinier region (Dervichian et al., 1952 ▶). Therefore, a constraint is imposed that the curves are non-increasing (within a tolerance) in the initial Guinier region. To approximate the Guinier region in the scattering curves in without iterating on R _g (radius of gyration) values, q _max = 1.33/R _g (Guinier & Fournet, 1955 ▶) and a fixed R _g = 40 Å are used. To allow for noise, this property is enforced only to within a tolerance ∊_Guinier: within the Guinier region, a given intensity is no more than (1 + ∊_Guinier) times the intensity at the next lower scattering angle. A reasonable value for ∊_Guinier can be estimated by examining some pure intensity curves that have been reconstructed from uncontaminated simulations with standard noise; a value of 2 × 10⁻² is used here. Note that this value is dependent on the extent of the noise and the spacing of the scattering angles. This constraint is formulated with a matrix G which, when multiplied by , gives the differences between (1 + ∊_Guinier) times a particular point and the next point, for points in the scattering curves in at q < q _max:

2.5.5. Constraint: molecular weights  

When considering a contaminant X that is a nonparticipating form of A (either monomer or aggregate), its native mass must be at least that of A, i.e. M _X > M _A. Thus, the zero-angle intensity of its scattering curve should be at least equal to that of I _A(0). Since the extrapolation to obtain I(0) requires an exponential fit (which would render the system nonlinear), the intensity at the smallest angle measured, I(q _min), is used instead:

where the scattering curves I _A and I _X (for A and the contaminant X) are particular vectors of .

Imposing this constraint on I(q _min) instead of I(0) results in negligible error, since, from the Guinier relationship,

Given that 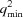is generally quite small (of the order of 10⁻⁶ in experimental data), the difference in radii of gyration is not large enough to impact the results substantially.

Furthermore, since a unique scattering curve for B has been found, its intensity at q _min can be used to constrain the intensity at q _min of the scattering curve for A and other forms (excluding the contaminant). For example, it is expected that

Essentially, this is encoding MSMRD (relative to the independent form B) as a constraint, but for intensities at q _min instead of at zero angle. As with most other constraints, a tolerance is used to allow for some noise. Thus, the approximate equality of the intensity ratio and the mass ratio is encoded as a constraint on the ratio between these two ratios – it must be within a tolerance ∊_MSMRD of the desired value of 1. A value of ∊_MSMRD = 0.1 has been found to work well for the present tests, but for other data this tolerance could potentially be tightened further, as long as feasible solutions still result. For the scattering from A (I _A) and every other mol­ecular species A _k B _l (I _AkBl), constraints are added of the form

where again the scattering curves I are particular vectors in .

2.5.6. Solving the system  

While the objective and constraints have been written in terms of and other matrices, these matrices can be reshaped into long vectors (i.e. by stacking columns). The combination of the objective function and constraints yields a convex quadratic optimization problem that can be solved by numerous solvers. If the quadratic optimization program is not feasible for a hypothesized association model, that model is discarded. If more than one feasible model were to remain, MSMRD values could be computed and the best selected, but that did not happen in the simulation studies presented below.

2.6. Implementation  

The methods have been implemented in a platform-independent Python package that is available from the authors upon request. The package calls the IBM ILOG CPLEX optimizer to solve the system of equations. The program allows a user to search over possible association models based on specifications provided via the command line or in an input file. The package contains implementations for both a contaminant-free search and an extension to handle non­participating monomers and homo-oligomeric contaminants. In addition to the methods in this paper, it also contains an implementation for homo-oligomeric association models from our previous work (Williamson et al., 2008 ▶).

To obtain the results presented below, coarse- and fine-grid searches for a one-stage model took less than a minute, while searches for a two-stage model took a few minutes on a single-core Intel Xeon 2.50 GHz processor. The three-stage searches took a few hours. Grid searches with contaminant for one-stage association took a few minutes, while contaminant searches for two-stage association took a few hours. The quadratic program solver usually took less than a minute.

3. Results  

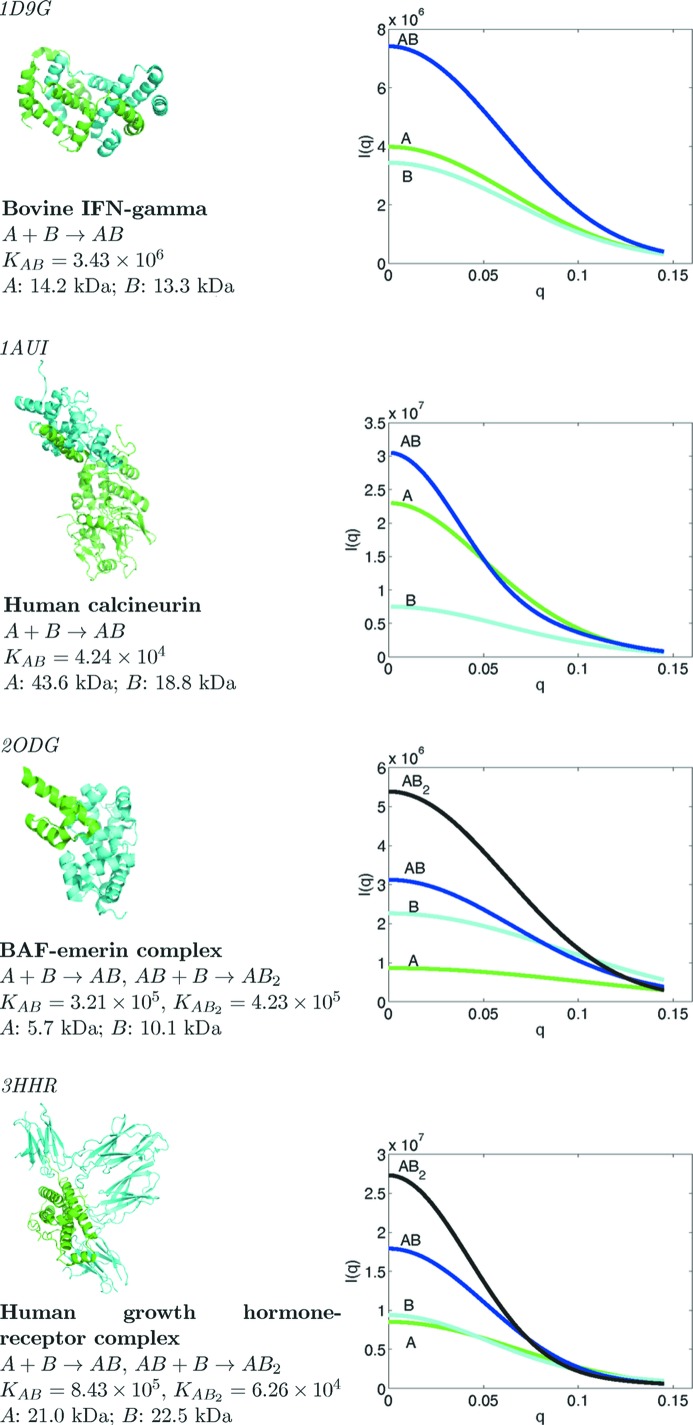
In order to evaluate the effectiveness of the present method in a range of scenarios, an extensive set of simulation studies were performed with different association pathways and association constants, and varying levels of random noise, data resolution and monomer size. Fig. 2 ▶ summarizes the complexes used in these studies, and illustrates their crystal structures and the simulated scattering curves of the monomers and intermediate and final oligomers at a constant mass concentration. The complex structures were taken from the Protein Data Bank (PDB; Berman et al., 2000 ▶) (PDB codes indicated), and monomer and intermediate complex structures were extracted. The association models for simulation were not taken from experimental data; instead, they were chosen to challenge the ability of the method to determine the correct model even in the presence of alternatives that have intermediate and final complexes of similar mass (note the similarity of the initial component masses in the bovine IFN-γ and human growth hormone-receptor cases). Association constants were chosen in the middle of a feasible range. However, the impact of the constants was explicitly assessed in one set of simulations.

Figure 2.

The four case studies discussed in this article.

It was found that as few as eight different initial concentrations provides a sufficient set of different scattering curves for subsequent reconstruction, and the results shown are based on eight for all test cases. The initial concentrations used (Supplementary Tables 1 and 21) are all in the 0.5–5.0 mg ml⁻¹ range, where SAS data are easily collected. They were chosen so as to yield a diverse set of row vectors (fractional masses) in the fractional mass matrix F, adequately sampling the space and ensuring that important vectors (scattering from intermediate and final complexes) are included in the low-rank approximation. Even so, the equilibrium mixtures are rarely more than 70% of one form. In practice, of course, F cannot be assessed initially, but it is still recommended that the user ensures that there is a diverse set of initial concentrations, with different combinations of low and high monomer concentrations. In the absence of approximate knowledge of the association constants that determine F, a first-round analysis can be used to identify a definitive set of initial concentrations from which to collect data. Pure monomer solutions (only A, only B) are included as initial components so as to characterize them better and account for their contributions to the mixtures. Of course, pure monomers may not be biochemically available, but the method is not dependent on this and any available components could be used.

The program CRYSOL (Svergun et al., 1995 ▶) was used at the default settings to simulate noiseless scattering intensities O from the three-dimensional structures of each initial component and complex. The noiseless equilibrium mixture intensities were then simply calculated as OF. Note that these curves include only the scattering within the initial components and complex members and do not capture contributions from any weak interparticle interactions. Noise E was then added, following the method employed by Williamson et al. (2008 ▶), to simulate realistic angle-dependent Gaussian noise based on noise levels observed in experimental samples. Ten data sets were generated for each example, with different random noise added for each data set.

While two one-stage associations and two two-stage associations were studied, detailed results are presented for only one of each and the second is summarized, since the results were similar in each category. We first show that the method yields the correct association model on the initial simulated data, for both one-stage and two-stage examples. We then demonstrate the robustness of the method to noise and investigate the range of association constants for which the method is applicable. Finally, we consider test cases with simulated contamination and present results from the expanded method that accounts for the contaminant.

3.1. Baseline simulations  

3.1.1. Bovine IFN-γ (one stage)  

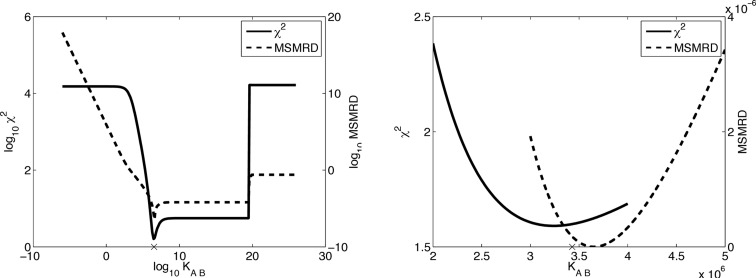
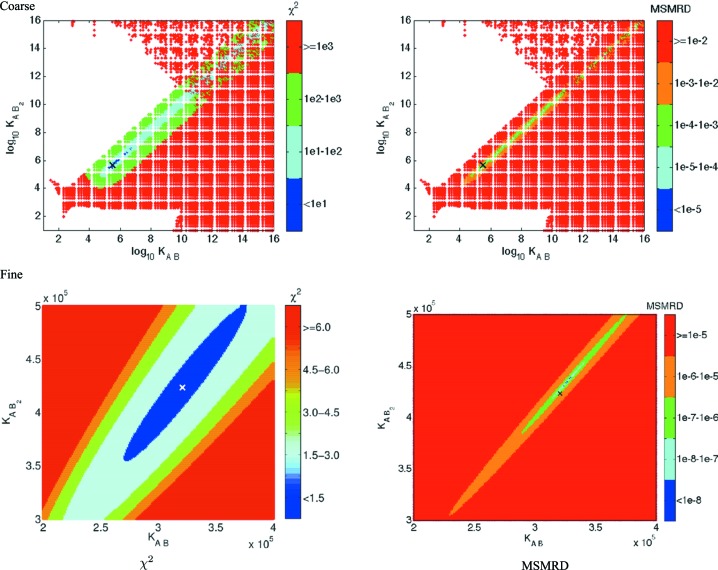
We first examine the results for one of the ten simulated data sets (i.e. one Gaussian noise matrix E), with the correct pathway A + B → AB and varying the association constants on a coarse grid (Fig. 3 ▶, left) and fine grid (Fig. 3 ▶, right). Both plots show a steep decline in χ² and MSMRD scores around the simulated association constant value (3.43 × 10⁶), with a minimum χ² of 1.59 at 3.34 × 10⁶ and a minimum MSMRD of 1.67 × 10⁻¹¹ at 3.65 × 10⁶. The close agreement of these association constants and the high quality of the scores under these complementary metrics gives confidence in this solution.

Figure 3.

Association constant searches for one bovine IFN-γ data set, for the correct A + B → AB pathway. The ‘×’ mark on the x axis indicates the simulated association constant (3.43 × 10⁶).

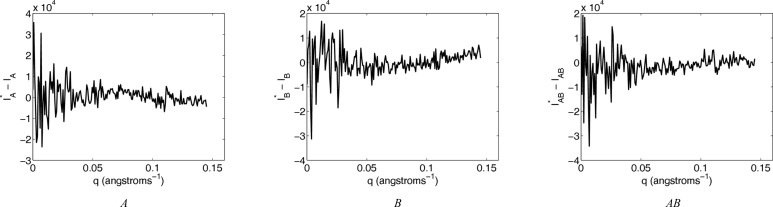
Whereas in an experimental setting one would not have access to the ‘true’ scattering curves of the various molecular species (O), here one does (from the CRYSOL calculation on the model components and complexes), and one can evaluate how well the reconstructed curves agree with them [, computed by equation (3)]. Fig. 4 ▶ shows the approximately random residuals between the reconstructed and simulated curves, at the association constant K _AB = 3.34 × 10⁶ which yields the best χ² score. [The apparent deviation from random residuals seen at higher resolution for component B (Fig. 4 ▶, middle) is not explained by deviation between simulated and best χ² association constants.] To quantify the extent of agreement, the median of the absolute relative deviation (MARD) is computed as a percentage deviation of the reconstructed curve from the simulated one; a MARD value close to zero indicates that the reconstructed curve is very close to the original noiseless CRYSOL curve. MARD scores confirm the agreement illustrated in the figure: A has a MARD of 0.24%, B 0.16% and AB 0.22%, averaged across the ten data sets with different simulated noise.

Figure 4.

Residuals between pure simulated scattering intensities and the reconstructed ones for bovine IFN-γ χ² optimum association models.

Table 1 ▶ summarizes the results of the best-scoring pathway (which is the correct one) over all ten simulated noisy data sets; Supplementary Table 3 includes results for alternatives. The A + B → AB pathway was always chosen and the average association constant was close to the simulated one, with only a small variation between data sets. Only the related two-stage pathways A + B → AB, AB + B → AB ₂ and A + B → AB, AB + A → A ₂ B obtained coarse-grid χ² scores (averaging 1.62 and 1.55, respectively) competitive with that of the correct model (1.53); the rest were much worse. Both alternative models extend the correct model with an additional association of weak affinity, keeping the A + B → AB association as the primary one. Any additional association has an adverse effect on the MSMRD scores (1.19 × 10⁻³ and 8.21 × 10⁻⁴, versus 3.74 × 10⁻⁷ for the correct model), as the low-angle data do not support an oligomer with a molecular weight corresponding to AB ₂ or A ₂ B. In addition, while the optimum association constants for χ² and MSMRD are very similar for the correct model, the best association constants by these two metrics are quite different for the alternative models. Furthermore, there is no choice of constants that scores moderately well under both metrics, and the association constants giving the best χ² score yield a poor MSMRD score and vice versa. For pathway A + B → AB, AB + B → AB ₂, the MSMRD for the association constant with the best χ² score averages 9.53 × 10⁻² across the ten data sets, versus an average best MSMRD of 1.19 × 10⁻³. On the other hand, the χ² score for the association constants with the best MSMRD score is 33.45 on average. These values are more than an order of magnitude worse than the best χ² and MSMRD scores for the correct pathway. Similar results are found for the second alternative pathway. Even though the χ² scores are not good discriminators, the substantial deterioration in the MSMRD and the disagreement between MSMRD and χ² metrics for the alternative models point to the correct A + B → AB pathway.

Table 1. Coarse- and fine-grid search results for the best-scoring (and correct) models for uncontaminated simulations, over ten sets of simulated noise.

Simulated association constants: bovine IFN-γ, K ₁ = 3.43 × 10⁶; BAF–emerin complex, K ₁ = 3.21 × 10⁵, K ₂ = 4.23 × 10⁵.

Search	K 1	K 2	Score
Bovine IFN-γ, A + B → AB
Coarse χ2	3.30 × 106 ± 4.8 × 105	–	1.53 ± 0.11
Coarse MSMRD	3.70 × 106 ± 4.8 × 105	–	3.74 × 10−7 ± 3.0 × 10−7
Fine χ2	3.40 × 106 ± 7.1 × 104	–	1.49 ± 0.12
Fine MSMRD	3.64 × 106 ± 5.2 × 105	–	1.82 × 10−11 ± 1.8 × 10−11
BAF–emerin complex, A + B → AB, AB + B → AB 2
Coarse χ2	3.00 × 105 ± 0.0	4.00 × 105 ± 0.0	1.17 ± 0.24
Coarse MSMRD	3.00 × 105 ± 0.0	4.00 × 105 ± 0.0	1.33 × 10−6 ± 6.8 × 10−7
Fine χ2	3.21 × 105 ± 4.5 × 103	4.24 × 105 ± 6.9 × 103	1.12 ± 0.24
Fine MSMRD	3.24 × 105 ± 1.3 × 104	4.29 × 105 ± 1.9 × 104	1.03 × 10−9 ± 6.6 × 10−10

3.1.2. BAF–emerin complex (two stage)  

Fig. 5 ▶ shows both χ² and MSMRD scores on the coarse and fine grids for the correct A + B → AB, AB + B → AB ₂ pathway, for one example noisy data set. As in the one-stage case, there are well defined minima, with the best association constants yielding much better χ² and MSMRD scores than nearby alternatives, at both coarse and fine resolutions. Again there is good agreement as to the best association constants under the two scores: χ² gives K _AB = 3.16 × 10⁵, K _AB2 = 4.16 × 10⁵, and MSMRD gives K _AB = 3.27 × 10⁵, K _AB2 = 4.35 × 10⁵, with the simulated constants being K _AB = 3.21 × 10⁵, K _AB2 = 4.23 × 10⁵. Interestingly, under both metrics, the best association constants lie on a diagonal line in which K _AB and K _AB2 increase at a similar rate, ensuring that if more AB is produced than the data dictate it is also converted to AB ₂. While this keeps the fraction of AB relatively constant, the resulting excessive depletion of A and excessive formation of AB ₂ yield worse scores at points along the diagonal line other than the minimum. The reconstructed intensities at the best association constants are quite similar to the original simulated noiseless ones, as illustrated in the residuals (not shown) and quantified by average MARD values of 0.08% for A, 0.08% for B, 0.15% for AB and 0.06% for AB ₂.

Figure 5.

Association constant searches for one BAF–emerin complex data set, for the correct A + B → AB, AB + B → AB ₂ pathway. The ‘×’ marks indicate the simulated association constants (K _AB = 3.21 × 10⁵, K _AB2 = 4.23 × 10⁵). The white regions in the coarse-grid plots indicate constants yielding nonphysical scattering curves (those with substantial negative intensities).

Table 1 ▶ summarizes the results from ten simulations for the correct, best-scoring model; Supplementary Table 4 includes those for alternatives. The best coarse-grid χ² score, averaging 1.17, is obtained by the correct pathway (A + B → AB, AB + B → AB ₂). The next best χ² scores, averaging 1.28 and 4.49, are obtained by alternative three-stage pathways that add weak association reactions AB ₂ + B → AB ₃ or AB ₂ + A → A ₂ B ₂ to the correct pathway. As before, larger changes in the MSMRD scores are seen. The first alternative (adding AB ₃) has an MSMRD score that is more than 40 times higher than the best MSMRD score (6.09 × 10⁻⁵, compared with 1.33 × 10⁻⁶ for the correct pathway). The second alternative (adding A ₂ B ₂) has an MSMRD score (2.50 × 10⁻³) that is almost 2000 times worse. Furthermore, comparing the best χ² association constants against the best MSMRD constants in these alternative pathways reveals that they differ by approximately 100 in K ₁ and 10³ in K ₂. In addition, as before, neither alternative pathway has a set of constants that score well under both metrics. Thus, using χ² and MSMRD scores together, the correct pathway can be determined.

3.2. Robustness to noise  

The simulated data sets include a realistic estimate of Gaussian noise found in experimental data sets at third-generation synchrotron sources (Williamson et al., 2008 ▶), but the present simulation framework enables easy assessment of how robust the method is to much noisier data. As one example, ten noisy data sets were generated for the one-stage bovine IFN-γ with the resolution-dependent Gaussian noise scaled up by a factor of two. The correct A + B → AB pathway was still the clear winner in all the data sets. It achieved a very good fine-grid χ² score (an average of 1.23 across ten data sets, compared with 1.49 with standard noise) at a nearly correct association constant (3.40 × 10⁶, the same as with standard noise and near the simulated value of 3.43 × 10⁶). It also achieved a good fine-grid MSMRD score (3.41 × 10⁻¹¹ compared with 1.82 × 10⁻¹⁴) with a good association constant (3.86 × 10⁶).

The performance of the method was then tested over a range of noise levels, increasing the Gaussian width up to five-fold, generating ten data sets for each noise level. The results were assessed in terms of identification of the association constant, as well as reconstruction of the underlying scattering curves of the monomers and oligomers. For association constants, the error was assessed with the absolute difference between the base-10 logs of the correct 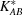and the inferred K _AB, i.e. . 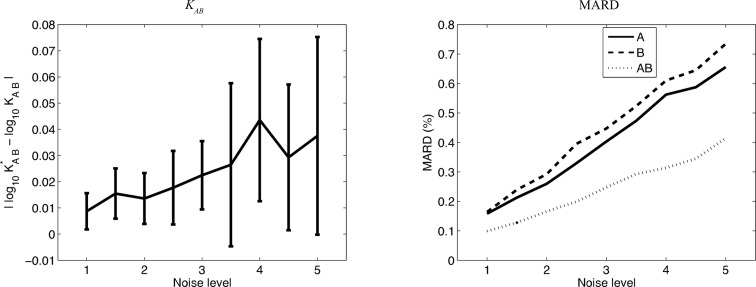For scattering curves, the evaluation is the MARD discussed above. Fig. 6 ▶ illustrates these error measures with respect to increasing noise (averaged over the ten data sets for each level). The figure shows that, as the noise increases, the best fine-grid points and reconstructions gradually become further away from the correct ones. Even at five times the noise, the errors in the association constants remain acceptable, approaching 10% (averaged across ten data sets), while the MARD values remain under 1% (0.6% for A, 0.7% for B and 0.4% for AB, averaged across ten data sets). Thus, we conclude that the method is indeed robust to such random noise. Robustness to some aspects of systematic noise (contamination with non­participating molecules) is discussed below.

Figure 6.

The effect of noise level (left) on the error in the association constant, assessed by the absolute difference in log₁₀ K _AB, and (right) on the reconstructed scattering curves, assessed by MARD. Values are for the bovine IFN-γ best χ² fine-grid point, averaged over ten data sets at each noise level. The association constant plot shows the means and standard deviations for the ten data sets at each noise level; only means are shown in the MARD plot, for clarity.

3.3. Robustness across ranges of association constants  

The ability of the method to recover the contribution from a particular species depends on that species making a non-negligible contribution to the mixture scattering data. That in turn depends on the association constants. The present simulations used physiologically reasonable constants, selected to ensure non-negligible quantities of each molecular species at equilibrium. However, since there is a wide range of reasonable values for weak association, a set of one- and two-stage simulations was conducted with varying association constant pairs to assess the range of values suitable for the method. For each association constant or pair of association constants, the simulated value was compared with the best χ² constants (results with MSMRD are similar and are not shown). Absolute log differences were used to assess the differences between the simulated and inferred values. For two association constants, the Euclidean distance d _E was evaluated

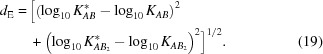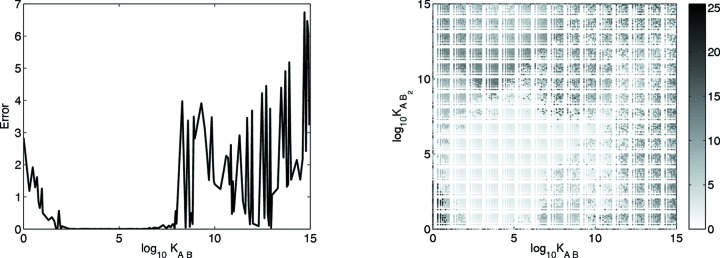
Fig. 7 ▶ shows the error over the range of association constant(s). For the one-stage bovine IFN-γ, the present method works best for values of K _AB between 100 and 10⁸. For the two-stage BAF–emerin complex, the method works best (i.e. has an absolute log difference of around 2 or less) for most combinations over a broad range of K _AB values between 10 and 10¹¹ and K _AB2 values between 100 and 10⁹. Poor scores for the one-stage association at low and high K _AB values can be attributed to near-zero fractional masses of the initial or final components at those extremes. Likewise, for the two-stage association, poor scores for low K _AB values can be attributed to the near-zero fractional mass of AB (and hence AB ₂) in such cases. The error is also large with high K _AB2 values, owing to the very small amount of AB remaining at equilibrium.

Figure 7.

The error in inferring the simulated association constant for (left) one-stage bovine IFN-γ and (right) two-stage BAF–emerin complex. The error for an association constant is the absolute log difference between the simulated and inferred association constants; for the two-stage case, the overall error is the square root of the sum of the squared errors.

3.4. Robustness to monomers and complex size and shape  

The performance of the present method was also studied on two other complexes that are quite different in molecular weight and structure from the two that have been discussed so far. While the main one-stage study, bovine IFN-γ, has monomers that are relatively small and close in molecular weight (14.2 and 13.3 kDa), the additional study, human calcineurin, has monomers that are larger and have very different molecular weights (43.6 and 18.8 kDa) and shapes. The main two-stage study, BAF–emerin complex, has monomers with weights of 5.7 and 10.1 kDa, while the additional study, HGH-receptor complex, has monomers with weights of 21.0 and 22.5 kDa and different shapes.

In both cases, the present method inferred the correct pathway and association constants and reconstructed scattering curves that are very similar to the simulated ones. For the one-stage human calcineurin (Supplementary Table 5), the χ² value averaged 1.08 over ten simulated data sets, with association constants averaging 4.24 × 10⁴ (which was the simulated value). The resulting MARDs for the best χ² association constant averaged 0.24% for A, 0.16% for B and 0.22% for AB. As in our initial one-stage study, an alternative two-stage model yielding both AB and AB ₂ scored well by χ² (1.28) but poorly by MSMRD (1.06 × 10⁻³), with substantial disagreement on the best association constants (K _AB = 4.30 × 10⁴, K _AB2 = 5.35 × 10² for χ², and K _AB = 3.00 × 10⁴, K _AB2 = 5.10 × 10² for MSMRD). The χ² score at the best MSMRD point and the MSMRD score at the best χ² point were also worse. Several other pathways scored moderately well by χ², but all of these could be eliminated by evaluating the MSMRD scores and the disagreement between the best association constants.

Similarly good results were seen for the HGH-receptor complex (Supplementary Table 6). The lowest χ² was on average 0.98 at association constants averaging K _AB = 8.43 × 10⁵, K _AB2 = 6.26 × 10⁴ (which were the simulated values). The average MARDs across ten data sets at the lowest χ² points were 0.08% for A, 0.09% for B, 0.10% for AB and 0.10% for AB ₂. Alternative models that extend the correct two-stage pathway with AB ₂ + A → A ₂ B ₂ or AB ₂ + B → AB ₃ third stages also have low χ² scores (1.38 and 1.33, respectively), but poorer MSMRD scores and large disagreement on the best association constants.

3.5. Contaminated data  

A frequent problem in the analysis of associating systems is the presence of ‘incompetent protein’ contaminants, either monomer protein that behaves similarly to ideal material during purification but does not participate in associations, or oligomers that do not dissociate (irreversible aggregates) (Xu, 2004 ▶). In both cases the protein appears in the initial concentrations but not in any complex. For example, we found in our previous work on homo-oligomers that the addition of 2% of another oligomeric form would lead to large χ² values and incorrect association constants and reconstructions (Williamson et al., 2008 ▶).

To test the robustness of the present method to such contaminants, a nonparticipating fraction of monomer A was used as a contaminant in the one-stage bovine IFN-γ. Also, a nonparticipating A ₁₃ aggregate was used in the two-stage BAF–emerin complex, using a single aggregated form to represent the total possible contribution from multiple aggregated forms. To construct an A ₁₃ structure for this simulation, copies of A were repeatedly docked together using the software GRAMM-X (Tovchigrechko & Vakser, 2006 ▶). Scattering curves from all forms were again simulated using CRYSOL. Data were simulated with off-grid values of 0.0047, 0.0113 and 0.0231 contaminant mass fraction in the initial mass of A, using the same association constants as before. Ten data sets were generated for each case with different random Gaussian noise.

First, the regular coarse- and fine-grid searches were performed on the simulated data with contaminants, assuming as in previous sections the absence of any contaminant (Supplementary Tables 7 and 8). All of the alternative (incorrect) association pathways were immediately eliminated owing to high χ² or inconsistency between best χ² and best MSMRD (not shown).

Using the correct association pathway for bovine IFN-γ, the χ² values increase monotonically with contaminant fraction. As expected, in the presence of a nonparticipating monomer, the apparent association constants also shift towards smaller values. When the contaminant fraction increases to 0.0231 the χ² score more than doubles, indicating a clear problem in the analysis. The MSMRD scores also increase significantly (although these scores do not have a standard baseline to reference).

The behavior of the BAF–emerin complex is similar. The χ² scores also increase monotonically with contaminant fractions. The behavior of the MSMRD score is more variable, perhaps because the A ₁₃ contaminant used here has a disproportionate effect on the I(0) values. For the 0.0231 contaminant fraction, even the coarse-grid search is unable to identify the nearest grid point. Here again, a significantly increased χ² and disagreement between the best χ² and best MSMRD association constants indicates problems for the 0.0113 and 0.0231 contaminant fractions. The increasing presence of the A ₁₃ contaminant shifts the association constants to larger values, forming more of the larger complexes.

In both cases, the presence (or suspicion) of an incorrect analysis (particularly disagreement between the best χ² and best MSMRD values) signals the need for a more sophisticated analysis. We have developed a convex quadratic optimization method specifically to deal with problems arising from nonparticipating contaminants.

Grid searches extended to include a contaminant fraction were performed for all cases. The coarse contaminant fraction grid dimension ranged from 0 to 0.1 in steps of 0.01. Fine-grid searches (including contaminant fraction) were then performed for all pathways with a χ² value for the extended coarse-grid search within 1.0 of the best χ² pathway (note that the MSMRD value cannot be used to assess the quality of these searches because scattering curves are only generated upon applying the quadratic optimization). The fine contaminant grid then ranged from the point below the identified coarse-grid contaminant fraction to that above it, with a step size of 0.001. The grid searches were performed considering either an A or B homo-oligomeric contaminant (but not both). Optimized scattering intensities were then computed for the best χ² fine-grid association constants by solving the quadratic program with constraints and parameter values as presented in Methods, §2.

Table 2 ▶ summarizes the fine-grid contaminant search results. For the one-stage bovine IFN-γ contaminated with nonparticipating A, three pathways passed the χ² cut-off: the correct model and the same two alternatives that were found in the baseline studies. While it is hard to distinguish the three solely on the basis of χ², the intensity reconstruction optimization procedure found no feasible solution for the alternative models but successfully yielded scattering curves for the correct model, in all ten data sets. For the two-stage BAF–emerin complex contaminated with the A ₁₃ aggregate, only the correct model passed the χ² filter and its intensity reconstruction optimization was successful. For both cases and at all contaminant levels, the identified fine-grid association constants and contaminant fractions are close to the simulated values (bovine IFN-γ: K ₁ = 3.43 × 10⁶; BAF–emerin complex: K ₁ = 3.21 × 10⁵ and K ₂ = 4.23 × 10⁵) and, for the higher contaminant fractions, notably closer than the values obtained in the contaminant-free searches.

Table 2. Fine-grid χ² results for contaminated simulations with coarse-grid χ² within 1.0 of the lowest scoring model.

Simulated association constants: Bovine IFN-γ, K ₁ = 3.43 × 10⁶; BAF–emerin complex, K ₁ = 3.21 × 10⁵, K ₂ = 4.23 × 10⁵.

Contamination	K 1	K 2	χ2	c A †	c B †
Bovine IFN-γ, A + B → AB
0.0000	4.80 × 106 ± 6.3 × 105		1.61 ± 0.1	4.10 × 10−3 ± 6.0 × 10−4 (×9)	2.00 × 10−3 ± 0.0 (×1)
0.0047	3.59 × 106 ± 3.6 × 105		1.51 ± 0.1	5.30 × 10−3 ± 9.5 × 10−4	N/A
0.0113	3.41 × 106 ± 1.3 × 105		1.43 ± 0.1	1.13 × 10−2 ± 6.7 × 10−4	N/A
0.0231	3.39 × 106 ± 1.7 × 105		1.46 ± 0.1	2.34 × 10−2 ± 5.2 × 10−4	N/A
Bovine IFN-γ, A + B → AB, AB + B → AB 2
0.0000	3.94 × 1013 ± 9.6 × 1013	1.01 × 1011 ± 2.0 × 1011	1.51 ± 0.1	5.18 × 10−2 ± 4.2 × 10−2 (×6)	1.08 × 10−2 ± 6.8 × 10−3 (×4)
0.0047	8.81 × 1014 ± 2.5 × 1015	2.70 × 1012 ± 7.6 × 1012	1.45 ± 0.2	5.39 × 10−2 ± 4.2 × 10−2	N/A
0.0113	5.39 × 1012 ± 1.1 × 1013	1.55 × 109 ± 3.2 × 109	1.42 ± 0.2	1.37 × 10−2 ± 8.6 × 10−3	N/A
0.0231	1.26 × 1014 ± 2.6 × 1014	1.94 × 1011 ± 4.1 × 1011	1.46 ± 0.1	3.11 × 10−2 ± 1.6 × 10−2	N/A
Bovine IFN-γ, A + B → AB, AB + A → A 2 B
0.0000	1.02 × 1010 ± 3.2 × 1010	1.33 × 106 ± 3.1 × 106	1.60 ± 0.1	N/A	1.70 × 10−2 ± 2.2 × 10−2
0.0047	3.91 × 1012 ± 1.2 × 1013	6.63 × 109 ± 2.1 × 1010	1.55 ± 0.3	N/A	1.66 × 10−2 ± 2.3 × 10−2
0.0113	7.25 × 106 ± 5.1 × 106	6.65 × 103 ± 9.1 × 103	1.40 ± 0.0	1.04 × 10−3 ± 8.4 × 10−4	N/A
0.0231	4.59 × 1010 ± 1.5 × 1011	8.75 × 105 ± 2.7 × 106	1.19 ± 0.4	2.24 × 10−2 ± 7.3 × 10−4 (×9)	8.00 × 10−2 ± 0.0 (×1)
BAF–emerin complex, A + B → AB, AB + B → AB 2
0.0000	5.44 × 105 ± 4.3 × 103	8.00 × 105 ± 0.0	1.78 ± 0.1	N/A	6.60 × 10−3 ± 5.2 × 10−4
0.0047	6.87 × 105 ± 9.2 × 105	1.04 × 106 ± 1.6 × 106	1.74 ± 0.0	1.00 × 10−2 ± 0.0 (×8)	8.50 × 10−3 ± 7.1 × 10−4 (×2)
0.0113	3.13 × 105 ± 1.2 × 104	4.08 × 105 ± 2.2 × 104	1.49 ± 0.1	1.18 × 10−2 ± 9.2 × 10−4	N/A
0.0231	3.60 × 105 ± 1.7 × 104	4.92 × 105 ± 3.0 × 104	1.56 ± 0.1	2.09 × 10−2 ± 8.8 × 10−4	N/A

^†The search considers only A or B contaminant. Rows with values for both c _A and c _B are the result of different identified contaminants for different simulations (number of times in parentheses).

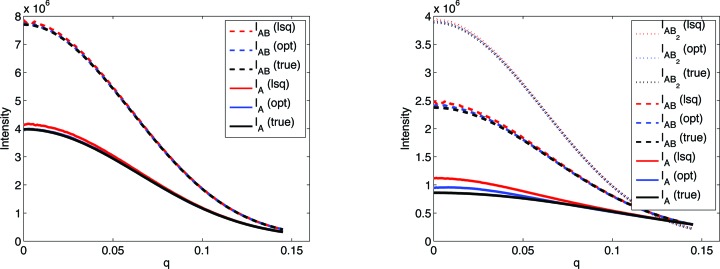
Scattering intensities optimized using the quadratic program (labeled OPT/opt) were compared with simulated intensities (labeled TRUE/true) and those computed by least squares (labeled LSQ/lsq), both visually (Fig. 8 ▶) and by calculating MARD (Table 3 ▶). Here the quadratic program is consistently successful. MARD scores are substantially improved for the optimized reconstructions, with the greatest improvement at the higher contaminant fractions, although even the lower ones benefit, presumably as a result of the added constraints. Examining the scattering curve reveals that the greatest deviations from the simulated data and the greatest improvement come at small q values. Note that I _B is an independent vector in the intensity matrix, and thus the MARD values are the same for the two methods. The reconstructed scattering curve for the contaminating molecule (not shown) was not a close approximation to the true curve, probably because of the extremely small fraction of contaminant in the solution.

Figure 8.

Simulated intensities compared with reconstructed ones computed by the quadratic program (opt) and the initial least squares (lsq), for one 0.0231 contaminant fraction data set of (left) bovine IFN-γ and (right) BAF–emerin complex. The I _B reconstruction, which is independent of contaminant, is not shown.

Table 3. MARDs (%) for contaminated reconstructions.

Contaminant fraction	Method	I A	I B	I AB	I AB2
Bovine IFN-γ
0.0000	LSQ	0.83 ± 0.2	0.28 ± 0.2	0.41 ± 0.1	–
	OPT	0.27 ± 0.1	0.24 ± 0.1	0.22 ± 0.1	–
0.0047	LSQ	0.53 ± 0.1	0.17 ± 0.0	0.17 ± 0.0	–
	OPT	0.20 ± 0.0	0.17 ± 0.0	0.09 ± 0.0	–
0.0113	LSQ	1.13 ± 0.1	0.16 ± 0.0	0.34 ± 0.0	–
	OPT	0.42 ± 0.0	0.16 ± 0.0	0.14 ± 0.0	–
0.0231	LSQ	2.28 ± 0.1	0.17 ± 0.0	0.69 ± 0.0	–
	OPT	0.83 ± 0.0	0.17 ± 0.0	0.29 ± 0.0	–
BAF–emerin complex
0.0000	LSQ	0.08 ± 0.0	0.64 ± 0.1	0.20 ± 0.0	0.20 ± 0.0
	OPT	Not feasible
0.0047	LSQ	2.32 ± 0.0	0.08 ± 0.0	0.85 ± 0.0	0.56 ± 0.0
	OPT	1.91 ± 0.0	0.08 ± 0.0	0.77 ± 0.1	0.53 ± 0.0
0.0113	LSQ	4.45 ± 0.1	0.08 ± 0.0	0.90 ± 0.1	0.42 ± 0.1
	OPT	2.41 ± 0.2	0.08 ± 0.0	0.56 ± 0.1	0.27 ± 0.1
0.0231	LSQ	8.72 ± 0.1	0.08 ± 0.0	1.41 ± 0.1	0.60 ± 0.1
	OPT	1.31 ± 0.1	0.08 ± 0.0	0.31 ± 0.1	0.21 ± 0.0

As a final test, contaminant grid searches were carried out on uncontaminated data (0.0000 entries in Tables 2 ▶ and 3 ▶). This approach did not perform as well as the contaminant-free search on uncontaminated data. As expected, fitting the additional contaminant parameter drives the association constants somewhat away from their best values.

3.6. Application of contaminant methods to homo-oligomers  

Contamination with aggregates proved to be a problem for our earlier method for characterizing homo-oligomers (Williamson et al., 2008 ▶). Thus, the present contaminant search and reconstruction were performed on the case studied previously: octameric purE from Escherichia coli (PDB code 1qcz; Mathews et al., 1999 ▶), under a monomer–tetramer–octamer association with a 2% mass fraction of a 16-mer as contaminant. The best association constants resulting from the contaminant search were K ₁₂ = 4.00 × 10¹², K ₂₃ = 1.25 × 10¹, close to the simulated association constants K ₁₂ = 2.87 × 10¹², K ₂₃ = 1.29 × 10¹, although the identified contaminant fraction was higher than simulated, at 6.6%. The association model found by the previous method (Williamson et al., 2008 ▶) was K ₁₂ = 3.46 × 10¹², K ₂₃ = 1.00 × 10¹, also close to the simulated association constants. However, the present reconstructed monomer scattering curve is much better than the previous one, whose χ² is four times worse. The optimized monomer intensity curve is much closer to the simulated curve than that computed by least squares (after a contaminant search) or that found without contaminant search [as done by Williamson et al. (2008 ▶)], especially at low q (Fig. 9 ▶). Thus, the contaminant search plus the quadratic program reconstruction produce a curve that closely approximates the true one, while the contaminant-free and least-squares reconstructions introduce substantial error. Note again that the least-squares curve is just one of the infinitely many satisfying solutions, and thus it is not too surprising that it is actually much worse. The curves for the tetramer and octamer are not plotted, since for both methods they are extremely similar to the true curves. These results demonstrate that the present method can also be profitably applied to homo-oligomers in the presence of contaminants.

Figure 9.

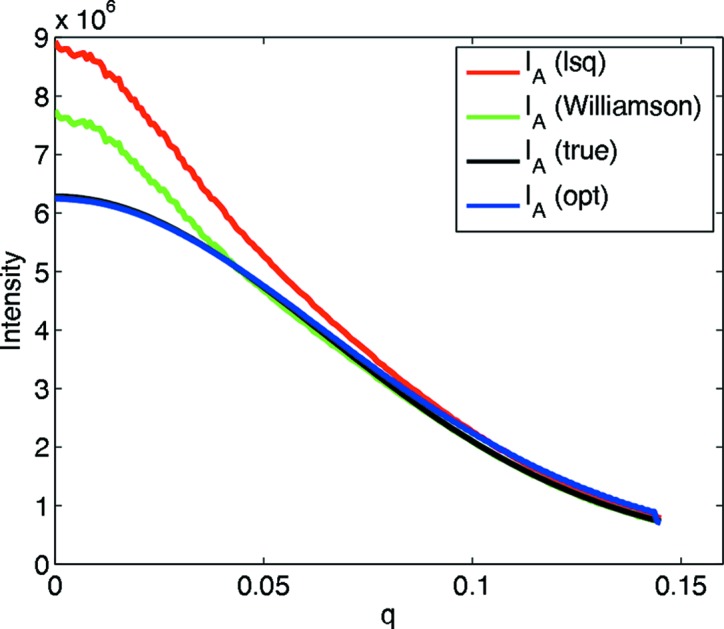
Reconstructed pure monomer intensity from a monomer–tetramer–octamer association contaminated with a 16-mer. I _A (Williamson) is computed using the original grid search with no contaminant fraction and subsequent intensity reconstruction, as done by Williamson et al. (2008 ▶).

4. Discussion  

We have presented a method to infer an association model (pathway and association constants), along with the underlying scattering curves of the initial components and intermediate and final complexes, from solution scattering data for a set of equilibrium mixtures undergoing hetero-association with different initial component concentrations. The method searches over possible association models and contaminant fractions, reconstructing the underlying scattering curves either by a least-squares method in the absence of ‘incompetent protein’ contaminants or by a convex quadratic program in their presence. The model and scattering curves are evaluated in terms of how well they can then reconstruct de-noised input data. Two complementary scores are used: a χ² to assess the overall fit between the data and the association model combined with reconstructed scattering, and the MSMRD to assess the consistency between the association model stoichiometry and the reconstructed scattering. The convex quadratic program provides an optimization-based method for the difficult problem of reconstructing the underlying scattering curves in the presence of either nonparticipating monomers or irreversible aggregates.

In a variety of simulated test cases covering one- and two-stage association pathways, this approach correctly determined the pathway, accurately estimated the association constants with generally less than 2% error and accurately reconstructed the scattering curves to within an average deviation of less than 0.25%. While such accuracy cannot be expected for all experimental scattering data, the potential for such accurate evaluation exists in the most favorable cases. The good accuracy for reconstructing the scattering curve bodes well for the application of three-dimensional structural modeling based on the reconstructed scattering curves. The χ² and MSMRD were found to be effective as complementary metrics. Cases where an alternative model with an extra association step obtained a fairly good χ² value could be ruled out by a greater MSMRD and inconsistency between the best-scoring association constants under one metric versus the other. The method was also found to be amenable to a range of association constants, Gaussian noise levels, different complex sizes and shapes, and contaminants.

The range of association constants that were found acceptable for the method (Fig. 7 ▶) compares well with the range of 10⁴–10⁹ routinely available from analytical ultracentrifugation (Lebowitz et al., 2002 ▶), while also revealing the molecular weight of each complex [via I(0) calculations] calibrated by the molecular weights of the initial components. At the same time, the SAS method provides complex scattering curves that can serve as the basis for three-dimensional reconstruction. In addition, this range of affinities is explored with the same fixed set of initial concentrations used in the earlier simulation. The initial concentrations could also be adjusted upwards to explore weaker interactions (limited by the solubility of the proteins) and downwards to explore stronger ones (limited by the strength of observed scattering). The strongest beamlines at third-generation sources can generate accurate scattering profiles at concentrations as low as 0.05 mg ml⁻¹ (Williamson & Friedman, unpublished results), a fact that also aids in the reduction of noise from interparticle interference (see below).

At realistic contaminant levels, the present method is able to reconstruct the scattering curves quite accurately, a result not possible by previous methods which assumed an absence of contaminants. While by no means perfect, the objective and set of constraints chosen here yield good solutions in practice. Smoothness is taken as the primary objective, and the potential for over-smoothing is mitigated by a counterbalancing constraint from the χ² constraint. Other constraints could potentially be incorporated in order to encode shape characteristics and relationships between the different forms. It is not possible to determine adequately the exact contaminant fraction or its scattering curve, but the incorporation of additional constraints could help. Extensions to other forms of contamination and systematic noise may be amenable to analogous techniques.

As discussed in the Introduction, we have focused only on the contributions from the modeled molecular species – initial components, higher-affinity intermediate and final complexes, and possibly static contaminants. Experimental scattering data also contain contributions from interparticle interference, arising from the lowest affinity, typically most transient, protein–protein complexes. A study of and extension to handle interparticle interference remains very interesting future work, which is likely to increase the power and applicability of this approach. There are several possible ways in which the method could be extended to account for this non-ideality. Some weak interparticle interactions of a different stoichiometry from the primary modeled association may become factored out as noise in the low-rank approximation or as residuals in the modeling. Other interparticle interactions may be captured as a form of explicit contaminant. Alternatively, data from dilution series towards zero concentrations (where these interactions become vanishingly small) could be collected and incorporated into the model. When the weak interactions are of the same stoichiometry as the modeled associations, they are linearly inseparable and thus cannot be directly accounted for in a ‘bottom-up’ analysis like that presented here. However, ‘top-down’ structural information could be exploited to constrain the scattering curves according to the structural characteristics of the monomers and complexes, a modification of our approach for NMR (Potluri et al., 2006 ▶; Martin et al., 2011 ▶; Chandola et al., 2011 ▶). Perhaps an iterative approach could even be employed, starting with an initial factorization as presented here, and then iteratively alternating between inferring a structure based on the current factorization and improving the derived model and curves based on the current structural information.

In the test cases, pure A and pure B were included as two of the samples. This suggests an alternative strategy to use the intensity curves of these pure samples to reduce the number of unknowns (removing known intensity column vectors for A and B in ) in the computations. However, when contaminants are present, there may be no such thing as a ‘pure’ sample. Likewise, this approach works with a self-associating system which does not contain pure monomers even at the lowest concentration. In preliminary studies (not shown), we have found that, even without using pure A and pure B in the set of samples, the correct model can still be obtained as long as the equilibrium mixtures contain sufficiently diverse concentrations of species.