Estimation of Extracellular Volume from Regularized Multi-Shell Diffusion MRI

Abstract

Diffusion MRI measures micron scale displacement of water molecules, providing unique insight into microstructural tissue architecture. However, current practical image resolution is in the millimeter scale, and thus diffusivities from many tissue compartments are averaged in each voxel, reducing the sensitivity and specificity of the measurement to subtle pathologies. Recent studies have pointed out that eliminating the contribution of extracellular water increases the sensitivity of the diffusion measures to tissue architecture. Moreover, in brain imaging, estimation of the extracellular volume appears to indicate pathological processes such as atrophy, edema and neuroinflammation. Here we study the free-water method, which assumes a bi-tensor model. We add low b-value shells to a regular DTI acquisition and present methods to improve the estimation of the model parameters using the extra information. In addition, we define a Laplace-Beltrami regularization operator that further stabilizes the multi-shell estimation.

1 Introduction

Diffusion MRI (dMRI) measures the displacement of water molecules, which in a typical brain imaging experiment displace a few tens of microns. This makes dMRI sensitive to normal and pathological architecture in the cellular scale. Indeed, dMRI based sequences, such as diffusion tensor imaging (DTI), have been found extremely useful in identifying subtle changes, especially in white-matter, that occur in normal development, as well as in many types of diseases, abnormalities and disorders [1]. Nevertheless, current image resolution is in the millimeter scale, introducing partial volume of different tissue types - white matter, gray matter, glia cells, cerebrospinal fluid (CSF) - which reduces the sensitivity and specificity of most indices derived from dMRI and DTI [2].

Correcting for extracellular water is required to eliminate CSF contamination, thus improving DTI’s sensitivity in the vicinity of the ventricles [3] and important for the delineation of fibers such as the fornix [4, 5]. Moreover, the fractional volume of the extracellular water, relative to the remaining hindered or restricted water molecules, appears to provide important information with regard to pathological processes that modify the interstitial extracellular space, such as edema [4], neuroinflammation [6] and atrophy [7]. Indeed, the extracellular volume was shown to be sensitive to pathologies that appear in aging [7], schizophrenia [8], Multiple-Sclerosis [6], and Alzheimer’s disease [9].

In this work we present a method to estimate the extracellular volume and the diffusivities of the remaining tissue using a multi-shell dMRI acquisition. Motivated by increasingly more designs that already choose multi-shell for clinical studies, we enable estimation of free-water from such acquisitions in a novel way that utilizes the additional information instead of discarding it.

2 The Free-Water Model

The free-water model estimates and corrects for the contribution of the extracellular space [4]. The model assumes that the diffusion signal originates from two molecular compartments, co-existing within a voxel, with slow exchange between the compartments [4]:

$$A_i(D,f)=fexp(-b_i{q}_i^T{Dq}_i)+(1-f)exp(-b_{i}d).$$ (1)

Here, A_i is the signal (normalized by the b₀) of the ith applied diffusion gradient with orientation q_i, and b-value b_i. The first term reflects the tissue compartment, where D is the diffusion tensor of this compartment and f is the relative contribution of the compartment. The second term reflects an isotropic compartment, with a fixed diffusion coefficient, d, set to the diffusion coefficient of water in body temperature, 3 × 10⁻³mm²/s. Thus, the isotropic compartment models free-water, i.e., molecules that do not experience hinderance. In a cellular environment such as brain tissue, free-water can only be in the extracellular space.

The free-water model adds only one more parameter, f, to the DTI model. However, unlike DTI, the fitting of this bi-exponential model is highly unstable [10]. Pierpaoli et al., proposed to stabilize the fit by measuring multiple b-shells that achieve high b-values, requiring a large number of measurements [11]. However, this approach required lengthy scans, and moreover, at high b-values the tissue compartment is no longer adequately described by a single exponent [10]. Pasternak et al., introduced a regularization framework that allowed the estimation of the free-water model from a single-shell DTI acquisition [4]. However, this method requires smoothing, which may reduce the sensitivity to subtle details or pathologies.

In our work we combine principles from these two approaches. Similar to [11], we acquire multi-shell data. However, our approach only requires lower b-valued shells. We present a novel way of estimating the free-water model parameters by separating the higher shells from the lower shells. We then use these estimates to initialize a spatial tensor regularization refinement step similar to [4], to result with the final estimates.

3 Multi-Shell Free-Water Estimation

Our approach has three steps. In the first step (Sec. 3.1) the diffusion tensor of the tissue compartment is estimated from the higher b-valued shells. In the second step (Sec. 3.2) the estimated tensors along with the lower b-valued shells are used to estimate the extracellular volume. In the final step (Sec. 3.3) we use these estimates as an initial guess to a regularized minimization process that takes in account the entire scope of the data.

3.1 Estimation of Free-Water Eliminated Tensors

The diffusivities of white and gray matter are considerably lower than those of free-water or CSF. Typically, in single shell DTI with a b-value around 1000 s/mm², healthy brain tissue has a quite homogeneous mean diffusivity of around 0.8mm²/sec, 3–4 times slower than free-water. Therefore, the free-water signal is expected to decay faster than tissue, e.g., with a b-value of 900mm²/sec the tissue decays to 49% of the signal while free-water decays to 7% of the signal. Figure (1) shows an example of a multi-shell acquisition for a range of b-values. This range is achieved by modifying the diffusion gradient amplitude for fixed diffusion times. As expected, the free-water signal (mainly seen in the ventricles and around the parenchyma) attenuates faster than other brain tissue. The free-water signal diminishes completely into the noise floor for the higher b-values.

Fig. 1. Multi-shell acquisition.

Diffusion signal for increasing b-values of (left to right) 0, 200, 900 and 1400 mm²/sec in a mid-sagittal plane. The signal from free-water, such as in the ventricles (red arrow), decays into the noise floor faster than the signal of brain tissue.

Also dependent on the b-value is the apparent diffusion coefficient of a partially volumed voxel, which can be expressed as [5]:

$$D^{\prime }=b_i^{-1}log(fexp(-b_i{q}_i^T{Dq}_i)+(1-f)exp(-b_{i}d)).$$ (2)

This means that D′ is not the average of the diffusivities of the two compartments, but is closer to D as b increases. Therefore, we suggest that a tensor estimated only from the higher b-valued shells (at least two shells are required), will minimize the contribution of the free-water and will be a good estimation for the tissue compartment tensor D. However, these shells cannot have a too-high b-value, for two reasons: (1) Sensitivity is reduced to tissue with high diffusivities, such as along axons, where the signal has already diminished in the higher b-values; (2) Since cellular tissue is heterogenous, the assumption of an exponential decay no longer holds for higher b-values [10], potentially biasing the estimated tensor.

We calculate D_H, the apparent diffusion tensor for the high b-valued shells, as an estimator for D by minimizing:

$$\sum _{i\in G_H}\Vert {\stackrel{\sim }{b}}_{0}exp(-b_i{q}_i^T{D}_H{q}_i)-E(q_i)\Vert ,$$ (3)

where G_H are the indexes of all the applied gradients within the high b-valued shells, and Ê(q_i) is the signal (not normalized by the acquired b₀) of these images. The acquired b₀ reflects the contribution of all spins within the voxel, including from free-water. Therefore, the estimation of D_H requires the estimation of b̃₀, which is the baseline image that would have been acquired in the case that the tensor D_H was the only component in the voxel. We minimize equation (3) using a linear least square (LLS) approach with ln(b̃₀) as one of the free parameters [3].

3.2 Estimation of Extracellular Volume

We estimate f, which reflects the extracellular relative volume in a voxel, using the low b-valued shells, which are in the range that still has signal from free-water. Given D_H as an estimate for D, we can calculate f_L as an estimate for f using LLS by defining:

$$f_L={(y^{T}y)}^{-1}{y}^{T}x,$$ (4)

where x = A_i/A₀ − exp(−b_id) and $y=exp(-b_i{q}_i^T{D}_H{q}_i)-exp(-b_{i}d)$, and i ∈ G_L being the indexes of the applied gradients in the low b-valued shells. A_i are the attenuation images defined in Eq. (1). Unlike our approach here, the single-shell free-water map estimation is initialized by the b₀ image alone, normalized by baseline values that assumed knowledge of voxels that have no tissue, and voxels that have no free-water [4]. This implicitly assumes that the T2 weighted images behave similarly across the entire brain, and that there are such baseline voxels. These assumptions are no longer required if using f_L and D_H as initialization.

3.3 Regularization of the Fitting

The initialization of the extracellular volume, f_L, and the tensor of the tissue compartment, D_H, were designed to be close to the real values, D and f, but could be biased due to either residuals of the free-water signal that remains in the higher b-valued shells, or due to high diffusivity within the tissue, the signal of which could disappear when using the higher b-valued shells. To avoid this potential bias we introduce a third step in which the entire information from all shells is fitted to the model. The fitting is initialized with the estimates provided in the previous two steps, and is stabilized by regularization. We use a regularization method based on the one proposed in [4] by minimizing the following functional:

$$L(D,f)={\int }_{\mathrm{\Omega }}\sum _{i\in G}\Vert A_i-{\widehat{A}}_i\Vert +\alpha \sqrt{\mid \gamma (D)\mid }.$$ (5)

Here, Ω includes all voxels of interest, G are the indexes of all applied gradients and A_i are their signal normalized by the b₀. The parameter α scales the contribution of the Polyakov action regularization term (typically α = 1 [4]), with |γ(D)| as the determinant of the induced metric. Using the Einstein summation convention this metric has the form γ_μν(x) = ∂_μXⁱ∂_νX^jh_ij(X). Differing from the implementation in [4] and following the findings in [12] we do not use an affine-invariant metric to describe distances between tensors but rather use a Euclidean metric and the canonical tensor representation. In a regularization scheme the effect of metric selection is minimal [12], yet here the Euclidean metric simplifies the calculations considerably. As a result the vector X has the elements $X=[D_{xx},D_{yy},D_{zz},2D_{xy},\sqrt{2}{D}_{yz},\sqrt{2}{D}_{xz},x,y,z]$. The matrix H = {h_ij} is the spatial-feature metric that for a Euclidean tensor space is simply a 9 × 9 diagonal matrix, with 1 for the last three diagonal entries (the spatial domain) and a constant for the remaining 6 diagonal entries. This leads to the motion equations for the six unique tensor elements, D^j with j ∈ {1, 2, …, 6}:

$$D_t^j=\sum _{i\in G}{b}_i(A_i-{\widehat{A}}_i)exp(-b_i{q}_i^T{Dq}_i)\left(q_i^T\frac{\partial D}{\partial X_j}{q}_i\right)+\frac{\alpha }{\sqrt{\mid \gamma \mid }}{\partial }_{\mu }\sqrt{\mid \gamma \mid }({\gamma }^{\mu \nu }{\partial }_{\nu }{X}^j)$$ (6)

and for the fractional volume parameter:

$$f_t=\sum _{i\in G}-b_i(A_i-{\widehat{A}}_i)(exp(-b_i{q}_i^T{D}_t{q}_i)-exp(-b_{i}d)).$$ (7)

Importantly, due to the use of the Euclidean metric, and unlike the motion equations derived in [4], equation (6) does not have any Christoffel numbers, and therefore its calculation is simpler and faster. The second term in equation (6) is the Laplace-Beltrami operator, which is a piece-wise smooth, edge preserving tensor regularization operator [4]. The final result is thus the parameters f and D that best fit the data while maintaining continuous tissue representation.

4 Experiments and Results

Multi-Shell Acquisition Schemes

We test the multi-shell estimation on two types of data sets that were obtained with multi-shells. The first data uses an acquisition optimized for the free-water estimation, having a single b=0, 3 × b=50, 6 × b=200, 10 × b=500, 30 × b=900 and 16 × b=1400, with gradient orientations designed as nested platonic solids, which means that each shell is rotationally invariant, and the shells complement each other to a rotationally invariant scheme. Data was acquired on a 1.5T scanner with 2.5mm isotropic voxels and takes 9:20 minutes. We use the b=1400 and b=900 shells to estimate D_H, and the remaining shells to estimate f_L. The second data set demonstrates adding lower shells to an existing DTI gradient scheme with b=900 and the scanner default 64 gradient orientations. We added a shell at b=400 with 10 measurements and a shell at b=100 with 6 measurements, adding 2:40 minutes to the acquisition time. We use the b=900 and b=400 shells to estimate D_H. We use b=100 and b=400 to estimate f_L. This data was acquired on a 3T scanner with 2mm isotropic voxels.

Implementation

All data was motion and eddy-current corrected. We used 3D-Slicer’s tensor estimation to calculate D_H by first omitting all images in G_L, including the b₀. We used Matlab (Natick, MA) to calculate f_L. The optimization was done using a Matlab code that was provided in [4]. The code was changed to accept multiple b-values, to regularize using a Euclidean metric, and to use D_H and f_L as initialization. The complete analysis for a whole brain takes less than 15 minutes on a 64-bit Linux machine with Xeon-E5530 processors, without taking advantage of multiple cores.

Optimized Multi-Shell Acquisition

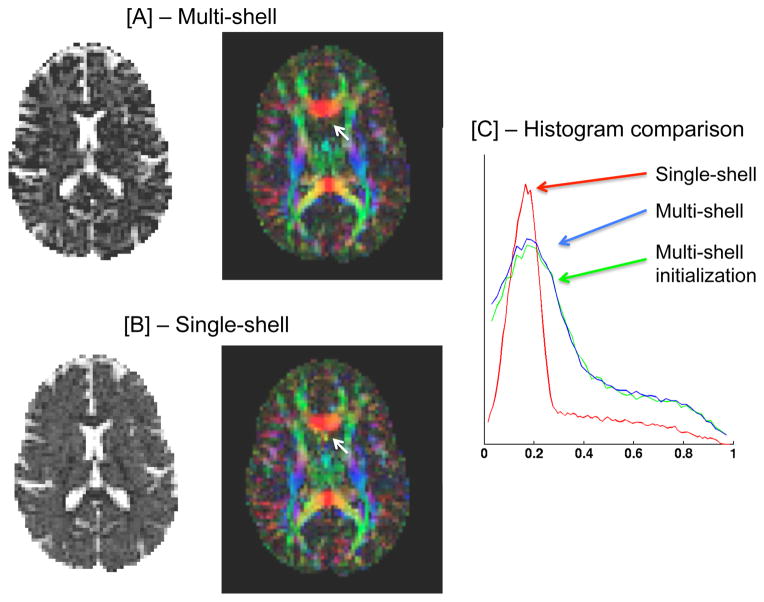
Both the multi-shell (Fig. 2[A]) and single-shell (using the b=900 shell; Fig. 2[B]) estimations provide similar free-water maps, showing high values in the ventricles, and low values in the brain tissue, nicely depicting the extracellular volume. The color by orientation maps are similar as well. To better evaluate the differences between the maps, we plot free-water maps using a color-scale that increases the visibility of the lower values. We can then see that the multi-shell maps are not as smoothed as the single-shell maps, although both estimations used the same Laplace-Beltrami regularization operator. As a result the multi-shell map is more detailed, allowing to better distinguish cortical structures. For this acquisition scheme, the initialization, f_L is very similar to the final multi-shell free-water map. Subtle changes between the maps can be seen in the histogram comparison (Fig. 2[C]). This means that in this case f_L is a good estimator for the extracellular volume. The histogram also demonstrated that most brain voxels have extracellular volume around the 0.2 value.

Fig. 2. Optimized multi-shell.

Our multi-shell regularized fitting provides a more detailed extracellular volume and tissue tensor maps [A], comparing with the regularized single-shell fitting [B]. Small details are preserved and there are less artifacts (white arrows). The initialization f_L is very close to the final convergence as can be seen in the histogram of the images [C].

Shells Added to a DTI Acquisition

This option suits cases where on-going DTI studies exist, but there is the opportunity to improve the acquisition by adding images to the existing protocol. In this case adding only lower shells is allowed, to prevent from changes in important imaging parameters such as echo time, repetition time and diffusion time that are required to accommodate the higher b-values. However, as can be seen in Fig. 3, the convergence point is no longer similar to the initialization point. The maps following regularization are smoother, but unlike the single-shell case, the details are better preserved during the regularization. The quality of the regularized images suggests that when the separability between shells is not sufficient, using the full proposed pipeline, including the regularization step is preferred.

Fig. 3. Modified DTI acquisition.

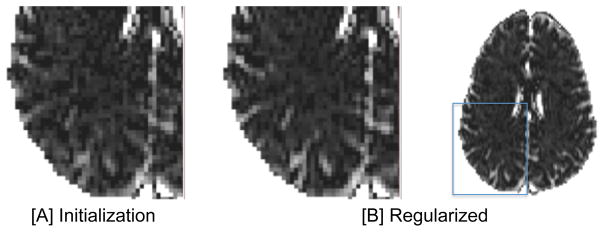
When there are residuals of free-water in the higher shells, the initialized free-water map [A] is different than the converged map following regularization [B]. The final map is less noisy and structures are accented. The higher quality of the regularized maps suggests that using the full proposed pipeline is preferred for this type of acquisition.

5 Discussion and Conclusions

Fitting the free-water model instead of the DTI model adds the extracellular volume as a new estimated biological parameter and provides tensor images that are more tissue specific [3–6]. We demonstrate that with a multi-shell data we can relax assumptions and dependency on regularization that is required when fitting the model from a single-shell data. We were able to estimate the extracellular volume from multi-shell data, achieving more detailed maps than single-shell maps. Although the difference is subtle, it could be important for studies of pathologies that slightly affect the extracellular space, such as neuroinflammation. For an optimized spread of a relatively small number of acquisitions in b-value shells within the DTI b-value range we can estimate the model parameters directly from the data, avoiding regularization. Future studies could further explore optimized scheme designs, and investigate the integration with other HARDI methods that acquire multiple-shells, in which case further parameters such as the diffusivity of the isotropic compartment, can be added.