Differentiation of the intracellular structure of slow- versus fast-twitch muscle fibers through evaluation of the dielectric properties of tissue

Abstract

Slow-twitch (type 1) skeletal muscle fibers have markedly greater mitochondrial content than fast-twitch (type 2) fibers. Accordingly, we sought to determine whether the dielectric properties of these two fiber types differed, consistent with their distinct intracellular morphologies. The longitudinal and transverse dielectric spectrum of the ex vivo rat soleus (a predominantly type 1 muscle) and the superficial layers of rat gastrocnemius (predominantly type 2) (n = 15) were measured in the 1 kHz–10 MHz frequency range and modeled to a resistivity Cole–Cole function. Major differences were especially apparent in the dielectric spectrum in the 1 to 10 MHz range. Specifically, the gastrocnemius demonstrated a well-defined, higher center frequency than the soleus muscle, whereas the soleus muscle showed a greater difference in the modeled zero and infinite resistivities than the gastrocnemius. These findings are consistent with the fact that soleus tissue has larger and more numerous mitochondria than gastrocnemius. Evaluation of tissue at high frequency could provide a novel approach for assessing intracellular structure in health and disease.

1. Introduction

During the last century, the dielectric properties of biological tissues over a wide frequency range were extensively investigated (Crile et al 1921, Schwan 1953, 1984, Schwan and Kay 1956, Stoy et al 1982, Geddes and Baker 1967, Pethig and Kell 1987, Gabriel et al 1996). Most of this knowledge was gathered by measuring a variety of ex vivo and in vivo animal tissues from 10⁻⁵ up to 10¹³ Hz via the technique of broadband spectroscopy (Kaatze 2013).

In contrast to these earlier studies, electrical impedance-based methods applied to the clinical evaluation of patients and animals on living tissue are usually performed at either a single frequency (generally 50 kHz) or by a sweeping frequency in the kHz to 1 MHz range (Faes et al 1999, Gabriel et al 2009) for determination of the state of organs (Gersing 1998), for example, to examine the electrical properties of the heart (Fallert et al 1993, Sanchez et al 2011) and lungs (Kimura et al 1994, Sanchez et al 2013d). The reason underlying this limited frequency range is that most relevant clinical information can be obtained within this narrow band of the dielectric spectrum.

The application of electrical impedance spectroscopy (EIS) specifically to the clinical muscle evaluation of patients and animals is known in the literature as electrical impedance myography (EIM) (Rutkove 2009). EIM has shown promise as a tool for the non-invasive, in vivo assessment of muscle status in a variety of conditions, ranging from amyotrophic lateral sclerosis (ALS) (Rutkove et al 2012) to primary muscle diseases (Tarulli et al 2005) to changes in muscle with disuse and ageing (Aaron et al 2006, Li et al 2013). In addition, the EIM technique may be able to detect patterns associated with primary nerve as compared to primary muscular conditions, making it a potentially useful diagnostic tool (Garmirian et al 2009). While early work in the area initially focused on applying just a single frequency of electrical current (Rutkove et al 2002), more recent studies have employed spectroscopic evaluation and these have revealed additional considerable value (Rutkove et al 2010, Wang et al 2011).

However, in order to accurately identify intracellular components of the skeletal muscle with EIS requires that frequencies above 1 MHz be used so that the cell membrane is effectively penetrated. The ability to evaluate the inner structures of the cell would be valuable since it could serve as a tool to assess conditions affecting mainly sub-cellular muscle components such as the mitochondria, the t-tubule system or the sarcomeres themselves (Sanger et al 2004). One challenge, however, is to determine whether or not the electrical current truly is detecting such intracellular components. Indeed, at high frequencies, it can become very difficult to disentangle true cellular data from the variety of errors inherent to the impedance spectroscopy techniques themselves (Bolton et al 1998).

Technical difficulties aside, one potential approach of experimentally identifying these distinctions would be to study two groups of muscle fibers from the same animal with distinctly different intracellular components. Fortunately, nature provides such a convenient opportunity. Specifically, mature muscle fibers are generally grouped into two broad classes of fibers: fast-twitch, commonly called type 2 fibers, and slow-twitch, commonly called type 1 fibers. Whereas there are also many subtypes of these fibers (e.g. type Ia, Ib, IIa, etc), the basic distinction between fast- and slow-twitch holds true in most appendicular muscles. Both fiber types have distinct morphology, with the slow-twitch being mainly oxidative and containing vast quantities of large mitochondria; the fast-twitch fibers, in contrast, mainly rely upon glycolytic processes, and thus have few and considerably smaller mitochondria. Thus, a comparison between the electrical properties of these two cell types would provide a straightforward approach for determining whether such intracellular differences can be identified.

In the present work, we study by comparing fibers from the rat soleus (mainly slow-twitch) and gastrocnemius (mainly fast-twitch) (Armstrong and Phelps 1984) the dielectric spectrum of type 1 and type 2 fibers in the 1 kHz–10 MHz frequency range. Our ultimate goal is to determine if it is possible to distinguish the mitochondrial content (size and density) of type 1 and type 2 muscle from the high-frequency content of the dielectric spectrum.

2. Methods

2.1. Animals

All procedures were approved by the Institutional Animal Care and Use Committee at Beth Israel Deaconess Medical Center. A total of 15 adult, healthy male Wistar rats of 14 weeks of age were obtained from Charles River Laboratories. Animals were allowed to acclimatize for a minimum of two days at our animal facility and fed a standard diet ad libitum.

2.2. Gastrocnemius and soleus muscle extraction

After placing the animal under 1% isoflurane anesthesia, the skin overlying the left hind limb was cut with scissors and the tissue dissected down to expose the entire gastrocnemius muscle. The animal was then killed via an intraperitoneal injection of FatalPlus® and the entire gastrocnemius muscle excised at its proximal extent just below the knee and distally by cutting the gastrocnemius tendon at its insertions, after removing the more superficial bicep femoris muscle. Of note, the animals were not exsanguinated at the time of sacrifice. After excising the gastrocnemius muscle, the soleus muscle was exposed and cut with scissors. With a scalpel, the soleus and gastrocnemius muscles were cut to approximately 5 × 5 mm² and 10 × 10 mm² respectively so as to fit in the two dielectric cells (described below).

3. Materials

3.1. Dielectric cell characteristics

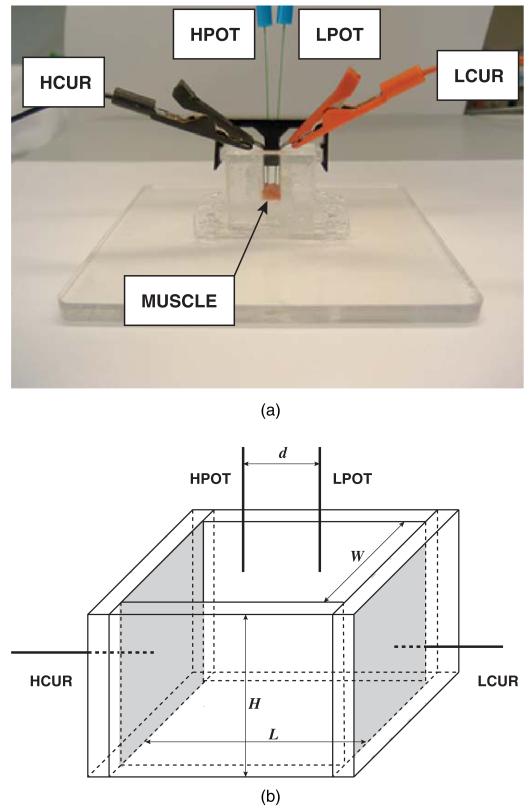
Figure 1 (top) shows a photo and a schematic of the Plexiglass dielectric measuring cell developed for the measurement of muscle dielectric properties. The dielectric cell consists of two flat plate stainless steel current electrodes, referred to as high and low current electrodes in figure 1 (bottom), contacting the entire side of the slab of muscle. Two disposable monopolar EMG needle electrodes (Carefusion reference 902-DMG50-TP) were used as voltage drop-measuring electrodes that projected through the holes of the tight-fitting cover. These voltage electrodes were inserted through the holes of the plastic cover so that they just contacted the surface of the muscle. We used two identical dielectric cells but with different geometrical dimensions since the extracted muscles were of different sizes. For measurements of the larger gastrocnemius, a cell W = 10 mm × L = 10 mm base and H = 10 mm high was used, the muscle was h = 5.1 ± 0.4 mm in height; voltage interelectrode distances were d = 4 and 6 mm (calculations of dielectric values were made using both sets and the average taken). While for the soleus, a W = 5 mm × L = 5 mm base, H = 5 mm high device was used, the muscle height being approximately h = 2.5 mm and voltage electrodes being placed at a single distance of d = 3 mm apart. Both gastrocnemius and soleus muscle were first placed in the cell with the fibers oriented perpendicularly to the metal plates, then removed and placed with the fibers placed parallel to the plates. To ensure consistent temperature, the entire cell was maintained at 37 °C through the use of a heating pad beneath the cell (not shown).

Figure 1.

(a) Image of the dielectric cell together with the four electrode-based electrical impedance measurement setup. The nomenclature for the electrodes is: high potential (HPOT), low potential (LPOT), high current (HCUR) and low current (LCUR). (b) Sketch of the dielectric cell for the impedance measurements. See text for details.

3.2. Impedance measuring device

Electrical impedance measurements were made with the EIM 1103 impedance spectroscopy system (Skulpt, Inc., Boston, MA) at f ∈ {1 kHz, 10 MHz} using a frequency sweep spectroscopy technique. In total, 41 logarithmically-spaced frequencies (10 frequencies per decade) were measured.

4. Data analysis and calibration

Resistance R(ω) (Ω) and reactance X(ω) (Ω) spectra were collected across the frequency range with ω = 2π f (s⁻¹) the (angular) frequency. Next, in order to calibrate the entire impedance measuring setup for potential measurement errors due to, for example, electrode polarization and stray capacitances, identical measurements were made with normal saline solution placed into both dielectric cells.

From the calibrated R(ω) and X(ω), the muscle conductivity σ (ω) (S m⁻¹) and the relative permittivity ε_r(ω) (dimensionless) were calculated as follows. By definition, the electrical impedance Z(ω) is expressed as

$$Z\left(\omega \right)=R\left(\omega \right)+\mathrm{j}X\left(\omega \right).$$ (1)

Considering the geometrical factor K (m⁻¹) of the impedance cell in figure 1, it follows that

$$Z\left(\omega \right)=\frac{K}{{\sigma }^{\ast }\left(\omega \right)},$$ (2)

with σ*(ω) (complex) conductivity defined as

$${\sigma }^{\ast }\left(\omega \right)=\sigma \left(\omega \right)+\mathrm{j}\omega {\epsilon }_0{\epsilon }_r\left(\omega \right),$$ (3)

and K

$$K=\frac{d}{A},$$ (4)

where ε₀ is the vacuum permittivity (ε₀ = 8.85 × 10⁻¹² F m⁻¹), d (m) is the distance between the voltage electrodes, A (m²) the cross-sectional area of the muscle given by A = W × h with W (m) the width of the dielectric cell and h (m) the muscle tissue sample height measured for each muscle (see section 3.1). By combining (1)–(3), it follows (Ahad et al 2009)

$$\{\begin{array}{c}\sigma \left(\omega \right)=K\frac{R\left(\omega \right)}{R^2\left(\omega \right)+X^2\left(\omega \right)}\hfill \\ {\epsilon }_r\left(\omega \right)=K\frac{X\left(\omega \right)}{\omega {\epsilon }_0\left(R^2\right(\omega )+X^2(\omega \left)\right)}.\hfill \end{array}\phantom{\}}$$ (5)

5. Procedure for data parametrization

The complex resistivity spectrum ρ* (ω) (Ω m) given by

$${\rho }^{\ast }\left(\omega \right)=\frac{1}{{\sigma }^{\ast }\left(\omega \right)},$$ (6)

was averaged for all animals’ data in both longitudinal and transverse directions. Data was fitted in MATLAB® (Natick, MA, USA) to the complex resistivity version of the Cole–Cole expression (Cole and Cole 1941), namely

$${\rho }^{\ast }\left(\omega \right)={\rho }_{\infty }+\frac{{\rho }_0-{\rho }_{\infty }}{1+{(\mathrm{j}\omega ∕{\omega }_c)}^{\alpha }},$$ (7)

with the weighted complex nonlinear least square method described in Sanchez et al (2013a). The model parameters are ρ₀ (Ω m) and ρ_∞ (Ω m) the resistivities at DC and ω → ∞ respectively, ω_c = 2π f_c (s⁻¹) the (angular) central frequency and the dimensionless empirical parameter α. The algorithm used was the Levenberg–Marquardt and the weights used were the standard error of the data. Finally, the numerical Jacobian matrix was calculated to estimate the standard errors in the model parameters. The number of maximum iteration and function evaluations were set to 10⁶. The desired tolerance was set to 10⁻¹². The initial values for the ρ₀ and ρ_∞ parameters were given from the initial and ending points of the resistivity magnitude spectrum. The initial central frequency was derived from the center frequency measured and the α parameter was initially set to 0.5.

6. Results

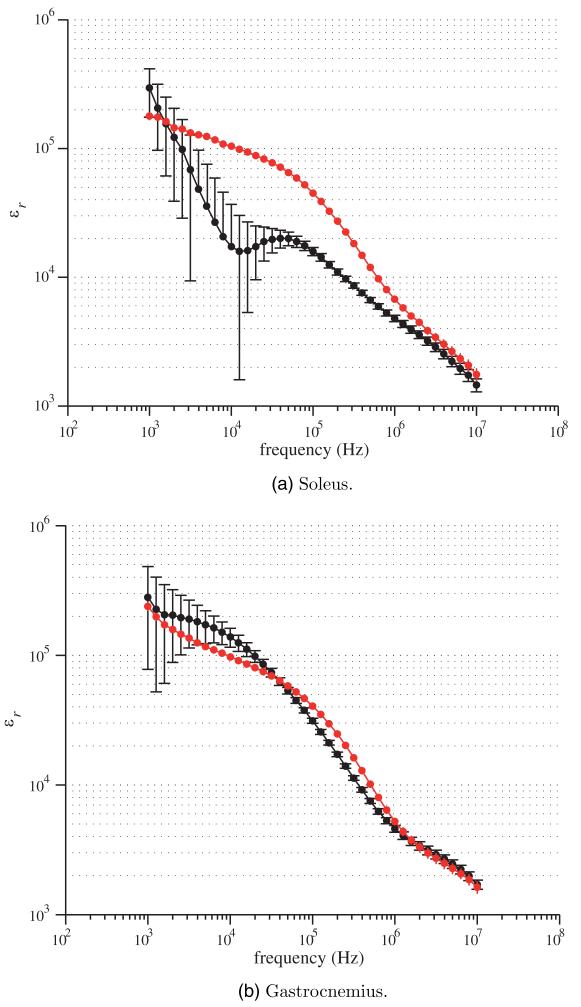
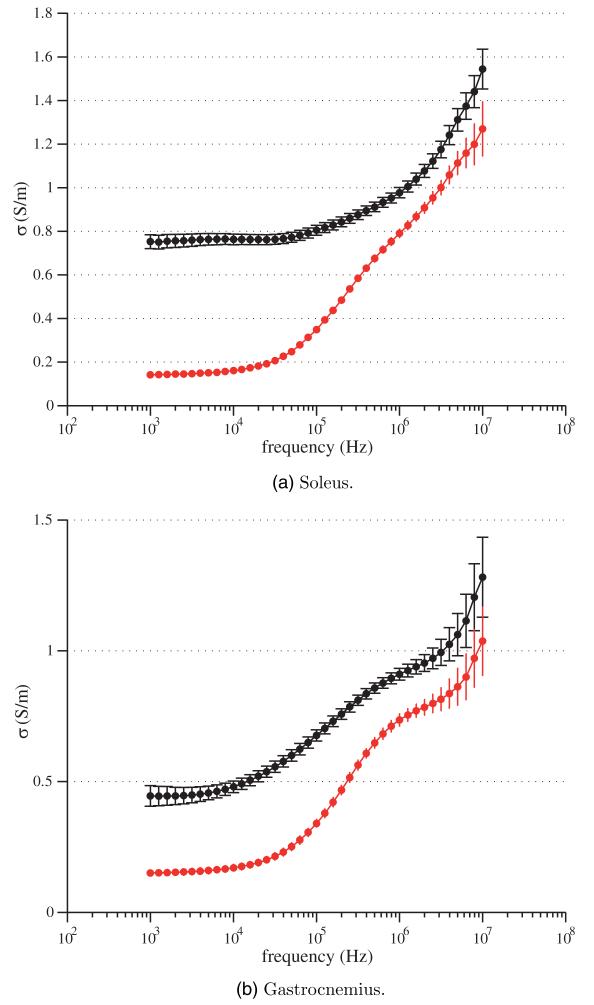
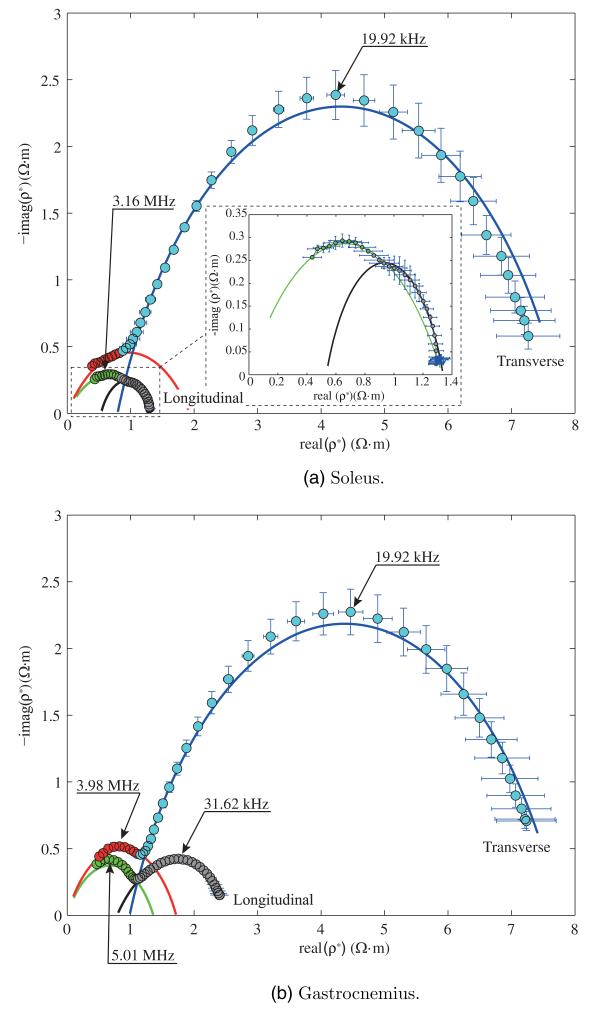
In what follows, the mean and the standard error of the mean for the relative permittivity and the conductivity spectra of soleus and gastrocnemius are shown graphically in figures 2 and 3 respectively for both longitudinal and transverse directions. As for the longitudinal measurements, the muscle was oriented such that the injected current between HCUR and LCUR electrodes was in the same direction as the muscle fibers determined by visual inspection. For the transversal measurements, the muscle was shifted 90° with respect to the longitudinal case. The complex resistivity plots and their fitting values are shown in figure 4 and table 1.

Figure 2.

Longitudinal (black) and transverse (red) relative permittivity spectrum ε_r(ω) (5). Mean values and standard errors shown.

Figure 3.

Longitudinal (black) and transverse (red) conductivity spectrum σ (ω) (5). Mean values and standard errors shown.

Figure 4.

Real versus imaginary part of the complex resistivity spectrum ρ*(ω) (6). Mean values and standard errors shown. The solid lines are the model fit (7) corresponding to color data code.

Table 1.

Estimated 1–10 MHz Cole–Cole resistivity model parameters (mean and standard error of the parameters shown).

	ρ0 (Ω m)	ρ∞ (Ω m)	fc (MHz)	α
Soleus longitudinal	1.33 ± 0.047	0 ± 0.039	2.88 ± 0.207	0.517 ± 0.029
Soleus transverse	1.93 ± 0.049	0 ± 0.103	1.20 ± 0.568	0.561 ± 0.095
Gastroc. longitudinal	1.36 ± 0.049	0 ± 0.146	4.41 ± 1.036	0.641 ± 0.065
Gastroc. transverse	1.72 ± 0.084	0 ± 0.070	3.55 ± 0.306	0.672 ± 0.048

7. Discussion

These results demonstrate for the first time differences in the frequency-dependent material properties of slow-twitch versus fast-twitch muscle fibers. Figures 2 and 3 show the electrical properties and their dependence with respect to the fiber orientation. The discussion that follows is made based on the interpretation of complex resistivity data shown in figure 4.

We initially hypothesized that we might be able to identify a second, high-frequency arc in the complex resistivity of slow-twitch soleus fibers given their substantially greater number of mitochondria (Ogata and Murata 1969) compared to the fast-twitch gastrocnemius. Unexpectedly, however, the complete high-frequency arc could be observed in the gastrocnemius data and not in the soleus data (see figure 4). We then sought explanations for this finding. At first, we considered the possibility that perhaps the upper high frequency (10 MHz) simply was still not high enough to capture the entire arc. However, on further review of older electron microscopy literature describing the morphology of these cells (Ogata and Murata 1969, Kayar et al 1988), it became clear that the mitochondria in the soleus were so large that their material properties could overlap those of the cells themselves. And indeed, this is borne out in the fitting of the high-frequency tail in the data that is buried in the low-frequency arc, which is supported by the fact that the soleus central frequency is smaller than the gastrocnemius central frequency in the transverse direction (1.20 MHz and 3.55 MHz respectively from table 1). Finally, additional evidence for our interpretation of the data is provided by the ρ₀ and ρ_∞ model values in table 1. The base of the arch defined by ρ₀ − ρ_∞ is much larger for soleus than for medial gastrocnemius, consistent with that fact that there are many more mitochondria in soleus than in gastrocnemius. The fitting parameters corresponding to low frequency data (<1 MHz) are shown in table 2.

Table 2.

Estimated 1 kHz–1 MHz Cole–Cole resistivity model parameters (mean and standard error of the parameters shown).

	ρ0 (Ω m)	ρ∞ (Ω m)	fc (MHz)	α
Soleus longitudinal	1.34 ± 0.007	0.53 ± 0.039	0.580 ± 0.062	0.695 ± 0.024
Soleus transverse	7.83 ± 0.110	0.79 ± 0.024	0.018 ± 0.001	0.736 ± 0.009
Gastroc. longitudinal	2.64 ± 0.027	0.79 ± 0.017	0.038 ± 0.002	0.528 ± 0.012
Gastroc. transverse	7.76 ± 0.088	0.98 ± 0.020	0.021 ± 0.001	0.729 ± 0.009

It is undoubtedly a simplistic explanation that these differences are based solely on the density of mitochondrial content and their dimensions. Whereas the number and size of mitochondria are perhaps the most obvious difference between slow- and fast-twitch muscle fibers, other differences are also present including variation in the density of the transverse tubule system, the amount of glycogen content, and the blood supply. Thus, it is conceivable that other variations in muscle structure are also playing a role in these results. For example, a primary vascular explanation certainly could play a role since the capillaries are considerably smaller than muscle fibers (approximately 5 μm in diameter as compared to 60 μm for muscle fibers) and denser in slow-twitch muscle (Sjogaard 1982). However, the overall capillary area makes up only a very small proportion of the entire muscle volume (on the order of 1–2% of the entire muscle volume based on data in (Lillioja et al 1987)) and thus is unlikely to contribute substantially to the overall impedance data. By their inherent nature, impedance measurements are non-specific and thus we cannot hope to identify a single specific mechanism underlying these findings, and yet of all explanations, the variation in mitochondrial size may be the most compelling.

The differences in the transverse and longitudinal data also deserve comment. First, as would be anticipated, in both muscles, the low-frequency imaginary part of the complex resistivity is considerably larger in the transverse direction as compared to the longitudinal since the electrical current needs to traverse a much greater number of cell membranes. Second, and perhaps of greatest interest and most easily appreciated in the gastrocnemius data, is that although the low-frequency arc shows a substantial anisotropy (i.e. the peak of imaginary part of the complex resistivity is 5× greater in the transverse direction than the longitudinal), the peak in the high-frequency arc, likely representing the mitochondria, demonstrates only slight anisotropy (approximately 1.2× greater in the transverse direction). This is exactly what is to be expected in that while the muscle fibers themselves are highly asymmetrical in structure, the mitochondria are only minimally so. This finding helps further support the premise that we really are measuring meaningful intracellular differences.

The identification and separation of these low- and high-frequency behaviors can provide a new and potentially innovative tool for the assessment of neuromuscular conditions and could open the door to new applications. These measurements were performed on excised tissue and simply for the purpose of evaluating whether high-frequency impedance-based techniques can effectively distinguish slow-twitch from fast-twitch muscle. However, there is nothing to preclude it being used in vivo to assess intracellular and extracellular content in various conditions. Of course, in such a setting, the actual material properties would not be directly obtained, but rather the geometry-dependent standard electrical impedance parameters. Yet, alterations in these parameters may be able to help distinguish between disease states. For example, it might be possible to use this approach to assess for primary mitochondrial conditions, in which mitochondria have markedly abnormal distribution and structure (Pfeffer and Chinnery 2013). Alternatively, it is possible that this approach could be used to evaluate other conditions with prominent intracellular abnormalities, such as lysosomal storage diseases, glycogen storage diseases, and congenital myopathies, including microtubular and nemaline rod myopathies. Perhaps more intriguingly, the technique could be used to assess the relative proportion of fast-twitch and slow-twitch fibers in relevant muscles of an individual, thus providing insights into their physical capabilities—i.e., what is the person’s intrinsic ability to sprint versus run long distances (Costill et al 1976, Gollnick et al 1972). Finally, the technique could serve as a useful measure of drug efficacy in diseases attempting to restore normal intracellular architecture such as enzyme replacement therapy in Pompe’s disease (Kishnani et al 2007).

There are a variety of technical limitations that should be noted beyond just the challenge of data interpretation. First, and undoubtedly most important, is the fact that it is technically difficult to obtain accurate measurements of the longitudinal soleus data. The muscle is relatively small and friable, and it was difficult to place it squarely in the impedance measuring cell to ensure that the current was flowing through the fiber ends. Perhaps not surprisingly, the resulting modeling of the soleus longitudinal data has considerable error, also in part due to the fact that we have a relatively small number of data points to fit. Second, no muscle is 100% fast-twitch or slow-twitch. Nature has fortunately provided us with one convenient example, but it is not perfect. Another approach to further explore this idea would be to do studies on single muscle fibers. Although this may seem daunting, techniques for evaluating the electrical and mechanical properties of single fibers are available. Third, data obtained are in a limited frequency range. Clearly, going up to higher frequency (e.g. 100 MHz) may have allowed us to more accurately model this high-frequency behavior for both muscle fiber types. Finally, although we did use 15 animals, using additional animals would have further reduced some of the noise and improved our fitting.

This effort represents only an initial step in the study of muscle ultrastructure using an electrical impedance-based method. As suggested, a logical next step would be to pursue these measurements up to even higher frequencies. Perhaps more practical, however, would be to perform such measurements in the clinical research setting. Whereas this study focused on excised tissue, it may be possible to extract similar values using surface measurements alone, making the technique useful in regular patient care. For example, it may be possible to obtain useful information on mitochondrial or other intracellular structures in healthy and diseased muscles and to evaluate the effect of therapy. Given the development of recently improved methods for the measurement of electrical impedance across a broad spectrum of frequencies including temporal information (Sanchez et al 2013b, 2013c), these goals should be within our reach.