Simulation of reaction diffusion processes over biologically relevant size and time scales using multi-GPU workstations

Abstract

Simulation of in vivo cellular processes with the reaction-diffusion master equation (RDME) is a computationally expensive task. Our previous software enabled simulation of inhomogeneous biochemical systems for small bacteria over long time scales using the MPD-RDME method on a single GPU. Simulations of larger eukaryotic systems exceed the on-board memory capacity of individual GPUs, and long time simulations of modest-sized cells such as yeast are impractical on a single GPU. We present a new multi-GPU parallel implementation of the MPD-RDME method based on a spatial decomposition approach that supports dynamic load balancing for workstations containing GPUs of varying performance and memory capacity. We take advantage of high-performance features of CUDA for peer-to-peer GPU memory transfers and evaluate the performance of our algorithms on state-of-the-art GPU devices. We present parallel e ciency and performance results for simulations using multiple GPUs as system size, particle counts, and number of reactions grow. We also demonstrate multi-GPU performance in simulations of the Min protein system in E. coli. Moreover, our multi-GPU decomposition and load balancing approach can be generalized to other lattice-based problems.

1. Introduction

Reaction diffusion processes are ubiquitous in biology. The random nature of gene expression and behavior of genetic switches was demonstrated by a series of pioneering experiments that have been recently reviewed [1]. These cellular processes are governed by stochastic interactions between a relatively small number of proteins and nucleic acids, giving rise to large fluctuations in the substances appearing in the underlying biochemical reactions. The distributions of copy numbers and phenotypic behavior of members within in a population of cells motivate a probabilistic formulation of the reactions rather than a deterministic one used to describe the mean behavior of chemical reactions with large concentrations of reactants. Even though cellular volumes range from only 1-1000 cubic microns, the cell has a crowded environment with many reactions being localized to particular parts of the cell requiring reactants to diffuse to the reaction sites. Stochastic modeling of a system of biochemical reactions at the cellular level can be divided into methods which handle spatial inhomogeneity such as the reaction-diffusion master equation (RDME), and those that assume a well-stirred environment like the chemical master equation (CME). Since the CME and RDME are both analytically intractable for systems of significant complexity, the reactions are generally studied using large ensembles of computationally generated trajectories (realizations) of the Markov processes and transition probabilities described by the master equations.

The CME assumes the reaction volume is well-stirred such that reactions are equally likely between any reactant molecules in the entire volume. For in vitro biochemical systems the well-stirred approximation proves reasonable [2], but spatial organization and molecular crowding inside cells bring this assumption into question for in vivo systems [3]. The RDME extends the master equation formalism of the CME to account for spatial degrees of freedom by dividing the system volume into discrete subvolumes with molecules diffusing between adjacent subvolumes and reacting only with other molecules in the local subvolume. In our previous studies of small bacteria and in vitro systems, we developed the Lattice Microbes software [3, 4] to e ciently sample trajectories from either the CME and RDME on high performance computing (HPC) infrastructure, taking advantage of attached GPUs or other many-core processors to increase performance.

To probabilistically study chemico-physical processes using the master equation formalism, one solves the time evolution of the probability P for the system to be in a given state x. In our treatment of the RDME for modeling chemical reactions under conditions of slow diffusion [5, 6, 7], the system's volume is divided into a set of uniform subvolumes with spacing λ and with the molecules in the system distributed amongst the subvolumes. Reactions occur only between molecules within a subvolume and each subvolume is considered to be well-stirred such that reactions within it follow standard kinetic theory and can be described by the CME solved using the Gillespie stochastic algorithm [8]. The CME using the Gillespie algorithms has already been applied by others to enzyme reactions obeying Michaelis–Menten kinetics [2]. Other more complex reaction schemes described by Hill functions can be broken down into elementary first and second order reactions and solved with either CME or RDME approaches. The Lattice Microbes software uses operator splitting to calculate the reaction and diffusion operations separately. Diffusion is accounted for by random transitions of molecular species between neighboring subvolumes at a predetermined time according to their macroscopic diffusion coe cient. The software combines the multiparticle (MP) method for diffusion developed by Chopard et al. [9] in lattice gas automata for reaction diffusion systems with Gillespie's stochastic simulator algorithm for reactions within the subvolumes. This approach is most similar to the Gillespie multi-particle (GMP) method first introduced by Rodríguez et al. [10]. Using the multiparticle diffusion (MPD) method, the diffusion operator of the RDME is parallelized for efficient calculation on a GPU at a per-subvolume granularity [11]. Uniquely, our MPD-RDME approach is of sufficient performance to permit the inclusion of in vivo crowding into the model, by constructing an approximation of the crowded cytoplasm using reflective sites.

The time evolution of the probability for the system to be in a specific state x (where x_v contains the number of molecules of each of N species in the ψ ∈ V subvolume) is the sum of the rates of change due to reaction and diffusion, as described by the operators R and D, respectively:

$$\begin{array}{cc}\hfill \mathcal{R}P(\mathbf{x},t)=& \sum _v^V\sum _r^R[-a_r\left({\mathbf{x}}_v\right)P({\mathbf{x}}_v,t)+a_r({\mathbf{x}}_v-{\mathbf{S}}_{\mathbf{r}})P({\mathbf{x}}_v-{\mathbf{S}}_{\mathbf{r}},t)]\hfill \\ \hfill \mathcal{D}P(\mathbf{x},t)=& \sum _v^V\sum _{\xi }^{\pm \widehat{i},\widehat{j},\widehat{k}}\sum _{\alpha }^N[-d^{\alpha }{x}_v^{\alpha }P(\mathbf{x},t)+d^{\alpha }(x_{v+\xi }^{\alpha }+1)P(\mathbf{x}+1_{v+\xi }^{\alpha }-1_v^{\alpha },t)]\hfill \\ \hfill \frac{dP(\mathbf{x},t)}{dt}=& \mathcal{R}P(\mathbf{x},t)+\mathcal{D}P(\mathbf{x},t).\hfill \end{array}$$

The reaction operator is simply the CME applied to each subvolume independently, where a_r(x) is the reaction propensity for reaction r of R and S is the N×R stoichiometric matrix describing the net change in molecule number when a reaction occurs. The diffusion operator describes the rate of change of the probability due to the molecules’ propensity to diffuse between the subvolumes. x^α_v is the number of molecules of species α ∈ N in subvolume v and d^α is the diffusive propensity for a molecule of species α to jump from subvolume v to neighboring subvolume v + ξ, which is related to its macroscopic diffusion coefficient by $d=\frac{{\lambda }^2}{D}$. The first part of the diffusion operator then is probability flux out of the current state due to molecules diffusing from subvolume to subvolume v + ξ, where ξ is a neighboring subvolume in the ±x, ±y, or ±z direction, as indicated by the î, ĵ, and k̂ units vectors. The second part of the diffusion operator describes probability flux into the current state due to molecules diffusing into the current subvolume from a neighboring subvolume. The 1^α _v syntax represents a single molecule of type α in subvolume v.

In our previous studies of small Escherichia coli (E. coli) bacteria with cellular volumes of 2-3 cubic microns and over one-half million obstacles fixed at lattice sites to represent the molecular crowding, the above time evolution equation was stochastically simulated on a single GPU to mimic the lac genetic switch controlling transitions between two distinct phenotypic states. The kinetic model involved 23 reactions for ten different molecular species which for the observed cellular concentrations resulted in 1 million active particles being simulated. The memory capacity and performance of a single GPU ultimately limits the number of particles, reactions, resolution, and size of the organism that can be simulated. These restrictions can be lifted to simulate larger organisms such as dividing bacteria and yeast over biologically relevant timescales by utilizing multiple GPU accelerators attached to a single workstation to carry out the MPD-RDME simulations.

The main target platforms for our multi-GPU MPD-RDME algorithm are multi-GPU workstations and HPC cluster nodes. These machines are composed of two or more GPUs connected to the host through a PCI Express (PCIe) bus. Modern GPUs are throughput-oriented devices with massively parallel architecture. State-of-the-art GPUs are capable of performing up to 4 trillion single-precision floating point operations per second (4 TFLOPS), and they contain their own high-bandwidth on-board memory subsystems capable of transferring data at rates of up to 250 GB/sec. Although a few multi-GPU laptop computers do exist, one of the GPUs is typically incorporated onto the main system board or within the CPU itself, and therefore does not have a high-bandwidth memory subsystem comparable to that of a traditional discrete GPU.

For computation of the MPD-RDME trajectory, a 3-dimensional regular lattice serves as a spatial representation for the system, with each lattice site describing the properties and state of a subvolume. A major limiting factor for the physical size of the biological system we wish to simulate is the amount of global memory available on the GPU to store the lattice. The GPU memory requirement is dependent on the lattice spacing and the maximum number of particles that can be stored per lattice site. Two to eight particles per lattice site can be expressed with a single 32-bit word [11], with a trade-off between the number of unique particle species that can be present in the simulation and the lattice site particle capacity. Alternatively, multiple 64-bit words can be used to express eight particles each [4] with a constant number of unique species. If the number of particles in a subvolume exceeds the capacity of a lattice site, the additional particles are considered to have overflowed the data structure and are added to a list to be re-integrated into the simulation at the end of the timestep [11]. Overflow handling is performed by the host CPU, so it is best to choose a lattice spacing and site capacity that will minimize the occurrence of these events, but these choices will impact the memory required to perform the simulation.

To overcome the limited memory capacity of a single GPU, our approach applies a spatial decomposition of the simulation lattice over multiple GPUs. This method has proven successful in other multiple-GPU parallelizations applied to 3D finite difference discretizations of the wave equation [12]. A multidimensional spatial decomposition is also applied in a number of packages that provide auto-parallelization of stencil kernels over regular lattices, such as Physis [13] and CaKernel [14]. Both Physis and CaKernel provide multiple GPU support via MPI that allows execution over multiple host machines to aggregate GPUs. Our approach targets a single workstation with multiple directly-attached GPUs, which neither CaKernel or Physis is optimized to handle. Our approach streamlines inter-GPU communication by establishing a unified memory address space between GPUs, and utilizes direct communication via PCIe DMA operations when possible. This allows us to o er powerful multi-GPU accelerated computations simply by having multiple GPUs present in the machine. Our approach does not rely on an MPI implementation to be installed or configured allowing for easier deployment and use, removing the requirement and burden of compiling MPI applications. The multi-process parallelization that MPI provides can not take advantage of the lowest latency communication channels between GPUs by directly using DMA operations over the PCI-Express bus to move information from one GPU to another. The domain of discrete particle diffusion is also difficult to express in the domain specific language that is provided by the automatic stencil frameworks. For example, Physis is optimized to operate on a periodic lattice of floating-point data types. Other works, such as PARTRANS [15], investigates single host, multi-GPU configurations as well. However, it is unable to have GPUs directly communicate as OpenCL lacks peer-to-peer GPU memory transfers. This multi-GPU implementation of the MPD-RDME algorithm has the additional benefit of bit-wise identical results with the single GPU version, which allows for trivial verification of correctness with respect to the single GPU implementation.

In principle, the aggregate arithmetic capabilities, memory capacities, and memory bandwidths provided by multi-GPU computers allow simulation of much larger biological systems than can fit onto a single GPU, as well as increasing simulation performance for smaller systems. Dynamic load balancing is used to tune the spatial decomposition in order to maximize performance, making optimal use of all GPU resources. In addition to assisting with increasing physical size, multi-GPU simulation is also helpful for reducing runtimes associated with increasing particle counts and larger numbers of reactions.

2. Methods

The adaptation of the MPD-RDME algorithm for parallel execution on multiple GPUs presents several challenges. First, the lattice must be dynamically distributed among GPUs using a spatial decomposition, which requires communication and synchronization to ensure data dependencies are satisfied. Next, MPD-RDME kernels must be modified to operate only on portions of the lattice at a time to facilitate concurrent overlap of communication with kernel execution. Finally, load balancing metrics need to be collected to optimize performance for inhomogeneous workloads and when utilizing accelerators with differing performance characteristics.

The majority of the kernel-level algorithms from the single GPU implementation [11] are kept intact during the process of moving to multiple GPUs. Only a few kernel modifications are required, as a GPU already performs work on a fine-grained level. Most of the challenges arise from efficiently performing the algorithm in a distributed memory environment.

2.1. Lattice Partitioning for Spatial Decomposition

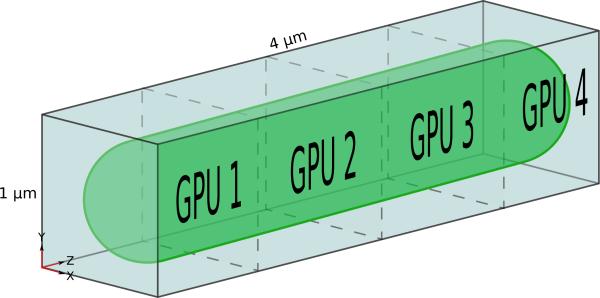
The lattice is stored in host memory as a 3-dimensional array, and when using a single GPU the lattice in GPU memory is laid out and sized identically. For multiple GPUs, as illustrated in Figure 1, the lattice is partitioned in one spatial dimension, creating a sublattice for each available GPU. The partitioning occurs in the z-dimension so that each sublattice is represented by a single contiguous memory region. The amount of data that must be communicated between adjacent sublattices is proportional to the cross-sectional area of the lattice when cut along the z-axis, therefore it is beneficial to performance to orient the simulated volume in a way that minimizes this area. Physically, E. coli cells are typically longer in one dimension, so the long axis of the bacterial cell is aligned with the lattice z-axis for the smallest cross-section. Other parallel decomposition schemes, such as a functional decomposition where diffusion and reactions are processed on different devices, would require that the full lattice be exchanged between devices at every step. A spatial decomposition allows for minimal data exchange, and distributing the lattice into the memory of multiple devices has the additional benefit of allowing for a lattice that would be too large for the on-board memory of any one GPU.

Figure 1.

Spatial decomposition of the RDME stochastic simulation onto four GPUs. The assigned GPU is responsible for storing and computing particle diffusions and reactions that occur within the region. Storing the lattice in distributed memory allows simulations of aggregate lattice sizes that exceed the memory capacity of a single GPU.

Each sublattice is extended to add an halo of lattice sites from each of the neighboring sublattices to account for diffusion on sublattice boundaries. The halo sites of each sublattice are redundantly calculated by the neighboring GPUs and allows the diffusion operator to be a communication-free operation, as all cells that the kernels must access are present in local GPU memory. At the end of every timestep, the halo sites are updated from the neighboring GPU. In the case of simulations with periodic boundary conditions, the first and last GPUs are also considered neighbors and their sublattices are extended as if they were adjacent.

The halo sites are redundantly simulated by both the GPU that “owns” that sublattice and the neighboring GPU. In order to preserve simulation consistency, random number generation for each stochastic event must be identical on both devices to arrive at the same outcome. To facilitate this, the random number generator is seeded with a combination of the current timestep and the index of the global lattice position. This is analogous to the single GPU implementation where the random seeds were derived from the global memory index of the lattice site. Using the global lattice position allows multiple GPUs to independently perform redundant work and arrive at identical results.

The lattice data structure has a finite number of particles that can be stored per site. It is possible that too many particles will need to occupy the same site and will have to overflow into a neighboring site. The list of overflow events must be examined every timestep to determine if there are any particles that must be relocated. The overflow list bu er is stored in host memory and is directly mapped into the GPU address space, enabling zero-copy memory accesses that fully overlap kernel execution and host-device memory transfers [16]. The use of the zero-copy scheme avoids the need for an explicit host-device memory copy to retrieve the overflow list thus improving performance, particularly when overflow exceptions are rare.

Parallel execution among GPUs is facilitated by a host thread that is spawned to control each GPU. A multi-threaded approach, as opposed to a multi-process approach, allows for efficient shared-memory communication between host threads, and avoids high GPU context switching overheads that would otherwise occur for multi-process access. The POSIX thread library provides mutexes and condition variables that are used for low-latency, inter-device synchronization and coordination via their controlling threads. Each thread is responsible for scheduling all kernel launches and memory transfers for its device. At the end of every timestep, the host threads perform a parallel sum reduction on the count of overflow events that occurred on the GPU during the timestep. If the sum is non-zero, sublattices are copied back to host memory for overflow resolution. The updated lattice is then returned to the GPUs, and simulation continues.

2.2. Hiding Inter-GPU Communication Latency

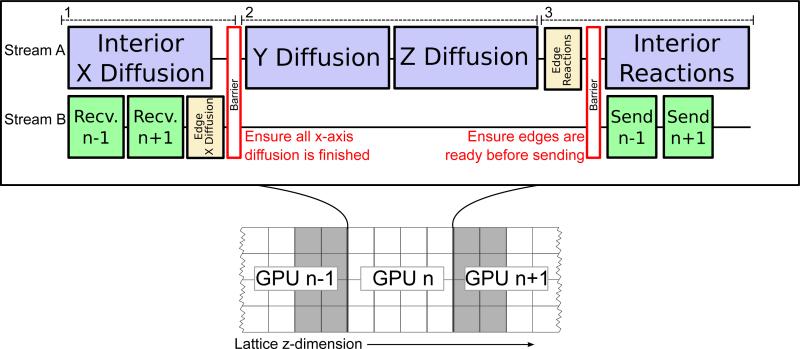
In order to reduce inter-GPU communication overhead, it is important to exploit the ability of the GPU hardware to overlap kernel execution with memory transfers [17, 18]. Before starting diffusion events, the halo sites of the sublattice must be updated with the current data from the neighboring GPU. Instead of waiting for any memory transfers to complete before beginning work, x-axis diffusion is broken into two separate parts. The first part is to compute x-axis diffusion events on the interior of the sublattice, and the second is x-axis diffusion in the halo regions. The interior diffusion events can be computed while performing the memory copies to update the halo. Once those memory transfers complete, the second part of x-axis diffusion performs updates on the halo region. Overlapping kernel execution and memory transfers requires the operations be performed in two independent asynchronous CUDA streams [19]. A CUDA stream is a queue of GPU operations such as kernel launches or memory transfers that are run in the order in which they are enqueued. The sequence of events across the two streams of every GPU is shown in Figure 2. In order to synchronize events between streams, a CUDA event is inserted in one stream, and a blocking operation waiting on that event is inserted into the other. We use this to block the execution of the y-axis and z-axis diffusion until both invocations of the x-axis kernel are complete. The y-axis and z-axis diffusion steps operate on the entire sublattice at once. The reaction kernel is also split in two parts. The first part computes reactions in sites that are halos in other sublattices, and the second part is the remaining interior of the sublattice. By computing the sites along the edge first, memory copies transferring that data to the neighboring GPUs can be overlapped with computation of the reactions on the interior.

Figure 2.

Execution of a timestep on each GPU is a three-phase process: On GPU n, the first phase processes x-axis diffusion on the interior (white area) of its sublattice while receiving the updated lattice state along the sublattice boundaries (gray) from neighboring GPUs (n – 1, n + 1). These operations are executed asynchronously on two CUDA streams to overlap peer-to-peer GPU memory copy operations with the computational kernels. X-axis diffusion is run on the sublattice edges once the receive operations complete. A stream/event barrier (red) synchronizes the two streams before continuing, ensuring that x-axis diffusion is complete across the entire sublattice and all memory transfers are complete. The second phase evaluates the y- and z-axis diffusion on the entire sublattice as sequential operations, and no communication with other GPUs is necessary. The third phase begins with the computation of reactions on the sublattice edges. The remaining sublattice interior is evaluated for reactions while the updated states of the two sublattice edges are asynchronously sent to the neighboring GPUs.

2.3. Host Machine NUMA Topology

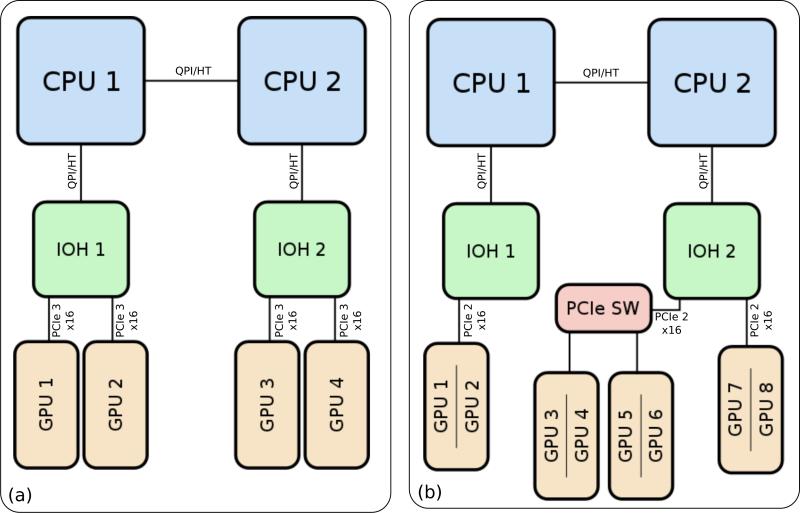
Modern computers are composed of a collection of tightly coupled network links that facilitate the movement of information between components. Figure 3 contains a block diagram illustrating the topological layout for the computers that were used in our multi-GPU performance analysis. The topology of the host machine must be considered as it has a strong influence on multi-GPU performance [20, 21]. Many multi-GPU computers contain multiple non-uniform memory access (NUMA) nodes and multiple I/O Hubs (IOH) to connect the host CPUs to the PCIe buses and other peripherals. NUMA describes the locality of memory to CPUs by defining a distance metric between processors and regions of memory with relation to how quickly a given processor can access that memory. Each IOH, like memory, also has an intrinsic locality in that there is similar non-uniformity in access times from different CPU sockets. There is a significant difference in the performance for transfers between a local GPU and a local memory bank, as opposed to a non-local GPU and a local memory bank, and furthermore, for a non-local GPU and a non-local memory bank [20, 21].

Figure 3.

Block diagrams of (a) A typical layout for a four GPU, dual IOH computer, and (b) an eight GPU node of the NCSA Forge cluster.

There are two methods for copying data between GPUs. The first method stages copies through host memory by copying the data from the source GPU to host memory and then copying from host memory to the destination GPU. The second method is direct peer-to-peer transfer, where the source GPU transfers data directly to the destination GPU over the PCIe bus. Peer-to-peer transfers require that participating GPUs support mapping of peer memory into their virtual address spaces and have associated hardware DMA support. When a GPU is able to directly access memory on a remote GPU as described above, the two GPUs are said to be “peered”. However, certain factors may prevent all GPUs from peering with each other. Non-peering GPUs are a result of multi-IOH computers which result in multiple roots in the PCIe bus topology. In these computers, direct memory transfers must traverse another internal network, e.g., HyperTransport (HT) or QuickPath Interconnect (QPI). Support for peer-to-peer transfers over HT exists, however there is currently no support for Intel-based chipsets that use QPI as an inter-processor network.

When GPUs are peered, halo sites are transferred directly to a bu er on the neighboring GPU after reactions are evaluated. A GPU only needs to perform a fast local memory copy to update its sublattice. If a pair of GPUs cannot be peered, communication between those devices must be bu ered through host memory. This can be transparently handled by the device driver and runtime library as an “unpeered” transfer, however we choose to handle it explicitly to control where the memory buffer is placed and to control the timing of the send and receive host-to-device memory copies that make up the exchange. The buffer is placed in host memory that is local to the receiving GPU, and is written to and read from with the CUDA asynchronous memory copy functions. To maximize the potential for peering of GPUs containing neighboring sublattices, it is important to map sublattices to GPUs such that communicating GPUs are under the same PCIe root whenever possible. This mapping reduces memory pressure caused by host memory accesses, thereby preventing the host memory controllers from becoming a communication bottleneck.

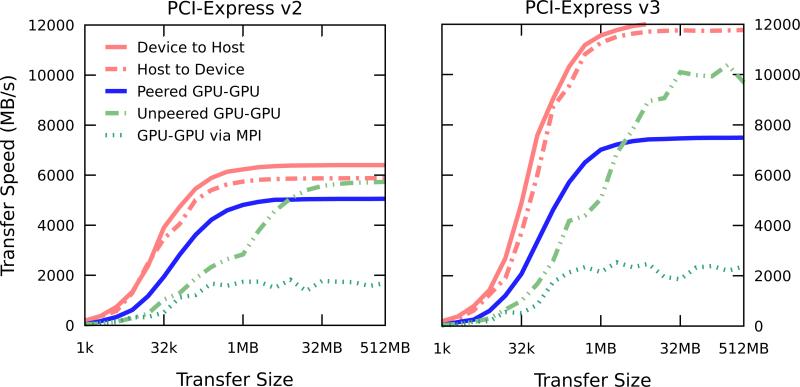
Figure 4 shows benchmarked data transfers for a range of payload sizes from host-to-GPU and between GPUs. A driver flag determined whether the GPUs link to the computer using the PCIe version 2 protocol or PCIe version 3 protocol. Each GPU has a full PCIe ×16 link to an IOH. When communicating with host memory, it is possible to fully utilize the bus as message sizes approach one megabyte in size. In PCIe 2 mode, we also start to observe peak throughput around this size for peered copies, but at a reduced rate. Non-peered PCIe 2 copies do not match the performance of peered copies as the copies are internally handled as a copy to host memory from the first GPU and then to the second GPU. However, the peered copy rate is lower than expected for PCIe 3, especially with respect to the PCIe 2 performance. This may not be a factor of the GPU hardware but may be a host machine chipset or driver anomaly that warrants further study. For comparison, an approach using MPI to do inter-process transfers with MPI Send and MPI Recv is shown to highlight potential gains in throughput from using direct peer-to-peer GPU memory transfers. In a latency-sensitive application, peered memory transfers are the best choice for inter-GPU communication.

Figure 4.

Inter-GPU and GPU-host memory copy speeds for PCIe 2.0 and PCIe 3.0 buses over a range of message sizes. Small transfers do not achieve high throughput due to being latency-bound. Larger transfers between the host and device are able to realize the full PCIe bandwidth. Direct peer-to-peer GPU memory copies o er higher bandwidth for smaller transfer sizes. Driver acceleration boosts unpeered GPU to GPU transfers, and we observe higher performance for those transfers than peered at large transfer sizes. The GPU-to-GPU transfer bandwidth for devices controlled by different MPI ranks is shown for comparison. MPI incurs high latency from copying data in host memory between rank processes as part of the GPU to GPU copy process. Tests were performed on a workstation containing a Supermicro X9DRG-QF motherboard with dual Xeon E5-2640 CPUs and four GTX680 GPUs using NVIDIA driver version 310.32 with the NVreg EnablePCIeGen3 option used to select between PCIe 2 and PCIe 3.

Memory copies to and from GPUs to the host memory lattice are optimized in regards to memory locality as well. The lattice is stored as a contiguous array of memory that can be directly indexed with the (x, y, z) coordinate for a site. Different GPUs access different slices of this array, so it is possible to optimize for NUMA locality here as well. Using the move pages Linux system call, we advise the kernel virtual memory subsystem to re-allocate slices of the lattice array to be physically stored in memory that will be local to the GPU that will be accessing it. The virtual memory addressing remains contiguous and the indexing into the array remains unchanged.

2.4. Capacity-Aware Heterogeneous GPU Load Balancing

By default, the lattice is partitioned into sublattices of equal sizes, presuming that all GPUs will complete their work at the same rate. To support instances when performance differs between GPUs, a dynamic load balancing approach is used to repartition the lattice among GPUs. At regular intervals, the load balancer compares the relative performance of each GPU. If a work imbalance is detected, the lattice is repartitioned to assign more lattice sites to GPUs that completed timesteps quicker than the other units.

One intuitive source of load imbalance arises in workstations where different models of GPUs are installed and some models are faster than others. The high performance GPU(s) are given larger sublattices compared to the lower performing GPUs. Another source of load imbalance can arise from spatial heterogeneity. Different densities of particles may be found in different spatial regions of the simulation, or some regions may have a larger number of reaction types that occur there, such as between mitochondria and cytoplasm. This localized area takes more time to compute, so smaller sublattices are given to those GPUs to compensate.

While the goal of load balancing is to equalize the runtime between heterogeneous GPUs, we must also consider available GPU memory when deciding how much of the lattice will be assigned to each GPU. Therefore, the load balancer must be aware of the memory capacity of each GPU and impose a constraint on the maximum size sublattice that each unit is able to support. In the case of a faster GPU with less device memory than other present GPUs, or in workstations with similarly-capable GPUs with different amounts of memory, a sub-optimal partitioning of the simulation may be necessary in order to avoid exceeding any GPU's memory capacity.

To assess the load balance across the system, the wall-clock time required to execute a timestep is collected and averaged for a batch of steps, which is then averaged among all GPUs to determine the mean compute time. The imbalance metric for a given GPU is its percentage difference from this mean time. A certain threshold for the imbalance metric must be crossed because the lattice cannot be divided at any arbitrary point along the z-axis. Only points that are integer multiples of the CUDA thread block size used for the z-dimension diffusion kernel are acceptable division points. Unless the sublattice is reduced by enough in the z-dimension, it does not result in a smaller CUDA thread block grid for the GPU to compute, because a partial block is still needed to cover the whole sublattice. Additionally, a partial block would also be needed on the neighboring GPU, resulting in more overall work.

3. Results

A number of variables affect the simulation performance of a single GPU and the parallel efficiency of multiple GPUs. The foremost factor affecting performance is the total number of lattice sites that result from the combination of the volume of the simulated cellular system and the choice of lattice spacing, which together determine the lattice dimensions. Since the multi-GPU algorithm detailed here uses a spatial decomposition, this is the one factor that our approach most directly addresses in our performance test simulations listed in Table 1. Other simulation parameters will have a noticeable e ect as well, such as the number of particles being simulated and the number of distinct reactions. We will explore the performance as a function of these parameters.

Table 1.

Description of performance test systems.

Representative Size	Physical Dimensions	Lattice Spacing	Lattice Dimensions	Timestep	Initial Particle Count
E. coli	1 μm × 1 μm × 2 μm	16 nm	64 × 64 × 128	50 μs	40,000
		8 nm	128 × 128 × 256	12.5 μs
Dividing E. coli	1 μm × 1 μm × 4 μm	16 nm	64 × 64 × 256	50 μs	80,000
		8 nm	128 × 128 × 512	12.5 μs
Yeast	4 μm × 4 μm × 4 μm	16 nm	256 × 256 × 256	50 μs	1,280,000
		8 nm	512 × 512 × 512	12.5 μs
Red Blood Cell	8 μm × 8 μm × 8 μm	16 nm	512 × 512 × 512	50 μs	10,240,000
		8 nm	1024 × 1024 × 1024	12.5 μs

Four different models with physical dimensions representative of various cellular systems were constructed at two lattice spacings, 16 nm and 8 nm. The number of particles were kept at a constant concentration for better comparability between systems. The initial particle count is assigned with species counts of A = C and B = D = 0. Diffusion constants for all species is 1 × 10^–12 m² s^–1. First-order reactions proceed at a rate of 1 s^–1 and second-order reactions at a rate of 1 × 10^–11 m^–1 s^–1.

3.1. Test Models

To evaluate multi-GPU performance as a function of lattice size, we have constructed a series of tests to mimic widely studied biological organisms of varying cell sizes, namely, E. coli, E.coli undergoing cell division, yeast, and red blood cells. For the purposes of comparison, each simulation assumes a spatially homogeneous volume with four different chemical species that interact via four reactions, A ⇋ B, B + C ⇌ D. The lattice data structure uses 32 bits for each site with four bits per particle and four bits for the site type. This configuration allows for as many as seven particles per site and for each site to be one of sixteen types, such as lattice sites representing the cytoplasm, membrane, or extracellular space. Our primary machine for performing the following performance tests is “Eir”, a dual-socket workstation with Intel Xeon E5-2640 six-core processors, with four NVIDIA GeForce GTX 680 GPUs, each attached to a dedicated PCIe 3.0 ×16 slot. To test larger biological systems with an increased quantity of GPU devices, we also made use of the NCSA Forge GPU cluster, comprised of compute nodes each containing two AMD Opteron 6136 “Magny-Cours” eight-core processors and eight NVIDIA Tesla M2070 GPUs. Finally, for tests of load balancing among heterogeneous GPUs, we used “Tokyo”, a dual-socket workstation with Intel Xeon X5550 4-core processors, with two NVIDIA Tesla K20c GPUs installed in dedicated PCIe 2 ×16 slots, and an external NVIDIA QuadroPlex 7000 chassis containing two NVIDIA Quadro 7000 GPUs cabled to a PCIe 2 ×16 slot. Hereafter, we refer to NVIDIA GeForce GTX 680 GPUs as “GTX680”, and NVIDIA Tesla M2070 GPUs as “M2070”.

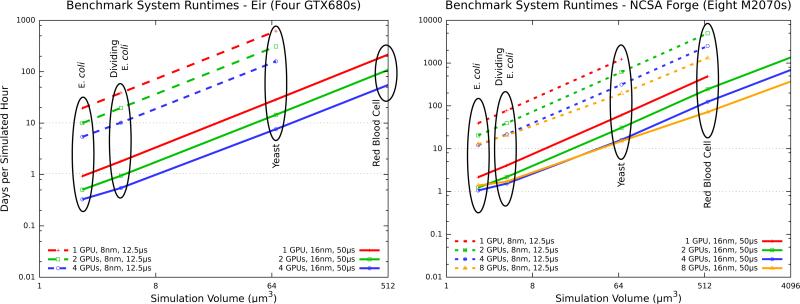
Each of the cellular test systems in Table 1 were run for a short simulated time and extrapolated to the wall time required for one simulated hour. The E. coli cell cycle is about one hour long, so it marks a reasonable goal for simulation length. The runtimes of the cellular performance test systems can be seen in Figure 5, and the achieved simulation runtime speed-ups are shown in Table 2. As the simulation volume increases, we observe a linear increase in runtime using a single GPU. Two and four GPUs provide a speedup over the single device, however for smaller volumes the benefit of four GPUs is less. Eight GPUs did not provide any speedup below 64 μm³ using a 16 nm lattice, but performs well for larger test systems. Note that tests using an 8 nm lattice spacing over a 16 nm lattice spacing also have a shorter timestep to conserve the diffusion coefficient values. Not only is the lattice eight times as large, but it also requires four times as many timesteps to achieve one simulated hour. We can see where the single-device limits begin to be overcome. With one M2070 GPU, it is not possible to simulate beyond 512 μm³ at 16 nm lattice spacing or beyond 64 μm³ with 8 nm lattice spacing. This is because the memory required exceeds the 6 GB on-board memory capacity of the M2070. The GTX680 GPU fares worse with its 2 GB on-board memory; even with four devices those limits can not be overcome. Multi-GPU computers make biological systems larger than E. coli possible, however very large cells are still not realizable on a single machine.

Figure 5.

Time required for simulating one hour of the performance test systems using multiple GPUs. Runtime grows with system volume in a nearly linear fashion. The simulations were run using four GTX680 GPUs and also with eight M2070 GPUs. The test systems are spatially homogeneous volumes simulating four reactions with four species (A ⇌ B, B + C ⇌ D) at constant density, with initial particle counts given in Table 1. Performance exhibits linear scaling as simulation volume increases on two and four GPUs, whereas using eight GPUs for the two smallest systems shows no benefit due to insufficient work per GPU.

Table 2.

Achieved n-fold speed-up from multi-GPU execution of benchmark systems.

Device	Spacing	GPUs	E. coli	Dividing E. coli	Yeast	Red Blood Cell
GTX680	16 nm	2	1.83	1.91	1.98	1.99
		4	2.84	3.30	3.78	3.91
M2070	16 nm	2	1.74	1.85	1.98	1.98
		4	2.04	2.64	3.79	3.91
		8	1.56	2.37	4.04	6.79
GTX680	8 nm	2	1.96	1.96	1.99	-
		4	3.61	3.81	3.88	-
M2070	8 nm	2	1.92	1.96	1.99	-
		4	3.27	3.59	3.91	-
		8	3.08	3.77	6.36	-

Large systems exhibit nearly linear scaling, with smaller systems performing well on lesser numbers of GPUs. For the red blood cell test, 8nm speed-up data is not available because it to large be run on one GPU for comparison.

3.2. Particle Concentration Affects Performance

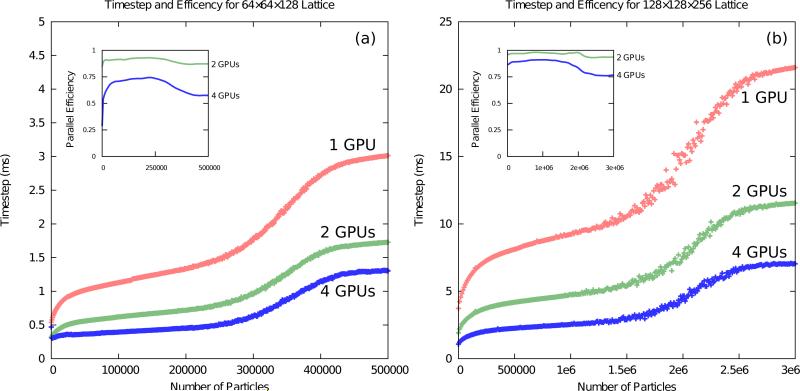
A greater number of particles in a simulation intuitively increases runtime. However, unlike volume, this relationship is not linear. At low particle counts there is little work to perform, but at high concentrations performance is strongly affected by site overflow exceptions because they are resolved by the CPU and involve additional serial overhead. We constructed a simulation to iteratively add particles to a fixed volume and chart performance, as shown in Figure 6. For a single GPU, runtime grows steeply at first until it nearly doubles. This can be explained by a work imbalance among blocks of each kernel launch. With low particle counts, some blocks are empty and they can be retired quicker than blocks that contain particles. After the initial rise, runtime grows linearly until site overflows begin to occur, and runtime exhibits a steep increase. At the upper-end of the second rise, overflows are occurring during every timestep and the cost of extra memory transfers to and from the host needed to resolve the overflow exceptions is a hindrance to simulation throughput.

Figure 6.

One, two, and four GPU performance and parallel efficiency as a function of mobile particles in the simulation. Graph (a) represents a simulation lattice of 64 × 64 × 128 and graph (b) is on a 128 × 128 × 256 lattice. Both simulated a single first-order reaction (A⇌B) with k_a→b = k_b→a = 1 s ⁻¹ and and D_A = D_B = 1 × 10⁻¹² m² s⁻¹. Every 100 steps, an additional 1000 copies of species A is randomly added into the volume. Inset shows the parallel efficiency achieved by multi-GPU execution. Runtime grows rapidly once lattice site overflows begin to occur, starting around 200,000 particles in (a) and 1.5 million in (b). Parallel efficiency drops due to increased serial work when handling overflows. Both tests were run on our “Eir” machine.

On multiple GPUs, the performance curve is similar, however the initial rise is flattened due to the grid size being smaller, and the linear growth is not as steep. As can be seen on the inset graphs of Figure 6, the parallel efficiency is maximal after the initial rise and remains steady until overflows start to occur. A spatial decomposition results in a distribution of particles among the sublattices and spreads the work among devices. The use of multiple GPUs is an effective approach for countering additional runtime as simulation particle counts increase.

3.3. Reactions in a Lattice Site are Independent of all Other Sites

Particles may only interact with other particles that are present in the same lattice site, and all sites can be processed independently as communication with neighboring sites is not required. With ideal load balancing, we expect linear performance gains from the use of multiple GPUs for computing reactions because the lattice sites are distributed among devices. However, quantifying the wall-clock cost of reactions is difficult. Not only is the performance determined by the number of reactions in the kinetic model, but the rate at which the reactions proceed and the number of substrate particles in the simulation also affect timings.

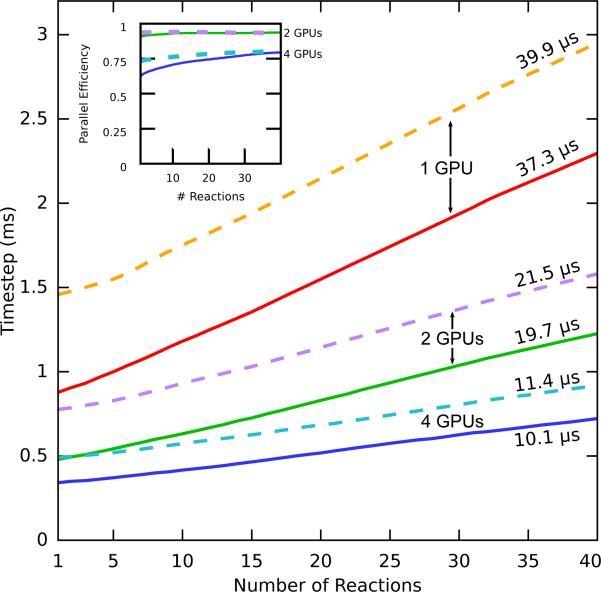
Consider the following test case to examine the effect from the quantity of reactions. Similar to the particle simulation test described above, a simulation was constructed to iteratively add one reaction and chart performance. All reactions are first-order reactions with a rate of 1 s⁻¹. Examining the slopes of the curves in Figure 7, it can be seen that for a system containing 100, 000 particles that runtime per timestep increases at a rate of 40 μs per reaction for a single GPU. When compared against the slopes of multi-GPU runs, the rate of growth is cut proportionally by the number of devices. With multiple GPUs, efficiency remains constant when increasing the quantity of reactions. The use of multiple GPUs is a therefore a key strategy for evaluation of large reaction networks.

Figure 7.

Linear time complexity of reaction processing can be seen in the comparison of simulation timestep lengths for varying quantities of distinct reaction types. A test system with 10,000 particles (solid lines) and another with 100,000 particles (dashed lines) were simulated in a 64 × 64 × 128 lattice with an increasing number of first-order reactions. Evaluating the slope of the regression line (written above the graph lines) serves as a metric for the growth in runtime from adding one more reaction. Multiple GPUs are effective at reducing this increase as the number of reactions increases. Each system was run on GTX680 GPUs on “Eir”.

3.4. Parallel Efficiency

The overall parallel efficiency of multi-GPU execution is affected by three factors: redundant computation, communication overhead, and inter-device synchronization. We can examine efficiency by considering the scalability of the three separate diffusion kernels and the reaction kernel separately. Redundant computations are performed by the x- and y-dimension diffusion kernels for the halo sites. Since the spatial decomposition is along the z-axis, the z-axis diffusion kernel only needs to read the halo sites but does not need to update them. Reactions are local to a lattice site and therefore the reaction kernel only needs to update sites in its sublattice and not the halo.

Ideally, communication overhead is negated by the ability to overlap computation and communication across multiple CUDA streams. This scheme imposes a deadline on computation such that overlapped communication can be considered free as long as the time required for the communication to complete does not exceed the time it takes to run the computation. The communication volume with each neighbor is 2×L_x×L_y lattice sites in size. For example, a lattice of dimensions 64 × 64 × 128 using a 32-bit site requires that 32 kB must be transferred to each neighbor. The profiled peer-to-peer transfer time for this copy size is on average 4.7 μs, which is shorter than either computation kernel that the communication overlaps with.

An added source of overhead is the parallel reduction that occurs after each timestep across all GPU threads for overflow detection. Each sublattice must be fully processed before the reduction on the number of overflow events can occur. This exposes any potential work imbalance as idle time for other threads. The synchronization requires more time as more devices are added, however adding devices decreases the time to compute the timestep. This results in an increased fraction of timestep run time that is spent on the barrier synchronization. This can be seen in profiling, and the per-operation times are described in Table 3.

Table 3.

Average kernel and message transfer times as reported by nvprof for the 64 × 64 × 128 and 128 × 128 × 256 benchmarks with GTX680s on “Eir”.

Lattice Dimensions	GPUs	Recv	X	Xedge	Y	Z	R	Redge	Send	Barrier	Timestep
64 × 64 × 128	1	-	22%	-	28%	28%	22%	-	-	-	1110 μs
64 × 64 × 128	2	.1%	21%	3%	27%	26%	18%	4%	1%	1%	615 μs
64 × 64 × 128	4	.2%	17%	5%	22%	21%	13%	6%	2%	14%	405 μs
128 × 128 × 256	1	-	24%	-	26%	27%	26%	-	-	-	5820 μs
128 × 128 × 256	2	.3%	23%	1%	26%	26%	24%	2%	1%	1%	3000 μs
128 × 128 × 256	4	.5%	22%	2%	25%	25%	21%	3%	2%	5%	1620 μs

X, Y, and Z represent respective diffusion kernel runtimes, and R represents reaction kernel runtime. X_edge and R_edge denote runtimes for the edge kernels. Send and receive times are included, however as they overlap with kernel execution, their time is not reflected in the timestep time. The edge kernels take the same amount of time to run regardless of the number of GPUs as the lattice volume that they operate on is fixed. The edge kernel time, along with the increasing average barrier time, are limits to scalability as GPU count increases.

3.5. Load Balancing

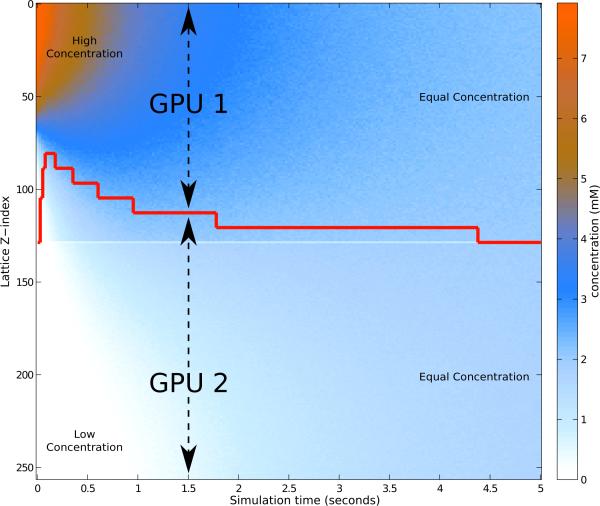
To demonstrate the ability to react to changes in workload due to the dynamics of the simulation, we constructed a model of simple diffusion across a barrier. A lattice of 128×128×256 with 16 nm lattice spacing is initialized with 500,000 particles in the upper quarter, and a barrier to slow down diffusion is placed in the middle of the simulated volume. The diffusion coefficient for the particles is 1 × 10⁻¹³ m² s⁻¹ in the barrier and 1 × 10⁻¹² m² s⁻¹ elsewhere. When run on two GPUs, the initial division of labor assigns the upper-half to the first GPU and the lower-half to the second. In this case, there are no reactions, so the work that a GPU must perform is correlated to the size of the sublattice that it must process and the number of particles located in that sublattice. Initially, work is imbalanced as the lower-half contains zero particles. As the simulation progresses, as seen in Figure 8, the distribution of particles begins to spread out in the upper-half, and around t = 0.5, particles begin to enter the lower-half. The red line in the figure represents how the volume is split into the sublattices for the two GPUs, and how the change in particle density over time causes those sublattices to be reshaped to better distribute the work. Every 25 ms the relative computation time is compared, and any imbalance is detected. The lattice distribution between devices is shifted to give a larger sublattice to the lower device, thus giving it a volume with particles to compute diffusion for. As the particles diffuse and become more uniformly distributed, the load balancer incrementally shifts to equalize work. Towards the end of the simulation, the particles are sufficiently distributed that the lattice is equally divided between the two GPUs.

Figure 8.

Load balancing distribution over time for a diffusion simulation on two GPUs. The time-varying spatially heterogeneous concentration of particles is represented in the graph with the vertical axis corresponding to lattice z-dimension, and color corresponding to particle concentration in that lattice plane. At t = 0, all of the particles are in the upper quarter of the volume, and a barrier in the center slows the flow of particles into the lower half of the volume. The red line indicates the spatial division of the lattice between the two GPUs over time as the load balancer reassigns work in response to changing particle densities.

The other application for load balancing is for handling GPU heterogeneity. In machines that have GPUs of differing computational ability, load balancing can help minimize runtime by assigning a larger portion of the lattice to faster devices. To test this aspect, we constructed “Tokyo”, a test machine containing two Tesla K20c cards and two Quadro 7000 cards, as described above. Running the large 16 nm “blood” performance test, load balancing boosted the simulation rate from 1.6 simulated seconds per hour to 2.1 seconds per hour, a 32% increase in throughput and would be a savings of 22 days to compute one full hour.

4. Case Study: Cell Division Regulation

The Min protein system of E. coli regulates the division process of the cell. This protein system has been well studied using both experimental and computational methods [22, 23, 24]. We use it as a case-study with increased complexity arising from the heterogeneity of the reactions. The system consists of three proteins, MinC, MinD, and MinE. MinD, upon phosphorylation, self-catalytically binds to the cell membrane, while MinE attaches to membrane-bound MinD and causes dephosphorylation, resulting in detachment. MinC attaches to membrane-bound MinD and inhibits FtsZ polymerization, which prevents cell constriction in those areas. One hallmark characteristic of this system is the periodic oscillation of MinD. The observation is that the reduced presence of the species in the center of the cell is what drives the location of cell constriction for division.

As bacteria undergoing cell division are elongated, the simulation volume is larger than our previous experiments on E. coli, allowing us to leverage the performance from multiple GPUs. Additionally, since we wish to capture the motion over a long period of time, multi-GPU execution helps realize this quickly.

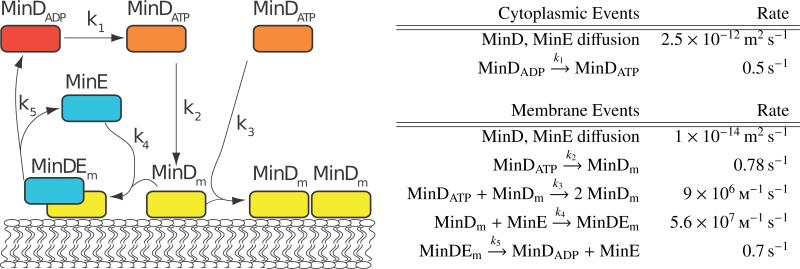
The simulation uses a 4 μm long E. coli cell undergoing cell division. The cell membrane geometry is constructed from a 3 μm long cylinder with a 1 μm diameter, and 1 μm diameter hemispheres on both ends. The model is discretized to a simulation lattice of dimensions 64 × 64 × 256 with 16 nm spacing, and simulated with a timestep of 50 μs. The kinetic model is adapted from Fange and Elf [23], which includes only experimentally known interactions between the Min proteins and is capable of replicating the characteristic features of the Min system. The implemented reactions can be seen in Figure 9 with their corresponding rate constants and diffusion coefficients. When the simulation starts, the initial species are randomly distributed within the cytoplasmic space, and no proteins are initially on the membrane. The amount of MinD present is equally split between MinD_ADP and MinD_ATP species with 1758 particles each. MinE has an initial count of 914 particles.

Figure 9.

Min protein system schematic and simulation parameters for the simplified model. Rates are shown for diffusion and reaction events. There are two site types in this simulation, cytoplasm and membrane. Each species has a specific diffusion rate within each site type, and reactions can progress at different rates (or not occur at all) depending on the site. The particle counts for t = 0 are shown in the right-hand table.

As the Min system involves reactions both on the membrane surface as well as the cytoplasm interior, we had to alter the set-up used in previous benchmarks. The out-most layer of lattice sites are designated as a distinct type (membrane) from the inner region of the cell. Unbound proteins can freely move between the two types of sites, but complexes associated to the membrane (designated with a subscript m) may only diffuse between membrane sites. With the exception of MinD phosphorylation which occurs in cytoplasmic sites, all other reactions occur within the membrane sites of the lattice.

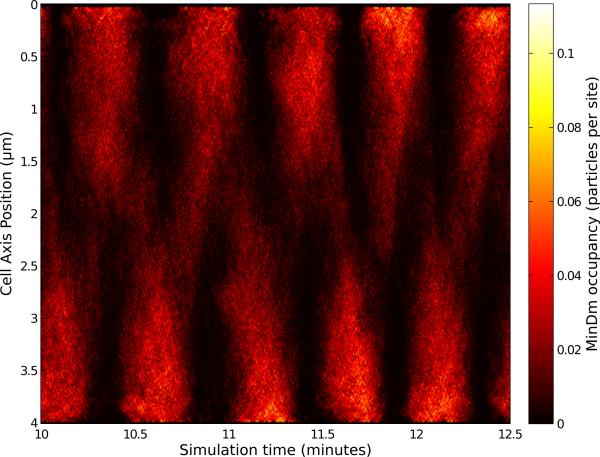
Even though the simulation is purely stochastic, the expected macroscopic time evolution of the system with the oscillatory behavior of the membrane-bound species is observed. In Figure 10, we track the location of MinD_m proteins along the cell over time, and present the average occupancy in terms of number of particles present versus the number of membrane lattice sites. The end to end oscillations are clearly visible.

Figure 10.

Periodic oscillations of the membrane bound MinD_m species can be seen in a space-time plot of the average occupancy. The occupancy is calculated from the number of proteins present within a plane along the z-axis divided by the number of membrane sites in that plane.

A single GTX680 GPU is able to simulate the Min system at a rate of 134 simulated seconds per wall-clock hour on the “Eir” machine described above. Using two and four GPUs we achieve a simulation rate of 249 and 384 seconds per hour, respectively. Comparing back to the benchmark systems discussed earlier, the speed-up shown in Table 2 for the dividing E. coli family was 1.91 and 3.30 for two and four GPUs. On this system, we observe speedups of 1.86 and 2.87. The parallel efficiency is lower but the overall simulation rate is higher – it would take only a bit over a day to compute a full hour of the simplified Min system as opposed to nearly two days for the benchmark model. With an initial count of 4430 particles and a lattice that contains one million sites, the expected concentration of particles per site is low. As some species are restricted to the membrane sites, the concentrations are locally higher in those areas of the lattice. This is still less than the 80,000 particles that were present in the benchmark test of the same lattice size. Refer back to Figure 6 and note the strong initial increase in runtime with added particles. While the Min system has more reactions than the benchmark, it is not a significant increase as compared to the additional runtime from the difference in particle counts. The benchmark systems, although lacking heterogeneity, are reasonable performance predictors for actual systems one wishes to study.

5. Discussion and Conclusion

We have shown that a one-dimensional spatial decomposition of the simulation lattice is an effective approach for use with the MPD-RDME operator implemented by the previous Lattice Microbes software [4]. Leveraging a moderate number of GPUs in a workstation, it enables effective use of advanced GPU hardware features such as peer-to-peer memory transfers for reducing communication bottlenecks via host memory by careful consideration of the overall hardware topology. Multiple GPUs help stem rising runtimes associated with the increase in physical size of the simulated biological system, with the addition of increased particle counts, and with the increased complexity from adding more reaction types to the simulation. We optimize performance via dynamic load balancing that can make efficient use of GPUs that have different levels of computational power, and adapt to performance changes and heterogeneity of work in the underlying simulation.

Practical matters involved in GPU hardware design and production costs are expected to begin favoring products that incorporate multiple GPU chips on a single circuit board. One of the key GPU performance characteristics, global memory bandwidth, is determined in part by the number of external pins on the GPU chip package, which is limited by the surface area of the GPU chip package. It is easy to see that for applications like Lattice Microbes, in which performance is ultimately bound by global memory bandwidth, that GPU products that incorporate multiple GPU chips per board can o er potentially greater performance per unit volume or per PCIe slot than single-chip GPU designs, at the cost of additional programming complexity.

Looking forward, although we expect that individual GPU performance will continue to increase, the computation rates required to maintain reasonable turnaround times for simulation of biological cells will eventually exceed the capabilities of multi-GPU workstations. Such challenging simulations will ultimately require the development of a new distributed memory parallelization layer for execution on large GPU clusters and supercomputers. Maintaining good parallel efficiency on distributed memory computers will require a multi-dimensional parallel decomposition scheme to provide a distributed memory implementation with sufficiently fine-grained work decomposition to exploit a large number of single- or multi-GPU compute nodes. Other challenges that will need to be solved for efficient scaling of a distributed memory parallel implementation include maximizing the use of advanced GPU and networking hardware features that enable zero-copy RDMA data transfers between GPUs on different nodes, and the development of efficient mechanisms for strided memory transfers for sublattice boundary exchanges when using 2-D or 3-D spatial decompositions.

Finally, the remaining major challenge will be handling lattice site overflow events in a distributed memory environment. We plan to first parallelize the process by allowing GPUs to resolve overflows without the CPU involvement. For situations where multiple sublattices are within the particle replacement search radius, a vote will need to be tal-lied on which volume can accommodate the particle at the smallest distance from the location where the exception occurred.

While the methods described here were applied to parallelization of Lattice Microbes over multiple GPUs, many of the approaches taken here are directly applicable to other grid-based calculations with similar nearest-neighbor data dependency patterns between grid cells. By segregating neighbor-dependent cells from independent cells and allowing the hardware to perform memory copy operations concurrently with calculations, highly efficient scaling onto multiple GPUs can be achieved.