Modeling delay in genetic networks: From delay birth-death processes to delay stochastic differential equations

Abstract

Delay is an important and ubiquitous aspect of many biochemical processes. For example, delay plays a central role in the dynamics of genetic regulatory networks as it stems from the sequential assembly of first mRNA and then protein. Genetic regulatory networks are therefore frequently modeled as stochastic birth-death processes with delay. Here, we examine the relationship between delay birth-death processes and their appropriate approximating delay chemical Langevin equations. We prove a quantitative bound on the error between the pathwise realizations of these two processes. Our results hold for both fixed delay and distributed delay. Simulations demonstrate that the delay chemical Langevin approximation is accurate even at moderate system sizes. It captures dynamical features such as the oscillatory behavior in negative feedback circuits, cross-correlations between nodes in a network, and spatial and temporal information in two commonly studied motifs of metastability in biochemical systems. Overall, these results provide a foundation for using delay stochastic differential equations to approximate the dynamics of birth-death processes with delay.

INTRODUCTION

Gene regulatory networks play a central role in cellular function by translating genotype into phenotype. By dynamically controlling gene expression, gene regulatory networks provide cells with a mechanism for responding to environmental challenges. Therefore, creating accurate mathematical models of gene regulation is a central goal of mathematical biology.

Delay in protein production can significantly affect the dynamics of gene regulatory networks. For example, delay can induce oscillations in systems with negative feedback,^{1, 2, 3, 4, 5, 6, 7} and has been implicated in the production of robust, tunable oscillations in synthetic gene circuits containing linked positive and negative feedback.^{8, 9} Indeed, delayed negative feedback is thought to govern the dynamics of circadian oscillators,^{10, 11} a hypothesis experimentally verified in mammalian cells.¹²

In genetic regulatory networks, noise and delay interact in subtle and complex ways. Delay can affect the stochastic properties of gene expression and hence the phenotype of the cell.^{2, 13, 14, 15, 16} It is well known that noise can induce switching in bistable genetic circuits;^{17, 18, 19, 20, 21, 22, 23, 24, 25, 26} the infusion of delay dramatically enhances the stability of such circuits²⁷ and can induce an analog of stochastic resonance.^{28, 29} Variability in the delay time (distributed delay) can accelerate signaling in transcriptional signaling cascades.³⁰

Given the importance of delay in gene regulatory networks, it is necessary to develop methods to simulate and analyze such systems across spatial scales. In the absence of delay, it is well known that chemical reaction networks are accurately modeled by ordinary differential equations (ODEs) in the thermodynamic limit, i.e., when molecule numbers are sufficiently large. When molecule numbers are small, however, stochastic effects can dominate. In this case, the chemical master equation (CME) describes the evolution of the probability density function over all states of the system. Gillespie's stochastic simulation algorithm (SSA)³¹ samples trajectories from the probability distribution described by the CME.

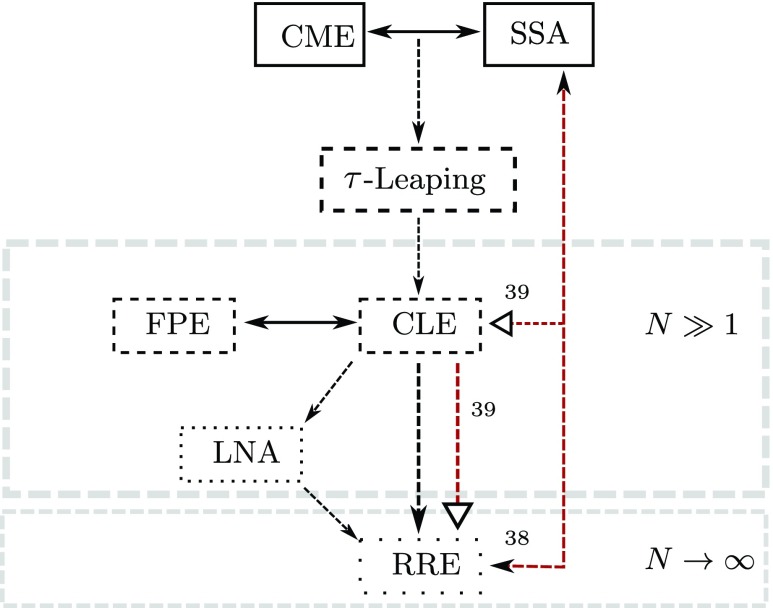
While exact, the CME is difficult to analyze and the SSA can be computationally expensive. To address these issues, a hierarchy of coarse-grained approximations of the SSA has been developed³² (see Figure 1): Spatially discrete approximations, such as τ-leaping^{33, 34, 35, 36} and K-leaping³⁷ trade exactness for efficiency. At the next level are chemical Langevin equations (CLEs), which are stochastic differential equations (SDEs) of dimension equal to the number of species in the biochemical system. CLEs offer two advantages. First, unlike the SSA, the well-developed ideas from random dynamical systems and stochastic differential equations apply to CLEs. Second, it is straightforward to simulate large systems using CLEs. Finally, in the thermodynamic limit, one arrives at the end of the Markovian hierarchy: the reaction rate equation (RRE).

Figure 1.

Schematic of the modeling hierarchy for biochemical systems. The black arrows link the various components of the theory for Markov systems (no delay); red arrows link the corresponding delay components. Numbers attached to arrows refer to papers that establish the corresponding links. Empty arrowheads denote heuristic derivations; in this paper, we rigorously establish the dSSA to dCLE and dCLE to dRRE links.

The Markovian hierarchy above (no delay) is well-understood,^{32, 40} but a complete analogue of the Markovian theory does not yet exist for systems with delay. The SSA has been generalized to a delay version – the dSSA – to allow for both fixed^{2, 41} and variable^{30, 38} delay. Notably, the modification of the SSA to incorporate non-Markov processes predates the dSSA;⁴² here, many exponential steps from a linear chain are replaced by a gamma-distributed delay. Some analogues of τ-leaping exist for systems with delay; see, e.g., D-leaping.⁴³

Several methods have been used to formally derive a delay chemical Langevin equation (dCLE) from the delay chemical master equation (dCME); see Sec. 4 for details. Brett and Galla³⁹ use the path integral formalism of Martin, Siggia, Rose, Janssen, and de Dominicis to derive a dCLE approximation without relying on a master equation. The Brett and Galla derivation produces the “correct” dCLE approximation of the underlying delay birth-death (dBD) process in the sense that the first and second moments of the dCLE match those of the dBD process. However, their derivation has some limitations (see Sec. 4). In particular, it gives no rigorous quantitative information about the distance between the dBD process and the dCLE; it does not clarify for what types of deterministic dynamics (in the thermodynamic limit) the dCLE accurately approximates the delay birth-death process, and on what timescales; and it does not clarify in what sense (distributionally or pathwise) the dCLE approximates the delay birth-death process. Our analysis answers these questions.

In this paper, we establish a rigorous link between dBD processes and dCLEs by proving that the distance between the dBD process and the correct approximating dCLE process converges to zero as system size tends to infinity (as measured by expectations of functionals of the processes). In particular, this result applies to all moments. It is natural to express distance in terms of expectations of functionals because the dBD process is spatially discrete while the correct dCLE produces continuous trajectories (see Figure 2). This first result is just a corollary of our main mathematical theorem. We rigorously estimate the probability that a trajectory of the correct dCLE remains inside a narrow tube around the corresponding trajectory of the dBD process. This quantitative tube estimate will allow practitioners to determine the accuracy of simulations of concrete biochemical reaction networks. The mathematical results hold for both fixed delay and distributed delay (see Figure 3a).

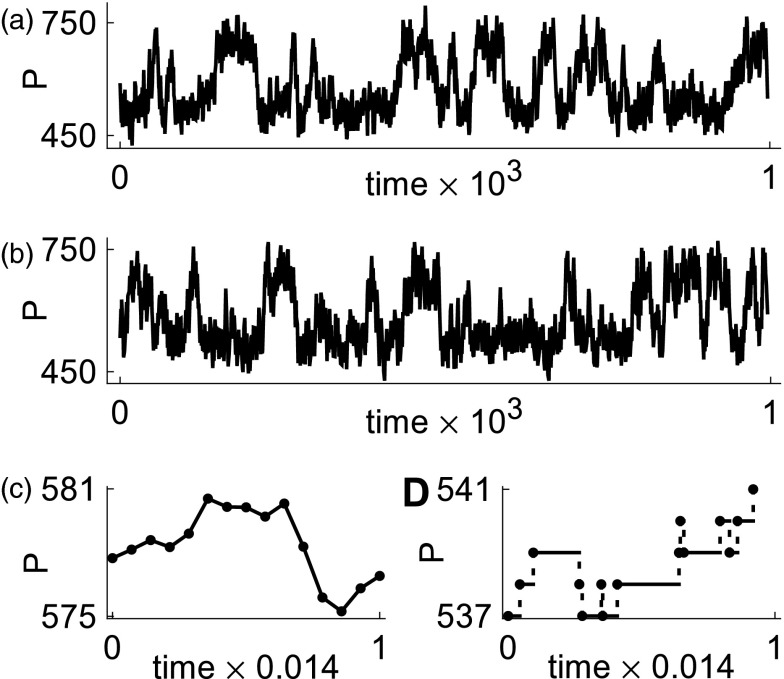
Figure 2.

(a) Typical trace obtained by using the dCLE. (b) Corresponding trace obtained using dSSA. By zooming into a small time segment, we see that the trace obtained from the dCLE (c) consists of equi-spaced time points (corresponding to an Euler discretization) and is continuous. The corresponding segment of the trace from the dSSA (d) consists of events that occur at random times and has jump discontinuities. The displayed traces were gathered after a long transient. The model simulated is the single-gene positive feedback model with N = 500; see Sec. 2C1.

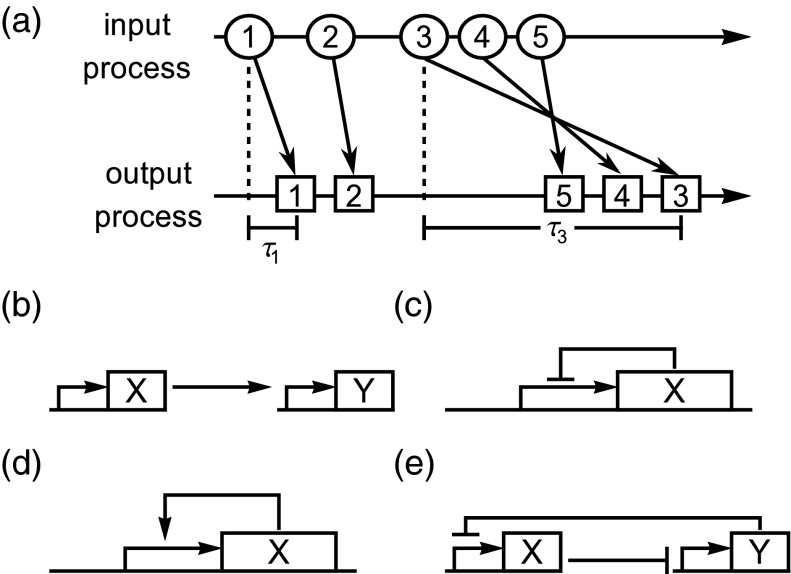
Figure 3.

(a) The effect of distributed delay on the protein production process. The “input process” is the first step in the transcription process, while the “output process” is the final mature product that enters the population. The time delay τ accounts for the lag between the initialization of transcription and the production of mature product. In a system with distributed delay, different production events can have different delay times; the order of the output process may therefore not match that of the input process. (b)–(e) Simulated gene regulatory network motifs: a transcriptional cascade (b), oscillators (c), and metastable systems (d) and (e).

The correct dCLE approximation is distinguished within the class of Gaussian approximations of the dBD process by the fact that it matches both the first and second moments of the dBD process. As we will see, it performs remarkably well at moderate system sizes in a number of dynamical settings: steady state dynamics, oscillatory dynamics, and certain metastable switches. We will demonstrate via simulation and argue mathematically using characteristic functions that no other Gaussian process with appropriately scaled noise performs as well. In the following, the term “dCLE” shall refer specifically to the dCLE derived by Brett and Galla³⁹ and expressed by 15, unless specifically stated otherwise. We provide a proof of our mathematical results in the supplementary material.⁴⁴

SIMULATIONS/OUTLINE AND INTERPRETATION OF RESULTS

Genetic regulatory networks may be simulated using an exact dSSA to account for transcriptional delay.^{2, 30, 38, 41} Here, we provide a heuristic derivation of a related dCLE, and show that in a number of concrete examples it provides an excellent approximation of the system (see Figure 3). These simulations raise the following questions: Is the dCLE approximation valid in general? Can the expected quality of the approximation be quantified in general? We answer these questions mathematically in Sec. 3.

We will adopt the following notation for reactions with delay:

$$X+Y\underset{\mu }{\overset{\alpha (X,Y)}{⇢}}Z.$$

Here, α(X, Y) denotes the rate of the reaction, the dashed arrow indicates a reaction with delay, and μ is a probability measure that describes the delay distribution. Solid arrows indicate reactions without delay.

A transcriptional cascade

First, we consider a transcriptional cascade with two genes that code for proteins X and Y. Protein X is produced at a basal rate; production of Y is induced by the presence of X. The state of the system is represented by an ordered pair (X, Y). Note that we use X and Y to denote both protein names and protein numbers. The reactions in the network, and the associated state change vectors v_i, are given by

$$\begin{array}{cc}\hfill \varnothing \underset{\mu }{\overset{a}{⇢}}X& v_1=(1,0),\hfill \end{array}$$ (1)

$$\begin{array}{cc}\hfill X\stackrel{b_{1}X}{\to }\varnothing & v_2=(-1,0),\hfill \end{array}$$ (2)

$$\begin{array}{cc}\hfill \varnothing \underset{\mu }{\overset{\psi \left(X\right)}{⇢}}Y& v_3=(0,1),\hfill \end{array}$$ (3)

$$\begin{array}{cc}\hfill Y\stackrel{b_{2}Y}{\to }\varnothing & v_4=(0,-1).\hfill \end{array}$$ (4)

This system can be simulated exactly using the dSSA: Suppose the state of the system and the reactions in the queue are known at time t₀ (the queued reactions can be thought of as the “input process”; see Figure 3a), and that the delay kernel μ is supported on a finite interval [0, τ₀].⁴⁵

1. Sample a waiting time t_w from an exponential distribution with parameter $A_0:=a+b_{1}X+\psi \left(X\right)+b_{2}Y$.

2. If there is a reaction in the queue that is scheduled to exit at time t_q < t₀ + t_w, advance to time t_q and set t₀ → t_q and $(X,Y)\mapsto (X,Y)+(v_i^{\left(1\right)},v_i^{\left(2\right)})$, where $v_i=(v_i^{\left(1\right)},v_i^{\left(2\right)})$ is the change in the system due to the scheduled reaction. Finally, sample a new waiting time for the next reaction.

3. If no reaction exits before t₀ + t_w, set t₀↦t₀ + t_w and sample a reaction type from the set {1, 2, 3, 4} with probabilities proportional to {a, b₁X, ψ(X), b₂Y}, respectively. If the reaction chosen is a non-delayed reaction, perform the update (X, Y) ↦ (X − 1, Y) (or (X, Y) ↦ (X, Y − 1)). However, if the reaction chosen is a delayed reaction, the state change vector (1, 0) (or (0, 1)) is put into the queue along with an exit time t_q. The difference τ = t_q − t₀ between the current and the exit time is sampled from the delay distribution μ.

We now heuristically derive the dCLE for the feed-forward system from this spatially discrete process.

Suppose the delay kernel μ is given by a probability density function κ supported on [0, τ₀] (dμ(s) = κ(s)ds). We first approximate the number of reactions that produce Y (Eq. 3) that will be completed within the interval [t₀, t₀ + Δ], where t₀ denotes the current time and Δ is a small increment. Since the production of Y involves delay, a reaction of this type that is completed within [t₀, t₀ + Δ] must have been initiated at some time within [t₀ − τ₀, t₀]. Let t₀ > t₀ − Δ > t₀ − 2Δ > ⋯ be the partition of [t₀ − τ₀, t₀] into intervals of length Δ. The (random) number of reactions completed within [t₀, t₀ + Δ] and initiated within [t₀ − (i + 1)Δ, t₀ − iΔ] may be approximated by a Poisson random variable with mean

$$\psi \left(X_{t_0-(i+1)\Delta }\right)\Delta ·\kappa \left((i+1)\Delta \right)\Delta .$$

Summing over i, the (random) number of reactions completed within [t₀, t₀ + Δ] may be approximated by a Poisson random variable with mean

$$\Delta \sum _i\left[\psi \left(X_{t_0-(i+1)\Delta }\right)\left(\kappa \left((i+1)\Delta \right)\Delta \right)\right];$$

this is a Riemann sum that approximates the integral

$$\Delta {\int }_0^{{\tau }_0}\psi \left(X_{t_0-s}\right)\kappa \left(s\right)\mathrm{d}s.$$

Known as τ-leaping, this line of reasoning produces a Poissonian approximation of the dBD process

$$\begin{array}{cc}\hfill \delta X_t& =\mathrm{Poisn}\left(a\Delta \right)-\mathrm{Poisn}\left(b_1{X}_t\Delta \right),\hfill \\ \hfill \delta Y_t& =\mathrm{Poisn}\left(\Delta {\int }_0^{{\tau }_0}\psi \left(X_{t-s}\right)\mathrm{d}\mu \left(s\right)\right)-\mathrm{Poisn}\left(b_2{Y}_t\Delta \right).\hfill \end{array}$$

Here, $\mathrm{Poisn}\left(\eta \right)$ denotes a Poisson random variable with mean η.

If these Poisson random variables have large mean, they can be approximated by normal random variables. For example, the Poisson variable representing the number of reactions that produce Y can be approximated by a normal random variable with mean and variance equal to $\Delta {\int }_0^{{\tau }_0}\psi \left(X_{t-s}\right)\mathrm{d}\mu \left(s\right)$. Since each reaction changes the state of either X or Y (but never both), it follows that the evolution of the system can be approximated by the stochastic difference equation

$$\begin{array}{cc}\hfill \delta X_t& =\Delta (a-b_1{X}_t)+\sqrt{\Delta (a+b_1{X}_t)}\mathcal{N}(0,1),\hfill \end{array}$$ (5a)

$$\begin{array}{ccc}\hfill \delta Y_t& =& \Delta \left({\int }_0^{{\tau }_0}\psi \left(X_{t-s}\right)\mathrm{d}\mu \left(s\right)-b_2{Y}_t\right)\hfill \\ & & +\sqrt{\Delta \left({\int }_0^{{\tau }_0}\psi \left(X_{t-s}\right)\mathrm{d}\mu \left(s\right)+b_2{Y}_t\right)}\mathcal{N}(0,1),\hfill \end{array}$$ (5b)

where $\mathcal{N}(0,1)$ is the standard normal random variable.

System 5 may be written in terms of concentrations. Let N be a system size parameter. We think of N as a characteristic system size; X_t/N and Y_t/N therefore represent fractions of this characteristic value. Writing x_t = X_t/N, y_t = Y_t/N, $\tilde{\psi }\left(x\right)=\psi \left(Nx\right)/N$, and assuming that the basal production rate a scales with N as $a=\tilde{a}N$, we obtain

$$\begin{array}{cc}\hfill \delta x_t& =\Delta (\tilde{a}-b_1{x}_t)+\frac{1}{\sqrt{N}}\sqrt{\Delta (\tilde{a}+b_1{x}_t)}\mathcal{N}(0,1),\hfill \end{array}$$ (6a)

$$\begin{array}{ccc}\hfill \delta y_t& =& \Delta \left({\int }_0^{{\tau }_0}\tilde{\psi }\left(x_{t-s}\right)\mathrm{d}\mu \left(s\right)-b_2{y}_t\right)\hfill \\ & & +\frac{1}{\sqrt{N}}\sqrt{\Delta \left({\int }_0^{{\tau }_0}\tilde{\psi }\left(x_{t-s}\right)\mathrm{d}\mu \left(s\right)+b_2{y}_t\right)}\mathcal{N}(0,1).\hfill \end{array}$$ (6b)

Equation 6 is the Euler–Maruyama type discretization of a delay stochastic differential equation (dSDE). Replacing Δ with dt and $\sqrt{\Delta }\mathcal{N}(0,1)$ with dW_t in 6, we obtain

$$\begin{array}{cc}\hfill \mathrm{d}{x}_t& =(\tilde{a}-b_1{x}_t)\mathrm{d}t+\frac{1}{\sqrt{N}}\sqrt{(\tilde{a}+b_1{x}_t)}\mathrm{d}{W}_t^1,\hfill \end{array}$$ (7a)

$$\begin{array}{ccc}\hfill \mathrm{d}{y}_t& =& \left({\int }_0^{{\tau }_0}\tilde{\psi }\left(x_{t-s}\right)\mathrm{d}\mu \left(s\right)-b_2{y}_t\right)\mathrm{d}t\hfill \\ & & +\frac{1}{\sqrt{N}}\sqrt{\left({\int }_0^{{\tau }_0}\tilde{\psi }\left(x_{t-s}\right)\mathrm{d}\mu \left(s\right)+b_2{y}_t\right)}\mathrm{d}{W}_t^2.\hfill \end{array}$$ (7b)

This is the dCLE for the transcriptional cascade in this section.

Taking the formal thermodynamic limit, N → ∞, in Eq. 7 yields the reaction rate equations derived in Ref. 38

$$\begin{array}{cc}\hfill \mathrm{d}{x}_t& =\left(\tilde{a}-b_1{x}_t\right)\mathrm{d}t,\hfill \end{array}$$ (8a)

$$\begin{array}{cc}\hfill \mathrm{d}{y}_t& =\left({\int }_0^{{\tau }_0}\tilde{\psi }\left(x_{t-s}\right)\mathrm{d}\mu \left(s\right)-b_2{y}_t\right)\mathrm{d}t.\hfill \end{array}$$ (8b)

The dynamics described by Eq. 8 are quite simple; if b₁ > 0 and b₂ > 0, then 8 has a globally attracting stable stationary point.

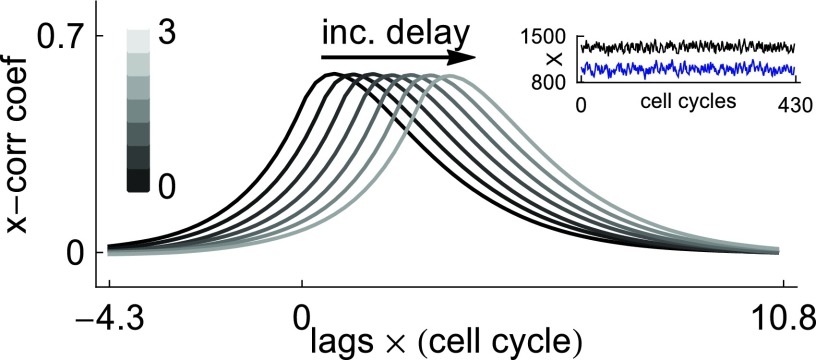
To test the validity of the dCLE approximation given in Eq. 7, we examine if it captures the interaction between the two proteins in our transcriptional cascade network. Figure 4 shows the cross correlation functions obtained by simulating the system with N = 1000 using dSSA. From left to right, the curves correspond to fixed delay τ increasing from 0 to 3. The corresponding cross correlation curves for the dCLE approximation 7 are indistinguishable from those obtained using dSSA.

Figure 4.

Cross correlation functions for the two-species feed-forward architecture at system size N = 1000. The inset shows sample trajectories for X (black; top) and Y (blue; bottom). The mean field model has a fixed point, and for this reason, stochastic dynamics stay within a neighborhood of this fixed point (see Theorem 1). However, the effect of increasing delay is clearly seen in the cross correlation function. The color bar displays the delay size corresponding to the cross correlation curves. Parameter values are given by $\tilde{\psi }\left(X\right)={\tilde{a}}_1{x}^3/(m^3+x^3)$, $\tilde{a}=0.92$, ${\tilde{a}}_1=1.39$, b₁ = b₂ = ln (2), m = 1.33, μ = δ_τ. The cross correlations have been normalized by dividing by the standard deviations σ_X and σ_Y of X and Y. Time has been normalized to cell cycle length.

In the heuristic derivation above, we first fix N and let Δ → 0 to obtain the dCLE; we then separately let N → ∞ to obtain the thermodynamic limit. Brett and Galla³⁹ also derive the dCLE by first fixing N and then sending Δ → 0. However, the two limits, Δ → 0 and N → ∞, cannot be taken independently; this is a common problem with heuristic derivations of stochastic differential equations, even in the absence of delay.⁴⁶ The time discretization, Δ, can be thought of as a sampling frequency, while the system size, N, determines the rate at which reactions fire. If N becomes too large for a given Δ, then the number of reactions that fire within [t, t + Δ] no longer follows a Poisson distribution with mean dependent only on the state of the system at time t. On the other hand, if N is too small for a given Δ, then the Poisson distribution cannot be approximated by a normal distribution. In order to rigorously derive the Langevin approximation and estimate the distance between the dBD and dCLE processes, we will have to take a careful limit by relating Δ to N (with Δ → 0 as N → ∞). We describe the proper scaling in Sec. 3.

Applied to the transcriptional cascade, our main mathematical result (Theorem 1 in Sec. 3) provides an explicit bound on the probability that the dCLE trajectory deviates from a narrow tube around the dBD trajectory (provided Δ is correctly scaled with respect to N).

In the previous example, the limiting deterministic system has a fixed point. Time series for the stochastic system therefore stay within a small neighborhood of this fixed point (see inset, Fig. 4). In the next example, we show that the dCLE approximation remains excellent even when the limiting deterministic dynamics are non-trivial. We consider a degrade-and-fire oscillator for which the limiting deterministic system has a limit cycle. The dCLE correctly captures the peak height and the inter-peak times for the dSSA realization of the degrade and fire oscillator, in addition to statistics such as the mean and variance. The approximation does not break down at small instantaneous protein numbers. Indeed, the mathematical theory developed in this work makes an important point: protein numbers at any particular time do not limit the quality of the dCLE approximation (in the presence of delay, or otherwise). Instead, the quality of the dCLE approximation depends on the latent parameter N. Theorem 1 makes this more precise: if one fixes the allowable error ɛ in the approximation of the dBD process by the dCLE process, then the time T during which the approximation error stays smaller than ɛ increases with N.

In the analysis of the previous example, and in the rest of this work, we make an assumption: There exists an integer N which describes the characteristic number of proteins in the system and all protein numbers and propensity functions can be scaled by this characteristic number. Because of this assumption, our setting is different from that of Gillespie,⁴⁷ who used the term chemical Langevin equation to differentiate his approximating Langevin equation from previous work such as that of van Kampen.⁴⁸ While we assume the existence of a system size parameter, we obtain the approximating Langevin equation without reference to a chemical master equation.

Degrade and fire oscillator

The degrade and fire oscillator depicted schematically in Figure 3c consists of a single autorepressive gene and corresponds to the reaction network

$$\begin{array}{cc}& \varnothing \underset{\mu }{\overset{\psi \left(X\right)}{⇢}}X\stackrel{\gamma X}{\to }\varnothing ,\hfill \\ & X+E\stackrel{\eta \left(X\right)}{\to }E.\hfill \end{array}$$

The production rate ψ(X) is given by ψ(X) = Nf(X/N), where f is the propensity function

$$f\left(x\right)=\frac{\alpha }{1+{\left(x/C_1\right)}^4};$$

the enzymatic degradation rate η(X) is given by η(X) = Ng(X/N). Here, g(x) = V_maxx/(K + x); K is the Michaelis-Menten constant, V_max the maximal enzymatic degradation rate, and γ the dilution rate coefficient. In the thermodynamic limit, the system is modeled by the delay differential equation

$$\frac{\mathrm{d}x}{\mathrm{d}t}={\int }_0^{{\tau }_0}\frac{\alpha }{1+{\left(\frac{x(t-s)}{C_1}\right)}^4}\mathrm{d}\mu \left(s\right)-\gamma x\left(t\right)-\frac{V_{max}x\left(t\right)}{K+x\left(t\right)}.$$ (9)

As before, x(t) denotes the concentration of protein X. We model the formation of functional repressor protein using distributed delay (described by the probability measure μ); this delayed negative feedback can induce oscillations.⁵ Figure 5a depicts a sample realization of the stochastic version of the degrade and fire oscillator (the finite system size regime) generated by dSSA.

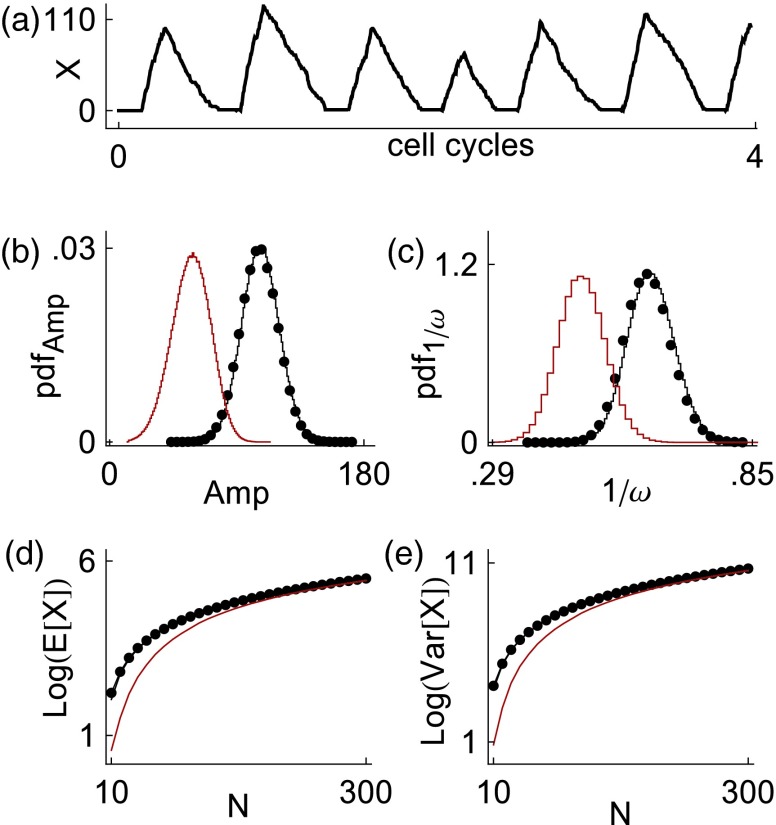
Figure 5.

Comparison of dSSA results to dSDE approximations for the degrade and fire oscillator. (a) depicts a stochastic realization of the oscillator generated by dSSA. We compare dSSA statistics (black dots in (b)–(e)) to those generated by the dCLE approximation given by Eq. 10 (black curves). We also show results for the dSDE approximation given by Eq. 11, obtained by removing delay from the diffusion term in Eq. 10 (red curves). At system size N = 50, the dCLE approximation given by Eq. 10 closely matches dSSA with respect to spike height distribution (b) and interspike interval distribution (c). In contrast, removing delay from the diffusion term results in a poor approximation of these distributions, as shown by the sizable shifts affecting the red curves. (d) and (e) illustrate mean repressor protein level and repressor protein variance, respectively, as functions of system size N. Equation 10 provides a good approximation for all simulated values of N while the performance of Eq. 11 improves as N increases. The quantity P represents protein number, not protein concentration. Parameter values are α = 20.8, C₁ = 0.04, β = ln (2), V_max = 5.55, γ₀ = 0.01, μ = δ_0.14. A soft boundary was added at 0 to ensure positivity.

The dCLE approximation is in this case given by

$$\begin{array}{ccc}\hfill \mathrm{d}{x}_t& =& {\int }_0^{{\tau }_0}f\left(x_{t-s}\right)\mathrm{d}\mu \left(s\right)-\gamma x_t-g\left(x_t\right)\mathrm{d}t\hfill \\ & & +\frac{1}{\sqrt{N}}{\left[{\int }_0^{{\tau }_0}f\left(x_{t-s}\right)\mathrm{d}\mu \left(s\right)+\gamma x_t+g\left(x_t\right)\right]}^{\frac{1}{2}}\mathrm{d}{W}_t.\hfill \end{array}$$ (10)

Figure 5 illustrates that Eq. 10 provides a good approximation of the dBD dynamics, even when system size is relatively small. At system size N = 50, the spike height distribution and interspike interval distribution obtained using the dSSA (black dots in Figures 5b, 5c) are nearly indistinguishable from those obtained using Eq. 10 (black curves in Figures 5b, 5c). Further, we see a close match with respect to mean repressor protein level and repressor protein variance across a range of system sizes (Figures 5d, 5e).

Interestingly, the dCLE approximation is very good even though the protein number approaches zero during part of the oscillation. This illustrates a central feature of the theory: the quality of the dCLE approximation is a function of a latent parameter N, not of the number of molecules present at any given time.

The exact form of the diffusion term is crucial to the accuracy of the dCLE approximation. If we remove delay from the diffusion term in Eq. 10, we obtain

$$\begin{array}{ccc}\hfill \mathrm{d}{x}_t& =& {\int }_0^{{\tau }_0}f\left(x_{t-s}\right)\mathrm{d}\mu \left(s\right)-\gamma x_t-g\left(x_t\right)\mathrm{d}t\hfill \\ & & +\frac{1}{\sqrt{N}}{\left[f\left(x_t\right)+\gamma x_t+g\left(x_t\right)\right]}^{1/2}\mathrm{d}{W}_t.\hfill \end{array}$$ (11)

At system size N = 50 (red curves in Figures 5b, 5c), dSDE 11 produces dramatically different results from those generated by the correct dCLE approximation. The performance of Eq. 11 improves as N increases (Figures 5d, 5e). This is expected, as both Eqs. 10, 11 converge weakly to Eq. 9 as N → ∞.

Metastable systems

Understanding metastability in stochastic systems is of fundamental importance in the study of biological switches.^{17, 18, 19, 20, 21, 22, 23, 24, 25, 26} While metastability is well understood mathematically in the absence of delay, understanding the impact of delay on metastability remains a major theoretical and computational challenge.^{27, 49, 50} We examine two canonical examples to show that for certain systems, the dCLE can be used to study the impact of delay on metastability: a positive feedback circuit and a co-repressive genetic toggle switch.

We offer a cautionary note before we proceed with the examples. Even in the Markovian context, SDE and Fokker-Planck modeling does not always accurately capture large deviations statistics associated with an underlying spatially discrete stochastic process. Existing work for systems without delay (see, e.g., Refs. ^{51, 52, 53}) illustrates the delicate relationship between continuum and discrete treatments of hitting times, extinction times, and the like. Determining when the dCLE accurately approximates the large deviations statistics of the underlying dBD process is an open problem.

Single species positive feedback circuit

The simplest metastable system consists of a single protein that drives its own production (Figure 3d). The chemical reaction network is given by

$$\varnothing \underset{\mu }{\overset{\psi \left(X\right)}{⇢}}X\stackrel{\gamma X}{\to }\varnothing$$

with ψ(X) = Nf(X/N) for the propensity

$$f\left(x\right)=\alpha +\frac{\beta x^b}{c^b+x^b}.$$

In the thermodynamic limit, the dynamics of this model are described by the DDE

$$\mathrm{d}{x}_t={\int }_0^{{\tau }_0}\alpha +\beta \frac{x{(t-s)}^b}{c^b+x{(t-s)}^b}\mathrm{d}\mu \left(s\right)-\gamma x\left(t\right)\mathrm{d}t.$$ (12)

Here, x represents protein concentration and b is the Hill coefficient. In the thermodynamic limit, there are two stable stationary states, x_l and x_h, as well as an unstable stationary state x_s. These states satisfy x_l < x_s < x_h.

In the stochastic (finite N) regime, the stationary states x_l and x_h become metastable. We simulate the metastable dynamics using dSSA and the dCLE approximation 15 given in this case by

$$\begin{array}{ccc}\hfill \mathrm{d}{x}_t& =& {\int }_0^{{\tau }_0}f\left(x_{t-s}\right)\mathrm{d}\mu \left(s\right)-\gamma x_t\mathrm{d}t\hfill \\ & & +\frac{1}{\sqrt{N}}{\left[{\int }_0^{{\tau }_0}f\left(x_{t-s}\right)\mathrm{d}\mu \left(s\right)+\gamma x_t\right]}^{\frac{1}{2}}\mathrm{d}{W}_t.\hfill \end{array}$$ (13)

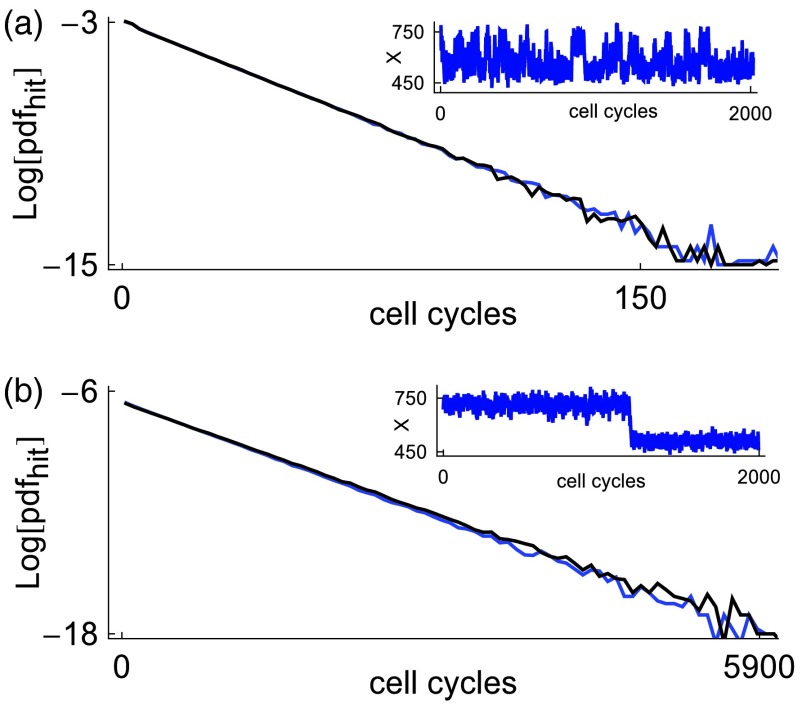
Figure 6 displays hitting time distributions for the dSSA simulations (black curves) and Eq. 13 (blue curves). A hitting time is defined as follows: We choose neighborhoods (x_l − δ_l, x_l + δ_l) and (x_s − δ_s, x_s + δ_s) of x_l and x_s, respectively. We start the clock when a trajectory enters (x_l − δ_l, x_l + δ_l) from the right. The clock is stopped when that trajectory first enters (x_s − δ_s, x_s + δ_s). A hitting time is the amount of time that elapses from clock start to clock stop. We see that for no delay (Figure 6a) and fixed delay τ = 1 (Fig. 6b), the dCLE approximation accurately captures the hitting time distributions for Hill coefficients increasing from 15 to 25. Hence, the dCLE approximation accurately captures the rare events associated with a spatially discrete delay stochastic process. This is significant because dSDEs are more amenable to large deviations theoretical analysis than their spatially discrete counterparts.

Figure 6.

Hitting time distributions for the positive feedback circuit. Black curves represent dSSA data; blue curves represent data from the dCLE approximation. (a) corresponds to the Markov case τ = 0 and a Hill coefficient of b = 15. (b) corresponds to a delay τ = 0.75 and b = 25. The tail of the hitting times distribution becomes longer with both increasing delay and increasing Hill coefficient b. The dCLE captures the lengthening of the tail due to both effects. Parameter values are α = 0.35, β = 0.15, c = 0.615, γ = ln (2), μ = δ_τ, N = 1000.

Hitting times increase dramatically as the delay increases from 0 to 1, in accord with earlier analysis.²⁷ A dramatic increase is also seen as the Hill coefficient increases. This is due to the fact that the potential wells around x_l and x_h deepen as b increases.

Co-repressive toggle switch

The co-repressive toggle switch (Figure 3e) is a two-dimensional metastable system described in the thermodynamic limit by the DDEs

$$\begin{array}{cc}\hfill \mathrm{d}{x}_t& ={\int }_0^{{\tau }_0}\frac{\beta }{1+y{(t-s)}^2/k}\mathrm{d}{\mu }_1\left(s\right)-\gamma x\mathrm{d}t,\hfill \end{array}$$ (14a)

$$\begin{array}{cc}\hfill \mathrm{d}{y}_t& ={\int }_0^{{\tau }_0}\frac{\beta }{1+x{(t-s)}^2/k}\mathrm{d}{\mu }_1\left(s\right)-\gamma y\mathrm{d}t.\hfill \end{array}$$ (14b)

The measure μ₁ describes the delay associated with production in this symmetric circuit. Equation 14 has two stable stationary points (x_l, y_h) and (x_h, y_l) separated by the unstable manifold associated with a saddle equilibrium point (x_s, y_s). In the stochastic (finite system size) regime, the stable stationary points become metastable. In this regime, a typical trajectory spends most of its time near the metastable points, occasionally moving between them.

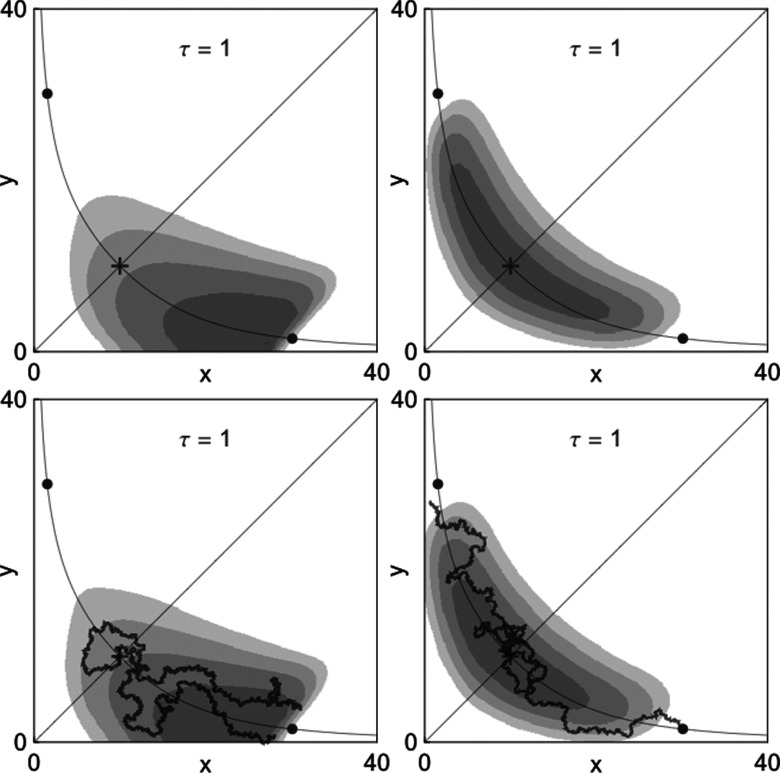
Figure 7 displays density plots corresponding to trajectories that either successfully transition between metastable states (four panels on the right) or make failed transition attempts (four panels on the left). Even for the moderate system size N = 30, the density plots generated by dSSA (top four panels) closely match those generated by the dCLE approximation in Eq. 15 (bottom four panels).

Figure 7.

Conditional density plots for the co-repressive toggle switch. The two left panels illustrate trajectories that leave a neighborhood of the stable point (x_h, y_l) and fall back into the same neighborhood before transitioning into a neighborhood of the stable point (x_l, y_h); displayed densities are conditioned on this set of trajectories. The two right panels illustrate trajectories that leave a neighborhood of (x_h, y_l) and transition to a neighborhood of (x_l, y_h) before falling back into the first neighborhood; displayed densities are conditioned on the set of such trajectories. Top panels correspond to dSSA; bottom panels correspond to dCLE. Cartoons of typical trajectories corresponding to failed transitions (left) and successful transitions (right) are shown for the dCLE process. Plots are shown for N = 30. The values of the other parameters are β = 0.73, k = 0.05, γ = ln (2).

Given the importance of rare events throughout stochastic dynamics, it is encouraging that the dCLE approximation captures well the dynamics of two popular biochemical motifs of metastability.

MAIN MATHEMATICAL RESULTS

The simulations thus far described suggest that the dCLE closely approximates the dBD process provided that the time increment Δ scales properly with N. Here, we mathematically quantify the quality of the approximation and we determine the optimal scaling of Δ.

The general biochemical setup is as follows. Consider a reaction network of D biochemical species and M possible reactions. We are interested in describing the dynamics as a function of a latent system parameter N, the system size. The state of the system at time t is described by the vector $B_N\left(t\right)\in {\mathbb{Z}}^D$ that lists the number of molecules of each species present at time t.

Each reaction R_j is described by the following:

• (a)A propensity function $f_j:{\mathbb{R}}^D\to {\mathbb{R}}^{+}$. The firing rate of reaction R_j is given by Nf_j(B_N(t)/N). It is reasonable to use propensity functions to model firing rates in well-mixed chemical systems.⁴⁷ We assume the propensities satisfy mild technical conditions;⁴⁴ these conditions are essentially always satisfied by chemical reaction networks. Examples include reactions of first and second order, Michaelis-Menten kinetics, and propensities of Hill type.
• (b)A state-change vector ${\mathit{v}}_j\in {\mathbb{Z}}^D$. The vector ${\mathit{v}}_j$ describes the change in the number of molecules of each species that results from the completion of a reaction of type j.
• (c)A probability measure μ_j that models the delay between the initiation and completion of a reaction of type j. We allow the delay to be distributed (μ_j has a density) or fixed (μ_j is a Dirac mass δ_τ at a fixed delay τ). For instantaneous reactions, μ_j = δ₀.

In order for the dCLE to closely approximate the dBD process, the time step Δ must be small enough so that the propensity functions remain essentially constant on time intervals of length Δ and large enough so that many reactions fire on such intervals. Gillespie⁴⁷ calls such a Δ a macroscopic infinitesimal time for the reaction network. The primary mathematical result of this paper provides a scaling of Δ as a function of N for which Δ is rigorously shown to be a macroscopic infinitesimal time for the reaction network. Further, we quantify the quality of the dCLE approximation: with high probability, the solution trajectory of the dCLE will remain inside a narrow tube around the solution trajectory of the dBD process. We state the main result precisely and then discuss implications.

Since B_N(t) is a vector of molecule numbers, we rescale by N to allow for a direct comparison of the dBD process and the dCLE. The correct dCLE approximation of (b_N(t)) = (B_N(t)/N) is given for 1 ⩽ k ⩽ D by

$$\begin{array}{ccc}\hfill \mathrm{d}{x}_k& =& \left(\sum _{j=1}^M{\int }_0^{{\tau }_0}{v}_{jk}{f}_j\left(\mathit{x}(t-s)\right)\mathrm{d}{\mu }_j\left(s\right)\right)\mathrm{d}t\hfill \\ & & +\frac{1}{\sqrt{N}}{\left(\Sigma \mathrm{d}\mathsf{W}\right)}_k,\hfill \end{array}$$ (15)

where W is a D-dimensional vector of independent standard Brownian motions and Σ² is given by

$${\Sigma }_{lm}^2=\sum _{j=1}^M{v}_{jl}{v}_{jm}{\int }_0^{{\tau }_0}{f}_j\left(\mathit{x}(t-s)\right)\mathrm{d}{\mu }_j\left(s\right).$$

Let ℓ_N denote the stochastic process defined by 15.

Theorem 1.For any fixed timeT > 0, Δ(N) = N^−1/4is a macroscopic infinitesimal time on [0, T]: There exist constantsK₁andK₂, depending only onTand the chemical reaction network, such that

$$\mathbb{P}\left(\underset{t\in [0,T]}{\max }‖b_N\left(t\right)-{\ell }_N\left(t\right)‖>\frac{K_1}{N^{1/8}}\right)⩽K_2{e}^{-\frac{1}{3}{N}^{1/4}}.$$ (16)

Theorem 1 has several interesting corollaries. First, for every continuous observable Ψ (real-valued function of trajectories of the processes), the difference between the expected value of Ψ with respect to the dBD and dCLE processes converges to zero as N → ∞. This implies in particular that the distance between every moment of the processes converges to zero as N → ∞. Second, since the right side of Eq. 16 is summable with respect to N, it follows from the Borel-Cantelli lemma that a trajectory of the dCLE process will, with probability one, lie within the tube of radius K₁/N^1/8 around the corresponding trajectory of the dBD process for all but finitely many values of N.

One would use Theorem 1 in a concrete situation by first fixing a desirable probability bound, say 1/1000. Using 16, one would then solve for the radius of the tube around the trajectory of the dBD process for which the dCLE trajectory will remain in this tube up to time T with probability at least 999/1000.

We prove Theorem 1 in three steps.⁴⁴ First, we prove that the family of measures on trajectories associated with b_N is a tight family, roughly meaning that they are all approximately supported on a common compact set of trajectories. Second, we prove a version of 16 for “discrete-time tubes” wherein the maximum on the left side of 16 is taken not over all t ∈ [0, T] but rather over only 0, Δ, 2Δ, …, (T/Δ)Δ. Third, we study the size of fluctuations of the dBD and dCLE processes on time intervals of length Δ in order to upgrade the discrete-time tube estimate to the continuous-time tube estimate 16. We determine the optimal scaling of Δ during this final step. At the beginning of the proof, we assume that Δ scales with N as Δ(N) = N^−α and then look for the optimal value of α. In order to both prove the discrete-time tube estimate and control fluctuations of the dCLE process on intervals of length Δ, we scale the radius r(N) of the continuous-time tube as

$$r\left(N\right)=\frac{C_1}{N^{\alpha /2}}+\frac{C_2}{N^{(1-3\alpha )/2}}.$$

The first term in the sum measures local fluctuations of the dCLE while the second comes from the proof of the discrete-time tube estimate. In order to minimize r(N), it is asymptotically optimal to have α = 1 − 3α, giving α = 1/4.

We conclude this section with a cautionary note about what the main theorem does not say. Theorem 1 is formulated for fixed time intervals: one must first fix T and only then allow N to vary. As a consequence, this theorem does not apply when one scales T with N such that T → ∞ as N → ∞, as one does in the large deviations context.

DISCUSSION

SDEs are one of our main tools for modeling noisy processes in nature. Interactions between the components of a system or network are frequently not instantaneous. It is therefore natural to include such delay into corresponding stochastic models. However, the relationship between dSDEs and the processes they model has not been fully established.

Delay stochastic differential equations have previously been formally derived from the dCME. Unlike the chemical master equation, however, the dCME is not closed; this complicates the derivation of dSDE approximations. Closure in this context means the following: Let P(n, t) denote the probability that the stochastic system is in state n at time t. The dCME expresses the time derivative of P(n, t) in terms of joint probabilities of the form P(j, t; k, t − τ) – the probability that the system is in state j at time t and was in state k at time t − τ, where τ is the delay. The one-point probability distribution P(·, t) is therefore expressed in terms of two-point joint distributions, resulting in a system that is not closed. Timescale separation assumptions have been used to close the dCME. If the delay time is large compared to the other timescales in the system, one may assume that events that occur at time t − τ are decoupled from those that occur at time t and close the dCME^{2, 54} by assuming the joint probabilities may be written as products

$$P(j,t;k,t-\tau )=P(j,t)P(k,t-\tau ).$$

Having closed the dCME, one may then derive dSDE approximations⁵⁴ as well as useful expressions for autocorrelations and power spectra.²

Approximations of dSDE type have also been derived using system size expansions such as van Kampen expansions^{48, 55} and Kramers-Moyal expansions for both fixed delay⁵⁶ and distributed delay.⁵⁷

Brett and Galla³⁹ use the path integral formalism of Martin, Siggia, Rose, Janssen, and de Dominicis to derive the dCLE without relying on the dCME. Using this formalism, a moment generating functional may be expressed in terms of the system size parameter N and the sampling rate Δ. In the continuous-time limit, Δ → 0, the dCLE may be inferred from the moment generating functional. However, the Brett and Galla derivation has some limitations. First, the Δ → 0 limit cannot be taken without simultaneously letting N → ∞. Intuitively, this is because as Δ → 0, the Gaussian approximation to the Poisson distribution with mean NλΔ breaks down unless the parameter Nλ simultaneously diverges to infinity. Second, the derivation gives no quantitative information about the distance between the dCLE and the original dBD process.

Here, we addressed these shortcomings. We proved rigorously that the dBD process can be approximated by a class of Gaussian processes that includes the dCLE. In particular, we established that for most biophysically relevant propensity functions, the dCLE process will approximate all moments of the dBD process. Our proof includes bounds on the quality of the approximation in terms of the time T for which the approximation is desired to hold and the characteristic system size N (see Theorem 1). The error bounds also indicate that the quality of the dCLE approximation worsens with increasing upper bounds on the reaction propensity functions and state-change vectors. Physically, this means that high reaction rates and reactions that cause large changes in the protein populations are detrimental to the quality of the dCLE approximation.

The dCLE is one of many Gaussian processes that approximate the dBD process. Among all Gaussian approximations with noise components that scale as $1/\sqrt{N}$, the dCLE is optimal because it is the only such approximation that exactly matches the first and second moments of the dBD process. We formally justify this assertion in the supplementary material⁴⁴ using characteristic functions. As our simulations of the degrade and fire oscillator demonstrate, the dCLE can significantly outperform other Gaussian approximations at moderate system sizes.

Nevertheless, the quantitative tube estimates in Theorem 1 apply to any Gaussian approximation of the dBD process provided the noise scales as $1/\sqrt{N}$. This is significant because it is often advantageous to use linear noise approximations of the dCLE. Delay appears in the drift component of a linear noise approximation but not in the diffusion component. Linear noise approximations are therefore easier to analyze than their dCLE counterparts. In particular, elements of the theory of large deviations for Markovian systems can be extended to SDEs with delay in the drift.⁵⁸

For metastable systems, our simulations indicate that the dCLE may capture both temporal information (such as hitting times for the positive feedback model; see Fig. 6) and spatial information (such as densities for trajectories corresponding to failed and successful transitions; see Fig. 7) for some examples. While SDE approximations (without delay) do not in general capture the dynamics in the presence of metastability even for Markov systems,^{51, 52, 53} our work suggests that dCLE approximations may be used, on a case by case basis, to study rare events for metastable biochemical systems.

We have made a number of simplifying assumptions in order to be able to prove the existence of a macroscopic infinitesimal time postulated by Gillespie.⁴⁷ In particular, we assumed the existence of a latent system size parameter N, in terms of which this macroscopic infinitesimal time Δ can be expressed. However, for many biochemical systems, it is often unclear what the system size is, and in this case, a more careful analysis will be required to rigorously justify the use of delay stochastic differential equations to approximate the dynamics of the underlying discrete systems. Further complications can arise when the system size itself changes as a function of time or if there is a scale separation between the fast and slow components of the system. In the non-delayed case, hybrid systems^{59, 60, 61} are often used to address these challenges. Developing a mathematical theory for hybrid systems in the presence of delays is an important future direction.

We have shown that the dCLE provides an accurate approximation of a number of stochastic processes. Although we chose gene regulatory networks in our examples, the theory is applicable to general birth-death processes with delayed events. SDEs, and the chemical Langevin equation in particular, are fundamental in modeling and understanding the behavior of natural and engineered systems. We therefore expect that the dCLE will be widely applicable when delays impact system dynamics.