Time-, frequency-, and wavevector-resolved x-ray diffraction from single molecules

Abstract

Using a quantum electrodynamic framework, we calculate the off-resonant scattering of a broadband X-ray pulse from a sample initially prepared in an arbitrary superposition of electronic states. The signal consists of single-particle (incoherent) and two-particle (coherent) contributions that carry different particle form factors that involve different material transitions. Single-molecule experiments involving incoherent scattering are more influenced by inelastic processes compared to bulk measurements. The conditions under which the technique directly measures charge densities (and can be considered as diffraction) as opposed to correlation functions of the charge-density are specified. The results are illustrated with time- and wavevector-resolved signals from a single amino acid molecule (cysteine) following an impulsive excitation by a stimulated X-ray Raman process resonant with the sulfur K-edge. Our theory and simulations can guide future experimental studies on the structures of nano-particles and proteins.

INTRODUCTION

X-ray techniques have long been applied to image the electronic charge density of atoms, molecules, and materials.^{1, 2, 3} Recently developed X-ray free electron laser sources, which generate short (attosecond), intense pulses, open up numerous potential applications for high temporal and spatial resolution studies.^{4, 5, 6, 7, 8, 9} One exciting application is the determination of molecular structure by X-ray diffraction of nanocrystals^{4, 10} avoiding the crystal growth process which is often the bottleneck in structure determination;^{11, 12} it may take decades to crystallize a complex protein. It is much easier to grow nanocrystals than the many-micrometers-sized samples required by conventional crystallography. This has been demonstrated experimentally in nanocrystals for the water splitting photosynthetic complex II,¹³ a mimivirus,¹⁴ and a membrane protein.^{4, 15}

Extending this idea all the way to the single-molecule level, totally removing “crystal” from crystallography is an intriguing possibility.^{16, 17, 18} Obtaining a protein structure by scattering from a single molecule is revolutionary. Many obstacles need to be overcome to accomplish this ambitious goal. For instance, the molecule will typically break down when subjected to such high fluxes. However, it has been argued^{16, 19, 20, 21} that, for sufficiently short pulses, the scattering occurs prior to photon damage, so that this should not affect the measured charge density. This point is still under debate.

In this paper, we consider the scattering of a broadband X-ray pulse from a system composed of a single, few, or many molecules prepared in a superposition of electronic states and show under what conditions the signal may be described solely by the time-dependent charge density. We assume that the X-ray pulse is off-resonance from any material transitions and that the pulse is sufficiently short so that the electrons in the sample do not appreciably re-arrange during the pulse time. The fluence is assumed sufficiently low so that the scattering is linear in pulse intensity. Scattering off non-stationary evolving states is an area of growing interest. When the time-dependent state of matter merely follows some classical parameter (as in the case of tracking the time-dependent melting of crystals^{8, 22}) no coherence of electronic states is prepared and the analysis of scattering is simplified considerably. Time-dependent diffraction can then be described by simply replacing the charge density in stationary diffraction by the time-dependent charge-density. The situation is more complex in pump-probe experiments in which a superposition of electronic states is prepared by the pump and is then probed by X-ray scattering. Such superpositions, which involve electronic coherence, can be prepared, e.g., by inelastic stimulated Raman processes,²³ a photoionization process,²⁴ off-resonant femtosecond pulses,²⁵ or high-intensity optical pumping.²⁶ Diffraction is a macroscopic, classical effect that involves the interference of wavefronts emanating from different sources treated at the level of Maxwell's equations.²⁷ A fundamental difficulty in extending it to single molecules is that X-ray scattering (as any light scattering) from a single molecule may not be thought of simply as a diffraction since it has both elastic (Thompson/Rayleigh) and an inelastic (Compton/Raman) components.²⁸ Using a quantum electrodynamic (QED) approach, we discuss and analyze the single-particle vs. the cooperative contributions to the signal. We find that the two terms carry different particle form factors that permit Raman scattering in different frequency ranges. Simulations are presented for the scattering of a broadband X-ray pulse from a single molecule of the amino acid cysteine either in the ground state or when prepared in a nonstationary state by a stimulated resonant X-ray Raman process with various delay times between preparation and the scattering event.

CLASSICAL THEORY OF DIFFRACTION

As the expressions developed in this paper bear a resemblance to the standard classical theory of diffraction, we review it briefly. The diffraction signal from a system initially in the ground state |g⟩ is

$$S\left(\mathbf{q}\right)\propto |{\sigma }_{gg}{\left(\mathbf{q}\right)|}^2,$$ (1)

where ${\sigma }_{gg}\left(\mathbf{q}\right)=⟨g|\widehat{\sigma }\left(\mathbf{q}\right)|g⟩$ is the ground state charge density in q-space and q ≡ k_s − k_p is the momentum transfer (k_s is the outgoing mode and k_p is the incoming mode). More generally, $\widehat{\sigma }\left(\mathbf{q}\right)$ is the Fourier transform of the charge-density operator

$$\widehat{\sigma }\left(\mathbf{q}\right)=\int d\mathbf{r}\widehat{\sigma }\left(\mathbf{r}\right)e^{-i\mathbf{q}·\mathbf{r}}.$$

Equation 1 assumes that the scattering is elastic and treats the entire sample as a single system (i.e., $\widehat{\sigma \left(\mathbf{r}\right)}$ is the electron density of the entire sample). A common approach to understanding diffraction patterns involves making an approximation on the structure of the electron density. For example, we may presume that the complete wavefunction is built up from single-electron wavefunctions and the total electron density is the sum of the densities associated with each electron wavefunction. If the system is composed of N identical particles and each electron is bound to a particle, then the amplitude of the signal from each particle carries a relative phase related to the particle position. The term “particle” is used here as a generic partitioning of the system and may stand for atoms as well as large (molecules) or small (unit cell) groups of atoms. Practically speaking, they should be large enough that the electron density between particles may be safely neglected and small enough that electronic structure calculations can be performed. Separating single- and multi-particle contributions yields for the intensity²⁷

$$S\left(\mathbf{q}\right)\propto |{\sigma }_{aa}{\left(\mathbf{q}\right)|}^2\left[N+\sum _{\alpha \ne \beta }{e}^{-i\mathbf{q}·{\mathbf{r}}_{\alpha \beta }}\right],$$ (2)

where r_αβ ≡ r_α − r_β is the position of particle α relative to β. Here, σ_aa(r) stands for the electron density in a single particle and σ_aa(q) is known as the particle form factor. Thus, the signal is factored into a product of the signals from the particle electron density and from the distribution of particles. The two terms in Eq. 2 both contribute linearly in N to the integrated signal.²⁹ However, the former yields a signal that is generally distributed throughout reciprocal space while the various terms in the α ≠ β summation carry different phases that cause a redistribution of the signal into points of constructive and destructive interference (a Bragg pattern for crystalline samples).³⁰

OFF-RESONANCE X-RAY SCATTERING SIGNALS

We calculate the X-ray scattering by a sample initially prepared in a non-stationary state using a quantum description of the field, in which radiation back-reaction (which leads to inelastic scattering) is naturally built in. Incorporation of the broad frequency bandwidth of incoming X-rays is an important point as ultra-short pulses need to outrun destruction in single-molecule scattering. We assume that the molecule is initially prepared in an arbitrary density matrix, representing a pure or mixed state such as photo-ions. We extend the quantum field formalism developed in Refs. ^{28, 32} for spontaneous emission of visible light to off-resonant X-ray scattering. Our calculation starts with the minimal-coupling Hamiltonian, which contains a term proportional to ${\widehat{\mathbf{A}}}^2\widehat{\sigma }$ as well as $\widehat{\mathbf{j}}·\widehat{\mathbf{A}}$ where $\widehat{\mathbf{j}}$ is the electronic current operator. The former describes instantaneous scattering where the electrons do not have the time to respond during the scattering process. The second term dominates resonant processes and allows for a delay between absorption and emission during which electronic rearrangement, ionization, and breakdown can occur. Since hard X-rays are always resonant with the electronic continua representing various ionized states, the relative role of the $\widehat{\mathbf{j}}·\widehat{\mathbf{A}}$ term should be investigated further in order to clarify how important are these processes. In our study, we treat only off-resonant scattering and therefore focus on the ${\widehat{\mathbf{A}}}^2$ term, which dominates such processes.^{33, 34}

In the interaction picture, the Hamiltonian is given by

$$\widehat{H}={\widehat{H}}_0+{\widehat{H}}^{\prime }\left(t\right),$$ (3)

where ${\widehat{H}}_0$ is the bare field and matter Hamiltonian while ${\widehat{H}}^{\prime }\left(t\right)$ is the field-matter coupling. Assuming the diffracting X-ray pulse is not resonant with any material transitions and its intensity is not too high, its interaction with the matter is given by³⁴

$${\widehat{H}}^{\prime }\left(t\right)=\frac{1}{2}\int d\mathbf{r}{\widehat{\mathbf{A}}}^2(\mathbf{r},t){\widehat{\sigma }}_T(\mathbf{r},t).$$ (4)

We consider a sample of N non-interacting, identical particles (molecules or atoms) indexed by α with non-overlapping charge distributions so that the total charge-density operator can be partitioned as ${\widehat{\sigma }}_T\left(\mathbf{r}\right)={\sum }_{\alpha }\widehat{\sigma }(\mathbf{r}-{\mathbf{r}}_{\alpha })$. The signal is given by the electric field intensity arriving at the detector and may be generally expressed as the overlap integral of a detector spectrogram (given in terms of the detection parameters) and a bare spectrogram (Eq. A9).

The scattering signal mode is initially in the vacuum state |0⟩⟨0|. Therefore, an interaction on both bra and ket of the field density matrix is required to generate the state |1⟩⟨1| which gives the signal. We thus expand the signal as

$$S(\overline{\omega },\overline{t},\overline{\mathbf{r}},\overline{\mathbf{k}})=\int dt\int d\mathbf{r}⟨{\mathbf{E}}^{\left(t\mathbf{r}f\mathbf{k}\right)†}(\mathbf{r},t){\mathbf{E}}^{\left(t\mathbf{r}f\mathbf{k}\right)}(\mathbf{r},t)⟩.$$ (5)

It is given in terms of the gated electric fields (defined in Appendix A), to second order in ${\widehat{H}}^{\prime }$ (Eq. 4). This naturally leads to a double sum ∑_{α, β} over the scatterers. Terms with α = β arise when the probe pulse is scattered off a single particle (Fig. 1a) and terms with α ≠ β describe two-particle scattering events (Fig. 1b). The former contains N terms which add incoherently (at the intensity level), giving a virtually isotropic signal. The latter, in contrast, is governed by N(N − 1) terms which carry different phase-factors and can interfere destructively or constructively (yielding the Bragg peaks in a crystalline sample or, more generally, a speckle pattern).²⁷ In general, both contributions must be considered as it is frequently not sufficient to sample a signal only at the points of constructive interference (Bragg diffraction) where the two-particle terms dominate.³⁵ In this paper, we refer to the single-particle contribution as “incoherent” and the two-particle contribution as “coherent” reflecting the way in which these contributions add (at the intensity versus amplitude level). In the X-ray community, incoherent is commonly taken to refer to inelastic contributions while coherent refers to elastic. The two nomenclatures coincide when considering scattering from the ground state because, as will be shown below, two-particle scattering from the ground state (or any population) is necessarily elastic while single-particle scattering from the ground state has only a single elastic term (or one term for each initially populated state). Two-particle scattering from a nonstationary superposition state, in contrast, has both elastic and inelastic terms which add coherently (since they are both proportional to a spatial phase-factor $e^{i\Delta \mathbf{k}·{\mathbf{r}}_{ab}}$ dependent on the distance between the two particles). On the other hand, the elastic terms from the single-particle scattering add incoherently since their spatial phase factors are canceled by the opposite-hermiticity interactions on the ket/bra.

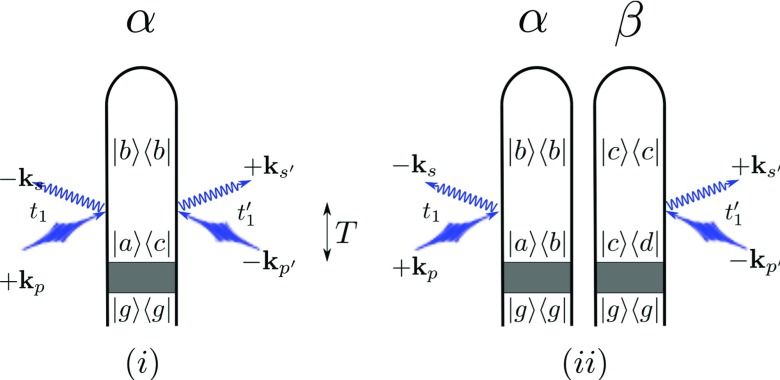
Figure 1.

Loop diagrams for incoherent (a) and coherent (b) X-ray scattering processes. The shaded area represents an unspecified process that prepares the system in an arbitrary state (|g⟩ is the electronic ground state). We denote modes of the pump with p and p^′ whereas s, s^′ represent relevant scattering modes (${\mathbf{k}}_{p^{(\prime )}}$ has frequency ${\omega }_{p^{(\prime )}}$ and ${\mathbf{k}}_{s^{(\prime )}}$ has frequency ${\omega }_{s^{(\prime )}}$). The time T between the termination of this preparation process and the central time of the scattered pulse is shown via the arrow in the center of the figure. Elastic scattering corresponds to ω_ab = ω_bc = 0 (i.e., ω_ac = 0 for the incoherent and ω_bc = ω_ed = 0 for the coherent contribution). Elastic scattering therefore originates from scattering off populations. For diagram rules, see Refs. ²⁸, ³¹.

In the coherent terms, the product of charge densities on different particles can be factorized and the signal is proportional to the modulus square of the single-particle electron density $\widehat{\sigma }\left(\mathbf{r}\right)$. Such factorization is not possible for the incoherent terms where the signal is given by a correlation function of the charge density rather than the charge density itself. As discussed below, restricting attention to elastic scattering reduces the correlation function to the modulus-square result and eliminates the need to consider the correlation function. Thus, the signal is expressible in terms of the charge-density alone either when the coherent contribution dominates or when attention is restricted to elastic scattering.

Figure 1 illustrates the incoherent (Fig. 1a) and coherent (Fig. 1b) scattering processes from a sample following preparation in a non-stationary electronic superposition state described by the density matrix $\widehat{\rho }={\sum }_{cb}{\rho }_{cb}|c⟩⟨b|$. The preparation process is represented by the gray box. In this paper, we will consider a Raman preparation process (in another work, we examine the case where the preparation process is itself an off-resonant scattering process³⁶). After the preparation process (which terminates at t = 0) the system evolves freely until an X-ray probe pulse with an experimentally controlled envelope centered at time T impinges on the sample and is scattered into a signal mode that is initially in a vacuum state. This signal photon is then finally absorbed by the detector. Time translation invariance of the matter correlation function implies the basic energy-conservation condition ${\omega }_p-{\omega }_{p^{\prime }}+{\omega }_{s^{\prime }}-{\omega }_s={\omega }_{ac}$ for an incoherent scattering event (Fig. 1a). Coherent scattering events (Fig. 1b) give two such conditions corresponding to the two diagrams ω_p − ω_s = ω_ab and ${\omega }_{p^{\prime }}-{\omega }_{s^{\prime }}={\omega }_{cd}$. For a broadband pulse in which ω_p and ${\omega }_{p^{\prime }}$ can differ appreciably, the signal will contain contributions from paths in which ω_s and ${\omega }_{s^{\prime }}$ take all possible values within this bandwidth. These can be controlled by pulse-shaping techniques as well as by the choice of detection parameters.³⁷

It follows from the diagrams that, since each particle must end the process in a population state and has only interactions on one side of the loop, coherent scattering from populations will always be Rayleigh type while Raman (inelastic) processes result from scattering off coherences. In contrast, the single-particle energy conservation condition for an initial population (i.e., ω_ac = 0) allows for inelastic processes.

FREQUENCY-GATED SIGNALS

Complete expressions for the signal which include arbitrary gating and pulse envelopes (i.e., the bare spectrograms) are given in Appendix B. In this section, we discuss the simpler signal that results when no time-gating is applied. The formulas are simplest when we employ delta functions for the detector spectrograms. As shown in Appendix A, we have separate detector spectrograms for the time-frequency gating and the space-propagation gating. As seen in Appendix B (Eqs. B22, B25), both coherent and incoherent bare spectrograms carry the delta function factor $\delta ({\mathbf{k}}^{\prime }-\frac{{\omega }^{\prime }}{c}{\widehat{\mathbf{r}}}^{\prime })$. This connects ω^′ to k′ in the usual way (though this is not automatic since the two are not a priori related in this way but rather both begin as separate gating variables) as well as fixing the direction of k′. For this reason, the logical choice for the spatial-propagation detector spectrogram is

$$W_D({\mathbf{r}}^{\prime },{\mathbf{k}}^{\prime };\overline{\mathbf{r}},\overline{\mathbf{k}})=\delta ({\mathbf{r}}^{\prime }-\overline{\mathbf{r}}).$$ (6)

This represents a spatially resolved signal; that is, the location of the detection event (the pixel location) is resolved. All signals considered in this paper use this choice.

If the detector spectrogram does not depend on t^′ (no time-gating is applied), we may separate the time-dependent phase factors from the auxiliary functions and carry out the time integration to give a factor of $\delta ({\omega }_p-{\omega }_{p^{\prime }}+{\tilde{\omega }}^{\prime }-\tilde{\omega })$. The signals are therefore given by

$$\begin{array}{cc}\hfill S_{\mathrm{coh}}(\overline{\omega },\overline{\mathbf{r}},\Lambda )=& K\int d{\omega }^{\prime }{\left|F_f({\omega }^{\prime },\overline{\omega })\right|}^2{\omega }^{\prime 2}\hfill \\ & \times \sum _{\alpha \beta }\int d{\omega }_{p}d{\omega }_{p^{\prime }}{A}_p\left({\omega }_p\right)A_p^{*}\left({\omega }_{p^{\prime }}\right)e^{-i(\mathbf{q}·{\mathbf{r}}_{\alpha }-{\mathbf{q}}^{\prime }·{\mathbf{r}}_{\beta })}\hfill \\ & \times ⟨\widehat{\sigma }(\mathbf{q},{\omega }^{\prime }-{\omega }_p)⟩⟨\widehat{\sigma }(-{\mathbf{q}}^{\prime },{\omega }_{p^{\prime }}-{\omega }^{\prime })⟩,\hfill \end{array}$$ (7)

$$\begin{array}{cc}\hfill S_{\mathrm{inc}}(\overline{\omega },\overline{\mathbf{r}},\Lambda )=& K\int d{\omega }^{\prime }{\left|F_f({\omega }^{\prime },\overline{\omega })\right|}^2{\omega }^{\prime 2}\hfill \\ & \times \sum _{\alpha }\int d{\omega }_{p}d{\omega }_{p^{\prime }}{A}_p\left({\omega }_p\right)A_p^{*}\left({\omega }_{p^{\prime }}\right)e^{-i(\mathbf{q}-{\mathbf{q}}^{\prime })·{\mathbf{r}}_{\alpha }}\hfill \\ & \times ⟨\widehat{\sigma }(-{\mathbf{q}}^{\prime },{\omega }_{p^{\prime }}-{\omega }^{\prime })\widehat{\sigma }(\mathbf{q},{\omega }^{\prime }-{\omega }_p)⟩,\hfill \end{array}$$ (8)

where ${\mathbf{q}}^{(\prime )}\equiv \frac{{\omega }^{\prime }}{c}\widehat{\overline{\mathbf{r}}}-{\mathbf{k}}_{p^{(\prime )}}$ is the momentum transfer, $F_f(\omega ,\overline{\omega })$ is the frequency gating function of Appendix A, and Λ stands for the set of parameters that define the external pulse envelopes (including ${\mathbf{k}}_{p^{(\prime )}}$). We approximate

$$\begin{array}{c}\hfill K=\frac{|\overline{\epsilon }\left({\widehat{\mathbf{k}}}_p\right)·{\mu }_D{|}^2}{72\pi c^4{r}^{\prime 2}}\end{array}$$ (9)

as a constant on the assumption that all pixels are roughly equidistant from the sample. In approaches to x-ray scattering that do not incorporate the detection event, the differential scattering cross section is calculated and found to be proportional to $r_0^2\left(\frac{{\omega }_s}{{\omega }_p}\right){|{\epsilon }_p·{\epsilon }_s|}^2$ with r₀ the classical electron radius. Our incorporation of the detection event included a summation over polarizations of the signal field and an averaging over initial polarizations and emission directions. This was shown to lead to the replacement ${\epsilon }_p·{\epsilon }_s\to \overline{\epsilon }\left({\widehat{\mathbf{k}}}_p\right)·{\mu }_D$ while the use of atomic units equates $r_0^2=\frac{1}{c^4}$. Finally, since we calculate the signal (defined as the expectation value of the gated electric field) by explicitly incorporating the detection event (which is linear in ω_s) our result is proportional to ${\omega }_s^2$. Recalling that $\mathbf{A}\left(\omega \right)\propto \frac{1}{\omega }\mathbf{E}\left(\omega \right)$, we see that our result carries the appropriate proportionality factors compared to the usual differential scattering cross section (Ref. ³⁴).

That the arguments of Eqs. 7, 8 are $\overline{\omega }$ and $\overline{\mathbf{r}}$ reflects the fact that they correspond to taking a spectrum at every pixel. Since the final observed signal frequency is $\overline{\omega }$, we may as well relabel it ω_s to make the interpretation more intuitive. Aside from the expected inverse-square dependence on $\overline{r}$, the signal only depends on $\overline{\mathbf{r}}$ through $\widehat{\overline{\mathbf{r}}}$, i.e., the direction vector pointing from the sample to the pixel. Since $\widehat{\overline{\mathbf{r}}}$ is the same as the direction of propagation of scattered light, this suggests representing the directional dependence by defining $\frac{{\omega }_s}{c}\widehat{\overline{\mathbf{r}}}\equiv {\mathbf{k}}_s$. Finally, it is important to note that, although these signals do not depend on time directly since we have assumed no time resolution (i.e., the pixels are simply left open to collect incoming light), the signal does depend parametrically on the central time of the incoming pulse through the field envelope A_p(ω) which carries a phase factor e^−iωT. Here, T is the central time of the pulse envelope and the zero of time is set at the end of the state preparation process (where the prepared state is presumed to be known). Since T therefore represents the time separation between state preparation and arrival of the center of the probe pulse and this is a key experimental control, we explicitly write this dependence in future expressions.

Eigenstate expansion of the frequency-resolved signal

In the following, we focus on the frequency-resolved signal because of its relative ease of interpretation. While this has not yet been demonstrated in the X-ray regime, it has been shown possible to discriminate a single wavelength component from multiwavelength scattering data in the EUV range.³⁸ From Eqs. 7, 8 with $|F_f({\omega }^{\prime },\overline{\omega }){|}^2=\delta ({\omega }^{\prime }-\overline{\omega })$, this signal is given by the sum of a coherent and an incoherent contribution which are related to the transition charge density σ_ab(q)

$$\begin{array}{cc}\hfill S({\mathbf{k}}_s,\Lambda )=& K\sum _{\alpha \ne \beta }\sum _{abcd}{\rho }_{ab}{\rho }_{cd}^{*}{\omega }_s^2{e}^{i({\omega }_{ba}T-{\mathbf{q}}_{ba}·{\mathbf{r}}_{\alpha })}{e}^{-i({\omega }_{dc}T-{\mathbf{q}}_{dc}·{\mathbf{r}}_{\beta })}\hfill \\ & \times {\mathcal{A}}_p({\omega }_s+{\omega }_{ba}){\mathcal{A}}_p^{*}({\omega }_s+{\omega }_{dc}){\sigma }_{ba}\left({\mathbf{q}}_{ba}\right){\sigma }_{dc}^{*}\left({\mathbf{q}}_{dc}\right)\hfill \\ & +K\sum _{\alpha }\sum _{abc}{\rho }_{ac}{\omega }_s^2{e}^{i({\omega }_{ba}T-{\mathbf{q}}_{ba}·{\mathbf{r}}_{\alpha })}{e}^{-i({\omega }_{bc}T-{\mathbf{q}}_{bc}·{\mathbf{r}}_{\alpha })}\hfill \\ & \times {\mathcal{A}}_p({\omega }_s+{\omega }_{ba}){\mathcal{A}}_p^{*}({\omega }_s+{\omega }_{bc}){\sigma }_{ba}\left({\mathbf{q}}_{ba}\right){\sigma }_{bc}^{*}\left({\mathbf{q}}_{bc}\right),\hfill \end{array}$$ (10)

where ${\mathcal{A}}_p\left(\omega \right)$ is the spectral envelope of the scattered pulse, σ_ij(q) are Fourier transformed matrix elements of the charge-density operator, and a,b,c, and d represent electronic states. We have also defined the momentum-transfer vector ${\mathbf{q}}_{ba}\equiv {\mathbf{k}}_s-\frac{{\omega }_s+{\omega }_{ba}}{c}{\widehat{\mathbf{k}}}_p$.

The signal is not generally related to the time-dependent, single-particle charge density but rather to its correlation function.^{34, 39} A compact expression for the total signal is

$$\begin{array}{cc}\hfill S_T({\mathbf{k}}_s,\Lambda )=& K\int d{\omega }^{\prime }{\left|F_f({\omega }^{\prime },\overline{\omega })\right|}^2{\omega }^{\prime 2}\int d{\omega }_{p}d{\omega }_{p^{\prime }}{A}_p\left({\omega }_p\right)\hfill \\ & \times A_p^{*}\left({\omega }_{p^{\prime }}\right)⟨{\widehat{\sigma }}_T(-{\mathbf{q}}^{\prime },{\omega }_{p^{\prime }}-{\omega }_s){\widehat{\sigma }}_T(\mathbf{q},{\omega }_s-{\omega }_p)⟩,\hfill \end{array}$$ (11)

where the correlation function of the total charge density operators may be expanded in terms of the single-particle densities as

$$\begin{array}{cc}& ⟨{\widehat{\sigma }}_T(-{\mathbf{q}}^{\prime },{\omega }_s-{\omega }_{p^{\prime }}){\widehat{\sigma }}_T(\mathbf{q},{\omega }_p-{\omega }_s)⟩\hfill \\ & =\sum _{\alpha }{e}^{-i(\mathbf{q}-{\mathbf{q}}^{\prime })·{\mathbf{r}}_{\alpha }}⟨\widehat{\sigma }(-{\mathbf{q}}^{\prime },{\omega }_s-{\omega }_{p^{\prime }})\widehat{\sigma }(\mathbf{q},{\omega }_p-{\omega }_s)⟩\hfill \\ & +\sum _{\alpha }\sum _{\beta \ne \alpha }{e}^{-i(\mathbf{q}·{\mathbf{r}}_{\alpha }-{\mathbf{q}}^{\prime }·{\mathbf{r}}_{\beta })}⟨\widehat{\sigma }(-{\mathbf{q}}^{\prime },{\omega }_s-{\omega }_{p^{\prime }})⟩⟨\widehat{\sigma }(\mathbf{q},{\omega }_p-{\omega }_s)⟩.\hfill \end{array}$$ (12)

For a macroscopic sample initially in the ground electronic state, the standard classical theory of diffraction gives the signal as the product of the modulus square of the single-particle momentum-space electron density (the form factor) and a structure factor which describes the interparticle distribution (Eq. 2).²⁷ This formula is used to invert the X-ray diffraction signal to obtain the ground state electron density once the “phase problem” is resolved.⁴⁰ Substituting Eq. 12 into 11 yields a close resemblance to the classical expression for X-ray diffraction except that the coherent and incoherent terms now carry different form-factors. Note that, if we restrict attention to elastic scattering, the correlation function in the incoherent term separates into a modulus square form and the two form factors are equal.

TIME- AND WAVEVECTOR-DEPENDENT X-RAY SCATTERING FROM A SINGLE CYSTEINE MOLECULE

Cysteine is a sulfur-containing amino acid which affects the secondary structure of many proteins because of the disulfide bonds it forms. It has been implicated in biological charge transfer in respiratory complexes.⁴¹ We have previously explored various resonant X-ray spectroscopic signals from this molecule, including stimulated X-ray Raman scattering (SXRS) and X-ray photon echo.^{42, 43} Below, we present calculations of off-resonant scattering from a single cysteine molecule (chemical structure and orientation shown in Fig. 2c). Details of the computational methodology can be found in Sec. 7.

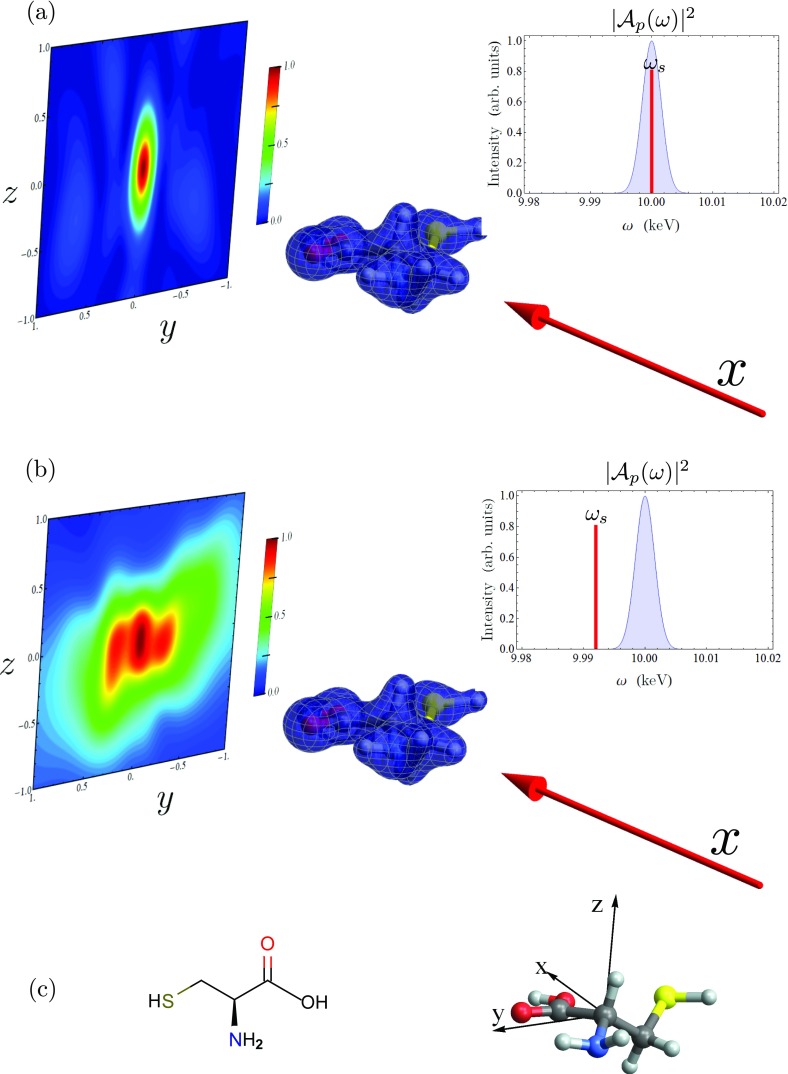
Figure 2.

Off-resonant scattering of a Gaussian X-ray pulse from cysteine for different detection frequencies. On the right, we show the pulse power spectrum in blue, with the detection frequency marked as a red line. The pulse propagation vector is shown as a red arrow, pointing at the molecule aligned in the lab frame, with the scattering pattern shown in the background. (a) The detection frequency ω_s is set equal to the pulse center frequency Ω_p, and the scattering signal is dominated by the elastic term. (b) The detection frequency is set to Ω_p − 9 eV, and the inelastic terms are dominant. (c) Chemical structure (left) and lab-frame orientation (right) of the cysteine molecule (O is red, S is green, N is blue, C is grey, H is white).

The scattering signal from the ground state (the second term in Eq. 10 with a = c = g, the ground state) is depicted in Figs. 2a, 2b. We also show the ground-state electron density, σ_gg(r), the pulse power spectrum, and the pulse wave vector for reference. As these calculations are for a single isolated molecule, we can restrict our scattering calculations to the second (incoherent) term in Eq. 10. We take the scattering pulse to be a transform-limited Gaussian

$${\mathcal{A}}_p\left(\omega \right)={\mathcal{A}}_p\sqrt{2\pi }{\tau }_p{e}^{-{\tau }_p^2{(\omega -{\Omega }_p)}^2/2}.$$ (13)

The center frequency Ω_p is set to 10 keV, and we take the direction of propagation to be in the positive x direction (for molecule orientation, see Fig. 2c). The pulse duration is τ_p = 300 as which corresponds to a fwhm bandwidth of 3.65 eV. Future progress in pulse-generation may make such experiments realizable. For this frequency range, the difference between $\tilde{\mathbf{q}}$ and q_ba for any two states a and b is negligibly small, and is ignored in the calculations presented herein.

We take the signal detectors to be on square grid, 2 cm in length on each side, located 1 cm from the molecule in the positive x direction (i.e., we detect forward-scattered light). This corresponds to a maximum detected scattering angle of 54.7°. We consider two different values for the detection frequency ω_s, one inside and one outside the pulse bandwidth. When we set the detection frequency equal to the pulse center frequency, we get the signal shown in Fig. 2a. This signal is dominated by the elastic scattering terms, where the scattering process does not change the state of the molecule. At this detection frequency, the elastic contribution is 4.4 × 10⁶ larger than the inelastic.

The elastic scattering term can be eliminated by moving the detection frequency outside the pulse bandwidth. In Fig. 2b, we show the scattering signal with a detection frequency ω_s = Ω_p − 9 eV. With this detection frequency, we see inelastic terms from valence states e whose excitation energy satisfies the condition that ω_eg + ω_s is within the pulse bandwidth. Therefore, all states with an energy between 4 and 12 eV will contribute. The scattering pattern resulting from the elastic and inelastic process are vastly different. The former is more strongly centered around the origin, corresponding to q = 0, and elongated in the z direction. The inelastic term, in addition to the feature at the origin, has two equal-intensity peaks at (y, z) = (−0.225 cm, −0.05 cm) and (0.25 cm, 0.0 cm), which, when converted to reciprocal space corresponds to (q_x, q_y, q_z) = (−0.08 a.u.⁻¹, −0.65 a.u.⁻¹, 0.0 a.u.⁻¹) and (−0.07 a.u.⁻¹, −0.60 a.u.⁻¹, −0.13 a.u.⁻¹), respectively.

We next turn to time-resolved scattering, in which an X-ray Raman preparation pulse ${\mathcal{A}}_R\left(\omega \right)$, resonant with the sulfur K edge, arrives at t = 0 followed by off-resonance scattering at time t = T. In this process, the Raman pulse acts twice on the same side of the loop, first promoting a sulfur 1s electron to the valence band before the transient core hole is filled by another valence electron. Because the Raman pulse is broadband, these two dipole interactions leave the molecule in a superposition of valence-excited states. This wavepacket is initially localized in the region surrounding the atom whose core is in resonance (sulfur in this case), but becomes delocalized across the molecule in a <5 fs time scale.^{44, 45}

The molecular density matrix immediately following the interaction with the first pulse is

$$\widehat{\rho }=i\widehat{\alpha }{\widehat{\rho }}_0-i{\widehat{\rho }}_0{\widehat{\alpha }}^{†},$$ (14)

where

$$\begin{array}{ccc}\hfill \widehat{\alpha }& =& \sum _{c,e}|e⟩\frac{({\mathit{\epsilon }}_R·{\mathit{\mu }}_{ec})({\mathit{\epsilon }}_R·{\mathit{\mu }}_{cg})}{2\pi }\hfill \\ & & \times {\int }_{-\infty }^{\infty }d\omega \frac{{\mathcal{A}}_R^{*}\left(\omega \right){\mathcal{A}}_R(\omega +{\omega }_{eg})}{\omega -{\omega }_{ce}+i{\Gamma }_c}⟨g|\hfill \end{array}$$ (15)

is the effective polarizability operator and ${\widehat{\rho }}_0$ is the initial (equilibrium) density matrix. In Eq. 15, ε_R is the polarization vector for the Raman pulse and μ_ec is the transition dipole between the valence-excited state e and the core-excited state c.

For a single-molecule system prepared in this manner (and with the simplification q → q₀), Eq. 10 assumes the form

$$\begin{array}{ccc}\hfill S({\mathit{k}}_s,T)& =& \sum _{e,e^{\prime }}i{\alpha }_{e,g}{e}^{-i{\omega }_{eg}T}{\mathcal{A}}_p({\omega }_s+{\omega }_{e^{\prime }e})\hfill \\ & & \times {\mathcal{A}}_p^{*}({\omega }_s+{\omega }_{e^{\prime }g}){\sigma }_{e^{\prime }e}\left(\tilde{\mathbf{q}}\right){\sigma }_{e^{\prime }g}^{*}\left(\tilde{\mathbf{q}}\right)+\mathrm{c}.\mathrm{c}.\hfill \end{array}$$ (16)

Note that any amplitude in the ground state after the Raman pulse has passed (terms in Eq. 16 where e = g) will contribute to a background, delay-time-independent signal, which can be filtered out. The remaining time-dependent scattering signal is a difference signal and will have positive and negative features, unlike the ground-state scattering signals from Fig. 2 which were only positive. The largest contributions will come from terms where e^′ in Eq. 16 is equal to either e or g.

We take the Raman pulse center frequency at the sulfur K-edge frequency Ω_R = 2.473 keV, and polarized along the x direction. The X-ray Raman signal is highly dependent upon the choice of polarization vector, and the nature of the underlying wavepacket is quite different for a y or z polarized pulses.⁴⁷ We take both the Raman and scattering pulses to be Gaussian with duration 100 as (fwhm of 10.96 eV). The broad bandwidth connects the ground state with the set of valence excited states, with energies between 5.7 eV and 9.0 eV. Figure 3 shows the time-dependent X-ray scattering signal for interpulse delays ranging from 0 to 20 fs. For each signal, we also show the transition density for the Raman wavepacket prior to interaction with the scattering pulse. This is defined by

$$\mathrm{Tr}\left[\widehat{\sigma }\left(\mathit{r}\right)\widehat{\rho }\right]=\sum _{e}i{\alpha }_{eg}{e}^{-i{\omega }_{eg}T}{\sigma }_{eg}\left(\mathit{r}\right)+\mathrm{c}.\mathrm{c}.$$ (17)

The left panel of Fig. 3 shows that the transition density is localized near the sulfur atom at T = 0 fs. In the supplementary material,⁴⁶ we show a movie of the time-dependent scattering signal and transition density for interpulse delays up to 20 fs. From the movie (see the supplementary material⁴⁶) and from Fig. 3 we see that there is a good deal more structure in the scattering signal along the y direction than along the z direction. This is consistent with the fact that the electronic motion induced by the Raman pulse is mostly in the y direction. While the correspondence between electronic motion in real space and the resulting scattering pattern is highly suggestive, it is not immediately apparent whether the transition density can be recovered from the scattering pattern alone. This is because the scattering pattern (Eq. 16) is not simply the Fourier transform of the density (Eq. 17).

Figure 3.

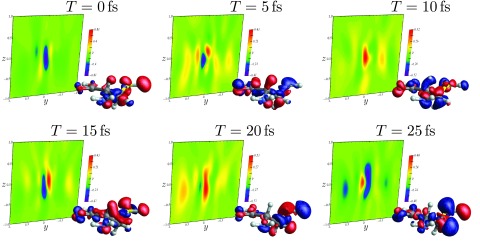
Background: time-dependent X-ray scattering (with ω_s = Ω_p) following X-ray Raman scattering (Eq. 16) for various interpulse delay times. Foreground: real-space transition charge densities for the Raman wavepacket (Eq. 17). Refer to Fig. 2c for the positions lab-frame orientation.

The scattering signal shows a complex dependence on time, reflecting interference between the many different electronic states which make up the superposition. The signal may not simply be thought of as a snapshot of the instantaneous time-dependent charge-density. The time variation strongly depends on the scattering direction, as can be seen in Fig. 4. Here, we depict the time evolution of six points from the T = 0 fs signal, corresponding to the highest and lowest peaks therein. Each trace has a beating pattern, representing a spatially resolved interferogram. Decay due to finite lifetime and dephasing is not included in the time-domain signals presented here. The contribution to the signal at a given detector due to a particular electronic coherence can be determined by Fourier transforming with respect to the delay time. This would give information on the transition density for the contributing excited states. However, we do not pursue this analysis here.

Figure 4.

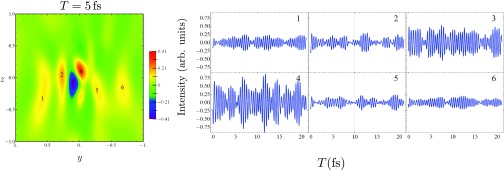
Time-dependence of the off-resonant X-ray scattering plot (with ω_s = Ω_p). Left: The scattering signal for T = 5 fs, with six different features labeled. Right: The evolution of these different features with increasing interpulse delay.

In Fig. 5, we show the variation of the time traces in Fig. 4 with the detection frequency ω_s. In the previous figures, ω_s was set equal to the scattering pulse center frequency, Ω_p. However, since purely elastic processes do not contribute to the time-dependent signal, the signal is larger for ω_s < Ω_p. The signal is maximized when, for a given e and e^′ from Eq. 16, both ${\omega }_s+{\omega }_{e^{\prime }e}$ and ${\omega }_s+{\omega }_{e^{\prime }g}$ lie within the pulse bandwidth.

Figure 5.

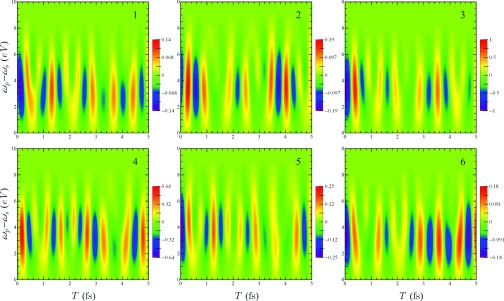
Variation of the six features in the T = 0 fs scattering signal in Fig. 5 with detection frequency ω_s and delay time T.

CONCLUSIONS

Coherent two-particle scattering from populations is an elastic process while coherent scattering from matter coherences is inelastic. Incoherent scattering, in contrast, generally produces both elastic and inelastic contributions regardless of the initial material state, as evident from Eq. 10. Thus, the coherent terms can only induce transitions between states populated by the material superposition state while the incoherent terms can induce transitions to any electronic state. Notably, the incoherent and coherent signals come with different particle form factors. Thus, the total signal may not be simply factored into the product of a particle form factor and a structure factor as in the classical theory. This issue had been addressed for X-ray scattering from a single hydrogen atom when it is prepared in a superposition state.³⁹ Our QED approach generalizes previous treatments^{34, 39} to properly account for arbitrary pulse bandshape, non-impulsive pulses, and detection details. The role of electronic coherence requires full account of frequency, time, and wavevector gated detection as is done here.

The present treatment fully incorporates inelastic scattering effects, which must be taken into account for single-molecule scattering. If the sample is initially in the ground state, the coherent scattering is entirely elastic and if the sample is prepared perturbatively, the coherent is dominated by elastic scattering while the incoherent terms are affected equally by the transition charge densities (σ_eg). Since light scattered from a single particle is not necessarily elastic and can change the state of the particle, obtaining the charge density from single-particle scattering will require distinguishing between the Rayleigh and Raman components. Furthermore, the total scattered intensity may not be fully described by the ground state charge density alone; it requires more information about electronic excited states of the particle, i.e., the transition charge densities. Our approach and simulations can provide valuable insight for future structural studies of proteins and nano-devices.

SIMULATION METHODS

The details of the electronic structure calculations can be found in Ref. 42, and are recounted briefly here. The optimized geometry of cysteine was obtained with the Gaussian09 package⁴⁸ at the B3LYP^{49, 50}/6-311G** level of theory. All time-dependent density functional theory (TDDFT) calculations were done at the CAM-B3LYP⁵¹/6-311++G(2d,2p) level of theory, and with the Tamm-Dancoff approximation (TDA).⁵² It was found that TDDFT with this type of long-range-corrected density functionals and diffused basis functions can describe Rydberg states well.^{53, 54} In these calculations, we include 50 valence excited states, with energies ranging from 5.4 eV to 9.0 eV. Core-excited states, in which a sulfur 1s electron is excited to the valence band, were calculated using restricted excitation window (REW) TDDFT with a locally modified version of NWChem code.^{55, 56} We also include 50 core-excited states for core excitations, with energies ranging from 2473.5 eV to 2495.9 eV (shifted to match experimental XANES results).

Transition density matrices between different valence excited states, which contribute to the summation in Eq. 9, are calculated using the CI coefficients from the TDDFT/TDA results, and are therefore in an unrelaxed sense. More accurate relaxed state-to-state transition density matrices could be calculated using the Z-vector method,^{57, 58} and this research is ongoing.

APPENDIX A: TIME-, FREQUENCY-, AND WAVEVECTOR-GATING OF SIGNALS

The signal is defined as the intensity of the detected electric field

$$S=\int dt\int d\mathbf{r}⟨{\mathbf{E}}^{†}(\mathbf{r},t)\mathbf{E}(\mathbf{r},t)⟩,$$ (A1)

where the detected electric field is represented as

$$\widehat{\mathbf{E}}(\mathbf{r},t)=\frac{1}{{\left(2\pi \right)}^4}\int d\omega \int d\mathbf{k}{e}^{-i\omega t+i\mathbf{k}·\mathbf{r}}\widehat{\mathbf{E}}(\mathbf{k},\omega ).$$ (A2)

Following the procedure outlined in Ref. 28, we add a series of gating functions to the detected electric field

$$\begin{array}{cc}& {\widehat{\mathbf{E}}}^{\left(t\right)}(\mathbf{r},t)=F_t(t,\overline{t})\widehat{\mathbf{E}}(\mathbf{r},t),\hfill \\ & {\widehat{\mathbf{E}}}^{\left(t\mathbf{r}\right)}(\mathbf{r},t)=F_{\mathbf{r}}(\mathbf{r},\overline{\mathbf{r}}){\widehat{\mathbf{E}}}^{\left(t\right)}(\mathbf{r},t),\hfill \\ \\ & {\widehat{\mathbf{E}}}^{\left(t\mathbf{r}f\right)}(\mathbf{r},t)=F_f(\omega ,\overline{\omega }){\widehat{\mathbf{E}}}^{\left(t\mathbf{r}\right)}(\mathbf{r},\omega ),\hfill \\ \hfill & {\widehat{\mathbf{E}}}^{\left(t\mathbf{r}f\mathbf{k}\right)}(\mathbf{r},t)=F_{\mathbf{k}}(\mathbf{k},\overline{\mathbf{k}}){\widehat{\mathbf{E}}}^{\left(t\mathbf{r}f\right)}(\mathbf{k},\omega ).\hfill \end{array}$$ (A3)

This gives

$$\begin{array}{cc}& {\widehat{\mathbf{E}}}^{\left(t\mathbf{r}f\mathbf{k}\right)}(\mathbf{r},t;\overline{t},\overline{\omega },\overline{\mathbf{r}},\overline{\mathbf{k}})\hfill \\ & =\int d{\mathbf{r}}^{\prime }\int d{t}^{\prime }\widehat{\mathbf{E}}({\mathbf{r}}^{\prime },t^{\prime })F_{\mathbf{k}}(\mathbf{r}-{\mathbf{r}}^{\prime },\mathbf{k})F_f(t-t^{\prime },\overline{\omega })\hfill \\ & \times F_{\mathbf{r}}({\mathbf{r}}^{\prime },\overline{\mathbf{r}})F_t(t^{\prime },\overline{t}).\hfill \end{array}$$ (A4)

The signal is then given by Eq. 5. We define the bare and detector spectrograms via

$$\begin{array}{ccc}& & W_B(t^{\prime },{\omega }^{\prime },{\mathbf{r}}^{\prime },{\mathbf{k}}^{\prime })\hfill \\ & & ={\int }_0^{\infty }d\tau e^{-i{\omega }^{\prime }\tau }\int d\mathbf{R}{e}^{i{\mathbf{k}}^{\prime }·\mathbf{R}}⟨\mathcal{T}{\widehat{\mathbf{E}}}_R^{†}({\mathbf{r}}^{\prime }+\mathbf{R}/2,t^{\prime }+\tau /2)\hfill \\ & & \times {\widehat{\mathbf{E}}}_L({\mathbf{r}}^{\prime }-\mathbf{R}/2,t^{\prime }-\tau /2)⟩,\hfill \end{array}$$ (A5)

$$\begin{array}{ccc}& & W_D(t^{\prime },{\omega }^{\prime },{\mathbf{r}}^{\prime },{\mathbf{k}}^{\prime };\overline{t},\overline{\omega },\overline{\mathbf{r}},\overline{\mathbf{k}})\hfill \\ & & =\int \frac{d\omega }{2\pi }{\left|F_f(\omega ,\overline{\omega })\right|}^2{W}_t(t^{\prime },{\omega }^{\prime }-\omega ,\overline{t})\hfill \\ & & \times \int \frac{d\mathbf{k}}{{\left(2\pi \right)}^3}{\left|F_{\mathbf{k}}(\mathbf{k},\overline{\mathbf{k}})\right|}^2{W}_{\mathbf{r}}({\mathbf{r}}^{\prime },{\mathbf{k}}^{\prime }-\mathbf{k},\overline{\mathbf{r}}),\hfill \end{array}$$ (A6)

where we have defined the auxiliary functions

$$W_t(t^{\prime },\omega ,\overline{t})\equiv \int d\tau F_t^{*}(t^{\prime }+\tau /2,\overline{t})F_t(t^{\prime }-\tau /2,\overline{t})e^{i\omega \tau }$$ (A7)

and

$$W_{\mathbf{r}}({\mathbf{r}}^{\prime },\mathbf{k},\overline{\mathbf{r}})\equiv \int d\mathbf{R}{F}_{\mathbf{r}}^{*}({\mathbf{r}}^{\prime }+\mathbf{R}/2,\overline{\mathbf{r}})F_{\mathbf{r}}({\mathbf{r}}^{\prime }-\mathbf{R}/2,\overline{\mathbf{r}})e^{-i\mathbf{k}·\mathbf{R}}.$$ (A8)

The signal is then given by the overlap of the two spectrograms

$$\begin{array}{ccc}\hfill S(\overline{t},\overline{\omega },\overline{\mathbf{k}},\overline{\mathbf{r}})& =& \int d{t}^{\prime }\frac{d{\omega }^{\prime }}{2\pi }\int d{\mathbf{r}}^{\prime }\frac{d{\mathbf{k}}^{\prime }}{{\left(2\pi \right)}^3}{W}_B(t^{\prime },{\omega }^{\prime },{\mathbf{r}}^{\prime },{\mathbf{k}}^{\prime })\hfill \\ & & \times W_D(t^{\prime },{\omega }^{\prime },{\mathbf{r}}^{\prime },{\mathbf{k}}^{\prime };\overline{t},\overline{\omega },\overline{\mathbf{k}},\overline{\mathbf{r}}).\hfill \end{array}$$ (A9)

For brevity, the following definitions are used in the derivations:

$$W_D(t^{\prime },{\omega }^{\prime };\overline{t},\overline{\omega })=\int \frac{d\omega }{2\pi }{\left|F_f(\omega ,\overline{\omega })\right|}^2{W}_t(t^{\prime },{\omega }^{\prime }-\omega ,\overline{t}),$$ (A10)

$$W_D({\mathbf{r}}^{\prime },{\mathbf{k}}^{\prime };\overline{\mathbf{r}},\overline{\mathbf{k}})=\int \frac{d\mathbf{k}}{{\left(2\pi \right)}^3}{\left|F_{\mathbf{k}}(\mathbf{k},\overline{\mathbf{k}})\right|}^2{W}_{\mathbf{r}}({\mathbf{r}}^{\prime },{\mathbf{k}}^{\prime }-\mathbf{k},\overline{\mathbf{r}}).$$ (A11)

APPENDIX B: DERIVATION OF THE BARE SPECTROGRAM

Beginning with Eq. A5, we expand it to leading order in H^′ (Eq. 1). This requires two interactions (one each for the ket and bra) since the signal mode is initially in a vacuum state

$$\begin{array}{cc}& W_B(t^{\prime },{\omega }^{\prime },{\mathbf{r}}^{\prime },{\mathbf{k}}^{\prime })\hfill \\ & =\sum _{{\mathbf{k}}_s,{\mathbf{k}}_{s^{\prime }}}\int d\tau e^{-i{\omega }^{\prime }\tau }\int d\mathbf{R}{e}^{i{\mathbf{k}}^{\prime }·\mathbf{R}}{\int }_{-\infty }^{t^{\prime }+\tau /2}d{t}_1^{\prime }{\int }_{-\infty }^{t^{\prime }-\tau /2}d{t}_1\hfill \\ & \times \int d{\mathbf{r}}_{1}d{\mathbf{r}}_1^{\prime }⟨{\widehat{\mathbf{E}}}_R^{\left(s^{\prime }\right)†}({\mathbf{r}}^{\prime }+\mathbf{R}/2,t^{\prime }+\tau /2)\hfill \\ & \times {\widehat{\mathbf{E}}}_L^{\left(s\right)}({\mathbf{r}}^{\prime }-\mathbf{R}/2,t^{\prime }-\tau /2){\widehat{\mathbf{A}}}_R^{\left(s^{\prime }\right)}({\mathbf{r}}_1^{\prime },t_1^{\prime })·{\widehat{\mathbf{A}}}_R^{\left(p\right)†}({\mathbf{r}}_1^{\prime },t_1^{\prime })\hfill \\ & \times {\widehat{\sigma }}_{T,R}({\mathbf{r}}_1^{\prime },t_1^{\prime }){\widehat{\mathbf{A}}}_L^{\left(s\right)†}({\mathbf{r}}_1,t_1)·{\widehat{\mathbf{A}}}_L^{\left(p\right)}({\mathbf{r}}_1,t_1){\widehat{\sigma }}_{T,L}({\mathbf{r}}_1,t_1){\rho }_T\left(0\right)⟩.\hfill \end{array}$$ (B1)

Here, the total density matrix is the direct product of field and matter density matrices immediately following state preparation (i.e., ρ_T(0) = ρ_F(0)⊗ρ_M(0)). The vector potential of the vacuum modes, ${\widehat{\mathbf{A}}}^{\left(s\right)}(\mathbf{r},t)$, is expanded as

$${\widehat{\mathbf{A}}}^{\left(s\right)}(\mathbf{r},t)=\sum _{{\mathbf{k}}_s,\nu }\sqrt{\frac{2\pi \hslash }{V{\omega }_s}}{\epsilon }^{\left(\nu \right)}\left({\widehat{\mathbf{k}}}_s\right){\widehat{a}}_{{\mathbf{k}}_s,\nu }{e}^{-i{\omega }_{s}t+i{\mathbf{k}}_s·\mathbf{r}}.$$ (B2)

Here, ${\widehat{a}}_{{\mathbf{k}}_s,\nu }$ is the annihilation operator for mode s and polarization ν, ${\epsilon }^{\left(\nu \right)}\left({\widehat{\mathbf{k}}}_s\right)$ is a unit vector in the direction of polarization, and V is the field quantization volume. The field operator is given by

$${\widehat{\mathbf{E}}}^{\left(s\right)}(\mathbf{r},t)=\sum _{{\mathbf{k}}_s,\nu }\sqrt{\frac{2\pi \hslash {\omega }_s}{V}}{\epsilon }^{\left(\nu \right)}\left({\widehat{\mathbf{k}}}_s\right){\widehat{a}}_{{\mathbf{k}}_s,\nu }{e}^{-i{\omega }_{s}t+i{\mathbf{k}}_s·\mathbf{r}},$$ (B3)

while the vector potential for the classical probe beam ${\widehat{\mathbf{A}}}^{\left(p\right)}(\mathbf{r},t)$ is represented as

$${\widehat{\mathbf{A}}}^{\left(p\right)}(\mathbf{r},t)=\sum _{\nu }{P}_{\nu }{\epsilon }^{\left(\nu \right)}\left({\widehat{\mathbf{k}}}_p\right)\int \frac{d{\omega }_p}{2\pi }{A}_p\left({\omega }_p\right)e^{-i{\omega }_{p}t+i{\mathbf{k}}_p·\mathbf{r}},$$ (B4)

where P_ν is the fraction of the probe pulse in polarization state ν and ${\epsilon }^{\left(\nu \right)}\left({\widehat{\mathbf{k}}}_p\right)$ is a unit vector in the direction of direction of polarization ν. Henceforth, we will use the shorthand ${\sum }_{\nu }{P}_{\nu }{\epsilon }^{\left(\nu \right)}\left({\widehat{\mathbf{k}}}_p\right)=\overline{\epsilon }\left({\widehat{\mathbf{k}}}_p\right)$ and assume a narrow beam so that ${\widehat{\mathbf{k}}}_p={\widehat{\mathbf{k}}}_{p^{\prime }}$. Note that, by starting the $t_1^{\prime }$ and t₁ integrations at −∞, we assume that the scattered pulse is well separated from the state preparation process. Inserting these definitions into Eq. B1, separating matter and field correlation functions (and evaluating the latter with the conditions described above), we obtain

$$\begin{array}{cc}& W_B(t^{\prime },{\omega }^{\prime },{\mathbf{r}}^{\prime },{\mathbf{k}}^{\prime })\hfill \\ & =\frac{1}{4V^2}\sum _{{\mathbf{k}}_s,{\mathbf{k}}_{s^{\prime }}}\int d\tau e^{-i{\omega }^{\prime }\tau }\int d\mathbf{R}{e}^{i{\mathbf{k}}^{\prime }·\mathbf{R}}{\int }_{-\infty }^{t^{\prime }+\tau /2}d{t}_1^{\prime }\hfill \\ & \times {\int }_{-\infty }^{t^{\prime }-\tau /2}d{t}_1{e}^{i{\omega }_{s^{\prime }}(t^{\prime }+\tau /2-t_1)-i{\omega }_s(t^{\prime }-\tau /2-t_1^{\prime })}\hfill \\ & \times \int d{\omega }_{p}d{\omega }_{p^{\prime }}{A}_p\left({\omega }_p\right)A_p^{*}\left({\omega }_{p^{\prime }}\right)e^{-i{\omega }_p{t}_1}{e}^{i{\omega }_{p^{\prime }}{t}_1^{\prime }}\hfill \\ & \times \int d{\mathbf{r}}_{1}d{\mathbf{r}}_1^{\prime }\sum _{\alpha ,\beta }^N\sum _{\lambda ,{\lambda }^{\prime }}({\epsilon }^{\left(\lambda \right)}\left({\widehat{\mathbf{k}}}_s\right)·\overline{\epsilon }\left({\widehat{\mathbf{k}}}_p\right))({\epsilon }^{\left({\lambda }^{\prime }\right)}\left({\widehat{\mathbf{k}}}_{s^{\prime }}\right)·\overline{\epsilon }\left({\widehat{\mathbf{k}}}_p\right))\hfill \\ & \times ({\epsilon }^{\left(\lambda \right)}\left({\widehat{\mathbf{k}}}_s\right)·{\mu }_D)({\epsilon }^{\left({\lambda }^{\prime }\right)}\left({\widehat{\mathbf{k}}}_{s^{\prime }}\right)·{\mu }_D)e^{i{\mathbf{k}}_s·({\mathbf{r}}^{\prime }-\mathbf{R}/2)}\hfill \\ & \times e^{-i{\mathbf{k}}_{s^{\prime }}·({\mathbf{r}}^{\prime }+\mathbf{R}/2)}{e}^{-i({\mathbf{k}}_s-{\mathbf{k}}_p)·{\mathbf{r}}_1}{e}^{i({\mathbf{k}}_{s^{\prime }}-{\mathbf{k}}_{p^{\prime }})·{\mathbf{r}}_1^{\prime }}\hfill \\ & \times ⟨{\widehat{\sigma }}_R^{\beta †}({\mathbf{r}}_1^{\prime },t_1^{\prime }){\widehat{\sigma }}_L^{\alpha }({\mathbf{r}}_1,t_1){\rho }_M\left(0\right)⟩,\hfill \end{array}$$ (B5)

where we have taken a dipolar-interaction model for the detection event with μ_D the dipole moment of the detector. We have also defined ${\widehat{\sigma }}^{\alpha }\left(\mathbf{r}\right)\equiv \widehat{\sigma }(\mathbf{r}-{\mathbf{r}}_{\alpha })$ so that ${\widehat{\sigma }}_T\left(\mathbf{r}\right)={\sum }_{\alpha }{\widehat{\sigma }}^{\alpha }\left(\mathbf{r}\right)$.

Coherent terms

We first examine the α ≠ β terms in the above. Assuming that the particles are uncorrelated, we have ρ_M(0) = ρ_α(0)⊗ρ_β(0). The correlation function therefore splits and we can separately collect factors associated with each particle. That is, we define

$$\begin{array}{cc}\hfill {\Pi }^{\left(\alpha \right)}(\mathbf{r},t)=& \frac{1}{2V}\sum _{{\mathbf{k}}_s,\lambda }{\int }_{-\infty }^{t}d{t}_1{e}^{-i{\omega }_s(t-t_1)}\hfill \\ & \times \int \frac{d{\omega }_p}{2\pi }{A}_p\left({\omega }_p\right)e^{-i{\omega }_p{t}_1}{e}^{i{\mathbf{k}}_s·\mathbf{r}}\hfill \\ & \times \int d{\mathbf{r}}_1({\epsilon }^{\left(\lambda \right)}\left({\widehat{\mathbf{k}}}_s\right)·\overline{\epsilon }\left({\widehat{\mathbf{k}}}_p\right))({\epsilon }^{\left(\lambda \right)}\left({\widehat{\mathbf{k}}}_s\right)·{\mu }_D)\hfill \\ & \times e^{-i({\mathbf{k}}_s-{\mathbf{k}}_p)·{\mathbf{r}}_1}{⟨{\widehat{\sigma }}^{\alpha }({\mathbf{r}}_1,t_1)⟩}_{\alpha },\hfill \end{array}$$ (B6)

where ⟨…⟩_α = Tr[…ρ_α(0)] is the trace over the product of the argument and the density matrix immediately after the state preparation process (ρ_α(0)). The coherent spectrogram is then given by

$$\begin{array}{cc}& W_{B,coh}(t^{\prime },{\omega }^{\prime },{\mathbf{r}}^{\prime },{\mathbf{k}}^{\prime })\hfill \\ & =\sum _{\alpha ,\beta }\int d\tau e^{-i{\omega }^{\prime }\tau }\int d\mathbf{R}{e}^{i{\mathbf{k}}^{\prime }·\mathbf{R}}{\Pi }^{\left(\alpha \right)}({\mathbf{r}}^{\prime }-\mathbf{R}/2,t^{\prime }-\tau /2)\hfill \\ & \times {\Pi }^{\left(\beta \right)†}({\mathbf{r}}^{\prime }+\mathbf{R}/2,t^{\prime }+\tau /2).\hfill \end{array}$$ (B7)

In order to carry out the integration over dt₁, we use the Fourier Transform

$${⟨{\widehat{\sigma }}^{\alpha }({\mathbf{r}}_1,t_1)⟩}_{\alpha }=\int \frac{d\tilde{\omega }}{2\pi }{e}^{i\tilde{\omega }{t}_1}{⟨{\widehat{\sigma }}^{\alpha }({\mathbf{r}}_1,\tilde{\omega })⟩}_{\alpha }.$$ (B8)

We thus have

$$\begin{array}{cc}\hfill {\Pi }^{\left(\alpha \right)}(\mathbf{r},t)=& \frac{1}{2V}\sum _{{\mathbf{k}}_s}\sum _{ij}{\overline{\epsilon }}_i\left({\widehat{\mathbf{k}}}_p\right){\mu }_{Dj}({\delta }_{ij}-{\widehat{k}}_{si}{\widehat{k}}_{sj})\hfill \\ & \times \int d{\mathbf{r}}_1\int \frac{d{\omega }_p}{2\pi }{A}_p\left({\omega }_p\right)\hfill \\ & \times \int \frac{d\tilde{\omega }}{2\pi }{⟨{\widehat{\sigma }}^{\alpha }({\mathbf{r}}_1,\tilde{\omega })⟩}_{\alpha }{e}^{i{\mathbf{k}}_s·\mathbf{r}}{e}^{-i({\mathbf{k}}_s-{\mathbf{k}}_p)·{\mathbf{r}}_1}{e}^{-i{\omega }_{s}t}\hfill \\ & \times {\int }_{-\infty }^{t}d{t}_1{e}^{i(\tilde{\omega }+{\omega }_s-{\omega }_p)t_1},\hfill \end{array}$$ (B9)

where we have also expanded the dot products of the polarizations and used the identity

$$\sum _{\lambda }{\epsilon }_i^{\left(\lambda \right)}\left({\widehat{\mathbf{k}}}_s\right){\epsilon }_j^{\left(\lambda \right)}\left({\widehat{\mathbf{k}}}_s\right)={\delta }_{ij}-{\widehat{k}}_{si}{\widehat{k}}_{sj}.$$ (B10)

We are now free to carry out the time integration

$${\int }_{-\infty }^t{e}^{i(\tilde{\omega }+{\omega }_s-{\omega }_p)t_1}=\frac{(-i)e^{i(\tilde{\omega }+{\omega }_s-{\omega }_p)t}}{\omega +{\omega }_s-{\omega }_p-i\eta },$$ (B11)

where η is a positive infinitesimal. We change the summation over k_s to an integration via

$$\frac{1}{V}\sum _{{\mathbf{k}}_s}\to \frac{1}{{\left(2\pi \right)}^3}\int d{\mathbf{k}}_{\mathbf{s}}=\int \frac{{\omega }_s^{2}d{\omega }_s}{{\left(2\pi c\right)}^3}d{\Omega }_s$$ (B12)

and make use of the relation⁵⁹

$$\int d{\Omega }_s({\delta }_{ij}-{\widehat{k}}_{si}{\widehat{k}}_{sj})e^{\pm i{\mathbf{k}}_s·\mathbf{r}}=(-{\nabla }^2{\delta }_{ij}+{\nabla }_i{\nabla }_j)\frac{\sin k_{s}r}{k_s^{3}r}.$$ (B13)

This gives

$$\begin{array}{cc}\hfill {\Pi }^{\left(\alpha \right)}(\mathbf{r},t)=& \frac{-i}{2{\left(2\pi \right)}^3}\sum _{ij}{\overline{\epsilon }}_i\left({\widehat{\mathbf{k}}}_p\right){\mu }_{Dj}(-{\nabla }^2{\delta }_{ij}+{\nabla }_i{\nabla }_j)\hfill \\ & \times \int d{\mathbf{r}}_1\int \frac{d{\omega }_p}{2\pi }{A}_p\left({\omega }_p\right)\hfill \\ & \times \int \frac{d\tilde{\omega }}{2\pi }{⟨{\widehat{\sigma }}^{\alpha }({\mathbf{r}}_1,\tilde{\omega })⟩}_{\alpha }{e}^{i{\mathbf{k}}_p·{\mathbf{r}}_1}{e}^{i(\tilde{\omega }-{\omega }_p)t}\hfill \\ & \times \int d{\omega }_s\frac{\sin {\omega }_s\tilde{r}/c}{{\omega }_s({\omega }_s-({\omega }_p-\tilde{\omega }+i\eta ))}\frac{1}{\tilde{r}},\hfill \end{array}$$ (B14)

where we have defined $\tilde{\mathbf{r}}=\mathbf{r}-{\mathbf{r}}_1$. The dω_s integral has poles at ω_s = 0 and ${\omega }_s={\omega }_p-\tilde{\omega }$. The term arising from the residue at the first pole will have a factor $\frac{1}{{\omega }_p-\tilde{\omega }}$. Because the interaction between the sample and the field is off-resonant, ω_p will not be close to any material frequency. The term arising from the residue of the pole at ω_s = 0 is negligible in such a process. Thus, we may perform the dω_s integration

$$\int d{\omega }_s\frac{\sin {\omega }_s\tilde{r}/c}{{\omega }_s({\omega }_s-({\omega }_p-\tilde{\omega }+i\eta ))}=\frac{\pi e^{i({\omega }_p-\tilde{\omega })\tilde{r}/c}}{{\omega }_p-\tilde{\omega }}.$$ (B15)

Using the identity

$$\begin{array}{cc}& (-{\nabla }^2{\delta }_{ij}+{\nabla }_i{\nabla }_j)e^{ikr}\hfill \\ & =\{({\delta }_{ij}-3{\widehat{r}}_i{\widehat{r}}_j)(ikr-1)+({\delta }_{ij}-{\widehat{r}}_i{\widehat{r}}_j)k^2{r}^2\}\frac{e^{ikr}}{r^2}\hfill \end{array}$$ (B16)

and rotationally averaging so that ${\widehat{r}}_i{\widehat{r}}_j=\frac{1}{3}{\delta }_{ij}$ results in

$$\begin{array}{cc}\hfill {\Pi }^{\left(\alpha \right)}(\mathbf{r},t)=& \frac{-i(\overline{\epsilon }\left({\widehat{\mathbf{k}}}_p\right)·{\mu }_D)}{6{\left(2\pi c\right)}^2\tilde{r}}\int \frac{d{\omega }_p}{2\pi }{A}_p\left({\omega }_p\right)\int \frac{d\tilde{\omega }}{2\pi }\hfill \\ & \times \int d{\mathbf{r}}_1{e}^{i{\mathbf{k}}_p·{\mathbf{r}}_1}{e}^{-i({\omega }_p-\tilde{\omega })(t-\tilde{r}/c)}({\omega }_p-\tilde{\omega })⟨{\widehat{\sigma }}^{\alpha }({\mathbf{r}}_1,\tilde{\omega })⟩.\hfill \end{array}$$ (B17)

Placing the origin within the sample and taking the detector to be far away (in comparison to the size of the sample) allows the approximation $\tilde{r}=|{\mathbf{r}}^{\prime }-\mathbf{R}/2-{\mathbf{r}}_1|\simeq r^{\prime }-{\widehat{\mathbf{r}}}^{\prime }·({\mathbf{r}}_1+\mathbf{R}/2)$. Where we have substituted r = r′ − R/2 since that is the point at which we will eventually evaluate Π^(α). Although we will later formally integrate over all R, this represents different detection locations and thus should only be carried out over the area of a detector pixel. The assumption that R is small compared to r^′ (the distance to the detector) is thus justified. Dropping the retardation due to r^′ (since this uniformly delays the signal by some constant due to travel time) and replacing the $\tilde{r}$ in the denominator by r^′ simplifies the expression yielding

$$\begin{array}{cc}& {\Pi }^{\left(\alpha \right)}({\mathbf{r}}^{\prime }-\mathbf{R}/2,t)\hfill \\ & =\frac{-i(\overline{\epsilon }\left({\widehat{\mathbf{k}}}_p\right)·{\mu }_D)}{6{\left(2\pi c\right)}^2\tilde{r}}\int d{\omega }_p{A}_p\left({\omega }_p\right)\hfill \\ & \times \int \frac{d\tilde{\omega }}{2\pi }{e}^{-i({\omega }_p-\tilde{\omega })(t-\frac{1}{c}{\widehat{\mathbf{r}}}^{\prime }·\mathbf{R}/2)}({\omega }_p-\tilde{\omega })⟨\widehat{\sigma }(\mathbf{Q}\left(\tilde{\omega }\right),\tilde{\omega })⟩e^{-i\mathbf{Q}\left(\tilde{\omega }\right)·{\mathbf{r}}_{\alpha }},\hfill \end{array}$$ (B18)

where we have also carried out the dr₁ integration via

$$\begin{array}{c}\hfill \int d\mathbf{r}{e}^{-i\mathbf{k}·\mathbf{r}}⟨{\widehat{\sigma }}^{\alpha }(\mathbf{r},\tilde{\omega })⟩=⟨\widehat{\sigma }(\mathbf{Q}\left(\tilde{\omega }\right),\tilde{\omega })⟩e^{-i\mathbf{Q}\left(\tilde{\omega }\right)·{\mathbf{r}}_{\alpha }}\end{array}$$ (B19)

with ${\mathbf{Q}}^{(\prime )}\left(\tilde{\omega }\right)\equiv \frac{1}{c}({\omega }_{p^{(\prime )}}-\tilde{\omega }){\widehat{\mathbf{r}}}^{\prime }-{\mathbf{k}}_{p^{(\prime )}}$. We are now in a position to perform the integrations over dτ and dR in Eq. B7

$$\begin{array}{c}\hfill \int d\tau e^{-i({\omega }^{\prime }-\frac{\Omega }{2})\tau }=2\pi \delta \left({\omega }^{\prime }-\frac{\Omega }{2}\right),\end{array}$$ (B20)

$$\begin{array}{c}\hfill \int d\mathbf{R}{e}^{-i({\mathbf{k}}^{\prime }-\frac{\Omega }{2c}{\widehat{\mathbf{r}}}^{\prime })·\mathbf{R}}={\left(2\pi \right)}^3\delta \left({\mathbf{k}}^{\prime }-\frac{\Omega }{2c}{\widehat{\mathbf{r}}}^{\prime }\right),\end{array}$$ (B21)

with $\Omega \equiv {\omega }_p+{\omega }_p^{\prime }-\tilde{\omega }-{\tilde{\omega }}^{\prime }$ defined for convenience. The bare coherent spectrogram is then

$$\begin{array}{cc}& W_{B,coh}(t^{\prime },{\omega }^{\prime },{\mathbf{r}}^{\prime },{\mathbf{k}}^{\prime })\hfill \\ & =\frac{|\overline{\epsilon }\left({\widehat{\mathbf{k}}}_p\right)·{\mu }_D{|}^2}{36{\left(2\pi \right)}^2{c}^4{r}^{\prime 2}}\sum _{\alpha }\sum _{\beta \ne \alpha }\int d{\omega }_{p}d{\omega }_{p^{\prime }}d\tilde{\omega }d{\tilde{\omega }}^{\prime }{A}_p\left({\omega }_p\right)\hfill \\ & \times A_p^{*}\left({\omega }_{p^{\prime }}\right)({\omega }_p-\tilde{\omega })({\omega }_{p^{\prime }}-{\tilde{\omega }}^{\prime }),\hfill \\ & ⟨\widehat{\sigma }(\mathbf{Q}\left(\tilde{\omega }\right),\tilde{\omega })⟩⟨\widehat{\sigma }(-{\mathbf{Q}}^{\prime }(-{\tilde{\omega }}^{\prime }),-{\tilde{\omega }}^{\prime })⟩e^{-i\mathbf{Q}\left(\tilde{\omega }\right)·{\mathbf{r}}_{\alpha }}{e}^{i{\mathbf{Q}}^{\prime }(-{\tilde{\omega }}^{\prime })·{\mathbf{r}}_{\beta }}\hfill \\ & \times e^{-i({\omega }_p-{\omega }_{p^{\prime }}+{\tilde{\omega }}^{\prime }-\tilde{\omega })t^{\prime }}\delta \left({\omega }^{\prime }-\frac{\Omega }{2}\right)\delta \left({\mathbf{k}}^{\prime }-\frac{\Omega }{2c}{\widehat{\mathbf{r}}}^{\prime }\right).\hfill \end{array}$$ (B22)

Incoherent terms

The incoherent (α = β) terms contain the correlation function

$$⟨\mathcal{T}{\widehat{\sigma }}_R^{\alpha †}({\mathbf{r}}_1^{\prime },t_1^{\prime }){\widehat{\sigma }}_L^{\alpha }({\mathbf{r}}_1,t_1)⟩.$$ (B23)

Since there is only one operator on each side of the density matrix, there is no time ordering ambiguity and we may drop T. The Hilbert space expression is then

$$Tr\left[{\widehat{\sigma }}^{\alpha †}({\mathbf{r}}_1^{\prime },t_1^{\prime }){\widehat{\sigma }}^{\alpha }({\mathbf{r}}_1,t_1){\rho }_{\alpha }\left(0\right)\right].$$ (B24)

Although we may not factor this into a product of correlation functions, we may still go through the same series of simplifications as in the coherent case resulting in

$$\begin{array}{cc}& W_{B,inc}(t^{\prime },{\omega }^{\prime },{\mathbf{r}}^{\prime },{\mathbf{k}}^{\prime })\hfill \\ & =2\pi K\sum _{\alpha }\int d{\omega }_{p}d{\omega }_{p^{\prime }}d\tilde{\omega }d{\tilde{\omega }}^{\prime }{A}_p\left({\omega }_p\right)\hfill \\ & \times A_p^{*}\left({\omega }_{p^{\prime }}\right)({\omega }_p-\tilde{\omega })({\omega }_{p^{\prime }}-{\tilde{\omega }}^{\prime })\hfill \\ & ⟨\widehat{\sigma }(-{\mathbf{Q}}^{\prime }(-{\tilde{\omega }}^{\prime }),-{\tilde{\omega }}^{\prime })\widehat{\sigma }(\mathbf{Q}\left(\tilde{\omega }\right),\tilde{\omega })⟩e^{-i(\mathbf{Q}\left(\tilde{\omega }\right)-{\mathbf{Q}}^{\prime }(-{\tilde{\omega }}^{\prime }))·{\mathbf{r}}_{\alpha }}\hfill \\ & \times e^{-i({\omega }_p-{\omega }_{p^{\prime }}+{\tilde{\omega }}^{\prime }-\tilde{\omega })t^{\prime }}\delta \left({\omega }^{\prime }-\frac{\Omega }{2}\right)\delta \left({\mathbf{k}}^{\prime }-\frac{\Omega }{2c}{\widehat{\mathbf{r}}}^{\prime }\right).\hfill \end{array}$$ (B25)

The total (incoherent plus coherent) bare spectrogram may also be written in a form similar to this

$$\begin{array}{cc}& W_{B,T}(t^{\prime },{\omega }^{\prime },{\mathbf{r}}^{\prime },{\mathbf{k}}^{\prime })\hfill \\ & =2\pi K\int d{\omega }_{p}d{\omega }_{p^{\prime }}d\tilde{\omega }d{\tilde{\omega }}^{\prime }{A}_p\left({\omega }_p\right)\hfill \\ & \times A_p^{*}\left({\omega }_{p^{\prime }}\right)({\omega }_p-\tilde{\omega })({\omega }_{p^{\prime }}-{\tilde{\omega }}^{\prime })\hfill \\ & ⟨{\widehat{\sigma }}_T(\mathbf{Q}\left(\tilde{\omega }\right),\tilde{\omega }){\widehat{\sigma }}_T(-{\mathbf{Q}}^{\prime }(-{\tilde{\omega }}^{\prime }),-{\tilde{\omega }}^{\prime })⟩\hfill \\ & \times e^{-i({\omega }_p-{\omega }_{p^{\prime }}+{\tilde{\omega }}^{\prime }-\tilde{\omega })t^{\prime }}\delta \left({\omega }^{\prime }-\frac{\Omega }{2}\right)\delta \left({\mathbf{k}}^{\prime }-\frac{\Omega }{2c}{\widehat{\mathbf{r}}}^{\prime }\right)\hfill \end{array}$$ (B26)

when given in terms of the total (many-particle) charge density.