Least Squares for Diffusion Tensor Estimation Revisited: Propagation of Uncertainty with Rician and non-Rician Signals

Abstract

Least Squares (LS) and its minimum variance counterpart, Weighted Least Squares (WLS), have become very popular when estimating the Diffusion Tensor (DT), to the point that they are the standard in most of the existing software for diffusion MRI. They are based on the linearization of the Stejskal-Tanner equation by means of the logarithmic compression of the diffusion signal. Due to the Rician nature of noise in traditional systems, a certain bias in the estimation is known to exist. This artifact has been made patent through some experimental set-ups, but it is not clear how the distortion translates in the reconstructed DT, and how important it is when compared to the other source of error contributing to the Mean Squared Error (MSE) in the estimate, i.e. the variance. In this paper we propose the analytical characterization of log-Rician noise and its propagation to the components of the DT through power series expansions. We conclude that even in highly noisy scenarios the bias for log-Rician signals remains moderate when compared to the corresponding variance. Yet, with the advent of Parallel Imaging (pMRI), the Rician model is not always valid. We make our analysis extensive to a number of modern acquisition techniques through the study of a more general Non Central-Chi (nc-χ) model. Since WLS techniques were initially designed bearing in mind Rician noise, it is not clear wether or not they still apply to pMRI. An important finding in our work is that the common implementation of WLS is nearly optimal when nc-χ noise is considered. Unfortunately, the bias in the estimation becomes far more important in this case, to the point that it may nearly overwhelm the variance in given situations. Furthermore, we evidence that such bias cannot be removed by increasing the number of acquired gradient directions. A number of experiments have been conducted that corroborate our analytical findings, while in vivo data have been used to test the actual relevance of the bias in the estimation.

1 Introduction

Diffusion Tensor Magnetic Resonance Imaging (DT-MRI) is a modality within Nuclear Magnetic Resonance (NMR) which exploits the diffusion of the spins associated to water molecules in the soft tissues to infer the macroscopic anisotropy of certain anatomies. Although other applications are possible, its clinical use is mostly devoted to neurosciences and brain imaging, where it has allowed tracking the principal directions and connectivity of nerve fibers in the white matter in vivo (Basser et al., 1994; Basser and Pierpaoli, 1996).

DT-MRI aims at characterizing the macroscopic statistics of the diffusion process at each imaged voxel. In the white matter, water molecules are supposed to move preferentially along the nerve fibers but not in the transverse directions, for which the myelin coats surrounding the neural axons restrict the diffusion. This assumption is reasonable as long as the diffusion time used in the experiment is short enough compared to the time scale of water exchange between compartments.

Although the statistics of diffusion in a restricted medium (neural axon) filled with an isotropic material (water) are rather complex, see Söderman and Jönsson (1995), the physical space of the voxel comprises a large number of pores containing a large number of water molecules each. If the pores are coherently oriented, the overall statistics will be the ensemble average of a large number of independent and roughly equally distributed individual statistics, yielding a 3-D multivariate Gaussian process with zero mean and anisotropic variance D, the so-called Diffusion Tensor (DT). As a covariance matrix, the DT can be represented as a 3 × 3 symmetric matrix with real, positive eigenvalues and orthogonal eigenvectors.

On the other hand, DT-MRI shows well-known limitations when the microscopic pores are not coherently oriented, as it is the case in scenarios of fibers crossing, bending, or kissing (Tuch, 2004; Wedeen et al., 2005). A number of approaches have appeared in the recent years to overcome these problems, such as Diffusion Spectrum Imaging (DSI) (Wedeen et al., 2005) or High Angular Resolution Diffusion Imaging (HARDI) (Jansons and Alexander, 2003; Özarslan et al., 2006; Tournier et al., 2007; Tristán-Vega et al., 2009b, 2010; Tuch, 2004). Despite this consideration, DT-MRI is nowadays a well-accepted and wide-spread technique, having shown its enormous potential for the diagnosis and treatment of several diseases including brain tumors and injuries, epilepsy, schizophrenia, or Alzheimer among others, see Sundgren et al. (2004); Taylor et al. (2004) for some reviews on this topic.

The ubiquitousness of DT-MRI applications justifies the importance of the research and development of new techniques for data processing and interpretation. At the heart of these techniques, especially those involving quantitative parameters, is the proper estimation of the DT from noisy MRI data sets. This is done by means of a Pulse Gradient Spin Echo (PGSE) sequence (Stejskal and Tanner, 1965): by applying a strong sensitizing pulsed gradient in the magnetic field, the obtained signals suffer a net attenuation compared to the unweighted T2 images. Such signals are the so-called Diffusion Weighted Images (DWI). Their attenuation strongly depends on the direction of the pulsed gradient, so that the larger fading corresponds to those orientations parallel to the primary directions in which the stochastic water diffusion proceeds.

Given the symmetry of the DT, only six free parameters are required to fully describe the diffusion process, which can be estimated by applying, at least, six different sensitizing gradients along independent directions (additionally, a T2 unweighted image is required to measure the attenuation). Then, a well posed linear system with six equations and six unknowns can be arranged and solved with standard methods. However, this former idea is not very useful in practice, since DWI are much more effected by acquisition noise, traditionally modeled as Rician distributed (Gudbjartsson and Patz, 1995), than anatomical MRI due to the strong attenuations necessary to measure diffusion (Basser and Pajevic, 2000). This artifact has lead to the use of redundant gradient directions to arrange an overdetermined system of linear equations which may be solved by means of Least Squares (LS) approaches.

A relevant reference in this sense is Salvador et al. (2005), since it formalizes the estimation based on Weighted Least Squares (WLS) and formally describes an iterative correction for WLS which is today a common methodology in DT-MRI software. For log-Rician distributed noise (coming from the linearization of the PGSE equation, see section 2.3), the author empirically derives the optimal weights to be used in order for the Gauss-Markov theorem to ensure that the estimate has minimum variance. Additionally, it is analytically evidenced that for a moderate Signal to Noise Ratio (SNR) the bias in the estimation is close to zero, and hence the estimator is the Best Linear Unbiased Estimator (BLUE) (Kay, 1993), which is to say that it is the optimal linear estimator in the sense of the Mean Squared Error (MSE).

Of course, other approaches for the estimation of the DT are possible, including: non-linear LS (Koay et al., 2006); LS with outlier rejection (Chang et al., 2005; Mangin et al., 2002); Maximum Likelihood (ML) and Maximum a Posteriori (MAP) estimation (Andersson, 2008; Landman et al., 2007); log-Euclidean computing to ensure the Positive Definite (PD) property of the DT (Arsigny et al., 2006; Fillard et al., 2007); variational frameworks featuring built-in spatial regularization (Tschumperle and Deriche, 2003; Wang et al., 2004); or sequential techniques for online estimation (Brion et al., 2010; Poupon et al., 2008) (which are indeed based on LS). Even so, LS and WLS are still the standard in most of DT-MRI software and commercial machinery due to their simplicity, computational efficiency, and optimality properties.

Since the work by Salvador appeared (and even before), some imaging protocols based on multiple-coil sensing have become very popular. Parallel Magnetic Resonance Imaging (pMRI) is based on the simultaneous acquisition of the different parts of the MRI volume by a number of independent coils with a given spatial distribution within the MRI scanner. It allows to reduce the geometric distortions produced by phase evolutions between subsequent echoes in Echo Planar Images (EPI), and to improve the SNR of the acquisitions by the combination of the signals proceeding from each of the radio frequency antennas. Under certain assumptions, the sum of their squared magnitudes (SoS) closely resembles the optimal combination in the sense of the MSE (Gilbert et al., 2007), and hence this is a popular approach. To reduce the geometric artifacts, the k-space at each receiver is subsampled, and the lost data is interpolated by somehow combining the redundant information. Despite the variety of techniques available, see Larkman and Nunes (2007) for a review, two of them are the most widely accepted today: Sensitivity Encoding (Pruessmann et al., 1999, SENSE), which performs the reconstruction of the composite signal from the signals at each coil in the spatial domain, and the GeneRalized Autocalibrated Partially Parallel Acquisition (Griswold et al., 2002, GRAPPA) protocol, which linearly interpolates the down-sampled k-space using a set of complex weights learnt from the low frequency spectrum (the so-called AutoCalibrating Signal, ACS). The latter has the additional advantage that it does not need a prior knowledge on the spatial sensitivity of the coils, hence the term Autocalibrated.

Naturally, the reconstruction procedure alters the statistics of the image (Thunberg and Zetterberg, 2007). With SENSE the noise can still be modeled as Rician, although a spatial pattern of variation of the noise power, the g-factor, is introduced (Larkman and Nunes, 2007). This is not an issue for the estimation of the DT as long as the estimator does not need to characterize the noise power, as it is the case with LS/WLS. However, the g-factor also stands for a decrease in the SNR which highly effects the bias in the calculation.

On the contrary, with fully sampled pMRI and also with GRAPPA, a whole complex spatial domain is reconstructed at each of the receiving coils which are further combined, in most of cases, using SoS. Obviously, the Rician statistics no longer apply to this case; if the signals at each coil are considered roughly uncorrelated, Non Central-Chi (nc-χ) statistics arise (Constantinides et al., 1997). However, this assumption is too coarse, and correlations between coils do exist (Aja-Fernández and Tristán-Vega, 2011; Thunberg and Zetterberg, 2007). Moreover, GRAPPA interpolation introduces very strong correlations between the channels. Nonetheless, it has been evidenced in a recent work that these correlations can be obviated with the introduction of an effective (reduced) number of receiving coils and an effective (increased) power of noise (Aja-Fernández and Tristán-Vega, 2011; Aja-Fernández et al., 2010b, 2011), so that the nc-χ can be considered general enough to model these signals. Additionally, GRAPPA images show also a spatial distribution of noise power similar to the g-factor in SENSE (Breuer et al., 2009).

pMRI systems are the standard today, to the point that they are used by all current scanner manufacturers. Given the concerns above, specially those referred to non-Rician signals, it remains evident that LS/WLS techniques for DT estimation have to be revisited. First, it is not clear whether or not the weights proposed by Salvador et al. (2005) for WLS are still valid with nc-χ signals. Second, even when the variance of the estimator were the minimum, certain biases might appear directly depending on the SNR. This artifact has been empirically reported even for Rician signals by Basser and Pajevic (2000); Jones and Basser (2004), and it is expected to become more noticeable with SENSE due to the amplification of the noise power associated to the g-factor. As a summary, it is not clear how pMRI/multi-coil reconstruction algorithms effect the estimation of the DT with LS/WLS.

In the present paper we propose an analytical study of the log-statistics of both Rician and nc-χ statistics, theoretically justifying and extending the findings in Salvador et al. (2005) to the nc-χ case (section 2.1). We use Taylor series to derive tractable, yet accurate expansions allowing easy intuitions on the behavior of noise-driven errors (section 2.2). These developments serve to generalize the popular WLS methodology to the nc-χ case, and to provide useful hints on when the error in the estimation can be reduced in a number of practical situations. The present work extends our preliminary results in Aja-Fernández et al. (2010a); Tristán-Vega et al. (2009a), providing full analytical derivations and applying a similar methodology for the ordinary LS, as well as illustrating our main results with in vivo data.

2 Methods

2.1 Theory

In this section we briefly review the principles underlying DT-MRI and the estimation of the DT, aiming to justify the importance of the statistics of noise in the logarithmic domain. The main results are the general model for noise in eq. 3 and the general model for the statistical parameters of noise in the logarithmic domain in eqs. 7 and 8. Both are novel contributions in our work, and apply for most of the nowadays MRI imaging protocols.

2.1.1 The DT model in diffusion MRI

When a short sensitizing gradient is applied along a unit direction g_i = [g_i,1, g_i,2, g_i,3]^T, the T2 baseline image, A₀, suffers an attenuation driven by the Stejskal-Tanner equation (Stejskal and Tanner, 1965):

$$A_i=A_0\exp \left(-b·{\mathbf{g}}_i^{T}D{\mathbf{g}}_i\right),\forall i=1\dots N,$$ (1)

where D is the diffusion tensor and b is a constant that comprises, along with the gyromagnetic ratio γ, the magnitude of the sensitizing gradients ∥G∥, the duration of the pulses δ, and the diffusion time Δ (LeBihan et al., 1986); the short pulses condition implies δ ≪ Δ.

2.1.2 Linearization of the Stejskal-Tanner equation

A straightforward way to estimate D is taking the logarithm of eq. 1:

$$\begin{array}{l}\log A_0-\log A_i=b·{\mathbf{g}}_i^{T}D{\mathbf{g}}_i\\ =b·[g_{i,1}^2,2g_{i,1}{g}_{i,2},2g_{i,1}{g}_{i,3},g_{i,2}^2,2g_{i,2}{g}_{i,3},g_{i,3}^2]\\ ·{[D_{11},D_{12},D_{13},D_{22},D_{23},D_{33}]}^T,{\{{\mathbf{g}}_i\}}_{i=1}^N,\end{array}$$ (2)

taking advantage of the symmetry of the DT. For N > 6, eq. 2 represents an overdetermined linear system with 6 unknowns (the 6 free components of D) and N equations, which can be easily solved with LS techniques.

2.1.3 General statistical characterization of noise in MRI

The signal M actually acquired is a noisy version of A in eq. 2. For fully sampled pMRI and GRAPPA with SoS combination, its Probability Density Function (PDF) corresponds to a nc-χ variable (Aja-Fernández et al., 2011)¹:

$$f_{M_L}(t;A_L,\sigma ,L)=\frac{A_L}{{\sigma }^2}{\left(\frac{t}{A_L}\right)}^L\exp \left(-\frac{t^2+A_L^2}{2{\sigma }^2}\right)I_{L-1}\left(\frac{A_{L}t}{{\sigma }^2}\right)u(t),$$ (3)

which stands for the probability (density) of obtaining a measurement t at a given voxel of the MRI volume, provided that 1) the ideal, noise-free signal is A_L, 2) the (effective) noise power in the image domain is σ², and 3) the (effective) number of coils is L. For a definition of these effective parameters, see Aja-Fernández et al. (2011). Finally, I_L−1 is the modified Bessel function of the first kind and order L − 1, and u(t) is Heaviside’s function. A_L is related to the in-phase component A_l,c and the quadrature component A_l,s of the complex signal at the l-th coil, A_l,c + jA_l,s, as:

$$A_L^2=\sum _{l=1}^L{|A_{l,c}+j{A}_{l,s}|}^2,$$ (4)

which is the ideal measurement in the absence of noise (i.e. with σ = 0). Consistently, if we consider a single coil system with L = 1, eq. 3 reduces to the Rician PDF traditionally considered for MRI data sets:

$$f_M(t;A,\sigma )=\frac{t}{{\sigma }^2}\exp \left(-\frac{t^2+A^2}{2{\sigma }^2}\right)I_0\left(\frac{\mathit{A\; t}}{{\sigma }^2}\right)u(t).$$ (5)

Therefore, the first meaningful remark is that the nc-χ statistics can be used as a general model for the noise distribution in MRI even with pMRI protocols, with or without subsampling (note that the effective value of L and σ has to be fixed accordingly), whenever SoS is used.

2.1.4 General statistical characterization of the log-statistics

From eq. 2, the linearized estimation of D requires the statistical characterization of log M (or log M_L). The corresponding PDF may be obtained from eq. 3 using the fundamental theorem of probability:

$$\begin{array}{c}{f}_{\log M_L}(t;A_L,\sigma ,L)=f_{M_L}({\log }^{-1}t;A_L,\sigma ,L)\frac{d{\log }^{-1}t}{\mathit{dt}}\\ =\frac{A_L^2}{{\sigma }^2}{\left(\frac{e^t}{A_L}\right)}^{L+1}\exp \left(\frac{-e^{2t}-A_L^2}{2{\sigma }^2}\right)I_{L-1}\left(\frac{A_L{e}^t}{{\sigma }^2}\right).\end{array}$$ (6)

whose mean μ = E{log M_L} and variance ν = Var{log M_L} are computed in Appendix A:

$$2\mu =\log (2{\sigma }^2)+\frac{\rho }{L}{}_{2}F_2(1,1:2,1+L;-\rho )+\psi (L);$$ (7)

$$\begin{array}{lll}4\nu & =& {\stackrel{\sim }{N}}_L(\rho )-2\log (2{\sigma }^2)\frac{\rho }{L}{}_{2}F_2(1,1:2,1+L;-\rho )\\ & & -{\left(\psi (L)+\frac{\rho }{L}{}_{2}F_2(1,1:2,1+L;-\rho )\right)}^2,\end{array}$$ (8)

where ρ is defined from the SNR, A_L/σ, as $\rho =\frac{1}{2}\mathrm{SN}{\mathrm{R}}^2=A_L^2/2{\sigma }^2$, and:

$${\stackrel{\sim }{N}}_L(z)=e^{-z}\sum _{k=0}^{\infty }\frac{z^k}{k!}\left(\psi {(k+L)}^2+{\psi }^{1)}(k+L)\right).$$

In the previous equations, ψ(·) is the polygamma function, ψ¹⁾ (·) is its first derivative, and ₂F₂(⋯) is the confluent hypergeometric function of the first kind (Abramowitz and Stegun, 1972). Particularizing eq. 7 for L = 1 and doing some algebra yields the result reported by (Salvador et al., 2005, eq. (11)):

$$E\{\log (M)\}=\frac{1}{2}{\mathrm{\Gamma }}^{(u)}\left(0,\frac{A^2}{2{\sigma }^2}\right)+\log (A),$$ (9)

with Γ^(u) the upper incomplete Gamma function. Hence, eq. 7 generalizes the analytical result in Salvador et al. (2005) to the nc-χ case, while eq. 8 is a novel contribution which has not been provided even for the Rician case.

2.2 Operative approximations to the log-statistics

Although eqs. 7 and 8 provide closed forms for the statistics of log-MRI signals, their complexity does not allow a further analysis. Instead, we use the following first-order approximations derived in Appendix B:

$$\begin{array}{lll}{\mathrm{bias}}^2\{\log M_L\}& =& {(E\{\log M_L\}-E\{\log A_L\})}^2\\ & =& \frac{{(L-1)}^2}{4}{\rho }^{-2}+O\left({\rho }^{-3}\right),\end{array}$$ (10)

$$\mathrm{Var}\{\log M_L\}=\frac{1}{2}{\rho }^{-1}-\frac{3L-4}{4}{\rho }^{-2}+O\left({\rho }^{-3}\right),$$ (11)

where Landau’s symbol O denotes the corresponding term decays as fast as its argument. Note in eq. 10 that the log-Rician bias drops to O(ρ⁻³). Indeed, we prove in Appendix C a much stronger condition: it drops to zero like exp(−ρ). This is consistent with the observation made by Salvador et al. (2005) that the bias in the Rician case should remain small for moderate SNR. At the same time, nc-χ signals are expected to show far larger biases (O(ρ⁻²)).

2.3 Estimation of the DT for nc-χ signals

In this section we introduce the problem statement of DT estimation as a linearized problem. The main results to highlight are: 1) The estimation is nearly unbiased in the Rician case, but not in the more general nc-χ case (section 2.3.1). 2) The usual implementation with WLS has nearly-minimum variance even in the general nc-χ case (section 2.3.3).

2.3.1 Linearized problem with log-nc-χ signals

The model in eq. 2 has to be rewritten in terms of the measured composite signals for each gradient direction g_i, say M_L,i:

$$\begin{array}{l}\log A_{L,0}-\log M_{L,i}\\ =\left[g_{i,1}^2,2g_{i,1}{g}_{i,2},2g_{i,1}{g}_{i,3},g_{i,2}^2,2g_{i,2}{g}_{i,3},g_{i,3}^2\right]\\ ·b{\left[D_{11},D_{12},D_{13},D_{22},D_{23},D_{33}\right]}^T+{\epsilon }_i,{\{{\mathbf{g}}_i\}}_{i=1}^N.\end{array}$$ (12)

As opposed to Salvador et al. (2005), we assume the baseline A_L,0 is known (noise-free). Since the SNR in the baseline image is far above that in the DWI, this assumption does not involve any substantial implication in our developments. From eq. B.3, ε_i has non-zero mean unless ρ is very large. This implies that the estimation of D will be notably biased except for the particular log-Rician case, that shows a bias in the order of exp(−ρ).

2.3.2 Solution based on (ordinary) LS

When no prior knowledge on the statistics of ε_i is available, the optimal solution to eq. 12 is given by the LS formulation (Kay, 1993):

$$\mathbf{X}={(G^{T}G)}^{-1}{G}^T\mathbf{Y},$$ (13)

where Y is an N × 1 vector comprising the DWI data, log(A_L,0) − log(M_L,i); X is the 6 × 1 vector of unknowns, (bD_ij); and G is the N × 6 concatenation of each row $[g_{i,1}^2,\dots ,g_{i,3}^2]$. This estimator has not minimum variance.

2.3.3 Solution based on WLS

If the variance of ε_i can be characterized, the linear estimator with the minimum variance is provided in Kay (1993):

$$\mathbf{X}={(G^T\mathit{WG})}^{-1}{G}^{T}W\mathbf{Y},$$ (14)

where W is the inverse of the covariance matrix of the data, C_YY. Since the noise in each DWI is independent, W reduces to a diagonal matrix of the form:

$$\begin{array}{lll}{W}_{\mathit{ii}}& =& {\mathrm{Var}}^{-1}\{{\mathbf{Y}}_i\}={\mathrm{Var}}^{-1}\{\log A_{L,0}-\log M_{L,i}\}\\ & =& {\mathrm{Var}}^{-1}\{\log M_{L,i}\}\simeq \frac{1}{{\rho }_i^{-1}/2-{\rho }_i^{-2}\left(3L-4\right)/4}\\ & \simeq & 2{\rho }_i+\left(3L-4\right),i=1\dots N,\end{array}$$ (15)

since A_L,0 is considered noise-free. Interestingly, the optimal weights are not proportional to ρ_i (i.e. to $A_{L,i}^2$), even for Rician noise, except for moderate-high SNR. However, we neglect the term (3L − 4) in eq. 15 for several reasons:

1. If 3L − 4 ≪ 2ρ_i, the estimator will very approximately resemble the one with minimum variance. In practice, effective values of L greater than 8-10 are hard to find (Aja-Fernández and Tristán-Vega, 2011; Aja-Fernández et al., 2011), translating in ρ_i ≫ 12.5 ⇒ A_L,i ≫ 5σ. This is not a very large value in the white matter for the b-values commonly used in DTI.

2. Such formulation is identical to that in Salvador et al. (2005), and is the one implemented in most of the software for the estimation of the DT.

3. That way it is not needed to know the value of σ, since any weight proportional to ρ_i (i.e. to $A_{L,i}^2$) can be used. Otherwise, we should estimate σ, losing one of the key advantages of WLS over ML.

To our knowledge, no justification had been given for the use of these weights other than the empirical study in Salvador et al. (2005). Finally, note the weights W_ii depend on A_L,i (not M_L,i), so they cannot be known a priori; this pitfall may be obviated by iteratively estimating X and updating W (Salvador et al., 2005). In what follows we assume W is known without uncertainty.

2.4 MSE in the components of the DT for LS and WLS

Once we have described the MSE in the log-signals in eqs. 10 and 11, we now study how this error is propagated to the DT when it is estimated as described in section 2.3. The MSE is computed as the sum of the variance plus the squared bias, and for WLS it is provided by Tristán-Vega et al. (2009a):

$$\begin{array}{ccc}\hfill C_{\mathbf{XX}}& =& L-\left(3L-4\right)L{G}^T\mathit{GL};\hfill \\ \hfill \zeta \{\mathbf{X}\}& =& \frac{N}{3}\left(L-1\right)\mathit{L\nu };\hfill \end{array}$$ (16)

$$\begin{array}{lll}\mathrm{MSE}& =& b^2\sum _{i=1}^3\sum _{j=i}^3{\mathrm{\Delta }}_{\mathit{ij}}^2=\mathrm{trace}\{C_{\mathbf{XX}}\}+{\Vert \mathrm{bias}\{\mathbf{X}\}\Vert }^2\\ & =& \mathrm{tr}(L)-\left(3L-4\right)\mathrm{tr}\left(L{G}^T\mathit{GL}\right)\\ & & +{\left(L-1\right)}^2{N}^2{\nu }^T{L}^2\nu ,\end{array}$$ (17)

where: L = (G^TWG)⁻¹ (symmetric); $\nu =\frac{1}{3}{[1,0,0,1,0,1]}^T$; C_XX is the covariance matrix of the error; ζ is its element-wise bias; Δ_ij stands for the error in the estimation of D_ij. For LS, the following values are derived in Appendix D:

$$\begin{array}{ccc}\hfill C_{\mathbf{XX}}& =& L^{\prime }{G}^T{W}^{-1}G{L}^{\prime }-\left(3L-4\right)L^{\prime }{G}^T{W}^{-2}G{L}^{\prime };\hfill \\ \hfill \zeta \{\mathbf{X}\}& =& (L-1)L^{\prime }{G}^T{W}^{-1}\mathbf{1},\hfill \end{array}$$ (18)

$$\begin{array}{lll}\mathrm{MSE}& =& \mathrm{tr}(L^{\prime }{G}^T{W}^{-1}G{L}^{\prime })\\ & & -\left(3L-4\right)\mathrm{tr}\left(L^{\prime }{G}^T{W}^{-2}G{L}^{\prime }\right)\\ & & +{(L-1)}^2{\mathbf{1}}^T{W}^{-1}G{L}^{\prime 2}{G}^T{W}^{-1}\mathbf{1},\end{array}$$ (19)

where 1 is an N × 1 vector of all ones and L′ = (G^T G)⁻¹. In the remaining, the following remarks will be useful:

1. Even if the weights W are nearly optimal, nc-χ signals introduce a certain bias, so the BLUE is (roughly) achieved only for Rician signals with WLS.

2. The size (trace, determinant) of G^TWG and G^T G asymptotically behaves like the number of gradients N (Tristán-Vega et al., 2009a). Hence, the size of L and L′ behaves like 1/N.

3. It follows that the variance, asymptotically driven by its first term tr(L) or tr(L′G^TW⁻¹GL′), decays like 1/N.

4. For the bias (WLS), N² cancels the 1/N² decay from L², being asymptotically constant with N. With LS, W⁻¹G and G^TW⁻¹ cancel L′².

5. The dependency with the SNR comes from L through W in WLS (or through W itself in LS): the variance decays as 1/ρ, and the squared bias as 1/ρ².

6. Finally, while the squared bias directly depends on L², the dominant term of the variance is constant with L.

3 Experiments and results

3.1 Accuracy of the Taylor series expansions

First of all, we test the correctness of eqs. 7 and 8 and the accuracy of the series expansions in eqs. 10 and 11. To that end, we have generated synthetic nc-χ signals following the first equality in eq. B.2, for different numbers of receiving coils L and for values of A_L/σ ranging from very low to very high SNR. The sample statistics thus obtained are compared to the true expressions, and to their counterparts computed from the series expansions, in Fig. 1. Obviously, the actual statistics perfectly fit the empirical values. As expected, the power series expansions are very accurate for large SNR, but show large deviations for smaller A_L/σ. Such deviation increases with the number L of antennas, but it can be concluded that the approximations are adequate for A_L/σ > 7 whenever L < 8. Although modern machinery may comprise up to 32 coils, noise correlations carry on a drastic reduction in the effective L which in practice makes it difficult to reach L > 10. With GRAPPA the SNR is lower, but at the same time the correlation-like artifacts reduce even more the effective number of coils L. Hence, our approximations are valid for a wide range of realistic cases. Of course, for L = 1 we come back to the Rician case, for which the bias is almost negligible.

Fig. 1.

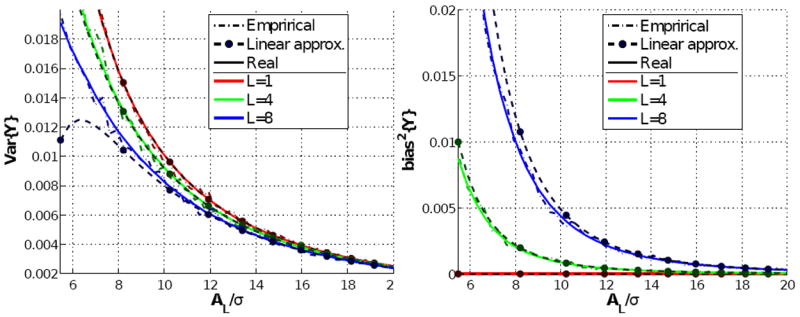
The variance (left) and the squared bias (right) of logarithmic nc-χ signals as a function of the normalized SNR, A_L/σ, and for different typical numbers of receiving coils. For each curve, we show: the true value theoretically obtained from eqs. 7 and 8; the first-order approximation we propose in eqs. 10 and 11; a sample estimate reckoned by means of Montecarlo simulation over a set of 2,000 independent samples.

3.2 Asymptotic behavior of the bias and the variance: isotropic case

As shown in previous sections, the bias and the variance suffer certain amplification with respect to the DWI after DT reconstruction, depending on the matrix G of gradient directions and the matrix W of signal amplitudes. We first consider a simplified scenario of isotropic diffusion, i.e. W = 2ρI_N for I_N the identity matrix. Note that in this case both LS and WLS converge to the same estimator: if all the samples show the same SNR, the Gauss-Markov theorem states that LS has minimum variance. In this case L = L′ = (G^T G)⁻¹ and either eq. 17 or (19) reduce to:

$$\mathrm{MSE}=\left(\frac{{\rho }^{-1}}{2}-(3L-4)\frac{{\rho }^{-2}}{4}\right)\mathrm{tr}\left({\left(G^{T}G\right)}^{-1}\right)+{\rho }^{-2}\frac{{\left(L-1\right)}^2{N}^2}{4}{\nu }^T{\left(G^{T}G\right)}^{-2}\nu .$$ (20)

From the previous equation, it remains evident that the study of L′ = (G^T G)⁻¹ is particularly useful. It is shown in appendix E that, if the gradients g_i are considered to be fairly distributed on the unit sphere, ν/∥ν∥ is an eigenvector of L′ associated to the eigenvalue 3/N. On the other hand, the trace of L′ can be evaluated for antipodal symmetric gradient directions, and the following expression results fairly accurate: tr((G^T G)⁻¹)≃ 29.3/N. Hence, the following approximation holds:

$$\begin{array}{lll}\mathrm{MSE}& \simeq & \frac{29.3}{N}\left(\frac{{\rho }^{-1}}{2}-(3L-4)\frac{{\rho }^{-2}}{4}\right)+{\rho }^{-2}\frac{9{\left(L-1\right)}^2{N}^2}{4N^2}{\nu }^T\frac{\nu {\nu }^T}{{\Vert \nu \Vert }^2}\nu \\ & =& \frac{29.3}{N}\left(\frac{{\rho }^{-1}}{2}-\left(3L-4\right)\frac{{\rho }^{-2}}{4}\right)+{\rho }^{-2}\frac{3{\left(L-1\right)}^2}{4},\end{array}$$ (21)

since the remaining eigenvectors of L′ are orthogonal to ν. The previous equation is quite illustrative: it explicitly shows that the squared bias does not depend on the number of gradients, while the variance linearly decreases with 1/N. Since the dominant term in the variance is the one in ρ⁻¹ (independent of L), it is also clear that the larger the number of receiving coils the more important the relative contribution of the bias to the MSE, which shall be only marginal for L = 1 (Rician noise). Fig. 2 quantitatively illustrates this reasoning. It aims at measuring the impact of the bias in the total MSE for different scenes: as an example, consider a system with effective L = 8, as chosen in the picture; with 51 gradient directions, the contribution of the bias is more important than that of the variance for all A_L/σ < 16.7 (ρ < 139.95). Alternatively, for L = 8 and a mean A_L/σ ≃ 17 in the DWI, it makes no sense to use more than 51 gradient directions (as long as the Gaussian assumption underlying the tensor model holds), since the dominant source of error is the bias and it cannot be reduced by increasing N. For lower SNR (say A_L/σ = 10, ρ = 50), the limiting number of gradients is as small as N = 15, so we may conclude that the bias in the estimations cannot be neglected in practical scenarios. As an additional remark, note that we are dealing with A_L/σ = 10, 17, which are well above the minimum value for which the power series expansions are reliable. Finally, let us consider the following example: suppose a GRAPPA reconstruction with effective L = 6, N = 15, and A_L/σ = 7.5 in our region of interest. From Fig. 2, increasing the number of gradients is not really worthy, since the squared bias will become higher than the variance and remain as a constant, residual error as N increases. In this situation, the only chance is to increase the SNR.

Fig. 2.

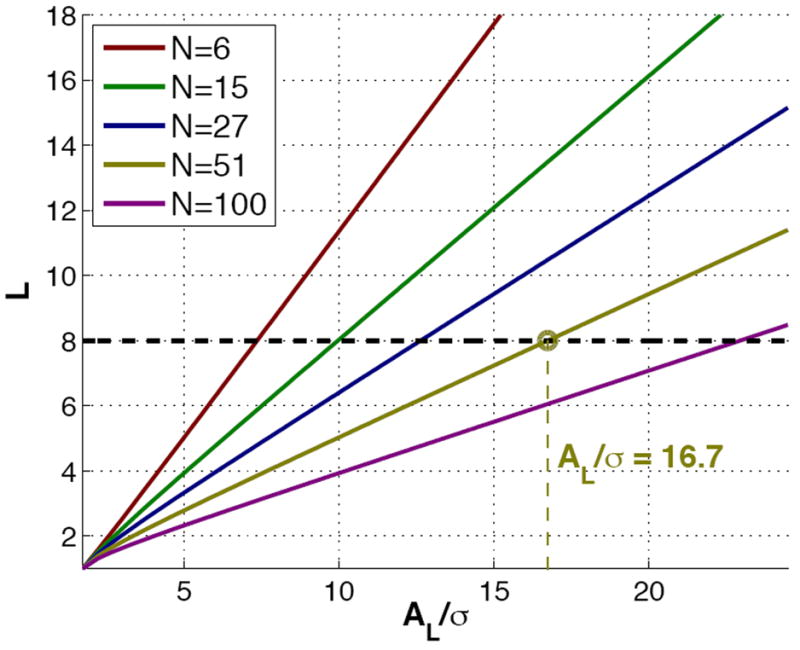
For each normalized SNR A_L/σ, we depict the minimum effective number of coils L such that the squared bias equals the variance in an isotropic scenario. The linear behavior is easily explained from eq. 21. Note also that for L = 1 (Rician noise) all the curves collapse to the point A_L/σ = 0: for Rician noise the bias is very small, so that we need a very low SNR to achieve a non-negligible bias.

3.3 Asymptotic behavior of the bias and the variance: anisotropic case

Of course, the most interesting case relies on anisotropic diffusion. To further test the conclusions above, we have designed a hypothetical system with typical values L = 8 (for other values of L, the linearity of the graphics in Fig. 2 allows to easily extrapolate the experiment), N = 15, 27, and 51, b = 1500s/mm², and Mean Diffusivity (MD) 0.8 · 10⁻³mm²/s. Now the diffusion is not isotropic; instead, we consider different Fractional Anisotropies (FA) for a prolate, cigar-shaped tensor (λ₁ > λ₂ = λ₃) and an oblate, disk-shaped tensor (λ₁ = λ₂ > λ₃). Fig. 3 shows the minimum value of the SNR for which the squared bias is kept below the variance, as a function of the FA, computed from eqs. 17 and 19. LS and WLS are not equivalent in this case, and as such they are considered separately². For FA= 0 we have an isotropic diffusion, and all the curves collapse to exactly the same point, which is the cut of the horizontal line L = 8 with each N = 15, 27, 51 in Fig. 2 (once attenuated by a factor exp(−b · MD)). As the FA increases, however, the squared bias becomes even more important, so that we need a SNR one order of magnitude higher to keep a relatively small bias contribution. Yet, the most conflicting case (the one requiring the largest SNR) arises with prolate tensors with large FA, which is indeed the most interesting one. For example, with N = 51 and FA= 0.8, the squared bias is greater than the variance for ρ₀ < 10⁴ (A_L0 < 140σ); though such SNR corresponds to the cleaner baseline image, it is still representative for white matter areas. Besides, for A_L0 ≃ 300σ (this SNR may be considered an upper limit for many realistic data sets) the bias will be roughly 1/4 of the variance, which is clearly not negligible.

Fig. 3.

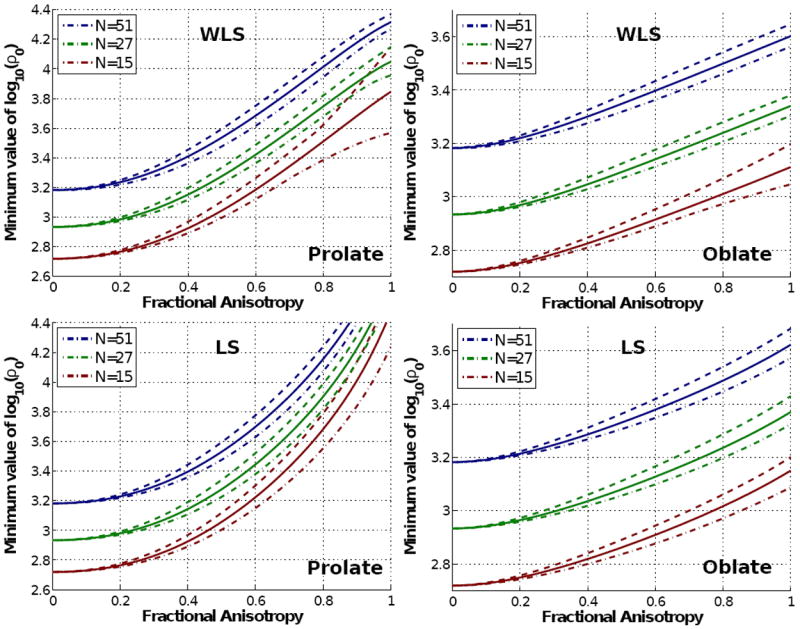
Log-plot of the minimum value of ${\rho }_0=A_{L,0}^2/2{\sigma }^2$ (related to the SNR in the baseline) which keeps the squared bias below the variance in the components of the DT for different tensor shapes. We show minimum, mean, and maximum values among all possible spatial orientations of the distinctive eigenvector of the tensor. The upper row shows the results for WLS reconstruction, and the bottom row those for LS.

With ordinary LS, the results are qualitatively similar, the bias gaining relative importance as the FA increases. Still, the minimum SNR for prolate tensors is slightly increased, approaching ρ₀ = 10⁵ (A_L = 450σ) in the worst case: the impact of the bias is at least as important as it is with WLS. Since the variance with LS is also higher, it remains evident that WLS is the preferred.

3.4 Numerical analysis of the error in the DT components (synthetic data)

The previous results are instructive and provide useful hints for the design of pMRI acquisitions. However, we have made certain assumptions that might introduce (hopefully low) systematic errors in our model. Mainly:

1. The weights used for WLS are not strictly the optimal.

2. We have considered the ideal weights for WLS are known a priori instead of estimated (the first two issues do not compromise the study for LS).

3. The T2-baseline image has been considered noise-free.

For these reasons, we have intended a series of experiments avoiding these modeling assumptions. A synthetic 128 × 128 synthetic 2-D tensor field ³ has been generated, see Fig. 4, comprising tensors with three different combinations of eigenvalues (mm²/s): [1.5 · 10⁻³, 0.4 · 10⁻³], [2 · 10⁻³, 0.1 · 10⁻³] and [2 · 10⁻³, 1.25 · 10⁻³]. DWI are simulated using eq. 1 for b = 1, 000 s/mm². Two scenarios are designed: (i) N = 16 gradients, ρ₀ = 1, 250 (A_L,0 = 1, 000, σ = 20); (ii) N = 8 gradients, ρ₀ = 2,500 (A_L,0 = 1, 000; $\sigma =20/\sqrt{2}\simeq 14.1$). Two cases are assumed:

1. nc-χ noise from fully sampled pMRI (hereafter, pMRI-SoS) with L = 8. A sensitivity map is coded for each coil so that $A_L^2={\sum }_l{A}_l^2$. The images at each coil are corrupted with a complex Gaussian noise N(0, σ²) and the composite image computed with SoS.

2. Standard Rician noise generated from one single receiving coil (L = 1; note we are considering one single coil with the same effective sensitivity as the whole 8-coil ensemble used for the nc-χ case).

Fig. 4.

The synthetic tensor fields generated. The Stejskal-Tanner equation is used to compute the synthetic DWI (possibly at each coil); the k-space is computed via the Fourier transform, and then corrupted with Gaussian noise. For pMRI-SoS the image domains at each coil are combined with SoS. Finally, iterative WLS is used to reconstruct the DT.

We use WLS in both cases to reconstruct the DT. In order to study the bias and the variance of the error in the estimation, data from 100 realizations of each experiment are considered (see Fig 4 for one such realization).

Fig. 5 shows the histograms of the estimated components of the tensor, with the ideal centroids marked as red spots. Our first point is that the dispersion of the clouds in both columns are comparable in all cases: doubling the number of gradient directions is exchangeable with doubling the input SNR. Comparing the offset of the clouds with respect to the noise-free centroids, it remains evident that the bias in the second scenario (right column) is smaller. Under the point of view of the output MSE, the second scenario is obviously preferable. As expected from our previous developments, nc-χ signals produce a significantly greater bias than Rician. In particular, single-coil, Rician acquisitions show a nearly negligible bias in all cases, as Appendix C suggests. Attending exclusively to the bias in the estimation of the DT, the acquisitions using SENSE are preferable to GRAPPA for a similar input SNR after pMRI reconstruction, since the former arise Rician signals meanwhile the noise statistics for the latter have to be characterized as nc-χ.

Fig. 5.

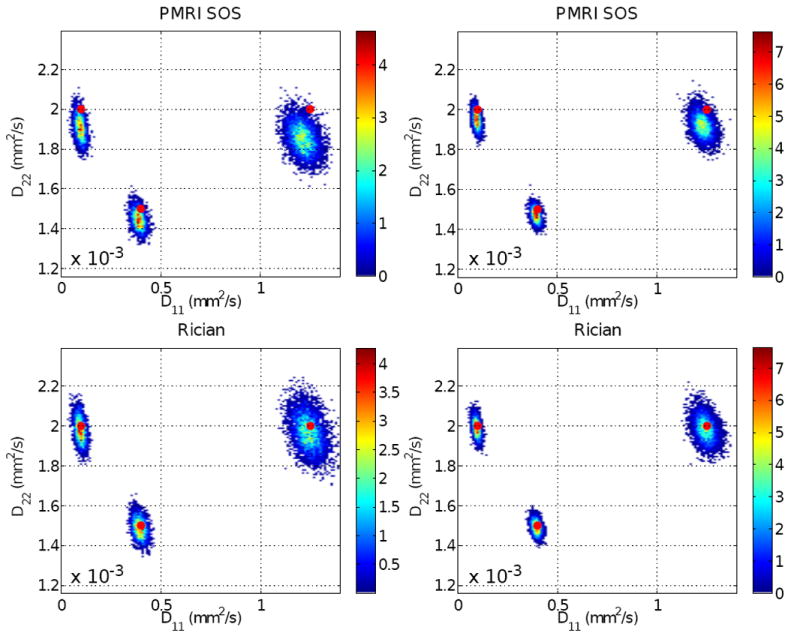
Histograms of the estimated (diagonal) components of the DT (note in Fig. 4 that the noise-free, ideal tensors are always diagonal). Left column: σ = 20, N = 16. Right column: σ = 14.1, N = 8. The value of ρ in the second column is twice that in the first column, but the number of gradients is halved so that the output variance is ideally the same.

To empirically check the impact of the analysis above on tensor-derived measures, we now study the behavior of the relative root MSE (rRMSE) in the estimated eigenvalues, $\widehat{{\lambda }_1}$ and $\widehat{{\lambda }_2}$, with respect to the ground-truth, λ₁ and λ₂:

$$\mathrm{rRMSE}=\frac{\sqrt{{\left(\widehat{{\lambda }_1}-{\lambda }_1\right)}^2+{\left(\widehat{{\lambda }_2}-{\lambda }_2\right)}^2}}{\max \{{\lambda }_1,{\lambda }_2\}},$$ (22)

against variations of both σ and N. With the setting-up described before, Fig. 6 shows the corresponding values, averaged for all realizations and pixels in the tensor field. The slope of the error as a function of the noise power σ is larger for nc-χ systems: for moderate-low SNR, the bias grows along with the variance, both of them perceptibly contributing to the rRMSE. For Rician systems, the bias is almost negligible, so that the rRMSE grows as long as the variance does. If we now consider the dependence with N, the rRMSE is monotonically reduced until a point where no further improvement is achieved: this is the point where the bias is dominant over the variance and it makes no sense to keep on increasing the number of gradients. This point is clearly reached before for nc-χ systems.

Fig. 6.

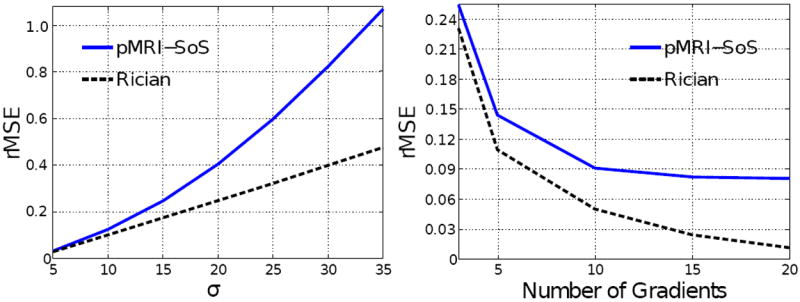
Evolution of the rRMSE in the estimated eigenvalues as a function of the power of noise in the receiver σ² (left: N = 5 gradients has been used; note in a 2-D scenario the minimum number of gradients to estimate the DT is N = 3) and the number of diffusion gradients N (right: σ = 10 has been used).

Though the numerical analysis performed above is limited to a few toy examples, it serves to conclude that the theoretical findings in the present paper apply even in non-ideal conditions (regarding our assumptions about the WLS weights and the noise power in the T2 baseline). To further justify this statement, we provide in the next section a final set of examples with in vivo data illustrating the accuracy of the model proposed.

3.5 Numerical analysis of the error in the DT components with in vivo data

For the last experiment, 20 identical and independent repetitions of a DWI data set with one baseline image and 15 gradient directions were successively taken from a healthy volunteer. To keep a reasonable acquisition time, one axial slice was collected in a 3T, 8-coil (without down-sampling) Philips scanner using a diffusion parameter b=1,200s/mm². The diffusion tensor at each voxel was estimated using standard WLS. Fig. 7 (a) shows the corresponding T2-baseline image and the color orientation map obtained. Figs. 7 (c) and (d) show respectively the squared bias and the variance computed either as sample estimates (left) or with the expressions provided in eq. 17 (right). Finally, Fig. 7 (b) shows the fraction of the MSE corresponding to the squared bias in each case.

Fig. 7.

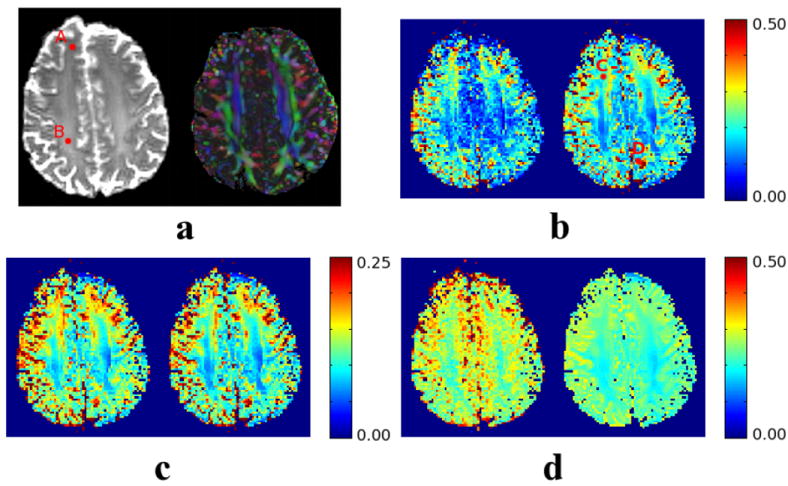
An axial slice of the brain of a healthy volunteer, acquired in a 3T, 8-coil Philips scanner. We show the baseline image and orientation color (a), and: the fraction of the MSE corresponding to the squared bias (b, relative units), the squared bias (c, absolute units), and the variance (d, absolute units). In all the cases, we show on the left hand side the sample values computed from 20 independent acquisitions and on the right hand side the values computed with our analytical expressions. The regions of interest are those corresponding to the white matter (vivid colors in a, right).

For the analytical computation of the bias and variance, we have computed the effective noise power ${\sigma }_{\mathrm{eff}}^2={0.085}^2$ and the effective number of coils L_eff = 4.2 (Aja-Fernández and Tristán-Vega, 2011). Note these values are quite different from the original σ² = 0.054 and L = 8 due to the noise correlations between the receivers. The first comment is that the SNR ρ in the baseline is well above the lower limit for which the series expansions are valid, at least in the white matter: in the locations flagged as A and B, they equal ρ_A = 96 and ρ_B = 280, hence we expect the analytical expressions to be faithful approximations of the sample computations. This assertion becomes clear comparing the squared bias and the variance in each case: the analytical bias is virtually identical to the estimated one, while a larger difference may be appreciated in the variance map. Note, however, these differences correspond to grey matter areas, for which the SNR in the DWI is typically much reduced and the series expansions are not reliable. In white matter areas, the approximations are still very accurate. Finally, the maps of the fraction of the MSE corresponding to the bias are also practically identical, at least for the regions of interest (white matter). Remarkably, this fraction may reach nearly 0.25 in C, meaning that the bias is one third of the variance, or even 0.5 in D, meaning that the squared bias equals the variance. Since the computation of the sample bias and variance avoids all the assumptions made throughout this paper, we may conclude our theoretical framework is representative enough of a real case. We would like to stress this experiment is not intended as a systematic empirical study of the error with real data, but as a means to validate the assumptions in our theoretical model. Such study would imply repeating the experiment for different b-values, input SNR, acquisition protocols, etc. Varying all these degrees of freedom for a one-subject, one-session acquisition is not feasible, and would require the design of an entire methodology to deal with this limitation.

4 Discussion

The analysis carried out suggests a number of interesting discussions. The most immediate is that the WLS formulation derived for Rician signals is equally valid for nc-χ distributions. In fact, these same weights can be used as long as the power of noise in each gradient image is similar, since the 1/A_i term comes from the logarithmic compression and not from the noise model itself. This result is especially relevant, since it allows concluding that the current WLS software available for both research tools and commercial machinery perfectly fits the characteristics of most pMRI protocols without any adaptation. Although, in a strict sense, the weights proportional to the squared envelope are not the optimal, we have proved that this is not the case in the conventional Rician case either; moreover, higher order terms may be neglected for moderate SNR permitting to obviate the characterization of the non-stationary power of noise.

In our study, the generalization of the Rician model to nc-χ statistics is critical. In fact, the latter can be seen as a canonical model for parallel and non-parallel MRI with SoS reconstruction. Although WLS are still (closely) valid and we have minimum variance, nc-χ signals drive to biases far larger compared to Rician, thus compromising the optimality of WLS which no longer approaches the BLUE: the larger the number of receiving coils L, the more important the effect of the bias. For GRAPPA, the k-space interpolation carries on a reduction on the effective L, so it seems that the problem could be alleviated; however, the interpolation notably worsens the SNR at the same time (in eq. 16, the decrease in L is compensated by the increase in the size of L through W⁻¹), so the artifact is even accentuated. Note that the same formalism, and hence the same comments, hold for fully sampled pMRI when correlations between the receiving antennas are considered (Aja-Fernández and Tristán-Vega, 2011). For L = 1 (Rician noise), the bias exponentially decays with the SNR, so it will be perceptible only for drastically low SNR.

While the variance in the estimation is easily reduced by increasing the number of acquired gradient directions N, the squared bias is asymptotically constant with this parameter. Paradoxically, some situations may arise in which the dominating source of error is the squared bias, and thus increasing the number of gradient directions does not necessarily improve the estimation. On the other hand, improving the SNR simultaneously reduces the variance (in the order of SNR⁻¹) and even more the bias (order SNR⁻²). This situation is more likely to arise with pMRI acquisitions, since the k-space subsampling induces a reduction in the SNR. While SENSE is borne with Rician noise and hence the bias will be kept in a reasonable level, GRAPPA systems show nc-χ noise, and thus the bias may become a very relevant issue.

Because of the previous concerns, the need for improving the input SNR becomes patent. The possibility of averaging the magnitude of the signals reconstructed from several independent acquisitions has been explored by Clarke et al. (2008). The authors propose to remove the bias inherent to this process with a simple profile-correction based on the ML estimate of the average (Sijbers et al., 1998). In terms of the output SNR in the tensor components, and for equivalent acquisition times, it results more profitable repeating the acquisition of each gradient direction than increasing the number of gradient directions themselves ⁴, as long as the number of averages is large enough for the bias removal to be reliable.

On the other hand, unbiased filtering is today a popular approach for a posteriori predicting the value of the unbiased signal out from noisy data, without substantially smoothing anatomical information, for Rician (Manjón et al., 2008; Tristán-Vega and Aja-Fernández, 2010; Tristán-Vega et al., 2011) and nc-χ data (Brion et al., 2011). Note we are only considering noise-driven artifacts, and leaving apart other sources of error like those coming from interpolation or characterization of coil sensitivities.

With regard to the use of LS instead of WLS, we have reasoned that the effect of the bias is asymptotically the same in both cases, so all the comments above hold for LS. Yet, this estimator has not minimum variance, so WLS is the preferred unless the computation time is an issue. WLS is slower for two reasons: first, the iterative computation of the weights in W; second, since W depends on the DWI signal itself, it does not allow the pre-computation of LG^TW as LS does with L′G^T.

As a final remark, the elegant algebraic formulation proposed for the error in the estimation has been possible because the DT linearly relates to the (log) DWI signal by means of a simple matrix product. This feature is shared by several of the most popular HARDI approaches, so a similar analytical study could be performed for Q-Balls (Tuch, 2004) or OPDT-like estimators (Tristán-Vega et al., 2010) by means of the spectral characterization of such matrices. The impact of Rician bias has been otherwise pointed out empirically by Clarke et al. (2008), so, in light of the present work, it is expected that some important distortions shall be driven by nc-χ signals. At the same time, the study carried out here for the DT components can be generalized to any measurement linearly related to them. For example, the considerations regarding the bias will be equally valid for the mean diffusivity. But if we study some other parameters like the FA, which is related to the DT components in a non-linear way, its estimation can be biased even when the DT components are not. In any case, the guidelines suggested here for the trade-off between the SNR and the number of gradients are still valid.

5 Conclusion

The analysis carried out in this paper applies for most of the nowadays imaging schemes, thanks to the generalization to a nc-χ model. Regardless of their simplicity, Least Squares approaches are still of high interest in the estimation of the DT: as long as log-statistics can be assimilated to Gaussian (i.e. for high enough SNR), WLS is indeed the optimal estimator (linear or nonlinear) in the sense of the MSE, being equivalent to ML with much lower complexity (Kay, 1993). However, important distortions may arise for medium-low SNR, which will obviously translate in systematic errors in the calculation of quantitative parameters of clinical interest such as the FA or the MD. These artifacts are especially annoying for nc-χ systems, for which the biases are far more important. Although it seems tempting to increase the number of acquired gradients to improve the estimation, we have evidenced that, for some scenarios, this procedure can be nearly worthless. The only chance in these situations is to improve the SNR by increasing the voxel size, averaging a set of independent magnitude signals (and correcting the profile to remove the bias), or filtering the data set. In fact, Fig. 3 itself provides useful quantitative hints for the design of DWI acquisitions depending on the input SNR, the required number of diffusion gradients, and the imaging protocol to be used.

A Statistical characterization of log-nc-χ signals

The expectation of D_L = log M_L can be computed from eq. 3 by considering the power series expansion of I_L−1:

$$\begin{array}{c}E\{D_L\}={\mathit{\int }}_{-\infty }^{\infty }t\frac{A_L^{1-L}}{{\sigma }^2}{e}^{(L+1)t}{e}^{-\frac{e^{2t}+A_L^2}{2{\sigma }^2}}{I}_{L-1}\left(\frac{A_L{e}^t}{{\sigma }^2}\right)\mathit{dt}\\ ={\mathit{\int }}_{-\infty }^{\infty }t\frac{A_L^{1-L}}{{\sigma }^2}{e}^{(L+1)t}{e}^{-\frac{e^{2t}+A_L^2}{2{\sigma }^2}}\sum _{k=0}^{\infty }\frac{{\left(\frac{A_L{e}^t}{2{\sigma }^2}\right)}^{2k+L-1}}{k!\mathrm{\Gamma }(L+k)}\mathit{dt}\\ =\sum _{k=0}^{\infty }\frac{2A_L^{2k}{e}^{-\frac{A_L^2}{2{\sigma }^2}}}{k!\mathrm{\Gamma }(L+k){\left(2{\sigma }^2\right)}^{L+2k}}{\mathit{\int }}_{-\infty }^{\infty }t{e}^{2(L+1)t}{e}^{-\frac{e^{2t}}{2{\sigma }^2}}\mathit{dt}.\end{array}$$ (A.1)

The previous integral can be expressed in terms of the polygamma function ψ (Abramowitz and Stegun, 1972):

$$E\{D_L\}=e^{-\frac{A_L^2}{2{\sigma }^2}}\sum _{k=0}^{\infty }{\left(\frac{A_L^2}{2{\sigma }^2}\right)}^k\frac{\log (2{\sigma }^2)+\psi (k+L)}{2k!},$$ (A.2)

which now depends only on $\rho =A_L^2/2{\sigma }^2$ and can be related to the confluent hypergeomteric function of the first kind (Abramowitz and Stegun, 1972):

$$E\{D_L\}=\frac{1}{2}\log (2{\sigma }^2)+\frac{\rho }{2L}{}_{2}F_2(1,1:2,1+L;-\rho )+\frac{1}{2}\psi (L),$$ (A.3)

To compute the variance, we first elaborate on the second order moment:

$$\begin{array}{l}E\{D_L^2\}={\mathit{\int }}_{-\infty }^{\infty }{t}^2\frac{A_L^{1-L}}{{\sigma }^2}{e}^{(L+1)t}{e}^{-\frac{e^{2t}+A_L^2}{2{\sigma }^2}}{I}_{L-1}\left(\frac{A_L{e}^t}{{\sigma }^2}\right)\mathit{dt}\\ ={\mathit{\int }}_{-\infty }^{\infty }{t}^2\frac{A_L^{1-L}}{{\sigma }^2}{e}^{(L+1)t}{e}^{-\frac{e^{2t}+A_L^2}{2{\sigma }^2}}\sum _{k=0}^{\infty }\frac{{\left(\frac{A_L{e}^t}{{\sigma }^2}\right)}^{2k+L-1}}{k!\mathrm{\Gamma }(L+k)}\mathit{dt}\\ =\sum _{k=0}^{\infty }\frac{2A_L^{2k}{e}^{-\frac{A_L^2}{2{\sigma }^2}}}{k!\mathrm{\Gamma }(L+k){(2{\sigma }^2)}^{L+2k}}{\mathit{\int }}_{-\infty }^{\infty }{t}^2{e}^{2(L+1)t}{e}^{-\frac{e^{2t}}{2{\sigma }^2}}\mathit{dt},\end{array}$$ (A.4)

and again the integral can be written in terms of the polygamma function and its derivative ψ¹⁾, depending only on ρ:

$$E\{D_L^2\}=\frac{e^{-\rho }}{4}\sum _{k=0}^{\infty }\frac{{\rho }^k}{k!}\left({(\psi {(k+L)}^2+\log (2{\sigma }^2))}^2+{\psi }^{1)}(k+L)\right).$$ (A.5)

In this case, only some of the terms in the summation drive to a hypergeometric function, compelling us to define the function:

$${\stackrel{\sim }{N}}_L(z)=e^{-z}\sum _{k=0}^{\infty }\frac{z^k}{k!}\left(\psi {(k+L)}^2+{\psi }^{1)}(k+L)\right),$$

which is depicted in Fig. 8. With this notation, we may write:

$$\begin{array}{c}E\{D_L^2\}=\frac{1}{4}(\log {(2{\sigma }^2)}^2+2\log (2{\sigma }^2)(\psi (L)\\ +\frac{\rho }{L}{}_{2}F_2(1,1:2,1+L;-\rho ))+{\stackrel{\sim }{N}}_L(\rho )).\end{array}$$ (A.6)

Fig. 8.

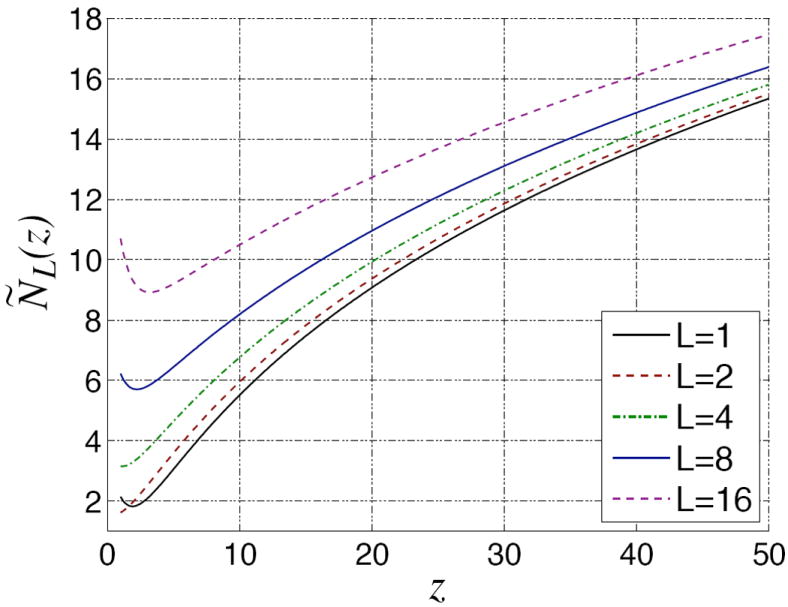
An sketch of the $\stackrel{\sim }{N_L}$ function for several values of L. It is continuous and shows a monotonic behavior in the range of interest.

Finally, the variance is computed as the mean squared value minus the squared mean of log M_L, yielding:

$$\begin{array}{lll}\mathrm{Var}\{D_L\}& =& \frac{{\stackrel{\sim }{N}}_L(\rho )}{4}-\log (2{\sigma }^2)\frac{\rho }{2L}{}_{2}F_2(1,1:2,1+L;-\rho )\\ & -& \frac{1}{4}{\left(\psi (L)+\frac{\rho }{L}{}_{2}F_2(1,1:2,1+L;-\rho )\right).}^2\end{array}$$ (A.7)

B Taylor series of the logarithmic statistical parameters

Since the MSE is the sum of the squared bias plus the variance, these are the parameters of interest. Without any loss of generality, we introduce a phase shift in eq (4) such that the same real signal A is acquired at all coils:

$$A_L=\sqrt{\sum _{l=1}^L{|A_{l,c}+j{A}_{l,s}|}^2}\equiv \sqrt{\sum _{l=1}^L{A}^2}=\sqrt{L}A.$$ (B.1)

Note the PDF of log M_L in eq. 6 depends only on the net squared signal $A_L^2$, so any combination of A_l whose squared sum yields $A_L^2$ will rise identical statistics. With this notation, the Taylor series expansion of log(M_L) for reasonable SNR (ρ > 20 ⇒ A_L > 6.3σ in the worst case, see Fig. 1) is:

$$\begin{array}{l}\log M_L=\frac{1}{2}\log \left(\sum _{l=1}^L{(A+n_{l,c})}^2+n_{l,s}^2\right)\\ =\log A_L+\frac{1}{AL}\sum _{l=1}^L{n}_{l,c}+\frac{1/2}{L{A}^2}\sum _{l=1}^L{n}_{l,s}^2\\ +\frac{1/2}{A^2{L}^2}\sum _{k=1,l=1}^L(L{\delta }_{kl}-2)n_{k,c}{n}_{l,c}+O\left(\frac{{\sigma }^3}{A^3}\right),\end{array}$$ (B.2)

with δ the Kronecker delta function and n_l,c, n_l,s ~ N (0, σ²) the uncorrelated noises in the complex domain. Though this Taylor series is only convergent for $A_L^2>{\sum }_{l=1}^L(2A{n}_{l,c}+n_{l,c}^2+n_{l,s}^2)$, in practice we are dropping the left tails of the Gaussians, which for any reasonable SNR will be negligible. It follows:

$$\begin{array}{lll}E\{\log M_L\}& =& \log A_L+(L-1)\frac{{\sigma }^2}{A_L^2}+O\left(\frac{{\sigma }^4}{A^4}\right)\\ & =& \log A_L+\frac{(L-1)}{2}{\rho }^{-1}+O\left({\rho }^{-2}\right).\end{array}$$ (B.3)

From eq. B.2, all the terms in σ³/A³ correspond to cross products comprising odd order moments of zero-mean Gaussians, so they are all identically zero and we gain one order of convergence up to σ⁴/A⁴. The result in eq. 10 becomes now obvious from the previous expression. For the variance, a parallel development of log M_L to order 3 yields the corresponding value in eq. 11.

C Bias of log-Rician signals

In the Rician case we have L = 1, so the bias in eq. 10 drops to O(ρ⁻³). Indeed, we may use the result in eq. 9 to write the bias in the form:

$$E\{\log (M)\}-\log (A)=\frac{1}{2}{\mathrm{\Gamma }}^{(u)}(0,\rho )=\frac{1}{2}{E}_1(\rho ),$$ (C.1)

where E₁ is the exponential integral function (Abramowitz and Stegun, 1972), which fulfills the following property for ρ > 0:

$$E_1(\rho )<\exp (-\rho )\log \left(1+\frac{1}{\rho }\right).$$ (C.2)

If we choose any positive ρ₀ > 0, the monotonicity of log(1+1/ρ) assures that the bias of log-Rician signals is bounded by log(1 + 1/ρ₀) exp(−ρ) for ρ > ρ₀ i.e., it decreases exponentially, hence faster than any negative power of ρ. As an illustration, suppose the DWI attenuation is 0.1, so the signal of interest is − log(0.1) ≃ 2.3. For SNR ρ = 1, the bias is in the order of 0.1 ≪ 2.3.

D Bias and variance in the DT with LS

From the closed form solution in eq. 13, the covariance matrix of the vector X of unknowns (tensor components) is easily computed using its definition:

$$\begin{array}{lll}{C}_{\mathbf{XX}}& =& E\{(\mathbf{X}-E\{\mathbf{X}\}){(\mathbf{X}-E\{\mathbf{X}\})}^T\}\\ & =& L^{\prime }{G}^T{C}_{\mathbf{YY}}G{L}^{\prime }\\ & =& L^{\prime }{G}^T\mathrm{diag}\left(\frac{1}{2}{\rho }_i^{-1}-\frac{3L-4}{4}{\rho }_i^{-2}\right)G{L}^{\prime }\\ & =& L^{\prime }{G}^T{W}^{-1}G{L}^{\prime }-\left(3L-4\right)L^{\prime }{G}^T{W}^{-2}G{L}^{\prime }.\end{array}$$ (D.1)

And for the vector bias:

$$\begin{array}{lll}\zeta \{\mathbf{X}\}& =& L^{\prime }{G}^T\zeta \{\mathbf{Y}\}=\frac{L-1}{2}{L}^{\prime }{G}^T{[{\rho }_1^{-1},\dots ,{\rho }_N^{-1}]}^T\\ & =& (L-1)L^{\prime }{G}^T{W}^{-1}\mathbf{1},\end{array}$$ (D.2)

where 1 is an N × 1 vector of all ones and L′ = (G^T G)⁻¹. The total MSE in eq. 19 for all tensor components comes from the sum of the trace of the covariance matrix in eq. D.1 and the squared norm of the bias in eq. D.2.

E Spectral characterization of L′ = (G^T G)⁻¹

The aim in this appendix is to show that ν/∥ν∥ is (approximately) and eigenvector of (G^T G)⁻¹ associated to the eigenvalue 3/N. It suffices to prove that ν/∥ν∥ is an eigenvector of G^T G associated to the eigenvalue N/3; applying the definition:

$$\begin{array}{lll}(G^{T}G)\frac{\nu }{\Vert \nu \Vert }& =& \frac{1}{\Vert \nu \Vert }{G}^T\left(G·{[1,0,0,1,0,1]}^T\right)=\frac{1}{\Vert \nu \Vert }{G}^T\left[\begin{array}{c}{g}_{1,1}^2+g_{1,2}^2+g_{1,3}^2\\ g_{2,1}^2+g_{2,2}^2+g_{2,3}^2\\ \dots \\ g_{N,1}^2+g_{N,2}^2+g_{N,3}^2\end{array}\right]\\ & =& \frac{1}{\Vert \nu \Vert }{G}^T\mathbf{1}=\frac{1}{\Vert \nu \Vert }\left[\begin{array}{c}{\sum }_{i=1}^N{g}_{i,1}^2\\ {\sum }_{i=1}^{N}2g_{i,1}{g}_{i,2}\\ \dots \\ {\sum }_{i=1}^N{g}_{i,3}^2\end{array}\right].\end{array}$$ (E.1)

Now, we realize that the g_i have to be fairly distributed on the surface of the unit sphere, so that we can model their components as independent, uniform random variables, g_j~U (−1, 1); although this assumption may seem naive, it accurately fits real scenarios even for small N. With this consideration, the above summations are seen as sample estimates of the moments of g_j:

$$\left(G^{T}G\right)\frac{\nu }{\Vert \nu \Vert }\simeq \frac{1}{\Vert \nu \Vert }\left[\begin{array}{c}N·E\{g_1^2\}\\ 2N·E\{g_1{g}_2\}\\ \dots \\ N·E\{g_3^2\}\end{array}\right]=\frac{N}{\Vert \nu \Vert }{\left[\frac{1}{3},0,0,\frac{1}{3},0,\frac{1}{3}\right]}^T=\frac{N}{3}\frac{\nu }{\Vert \nu \Vert }.$$ (E.2)