Abstract
We used computer simulation to understand the functional relationships between motor (dynein, HSET, and Eg5) and non-motor (NuMA) proteins involved in microtubule aster organization. The simulation accurately predicted microtubule organization under all combinations of motor and non-motor proteins, provided that microtubule cross-links at minus-ends were dynamic, and dynein and HSET were restricted to cross-linking microtubules in parallel orientation only. A mechanistic model was derived from these data in which a combination of two aggregate properties, Net Minus-end–directed Force and microtubule Cross-linking Orientation Bias, determine microtubule organization. This model uses motor and non-motor proteins, accounts for motor antagonism, and predicts that alterations in microtubule Cross-linking Orientation Bias should compensate for imbalances in motor force during microtubule aster formation. We tested this prediction in the mammalian mitotic extract and, consistent with the model, found that increasing the contribution of microtubule cross-linking by NuMA compensated for the loss of Eg5 motor activity. Thus, this model proposes a precise mechanism of action of each noncentrosomal protein during microtubule aster organization and suggests that microtubule organization in spindles involves both motile forces from motors and static forces from non-motor cross-linking proteins.
INTRODUCTION
Chromosome movement and segregation during both mitosis and meiosis are driven by a complex microtubule-based structure called the spindle (Rieder, 1981; Mitchison et al., 1986; McIntosh and Koonce, 1989; Hyman and Karsenti, 1996; Compton, 2000; Sharp et al., 2000). Plus-ends of spindle microtubules extend toward either the cell periphery where they contact the cell cortex or the spindle midzone where many contact chromosome arms and kinetochores. Minus-ends of spindle microtubules are focused at spindle poles, the sites to which chromatids segregate at anaphase.
In many cell types, centrosomes are located at spindle poles as a consequence of their role in microtubule nucleation. However, centrosomes are not necessary for spindle pole organization or function, as demonstrated by the lack of centrosomes in some cell types (Szollosi et al., 1972) and experiments where centrosomes have been eliminated from cells (Nicklas, 1989; Khodjakov et al., 2000). Instead, microtubule minus-ends are focused at spindle poles by noncentrosomal proteins, including the structural protein NuMA and microtubule motor proteins dynein (with its activating complex dynactin), HSET, and Eg5 (Merdes and Cleveland, 1997; Compton, 1998). These proteins work in concert to focus microtubule minus-ends and tether centrosomes to the spindle pole through microtubule cross-linking and/or motor activity (Gaglio et al., 1995, 1996, 1997; Echeverri et al., 1996; Heald et al., 1996, 1998; Merdes et al., 1996, 2000; Mountain et al., 1999).
To investigate mechanisms involved in microtubule focusing at spindle poles by these noncentrosomal proteins, we developed a cell-free system derived from synchronized cultured cells (Gaglio et al., 1995). As in mitotic cells, microtubule minus-end focusing in these extracts is driven by the structural protein NuMA and motor proteins dynein (with its activating complex dynactin), HSET, and Eg5 (Gaglio et al., 1995, 1996, 1997; Mountain et al., 1999). However, in the absence of spatial cues normally provided by cellular constituents, taxol-stabilized microtubules in these extracts form radial arrays or asters. Extensive biochemical characterization of these microtubule asters indicates that the five noncentrosomal proteins mentioned above are the only proteins responsible for microtubule aster organization (Mountain et al., 1999; Mack and Compton, 2001; see also Garrett et al., 2002). Depending on which of these proteins are present in the extract, three different microtubule arrangements are observed (Figure 1). In control extracts, where all five proteins are present, microtubules form tightly focused asters with NuMA concentrated at the central core (Figure 1A). If Eg5 is inhibited, then microtubules are arranged in asters, but NuMA is not tightly focused at the central core, and microtubule minus-ends are loosely focused at the vertex (Figure 1, A and B). If NuMA, dynein, or HSET are perturbed, microtubules remain randomly dispersed (Figure 1A).
Figure 1.
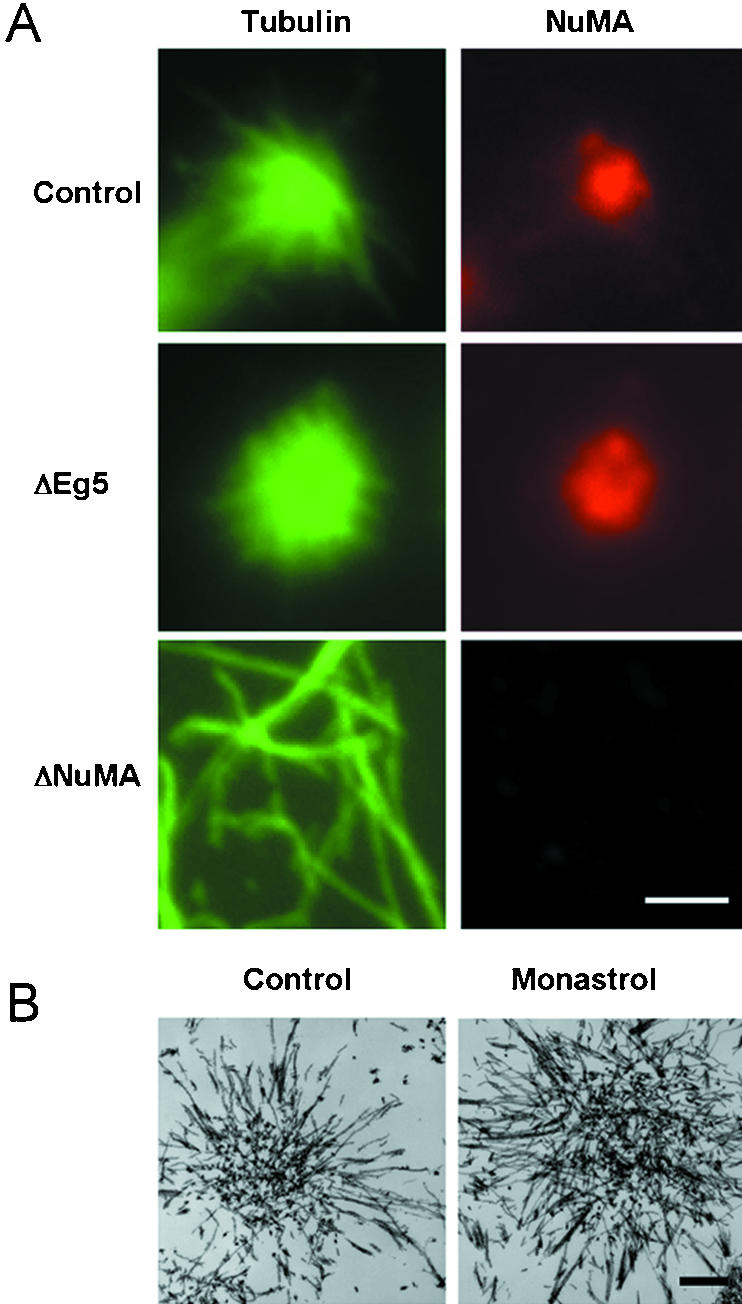
Three arrangements of microtubules observed in a mammalian mitotic extract. (A) Microtubule structures in mammalian mitotic extracts that were untreated (control), depleted of the plus-end–directed motor Eg5 (ΔEg5), or depleted of NuMA (ΔNuMA) were visualized by staining for tubulin or NuMA as indicated. (B) Microtubule structures formed in untreated (control) or monastrol-treated (monastrol) mitotic extracts were fixed, processed, and visualized by transmission electron microscopy. Bar, 5 μm (A); 1 μm (B).
In addition to inhibiting each protein alone, we have also performed a series of combinatorial inhibitions that revealed important functional relationships among these proteins (Table 1). Some of the functional relationships can be interpreted in a straightforward way. For example, because microtubule asters have minus-ends focused at vertices, it is obvious why the minus-end–directed motor activity of either or both dynein or HSET must be present in the extract for aster organization (Table 1, lines 1, 5, 8–10). Also, motors of opposite directionality act antagonistically, because tightly focused asters can be restored to extracts lacking HSET or dynein activity by simultaneously inhibiting Eg5 (Table 1, lines 3 and 9 and lines 4 and 10). Other functional relationships cannot be explained so simply. For example, when either dynein or HSET is the sole motor present, NuMA is essential for microtubule organization (Table 1, lines 9 and 10), but when both dynein and HSET are present NuMA is dispensable (Table 1, line 8). Also, it is not clear why Eg5 inhibition should restore microtubule organization to extracts lacking NuMA (Table 1, lines 2 and 8). Thus, a complete mechanistic explanation for microtubule organization at spindle poles requires the precise definition of the molecular mechanism of each component and the explanation of functional relationships between those components. Unfortunately, it is currently impossible to address these issues by reconstituting microtubule aster organization by using purified proteins because technical limitations limit availability of functionally active pure proteins. Even if functionally active forms of all these proteins were available, a full understanding of the mechanisms involved would only be revealed if microtubule cross-linking and motor activities could be evaluated independently. Such fine-grained control of motor behavior is not possible with current biochemical techniques. Thus, we used computer simulation to investigate how these proteins contribute to microtubule aster organization.
Table 1.
Combinatorial immunodepletions performed in a mammalian mitotic extract
| Depletion | Remaining | Aster focusing | Reference | |
|---|---|---|---|---|
| 1 | None | D, H, N, E | Tightly focused | 1, 2 |
| 2 | N | D, H, E | No organization | 1 |
| 3 | H | D, N, E | No organization | 2 |
| 4 | D | H, N, E | No organization | 1, 2 |
| 5 | E | D, H, N | Loosely focused | 1, 2 |
| 6 | N, H | D, E | No organization | 2 |
| 7 | N, D | H, E | No organization | 1 |
| 8 | N, E | D, H | Loosely focused | 1 |
| 9 | H, E | D, N | Tightly focused | 2 |
| 10 | D, E | H, N | Tightly focused | 1, 2 |
| 11 | H, D | N, E | No organization | 2 |
| 12 | N, H, E | D | Not done | |
| 13 | N, D, E | H | No organization | 1 |
| 14 | H, D, E | N | No organization | 2 |
| 15 | N, H, D | E | Not done |
MATERIALS AND METHODS
Cell Culture
Mammalian HeLa cells were maintained in DMEM containing 10% fetal calf serum, 50 IU/ml penicillin, and 50 μg/ml streptomycin. Cells were grown at 37°C in a humidified incubator in a 5% CO2 atmosphere.
Antibodies
The mouse mAb DM1A (Sigma-Aldrich) was used to detect tubulin, a rabbit polyclonal antibody was used to detect NuMA (Gaglio et al., 1995), and a rabbit polyclonal antibody was used to detect Eg5 (Mountain et al., 1999).
Preparation and Immunodepletion of Mitotic Extracts
Mitotic extracts from HeLa cells were prepared according to Gaglio et al. (1995). Immunodepletion of Eg5 was carried out according the Gaglio et al. (1996) and verified by immunoblotting. Electron microscopy was performed according to Dionne et al. (1999). Indirect immunofluorescence microscopy of microtubule asters was performed according to Gaglio et al. (1995). Images were collected on a Zeiss Axioplan 2 microscope equipped with a Hamamatsu Orca II charge-couple device camera. The diameter of aster cores was determined by measuring the area occupied by NuMA by using the measurement tool in the Openlab software (Improvision, Lexington, MA). All images were contrast enhanced identically and identical thresholding was performed to specify the boundaries of NuMA staining at the core of microtubule asters. Two measurements, perpendicular to each other, were conducted on each aster to eliminate effects of any asymmetries in the distribution of NuMA at the center of the asters.
Computer Simulation
The simulation was prototyped in MATLAB, and written in C++ (code is available upon request). Code was optimized to run parallel on a Linux-based Beowulf cluster (14 nodes or processors, 1.3 MHz each), with each node of the cluster dedicated to a single run at a time. The data was then written to files that were subsequently analyzed using routines written in MATLAB. If appreciable microtubule organization occurred, then the final frame of the simulation was adjusted to place the microtubule aster in the center.
We used an iterative Monte Carlo method to simulate the process of microtubule organization in a mammalian mitotic extract. The simulation was designed as a two-dimensional approximation of a three-dimensional process consistent with other computer simulations (Odde and Buettner, 1995; Nedelec et al., 1997). The simulation area was arbitrarily designated to be 12.3 × 12.3 μm (150 μm2) for 15 microtubules, or 17.3 × 17.3 μm (300 μm2) for 30 microtubules (Table 2). The edges of the simulation area were dealt with using periodic boundary conditions to eliminate edge effects and prevent component dilution due to diffusion.
Table 2.
Physical parameters and biological model of the computer simulation

Each simulation is initiated with a randomized distribution of microtubules and motors. The simulation first determines whether any motors are connected to microtubules. We arbitrarily defined an interaction range of 20 nm for motors, such that a motor within 20 nm of a microtubule is classified as bound to the microtubule, provided it satisfies binding angle restrictions (see below). The simulation then calculates the force applied to microtubules by motors bound to them using Newtonian mechanics, and moves microtubules an appropriate distance. The simulation also moves any microtubules connected to microtubules being moved. After accounting for all motor-driven movements, the simulation then moves all components by Brownian motion. Final positions at the end of each iteration become initial positions in the succeeding iteration, which proceeds in the same way as described above. Each iteration of the simulation corresponds to 1 s of simulated time (Table 2), and simulations are performed for 1500 s. This length of time (25 min) corresponds closely to the amount of time required for asters to organize in the mitotic extract system (Gaglio et al., 1995). Simulations run up to 5000 s showed no appreciable differences in the degree of microtubules organization, suggesting 1500 s is a sufficient length of time for steady-state conditions to be reached.
Brownian motion was calibrated from previously published time-lapse traces of single microtubules attached to a glass coverslip via a single kinesin motor (Howard et al., 1989) and differential interference contrast time-lapse video sequences of particle movement in living cells (video courtesy of M. Gordon, Dartmouth Medical School, Hanover, NH). These data were used to train the rate and extent of translational and rotational Brownian motion in the simulation. The amplitude of Brownian motion was adjusted for each component of the simulation based on surface area, and a probabilistic function was implemented to ensure that Brownian motion closely resembled experimentally determined motion.
Microtubules were modeled as 5-μm rigid rods without dynamics (Table 2). Because microtubules in the mitotic extract are stabilized with taxol, this assumption accurately reflects conditions in the extract, and simplifies computational analysis.
Eg5 was simulated as a bipolar motor with motor domains at each end (Table 2; Kashina et al., 1996). Dynein and HSET were modeled with motor domains at one end and non-motor microtubule binding domains at the other end (Table 2; Gill et al., 1991; Chandra et al., 1993; Kuriyama et al., 1995; Heald et al., 1996; 1998; Matuliene et al., 1999). Motors were modeled as inflexible and with a binding angle on microtubules that could not exceed 42° away from the perpendicular. These restrictions were based on biophysical data for Eg5 (Kashina et al., 1996) and were applied to all three motors. Off-rates for the non-motor microtubule binding domains of dynein and HSET were set so that 50% of motors were bound to microtubules at steady state (Table 2).
Simulation of microtubule movement relied on Newtonian mechanics. The mitotic extract is a concentrated protein solution that will possess a relatively high viscous friction coefficient. Thus, the dominant force retarding microtubule movement will be linear viscous friction and inertia is negligible (Berg, 1993; Nedelec, 2002). Under these conditions, microtubule movement can be considered to occur in an overdamped manner (Howard, 2001) and microtubule movement decelerates rapidly upon motor inactivation (Supplemental Figure 1C). Therefore, force incident on a microtubule from a motor goes toward acceleration of the microtubule and overcoming viscous friction, giving the equation F = ma + bv (equation 2.4 from Howard, 2001). The viscous friction coefficient (b) was determined from force velocity relationships for conventional kinesin (Svoboda and Block, 1994) and was 6.25 × 10–6 Ns m–1. This value was independently validated with data showing the relationship between force and velocity for kinesin in optical trapping experiments. Every 1 pN of applied force linearly reduced the velocity of bead movement by 0.16 μm s–1 (Svoboda and Block, 1994), a result consistent with the value of the viscous friction coefficient derived here. Because viscous friction is a property of the solution that impedes microtubule movement driven by motors, use of conventional kinesin data to calculate this parameter is valid. The measurements of kinesin force and velocity were made in a cell-free solution, so the results can be considered to be broadly applicable to our system. It has also been argued that in vivo and in vitro motor velocities are equivalent (see Table 13.1 in Howard, 2001). Because the velocity of a motor in a viscous system is a function of the viscous friction coefficient, an absence of variation in motor velocities in these cases suggests the variation in viscous friction between systems is minimal. The response time for motor movement at full velocity was 3 ps in the simulation (Supplemental Figure 1D). This indicates that motors have essentially on/off kinetics with respect to movement at full velocity. This also provides an independent validation of our viscous friction coefficient as Howard (2001) calculated the same response time for a similarly sized particle. Finally, the mitotic extract is supplemented with ATP to 2.5 mM, a concentration in vast excess to the measured threshold where motor velocity diminishes due to delays in the chemical cycle for motor movement (Howard et al., 1989; Visscher et al., 1999). Thus, ATP was not limiting in the simulation and each motor was permitted to move at full velocity.
NuMA was implemented as an activity that would cross-link adjacent microtubules at their minus-ends and was referred to as Minus-End Cross-linking in this context (Table 2). We chose to simulate NuMA in this manner based on various data, including the localization of NuMA to microtubule minus-ends in spindles (Dionne et al., 1999), the ability of NuMA to cross-link microtubules (Haren and Merdes, 2002), and the loss of microtubule cross-linking at minus-ends when NuMA function is perturbed (Gaglio et al., 1996; Merdes et al., 1996). Moreover, although NuMA may use dynein motor function to facilitate its localization to microtubule minus-ends, it can act independently of dynein as demonstrated by its concentration at aster cores in the absence of dynein (Gaglio et al., 1996). To implement Minus-End Cross-linking in the simulation the region of the microtubule possessing the cross-linking activity or stickiness extended 0.5 μm from the minus-end. This stickiness extended 0.1 μm outward from the microtubule sidewall, forming a “sticky” rectangle 0.2 × 0.5 μm wide at the minus-end of each microtubule (Table 2, line 8). These dimensions were selected based on both the distribution of microtubule minus-ends and the localization of NuMA at spindle poles determined by electron microscopy (Dionne et al., 1999). If any part of this rectangular area of one microtubule intersects the rectangular area at the minus-end of another microtubule, then the two microtubules will be cross-linked to each other via these sticky regions. An off-rate for Minus-End Cross-linking was set based on the intuitive finding that microtubule asters form through Minus-End Cross-linking alone if it cross-links microtubules irreversibly (Table 2).
We assumed all three classes of motors act independently in the simulation. This assumption is justified because immunodepletion of any one class of motor does not affect microtubule-binding efficiency of any of the others (Gaglio et al., 1996; Mountain et al., 1999). Furthermore, microtubules being moved by kinesin and ciliary dynein simultaneously undergo a form of oscillatory behavior (directional instability), suggesting motors are acting independently and at any given time, only one motor molecule on a microtubule is actively generating movement (Vale et al., 1992). We also assumed that the velocity of a microtubule being moved by multiple motors of the same species is independent of motor density because it has been shown that the velocity of microtubule movement by such singly acting motors is independent of motor density (Vale et al., 1992; Malik et al., 1994). The resistance from cross-linked motors bound in the tight binding state of their mechanochemical cycle is not addressed in this model as will be addressed in DISCUSSION.
Each motor and the non-motor protein NuMA are capable of cross-linking microtubules (Kuriyama et al., 1995; Heald et al., 1996; Kashina et al., 1996; Mountain et al., 1999; Dionne et al., 1999; Haren and Merdes, 2002). Cross-linked microtubules with minus-ends pointed in the same direction were designated as parallel in orientation. Cross-linked microtubules where the minus-end of one microtubule pointed in the same direction as the plus-end of the adjacent microtubule were designated as antiparallel in orientation (Table 2).
Net motor force on a microtubule was calculated by vector addition of the forces provided by each motor species with one or more members present on the microtubule. This net motor force was then compared against the minus-end cross-linking threshold, and if the net force acting on the microtubule minus-ends exceeded the threshold, the cross-link was broken and the force threshold was subtracted from the net force on the cross-link. If the net force acting on the microtubule minus-ends did not exceed the threshold, net force on the cross-link was set to zero and the minus-ends stayed together.
A thorough computational verification of the program was performed as it was written. The code was written in a modular manner. Modules encoding the most basic system properties (e.g., Brownian motion, motor-driven movement of single microtubules) were implemented first. Every module was first tested independently to ensure that it correctly encoded system behavior. For example, microtubule displacement measurements and acceleration-deceleration curves (Supplemental Figure 1) were used to computationally verify the behavior of the single microtubule movement module. Modules were then assembled into larger functional units that encoded more complex system behaviors (e.g., motor-driven movement of microtubule pairs) and at this point these modules were once again tested to ensure the correctness of the code. For example, a test suite of several different microtubule configurations was used to determine the proper behavior of microtubule pairs (Supplemental Figure 2). In each case, visual inspection of the final positions of the microtubule pairs, coupled with the distances moved by each microtubule in the pair, provided the necessary computational verification. Finally, the movement of whole systems of microtubules was verified by generating frame-by-frame animations of the output.
Finally, we developed two metrics to evaluate the degree of microtubule organization in the simulation. One metric (microtubules bound at minus-end) counts the total number of microtubules bound to one another with their minus-ends overlapping in the final frame. For this purpose, the terminal 0.5 μm of the microtubule is defined as the minus-end. The other metric (minus-end area) is a measure of the area occupied by minus-ends of microtubules whose minus-ends overlap in the largest aggregate of microtubules in the final frame. This area is measured by determining the convex hull of minus-ends, which is the smallest convex polygon that contains all minus-ends (www.cs.princeton.edu/~ah/alg_anim/version1/ConvexHull.html). These two metrics, when applied to the simulation, are sufficient to discriminate between the three possible outcomes: tightly focused asters, loosely focused asters, and no organization. These are the arrangements observed in the mitotic extract (Figure 1 and Table 1).
RESULTS
Modeling Microtubule Aster Formation
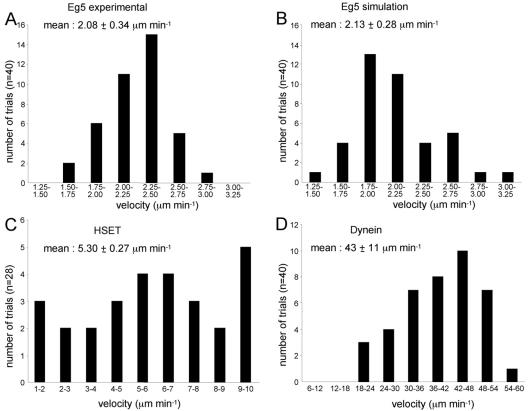
Velocities of microtubule movement by Eg5, HSET, and dynein have been published previously (Sawin et al., 1992; King and Schroer, 2000; DeLuca et al., 2001). We used these velocities to implement the movement of single microtubules by motors in the simulation (Figure 2). For variance around the mean, we included a probabilistic function to mimic a time delay at each step of the motors in accordance with data from Visscher et al. (1999) (Supplemental Figure 1, A and B). With these parameters, 40 trials of Eg5-mediated motility generated an average velocity of 2.13 μm min–1 (Figure 2B) that was very similar to the published velocity of Eg5-mediated motility (2.08 μm min–1; Sawin et al., 1992; Figure 2A). For each motor species, simulated motors had a mean velocity that was not significantly different from the experimentally determined velocities (t test, p < 0.05).
Figure 2.
Velocities of movement of single microtubules moved by motors in the simulation. (A) Velocity measurements of 40 trials of single microtubule movement by the plus-end–directed motor Eg5 (taken from Sawin et al., 1992). (B–D) Velocity measurements of 40 trials of single microtubule movement by the simulated activities of the plus-end–directed motor Eg5, the minus-end–directed motor HSET, and the minus-end–directed motor dynein as indicated.
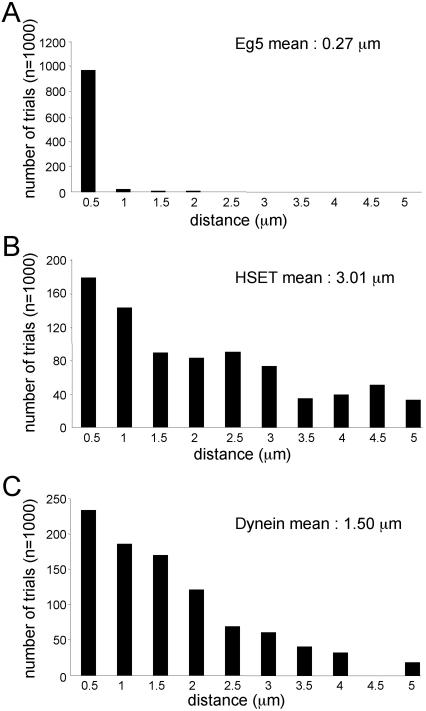
To regulate motor run lengths, a probabilistic function that a motor would spontaneously detach from a microtubule was implemented for each motor in the simulation. The magnitude of this probability differed for each motor and was determined empirically, such that simulated run lengths of HSET, Eg5, and dynein averaged 3.01, 0.27, and 1.5 μm, respectively (Figure 3). The average run length of dynein in the simulation was implemented to match the average run length for dynein/dynactin complexes determined using single motor motility assays (King and Schroer, 2000). We simulated dynein as associated with dynactin to reduce simulation complexity. This assumption is justified because dynein has not been shown to act on spindles without being associated with dynactin. The average run length of HSET in the simulation was implemented to match the average run length of native HSET determined using multiple motor motility assays (DeLuca et al., 2001). Finally, run lengths for native Eg5 have not been reported. In this case, we set the probability of detachment of Eg5 from microtubules so that ∼50% of Eg5 motors were bound to microtubules at steady state. This matches the distribution of Eg5 between the soluble and aster-containing pellet fractions determined using immunoblots of the mitotic extract (Figures 11B and 12B, control samples).
Figure 3.
Run length of microtubule motors in the simulation. The distance (micrometers) traveled before dissociation from the microtubule by the motors Eg5 (A), HSET (B), and dynein (C) in 1000 independent trials of motor movement on single microtubules.
Figure 11.
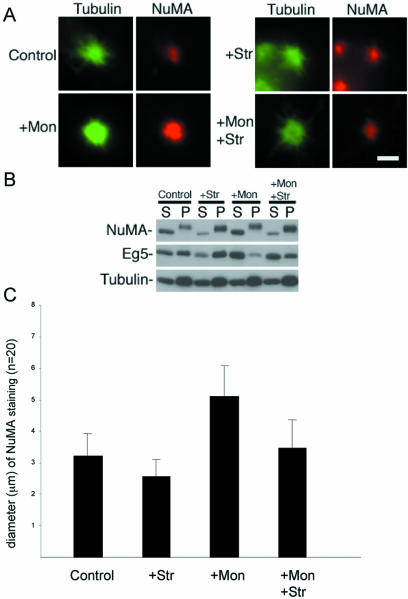
Formation of tightly focused asters in the absence of Eg5 activity by inhibition of protein kinase activity. The mammalian mitotic extract was treated with the Eg5 inhibitor monastrol (100 μM) or the protein kinase inhibitor staurosporine (1 μM) as indicated. (A) Microtubule polymerization was then stimulated by the addition of taxol and ATP and incubation at 33°C, and the resulting structures were analyzed by immunofluorescence microscopy by using antibodies specific for tubulin and NuMA as indicated. (B) The extract was separated into 10,000g soluble (S) and insoluble (P) fractions after induction of microtubule polymerization. These fractions were subjected to immunoblot analysis using antibodies specific for NuMA, Eg5, and tubulin as indicated. (C) Diameter of NuMA staining in 20 randomly selected asters under each condition was analyzed by taking two perpendicular measurements of each aster.
Figure 12.
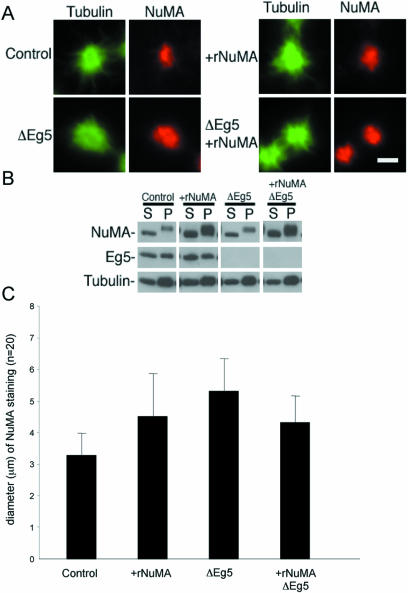
Formation of tightly focused asters in the absence of Eg5 by addition of recombinant NuMA. The mammalian mitotic extract was depleted of Eg5 and/or supplemented with recombinant NuMA as indicated. (A) Microtubule polymerization was then stimulated by the addition of taxol and ATP and incubation at 33°C, and the resulting structures were analyzed by immunofluorescence microscopy by using antibodies specific for tubulin and NuMA as indicated. (B) The extract was separated into 10,000g soluble (S) and insoluble (P) fractions after induction of microtubule polymerization. These fractions were subjected to immunoblot analysis using antibodies specific for NuMA, Eg5, and tubulin as indicated. (C) Diameter of NuMA staining in 20 randomly selected asters under each condition was analyzed by taking two perpendicular measurements of each aster.
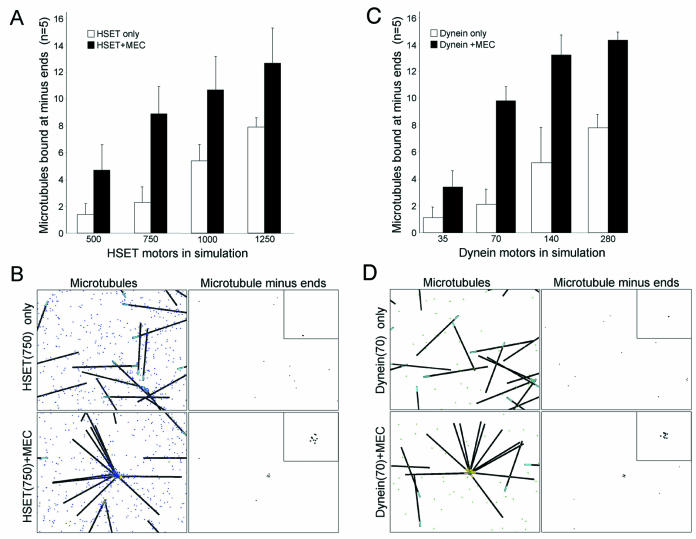
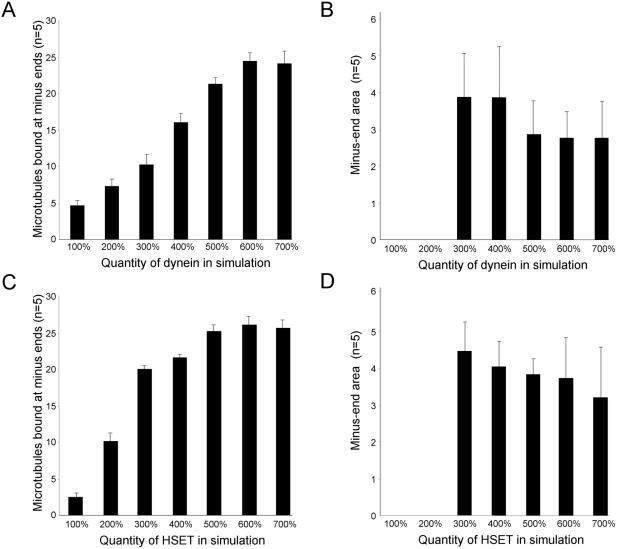
We used a linear optimization strategy based on the information contained in Table 1 to determine the quantity of each motor in the simulation. For example, when dynein, Eg5, and NuMA are depleted simultaneously, HSET alone is insufficient to overcome the dispersive effect of Brownian motion and organize microtubules into asters (Table 1, line 13). However, the motor activity of HSET is sufficient to organize microtubule asters if NuMA is present (when Eg5 and dynein are depleted simultaneously) (Table 1, line 10). Based on these data, we increased the quantity of HSET with and without Minus-End Cross-linking in the simulation, and determined the degree of microtubule organization (Figure 4, A and B). Increasing the quantity of HSET from 500 to 1250 resulted in a linear increase in the number of microtubules bound when HSET alone is present (from ∼10 to 50%). In the presence of Minus-End Cross-linking activity, the number of microtubules bound increased significantly at each quantity of HSET (Figure 4A). From these data, we selected a quantity of 750 HSET for the simulation (for 15 microtubules in a 150-μm2 area). This was the highest quantity of HSET that organized microtubules in the presence of Minus-End Cross-linking activity, but failed to organize microtubules when present alone (Figure 4B). Using a similar strategy we selected 70 dynein for the simulation (for 15 microtubules in a 150-μm2 area). This was the highest quantity of dynein that organized microtubules in the presence of Minus-End Cross-linking activity, but failed to organize microtubules when present alone (Figure 4, C and D).
Figure 4.
Optimization of HSET and dynein quantities in the simulation. (A and C) Number of microtubules bound at minus-ends was determined in five independent trials of 15 microtubules (in a 150-μm2 area) with HSET (A) or dynein (C) alone (white bars) or with minus-end cross-linking (MEC) (black bars). The quantities of HSET and dynein were varied as indicated. (B and D) Representative images of microtubules and microtubule minus-ends from the final time point from simulations with HSET or HSET + MEC (B) and dynein or dynein + MEC (D). HSET and dynein are represented as blue and green dots, respectively. Microtubules are represented as black line with minus-ends colored cyan (unbound) or yellow (bound). Microtubule minus-ends are represented as black spots. Inset is 5× magnification to highlight the position of microtubule minus-ends.
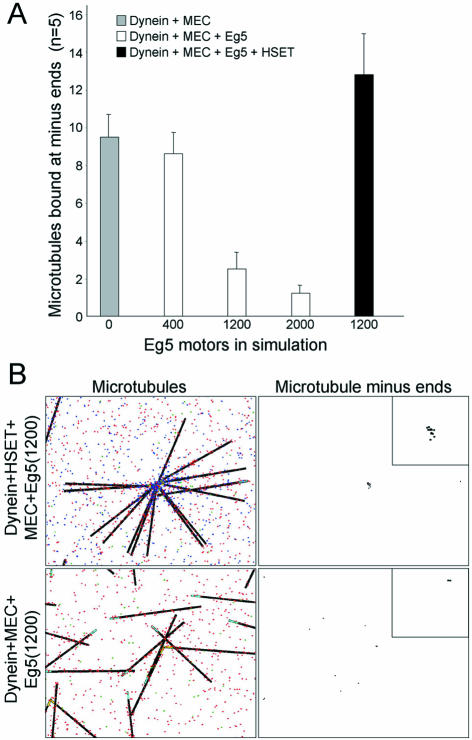
We also used the data in Table 1 to determine the quantity of Eg5. These data show the concentration of Eg5 in the mitotic extract must be sufficient to destabilize asters formed when either HSET and NuMA or dynein and NuMA are present (Table 1, lines 3 and 4). Based on this information, we increased the quantity of Eg5 in the simulation in the presence of dynein and Minus-End Cross-linking activity (Figure 5). Increasing the quantity of Eg5 from 400 to 2000 led to a linear decrease in the number of microtubules bound in the presence of dynein and Minus-End Cross-linking activity (Figure 5A). From these data, we selected 1200 Eg5 for the simulation (for 15 microtubules in a 150-μm2 area). This was the highest quantity of Eg5 sufficient to destabilize microtubule aster formation by dynein and Minus-End Cross-linking without affecting aster formation by dynein, Minus-End Cross-linking and HSET (Figure 5B).
Figure 5.
Optimization of Eg5 quantity in the simulation. (A) Number of microtubules bound at minus-ends was determined in five independent trials of 15 microtubules (in a 150-μm2 area) with dynein + MEC (gray bars), dynein + minus-end cross-linking (MEC) + Eg5 (white bars), or dynein + MEC + Eg5 + HSET (black bar). The quantity of Eg5 was varied as indicated. (B) Representative images of microtubules and microtubule minus-ends from the final time point from simulations with dynein + HSET + MEC + Eg5 or dynein + MEC + Eg5. Eg5, HSET, and dynein are represented as red, blue, and green dots, respectively. Microtubules are represented as black line with minus-ends colored cyan (unbound) or yellow (bound). Microtubule minus-ends are represented as black spots. Inset is 5× magnification to highlight the position of microtubule minus-ends.
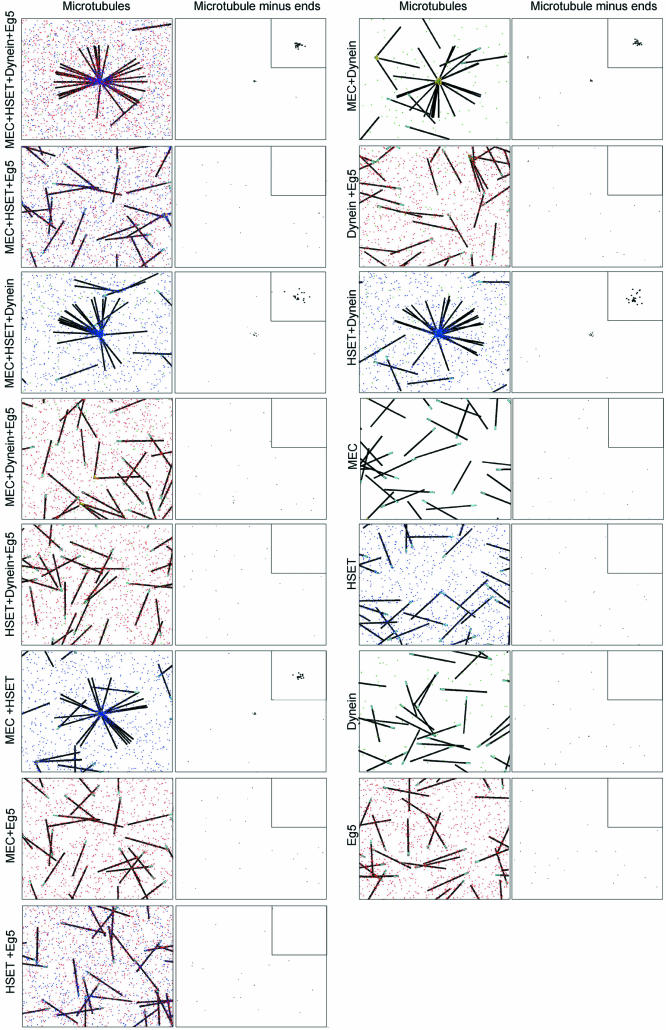
Using biophysical properties of each component at the quantities determined, we attempted to replicate results from the mitotic extract present in Table 1. Simulations were performed with 15 microtubules and all possible combinations of dynein, HSET, Minus-End Cross-linking, and Eg5. These trials demonstrated that when all four components (dynein, HSET, Minus-End Cross-linking, and Eg5) were present, microtubules organized into asters with tightly focused cores (Figure 5B, top). This was the expected result based on data in Table 1. Also, microtubules were randomly dispersed and failed to organize if only HSET was removed (Figure 5B, bottom). This was the expected result of an HSET depletion based on data in Table 1. Indeed, the simulation accurately replicated all combinations represented in Table 1 that led to either tightly focused asters or randomly distributed microtubules. However, asters formed with dynein and HSET or dynein, HSET, and Minus-End Cross-linking were focused to the same extent as asters formed with dynein, HSET, Eg5, and Minus-End Cross-linking. This was inconsistent with loosely focused asters expected based on the data in Table 1 (lines 5 and 8) and indicated that the biological model underlying the simulation was incomplete.
To modify the biological model underlying the simulation, we first focused on the combination containing HSET and dynein only. This combination contains the fewest components that yields loosely focused microtubule asters (Table 1, line 8). Initially, we varied the quantity of either or both HSET (250–750) and dynein (18–70). In some of these cases, total motor activity failed to reach an appropriate threshold and microtubules did not organize efficiently as expected from the titrations of each motor alone. In all other cases, microtubules organized into asters, but microtubule minus-ends occupied areas that were consistent with tightly focused asters (t test, p > 0.05 compared with results obtained with all components present). These data indicate that there is no unique quantity of HSET and/or dynein that yields loosely focused asters and that the way in which we simulate HSET and/or dynein activity must be qualitatively changed. The qualitative change we made was to limit HSET and dynein to cross-linking only those pairs of microtubules that lie parallel to one another with respect to their plus- and minus-ends (refer to Table 2 and MATERIALS AND METHODS for a definition of microtubule orientation). To determine whether this restriction affected microtubule organization in the simulation, we compared microtubule organization by dynein and HSET together where dynein and HSET were permitted to cross-link microtubules indiscriminately (in either parallel or antiparallel orientation) or parallel only (Figure 6). At the quantities of each motor determined in Figure 4, restricting dynein and HSET to cross-linking parallel microtubule pairs does not diminish their ability to overcome the dispersive effects of Brownian motion and organize microtubules into asters (Figure 6A). However, microtubule minus-ends occupied a significantly larger area when dynein and HSET were restricted to parallel microtubule pairs only compared with when they cross-link microtubules indiscriminately (t test, p < 0.05). Thus, restricting the ability of dynein and HSET to cross-link microtubules in parallel orientation only succeeded in generating loosely focused microtubule asters consistent with the data in Table 1.
Figure 6.
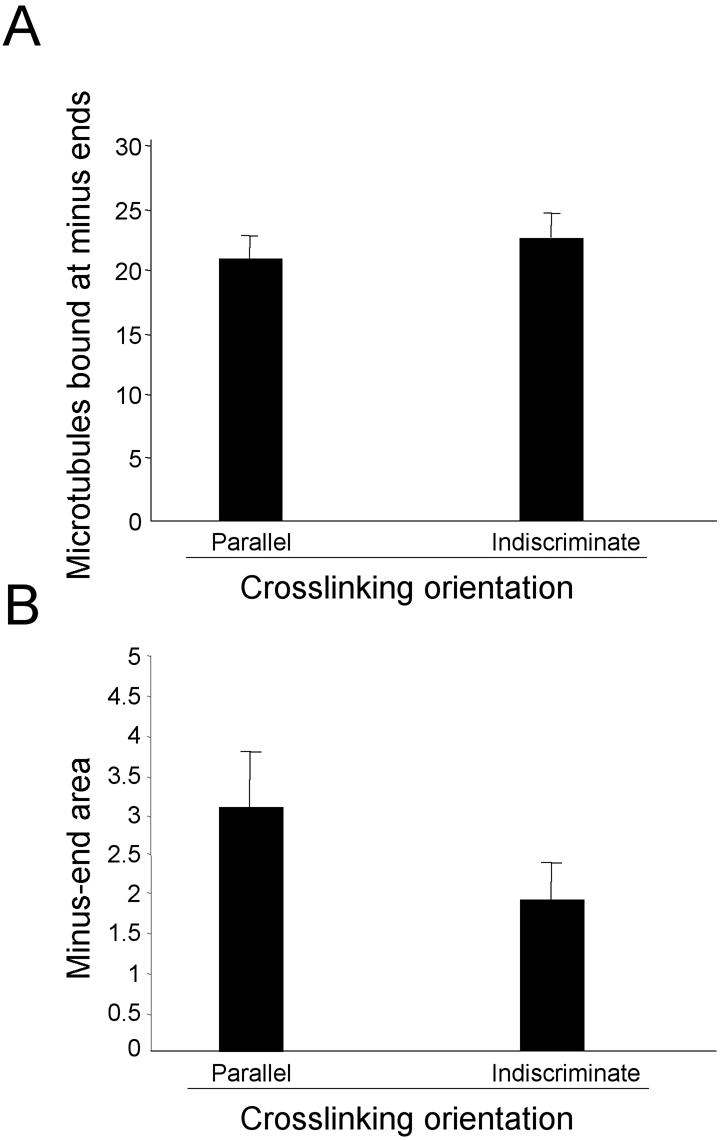
Microtubule organization depends on restrictions on the cross-linking orientation of dynein and HSET. The number of microtubules bound at minus-ends (A) and the area occupied by microtubule minus-ends in the largest aggregate (B) were determined in five independent trials of 30 microtubules (in a 300-μm2 area) when HSET and dynein were allowed to cross-link microtubules indiscriminately or in parallel orientation only.
The final combination in Table 1 that the simulation failed to accurately predict was when Eg5 was depleted, leaving HSET, dynein, and NuMA in the extract (Table 1, line 5). Loosely focused asters form in that combination (Figure 1), whereas the simulation produced tightly focused asters. The only difference between the combination containing dynein and NuMA (Table 1, line 9) (or HSET and NuMA) and the combination containing dynein, HSET, and NuMA (Table 1, line 5) is the presence of two minus-end–directed motors instead of one, yet that difference is sufficient to alter the degree to which microtubule minus-ends are focused at the center of asters. Based on that single difference, we postulated that the force exerted by the combined action of two minus-end–directed motors (dynein and HSET) would be greater than the force exerted by either dynein or HSET alone. The increase in force from two motors acting simultaneously would be sufficient to disrupt NuMA-dependent cross-links at microtubule minus-ends. This would render NuMA ineffective, making the combination containing dynein, HSET, and NuMA equivalent to dynein and HSET, which yields loosely focused asters. To implement such a force-dependent disruption of NuMA cross-links, we applied a force-sensitive threshold to Minus-End Cross-linking activity in the simulation. This threshold was set to 2.1 pN, a value determined empirically. To determine whether this restriction altered organization of microtubule asters, we compared the outcome of simulations in which Minus-End Cross-linking was either sensitive to Net Minus-end–directed Force, or insensitive. We did this comparison in the presence and absence of restrictions on dynein and HSET's ability to cross-link microtubules (parallel only and indiscriminate; Figure 7). Applying a threshold to the ability of Minus-End Cross-linking to withstand force exerted on it does not diminish the ability of HSET and dynein to organize microtubules into asters (Figure 7A). As expected, if Minus-End Cross-linking is insensitive to force or if dynein and HSET cross-link microtubules indiscriminately, tightly focused asters were observed (Figure 7B). In contrast, microtubule minus-ends occupied a significantly larger area if Minus-End Cross-linking activity was force sensitive, and dynein and HSET were restricted to cross-linking microtubules in a parallel-only orientation (t test, p < 0.05, comparison with force-insensitive control). These results demonstrate that Minus-End Cross-linking activity must be force-sensitive to generate loosely focused asters when dynein, HSET, and Minus-End Cross-linking are present as expected from Table 1. These results also demonstrate that both Minus-End Cross-linking force-sensitivity and parallel-only restrictions on dynein and HSET must be implemented for loosely focused asters to form in the combination containing dynein, HSET and Minus-End Cross-linking.
Figure 7.
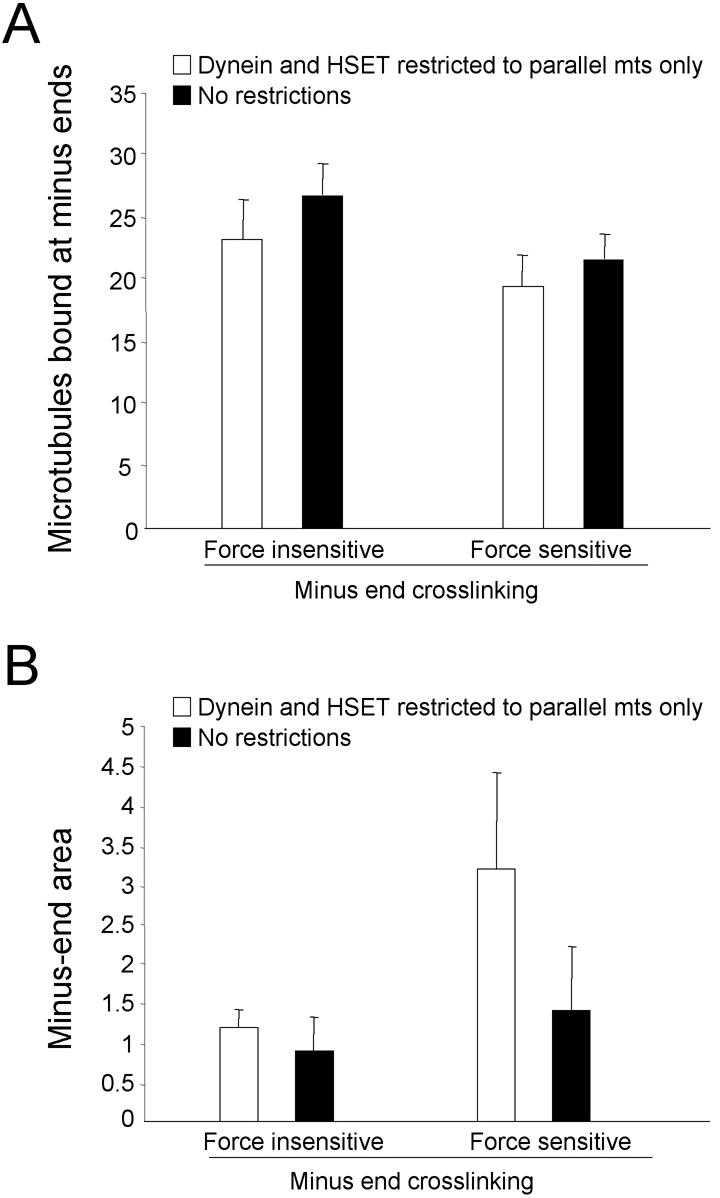
Microtubule organization depends on making minus-end cross-linking (MEC) sensitive to force incident on it. The number of microtubules bound at minus-ends (A) and the area occupied by microtubule minus-ends in the largest aggregate (B) were determined in five independent trials of 30 microtubules (in a 300-μm2 area) when MEC was force sensitive or force insensitive as indicated. HSET and dynein were allowed to cross-link microtubules indiscriminately (white bars) or in parallel orientation only (black bars).
The simulation was now run with 30 microtubules and with appropriately scaled quantities of dynein, HSET, Eg5, and Minus-End Cross-linking in all possible combinations (Figure 8). The results were compared with results of combinatorial depletions from the mitotic extract (Tables 1 and 3). In the revised configuration, in which dynein and HSET were restricted to cross-linking microtubules in parallel orientation only and Minus-End Cross-linking was force sensitive, the simulation accurately replicated microtubule organization in all combinations (Figure 8 and Table 3). Three combinations (dynein and Minus-End Cross-linking, HSET and Minus-End Cross-linking, as well as HSET, Eg5, dynein, and Minus-End Cross-linking) showed efficient microtubule organization (60–65%) and tightly focused microtubule minus-ends (2–2.6 μm2) (Table 3). Two combinations (dynein and HSET, and dynein, HSET, and Minus-End Cross-linking) showed efficient microtubule organization (60–65%) and loosely focused microtubule minus-ends (4.5–6 μm2) (Table 3). All other combinations resulted in randomly dispersed microtubules with <20% microtubules bound in the final frame (Table 3).
Figure 8.
Simulation accurately replicates microtubule organization in all the combinations in a mammalian mitotic extract. Representative images of microtubule organization in the final time point from simulations (30 microtubules in a 300-μm2 area) with all possible combinations of dynein, HSET, Eg5, and minus-end cross-linking (MEC) as indicated. Eg5, HSET, and dynein are represented as red, blue, and green dots, respectively. Microtubules are represented as black line with minus-ends colored cyan (unbound) or yellow (bound). Microtubule minus-ends are represented as black spots. Inset is 5× magnification to highlight the position of microtubule minus-ends.
Table 3.
Summary of combinatorial immunodepletions modeled in the simulation
| Components | No. mts bounda | Minus-end areaa | Conclusion | Table 1 concordance |
|---|---|---|---|---|
| D, H, M, E | 26.4 ± 3.5 | 2.1 ± 0.8 | Tightly focused | Yes |
| D, H, E | 3.8 ± 2.1 | No organization | Yes | |
| D, M, E | 5.1 ± 2.2 | No organization | Yes | |
| H, M, E | 6.9 ± 3.1 | No organization | Yes | |
| D, H, M | 22.7 ± 2.0 | 4.4 ± 0.6 | Loosely focused | Yes |
| D, E | 5.2 ± 3.0 | No organization | Yes | |
| H, E | 2.2 ± 1.3 | No organization | Yes | |
| D, H | 20.2 ± 3.6 | 5.0 ± 1.2 | Loosely focused | Yes |
| D, M | 21.9 ± 3.7 | 2.2 ± 0.5 | Tightly focused | Yes |
| H, M | 21.0 ± 2.9 | 2.6 ± 0.7 | Tightly focused | Yes |
| M, E | 2.2 ± 0.6 | No organization | Yes | |
| D | 3.2 ± 0.9 | No organization | N/A | |
| H | 2.4 ± 1.8 | No organization | Yes | |
| M | 4.8 ± 2.8 | No organization | Yes | |
| E | 0.7 ± 0.2 | No organization | N/A |
mts, microtubules.
Ten trials of 30 microtubules each.
In iteratively refining the simulation to replicate known experimental data from the mitotic extract, it became clear the degree of microtubule organization relies on two aggregate properties to overcome the dispersive effect of Brownian motion. One property was Net Minus-end–directed Force. The magnitude of minus-end–directed force will be an aggregate property that depends on which motors are present, because there will be antagonism between the plus- and minus-end–directed motors. The second property was the propensity of microtubules in the extract to be cross-linked in parallel or antiparallel orientation which we refer to as microtubule Cross-linking Orientation Bias. This is also an aggregate property that will depend on the individual components present as the simulation now places restrictions on the cross-linking properties of some components. Cross-linking Orientation Bias for most combinations is intuitively obvious, such as when all components cross-link microtubules in parallel orientation only (e.g., dynein and HSET), or when all components cross-link indiscriminately in either parallel or antiparallel orientation (e.g., Minus-End Cross-linking and Eg5). If there are two components cross-linking parallel only and one cross-linking indiscriminately (e.g., HSET, dynein and Eg5), then aggregate Cross-linking Orientation Bias is defined as parallel. Similarly, if there are two components cross-linking indiscriminately and one cross-linking parallel only (e.g., dynein, Minus-End Cross-linking, and Eg5), then aggregate Cross-linking Orientation Bias is defined as indiscriminate. The only combination that required us to specify an additional rule is when even numbers of components cross-linking parallel only and indiscriminately are present (e.g., dynein and Minus-End Cross-linking or dynein, HSET, Eg5, and Minus-End Cross-linking). In those combinations, we defined Cross-linking Orientation Bias as indiscriminate.
These results lead to a model for microtubule organization in this system that is based on two aggregate properties: Net Minus-end–directed Force and Cross-linking Orientation Bias (Table 4). Each aggregate property is determined by properties inherent to individual components present in a given combination. These two properties, together, are sufficient to predict the organization of microtubules in all combinations observed experimentally in Table 1. For example, tightly focused microtubule asters are predicted to form when HSET and Minus-End Cross-linking are present because Net Minus-end–directed Force is strong (HSET is unopposed) and microtubule cross-linking is indiscriminate (because Minus-End Cross-linking is present). When HSET, dynein, Eg5, and Minus-End Cross-linking are present, tightly focused asters are formed as Net Minus-end–directed Force is weak (HSET and dynein are opposed by Eg5) and Cross-linking Orientation Bias is indiscriminate (because both Minus-End Cross-linking and Eg5 are present). Loosely focused asters are predicted to form when dynein and HSET are present, because Net Minus-end–directed Force is strong (both motors are unopposed) and Cross-linking Orientation Bias is parallel (no indiscriminately cross-linking components are present). Finally, when Net Minus-end–directed Force is insufficient (e.g., the Eg5 and Minus-End Cross-linking combination, where Net Motor Force is plus-end directed), microtubules will fail to organize and be randomly distributed.
Table 4.
Model for organization of microtubules in a mammalian mitotic extract
| Microtubule cross-linking bias
|
|||
|---|---|---|---|
| Indiscriminate | Parallel | ||
| Net minus-end—directed force | Strong | Tightly focused | Loosely focused |
| Weak | Tightly focused | ||
| None | |||
Evaluation of the Model for Microtubule Aster Organization
Two constraints were needed for the simulation to accurately predict microtubule organization as it occurs in the mammalian mitotic extract. One constraint was that Minus-End Cross-linking must be sensitive to the force incident on it and that constraint will require direct biophysical measurements to test. The other constraint was that microtubule cross-linking orientation was restricted for some but not all components. The initial choice of cross-linking restrictions was driven by a specific combination (dynein and HSET only), and we needed to explore all other possibilities. Thus, we systematically altered the cross-linking bias of each component from parallel-only to indiscriminate (we did not examine restricting components to antiparallel microtubule cross-linking only as that is incompatible with microtubule aster organization in which microtubule minus-ends are focused at the aster vertex). We then performed simulations with combinations that generated asters in which all 16 possible permutation of cross-linking bias were tested (Table 5 and Supplementary Table). Based on these simulations, the only permutation of cross-linking bias that demonstrated complete concordance with the data in Table 1 was with dynein and HSET restricted to cross-linking parallel microtubules only and Minus-End Cross-linking and Eg5 unrestricted (cross-linking microtubules indiscriminately). All other permutations fail to replicate the data in Table 1 in at least one combination (Table 5 and Supplementary Table), and most permutations fail in multiple combinations. Permitting Eg5 to cross-link microtubules indiscriminately is entirely consistent with localization studies showing Eg5 associated with both parallel and antiparallel microtubule populations in spindles (Sawin et al., 1992; Sharp et al., 1999). Also, restricting dynein and HSET to parallel-only microtubule cross-linking is entirely consistent with their localization to parallel microtubule populations in spindles (Steuer et al., 1990; Kuriyama et al., 1995; Matuliene et al., 1999; Mountain et al., 1999), the parallel-only microtubule bundles formed by overexpression of the hamster homologue of HSET (CHO2) in insect cells (Sharp et al., 1997), and the dynein-dependent focusing of parallel oriented polarity-marked microtubules at spindle poles in frog egg extracts (Heald et al., 1996, 1998). Permitting Minus-End Cross-linking to cross-link microtubules indiscriminately is somewhat counterintuitive given that Minus-End Cross-linking in the simulation represents NuMA in the mitotic extract. Although NuMA may have the capacity to cross-link microtubule minus-ends indiscriminately (as we have simulated Minus-End Cross-linking activity), in mitotic cells where the positions of microtubule minus-ends are restricted by centrosomes, the opportunity for antiparallel microtubule minus-end cross-linking presents itself so seldom that it may go unobserved.
Table 5.
Summary of evaluations of alternative cross-linking orientation biases
| Orientation restriction | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dynein | P | P | P | P | I | I | I | I | P | P | P | P | I | I | I | I | |
| HSET | P | P | P | P | P | P | P | P | I | I | I | I | I | I | I | I | |
| MEB | P | P | I | I | P | P | I | I | P | P | I | I | P | P | I | I | |
| Eg5
|
P
|
I
|
P
|
I
|
P
|
I
|
P
|
I
|
P
|
I
|
P
|
I
|
P
|
I
|
P
|
I
|
|
| dhme | - | - | - | + | - | + | + | + | - | + | + | + | + | + | + | + | |
| Simulation cases | dhm | + | + | + | + | + | + | - | - | - | - | - | - | - | - | - | - |
| dm | - | - | + | + | - | - | + | + | - | - | + | + | - | - | + | + | |
| hm | - | - | + | + | - | - | + | + | - | - | + | + | - | - | + | + | |
| dh | + | + | + | + | - | - | - | - | - | - | - | - | - | - | - | - | |
D, dynein; E, Eg5; H, HSET; I, indiscriminate; M, minus-end cross-linking; P, parallel.
+, simulation outcome is not significantly different from combinatorial immunodepletion result (p > 0.05).
-, simulation outcome is significantly different from combinatorial immunodepletion result (p < 0.05).
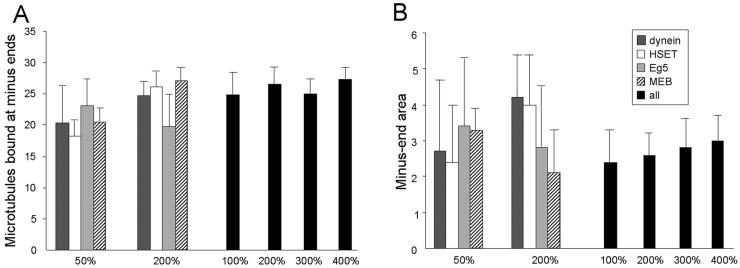
Next, we evaluated whether the simulation was robust to minor alterations in the quantity of individual components (Figure 9). Decreasing the quantity of dynein or HSET to 50% or increasing the quantity of Eg5 or Minus-End Cross-linking (by reducing off-rate) to 200% had no significant effect on microtubule organization. In contrast, increasing the quantities of dynein or HSET to 200%, or decreasing the quantity of Eg5 or Minus-End Cross-linking (by increasing off-rate) to 50% led to asters that were significantly less tightly focused than controls (t test, p < 0.05). Thus, the simulation is robust to minor perturbations in the quantity of single components, but only if those changes decrease Net Minus-end–directed Force or increase indiscriminate cross-linking.
Figure 9.
Robustness analysis for the simulation. The number of microtubules bound at minus-ends (A) and the area occupied by microtubule minus-ends in the largest aggregate (B) were determined in five independent trials of 30 microtubules (in a 300-μm2 area) when the quantities of dynein (dark gray bars), HSET (white bars), Eg5 (light gray bars), or minus-end cross-linking (MEC) (hatched bars) were varied individually or together (black bars) as indicated.
The inverse relationship observed between Net Minus-end–directed Force and indiscriminate cross-linking in these analyses suggested that the ratios of these activities might be more critical than the quantities of any one component. To test this, we increased the quantities of Eg5, dynein, HSET, and Minus-End Cross-linking (by reducing the off-rate), to 200, 300, and 400% and compared the outcome with the observed result (Figure 9). In each case, asters form with tightly focused cores whose area is not significantly different from the starting condition (t test, p > 0.05). These results demonstrate that the simulation can tolerate substantial changes in the quantities of individual components, provided the ratios of the components stay within the range over which the simulation has been trained. This is significant because the key requirement is the appropriate ratio of activities, and not the absolute quantity of any one component. This minimizes the impact of any errors that might be inherent in our initial estimates for the quantities of each component.
An explicit feature of the model is that both parallel and indiscriminate microtubule cross-linking contribute to microtubule aster formation, which emphasizes the quality of microtubule cross-linking and not necessarily the quantity microtubule cross-linking. To determine whether increasing only the quantity of microtubule cross-linking affected microtubule organization in asters, we ran simulations where we increased the quantity of dynein or HSET alone in increments of 100% up to 700% (Figure 10). Both dynein and HSET organized a significant fraction of microtubules into asters when present at quantities of 300% or higher. In each case where asters were organized by HSET, the area occupied by microtubule minus-ends was significantly different from tightly focused asters under control conditions (t test, p < 0.05). Similarly, increasing dynein quantities up to 500% generated asters whose minus-end area was significantly larger than controls (t test, p < 0.05, for 500%, p = 0.043). However, at 600 and 700%, asters formed with cores whose minus-end area was not significantly larger than controls (t test, p > 0.05). These results demonstrate that tightly focused asters can form under conditions of parallel-only cross-linking, provided the quantity of cross-linking is sufficiently high. However, these results do not eliminate the contribution of some degree of antiparallel cross-linking in aster organization. HSET alone failed to generate asters at quantities up to 700% of the original quantity, and dynein alone was only successful in generating tightly focused asters at 600% or greater. Thus, the tightly focused microtubule asters that form when the quantity of components is specified by data in Table 1 indicate that indiscriminate microtubule cross-linking plays a significant role in determining the state of microtubule organization.
Figure 10.
Increasing the quantity of HSET or dynein in the simulation. The number of microtubules bound at minus-ends (A) and the area occupied by microtubule minus-ends in the largest aggregate (B) were determined in five independent trials of 30 microtubules (in a 300-μm2 area) when the quantities of dynein (A and B) or HSET (C and D) were increased as indicated.
Finally, based on the relationship between Net Minus-end–directed Force and Cross-linking Orientation Bias, the model predicts that loosely focused asters formed under conditions of strong Net Minus-end–directed Force and parallel microtubule cross-linking bias could be converted to tightly focused asters merely by increasing the quantity of indiscriminate microtubule cross-linking (Table 4). Specifically, it should be possible to convert loosely focused asters formed in the absence of Eg5 activity into tightly focused asters by increasing the quantity of indiscriminate cross-linking provided by NuMA.
To test this prediction, Eg5 activity in the mitotic extract was inhibited with monastrol (Mayer et al., 1999). The quantity of NuMA bound to microtubules in the mitotic extract was increased by treatment with the protein kinase inhibitor staurosporine (Compton, unpublished observation). Under control conditions, microtubule asters formed with tightly focused cores (∼3.2 μm in diameter), as judged by the diameter of NuMA staining (Figure 11, A and C). An appreciable amount of both NuMA and Eg5 was associated with asters in the insoluble fraction (Figure 11B). Treatment of the extract with monastrol resulted in microtubule asters with loosely focused cores (∼5.1 μm in diameter; Figure 11, A and C). Monastrol did not alter the distribution of NuMA between the soluble and insoluble fractions, but it seemed to reduce the efficiency with which Eg5 associated with microtubule asters in the insoluble fraction (Figure 11B). Treatment of the extract with staurosporine did not alter microtubule aster organization, although the cores were slightly more tightly focused relative to control (∼2.6 μm in diameter; Figure 11, A and C). Staurosporine significantly increased the efficiency with which NuMA associated with microtubule asters in the insoluble fraction (Figure 11B). Simultaneous treatment of the extract with staurosporine and monastrol led to microtubule asters that had tightly focused cores (∼3.5 μm in diameter), with diameters not significantly different from controls (t test, p > 0.05; Figure 11C). These results suggest that increasing the quantity of NuMA on microtubule asters overcomes deficits in Eg5 activity and converts loosely focused asters into tightly focused asters.
To eliminate the possibility of artifacts associated with pleiotropic drug effects, we repeated this experiment by using a strategy that did not rely on drugs. Eg5 was depleted using a specific antibody, and the quantity of NuMA was increased by addition of the purified recombinant protein (Figure 12). Immunoblots verified that Eg5 was depleted completely from the extract (Figure 12B) and the added recombinant NuMA significantly increased (approximately threefold) the quantity of NuMA in the aster-containing insoluble fraction (Figure 12B). As expected, the depletion of Eg5 resulted in loosely focused microtubule asters (∼5.2 μm in diameter compared with 3.2 μm in control; Figure 12, A and C). Addition of recombinant NuMA to the Eg5-depleted extract resulted in microtubule asters with core diameters (∼4.3 μm) significantly smaller than those found in the absence of Eg5 alone (t test, p < 0.05). The diameter of aster cores in this situation was not significantly different from when recombinant NuMA was added alone (∼4.4 μm; t test, p > 0.05). These data are similar to the data obtained by drug inhibition. These experiments confirm the prediction from the model that increasing indiscriminate microtubule cross-linking can compensate for imbalances in motor force.
DISCUSSION
We used computer simulation to build a model for microtubule organization driven by noncentrosomal motor and nonmotor proteins in a mammalian mitotic extract. The simulation was trained using experimental data (Table 1) by comparing simulation outcomes to experimental outcomes, and iteratively refining the underlying biological assumptions accordingly. Thus, the strength of the computer simulation, and the validity of any conclusions we draw from it, depend on the accuracy of the data from the combinatorial inhibitions in the mammalian mitotic extract (Table 1). A number of independent observations indicate that the experimental data in Table 1 is a reliable data set on which to train the simulation. For example, extensive biochemical characterizations of the mitotic extract indicate that the specific motor and non-motor proteins represented in the simulation are the only components that contribute to microtubule aster organization (Gaglio et al., 1995; Mountain et al., 1999; Mack and Compton, 2001). Also, antagonism between oppositely oriented motors, an explicit feature of the model presented here, has been well documented in many different experimental systems ranging from yeast to human (Pidoux et al., 1996; Saunders et al., 1997; Mountain et al., 1999; Sharp et al., 1999).
It is interesting to note that, by extrapolation (assuming a cell with dimensions 20 × 20 × 20 μm), the quantities of dynein, HSET, and Eg5 used in the simulation are ∼2 × 105, ∼1 × 106, and ∼2 × 106 molecules/cell, respectively. HSET and Eg5 have both been reported at ∼5 × 106 molecules/cell (Mountain et al., 1999; Kapoor and Mitchison, 2001). Dynein has been reported at ∼3 × 106 molecules/cell, but only ∼3% (∼1 × 105) of dynein functionally participates in spindle pole organization (Merdes et al., 1996). Thus, the motor quantities used in the simulation compare favorably to the concentrations determined for these motors in cells and/or mitotic extracts.
We simulated the activity of each component to match published biophysical properties as closely as possible. However, there are limitations in published data that might impact our simulation. For example, motors attached to microtubules that are inactive at any given iteration of the simulation would contribute a drag force on microtubule movement (Vale et al., 1992), but we have not implemented such a drag force because biophysical data defining the magnitude of that force are scant, at best. Also, run lengths for some motors have not been established using single motor motility assays, and some in vitro biochemical data suggest that the HSET (Ncd) and Eg5 classes of kinesin-related motors do not move processively on microtubules (Crevel et al., 1997; deCastro et al., 2001). However, Crevel et al. (1997) did not present evidence verifying that the bacterially expressed motors tested were dimeric, and deCastro et al. (2001) performed experiments at limiting ATP concentration, which could reduce measured run lengths by exaggerating the dissociation of the motor between steps. The simulation used here assumed each motor was dimeric (Table 2) and was performed without limitations on ATP concentration consistent with conditions in the mitotic extract. Moreover, we ran simulations with either or both Eg5 and HSET motors being nonprocessive. The results of each of those simulations yielded results identical to the complete absence of the motor(s), even when the quantity of each motor was increased fivefold. Thus, if these motors move nonprocessively, then we would need greater than fivefold increases in their quantities to get the same effective force generation (Nedelec et al., 1997; Surrey et al., 2001). Finally, it has been demonstrated that single-headed kinesin motors that lack processive movement generate motility over long distances in gliding assays if more than three motors bind to a single microtubule (Hancock and Howard, 1998). At the quantities of HSET and Eg5 used in our simulation virtually every microtubule had more than one motor bound (Figure 8; e.g., for HSET, there are ∼20–30 motors bound to adjacent MTs in the combinations containing either all components or just HSET + MEC). This indicates that HSET and Eg5 could power microtubule movement with substantial run lengths in our simulation even if we overestimated their individual processivities.
Comparison to Previous Computer Simulations of Microtubule Organization
Our approach is broadly consistent with computer simulations of motor-driven microtubule organization done previously (Nedelec et al., 1997; Surrey et al., 2001; Nedelec, 2002; Cytrynbaum et al., 2003). Conceptually, the most important similarity between our results and those of others is that microtubule organization into asters requires both cross-linking and motor activity (Verde et al., 1991; Nedelec et al., 1997; Nedelec et al., 2001). Another important similarity is that microtubule motor activity is an aggregate property reflecting multiple motor attributes, including velocity, run length, and concentration (Nedelec et al., 1997; Surrey et al., 2001).
In contrast, there are a number of important differences between our simulation and those done previously. Many of these differences arise because we sought to understand the mechanism of microtubule organization into asters as it occurs in a mammalian mitotic extract. This differs from the approach of others who have sought to achieve a theoretical understanding of the parameters responsible for microtubule organization (Nedelec et al., 1997; Surrey et al., 2001). For example, by simulating NuMA as Minus-End Cross-linking activity, our simulation obtained asters without assistance from edge effects and without pausing motors at microtubule ends. Both edge effects and motor pausing at microtubule ends have been shown to facilitate microtubule organization (Nedelec et al., 1997; Surrey et al., 2001). These differences provide the most likely explanation for why motors acting alone were not capable of organizing microtubules into asters in either our simulation or the mammalian mitotic extract (Gaglio et al., 1996; Mountain et al., 1999).
Our simulation also exhibits antagonism between oppositely oriented motors when motors act independently of each other without physically interacting. Other simulations treat motors as protein complexes where motors of either the same or different types are physically associated with one another (Nedelec et al., 1997; Nedelec, 2002). Immunoprecipitation experiments demonstrate that none of the motor and non-motor components responsible for microtubule minus-end focusing in the mammalian mitotic extract system are associated with any of the others (Gaglio et al., 1996; Mountain et al., 1999).
Our simulation also addresses the contribution of a nonmotor component explicitly. As discussed below, non-motor components make a significant contribution to microtubule minus-end focusing in the extract. No other computer simulations have evaluated either the contribution of non-motor components or the functional relationship between nonmotor components and motors during microtubule organization. This will be an important concept to expand in the future as increasing numbers of non-motor proteins involved in spindle organization are identified (e.g., TOGp, TPX2, astrin, and TACC).
By training our computer simulation to the outcomes from the combinatorial inhibition of components in a mammalian mitotic extract (Table 1), we have been compelled to develop a model that accounts for both tightly and loosely focused asters. The efficiency of microtubule organization (as judged by numbers of microtubules bound at minus-ends) is similar between tightly and loosely focused asters, indicating that these two arrangements represent different steady-state configurations. Our simulation accounts for these two arrangements in a direct manner, and building the simulation to account for both tightly and loosely focused asters gave us analytical leverage that would not have been possible if we had to account for merely two conditions, organized or not organized. This differs from previous simulations, where differing microtubule arrangements occurred with assistance of edge effects (Nedelec et al., 1997).
Relationship between Net Minus-End–directed Force and Microtubule Cross-linking Orientation Bias
Microtubule organization in our system is determined by the combination of two aggregate properties, Net Minus-end–directed Force and microtubule Cross-linking Orientation Bias (Table 4). We developed this model through simulating microtubule aster organization as it occurs in a mammalian mitotic extract. Despite this focus, there are general principles about microtubule organization implicit in the model that can be broadly applied to mitotic spindles in living cells.
One general principle is that microtubule motors provide both motile force and microtubule cross-linking activities, and the orientation that motors cross-link microtubules has an impact on microtubule minus-end focusing. Minus-end–directed microtubule motor activity is essential for microtubule organization into asters and at spindle poles. Our results indicate that dynein and HSET must be restricted to cross-linking microtubules in parallel orientation only, and that they cross-link microtubules through motor and non-motor microtubule binding domains. These two features of microtubule cross-linking are compatible with the observed dynein-dependent poleward translocation of polarity-marked microtubules on spindles in frog egg extracts (Heald et al., 1996, 1998). This also provides a straight forward explanation for the sliding of both kinetochore fiber and peripheral microtubule minus-ends toward spindle poles that has been recently revealed in green fluorescent protein-tubulin–expressing living cells (Khodjakov et al., 2003; Tulu et al., 2003).
The magnitude of minus-end–directed force in this system is determined by the sum of force provided by the motors present in any given combination. Thus, antagonism between motors of opposite polarity is an explicit feature of the model consistent with the observed antagonism between motors of opposite polarity in many different experimental systems (Pidoux et al., 1996; Saunders et al., 1997; Mountain et al., 1999; Sharp et al., 1999). Because we simulated motors acting independently, this result suggests that antagonism between motors of opposite polarities can arise from force vector summation rather than direct physical interaction. This is an intuitively obvious corollary of the behavior of rigid bodies if the motors are acting on the same set of microtubules, as implied in some models for motor antagonism (Sharp et al., 2000). However, this view is not limited to that specific context and may also be applied to situations where motors act on different sets of microtubules. For example, in budding yeast, motors contribute to spindle function by acting on microtubule populations in both the cytoplasm and nucleus (reviewed by Hildebrandt and Hoyt, 2000).
Another general principle is that non-motor proteins provide static microtubule cross-links, and the orientation in which non-motor proteins cross-link microtubules has an impact on microtubule minus-end focusing. We have focused on NuMA due to its role in microtubule aster organization. However, this principle may be applied to other non-motor spindle proteins. For example, the non-motor spindle protein PRC1/Ase1p most likely contributes to spindle organization by cross-linking microtubules in antiparallel orientation only in the spindle midzone (Mollinari et al., 2002; Schuyler et al., 2003).
A third general principle is that static microtubule cross-links provided by non-motor proteins are sensitive to shear force generated by motors. Such a relationship between force and cross-linking has been investigated using actin networks. Xu et al. (1998) demonstrated that the more heavily cross-linked an actin/actinin network, the greater its viscoelastic coefficient and the more resistant it is to shear force. This result is a direct measurement of the relationship between force and cross-linking in the actin system and is consistent with our inference about the relationship between force and cross-linking in our simulation. In our simulation minus-end cross-links are literally broken if the net force on the cross-linked microtubules exceeds a specified threshold. It seems plausible that such a direct mechanism of cross-link breakage could occur in the mitotic extract or living cells, but we readily acknowledge the possibility that similar reductions in microtubule cross-linking could be obtained through indirect mechanisms if posttranslational modifications or microtubule binding affinities of cross-linking proteins are sensitive to motor forces.
Because the force of minus-end cross-linking in our simulation is akin to static friction, it acts in opposition to shear force generated through plus-end–or minus-end–directed motor activity. In our simulation, dynein and HSET generate significant shear force between two microtubules as they transport one microtubule as cargo along a second microtubule. In contrast, as a bipolar motor that cross-links microtubules by motor domains alone, Eg5's contribution to shear force depends on the orientation of its cross-linking. When cross-linking microtubules in a parallel-only orientation, Eg5 does not contribute shear force as it moves toward both microtubule ends at the same velocity. When cross-linking microtubules in an antiparallel orientation, Eg5 generates shear force as it slides one microtubule past the other, but such activity has very little impact on microtubule asters formed in this simulation because microtubule minus-ends of most antiparallel microtubule pairs are not adjacent to one another. However, it is interesting to note that Eg5 acting on antiparallel microtubules would generate shear force in the context of a bipolar spindle. As Eg5 slides microtubules past one another, the minus-ends of those microtubules will experience shear force relative to other microtubules at spindle poles where different classes of spindle microtubule converge.
The last general principle is that Net Minus-end–directed Force and microtubule Cross-linking Orientation Bias combine to determine microtubule organization. However, the interplay between Net Minus-end–directed Force and Cross-linking Orientation Bias is complex. For example, when dynein and minus-end cross-linking are present, weak net minus-end–directed motor force cooperates with indiscriminate microtubule cross-linking to organize tightly focused microtubule asters. In contrast, when dynein, HSET, and minus-end cross-linking are present, strong motor force has an adverse effect on microtubule cross-linking because it overwhelms minus-end cross-linking to generate loosely focused asters.
In this context, the model proposed here offers a straight-forward explanation for the formation of rosette-like spindle aggregates that form upon inhibition of Eg5 activity in frog egg extracts (Sawin et al., 1992). In the absence of Eg5 activity, the model states that Net Minus-end–directed Force will be strong and Cross-linking Orientation Bias will be predominantly parallel. That condition favors the lateral association of monopolar spindles into rosette-like arrangements in the context of an extract where multiple monopolar spindles mingle.
Collectively, these results support the idea that spindle poles are sites of force integration. Our work has focused only on those forces that directly participate in spindle pole organization, and demonstrates that motile and static forces are integrated at microtubule aster vertices through microtubule cross-links at microtubule minus-ends. However, because most spindle microtubules are cross-linked together at spindle poles, most, if not all, forces acting on spindle microtubules will be integrated at spindle poles. Evidence for this comes from the recently uncovered functional relationship between NuMA and the chromokinesin Kid (Levesque et al., 2003). Kid uses nonkinetochore microtubules to generate polar ejection force on chromosome arms (Antonio et al., 2000; Funabiki and Murray, 2000; Levesque and Compton, 2001). That activity generates an equal and opposite force that pushes nonkinetochore microtubules toward spindle poles where NuMA cross-links their minus-ends to minus-ends of other spindle microtubules. Interestingly, if Kid-generated force is inhibited, then NuMA is dispensable for microtubule organization at spindle poles, consistent with the relationship between cross-linking and motor forces described by this model. The magnitude of force generated by Kid calculated from motility data (4.1 pN; Yajima et al., 2003) or theoretical arguments (∼1 pN; Marshall et al., 2001) is similar to the magnitude of the force threshold we applied to break minus-end cross-linking activity in the simulation (2.1 pN). This suggests that our estimates for these forces are within a physiological range.
In conclusion, we have developed a model of microtubule organization that accurately describes the mechanism by which microtubules are organized into asters in a mammalian mitotic extract. Furthermore, the model is capable of experimental predictions that were not intuitively obvious before when the model was built, and we have demonstrated that the outcome of those experiments is consistent with the predictions (Figures 11 and 12). In spite of this, it remains a formal possibility that other models based on different mechanisms of action of the specific components will also provide accurate descriptions of microtubule organization in the mammalian mitotic extract. We favor the current model because it requires minimal (two) constraints to be applied to the biological components and is consistent with many other aspects of how these components act both in vitro and in vivo. Thus, the model developed here is a reasonable first approximation of the mechanistic processes underlying microtubule organization by motor and non-motor microtubule binding proteins.
Supplementary Material
Acknowledgments
We thank Laura Ray (Thayer School of Engineering, Dartmouth College) and Daniela Rus (Department of Computer Science, Dartmouth College) for input into the physical modeling and algorithmic refinements to the code. We also acknowledge David Odde who suggested the use of periodic boundary conditions and David Jewell and Susan Schwartz for assistance in porting the simulation code to a Linux platform. We also thank Susan Gilbert for helpful discussion of motor motility. This work was supported by a grant from the National Institutes of Health (GM-51542).
Article published online ahead of print. Mol. Biol. Cell 10.1091/mbc.E03–08–0579. Article and publication date are available at www.molbiolcell.org/cgi/doi/10.1091/mbc.E03–08–0579.
Online version of this article contains supporting material. Online version available at www.molbiolcell.org.
References
- Antonio, C., Ferby, I., Wilhelm, H., Jones, M., Karsenti, E., Nebreda, A.R., and Vernos, I. (2000). Xkid, a chromokinesin required for chromosome alignment on the metaphase plate. Cell. 102, 425–435. [DOI] [PubMed] [Google Scholar]
- Berg, H. (1993). Random Walks in Biology, Princeton, NJ: Princeton University Press.
- Chandra, R., Salmon, E.D., Erickson, H.P., Lockhart, A., and Endow, S.A. (1993). Structural and functional domains of the Drosophila Ncd microtubule motor protein. J. Biol. Chem. 268, 9005–9013. [PubMed] [Google Scholar]
- Compton, D.A. (1998). Focusing on spindle poles. J. Cell Sci. 111, 1477–1481. [DOI] [PubMed] [Google Scholar]
- Compton, D.A. (2000). Spindle assembly in animal cells. Annu. Rev. Biochem. 69, 95–114. [DOI] [PubMed] [Google Scholar]
- Crevel, I.M., Lockhart, A., and Cross, R.A. (1997). Kinetic evidence for low chemical processivity in Ncd and Eg5. J. Mol. Biol. 273, 160–170. [DOI] [PubMed] [Google Scholar]
- Cytrynbaum, E.N., Scholey, J.M., and Mogilner, A. (2003). A force balance model of early spindle pole separation in Drosophila embryos. Biophys. J. 84, 757–769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- deCastro, M.J., Foundcave, R.M., Clarke, L.A., Schmidt, C.F., and Stewart, R.J. (2001). Working strokes by single molecules of the kinesin-related microtubule motor Ncd. Nat. Cell Biol. 2, 724–729. [DOI] [PubMed] [Google Scholar]
- DeLuca, J.G., Newton, C.N., Himes, R.H., Jordan, M.A., and Wilson, L. (2001). Purification and characterization of native conventional kinesin, HSET, and CENP-E from mitotic HeLa cells. J. Biol. Chem. 276, 28014–28021. [DOI] [PubMed] [Google Scholar]
- Dionne, M.A., Howard, L., and Compton, D.A. (1999). NuMA is a component of an insoluble matrix at mitotic spindle poles. Cell Motil. Cytoskeleton 42, 189–203. [DOI] [PubMed] [Google Scholar]
- Echeverri, C.J., Paschal, B.M., Vaughan, K.T., and Vallee, R.B. (1996). Molecular characterization of the 50-kD subunit of dynactin reveals function for the complex in chromosome alignment and spindle organization during mitosis. J. Cell Biol. 132, 617–633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Funabiki, H., and Murray, A.W. (2000). The Xenopus chromokinesin Xkid is essential for metaphase chromosome alignment and must be degraded to allow anaphase chromosome movement. Cell 102, 411–424. [DOI] [PubMed] [Google Scholar]
- Gaglio, T., Dionne, M.A., and Compton, D.A. (1997). Mitotic spindle poles are organized by structural and motor proteins in addition to centrosomes. J. Cell Biol. 138, 1055–1066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaglio, T., Saredi, A., Bingham, J.R., Hasbani, M.J., Gill, S.R., Schroer, T.A., and Compton, D.A. (1996). Opposing motor activities are required for the organization of the mammalian mitotic spindle pole. J. Cell Biol. 135, 399–414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaglio, T., Saredi, A., and Compton, D.A. (1995). NuMA is required for the organization of microtubules into aster-like mitotic arrays. J. Cell Biol. 131, 693–708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garrett, S., Auer, K., Compton, D.A., and Kapoor, T.M. (2002). hTPX2 is required for normal spindle morphology and centrosome integrity during vertebrate cell division. Curr. Biol. 23, 2055–2059. [DOI] [PubMed] [Google Scholar]
- Gill, S.R., Schroer, T.A., Szilak, I., Steuer, E.R., Sheetz, M.P., and Cleveland, D.W. (1991). Dynactin, a conserved, ubiquitously expressed component of an activator of vesicle motility mediated by cytoplasmic dynein. J. Cell Biol. 115, 1639–1650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hancock, W.O., and Howard, J. (1998). Processivity of the motor protein kinesin requires two heads. J. Cell Biol. 140, 1395–1405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haren, L., and Merdes, A. (2002). Direct binding of NuMA to tubulin is mediated by a novel sequence motif in the tail domain that bundles and stabilizes microtubules. J. Cell Sci. 115, 1815–1824. [DOI] [PubMed] [Google Scholar]
- Heald, R., Tournebize, R., Blank, T., Sandaltzopoulos, R., Becker, P., Hyman, A,. and Karsenti, E. (1996). Self-organization of microtubules into bipolar spindles around artificial chromosomes in Xenopus egg extracts. Nature 382, 420–425. [DOI] [PubMed] [Google Scholar]
- Heald, R., Tournebize, R., Habermann, A., Karsenti, E., and Hyman, A. (1998). Spindle assembly in Xenopus egg extracts: respective roles of centrosomes and microtubule self-organization. J. Cell Biol. 138, 615–628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hildebrandt, E.R., and Hoyt, M.A. (2000). Mitotic motors in Saccharomyces cerevisiae. Biochim. Biophys. Acta 1496, 99–116. [DOI] [PubMed] [Google Scholar]
- Howard, J., Hudspeth, A.J., and Vale, R.D. (1989). Movement of microtubules by single kinesin molecules. Nature 342, 154–158. [DOI] [PubMed] [Google Scholar]
- Howard, J. (2001). Mechanics of Motor Proteins and the Cytoskeleton, Sunderland, MA: Sinauer Press.
- Hyman, A.A., and Karsenti, E. (1996). Morphogenetic properties of microtubules and mitotic spindle assembly. Cell 84, 401–410. [DOI] [PubMed] [Google Scholar]
- Kapoor, T.M., and Mitchison, T.J. (2001). Eg5 is static in bipolar spindles relative to tubulin: evidence for a static spindle matrix. J. Cell Biol. 154, 1125–1133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kashina, A.S., Baskin, R.J., Cole, D.G., Wedaman, K.P., Saxton, W.M., and Scholey J.M.M. (1996). A bipolar kinesin. Nature 379, 270–272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khodjakov, A., Cole, R.W., Oakley, B.R., and Rieder, C.L. (2000). Centrosome-independent mitotic spindle formation in vertebrates. Curr. Biol. 10, 59–67. [DOI] [PubMed] [Google Scholar]
- Khodjakov, A., Copenagle, L., Gordon, M.B., Compton, D.A., and Kapoor, T.M. (2003). Minus-end capture of preformed kinetochore fibers contributes to spindle morphogenesis. J. Cell Biol. 160, 671–683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King, S.J., and Schroer, T.A. (2000). Dynactin increases the processivity of the cytoplasmic dynein motor. Nat. Cell Biol. 2, 20–24. [DOI] [PubMed] [Google Scholar]
- Kuriyama, R., Kofron, M., Essner, R., Kato, T., Dragas-Granoic, S., Omoto, C.K., and Khodjakov, A. (1995). Characterization of a minus end-directed kinesin-like motor protein from cultured mammalian cells. J. Cell Biol. 129, 1049–1059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levesque, A.A., and Compton, D.A. (2001). The chromokinesin Kid is necessary for chromosome arm orientation and oscillation, but not congression, on mitotic spindles. J. Cell Biol. 154, 1135–1146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levesque, A.A., Howard, L., Gordon, M.B., and Compton, D.A. (2003). A functional relationship between NuMA and Kid is involved in both spindle organization and chromosome alignment in vertebrate cells. Mol. Biol. Cell 14, 3541–3552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mack, G.J., and Compton, D.A. (2001). Analysis of mitotic microtubule-associated proteins using mass spectrometry identifies astrin, a spindle-associated protein. Proc. Natl. Acad. Sci. USA 98, 14434–14439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malik, F., Brillinger, D., and Vale, R.D. (1994). High-resolution tracking of microtubule motility driven by a single kinesin motor. Proc. Natl. Acad. Sci. USA 91, 4584–4588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marshall, W.F., Marko, J.F., Agard, D.A., and Sedat, J.W. (2001). Chromosome elasticity and mitotic polar ejection force measured in living Drosophila embryos by four-dimensional microscopy-based motion analysis. Curr. Biol. 11, 569–578. [DOI] [PubMed] [Google Scholar]
- Matuliene, J., Essner, R., Ryu, J., Hamaguchi, Y., Baas, P.W., Haraguchi, T., Hiraoka, Y., and Kuriyama, R. (1999). Function of a minus-end-directed kinesin-like motor protein in mammalian cells. J. Cell Sci. 112, 4041–4050. [DOI] [PubMed] [Google Scholar]
- Mayer, T.U., Kapoor, T.M., Haggarty, S.J., King, R.W., Schreiber, S.L., and Mitchison, T.J. (1999). Small molecule inhibitor of mitotic spindle bipolarity identified in a phenotype-based screen. Science 286, 971–974. [DOI] [PubMed] [Google Scholar]
- McIntosh, J.R., and Koonce, M.P. (1989). The mitotic spindle. Science 246, 622–628. [DOI] [PubMed] [Google Scholar]
- Merdes, A., and Cleveland, D.W. (1997). Pathways of spindle pole formation: different mechanisms; conserved components. J. Cell Biol. 138, 953–956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merdes, A., Heald, R., Samejima, K., Earnshaw, W.C., and Cleveland, D.W. (2000). Formation of spindle poles by dynein/dynactin-dependent transport of NuMA. J. Cell Biol. 149, 851–862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merdes, A., Ramyar, K., Vechio, J.D., and Cleveland, D.W. (1996). A complex of NuMA and cytoplasmic dynein is essential for mitotic spindle assembly. Cell 87, 447–458. [DOI] [PubMed] [Google Scholar]
- Mitchison, T.J., Evans, L., Schulze, E., and Kirschner, M. (1986). Beyond self-assembly: from microtubules to morphogenesis. Cell 45, 515–27. [DOI] [PubMed] [Google Scholar]
- Mollinari, C., Kleman, J.P., Jiang, W., Schoehn, G., Hunter, T., and Margolis, R.L. (2002). PRC1 is a microtubule binding and bundling protein essential to maintain the mitotic spindle midzone. J. Cell Biol. 157, 1175–1186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mountain, V., Simerly, C., Howard, L., Ando, A., Schatten, G., and Compton, D.A. (1999). The kinesin-related protein, HSET, opposes the activity of Eg5 and crosslinks microtubules in the mammalian mitotic spindle. J. Cell Biol. 147, 351–365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nedelec, F. (2002). Computer simulations reveal motor properties generating stable antiparallel microtubule interactions. J. Cell Biol. 158, 1005–1015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nedelec, F., Surrey, T., and Maggs A.C. (2001). Dynamic concentration of motors in microtubule arrays. Phys. Rev. Lett. 14, 3192–3195. [DOI] [PubMed] [Google Scholar]
- Nedelec, F.J., Surrey, T., Maggs, A.C., and Leibler, S. (1997). Self-organization of microtubules and motors. Nature 389, 305–308. [DOI] [PubMed] [Google Scholar]
- Nicklas, R.B. (1989). The motor for poleward chromosome movement in anaphase is in or near the kinetochore. J. Cell Biol. 109, 2245–2255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Odde, D.J., and Buettner, H.M. (1995). Time series characterization of simulated microtubule dynamics in the nerve growth cone. Ann. Biomed. Eng. 23, 268–286. [DOI] [PubMed] [Google Scholar]
- Pidoux, A.L., LeDizet, M., and Cande, W.Z. (1996). Fission yeast pkl1 is a kinesin-related protein involved in mitotic spindle function. Mol. Biol. Cell 7, 1639–1655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rieder, C.L. (1981). The structure of the cold-stable kinetochore fiber in metaphase PtK1 cells. Chromosoma 84, 145–158. [DOI] [PubMed] [Google Scholar]
- Saunders, W., Lengyel, V., and Hoyt, M.A. (1997). Mitotic spindle function in Saccharomyces cerevisiae requires a balance between different types of kinesin-related motors. Mol. Biol. Cell 8, 1025–1033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sawin, K.E., LeGuellec, K., Philippe, M., and Mitchison, T.J. (1992). Mitotic spindle organization by a plus end-directed microtubule motor. Nature 359, 540–543. [DOI] [PubMed] [Google Scholar]
- Schuyler, S.C., Lin, J.Y., and Pellman, D. (2003). The molecular function of Ase1p: evidence for a MAP-dependent midzone-specific spindle matrix. J. Cell Biol. 160, 517–528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp, D.J., Kuriyama, R., Essner, R., and Baas, P.W. (1997). Expression of a minus-end-directed motor protein induces Sf9 cells to form axon-like processes with uniform microtubule polarity orientation. J. Cell Sci. 110, 2373–2380. [DOI] [PubMed] [Google Scholar]
- Sharp, D.J., Rogers, G.C., and Scholey, J.M. (2000). Microtubule motors in mitosis. Nature 407, 41–47. [DOI] [PubMed] [Google Scholar]
- Sharp, D.J., Yu, K.R., Sisson, J.C., Sullivan, W., and Scholey, J.M. (1999). Antagonistic microtubule-sliding motors position mitotic centrosomes in Drosophila early embryos. Nat. Cell Biol. 1, 51–54. [DOI] [PubMed] [Google Scholar]
- Steuer, E.R., Wordeman, L., Schroer, T.A., and Sheetz, M.P. (1990). Localization of cytoplasmic dynein to mitotic spindles and kinetochores. Nature 345, 266–268. [DOI] [PubMed] [Google Scholar]
- Surrey, T., Nedelec, F., Leibler, S., and Karsenti, E. (2001). Physical properties determining self-organization of motors and microtubules. Science 292, 1167–1171. [DOI] [PubMed] [Google Scholar]
- Svoboda, K., and Block, S.M. (1994). Force and velocity measured for single kinesin molecules. Cell 77, 773–784. [DOI] [PubMed] [Google Scholar]
- Szollosi, D., Clarco, P., and Donahue, R.P. (1972). Absence of centrioles in the first and second meiotic spindles of mouse oocytes. J. Cell Sci. 11, 521–531. [DOI] [PubMed] [Google Scholar]
- Tulu, U.S., Rusan, N.M., and Wadsworth, P. (2003). Peripheral, non-centrosome-associated microtubules contribute to spindle formation in centrosome-containing cells. Curr. Biol. 13, 1894–1899. [DOI] [PubMed] [Google Scholar]
- Vale, R.D., Malik, F., and Brown, D. (1992). Directional instability of microtubule transport in the presence of kinesin and dynein, two opposite polarity motor proteins. J. Cell Biol. 119, 1589–1596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verde, F., Berrez, J.M., Antony, C., and Karsenti, E. (1991). Taxol-induced microtubule asters in mitotic extracts of Xenopus eggs: requirement for phosphorylated factors and cytoplasmic dynein. J. Cell Biol. 112, 1177–1187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visscher, K., Schnitzer, M.J., and Block, S.M. (1999). Single kinesin molecules studied with a molecular force clamp. Nature 400, 184–189. [DOI] [PubMed] [Google Scholar]
- Xu, J., Wirtz, D., and Pollard, T.D. (1998). Dynamic crosslinking by alpha-actinin determines the mechanical properties of actin filament networks. J. Biol. Chem. 273, 9570–9576. [DOI] [PubMed] [Google Scholar]
- Yajima, J., Edamatsu, M., Watai-Nishii, J., Tokai-Nishizumi, N., Yamamoto, T., and Toyoshima, Y.Y. (2003). The human chromokinesin Kid is a plus end-directed microtubule-based motor. EMBO J. 22, 1067–1074. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.