Organization of the mitotic chromosome

Abstract

Mitotic chromosomes are among the most recognizable structures in the cell, yet for over a century their internal organization remains largely unsolved. We applied chromosome conformation capture methods, 5C and Hi-C, across the cell cycle and revealed two alternative three-dimensional folding states of the human genome. We show that the highly compartmentalized and cell-type-specific organization described previously for non-synchronous cells is restricted to interphase. In metaphase, we identify a homogenous folding state, which is locus-independent, common to all chromosomes, and consistent among cell types, suggesting a general principle of metaphase chromosome organization. Using polymer simulations, we find that metaphase Hi-C data is inconsistent with classic hierarchical models, and is instead best described by a linearly-organized longitudinally compressed array of consecutive chromatin loops.

Introduction

The three-dimensional organization of genomes plays critical roles in regulating chromosomal processes, including gene regulation, DNA replication, and genome stability (1–4). During the cell cycle, chromosomes transition between two distinct folding states: interphase and metaphase. Interphase chromosomes are relatively decondensed and acquire a cell-type-specific spatial organization. In preparation for cell division, chromosomes undergo extensive spatial re-organization and eventually shut down most transcription. This process culminates in a highly condensed and morphologically reproducible metaphase chromosome state.

Chromosome conformation capture (3C)-based methods extend previous characterizations of interphase chromosomes by detecting physical contact frequencies between pairs of genomic loci (2, 5, 6). During interphase, chromosomes occupy individual territories and are compartmentalized at several hierarchical levels: large multi-Mb active A- and inactive B-compartments (7), and smaller sub-Mb Topologically Associating Domains (TADs) (8–10). At ~100Kb scales chromatin looping interactions connect genes to distal regulatory elements, mediating long-range gene regulation (11).

The internal organization of mitotic chromosomes remains enigmatic (12–15). Based on studies using light microscopy, electron microscopy, tomography, and mechanical measurements, several models of mitotic chromosomes have been proposed. These models can be subdivided into three groups (16, 17): loops-on-a-scaffold models (15, 18, 19), hierarchical models of increasingly thicker coiled or looped fibers (20, 21), and network models, which describe mitotic chromosomes as highly cross-linked gels (22, 23), as well as models that combine these different features (24).

Here we applied 5C (25) and Hi-C (7) to study the spatial organization of human chromosomes during the cell cycle, revealing two alternate folding states. Using polymer simulations, we evaluated existing and new models of metaphase chromosome organization and propose that metaphase organization can emerge through a two-stage process: linear compaction by consecutive chromatin loops, potentially generated by SMC complexes, followed by axial compression.

Results

Changes in chromosome organization during the cell cycle

For our initial studies we used HeLa S3 cells because large and homogeneous populations of these cells at various stages of the cell cycle can be obtained relatively easily and efficiently (Figure S1). The HeLa S3 karyotype is complex, but stable. We focused analyses on intra-chromosomal data from six chromosomes that appear normal, as judged by SKY/M-FISH and Hi-C (Figures S2, S3). Further, our analyses use ICE (26), which corrects for biases in sequencing coverage that may arise due to copy-number alterations.

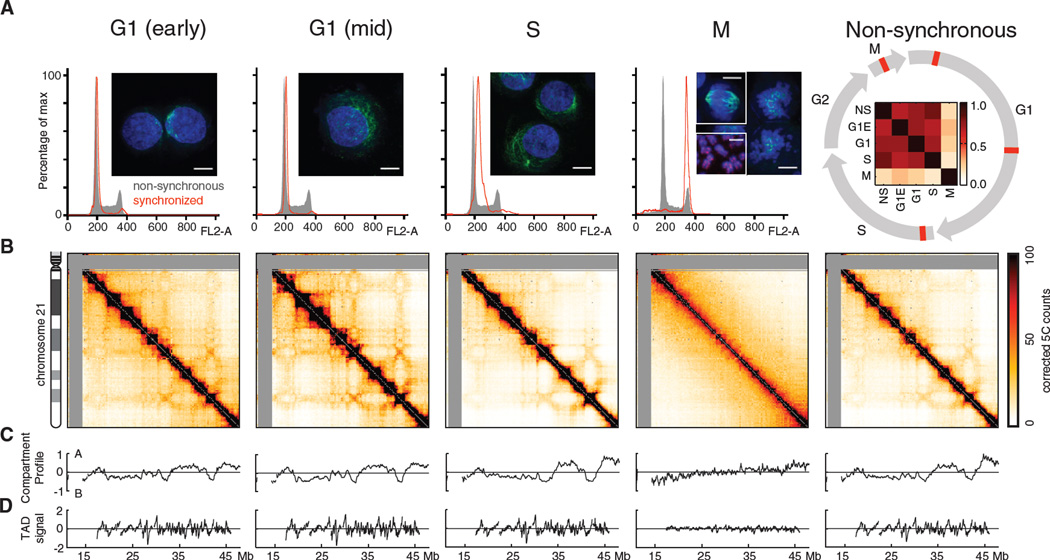
We used 5C technology to study the organization of small and un-rearranged chromosome Chr. 21 at different time points throughout the cell cycle (Figure 1). We interrogated long-range interactions using a pool of 5C primers, which cover the length of chromosome 21 with an average spacing of 25kb (Methods). We studied early G1 and mid-G1 cells, thymidine-arrested early S-phase cells and nocodazole-arrested prometaphase (“mitotic”) cultures (Figures 1, S1, S4, Methods). We find that nocodazole treatment up to 12 hours leads to some gradual shortening of mitotic chromosomes but Hi-C analyses for 3, 7, and 12 hours incubation yield overall very similar results (Figure S5). Sister chromatid arms are separate and no longer intertwined in nocodazole-arrested cells (Figure 1A).

Figure 1. Organization of chromosome 21 through the cell cycle.

(A). FACS profiles and microscopy images of cell populations analyzed in this study. Images show DAPI-stained DNA (blue) and alpha-tubulin (green), scale bars are one micron. Image under M shows cells arrested in metaphase (12 hours nocodazole); top left inset shows cells with intact spindle; right half shows nocodazole-arrested metaphase chromosomes with disrupted spindles; bottom inset shows arrested chromosomes stained for SMC2, showing separated sister chromatids. (Right) Non-synchronous population consists of a mixture of all cell-cycle phases. Circular diagram shows cell cycle, with red markers indicating studied synchronization samples. Inside of cell-cycle circle: correlation matrix between 5C interaction patterns of both non-synchronous cells and all studied stages of the cell cycle (Methods). (B). Corrected 5C matrices of chromosome 21 for these cell populations; raw 5C data were binned to 250 Kb with a 50 Kb sliding window, and corrected using ICE. Grey regions are not interrogated in this study. (C). A/B compartment profile for each data set. (D). TAD signal for each data set.

The interaction patterns for early G1, mid G1, and S-phase are highly correlated with each other and with the pattern obtained with non-synchronous cells (Spearman r > .67, P << 10⁻¹⁰, Figure 1A, Methods). For these cell cycle phases, the interaction maps display similar plaid patterns of regional enrichment or depletion of long-range interactions (Figure 1). A similar plaid pattern was previously observed for non-synchronous cells, which are mainly (97%) in interphase and has been interpreted to reflect spatial separation of chromosomes in A/B compartments (see below, and (7)).

In mitotic cells, however, the interaction map changes dramatically, and the plaid pattern disappears. The mitotic interaction pattern displays a low correlation with those for all other cell cycle phases (Spearman r <.27, P << 10⁻¹⁰, Figure 1b). Thus, we identify two distinct chromosome folding states in the cell cycle.

Loss of chromosome compartments and TADs in metaphase

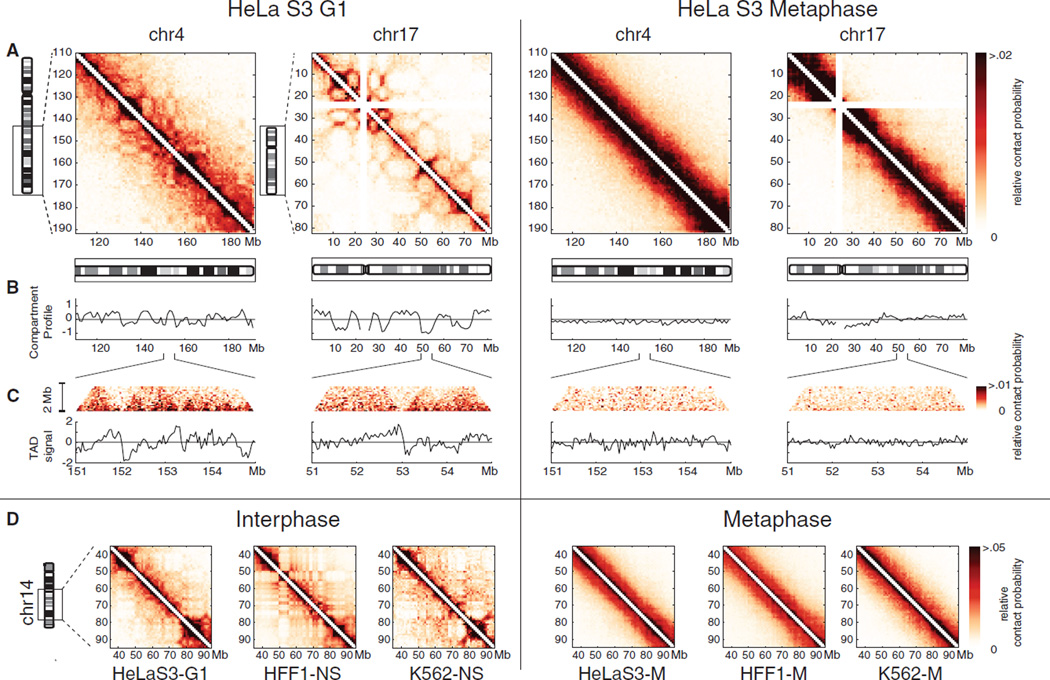
Next, we used Hi-C (7) to perform a genome-wide analysis of the mitotic and mid-G1 states, as these represent the two most distinct states (Figure 2, S6). We then used both 5C and Hi-C data to study features of chromosome organization at different levels: compartments at the chromosome scale, and TADs at the sub-megabase scale. Using eigenvector decomposition, ICE (26), we obtained compartment profiles. In G1, an alternating compartment profile and preferential interactions among regions within the same compartment type (Figure S7) are observed (Figure 2B), which is in agreement with previous studies on non-synchronized cells (7, 27). Compartment profiles extracted from 5C agree with Hi-C on chr21 (Figure S8), and are highly correlated in early G1, mid G1 and S-phase cells (Spearman r > 0.85, P << 10⁻¹⁰).

Figure 2. Hi-C analysis of chromosome organization in G1 and Mitotic cells.

(A) Relative Hi-C contact probability maps for chromosome 17 and an equally sized 82 Mb region of chromosome 4, at 1Mb resolution. M-phase arrest: 12 hours nocodazole. (B) A/B compartment profile for these regions. (C) Zoom-in of 4Mb sub-regions. (Top) Region of a contact map at 40Kb resolution. (Bottom) TAD signal for this region. (D) Hi-C contact probability maps for a region of chromosome 14 in interphase and metaphase. Displayed are HeLaS3-G1, HFF1-NS (non-synchronous), and published K562-NS (7) datasets (left) and HeLaS3-M, HFF1-M, and K562-M datasets (right).

In mitotic cells, compartmentalization disappears across the genome (Figures 1, 2), as eigenvector decomposition does not detect a compartment profile which alternates along the length of a chromosomal arm. Consistently, preferential interactions between compartments extracted from G1 Hi-C data, or between regions with similar GC content or similar interphase chromatin marks, are lost in mitosis (Figure S7).

At a sub-megabase scale, chromosomes have been found to be composed of TADs (9, 10). A TAD is a contiguous chromosomal region that largely interacts with itself and is relatively insulated from its direct genomic neighbors. TADs have been identified by their pattern of preferential upstream or downstream interactions: largely downstream at the start of a TAD, and largely upstream at the end (9). We quantify the TAD signal by the log2-ratio of upstream to downstream interactions of each genomic region. In interphase, the TAD signal is prominent along all chromosomes (Figure 1, 2C), consistent between Hi-C and 5C on chr21 (r=0.73, P<10⁻¹⁰) and is more prominent in mid-G1 cells than in early G1 and S phases.

In mitotic cells, the amplitude of the TAD signal is strongly reduced across all chromosomes; this is confirmed by 5C on chromosome 21. The residual variation in the TAD signal in mitotic cells can be explained by the presence of around 15% non-mitotic cells in nocodazole-arrested cultures (Figure S9). A high-synchrony (98%) mitotic dataset displays further loss of TADs (Fig S10). Hi-C performed at 4-fold lower formaldehyde concentration (0.25%) showed similar results, indicating that loss of compartments and TADs is not due to over cross-linking of condensed chromosomes (Figures S11, S12). We conclude that the presence of large-scale compartments and sub-Mb TADs is mostly lost in metaphase.

We repeated the analysis of interphase and metaphase chromosome conformation in two additional cell types: erythroid K562 cells and primary human foreskin fibroblasts (HFF1) (Figure 2D, S13, S14). In interphase, all three cell types display A/B compartments, but their locations are different (Figure S15). In contrast, the Hi-C data for mitotic chromosomes are strikingly similar for all three cell-types, showing loss of compartments and TADs, leaqding to virtually identical homogeneous interaction maps for all chromosomes. Thus, during the cell cycle chromosomes alternate between cell-type specific interphase organizations and a universal cell-type and chromosome-type invariant mitotic conformation.

Two levels of organization of mitotic chromosomes

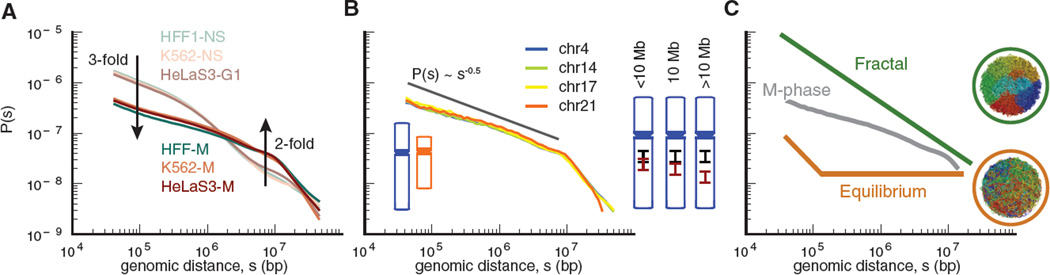
Since chromosomes can be understood as long polymers, we examined how the contact probability P(s) derived from Hi-C maps depends upon genomic distance, s, between a pair of loci in each chromosomal arm (Figure 3). This dependence is informative of the underlying polymer state (28–30). P(s) for interphase and mitotic chromosomes are strikingly different, while being highly consistent among cell types (Figure 3A). In contrast to interphase, mitotic chromosomes display a slow decrease in contact probability P(s)~s^−0.5 from 100Kb to 10Mb, followed by a rapid fall-off at ~10Mb. These features are observed for all chromosomes irrespective of their lengths (Figure 3B), and are robust to details of a Hi-C experiment and methods used to compute P(s) (Figures S16).

Figure 3. Contact probability as a function of genomic distance.

To compare experiments with different numbers of reads, here and below all P(s) plots are normalized to integrate to one. (A). Contact probability for interphase and mitotic cells averaged over all chromosomes; datasets as in Fig 2D. Arrows indicate fold-change from interphase to metaphase. (B). Contact probability for individual HeLa S3 mitotic chromosomes, compared with P(s)~s^−0.5. Diagrams on the right illustrate that loci separated by fewer than 10Mb occupy overlapping longitudinal positions, whereas loci separated by more than 10Mb rarely overlap. (C). Mitotic P(s) below 10Mb plotted against schematic P(s) for fractal and equilibrium globule states. Insets show spatial organization of simulated polymer fibers for each state, where fibers (here and below) are colored from blue to red along their lengths. Observed P(s) for mitotic chromosomes falls in-between that of an equilibrium globule, where regions of the polymer are highly mixed, and a fractal globule, where different regions are spatially segregated.

The two regimes in metaphase P(s) suggest that chromatin is organized differently above and below 10Mb. Regions separated by more than 10Mb rarely contact each other and thus occupy distinct spatial positions; this is consistent with the known linear organization of mitotic chromosomes, where consecutive regions occupy consecutive longitudinal positions (below). In contrast, loci within any continuous 10Mb region frequently contact each other. Thus mitotic chromosomes can be considered as a linearly ordered structure above 10Mb consisting of spatially mixed layers of ~10Mb (Figure 3B).

To understand mitotic chromosome organization within a 10Mb layer we compared the observed P(s) with that of the equilibrium globule and fractal globule polymer states. A fractal globule state has P(s)~s⁻¹ and is characterized by spatial segregation of different regions (Figure 3C). Conversely, the equilibrium globule state exhibits a plateau in P(s) (i.e. P(s) ~ s⁰), and is characterized by a high degree of mixing between different regions of the polymer. The observed P(s)~s^−0.5 in metaphase falls in-between P(s) for these two states indicating an intermediate level of spatial mixing. Thus, while previous work found that a fractal globule state was consistent with interphase P(s) from 500kb to 7Mb (7), a different polymer model is needed to account for the greatly different P(s) for mitotic chromosomes.

Polymer modeling of mitotic chromosome organization

We next developed and tested polymer models of the final folded state of a mitotic chromosome. Since details of the folding pathway and initial conformations are unknown, we studied equilibrium polymer models (Methods). For each model, we generated an ensemble of conformations, simulated Hi-C experiments of this ensemble, and evaluated its ability to reproduce the main features of the Hi-C data: the observed P(s) (Figure 3B) and a homogeneous ensemble-average interaction map (Figure 1, 2, S17). We additionally required that models have the known cylindrical chromosome geometry, chromatin packing density (~70Mb per 1um of chromatid (31)) and linear organization of mitotic chromatids (32). We modeled 77Mb of chromatin (e.g. chr17: 1um long and 0.5um in diameter) as a polymer of 128,000 monomers, each representing 3 nucleosomes (about 600bp), with a diameter of 10nm and a persistence length of 4 monomers (10–12 nucleosomes) (33). We chose these parameters to best represent a 10nm fiber (Methods), as the pervasiveness of the 30nm fiber in vivo has become increasingly contested (22, 34, 35). Further simulations have shown that our main results hold for a 30nm fiber, as well as for a more flexible 10nm fiber (Figure S18), and our results are relatively insensitive to the local structure of the chromatin fiber. Polymer models were simulated using Langevin dynamics with interactions and constraints specific to each model. We account for topoisomerase II activity (36, 37) by allowing chromatin fibers to pass through each other and thus change the topological state of a chromosome (Methods, (38)); this is accomplished by setting a finite energy cost for two monomers to occupy the same volume.

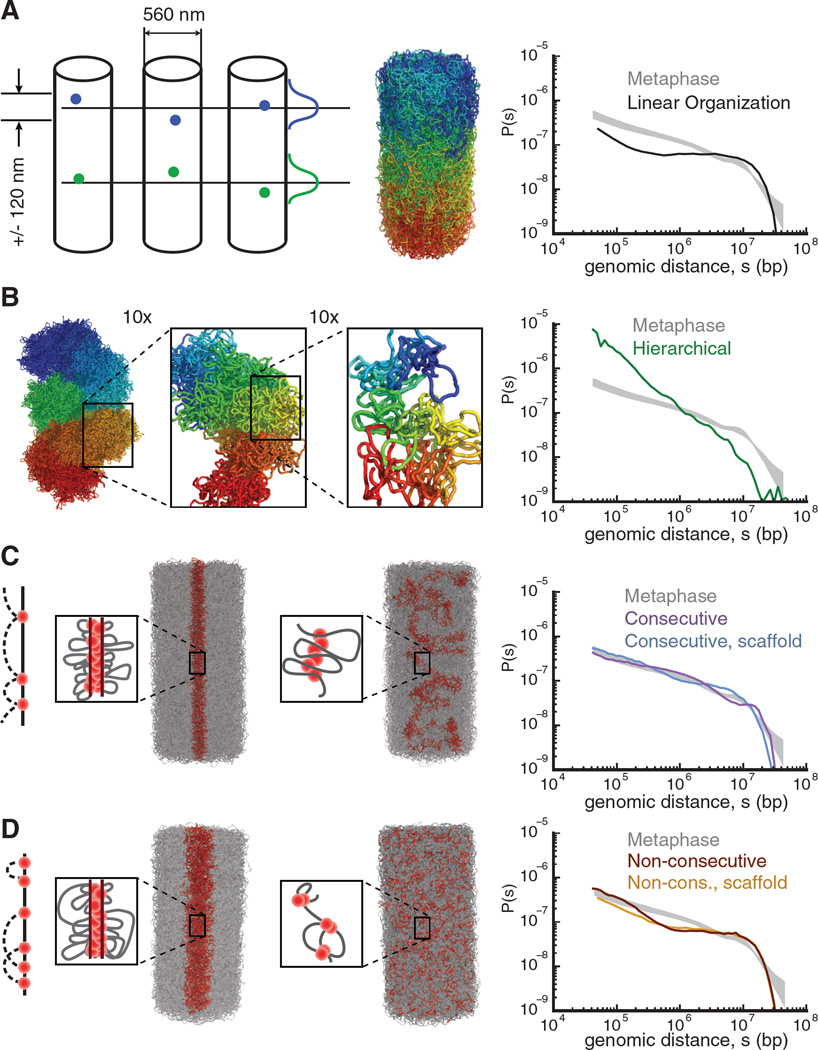
First, we tested if an equilibrium model with a combination of cylindrical geometry and linear organization is sufficient to reproduce the observed P(s) (Figure 4A, S19). This model imposes linear organization by constraining monomers to have reproducible mean longitudinal positions with a 120nm standard deviation along the axis of the chromosome, as observed using microscopy (32). Simulations of this model generate a layered chromosome conformation where the fall-off in contact probability P(s) naturally emerges at about 10Mb, demonstrating that linear organization and a fall-off in contact probability are connected (also Figure S19, Movie M1). However, in contrast to the Hi-C data, models constrained only by cylindrical geometry and linear organization produce P(s) with a plateau from 200kb to 10Mb (Figure 4A), and are highly mixed within a layer, similar to an equilibrium globule (Figure 3C, S20).

Figure 4. Polymer models of mitotic chromosome organization (left) and their corresponding P(s) (right).

Experimental P(s) in metaphase (grey shaded area) is bounded by minimum and maximum P(s) calculated from six independent Hi-C datasets (three cell lines).

(A) Linear organization model: each monomer is constrained to have reproducible mean longitudinal positions with 120nm standard deviation (illustrated in the diagram, next to an example of a polymer conformation for this model). (B) Hierarchical model formed by successively folding the fiber into a next level fiber, here using loops with average length of 9kb, 240kb and 4.8Mb; conformation colored from blue to red at each level of magnification (Figures S13, S14). (C) Models with consecutive loops, cylindrical geometry, and linear organization. Bases of the loops (red) are either free (left) or attracted to a central scaffold (middle). For optimal loop sizes, P(s) curves for these models approach experimental P(s). (D) Models with non-consecutive loops, cylindrical geometry and linear organization, either free (left) or attracted to a central scaffold (middle). Non-consecutive loops are obtained by randomizing positions of consecutive loop bases, while maintaining loop lengths. Models with non-consecutive loops have worse agreement with metaphase P(s) than models with consecutive loops (Figure S15).

We evaluated two major classes of models for mitotic chromosomes: hierarchical models (20, 21) and loops/scaffold models (15, 18, 19). In hierarchical models, the chromatin fiber is successively folded into a thicker fiber at each hierarchical level. Models with both looping and solenoidal twisting at each level were implemented by constraints on distances and angles between subsets of monomers (Figure 4B, S21, S22). We found that although hierarchical folding can produce chromosomes with the correct geometry and linear organization, the contact probability for these models decreased much more sharply than observed in Hi-C (Figure 4B, S22). This indicates that hierarchical models overly constrain the chromatin fiber, as most of the contacts occur locally, within the first- and second-level fibers.

To study models with loops emanating from a scaffold (17, 18), we induced formation of consecutive loops, attracted their bases to a central scaffold, and imposed linear ordering and cylindrical geometry (Figure 4C, Movie M2). To form consecutive loops we chose a random subset of genomic positions as loop bases; each loop base was then connected by harmonic bonds to immediately preceding and subsequent loop bases along the chromosome (Methods). This process forms an array of consecutive non-overlapping loops with an exponential distribution of loop lengths. For each average loop length, we equilibrated the system (Figure S23) and found that chromosome models with 80kb average loop size closely reproduce experimental P(s) (Figure 4C, S18), and yield moderately mixed chromatin organization within layers (Figure S20, Movie M3, Movie M4). Surprisingly, a scaffold-free model with consecutive 120Kb loops still achieved good agreement with experimental P(s) (Figure 4C, S18). This stems from the spatial proximity of neighboring consecutive loops, and explains how short-range interactions (~100 Kb) can increase contact probabilities over much longer ranges (~5 Mb) (Figure S24). Loop sizes for our best-fitting models closely agree with earlier measurements: 80Kb (39) ; 30–90Kb (18), 83 +/−29Kb (40).

Models with only attraction to a scaffold (Figure S19), or with non-consecutive loops (Figure 4D), are inconsistent with experimental P(s). Additionally, cell-to-cell variability in loop positions and sizes is required to reproduce the homogenous population-averaged Hi-C maps (Figure S17). Taken together, stochastic arrays of consecutive loops, either on or off the scaffold, are essential for agreement with Hi-C data.

A two-step process for mitotic chromosome folding

In our polymer models, mitotic chromosome organization is described by two main features: arrays of consecutive 80–120kb loops and linear ordering of loci separated by more than 10Mb. Consecutive loops could be formed by linear compaction of the chromatin fiber (41) by loop-extruding SMC-containing complexes in early prophase, e.g. as proposed by Alipour and Marko (42). Arrays of loops have also been proposed for mitotic and meiotic chromosome organization based on cytological and molecular considerations (43). Consecutive loops resemble a polymer bottlebrush model (Fig 5, S24), which has previously been suggested as a model for condensed chromosomes (33). The second feature, linear ordering above 10Mb, was imposed in our consecutive loop models of the final folded state (Figure 4C), but could emerge naturally from axial compression of long prophase chromosomes, e.g. (19, 37, 41, 43). Compression cannot be accomplished by increased chromatin-chromatin affinity alone, as this would lead to condensation into a globular geometry (17, 33, 42). However, mechanisms that locally compress the backbone formed by loop bases naturally allow for active anisotropic compression into a shorter and thicker chromosome, with the same width regardless of chromosome length (14). Additionally, differences in the duration or efficiency of the first and second stages of chromosomal condensation provide a natural mechanism for condensation-related proteins to separately affect mitotic chromosome length and width (23).

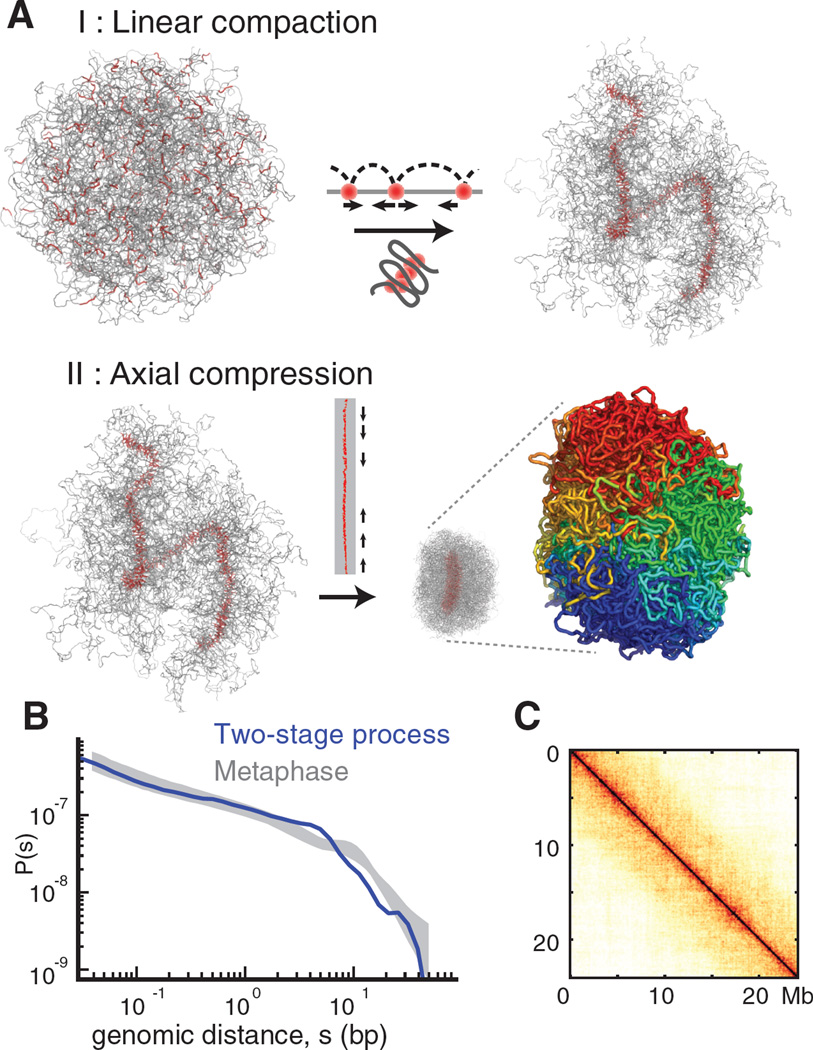
Figure 5. A two-stage process of mitotic chromosome folding.

(A). Stage I: linear compaction by formation of consecutive chromosomal loops leads to the formation of a fiber of loop bases. Stage II: homogeneous axial compression of the fiber’s backbone leads to formation of a dense chromosome. This two-stage process produces a chromosome with the appropriate cylindrical geometry and linear organization (genomic position is indicated by the coloring from blue to red). (B) Contact probability P(s) for the two-stage process compared with observed P(s) (grey shaded area as in Figure 4). (C). Average contact map for chromosomes folded by two-stage process.

These considerations led us to propose a model where mitotic chromosomes are formed by a two-stage process (Figure 5): first, an interphase chromosome is linearly compacted into an array of consecutive loops, forming a prophase-like chromatid of ~5um in length and ~1um in diameter. Second, this chromatid undergoes homogeneous axial compression (Methods).

We simulated the first state by creating an array of consecutive loops, i.e. without explicitly modeling loop extrusion (see above). To simulate the second stage, we imposed interactions between nearby loop bases, and concomitantly condensed loops using poor solvent conditions. Resulted conformations naturally acquire cylindrical chromosomal geometry, linear ordering and demonstrate good agreement with experimental Hi-C and microscopy data (Figure 5, S20, Movie M5, M6).

Discussion

The interphase and mitotic states represent two functionally distinct three-dimensional organizations of the genome. We find that mitotic chromosomes preserve few if any of the structural features that define interphase chromosomes. Remarkably, we find that metaphase chromosomes acquire a similar organization in different cell types. This raises the important question of how epigenetic information is inherited through mitosis, when transcription largely ceases and many proteins, including RNA polymerase, dissociate from chromosomes. Current models of epigenetic memory involve retention of key transcription factors and chromatin architectural proteins at specific loci (“bookmarking” (44)), but roles of higher-order chromatin folding have also been proposed (45). In mitotic chromosomes, we not only find that the large-scale spatial segregation into cell-type specific A/B compartments is lost but that locally folded and conservative between cell-types TADs are also largely absent. Additionally, the homogeneous mitotic interaction maps show no evidence for the emergence of new compartments, including a lack of preferential interactions within chromosomal bands. These observations imply that higher order chromatin structures have to form de novo in early G1 and do not themselves carry epigenetic memory. It is possible that their re-emergence in early G1 is driven by histone marks, DNA methylation, and protein complexes that remain on DNA through mitosis, e.g. at TAD boundaries (46), or at key gene regulatory elements (47).

Our proposed model of a metaphase chromosome as a compressed array of consecutive loops (Fig 4C) is supported by several previously described structural features. Imaging studies have shown that individual loci do not occupy reproducible axial positions (32). Additionally, contiguous chromosomal regions of <1Mb do not fill a full radial cross-section of the chromosome while regions of several Mb do (48). Reproduced by our model, these features are consistent with incomplete mixing within a 10Mb layer (Figure S20). Average loop lengths of 80–120Kb, which best reproduce experimental P(s) in our models, agree with previous estimations of loop lengths (18, 39, 40). We remain agnostic about the role of a scaffold, as models with compact, diffuse, or no scaffold agree equally well with Hi-C data (Figure S26). Further, the loops in our models are irregular and would form a uniform density ‘melt’, consistent with recent EM and SAXS studies (22, 49) (Figure S20).

One important aspect makes our proposed model of the mitotic chromosome different from earlier proposals. Several classical models assumed a highly structured folding with regular solenoids, loops of fixed length, or distinct hierarchical levels. Our model achieves agreement with earlier experiments and our Hi-C data by incorporating variability at all levels of assembly: cell-to-cell differences in loop positions and lengths, and substantial mixing within a 10Mb layer. Moreover, classical models of solenoidal and hierarchical folding would require machinery able to manipulate chromatin at the micron and multi-megabase scale; similarly, a recently proposed polymer model (50) implies a mechanism to control the formation of long-range loops. Our model, on the contrary, proposes largely local loop formation followed by a linear compression of the resulting backbone of loop bases, allowing the rest of the chromatin fiber to stay in a largely disordered ensemble. The use of local folding mechanisms and the lack of strict sequence-driven control makes this two-stage folding mechanism robust with respect to chromosome sizes, compositions and genomic rearrangements. We note that the current resolution of our data does not rule out the use of different subsets of specific sequence elements as loop bases in different cells.

Future studies performed at higher resolution, e.g. through deeper sequencing of Hi-C libraries, single-cell Hi-C and at multiple timepoints through prophase and telophase-early G1, may lead to insights into the finer-scale organization of chromosomes and the intricate folding pathways that connect interphase and mitotic chromosome structures.