Array-Optimized Composite Pulse for Excellent Whole-Brain Homogeneity in High-Field MRI

Abstract

A number of methods to improve excitation homogeneity in high-field MRI have been proposed, and some of these methods rely on separate control of radiofrequency (RF) coils in a transmit array. In this work we combine accurate RF field calculations and the Bloch equation to demonstrate that by using a sequence of pulses with individually optimized current distributions (i.e., an array-optimized composite pulse), one can achieve remarkably homogeneous distributions of available signal intensity over the entire brain volume. This homogeneity is greater than that achievable using the same transmit array to produce either a single optimized (or RF shimmed) pulse or a single RF shimmed field distribution in a standard 90x-90y composite pulse arrangement. Simulations indicate that with a very simple array-optimized composite pulse, excellent whole-brain excitation homogeneity can be achieved at up to 600 MHz.

The advancement to higher static magnetic (B₀) field strengths and concomitant higher radiofrequency (RF) magnetic (B₁) field frequencies necessitates the design of magnetic resonance imaging (MRI) technologies with an increased consideration of the field-perturbation effects of human tissue. In recent years a number of methods to alleviate image artifacts related to RF wavelength effects in high-field MRI have been proposed, and some of these methods rely on separate control of RF coils in a transmit array. In this work we refer to the two most commonly discussed methods as “RF shimming” and “multicoil tailored pulses.” With RF shimming the current magnitudes and phases of coils in a transmit array (or impedances of elements in a volume coil) are adjusted individually to produce a homogeneous RF field or RF excitation within a target region (1–3). This can be viewed as using multiple RF field sources to find an advantageous field distribution within the bounds of the Maxwell equations. In contrast, tailored pulses are designed around the highly-shaped, coordinated simultaneous pulsing of RF and gradient coils to achieve spatially-selective excitation based primarily on the use of the Bloch equations and predefined k-space trajectories (4). The resulting excitation distribution is very flexible. It seems to be limited more by the imagination of the pulse designer than by the Maxwell equations (5), but requires very long RF pulses. Tailored RF pulses have been used successfully to compensate for RF inhomogeneity (6). Additionally, multicoil tailored RF pulses, in the specific form of transmit (SENSE) (7), have successfully been used to perform spatially-selective excitations with reduced pulse durations (8).

One previously published work is especially worthy of mention here because of its relation to the method we propose. Ledden and Cheng (9) proposed pulsing each of eight coils at separate times in quick succession. Unfortunately, in their mathematical treatment they failed to consider the vector nature of either the spin magnetization or the appropriate portion of the applied RF magnetic field, and assumed that the result of the proposed composite pulse would be equivalent to that obtained by merely summing the magnitudes of the fields from the eight separate coils. In our earlier investigations into using a sequence of pulses with different field distributions (starting in 2003), we showed that by pulsing different coils sequentially it is not possible to produce the effect of merely summing the separate expected flip angle magnitudes (10), as Ledden and Cheng assumed (9).

A logical progression from single RF-shimmed pulses is to use array-optimized composite pulses. Composite pulses have successfully been used with single coils to improve the homogeneity of the flip angle despite an inhomogeneous RF field (11,12). When used with a single excitation coil, they are theoretically more limited than tailored pulses in producing homogeneous excitations with a given single inhomogeneous field distribution, but do not require the long, complex, simultaneous shaped RF and gradient pulses. Here we combine accurate full-Maxwell field simulations and the Bloch equation to show that by adjusting individual coil currents in a sequence of pulses through a transmit array, one can achieve remarkably homogeneous whole-brain excitations at up to 600 MHz.

MATERIALS AND METHODS

To calculate the degree of spin excitation induced by the applied RF fields over time, we tracked the magnetization vector by numerically implementing a portion of the Bloch equation:

$$\frac{\mathrm{d}\mathbf{M}}{\text{dt}}=\mathbf{M}\times \sum _{\mathrm{n}}{\mathbf{B}}_{1\mathrm{n}}^{+},$$ [1]

where M and ${\mathbf{B}}_1^{+}$ are defined in the rotating frame. Here M represents the net spin magnetization vector. The initial state of M (M₀) was oriented with B₀ and assigned a magnitude of 1.0 in white matter, gray matter, and CSF within the brain, and of 0.0 elsewhere for simplicity. Because the available signal intensity distribution was calculated immediately after the excitation pulse or pulses, the relaxation terms of the Bloch equation were considered irrelevant and thus are not included in the above equation. The summation is performed over the n coils of the transmit array. ${\mathbf{B}}_1^{+}$ for each coil is calculated using previously published methods (13) and represented as a vector in the rotating frame. We implemented Eq. [1] using rotation operations (i.e., rotating the orientation of M at a certain location about ${\sum }_n{\mathbf{B}}_{1\mathrm{n}}^{+}$ at the same location). This rotation occurred at a frequency proportional to $\Vert {\sum }_{\mathrm{n}}{\mathbf{B}}_{1\mathrm{n}}^{+}\Vert$ by the gyromagnetic ratio of ¹H (γ = 42.58 MHz/T) for a pulse duration of τ. In these simulations τ = 3.0 ms for each individual pulse, including each of the two component pulses of the composite pulse.

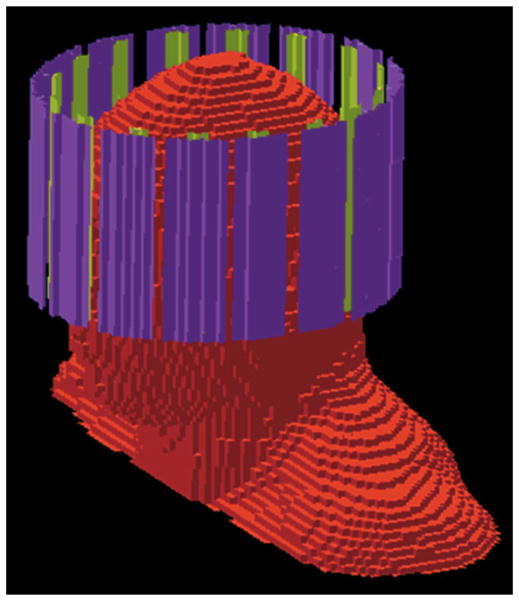
The FDTD method was used to calculate the ${\mathbf{B}}_1^{+}$ field distribution of each of 16 stripline elements in an array about the head (Fig. 1). The creation of the head model was described previously (13), as were the array geometry and calculation methods used (14). The array was based on designs developed at the University of Minnesota (15). Briefly, a 16-element, elliptical, stripline coil array was modeled about an anatomically accurate, multi-tissue human head model. Each element of the array was modeled as a 2-cm-wide, 15-cm-long thin strip of copper oriented in the longitudinal direction and placed with equal spacing on the surface of an ellipse with a long (anterior–posterior) axis of 24 cm and a short (left–right) axis of 21 cm. Both ends of each element were connected (with thin wires in a roughly radial direction) to a slotted elliptical shield of copper (15 cm long, long axis = 27 cm, short axis = 23 cm) modeled concentrically with the array. One current source was placed in each radially oriented wire (two per element) with sources at opposite ends of a given element having equal magnitudes and phases and being oriented in opposite directions. The head and array were modeled at a resolution of 5 mm. The finite-difference time-domain (FDTD) method was used to calculate the field produced by each element driven individually using the FDTD method at 600 MHz. The electrical properties of tissues at these frequencies were obtained from the literature (16). All FDTD calculations were performed with the aid of commercially available software (xFDTD; Remcom, Inc.; State College, PA, USA).

FIG. 1.

Geometry of the human head model in a 16-element transmit array. The inner and outer conductors of each array element are colored green and purple, respectively. All tissues throughout the head were accurately represented in each field calculation.

The distribution of the available signal intensity, or the magnitude of the transverse component of M (M_t) throughout the brain, was calculated for four different cases: 1) after a single RF pulse with an array having a current distribution similar to that in a typical volume coil (“original”); 2) after a single pulse with an RF-shimmed transmit array (“RF shimmed”); 3) after a two-pulse composite pulse with a transmit array in which current magnitudes and phases of the first component pulse are equal to those in case 2, and those of the second component pulse are merely phase shifted by 90° (“composite shimmed”); and 4) after a two-pulse array-optimized composite pulse with a transmit array in which current magnitudes and phases in both component pulses have been optimized to produce the most homogeneous M_t at the end of the second component pulse (“optimized composite”). Note that the composite-shimmed case is equivalent to the RF-shimmed pulse being applied in a 90x-90y composite pulse configuration.

Two of the cases described above—RF shimmed and optimized composite—require the use of an optimization routine to determine the magnitudes and phases of individual coil currents to produce an optimally homogeneous M_t distribution after the excitation pulses or pulses. To optimize the spatial homogeneity of M_t, we utilized the results of the field calculations for all individual coils in in-house-built, simple optimization routines using Matlab (The MathWorks, Natick, MA, USA). The magnitudes and phases of the individual coil currents were varied incrementally and sequentially with the goal of improving the homogeneity of M_t after either a single pulse (for the RF-shimmed case), or after a sequence of two pulses (for composite pulse cases). The entire distribution of the ${\mathbf{B}}_1^{+}$ magnitude and orientation for each coil were multiplied or shifted (respectively) according to the magnitude and phase of the current driven in that coil. For the optimization results shown here, the sum of M_t at all locations in the brain was maximized. This brings M_t closer to 1.0 (its maximum possible value) throughout the brain, and thus also improves its homogeneity. We used a previously described optimization routine (14), but with twice as many variables (magnitude and phase in each coil for each of two pulses) for the optimized-composite pulse (with two pulses) than for the RF-shimmed pulse (with only one pulse). The starting point (before optimization) for the RF-shimmed pulse was the current magnitude and phases of the original case, and the starting point for the optimized-composite pulse was the current magnitudes and phases of the two pulses in the composite-shimmed case. Maximizing the sum of M_t is one approach to optimization; however, to show some of the flexibility of the method, we also optimized a multicoil composite pulse by using the least-squares approach of minimizing the sum of the squares of the differences between M_t and 1.0.

RESULTS

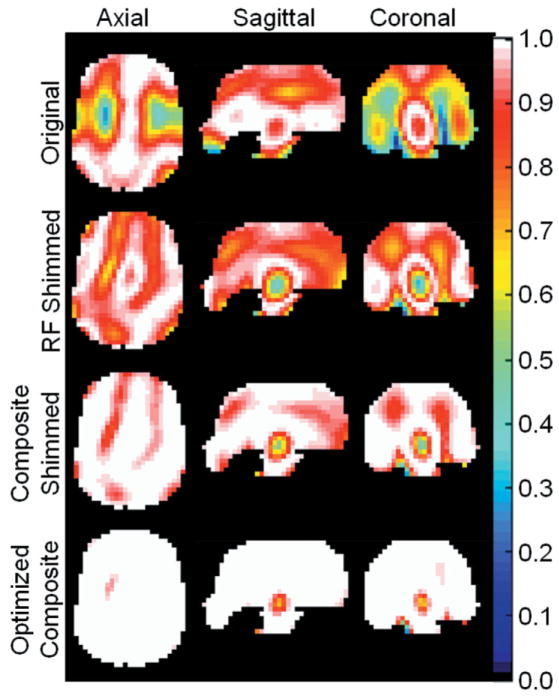
A representation of the head model in the 16-element array is given in Fig. 1. Figure 2 shows M_t throughout the brain at 600 MHz (for ¹H imaging at 14T) calculated using each of the four cases described. Because M was assigned a magnitude of 1.0 throughout the brain (and zero elsewhere), the maximum possibility for M_t is also 1.0. An M_t of 1.0 indicates that the magnetization vector is entirely in the transverse plane, or that the flip angle is exactly 90° from the orientation of the B₀ field. Also because M was assigned a magnitude of one, the size of M_t is equal to the absolute value of the sine of the flip angle at each location. As should be expected, the homogeneity of M_t increases with the following progression: original, RF shimmed, composite shimmed, and optimized composite. The mean ± standard deviation (SD) for M_t in this same progression is 0.821 ± 0.177, 0.896 ± 0.100, 0.967 ± 0.056, and 0.992 ± 0.016. The optimized-composite pulse results in very good excitation (white in Fig. 2, indicating M_t > 0.984) in nearly the entire brain volume, even at 600 MHz. Simulations at the lower frequencies currently used in practice produced only more homogeneous results. Figure 3 shows M_t on the same three slices with the same color scale as in Fig. 2 for an array-optimized composite pulse. We minimized the sum of the squares of the differences between M_t and 1.0 during optimization instead of maximizing the sum of M_t, as was done for the results in Fig. 2.

FIG. 2.

Magnitude of the transverse component of the magnetization vector M_t (the maximum possible value is 1.0 throughout the brain, and zero elsewhere) on axial, sagittal, and coronal slices through the middle of the brain for four different cases: 1) after a single RF pulse with an array having a current distribution similar to that in a typical volume coil (“original”); 2) after a single pulse with an RF-shimmed transmit array (“RF shimmed”); 3) after a two-pulse composite pulse with a transmit array in which current magnitudes and phases of the first pulse are equal to those in case 2, and those of the second pulse are merely phase shifted by 90° (“composite shimmed”); and 4) after a two-pulse array-optimized composite pulse with a transmit array in which current magnitudes and phases in both pulses have been optimized to produce the most homogeneous M_t at the end of the second pulse (“optimized composite”). It can be seen that M_t becomes both more homogeneous and stronger throughout the brain in the progression shown. The optimizations were performed for the whole brain volume simultaneously, and results are shown for 600 MHz (14T).

FIG. 3.

Distribution of M_t throughout the brain at 600 MHz for an array-optimized composite pulse as in the bottom row of Fig. 2, but with improved excitation in the center at the cost of slightly lower homogeneity throughout the remainder of the brain. This was accomplished by minimizing the sum of the squares of the differences between M_t and 1.0 during optimization instead of maximizing the sum of the M_t, as was done for Fig. 2.

DISCUSSION

In this work we investigated the possibility of capitalizing on the combined use of array coil technology and composite pulse concepts to produce homogeneous whole-brain excitation pulses for high-field MRI. The results obtained at 600 MHz clearly demonstrate the advantages of combining technologies to overcome RF field distortions from the hardware end with techniques developed to reduce the effects of these distortions utilizing spin excitation principles. Other methods that capitalize on combining these techniques and technologies with multicoil tailored RF pulses, such as transmit SENSE, have been presented (7). However, whereas most previous pulse designs were based on analytical derivations, our approach is largely numerically driven, and may yield results that could not easily be derived otherwise.

In the future it should be possible to capitalize further on the technology of RF array hardware and the wealth of methods developed in RF pulse design. Unlike multicoil tailored RF pulses, such as transmit SENSE, array-optimized composite pulses do not require different waveforms in each coil. It may be possible to implement such pulses with many existing spectrometers after augmenting them with an electronically controlled system to split a single excitation waveform into several channels, and then phase shifting, attenuating, and amplifying the channels separately, as has been done for RF shimming (17).

From a simple perspective, using multiple pulses in quick succession with a transmit array increases the number of variables that can be adjusted (magnitude and phase of each current in each pulse) to produce a homogeneous distribution in flip angle or available signal intensity. Having more degrees of freedom both permits greater flexibility in the final result and requires consideration of more possibilities in an optimization routine. While for very small flip angles the advantages of such an array-optimized composite pulse may be limited (10), for larger flip angles the advantages are clear (Fig. 2). Larger flip angles and more pulses (such as a three-pulse 180° version based on the well-known 90x-180y-90x composite pulse (11)) should yield more impressive results than those shown here. Also, though our earlier investigation into the use of this method for very small flip angles showed no advantage over RF shimming alone, there are more sophisticated composite pulses for fairly low flip angles (18) that might be used as a basis for more successful low-flip-angle attempts in the future. It should be possible to implement a slice-selective version of array-optimized composite pulses with a variety of creative yet fairly straightforward methods (12,18,19). Although we did not investigate the effects of resonance frequency offset (e.g., due to B₀ inhomogeneities) in this work, some composite pulses are known to perform well in the presence of such offsets (11), and it is conceivable that such offsets could also be considered during the optimization procedure.

As shown on the bottom row of Fig. 2, the array-optimized composite pulse results in a small region of smaller M_t (as low as 0.68) near the center of the brain, where the final flip angle is slightly greater than 90°. There is considerable flexibility in the method illustrated here, however, and a slight modification can result in improved homogeneity in this region. For example, Fig. 3 shows M_t on the same three slices with the same color scale as in Fig. 2, but using different criteria during optimization. M_t near the center of the brain is now much closer to 1.0 (no lower than 0.85), but M_t at many locations outside this is slightly lower (still greater than 0.95) than in Fig. 2.

Because some image reconstruction methods effectively remove the coil receptivity distribution from the final images, depending on the method used for image reconstruction and the efficacy of its implementation, in theory the signal intensity on the final images can be as homogeneous as the available signal intensity shown here with regard to the RF fields (14).

The distribution of $\Vert {\sum }_{\mathrm{n}}{\mathbf{B}}_{1\mathrm{n}}^{+}\Vert$ in the two pulses of the optimized-composite case is much different from that in the two pulses of the composite-shimmed case. For the composite-shimmed case, the field magnitude is identical at every location in both pulses, but in the optimized-composite case the field magnitude of the second pulse is approximately 1.6–2.3 times greater than that in the first pulse. Similarly, while the phase of the second pulse is exactly 90° greater than that of the first pulse in the composite-shimmed case, it ranges from approximately 95° to 115° greater than the first pulse in the optimized-composite case. While it is possible to think of potential general advantages to this arrangement in the optimized-composite case, it is difficult to make generalizations. For example, in similar optimizations for 400 MHz (not shown here), the magnitude of the second pulse ends up being weaker than that of the first pulse in the optimized-composite case. At 400 MHz the array-optimized composite pulse produces practically perfect excitation throughout the entire brain.

One obvious concern that arises when more RF pulses are added is the effect on specific absorption rate (SAR). We expect the increase in the number of RF pulses to result in an increase in average SAR for a given sequence. The result on local SAR, however, is unclear at this point. Because the two different pulses will have different SAR distributions and (potentially) different locations of “hot spots,” it may actually be possible to use array-optimized composite pulse designs to reduce the local SAR levels. Previous simulations have shown that it is possible to consider both local SAR and B₁ homogeneity during optimization to find current distributions that both improve RF homogeneity and reduce local SAR levels during a single pulse (20). However, it may be difficult to implement this in practice, since SAR distributions for a given coil-driving configuration can vary dramatically between individuals (21), and it is not feasible to model each subject before imaging.

Another question arises regarding the sensitivity of this method to subject geometry and motion or change in position. A previous study (22) indicated that the optimum current distribution for RF shimming depended strongly on both of these practical aspects of MRI, but it has also been shown that a compromising drive configuration that yields somewhat improved results for multiple subjects can be achieved in some cases (20). One can expect that a dependence on geometry or change in position would also exist to some degree for optimized composite pulses, with the strength of the dependence increasing with B₁ field frequency.

The method described in this work might be seen as a discrete point on a continuum of solutions to RF inhomogeneity problems between methods that rely primarily on hardware advancements (e.g., RF shimming) and those that utilize much more complex consideration and manipulation of the magnetization with much more elaborate pulsing techniques (e.g., transmit SENSE). Another set of approaches employs combinations of separate complete images acquired with different RF excitations (23,24), but has significant consequences, at least in terms of total acquisition time. As the methods become more complex, the possibility of overcoming RF inhomogeneity may become more certain, but other problems, such as long pulse durations and complex pulse design and implementation, may arise. The array-optimized composite pulse will be able to provide excellent homogeneity with relatively minor increases in pulse duration and complexity of design, using much of the same methods and technologies that are currently being developed for RF shimming.