Priming by the variability of visual information

Significance

Sensory systems in the mammalian brain adapt to the context provided by the local environment. The high-level statistics of visual information, such as the central tendency (mean) or heterogeneity (variance) of features or objects, provide important contextual cues for perception. Here, we show that participants categorize a “target” array faster when it occurs in the context of a preceding “prime” array with similar levels feature variance, even when prime and target features are drawn from different categories. This finding suggests that humans rapidly extract and adapt to the variance of visual information. Adaptation to variance may facilitate gain control in heterogeneous or cluttered environments, and contribute to ecologically important behaviors, such as detection in camouflage.

Abstract

According to recent theories, perception relies on summary representations that encode statistical information about the sensory environment. Here, we used perceptual priming to characterize the representations that mediate categorization of a complex visual array. Observers judged the average shape or color of a target visual array that was preceded by an irrelevant prime array. Manipulating the variability of task-relevant and task-irrelevant feature information in the prime and target orthogonally, we found that observers were faster to respond when the variability of feature information in the prime and target arrays matched. Critically, this effect occurred irrespective of whether the element-by-element features in the prime and target array overlapped or not, and was even present when prime and target features were drawn from opposing categories. This “priming by variance” phenomenon occurred with prime–target intervals as short as 100 ms. Further experiments showed that this effect did not depend on resource allocation, and occurred even when prime and target did not share the same spatial location. These results suggest that human observers adapt to the variability of visual information, and provide evidence for the existence of a low-level mechanism by which the range or dispersion of visual information is rapidly extracted. This information may in turn help to set the gain of neuronal processing during perceptual choice.

What information do sensory systems represent, and how do their computations allow us to make judgments about the external world? Canonical theories in perception and cognition suggest that visual neurons code exhaustively for the features or objects that populate natural scenes, from primitive colors and shapes to complex high-dimensional items, such as faces (1, 2). However, any theory of visual representation must account for two striking findings. First, visual judgments can be remarkably blind to local detail: for example, when observers fail to notice the removal of an object from a cluttered natural image, at least when it is outside of the focus of attention (3, 4). Second, both humans and monkeys are extremely good at extracting high-level information (e.g., the presence of an animal or a navigable path) from a scene in a single, rapid glance, despite the almost endless variability in natural images (5–10). One alternative theory that can account for both of these findings argues that the visual system rapidly computes “summary” statistical information about a scene (e.g., the average size of all of the round objects) as opposed to specific features (e.g., the presence of a large round object) (11–13). Encoding summary statistics might offer a crude but efficient representation of the visual world (14) that would facilitate rapid, accurate decisions that are critical for survival (e.g., whether to flee in the face of impending predation, and which route to take), but at the cost of discarding visual detail outside of the focus of attention. However, our understanding of the nature and limits of these summary representations is rudimentary, and the very notion that observers extract summary statistics from a scene continues to be hotly debated (15–17).

To date, a great deal of research has focused on demonstrating that observers encode the central tendency of sensory data: humans can accurately estimate mean feature information from arrays of simple features (11, 13, 18–21), complex shapes or letters (22), or human faces (23, 24), even when discrimination of individual array elements is at chance. However, limited consideration has been given to whether the visual system represents the dispersion (variability) of available visual information. (but see ref. 25) The variability of visual information is a key descriptor of the visual world, pertaining to the range, uniqueness, and spacing of feature information, and is likely to be useful for a range of ecologically pertinent visual functions, such as discriminating among textures (e.g., bark or leaf shape) or detecting objects in camouflage (26).

Human judgments about complex natural scenes are resource-limited, and the brain has evolved to capitalize on autocorrelation in sensory signals to interpret the visual world, for example by adapting information processing to the context provided by the recent stimulation history. This mechanism is visible in well-established behavioral phenomena, such as priming, in which judgments about a stimulus that shares perceptual or conceptual features with its predecessor are faster or more accurate (27). However, variability in visual features is also autocorrelated across time; for example, crossing a desert might lead to sustained periods of relatively low variance in feature information, whereas trekking through the rainforest will lead to prolonged experience of high visual variability. If the visual system encodes variability information about when presented with stimulation, then we should observe “priming by variance,” the facilitation of responses to visual arrays that are preceded by a prime array with similar levels of feature variance. Here, we describe three experiments in which we tested and confirmed this prediction. We observed that classification performance was facilitated when the variability of a prime and target array matched, independent of the similarity of individual elements and of whether the feature information in the two arrays belonged to the same category or different categories. This priming effect was visible with prime–target intervals as short as 100 ms. The existence of this phenomenon not only provides compelling new evidence for statistical representations in human visual perception, but hints at the existence of a mechanism by which the gain of visual processing is calibrated to account for the likely dispersion of information in a natural scene.

Results

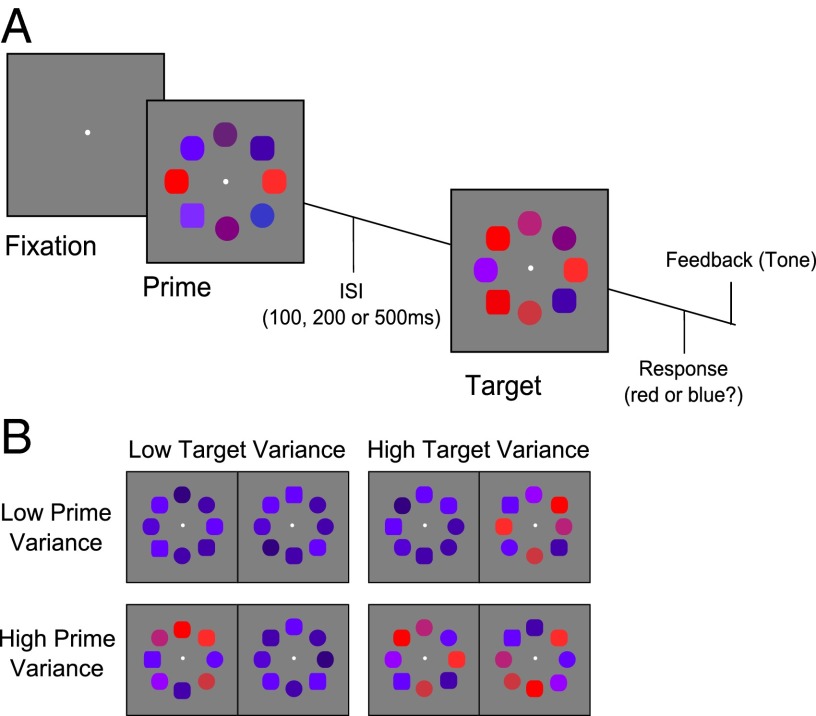
On each trial, observers viewed two successive arrays each composed of eight colored shapes (“squircles”) arranged in a ring around fixation (Fig. 1). The task was to categorize the later (“target”) array on the basis of its average color or shape, ignoring the earlier 100-ms duration (“prime”) array that preceded it by 100, 200, or 500 ms. Each of the eight elements in both target and prime arrays took on a color value (red to blue) and shape value (square to circle) continuously parameterized in the range −1 to +1, and on each trial these feature values were drawn pseudorandomly from a Gaussian normal distribution with mean μ or −μ and variance σ². One dimension (color or shape, manipulated between subjects) was designated task-relevant and the other was task-irrelevant. Observers judged whether the mean feature value for the task-relevant dimension was greater or less than zero (e.g., red vs. blue, square vs. circle).

Fig. 1.

Task description. (A) Trial sequence. Observers were asked to classify a target array based on either the average color (red vs. blue) or shape (square vs. circle). Only one dimension was relevant for the duration of the session. Preceding the target array was an irrelevant prime array, which could appear with a PTI of 100, 200, or 500 ms. Auditory feedback was given immediately following the response. (B) Examples of prime (P) and target (T) arrays with high and low variance on the color dimensions. Response time facilitation was observed when the variance matched (Upper Left, Lower Right).

Experiment 1.

In Exp. 1 (n = 40), we manipulated the variance (high vs. low) of both task-relevant and task-irrelevant dimensions for both prime and target arrays independently (Fig. 1). This process allowed us to assess how variability of the prime and target distributions, and (critically) the congruence between their variances, influenced response times (RTs) independently for task-relevant and task-irrelevant feature dimensions. In what follows, all analyses were conducted on log-transformed RTs greater than 300 ms from correct trials only.

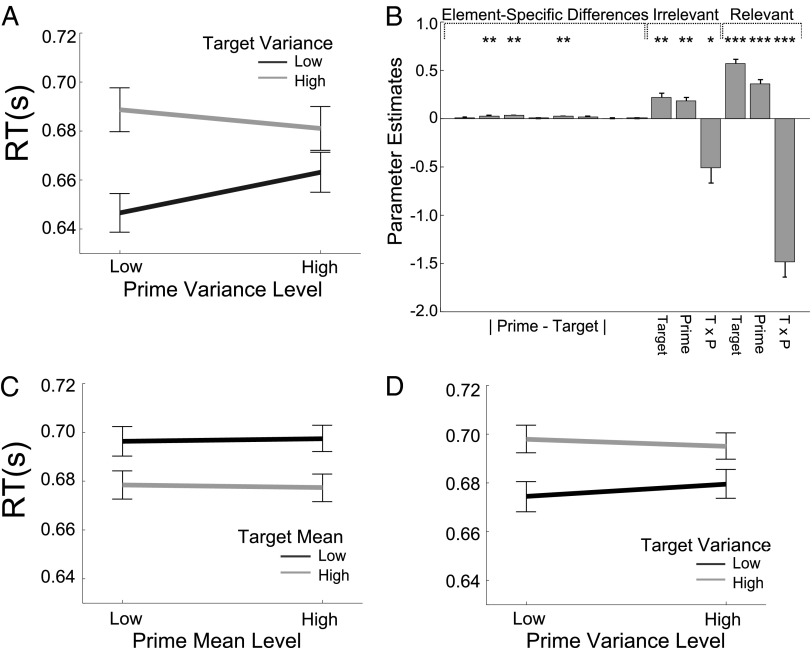
As expected, participants responded faster on trials where the prime and target features were drawn from distributions with the same mean value (i.e., from the same category) [F_{(1, 39)} = 23.0, P < 0.001]. Moreover, increased prime and target variance both slowed response times [prime: F_{(1, 39)} = 5.24, P < 0.028; target: F_{(1, 39)} = 76.9, P < 0.001] (Table S1, Exp. 1). Critically however, the congruity of the variance of the prime and target arrays influenced behavior, with faster responses for trials where the prime and target arrays had the same variance (either high or low), relative to trials where their variance was different (Fig. 2A). This result was reflected in a significant prime × target variance interaction on RT [F_(1,39) = 27.5, P < 0.001]. There was no prime × target interaction on accuracy [F_{(1, 39)} = 0.775, P = 0.384], suggesting that this effect is a facilitation in processing, rather than a because of a change in speed-accuracy trade-off. The variance of the prime did not impair accuracy, whereas the target variance did [F_{(1, 39)} = 16.0, P < 0.001], as previously reported (18).

Fig. 2.

Variance priming. (A) Mean RTs for both levels of prime variance (x axis; high or low) and both levels of target variance (lines; high vs. low). Error bars are SEM. (B) Regression weights are plotted for element-specific differences (|prime–target|), variance of the target (Target), prime (Prime) and their interaction (T × P) for the irrelevant and the relevant dimension. *P < 0.05, **P < 0.01, or ***P < 0.001. (C) Mean RTs from Exp. 2 for both levels of prime mean distance to category boundary (x axis) and both levels of target mean distance to category boundary (lines). Error bars as for A. (D) Mean RTs from Exp. 2 for both levels of prime variance (x axis) and both levels of target variance (lines). Error bars as for A.

To test whether these findings could be explained by the overlap in individual features between the prime and target arrays, we turned to multiple regression. The prime array variance, target array variance, and their interaction were entered as rival predictors of RT alongside additional regressors encoding the absolute prime–target feature difference for each of the eight elements in the array (Fig. 2B), and t tests were used to assess the deviance of the resulting parameter estimates from zero. Parameter estimates associated with prime array variance and target array variance were both positive [prime: t₍₃₉₎ = 4.24, P < 0.001; target: t₍₃₉₎ = 6.54, P < 0.001], consistent with the previously described detrimental impact of high-variance arrays on decision latencies (18), whereas those associated with interaction between prime and target variance were negative [t₍₃₉₎ = 4.79, P < 0.001], consistent with the abovementioned observation that similar variance in the prime and the target facilitated responding. Crucially, these effects persisted even when the eight element-specific differences had been partialled out, indicating that it is a summary statistical representation—not feature information—that is driving priming by the variance.

One alternative explanation not ruled out by these analyses is that RT might be faster when the prime and target offer compatible information about which response to make, but that this response compatibility effect is dampened under high variance. To test this hypothesis, we constructed two further nuisance regressors that encoded (i) the compatibility between prime (P) and target (T) (i.e., the absolute of the difference between their task-relevant features |ΣP_1–8–T_1–8|), and (ii) the interaction between this quantity and target variance. Repeating the regression analyses described above yielded a weak trend toward a main effect of response compatibility [t₍₃₉₎ = 1.40, P < 0.09], but no reliable interaction between compatibility and variance (P < 0.25). Critically, the interaction between prime and target variance remained strongly significant [t₍₃₉₎ = 5.10, P < 0.001]. Very similar results were obtained using a measure of the absolute activation provided by both prime and target (i.e., |ΣP_1–8+T_1–8|). These analyses, which are described in Fig. S1, suggest that our effects are not driven by response compatibility.

To better characterize the processing stage at which priming by variance occurs, we included both task-relevant and irrelevant target variance, prime variance, and their interaction in a further analysis. Although weaker than for the task-relevant dimension, the congruity of prime–target variance for the task-irrelevant feature values also facilitated behavior [t₍₃₉₎ = 1.72, P < 0.05], consistent with an early, automatic phenomenon (Fig. 2B). Interestingly, however, there was no cross-over variance priming between task-relevant and task-irrelevant dimensions for these trials; that is, the variance of the task-relevant features for the prime did not interact with the variance of the task-irrelevant features for the target [t₍₃₉₎ = 0.02, P = 0.510] or vice versa [t₍₃₉₎ = 0.52 P = 0.300]. In other words, variance priming does not depend on feature-based attention, but does seem to occur within feature-specific channels. Moreover, the existence of independent priming effects for relevant and irrelevant dimensions is hard to reconcile with any explanation based on response compatibility, because no meaningful response mappings were assigned to the irrelevant dimension.

Experiment 2.

One outstanding possibility is that facilitatory effects of congruent prime–target array variance could be secondary to nonspecific aspects of the task, such as the relative level of cognitive resources required to judge high- and low-variance arrays. For example, high-variance prime arrays might engage attentional or control processes that confer disproportionate benefit on processing of the high-variance target array, an explanation that has been invoked to account for adaptation to conflict between sequential trials (28, 29). To test this possibility, we capitalized on the previous observation that the absolute mean feature value of the array |μ| (i.e., proximity of the mean to the category boundary, at x = 0) impacts decisions and their latencies in a similar fashion to array variability σ², with no interaction between the two factors (18). In a second experiment, we again manipulated array variance (high vs. low) but varied array mean μ at four symmetric levels around zero (μ₂, μ₁, −μ₁, −μ₂, where μ₂ > μ₁). This process allowed us to compare how (i) the congruity of variance (high and low) and (ii) congruity of absolute mean (μ₂ and μ₁) influenced performance. If the variance priming observed in Exp. 1 is because of nonspecific effects, we would expect to additionally see priming by the absolute mean of array information. If it is specific to the range or dispersion of the information in the prime, then we would expect to replicate Exp. 1 in the absence of any priming by absolute mean.

In Exp. 2, we replicated the phenomenon of variance priming reported above, with faster RTs for trials on which the prime–target array variance was consistent [F_{(1, 38)} = 5.03, P < 0.04]. Additionally, we observed the anticipated facilitatory influence of category congruity between prime and target [F_{(1, 38)} = 20.9, P < 0.001]. As expected, absolute target array mean had a main effect on response times [low |μ| > high |μ|, F_{(1, 38)} = 63.6, P < 0.001] along with target array variance [high σ > low σ, F_{(1, 38)} = 37.8, P < 0.001]. Critically however, congruity in absolute mean (and thus, degree of response conflict) had no facilitatory effect on decision latencies [F_{(1, 38)} = 0.195, P = 0.661] (Fig. 2 C and D and Table S1, Exp. 2, Variance and Mean). This result occurred despite this equivalence between the way that target array |μ| and σ influenced responding: the main effect of mean on RTs (low mean RT = 698 ms; high mean RT = 679 ms, difference = 19 ms) was comparable with the main effect of variance (low variance RT = 678 ms; high variance RT = 698 ms, difference = 20 ms). It is thus unlikely that the manipulation of mean was simply too weak to observe similar priming effects to the variance. As for Exp. 1, these results cannot be accounted for by a speed accuracy trade-off, with no significant prime × target interaction on accuracy for either variance [F_{(1, 38)} = 0.015, P = 0.902] or absolute mean [F_{(1, 38)} = 1.49, P = 0.230]. Together, these analyses seem to rule out nonspecific explanations based on resource recruitment or adaptation to conflict.

The Influence of Prime–Target Interval.

If summary statistical information is to benefit rapid object perception, it must be encoded within just a few hundred milliseconds (5, 6). To assess the latency with which perceptual variance influences behavior, we collapsed across data from Exps. 1 and 2, and compared variance priming at the three levels of prime–target interval (PTI) used (100, 200, 500 ms). The prime–target variance interaction was significant when considering only those trials with PTI of 100 ms [F_{(1, 78)} = 18.4, P < 0.001] and 200 ms [F_{(1, 78)} = 8.74, P < 0.004]; and although the interaction failed to achieve significance for the 500-ms trials [F_{(1, 78)} = 2.73, P = 0.102], there was no three-way interaction between prime variance, target variance, and PTI [F_{(2, 147)} = 1.97, P = 0.146] (Table S2). This finding suggests that the effect begins very early and persists for several hundred milliseconds (Fig. 3).

Fig. 3.

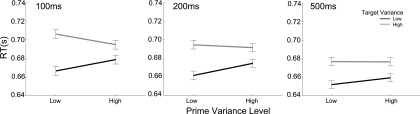
Variance priming across the three PTIs. The extent of the variance priming effect is plotted for trials grouped by the three levels of PTI, from Left to Right: 100, 200, and 500 ms. Axes are as for Fig. 2A.

Experiment 3.

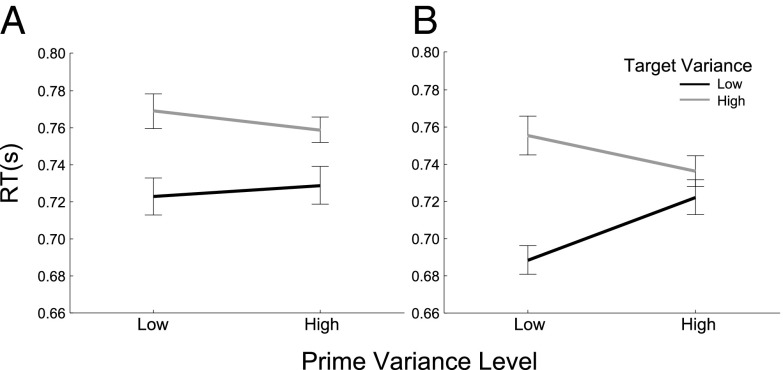
If the encoding of array variability contributes to rapid detection and recognition, then one would not expect its influence to be tied to a specific spatial location. To test the spatial specificity of variance priming, we conducted a third experiment in which the radius of the prime and target arrays were manipulated, such that either they were overlapping or one fell concentrically within the other. A facilitatory effect of variance congruity on RT was again observed when the arrays were spatially overlapping, replicating the findings of the previous two experiments [F_{(1, 13)} = 15.4, P < 0.002]. The effect was again observed at both 100 ms [F_{(1, 13)} = 24.7, P < 0.001] and 200 ms [F_{(1, 13)} = 4.90, P < 0.046] PTI (there were no 500-ms PTI trials in Exp. 3). To explore the data further, we created a summary measure of variance priming by subtracting the RT difference for each combination of congruent and incongruent different trials (high/high – high/low) – (low/high – low/low). Variance priming was significant when the prime array was large, irrespective of whether the target array was large [t_{(1, 13)} = 4.24, P < 0.001] or small [t_{(1, 13)} = 2.87, P < 0.01]. It was also significant when the target and prime array were both small [t_{(1, 13)} = 2.13, P < 0.03]. Only when the prime array was small and the target was large did the effect evaporate (P = 0.28) (Fig. 4). However, neither the main effect of prime array size (P = 0.20), target array size (P = 0.70), or their interaction (P = 0.20) on variance priming were significant. Thus, variance priming does not depend on spatial overlap between prime and target.

Fig. 4.

Variance priming for spatially nonoverlapping prime–target pairs. Mean RTs plotted for each combination of prime variance (high vs. low) and target variance (high vs. low). Data are from Exp. 3 (A) trials in which the prime array appeared within the spatial boundary of the target array, and (small-large) (B) for the reverse spatial organization (large-small).

Variance Priming Across the Category Boundary.

Finally, the strongest demonstration of priming by variability would be that the congruity of prime–target variance can still facilitate responding even when prime and target are drawn from different categories (trials; e.g., red mean prime, blue mean target). We assessed this by pooling across data from all three experiments and repeating the regression analyses described above, including independent predictors for switch (prime and target from different category) and stay (same category) trials. For this analysis, we excluded data from the 500-ms condition for which variance priming was not significant (see Tables S3 and S4 for further results including all conditions). Critically, although variance priming was stronger for stay trials [prime variance × target variance × same/different category interaction, F_{(1, 92)} = 18.0, P < 0.001], it was independently significant for both stay [t₍₉₂₎ = 7.31, P < 0.001] and switch [t₍₉₂₎ = 1.73, P < 0.05] trials (Fig. 5). Individually, the effect was significant on switch trials for Exp. 1 [t₍₃₉₎ = 1.79, P < 0.05] and Exp. 3 [t₍₁₃₎ = 2.24, P < 0.03], but not Exp. 2 [t₍₃₈₎ = 0.69, P = 0.751] (see Table S5 for full ANOVA results on RTs). Together, these results imply that priming by the variance of a visual array can occur entirely independently of the mean feature values of the prime and target arrays.

Fig. 5.

Regression weights for variance priming on category congruent (stay) and incongruent trials (switch). Regression weights are plotted for the variance of the target, prime, and their interaction. Data included from the 100- and 200-ms PTI conditions across all experiments. Trials are split by whether the prime and target belong to the same category (light gray bars, “stay”) or whether the categories differ (dark gray bars, “switch”). *P < 0.05, **P < 0.01, or ***P < 0.001.

Finally, we assessed the strength of the priming by variance account in the data collapsed across all experiments as described above. When all subjects were included in a single analysis, the prime variance × target variance interaction was highly significant [F_{(1, 92)} = 40.8, P < 0.001]. It was also significant independently for judgments about color [F_{(1, 52)} = 33.9, P < 0.001] and shape [F_{(1, 39)} = 9.21, P < 0.004] in roughly equal measure. Of note, the difference in RT between low/low and high/low conditions [t₍₉₂₎ = 5.96, P < 0.001] and high/high and low/high conditions [t₍₉₂₎ = 3.02, P < 0.004] were both independently significant. This latter finding rules out a ceiling effect on a response compatibility effect as an explanation for our findings.

Discussion

Priming is one of the most basic and well-established phenomena in the psychological literature, and has classically been used to probe the nature of the representations underlying perception and cognition (27). Most demonstrations of priming occur when judgment of a target stimulus is facilitated by the prior presentation of an irrelevant prime with which it shares perceptual, semantic, or conceptual features (30, 31). Here, we describe an instance in which a facilitatory relationship between prime and target is observed even though they share no overlapping features. Rather, we observed that judgments about a target visual array were facilitated when the feature variance of a target visual array matched that of a preceding prime array, irrespective of whether the mean feature information overlapped or not. This observation provides evidence for a new sort of priming that does not relate to the perceptual or the semantic features of the stimulus, but rather to its statistics: priming by the variance of visual information. Importantly, this variance priming effect could not be explained uniquely by priming at the level of individual elements. We demonstrate this with two classes of analysis. First, the effect remained robust even after accounting for any residual variability associated with the divergence between each individual element of the prime and target arrays. Second, the effect was significant even for switch trials (i.e., those for which the prime and target were drawn from different categories). These statistical representations might be useful for the rapid extraction of summary information (or “gist”) from a visual scene.

A number of strands of evidence in our data suggest that variance priming is a fast and automatic process. First, variance priming occurred even for PTIs of as short as 100 ms (i.e., with a latency that could contribute to very rapid categorization of information in a visual scene) (6). Second, variance priming occurred for both task-relevant and task-irrelevant array dimensions; it did not depend on the feature that was currently being attended. Interestingly, however, we observed no priming across the task-relevant and task-irrelevant dimensions. One interpretation of this finding is that this priming occurs within tightly constrained channels that process only a single visual dimension, such as shape or color. In other words, representations of variability are tied to specific features and do not simply encode the general level of order or disorder in a visual scene; this also points to variance priming being an early, automatic process.

Another interesting feature of the effect is that it occurred even when prime and target occupied different spatial locations, as inner and outer concentric rings around fixation. Interestingly, this effect was only observed when the prime array encompassed the target array spatially, and not vice versa. One possibility is that the spatial extent of the prime sets the range over which summary statistical extraction might occur. However, the four-way interaction between prime variance, target variance, prime size, and array size failed to achieve significance, so this effect merits further investigation.

Variance priming is somewhat reminiscent of the phenomenon of conflict adaptation, whereby responses made in the face of conflicting information are facilitated if information on the previous trial was also incompatible (28, 29). Conflict adaptation, like the variance priming effect we report here, will transfer across specific features within a task, for example when a response to the word “green” presented in red ink facilitates subsequent responding to “yellow” in blue ink (32). However, the findings reported here cannot merely be explained by conflict adaptation. In Exp. 2, we deliberately varied the degree of response conflict engendered by prime and target, by varying the proximity of array mean to the category boundary, but no compatibility effects were observed for response conflict, presumably because the prime was task-irrelevant. In other words, the locus of variance adaptation appeared to be much earlier than that for conflict adaptation, a view that is supported by the current finding that prime–target compatibility, even between the variance of task-irrelevant features, had an impact of decision latencies.

Conversely, however, it is possible that conflict adaptation may be partly accounted for by variance adaptation. Conflict adaptation partly reflects the biasing of resources to a given task, as evidence by neural amplification of task-relevant sensory regions in response to previous trial conflict (33) and the failure of conflict adaptation to transfer between tasks on switch trials (34, 35). However, there is evidence that it is influenced by more automatic mechanisms. First, conflict adaptation is strongest at short interstimulus intervals (∼500 ms) and declines thereafter (36). Here, variance adaptation was observed to occur very rapidly, with maximal effects at prime–target intervals of < 200 ms, and some loss of statistical power by 500 ms. Second, simply cueing participants that a trial will be congruent has an additional facilitatory effect (37). In other words, it is possible that some of the sequential congruency advantage on paradigms, such as the Stroop task, may reflect adaptation to the dispersion in visual features between successive trials. However, the relationship between variance priming and conflict adaptation could be better assessed by comparing sequential judgments of arrays with differing variance in a task with no intervening prime.

Another possible account for our findings is that the interaction between prime and target variance occurs because any facilitatory effects of prime–target response compatibility are dampened when the prime array is highly variable. We conducted three analyses that argue strongly against this view. First, when we included regressors for response compatibility and its interaction with variance in our regression analysis, the variance priming effect persisted. Second, we note that the effect was present for the irrelevant dimension, for which no responses were assigned. Third, we show that not only are low/low variance trials faster than low/high variance trials, but high/high variance trials are faster than high/low variance trials. In other words, the interaction crosses over and our effects cannot be explained by a ceiling on compatibility.

One likely function for adaptation to variance is that it helps rapidly adjust the gain range of visual processing to suit the current environment. Gain control is a major computational challenge for the visual system, as the number of possible objects and features that could be observed at any one time is virtually limitless, and efficiency will be maximized if the visual system is most sensitive to those that are likely to occur. Indeed, neural responses adapt to the variability of low-level sensory input across time, both in the visual (38) and auditory (39) domains. Similarly, extracting the gist of a scene—coarse information about the statistics of the information—could help calibrate visual processing so that likely features are processed with maximal gain (40). Representations of feature variability may also contribute to texture perception or contribute to the detection of objects in camouflage (26) or visual search (41). One outstanding question is whether adaptation to variability in our experiment is driven by an adaptation to the range of information available. Unfortunately these two quantities were too highly correlated to be disentangled in our paradigm.

An obvious further question pertains to the neural structures that are sensitive to variance adaptation. Two likely candidates present themselves. First, variance adaptation may depend on high-level representations in the ventral stream that have extracted abstract, correlated structure throughout visual development, and come to represent the variance in a fashion untied to the specific input (42). Second, variance adaptation may depend on dorsal stream structures that are conjectured to support gist-based retrieval (43) and are involved in controlling covert attention and saccadic exploration of a scene (44). We hope that future research will arbitrate among these possibilities.

Methods

Participants.

A total of 94 right-handed volunteers (reporting normal or corrected-normal vision and no history of neurological problems) participated in the three experiments (Exp. 1, n = 40; Exp. 2, n = 40; Exp. 3, n = 14). One participant was excluded from Exp. 2 because of data loss in one condition. The subjects provided informed consent and received £10/h. The study was approved by the Oxford University Medical Sciences Division Ethics Committee (approval no. MSD/IDREC/C1/2009/1).

Stimuli.

Stimuli were created and displayed using PsychToolBox (www.psychtoolbox.org) for MATLAB (Mathworks). Stimuli were presented on an equiluminant gray background, of a 17-inch LCD monitor with a resolution of 1,280 × 1,024 pixels, viewed from a distance of ∼80 cm. Every stimulus was an array of eight elements. On each trial, participants viewed two sequentially presented arrays of eight elements (colored shapes). In Exps. 1 and 2, elements were arranged in a circular formation with a radius of ∼3° visual angle around a central fixation point (Fig. 1A). In Exp. 3, an additional ring with a radius of ∼5° visual angle was used. Within each array, elements were equally spaced, equiluminant, and covered an equal area on the screen. Individual elements were defined by a shape parameter (S) a color parameter (C) taking values between −1 (most blue/round) and +1 (most red/square) (for full details, see Supporting Information). For each array, the eight values of the S (or C) parameter were drawn from a normal distribution, the mean μ and variance σ² of which were controlled by design. Feature values were resampled until sample statistics fell within 0.1% of μ and σ².

Task.

For Exps. 1 and 2, which dimension was task-relevant (color or shape) was counterbalanced across subjects. For Exp. 3, participants judged only color, which had given slightly more robust effects in the previous experiments. Only one dimension (shape or color) was the decision-relevant dimension within a single session, and participants were instructed to ignore the other dimension.

Thresholding.

To equalize difficulty across participants and task type (shape or color), we used an adaptive procedure in which participants made judgments about a target array preceded by a prime array, as in the main task. Each thresholding run was 144 trials long. For Exp. 1, the task-relevant mean μ was titrated until performance reached 80% correct on each dimension (shape and color). For Exp. 2, performance was titrated to 75% (μ₁) and 85% (μ₂) for the relevant dimension (either color or shape). For all experiments, the task-relevant variance σ² could take one of two values (0.15, 0.3); in Exp. 1, the task-irrelevant variance could also take on these values; in Exps. 2 and 3, σ² was fixed at 0.15.

Design.

For Exp. 1, we manipulated five orthogonal factors: the variance of the prime and the target on the task-relevant and task-irrelevant dimensions, and the congruity of the prime category and the target category on the task-relevant dimension. For Exp. 2, we varied orthogonally five factors: the absolute level of mean (μ₁ and μ₂) of the prime and target arrays for each category, and the task-relevant variance of prime and target arrays, but fixed the task-irrelevant variance and the prime–target congruency with respect to the task-relevant mean.

For Exp. 3, we once again fixed the mean to just μ or −μ, but we crossed prime and target array variance with a new factor that encoded the location of the circular prime and target arrays (inner vs. outer ring). The design was thus: target array task-relevant variance (high, low) × prime array task-relevant variance (high, low) × target array location (inner, outer) × prime array location (inner, outer).

Task and Procedure.

On each trial, a white fixation point (5-pixel radius) appeared in the center of the screen, followed after 500 ms by the prime array. The prime duration was 100 ms. The target array appeared after a variable PTI (100, 200, or 500 ms). Participants had up to 1.5 s to respond to the target using the computer mouse. The target array remained on screen until the response. Response mapping were fully counterbalanced across participants. After a response was made, auditory feedback was given immediately. A high tone (1,200 Hz) indicated a correct response whereas a low tone (400 Hz) indicated an incorrect response. Twenty practice trials were given before continuing to the main experiment, which consisted of 768 trials (512 trials for Exp. 3), with short breaks approximately every 80 trials.

Analysis.

We log-transformed reaction times for correct trials and analyzed the relative influence of the different factors using ANOVAs and multiple regression. An α of P < 0.05 was used for all statistical reporting.