Epitaxial superlattices with titanium nitride as a plasmonic component for optical hyperbolic metamaterials

Significance

Plasmonic and metamaterial devices require high-performance material building blocks, both plasmonic and dielectric, to be useful in any real-world application. Here, we develop both plasmonic and dielectric materials that can be grown epitaxially into ultrathin and ultrasmooth layers with sharp interfaces. We show that a superlattice consisting of titanium nitride as a plasmonic component behaves as an optical hyperbolic metamaterial and exhibits extremely high photonic density of states.

Abstract

Titanium nitride (TiN) is a plasmonic material having optical properties resembling gold. Unlike gold, however, TiN is complementary metal oxide semiconductor-compatible, mechanically strong, and thermally stable at higher temperatures. Additionally, TiN exhibits low-index surfaces with surface energies that are lower than those of the noble metals which facilitates the growth of smooth, ultrathin crystalline films. Such films are crucial in constructing low-loss, high-performance plasmonic and metamaterial devices including hyperbolic metamaterials (HMMs). HMMs have been shown to exhibit exotic optical properties, including extremely high broadband photonic densities of states (PDOS), which are useful in quantum plasmonic applications. However, the extent to which the exotic properties of HMMs can be realized has been seriously limited by fabrication constraints and material properties. Here, we address these issues by realizing an epitaxial superlattice as an HMM. The superlattice consists of ultrasmooth layers as thin as 5 nm and exhibits sharp interfaces which are essential for high-quality HMM devices. Our study reveals that such a TiN-based superlattice HMM provides a higher PDOS enhancement than gold- or silver-based HMMs.

Metamaterials are artificially created materials with subwavelength building blocks and unconventional electromagnetic properties that enable devices with unique functionalities (1, 2). For example, highly anisotropic metamaterials that consist of deeply subwavelength dielectric–metallic multilayers can effectively act as a material that is metallic in one or two directions and dielectric in the other (3, 4). In such metamaterials, light encounters extreme anisotropy, resulting in a hyperbolic dispersion relation (therefore these materials are referred to as “hyperbolic metamaterials,” HMMs), which causes dramatic changes in the light's behavior (5–7). HMMs enable many exotic devices for subwavelength-resolution imaging (5, 8–10), ultracompact resonators (11), highly sensitive sensors (12), and could lead to breakthrough quantum technologies (7, 13). The recent discovery of the enhancement of the photonic density of states (PDOS) within a broad bandwidth in HMMs could revolutionize PDOS engineering (14–17), enabling light sources with dramatically increased photon extraction and ultimately leading to nonresonant single-photon sources (6). These HMMs can be combined with wide-spectrum, room-temperature quantum emitters [such as quantum dots and nitrogen-vacancy color centers in diamonds (18)] to provide greatly enhanced spontaneous emission rates (19). Additionally, HMMs can transform an isotropic spontaneous emission profile into a directional one, leading to new types of light sources (20). Rather than obeying Planck’s law, an extreme PDOS enhancement enables near-field thermal radiation arising from the HMM to be significantly enhanced compared with the near-field thermal radiation from a dielectric (21). Moreover, the thermal conductivity of such metamaterials can exceed the dependence predicted by Stefan–Boltzmann law, opening up the possibility of addressing the critical need in the field of integrated circuits to find efficient cooling schemes to overcome the current problem of excessive heating (22).

The realization of good optical HMM devices is hindered by the fact that metals (used as HMM subwavelength building blocks) with their large negative permittivity and high losses in the optical frequency range are detrimental to HMM performance. It is also difficult to pattern noble metals into the ultrathin films or high-aspect ratio nanowires necessary for building HMMs (23, 24). There are two methods of realizing HMMs: embedding metal nanowires in a dielectric host (25–27), and stacking alternating planar layers of metal and dielectric (5, 8). Between the two approaches to build HMMs, planar HMMs are important from a technological point of view, as they can be easily integrated into existing processing lines that use planar fabrication technology. For multilayered HMMs, to achieve a significant enhancement of the PDOS, the individual HMM layers need to be as thin as possible [PDOS in an HMM is inversely related to the cube of the layer thickness (13, 28)]. Noble metal films (such as gold or silver) currently used to create HMM structures possess very high surface energies and high mobilities of atoms on the surface and hence cannot be patterned into ultrathin layers without compromising their quality, resulting in additional losses (29). Thus, the realization of metal-based HMMs with deep subwavelength layers and good optical performance is extremely challenging. Moreover, neither gold nor silver offers thermal stability and silicon CMOS compatibility required for the technology-driven applications mentioned above (24).

Alternative Materials

As an alternative to gold and silver, titanium nitride (TiN) [which has recently been suggested as a good alternative to replace noble metals in optical metamaterials applications (23, 30)] has optical properties similar to those of gold (31, 32), but is CMOS-compatible, has extreme thermal stability (melting point >2,700 °C), and can be grown epitaxially as an ultrathin crystalline layer of high quality on various substrates (such as sapphire, MgO, and silicon) (30, 33, 34). Moreover, unlike gold, titanium nitride can be nonstoichiometric such that its optical properties can be adjusted–tailored within a certain range (30). This material is of significant interest for biological applications because TiN is a biocompatible, mechanically tough, chemically and thermally stable ceramic that exhibits localized surface plasmon resonance in the biological transparency window (700–1,000 nm) (35). Also, TiN may be useful in plasmonic heating applications (36) because TiN nanoparticles have a large absorption cross-section at the surface plasmon resonance and TiN has an extremely high melting point. It has been suggested that the thermal stability of TiN makes it a better plasmonic material for thermal radiation engineering and thermophotovoltaic applications (37).

It is not enough to only have a good plasmonic material for building optical metamaterials with high performance suitable for realization of practical devices. It is crucial to have a good dielectric material as well; a dielectric that can be integrated with the plasmonic material component without compromising the material–structural quality or optical properties. For example, single-crystal epitaxial film of TiN requires a dielectric that can also grow epitaxially on TiN. Clearly, the possibility of growing both metal and dielectric material components as a whole epitaxial system is indispensable for realizing high-performance metamaterials. Despite the obvious need, the knowledge of material classes that could be used to grow such binary superlattice metamaterials is largely missing. One of the stumbling blocks is the fact that common dielectrics (such as silica, alumina, and other oxides) cannot be used in combination with metallic components (transition metal nitrides) because the deposition processes are not compatible with each other. In addition, both the plasmonic and dielectric components should be materials with relatively low surface energies to promote layer-by-layer growth with ultrasmooth surfaces. Above all, the requirement that both the materials should possess the same or compatible crystal structures with tolerable lattice mismatch presents as a real challenge in the material selection. In general, a lattice mismatch of less than 5% is necessary for growing epitaxial quality films. Meeting all of these requirements simultaneously requires meticulous efforts in engineering the material building blocks. In this work, we engineer a dielectric material that can grow epitaxial on TiN, form sharp interfaces, produce ultrasmooth surfaces, and possess desired optical properties. This work extends the realm of possible applications of TiN in plasmonics and metamaterials and, demonstrates HMMs using TiN as a plasmonic material operating in the visible frequency range.

Results and Discussion

In our experiments, we developed an approach to grow alternating layers of TiN and a low-loss dielectric epitaxially. To build an epitaxial metal–dielectric superlattice consisting of TiN as a plasmonic material, the dielectric material needs to have the same crystal structure (rocksalt) and lattice constant (4.24 Ǻ) as TiN. In addition, the dielectric material should belong to the nitride family of ceramics with low surface energy. AlN is a low-loss dielectric in the visible spectral range that can be engineered to grow epitaxially on TiN. AlN naturally occurs in wurtzite phase and may be stabilized in cubic phase (matching TiN lattice) if a thin AlN layer is sandwiched between TiN layers (38). However, the critical thickness for stabilizing the cubic phase of AlN on TiN–AlN superlattices is less than 2.5 nm (38), which is not suitable for practical applications. Although AlN in its stable form has a hexagonal lattice structure, it also has a high-pressure cubic phase with a lattice constant of 4.08 Ǻ (39). Without the restrictions on thickness or pressure, AlN may be stabilized in cubic phase matching lattice with TiN by alloying it with ScN. Here, we show stabilization of the cubic phase of Al_xSc_1-xN by alloying AlN with scandium nitride (ScN), and deposit cubic TiN–(Al,Sc)N superlattices. Al_xSc_1-xN alloy allowed stable cubic phase for small Sc concentration (x $\le$ 0.88) and yielded high critical thicknesses (in excess of 1 μm) to maintain its cubic structure (Fig. S1). An aluminum concentration of 72% in Al_xSc_1-xN (estimated with Rutherford backscattering spectrometry) was found to be suitable for lattice matching with TiN.

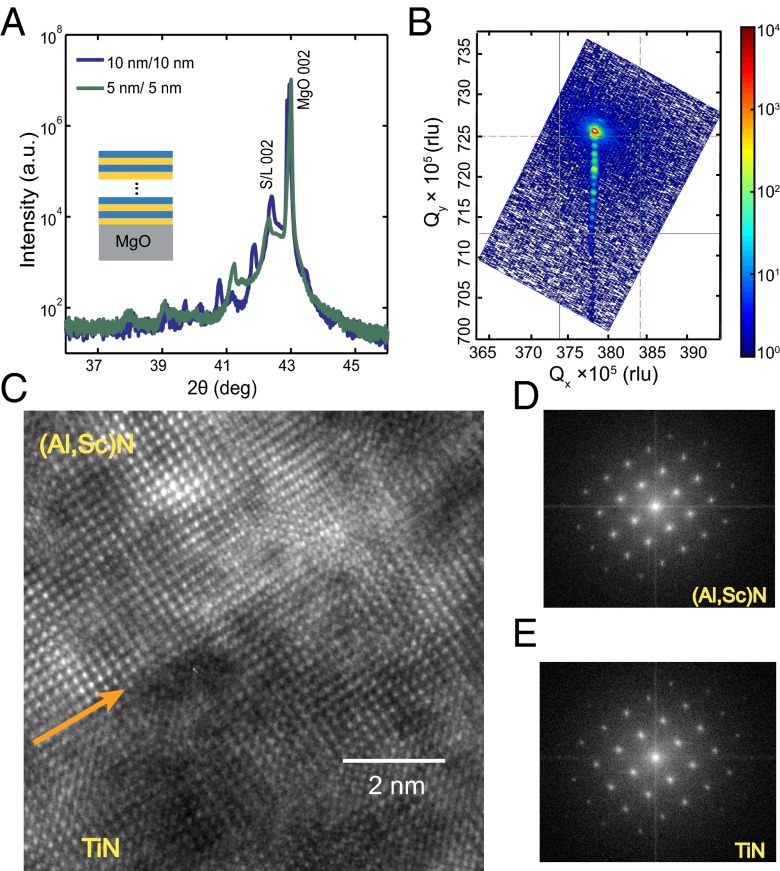
Superlattices consisting of TiN and Al_0.72Sc_0.28N alternating layers of equal thickness were grown on [001] MgO substrates. The X-ray diffraction analysis (symmetric 2θ–ω spectra in Fig. 1A and the reciprocal space X-ray map in Fig. 1B) along with the high-resolution transmission electron microscopic (HRTEM) images (Fig. 1C) suggest that the superlattices grow with a (001) orientation on the [001] MgO substrates having a cube-on-cube epitaxial relationship with (Al,Sc)N(001)[100]||TiN(001)[100] and TiN(001)[100]||MgO(001)[100]. The principal 002 diffraction peak is located at 2θ = 42.4°, suggesting an out-of-plane lattice constant of 4.25 Ǻ. Strong satellite fringes due to the X-ray interference at metal–dielectric interfaces are clearly visible (in Fig. 1 A and B), indicating that the interfaces are sharp and abrupt. This conclusion was further confirmed by the TEM images. The full width at half maximum of the rocking curve (ω-scan) has a very small value of 0.065°, suggesting a small degree of mosaicity. The vertical alignment of the main 024 peak of the superlattice, the substrate (MgO), and the satellite fringes in the reciprocal space X-ray map indicate that the superlattices are pesudomorphic, i.e., the in-plane lattice constant of the constituent TiN and (Al,Sc)N layers are identical to that of MgO (4.21 Ǻ). In the out-of-plane direction the TiN layers have a lattice constant of 4.23Ǻ, which is very close to its bulk value of 4.24 Ǻ, whereas the (Al,Sc)N layers have an out-of-plane lattice constant of 4.26 Ǻ.

Fig. 1.

Characterization of the microstructure of the superlattice. (A) X-ray diffraction plot for two binary superlattices of TiN and (Al,Sc)N with 5- and 10-nm-thick constituent layers. The peaks corresponding to the substrate and superlattice (S/L) are marked. The smaller peaks to the left of S/L 002 are the satellite peaks arising from superlattice reflections. (B) Reciprocal space map of TiN–(Al,Sc)N superlattice grown on [001] MgO substrate. (C) HRTEM image showing the interface of TiN and (Al,Sc)N in the superlattice; (D and E) Fast Fourier transforms corresponding to the diffractograms on the either sides of the interface imaged in C.

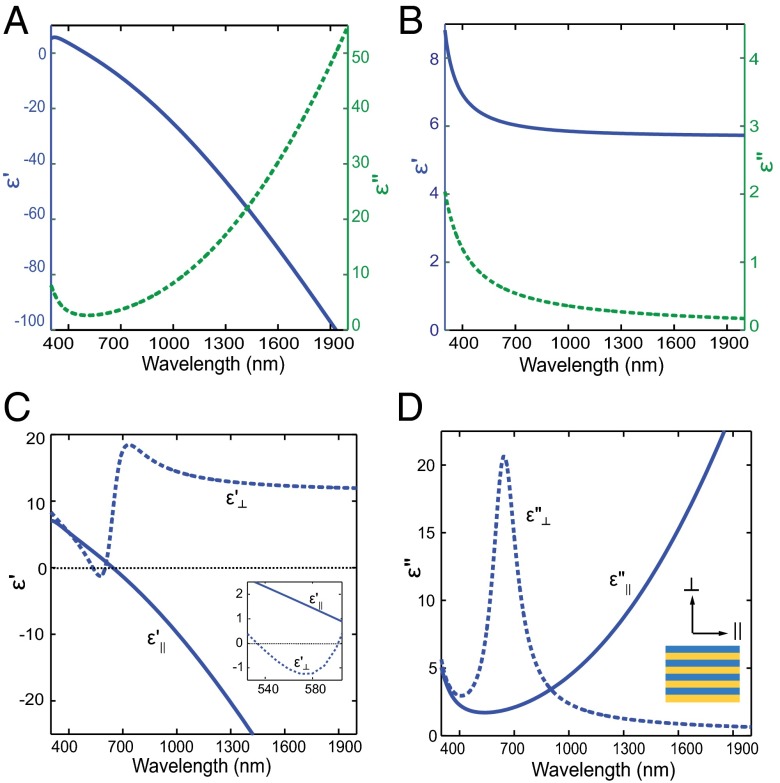
The optical properties of the superlattice consisting of 5-nm-thick layers of TiN and (Al,Sc)N, characterized using a spectroscopic ellipsometer, are shown in Fig. 2. Fig. 2 A and B shows the dielectric constants of TiN and (Al,Sc)N that constitute the superlattice retrieved from our ellipsometry measurements. TiN is metallic (real part of the dielectric permittivity ε′ < 0) for wavelengths longer than 510 nm and (Al,Sc)N is dielectric throughout the visible and near-infrared ranges. Besides a change in the crystal structure to a rocksalt configuration, the addition of Sc to AlN reduces its bandgap, which may be noticed by the spectral location of the absorption edge (around 450-nm wavelength). Because the superlattice is composed of layers much smaller than the wavelength of light, it can be approximated by a uniaxial anisotropic effective medium (40). The dielectric functions in the direction normal to the plane of the layers (${\epsilon }_{\perp }$) and parallel to plane of the layers (${\epsilon }_{\parallel }$) are as shown in Fig. 2 C and D. The real parts of the dielectric functions (Fig. 2C) exhibit opposite signs in the wavelength ranges from 540 to 600 nm and for λ > 650 nm, which produces a hyperbolic dispersion. In the 540–600-nm range, the dispersion is transverse-positive (41) or type 1 (${\epsilon }_{\perp }^{\prime }$ < 0, ${\epsilon }_{\parallel }^{\prime }$ > 0), which is useful in building devices such as a hyperlens (5). For wavelengths longer than 650 nm, the dispersion is transverse-negative or type 2 (${\epsilon }_{\perp }^{\prime }$ > 0, ${\epsilon }_{\parallel }^{\prime }$ < 0), which is useful for applications where PDOS enhancement is desirable (6). The losses in this HMM were low enough to measure more than 15% transmittance from a 160-nm-thick superlattice at approximately a 600-nm wavelength (Fig. S2). In this context of losses, note that epitaxial quality films are important for achieving low-loss operation. As expected, polycrystalline films of both TiN and (Al,Sc)N showed higher optical losses (Fig. S3). More information on the optical properties of polycrystalline films may be found in SI Text, section 3. Note that a 160-nm-thick HMM built from similar alternating layers of noble metals (if one could make them continuous at such a small thickness) and any dielectric would have less than 1% transmittance (42) in the same spectral range.

Fig. 2.

Dielectric functions (measured using spectroscopic ellipsometry) of (A) TiN and (B) (Al,Sc)N that constitute the fabricated superlattices (48 layers of 5 nm each) together with (C) the real and (D) imaginary parts of the dielectric functions of the effective medium that approximates the superlattice. The effective medium approximation uses uniaxial medium with different permittivities in the directions parallel ($\parallel$) and perpendicular ($\perp$) to layers of the superlattice. The inset in C zooms into the wavelength range 525–600 nm.

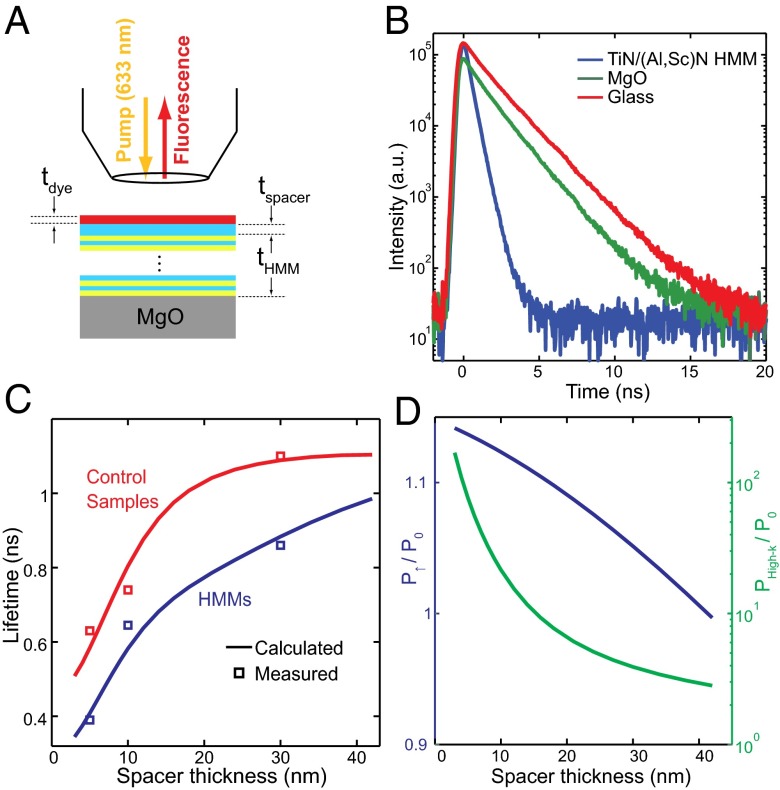
The small losses and ultrathin layers are expected to significantly increase the enhancement of PDOS in the HMM (13). To verify this prediction, we placed an emitter (LD-800 dye molecule) close to the surface of the HMM [separated by a spacer layer made of (Al,Sc)N] and measure its lifetime (42) (Fig. 3A). The wavelength of peak emission of the dye was measured to be about 720 nm. For the lifetime measurements, in addition to the superlattice HMM samples, control samples were also prepared which had a thin layer of metal (of the same thickness as in the superlattice) and a layer of spacer (of the same thickness as in the superlattice sample) on top.

Fig. 3.

Experiments to probe the photonic density of states of an HMM. (A) The schematic showing the sample geometry and the experiment configuration. (B) Measured spontaneous emission vs. time profiles from dye molecules placed on top of TiN–(Al,Sc)N superlattice with individual layers 10 nm thick, bare MgO and bare glass substrates. (C) Lifetimes of dye molecules on TiN–(Al,Sc)N HMMs or 10-nm TiN film (control) as a function of the distance from the top metal surface of the sample. The HMMs are composed of 24 layers, each being 10 nm thick. The dye layer is separated from HMM–control sample surface by (Al,Sc)N spacer layer. The calculated emitter lifetimes (solid line) for different spacer layer thickness were fit to the measured values (squares). (D) Calculated normalized power (SI Text) radiated from the emitter into low-k modes that propagate in the upper-half-plane (left axis) and high-k modes that propagate only in the HMM (right axis). Note significant (about two orders of magnitude) increase of the power radiated into high-k modes with the decreasing spacer thickness.

Fig. 3B shows the lifetime measurements on TiN–(Al,Sc)N HMM with 10-nm-thick individual layers, consisting of 12 pairs of layers plus an additional spacer layer on top. The spacer layer was made of the same dielectric, (Al,Sc)N, used in the HMM. The lifetimes were extracted by fitting single exponent to the intensity vs. time curves obtained from time-correlated single-photon counting (TCSPC). Single exponent was sufficient to fit the TCSPC data and the lifetimes of the emitters were quite uniform throughout the sample, resulting in a SD of the measured lifetimes smaller than 0.012 ns (Fig. S4). Three such HMMs with three different spacer layer thicknesses were fabricated. An approximately 11-nm-thick layer containing dispersed dye molecules was spin-coated on top of the HMMs. The results of the lifetime measurements are shown in Fig. 3C. The HMM with the thinnest spacer layer of 5 nm shows the smallest lifetime whereas the HMMs with the thicker spacer layers (10 and 30 nm) show much larger lifetimes. This is because the emitter, which is closer to the surface of HMM, couples light more effectively into the HMM from a very broad range of wavevectors (k) that includes not only those wavevectors supported by vacuum, but also those with significantly higher wavevectors (high-k modes). Hence, more radiation channels are available for the emitter to radiate into the HMM propagating high-k modes, which reduces the lifetime. This trend was discussed by Jacob et al. (13), where they predicted a cubed dependence of the emitter lifetime as a function of the distance of the emitter from the HMM surface. A nearly lossless HMM and an ideal emitter (quantum yield of 100%) would show such a dependence.

However, in practice, HMMs have significant losses and the emitter is nonideal (42). To predict the lifetime of the dye molecules placed on the top of HMM with different spacer thicknesses, we use local density of states calculations (SI Text) (28, 43). If the radiation from the dipole μ(r₀) is scattered by the HMM, and if the scattered field strength is E_s(r), then the power (P) radiated by the dipole may be calculated from Eq. 1 (43). If the dipole emitter has less than a 100% intrinsic quantum yield (Q), the spontaneous emission rate (Γ) of the emitter may be calculated using Eq. 2 (43). P₀ and Γ₀ are the power and emission rates of the emitter in vacuum, respectively.

$$\frac{P}{P_0}=1+\frac{6\pi {\epsilon }_0}{{\left|\mathit{\mu }\right|}^2}\frac{1}{k^3}Im\{{\mathit{\mu }}^{\ast }.{\mathit{E}}_{\mathit{s}}\left({\mathit{r}}_0\right)\},$$ [1]

$$\frac{\Gamma }{{\Gamma }_0}=\left(1-Q\right)+Q\frac{P}{P_0}.$$ [2]

Our calculations were fit to the experimental observations using quantum yield as a fitting parameter. The quantum yield used for fitting was 7.8%, which is reasonable for LD-800 dye dispersed in SU-8 solution (42). The good agreement between calculated and measured lifetimes confirms the enhancement of PDOS provided by TiN–(Al,Sc)N HMMs. To assess the role of surface plasmon-polaritons (SPPs) in enhancing the PDOS (44), we prepared control samples consisting of 10-nm TiN films on MgO substrates with a top (Al,Sc)N spacer layer. The spacer layer was 5-, 10-, and 30-nm thick in three different samples. The dye layer was spin-coated on top of these control samples by exactly the same protocol as used on the HMMs. The results of lifetime measurements on these control samples are also shown in Fig. 3C. The control samples provide enhancement in the emission rate by nearly two times (in comparison with emission rate on bare glass) due to excitation of SPPs at the top and bottom interfaces of the TiN film (42). However, the emission rate enhancements observed in the control samples are smaller than those provided by HMMs by approximately two times. Note that lifetime reduction by 2 times implies nearly 20 times higher PDOS because the quantum yield of the emitter is nearly 10%. Thus, the PDOS in HMMs is enhanced significantly compared with the control samples.

The high-k channels into which the dye molecule emits are confined only to the HMM because no other surrounding medium supports them (13). Hence, these photons do not reach the detector, causing a reduction in the apparent quantum yield (42). Table 1 shows the calculation of the normalized radiative decay rates (Γ_r) and quantum yield for HMMs (42) with different spacer thicknesses. The quantum yield of the dye has reduced drastically and the radiative decay rate (here “radiative” means the radiation that reaches the detector) is much smaller than that on glass. The reason for this can be understood better with the help of Fig. 3D. When the spacer thickness is small, the emitters emit most of their power into high-k modes in the HMM (note, for example, the 10-fold increase in the power emitted into high-k modes when the spacer thickness is reduced from 40 nm to below 20 nm; Fig. 3D). The power emitted into low-k modes that reaches the detector (upper-half space), denoted as P_↑, is a tiny fraction of the total power for spacer layer thicknesses less than 30 nm, leading to the small apparent quantum yield of the dye on HMMs with a thin spacer. As the spacer layer is thinned, the power radiated to the upper-half space (to detector) increases slightly (Fig. 3D). Hence, the radiative decay rate also increases slightly as the spacer layer thickness is decreased. The extremely small apparent quantum yield is a clear indication that the emitters are effectively probing the high PDOS of the HMMs.

Table 1.

Radiative decay rate calculated from measured absorption, fluorescence, and net lifetime for TiN–(Al,Sc)N HMMs consisting of 24 layers of 10 nm each with different spacer layer thickness

Spacer thickness, nm	Measured lifetime, ns	Apparent quantum yield, normalized to that on glass	$\frac{{\left({\Gamma }_{\text{r}}\right)}_{\mathrm{HMM}}}{{\left({\Gamma }_{\text{r}}\right)}_{\mathrm{glass}}}$
5	0.39	0.0540	0.2909
10	0.65	0.0774	0.2502
30	0.85	0.0616	0.1522

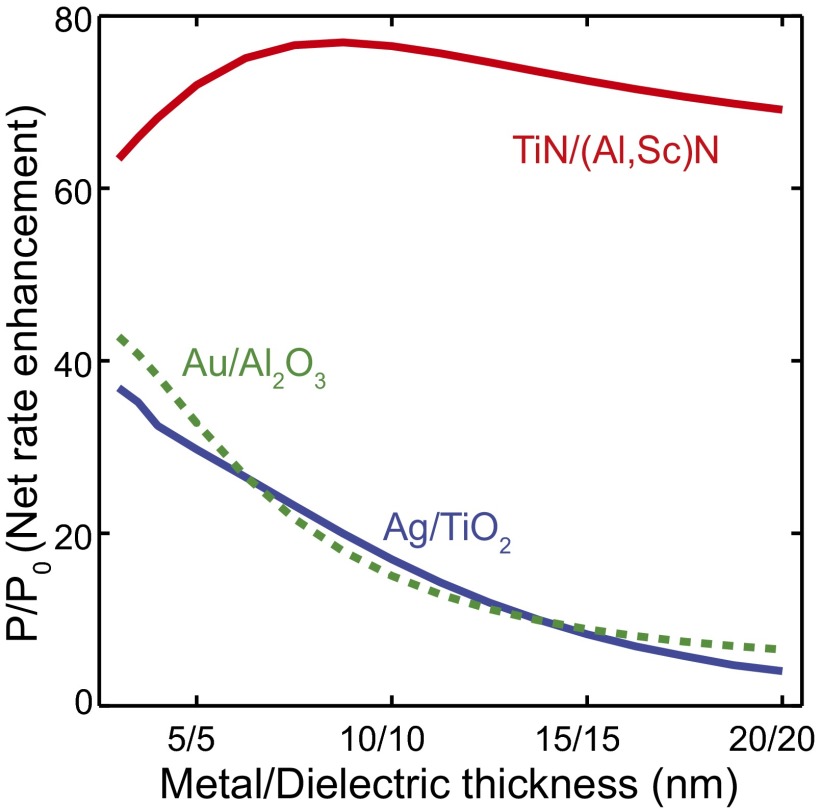
The PDOS of the superlattice HMMs is also predicted to be dependent on the thickness of the constituent layers (13, 28). The largest k vector of the photon that can propagate in the HMM depends inversely on the layer thickness. This increases the PDOS of the HMM because there are more high-k modes available for the emitter to radiate into. The limit to PDOS enhancement in HMMs is, in general, imposed by the individual layer thickness. However, when the layers are made extremely thin, the PDOS enhancement may be also limited by losses rather than the individual layer thickness (13). Fig. 4 shows the calculated normalized net power (into all possible propagating modes including high-k modes) radiated by emitters placed on the top of HMMs composed of metal–dielectric layers of different thicknesses. For ideal emitters, this quantity is identical to the net enhancement in the spontaneous decay rate. For TiN–(Al,Sc)N HMMs, reducing the individual layer thickness increases the emission rate until the thickness reaches ∼7 nm. For layers thinner than 7 nm, losses start dominating, limiting the enhancement factor even before other effects such as nonlocality (45) begin to limit the enhancement in the PDOS. This explanation correlates well with the measured lifetimes of dye molecules placed on TiN–(Al,Sc)N HMMs with 5- and 10-nm individual layers. The dye lifetime measured on TiN–(Al,Sc)N superlattice composed of 5-nm layers was 0.3985 ns, which is only slightly higher than that measured for the superlattice with 10-nm layers (0.390 ns).

Fig. 4.

Calculated net emission rate enhancement factor (Eq. 1) for an ideal emitter emitting at λ = 720 nm as a function of the superlattice periodicity. All calculations were performed assuming that the emitters are separated from the HMM surface by a 5-nm-thick spacer made from the dielectric that constitutes the superlattice. The enhancement factor is averaged to account for the spread of the emitters as in the layer of dye, over a distance of 11 nm. The orientation of the dipoles is assumed to be equally probable in all directions. The optical constants of Au and Ag are from Johnson and Christy (49).

Fig. 4 also provides insight into what plasmonic material would provide larger PDOS in the HMM. It turns out that the choice of the best materials to achieve the highest PDOS is not dictated by the lowest losses only. This is because the penetration depth of light into the HMM depends both on the real and the imaginary parts of the permittivity of the metal. A large negative permittivity would limit the penetration of light into the structure, even more severely for higher-k waves. This is the reason why HMMs composed of noble metals perform poorly. As a fair comparison, gold-based HMMs using the same dye emitters as our experiments and having similar quantum yield (42) showed lifetime reduction of less than 1.5 times, whereas TiN–(Al,Sc)N HMMs produce about 5.5 times reduction in the lifetime. A fair comparison with other reports is possible if quantum yields of the emitters used in the experiments are known. Without the knowledge of the quantum yield of the emitters used in the particular experiment, the observed lifetime reduction alone cannot provide any quantitative estimate of the PDOS enhancement. Thus, it is fair to conclude that the calculated PDOS enhancement effects as shown in Fig. 4 agree with experiments reported here and in ref. 42. This indicates that TiN as a plasmonic material is a better choice for building HMMs with high PDOS in the visible spectrum. The benefit of the low loss of noble metals can be observed only when the layers have been made so thin that enough light can penetrate into these HMMs. This means that the curves in Fig. 4 corresponding to noble metals would show a maximum in enhancement only for much thinner layers. Unfortunately this requires noble metal layers to be fabricated as thin as a couple of nanometers, which is a large fabrication challenge. Moreover, losses increase dramatically when noble metal layers are as thin as a few nanometers (29). Also, nonlocal effects become important and limit the PDOS enhancement for extremely thin layers (45). Thus, optical properties of TiN (specifically, smaller in the magnitude of the negative real part of the permittivity) as well as the possibility of epitaxially growing ultrasmooth and ultrathin layers, make this ceramic material a better alternative to obtain a higher PDOS in HMMs. This fabrication technique could be extended to CMOS platform given that TiN is a CMOS-compatible material, and it is possible to grow TiN epitaxially on (100) silicon using a thicker TiN buffer layer (34). Given the other advantages of TiN as a plasmonic material, our study opens up research opportunities not only in the field of HMMs, but also for many other plasmonic and metamaterials applications. For example, ultrathin metal films show strong quantum effects (46) and plasmonics at ultrasmall gaps (47, 48), which form the bases of the field of quantum plasmonics.

In conclusion, using titanium nitride in hyperbolic metamaterials instead of noble metals opens remarkable possibilities for this important class of optical metamaterials. This work paves the way toward the realization of practical HMM devices that have high-performance, CMOS- and biocompatibility, thermal stability, and tunable optical properties. Using TiN as a plasmonic material enables high-performance binary superlattice HMMs, consisting of ultrathin smooth epitaxial layers that can unlock the full range of exciting properties of hyperbolic metamaterials. High-performance, low-loss TiN-based metamaterials could also lead to a new generation of light sources and devices for quantum optical technologies. This demonstration provides guidance on how to choose the right materials and fabrication techniques. Also, it elucidates the importance of applying the principles of materials science and engineering in solving critical problems of optical metamaterials to advance plasmonics and metamaterials to next-generation technologies.

Methods

TiN–(Al,Sc)N superlattices were deposited on (001)-oriented MgO substrates using reactive dc magnetron sputtering in a load-locked turbomolecular pumped high-vacuum deposition system with a base pressure of (2–5) × 10⁻⁸ Torr (PVD Products, Inc.). The growth chamber had the capability to accommodate four targets and was equipped with three dc power supplies. Before the deposition the substrates were cleaned in acetone and methanol and dried in nitrogen gas. The Ti (99.99% purity), Al (99.99% purity), and Sc (99.99% purity) targets had dimensions of 2-in. diameter and 0.25-in. thickness. All depositions were performed with an Ar–N₂ mixture with the flow rates of Ar and N₂ being 4 and 6 standard cubic cm per min, respectively, and a deposition gas pressure of 10 mTorr. The targets were sputtered in constant power mode. Whereas the Ti target was fixed at 200 W, the Al and Sc target powers were varied to achieve the desired stoichiometry of (Al,Sc)N alloy layers, i.e., Al_0.7Sc_0.3N. The substrates were maintained at 750 °C during deposition, as determined using an infrared pyrometer operated in the wavelength range of 0.8–1.1 μm, together with a thermocouple.

The crystal orientation, texture, and epitaxial relationship of the superlattices were determined by high-resolution X-ray diffraction and HRTEM using Cu Kα1 radiation in a Panalytical X-ray diffractrometer and an FEI 80–300-KeV transmission electron microscope. The period thicknesses of the superlattices were determined from the separation of the satellite peaks in the 2$\theta -\omega$ diffraction pattern of the superlattice as well as X-ray reflectivity measurements. Cross-sectional TEM samples structures were prepared on an FEI Nova 200 NanoLab DualBeam SEM/Focused Ion Beam using standard lift-out technique equipped with a Klocke nanomanipulator.

The dye layer on top of MgO, glass, superlattice samples, and control samples was prepared by the following method: 100-μM concentration of LD-800 dye dispersed in 1:7 diluted SU8-200 polymer was sonicated for 5 min before spin-coating it on top of all samples to achieve about 11-nm-thick dye layer. The thickness of the dye layer was measured by spectroscopic ellipsometer (J.A. Woollam Co.).

Fluorescence lifetime imaging microscopy measurements were performed based on a customized confocal microscopy (Microtime 200, PicoQuant GmbH) with TCSPC in time-tagged time-resolved mode (Time Harp 200, PicoQuant GmbH, Berlin, Germany). A picosecond pulsed 633-nm laser line was used as an excitation source for LD-800 dyes via 50×/0.75 N.A. objective (Olympus Inc.). The fluorescence signal was collected using the same objective backwardly and filtered from the excitation light by a dichroic mirror (z467/638rpc, Chroma). The overall fluorescence signal was further spectrally and spatially filtered by a 50-μm pinhole to exclude the background noise and out-of-focus fluorescence, and finally recorded by single-photon avalanche photodiodes (SPCM-AQR-14, PerkinElmer) after passing the 685-70 (Chroma) band-pass filter (685-70 means that the filter is centered at 685 nm with a bandwidth of 70 nm). The average lifetimes of the dye molecules are calculated by fitting measured spontaneous decay curves with multiple exponential equations.