A seismologically consistent compositional model of Earth’s core

Significance

It is well known that Earth’s core is made primarily of iron, alloyed with ∼5% nickel and some lighter elements, such as carbon, oxygen, silicon, or sulfur. The amount as well as the chemistry of the light elements is poorly known and still a matter of considerable debate. In this paper we calculate the seismic signature of iron-rich light-element alloys and compare them to the seismic properties of Earth’s core. We find that oxygen is required as a major light element in the core, whereas silicon, sulfur, and carbon are not required. We also find that silicon concentration in the core cannot be higher than 4.5%, and sulfur concentration cannot be higher than 2.4%.

Abstract

Earth’s core is less dense than iron, and therefore it must contain “light elements,” such as S, Si, O, or C. We use ab initio molecular dynamics to calculate the density and bulk sound velocity in liquid metal alloys at the pressure and temperature conditions of Earth's outer core. We compare the velocity and density for any composition in the (Fe–Ni, C, O, Si, S) system to radial seismological models and find a range of compositional models that fit the seismological data. We find no oxygen-free composition that fits the seismological data, and therefore our results indicate that oxygen is always required in the outer core. An oxygen-rich core is a strong indication of high-pressure and high-temperature conditions of core differentiation in a deep magma ocean with an FeO concentration (oxygen fugacity) higher than that of the present-day mantle.

From the analysis of iron meteorites and the observation of Earth’s moment of inertia, we know that the primary constituent of Earth’s core is an iron alloy (1) with Fe/Ni∼16 (2, 3). Comparing seismic travel times in the core with experimental shockwave measurements, Birch (1) proposed that the core is lighter than pure iron. Shockwave and static diamond anvil cell (DAC) experiments have further constrained the core’s density deficit (with respect to pure iron) to be between 5 and 10% (4). This requires lower atomic weight elements to be present as additional constituents—so-called light elements. Moreover, the density jump at the inner core boundary (ICB) between the solid inner core and liquid outer core is ∼4.5% (5), too large to be due to just the solid–liquid phase transition, and indicates that the outer core contains more light elements (∼5–10%) than the inner core (∼2–3%). The prime light-element candidates for the core, taking into account cosmochemical and petrological constraints, are silicon, sulfur, carbon, oxygen, and hydrogen (6). Models for core composition allow in principio a mixture of several light elements, and many arguments have been put forward over the years for and against each of the elements (2, 7, 8).

Silicon, sulfur, and carbon are rather soluble in iron at all conditions and were originally quite sensibly proposed as the most valid candidates. They are compatible with low-pressure core formation models, either in a shallow magma ocean or in the differentiated accretionary material. The solubility of these elements in molten iron coexisting with silicate melt would be several percent (9), even at low pressures. On the other hand, oxygen solubility is much more limited at low pressures, and DAC experiments show that oxygen can be introduced in the core by reaction with the molten mantle at high pressures and temperatures (10, 11). Oxygen thus became a natural candidate with the introduction of the “deep magma ocean” models (12–15) of core formation. Additional support for oxygen in the core comes from the fact that oxygen is the only light element to be highly incompatible in solid iron; therefore most of the oxygen would be expelled from the growing inner core and remain in the outer core (7, 8), hence elegantly accounting for the problem of the large density contrast between the inner and outer core. Hydrogen is extremely volatile and is thought to have been brought to Earth during late accretion (16, 17), after the core had formed. In this case, it would be essentially nonexistent in the proto-Earth during core formation and not a likely candidate for the light element in the core.

The literature offers a wide range (3, 2, 7, 8, 10, 11, 18, 19) of plausible estimates for the light-element composition of the core (SI Appendix, section 1). To constrain these further, we need to assess whether the compositional model for the core matches the seismically observed density and sound velocity of the core. As the core is 95% molten, this analysis has not been possible due to the lack of density and velocity data on (Fe–Ni)–C–O–Si–S liquid alloys under core conditions. Measuring bulk sound velocities and densities in molten Fe alloys at core conditions lies currently beyond the capability of experimentation. An alternative is to use ab initio simulations to interpret seismic observations (20) in terms of outer core composition. We therefore calculated the density and bulk sound velocity of liquid alloys in the (Fe–Ni)–C–O–Si–S system using ab initio molecular dynamics. We then compared the properties of the molten alloys directly with the primary geophysical observations [e.g., density and bulk sound velocity obtained (21) from radial seismic models]. This allowed us to identify the subset of compositions that match the constraints and, finally, to propose a seismologically constrained compositional model of Earth’s core.

The simulations were performed on liquid iron binaries (Fe_1−xNi_x; Fe_1−xC_x; Fe_1−xO_x; Fe_1−xSi_x; Fe_1−xS_x) at two different concentrations (x = 8.3 and 16.7 mol%) at the pressure and temperature conditions of the core–mantle boundary (CMB) and the ICB (on the outer core side). Details about the simulations can be found in the SI Appendix, section 2.

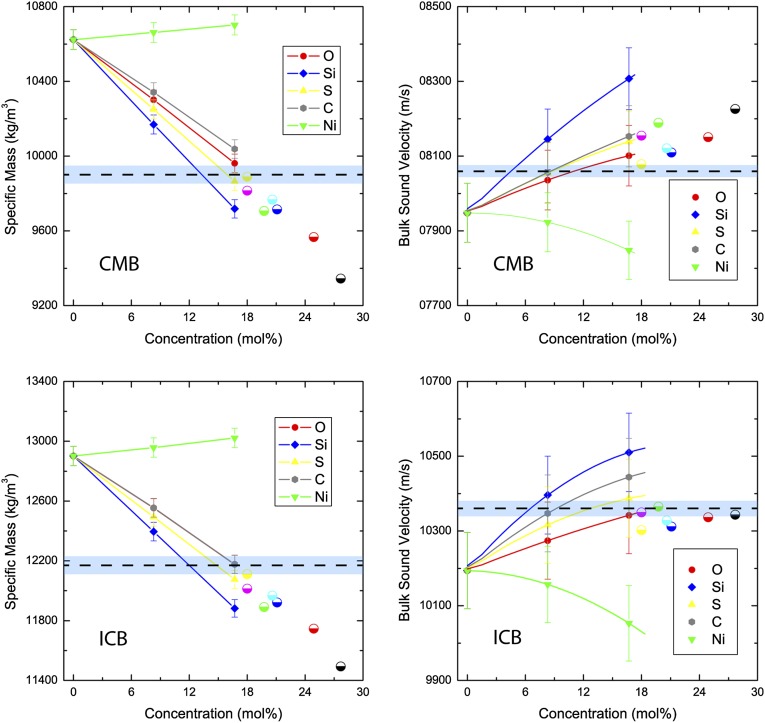
We calculated the densities with a statistical uncertainty (1σ) of 0.15% and bulk sound velocities with a statistical uncertainty (1σ) of 0.8%. These are reported in Fig. 1. We combined the binary data assuming ideal mixing to obtain the density and bulk sound speed for any composition in the (Fe–Ni)–C–O–Si–S system as $\rho ={\displaystyle \sum x_i{\rho }_i}$ and $V_{\mathrm{\Phi }}=\sqrt{\frac{K}{\rho }}$ where $\frac{1}{K}={\displaystyle \sum \frac{x_i}{K_i}}$. ρ is the density of the mixture, K its bulk modulus, V_Φ its bulk sound velocity, and x_i, ρ_i, and K_i, are the volume fraction, density, and bulk modulus of the Fe–X_i component, respectively. Ideal mixing has been the standard working hypothesis in this kind of study (6, 19, 22) and will need to be verified by future work. However, our study reinforces this hypothesis by showing that (i) the binary systems are perfectly ideal (as can be seen by the perfectly linear fits of density versus concentration) and (ii) our calculations were compared with existing shockwave data (19, 22–24) on molten Fe, Fe–O, and Fe–S alloys and found them to be in excellent agreement (SI Appendix, section 3). It should also be noted that high-pressure experiments have shown that miscibility gaps vanish at high pressures (25–28), hence also indicating that high-density liquids tend to have a simpler thermodynamic behavior than their low-pressure counterpart.

Fig. 1.

Density (Left) and bulk sound velocity (Right) of molten Fe-Ni, Fe-C, Fe-O, Fe-Si, and Fe-S alloys as a function of concentration at CMB (Upper) and ICB (Lower) conditions. The calculations are represented by full symbols, and the lines are fits to the data (density, linear; bulk sound velocity, quadratic). Note that the densities of C and O at the ICB overlap and are indistinguishable. The horizontal dashed line represents the seismological “target value,” and the shaded area represents its uncertainty. The half-filled circular points are the calculated density and bulk sound velocity for various core compositional models proposed in the literature—black (2), red (10), blue (11), green (8), purple, Si from ref. 7; light blue, S from ref. 7.

We calculated ρ_CMB, ρ_ICB, V_ϕ,CMB, and V_ϕ,ICB for various outer core compositional models in the literature, derived from both experimental and theoretical models (2, 7, 8, 10, 11). These are reported in Fig. 1, alongside the binary data. Except for the ab initio model of Alfè et al. (7), all of the models overestimate the concentration of light elements, yielding densities that are too low. The velocities for the various core compositions are generally higher than observed at the CMB, another indication that the light-element concentration was overestimated.

Assuming a chemically homogeneous outer core, we can constrain its composition by finding all possible combinations of light-element concentrations for which their densities and velocities match those of the Preliminary Reference Earth Model simultaneously at the CMB and ICB. The Fe/Ni ratio in chondrites shows very little variance, so we fix Fe/Ni at 16 (2, 3). The CMB temperature is fixed at T_CMB = 4,300 K so that the ICB temperature (calculated along the isentrope) is T_ICB = 6,300 K (SI Appendix, section 2), which is consistent with iron melting at the ICB (6, 29). The results for other temperature profiles are also tested. We generated over 100 million combinations of (x_O, x_Si, x_S, x_C), never exceeding a threshold of 25 mol% for any single light element, and calculated their densities and bulk sound velocities. We kept the compositions that satisfy the four seismological constraints (ρ_CMB, ρ_ICB, V_ϕ,CMB, V_ϕ,ICB) while propagating all uncertainties (0.15% on calculated densities, 0.5% on seismic densities, 0.8% on calculated velocities, and 0.2% on seismic velocities) in our multicomponent model to obtain a seismologically constrained core compositions.

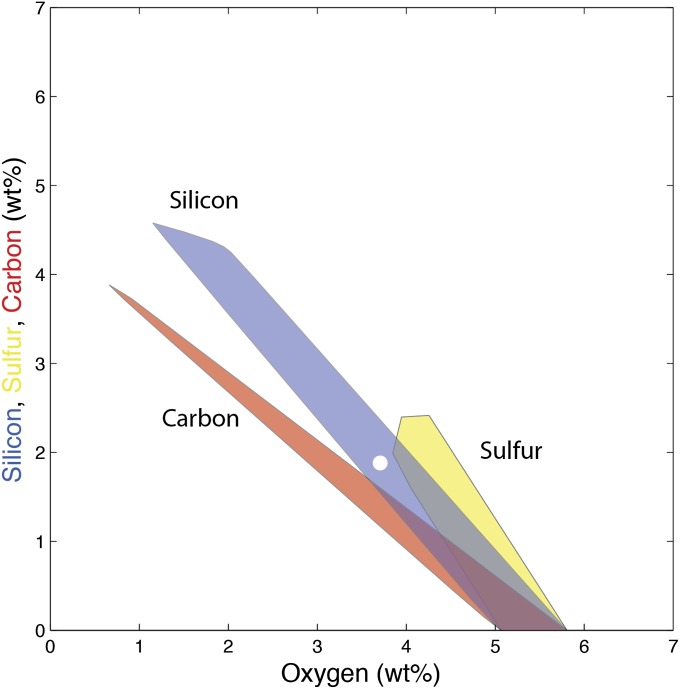
The first striking observation is that all of our solutions contain oxygen, and there are no solutions in an oxygen-free system. Second, there is a valid core composition with oxygen being the only light element (5.4 ± 0.4%) [all percentages are in weight (wt%) except where otherwise noted], alloyed with Fe–Ni. No other element is able to satisfy the constraints alone. Finally, the maximum concentrations permissible for silicon and sulfur concentrations are rather low, 4.5 and 2.4%, respectively. To visualize the complex solution space, we first plotted the ternary solution spaces: (Fe–Ni)–O–Si, (Fe–Ni)–O–C, and (Fe–Ni)–O–S in Fig. 2 [the other three ternaries, (Fe–Ni)–Si–S, (Fe–Ni)–Si–C, and (Fe–Ni)–S–C, have no solution]. From all those acceptable compositions, we have calculated the best numerical solution: it is a core that contains 3.7% O, 1.9% Si, and no sulfur or carbon (SI Appendix, Table S2), a composition indicated by a white circle in Fig. 2.

Fig. 2.

Range of core compositions compatible with seismic observations. Each shaded area represents the ternary solution space that satisfies the seismic density and bulk sound velocity at the top and bottom of the outer core (Fe₉₄Ni₆–O–Si, blue; Fe₉₄Ni₆–O–C, red; and Fe₉₄Ni₆–O–S, yellow). There is no solution for the other ternaries (Fe₉₄Ni₆–Si–S, Fe₉₄Ni₆–Si–C, and Fe₉₄Ni₆–S–C). This shows that oxygen is always required to match the seismic data. The best numerical fit is shown by the white circle corresponding to 3.7% O, 1.9% Si, 0% S, and 0% C.

We can further constrain our compositional model by using inner-core compositional models and experimental metal–silicate partitioning data. Recent studies have proposed that the inner core is a Fe–Ni–Si alloy containing between 1 and 2% silicon (8, 30). Because the inner core is growing from the outer core, and these are in chemical equilibrium, then the outer core should also contain silicon, between 1.2 and 3.6% [assuming a liquid/solid partition coefficient (7) of 1.5 ± 0.3 for silicon]. Moreover, core formation experiments place a tight constraint (12, 31–35) on oxygen solubility in molten iron: incorporating large amounts of oxygen in a core-forming metal in equilibrium with a molten silicate requires very high temperatures. In those conditions, silicon will always be incorporated in the metal as well (31, 34, 35).

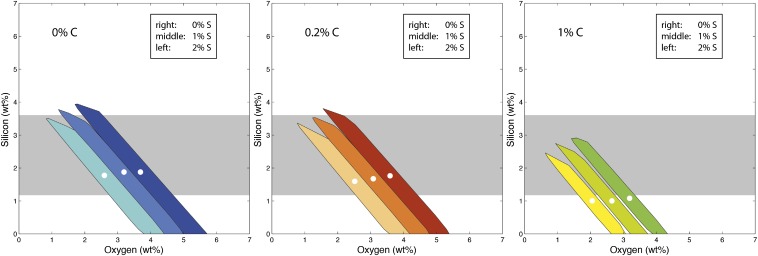
With oxygen being required from outer-core seismology and silicon being required from inner-core seismology as well as metal–silicate partitioning, our model leaves little room for other light elements such as sulfur and carbon. This is in agreement with recent results obtained by first principles’ simulations of metal–silicate equilibrium (36). These suggest that the main core components are Si and O, whereas volatile element contents such as C and H lie well below the 1% and 1,000 ppm threshold, respectively. We therefore focused our attention on the (Fe–Ni)–O–Si system and evaluated the influence of varying S and C contents on the final Si and O content. We plotted the (Fe–Ni)–O–Si solution space calculated when incorporating carbon (0, 0.2, and 1%) and/or sulfur (0, 1, and 2%) in Fig. 3. As expected, adding S and/or C in the core reduces the range of acceptable O–Si concentrations as major elements and has a more pronounced effect on oxygen rather than silicon. However, the picture remains qualitatively the same, and oxygen is always required in the core.

Fig. 3.

Range of O and Si compositions compatible with seismic observations, calculated for varying S and C concentrations. Each panel corresponds to a fixed carbon content: (Left) 0% C; (Center) 0.2% C; (Right) 1% C. In each panel, we calculate three sulfur concentrations: dark (0% S), light (1% S), and lighter (2% S). For each of the nine S–C combinations plotted, we calculate the best numerical fit represented by a white circle. The horizontal gray band represents the outer-core silicon concentration range required by inner-core models (7, 8, 30).

All these results are based on a core–mantle boundary temperature of 4,300 K, a condition that was chosen so that the inner-core boundary temperature (calculated along the isentrope) falls on the melting temperature of iron (6, 29). To verify that our solution is robust, we checked the sensitivity to temperature. We performed the same calculations for a range of CMB temperatures from 3,800 to 4,700 K, with ICB temperatures ranging from 5,500 to 6,900 K, respectively. The calculations are reported in the SI Appendix, sections 5 and 6. Higher temperatures make for less light elements, and conversely, a core at lower temperature requires more light elements. The solution spaces shift to higher or lower concentrations with T, but the general topology of the solution, and our conclusions, remains unchanged.

This study shows that oxygen is present, and likely in high concentrations, in the outer core. Because the solubility of oxygen in iron requires high temperatures and high FeO concentration (oxygen fugacity) in coexisting silicate melts, our observation strongly favors models of core formation in a deep magma ocean (35) under relatively oxidizing conditions (magma ocean FeO content higher than that of the present-day mantle) or by merging of several large protoplanets that have experienced such conditions (37, 38). A core with high oxygen content is consistent with inner-core models (8, 30) and helps explain the large density contrast at the ICB. It has been proposed that oxygen (33) is a light element whose presence in the core dramatically changes the activity of V and Cr during metal–silicate equilibrium, modifying their partition coefficients to reach concentrations in the mantle in accord with geochemical observation, as long as the core contains 3–6% oxygen (34, 35); such contents fall in the range of our solutions. Combining the geophysical constraints (from this work) with geochemical constraints (siderophile trace-element partitioning) should be a very effective tool to further constrain core formation scenarios as well as the chemical environment that prevailed during terrestrial accretion.