Response of Escherichia coli growth rate to osmotic shock

Significance

The peptidoglycan cell wall is a universal feature of bacteria that determines their shape, their effect on the human immune system, and their susceptibility to many of our front-line antibiotics. Therefore, it is essential to understand the physiology of this structure. Here, we examine the fundamental biomechanical and biochemical processes that drive cell-wall expansion during cell growth. We demonstrate that, contrary to a long-standing hypothesis, osmotic pressure is not essential for cell-wall expansion of the model bacterium Escherichia coli and that growth of this organism is robust to changes in osmotic pressure. This may be an important adaptation for an enteric bacterium, which regularly faces drastic changes in its osmotic environment during entry and exit from the intestine.

Abstract

It has long been proposed that turgor pressure plays an essential role during bacterial growth by driving mechanical expansion of the cell wall. This hypothesis is based on analogy to plant cells, for which this mechanism has been established, and on experiments in which the growth rate of bacterial cultures was observed to decrease as the osmolarity of the growth medium was increased. To distinguish the effect of turgor pressure from pressure-independent effects that osmolarity might have on cell growth, we monitored the elongation of single Escherichia coli cells while rapidly changing the osmolarity of their media. By plasmolyzing cells, we found that cell-wall elastic strain did not scale with growth rate, suggesting that pressure does not drive cell-wall expansion. Furthermore, in response to hyper- and hypoosmotic shock, E. coli cells resumed their preshock growth rate and relaxed to their steady-state rate after several minutes, demonstrating that osmolarity modulates growth rate slowly, independently of pressure. Oscillatory hyperosmotic shock revealed that although plasmolysis slowed cell elongation, the cells nevertheless “stored” growth such that once turgor was reestablished the cells elongated to the length that they would have attained had they never been plasmolyzed. Finally, MreB dynamics were unaffected by osmotic shock. These results reveal the simple nature of E. coli cell-wall expansion: that the rate of expansion is determined by the rate of peptidoglycan insertion and insertion is not directly dependent on turgor pressure, but that pressure does play a basic role whereby it enables full extension of recently inserted peptidoglycan.

Cell growth is the result of a complex system of biochemical processes and mechanical forces. For bacterial, plant, and fungal cells, growth requires both the synthesis of cytoplasmic components and the expansion of the cell wall, a stiff polymeric network that encloses these cells. It is well established that plant cells use turgor pressure, the outward normal force exerted by the cytoplasm on the cell wall, to drive mechanical expansion of the cell wall during growth (1, 2). In contrast, our understanding of the physical mechanisms of cell-wall expansion in bacteria is limited. Furthermore, the bacterial cell wall is distinct from its eukaryotic counterparts in both ultrastructure and chemical composition. In particular, the peptidoglycan cell wall of Gram-negative bacteria is extremely thin, comprising perhaps a molecular monolayer (3). This raises the question of whether these organisms require turgor pressure for cell-wall expansion, or whether they use a different strategy than organisms with thicker walls.

Turgor pressure is established within cells according to the Morse equation, $P=RT\left(C_{\mathrm{in}}-C_{\mathrm{out}}\right)$, where $C_{\mathrm{in}}$ is the osmolarity of the cytoplasm, $C_{\mathrm{out}}$ is the osmolarity of the extracellular medium, R is the gas constant, and T is the temperature. In the Gram-negative bacterium Escherichia coli, P has been estimated to be 1–3 atm (4, 5). A primary role of the cell wall is to bear this load by balancing it with mechanical stress, thereby preventing cell lysis. In 1924, Walter proposed a theory of bacterial growth based on the premise that mechanical stress, in turn, is responsible for stretching the cell wall during growth (6). In support of this theory, he and others showed that the growth rate of a number of bacterial species, including E. coli, decreases as the osmolarity of their growth medium is increased (6–9) (Fig. 1A). This result would be predicted by the Morse equation if growth rate, $\dot{e},$ scaled with pressure: $\dot{e}\sim P\sim -C_{\mathrm{out}}$. The decrease in growth rate did not depend on the chemical used to modulate the osmolarity, which demonstrated that this effect was not due to specific, toxic reactions. More recently, several theoretical studies have offered plausible molecular mechanisms by which turgor pressure could drive cell-wall expansion. These theories range from ones in which the cell wall is irreversibly stretched by turgor pressure when peptidoglycan cross-links are hydrolyzed (10, 11) to ones in which the rate of peptidoglycan biosynthesis is directly dependent on turgor pressure (12, 13). Two of these theories explicitly predict the scaling between cellular growth rate and pressure (12, 13), providing possible explanations of the classic experiments (6–9).

Fig. 1.

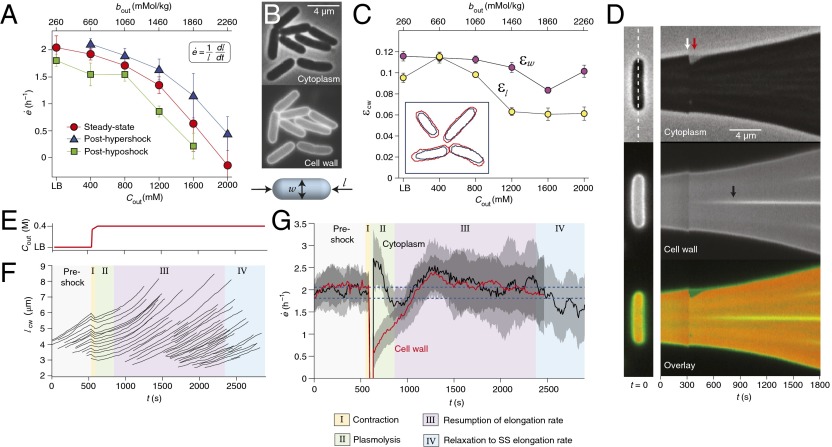
E. coli cells maintain their elongation rate after hyperosmotic shock. (A) The population-averaged steady-state elongation rate as a function of the concentration of sorbitol in the growth medium, $C_{\mathrm{out}}$ (red circles). Also shown are the population-averaged elongation rates during phase III of recovery from a 400 mM hyperosmotic shock (blue triangles) and immediately after a 400 mM hypoosmotic shock (green squares). Each data point is averaged over 20–100 cells. Error bars indicate ±1 SE. (Inset) Definition of elongation rate. (B) E. coli stained with fluorescent WGA, imaged with phase and epifluorescence microscopy. (Lower) Schematic defining the length and width of a rod-shaped cell. (C) Longitudinal strain, ${\epsilon }_l$, and radial strain, ${\epsilon }_w$, as a function of medium osmolarity. Error bars indicate ±1 SE. (Inset) Tracked outlines of the wall of four cells before (red) and after (blue) plasmolysis. (D) (Left) Initial images of a single cell: phase, epifluorescence, and overlay. In the overlay, the epifluorescence kymograph is false-colored green and the inverse of the phase kymograph is false-colored red. (Right) Kymographs of this cell elongating and dividing during a 400 mM hyperosmotic shock. The kymographs consist of a montage of a one-pixel-wide region around the long axis of the cell, indicated by the dashed line. The white arrow indicates the time of the shock. The red arrow indicates the period of plasmolysis during which the cytoplasm is shorter than the cell wall. The black arrow indicates the formation of a septum during cell division. (E) The concentration of sorbitol in the growth medium versus time during a hyperosmotic shock. (F) The length of the cell walls of representative cells during the same shock. The background colors indicate the four phases of response. (G) The population-averaged elongation rate of both the cytoplasm and the cell wall during the same shock (n = 42 cells). The data were smoothed with a moving-average filter with a 2-min window for illustrative purposes. The blue dotted lines indicate the steady-state elongation rates in LB (upper line) and LB+400 mM sorbitol (lower line). The confidence intervals indicate ±1 SE. The cell wall could not be tracked indefinitely owing to dilution of the cell-wall stain. (Lower) Key describing the four phases of response to hyperosmotic shock.

However, bacterial cells possess several mechanisms for regulating their cytoplasmic osmolarity in response to changes in their external osmotic environment (14). Specifically, E. coli imports and synthesizes compatible solutes, and imports ions, in response to high external osmolarities (15). For example, the concentration of potassium ions in the cytoplasm scales as the external osmolality (16). Therefore, it is unclear whether raising medium osmolarity actually causes a decrease in turgor pressure over long time scales. The inverse correlation between growth rate and medium osmolarity could result from another osmotic effect such as altered water potential within the cell, which could affect, for example, protein folding (17) or signaling (18). We sought to distinguish between these possibilities by measuring the elastic strain within the cell wall as a function of medium osmolarity and by determining the time scale over which osmotic shock (acute changes in medium osmolarity) modulates growth rate and cell-wall synthesis. If growth rate scales with turgor pressure, then (i) growth rate should also scale with cell-wall elastic strain, and therefore elastic strain should decrease with increasing medium osmolarity, and (ii) growth rate, and perhaps the rate of cell-wall synthesis, should rapidly change upon osmotic shock. However, if medium osmolarity modulates growth rate independently of pressure, these processes may adapt more slowly to changes in osmolarity.

We found that elastic strain decreases only moderately with increasing medium osmolarity. By measuring the growth-rate response of E. coli across time scales that spanned four orders of magnitude we concluded that osmotic shock had little effect on growth rate, except in the case of plasmolysis (when P ≤ 0, causing the cytoplasm to separate from the cell wall). The growth rate of E. coli adapted slowly to changes in medium osmolarity, over the course of tens of minutes. Furthermore, when turgor pressure was restored after slight plasmolysis, E. coli cells quickly elongated to the length that they would have attained had they never been plasmolyzed. From this result, we inferred that peptidoglycan synthesis is insensitive to changes in turgor pressure. In support of this hypothesis, we found that the speed of MreB, a protein whose motion is dependent on peptidoglycan synthesis (19–21), is largely unaffected by osmotic shock. Therefore, our results demonstrate that cell-wall biosynthesis is the rate-limiting factor in cell-wall expansion and that turgor pressure is not required for cell-wall biosynthesis, but that pressure does play a simple role whereby it stretches recently assembled, unextended peptidoglycan.

Results

Under favorable, chemostatic conditions, single-cell elongation of E. coli can be accurately described by an exponential function (22), and it is therefore useful to define growth rate as a relative rate of elongation, $\dot{e}=\left(dl/dt\right)/l$, where l is the length of the cell (Fig. 1C). This empirical quantity accounts for reversible elongation of the cell, in which the cytoplasm acquires water and the cell wall stretches elastically, as well as irreversible elongation, in which uptake of water is accompanied by synthesis, hydrolysis, and/or reorganization of the cell wall. Whereas reversible elongation results from changes in turgor pressure, irreversible elongation occurs during steady-state growth. Our goal was to determine whether irreversible elongation, like reversible elongation, is pressure-dependent.

Cell-Wall Strain Varies Weakly with Medium Osmolarity.

To do so, we used phase-contrast microscopy to measure the steady-state elongation rate of single E. coli cells as a function of medium osmolarity. Steady-state elongation was achieved by culturing the bacteria in chemostatic conditions using a microfluidic flow cell. We found a negative relationship between elongation rate and osmolarity (Fig. 1A), in agreement with the population-level measurements (7–9).

To determine whether this negative dependence was pressure-mediated, or whether it was due to other effects of osmolarity on elongation rate, we first inquired whether turgor pressure exhibited a similar negative dependence on medium osmolarity. Although the small size of bacterial cells precludes direct measurement of turgor pressure with a capillary probe, we could quantify the elastic strain within the cell wall (the extent to which it is stretched by pressure) by plasmolyzing the cells, thereby depleting the force exerted by the cytoplasm on the wall, and measuring the resulting contraction of the wall. To achieve this, we labeled the cells with fluorescent wheat germ agglutinin (WGA), a specific cell-wall marker for E. coli (23), and recorded time-lapse images of cells using phase-contrast and epifluorescence microscopy (Fig. 1B) while subjecting them to large (≥1 M) hyperosmotic shock.

We found that the longitudinal strain within the cell wall, ${\epsilon }_l=\left(l-l_0\right)/l_0$, where $l_0$ is the length of the cell wall immediately after plasmolysis, decreased moderately with medium osmolarity (Fig. 1C). However, the radial strain, ${\epsilon }_w=\left(w-w_0\right)/w_0$, decreased very little. Notably, there is large elastic strain at osmolarities that quench elongation. Although from these measurements we could not rule out the possibility that pressure was changing more than was evidenced by elastic strain owing to nonlinear mechanical properties of the cell wall (Fig. 1A), the observation that medium osmolarity does not reduce cell-wall elastic strain to the same degree that it reduces elongation rate argues against a role for turgor pressure in determining elongation rate.

E. coli Maintains Its Elongation Rate After Osmotic Shock.

Therefore, as an independent means of probing this relationship, we next measured the time scale over which elongation rate relaxes to its steady-state value in response to osmotic shock. Because hyperosmotic shock dehydrates E. coli cells within seconds (Fig. S1) (24), we expected that if turgor pressure determines the rate of cell-wall expansion, then the elongation rate would rapidly fall to its new steady-state value.

To test this hypothesis, we monitored the elongation of the cytoplasm and the cell wall during a 400 mM hyperosmotic shock (Fig. 1 D–G and Fig. S2). The elongation-rate response of the cells was characterized by four phases (Fig. 1 F and G). During the shock (phase I), both the cytoplasm and the cell wall rapidly shrank owing to dehydration of the cell (Fig. 1 D and F and Fig. S2B). The cytoplasm shrank more than the cell wall (Fig. 1D), that is, the cells became plasmolyzed. In agreement with previous observations (25, 26), separation between the cytoplasm and the wall was most commonly observed at one or both poles of the cells (Fig. S2A). Immediately following the shock (phase II), the cytoplasm rapidly elongated for several minutes whereas the cell wall elongated at a slower rate (Fig. 1G). During the tens of minutes after recovery from plasmolysis (phase III), the cells elongated at a rate approximately equal to the preshock elongation rate, and therefore faster than their steady-state value at the new osmolarity (Fig. 1 A and G). Finally, the elongation rate of the cells decreased to its steady-state value (phase IV). To ensure that this drop in elongation rate was not due to phototoxicity, we repeated the experiment without fluorescence excitation and observed similar results (Fig. S2D). These behaviors were independent of the preshock osmolarity (Fig. 1A), except that for high preshock osmolarities the majority of the cells did not become plasmolyzed (Fig. S2C).

The observation that cells resumed their preshock elongation rate for several minutes after recovery from plasmolysis demonstrates that, whereas turgor pressure changes within seconds upon osmotic shock, elongation rate is apparently determined by variables that vary slowly, on the order of tens of minutes after a shock. Strikingly, we observed a significant rate of cell-wall elongation even during plasmolysis (Fig. 1G, phase II), which demonstrates that turgor pressure is not even required for cell-wall elongation. This elongation may reflect the basal rate of cell-wall synthesis in the absence of turgor. Taken together, these data demonstrate that the rate of cell-wall expansion during cell growth is not dictated by mechanical stress.

Finally, we found that E. coli cells also resume their original elongation rate after a 400 mM hypoosmotic shock and accelerate to their steady-state value over the course of several minutes (Fig. 1A and Fig. S3). These data confirm that elongation rate responds slowly to shifts in external osmolarity, which supports the idea that elongation is not pressure-mediated.

E. coli Stores Growth During Oscillatory Hyperosmotic Shock.

To confirm that reducing turgor pressure does not affect the rate of cell elongation, we next examined cell growth at shorter time scales after hyperosmotic shock. E. coli responds to hyperosmotic shock by importing potassium, as well as compatible solutes such as proline and glycine betaine, if they are present (27). Potassium takes several minutes to accumulate in the cytoplasm (28), whereas the time required for activation of the broad-specificity compatible solute transporter ProP is <1 min (29). In addition, E. coli recovers from plasmolysis within several minutes after moderate hyperosmotic shocks (Fig. 1G) (24), suggesting that osmoregulation occurs on the minute time scale. Therefore, we wished to determine whether elongation rate was pressure-dependent at shorter time scales, <1 min after hyperosmotic shock, before osmoregulatory mechanisms are able to achieve osmotic homeostasis.

It is difficult to measure elongation rates at subminute time scales owing to the small size of bacteria: in lysogeny broth (LB), E. coli cells elongate at ∼2 h⁻¹ (Fig. 1A), which is equivalent to ∼2 nm/s. To precisely measure elongation rates on short time scales, despite the optical diffraction limit, we combined three strategies: (i) We determined cell boundaries to subpixel resolution and were then able to discern changes in cell length below the diffraction limit (SI Materials and Methods and Figs. S4 and S5); (ii) we averaged the elongation rate over a population of cells; and (iii) we averaged the elongation rate of these populations over many successive identical osmotic shocks. To achieve the latter, we used a microfluidic chamber to subject the cells to oscillatory hyperosmotic shock during which, after initial incubation in LB, the medium was repeatedly exchanged for LB concentrated with sorbitol (Fig. 2A and Movie S1). We examined the effects of relatively small-amplitude osmotic shocks, <300 mM, to avoid significant plasmolysis, and because within this range the variation in steady-state elongation rate is relatively small (Fig. 1A). Thus, larger variations in elongation rate that result from osmotic shocks of this magnitude are likely to be due to changes in turgor pressure.

Fig. 2.

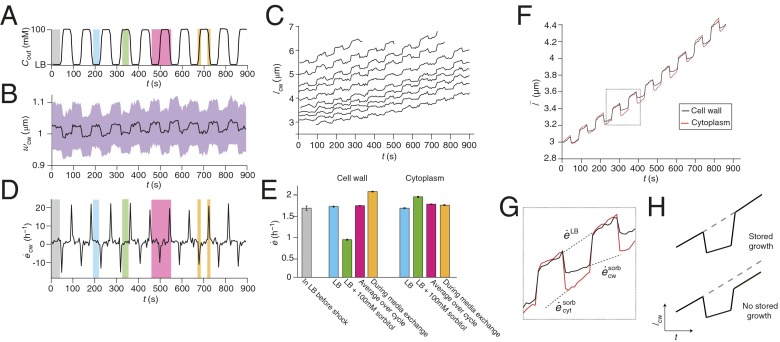
Hyperosmotic shock results in stored growth. (A) The concentration of sorbitol in the growth medium during a 100 mM oscillatory hyperosmotic shock with a 90-s period. The various phases of the oscillatory cycle are highlighted in different colors. (B) The population-averaged width of the cell wall during the shock (n = 37). The confidence intervals (purple region) indicate ±1 SD. (C) The length of the cell walls of representative cells during the shock. (D) The population-averaged elongation rate of the cell wall during the shock. (E) The population-averaged elongation rate of the cytoplasm and the cell wall during each phase of the oscillatory cycle. Error bars indicate ±1 SE. (F) The effective population-averaged length of the cytoplasm and cell wall obtained by integrating their average elongation rate (Materials and Methods). (G) Zoom-in of two cycles from F; dashed lines indicate the elongation rates of the cytoplasm and cell wall in LB+sorbitol (${\dot{e}}_{\mathrm{cyt}}^{\mathrm{sorb}}$ and ${\dot{e}}_{\mathrm{cw}}^{\mathrm{sorb}}$, respectively) and in LB (${\dot{e}}^{\mathrm{LB}}$). (H) Schematic illustrating predicted behavior of cell-wall length for two scenarios: (above) hyperosmotic shock reduces elongation rate but growth is stored; (below) hyperosmotic shock reduces elongation rate and growth is not stored.

We found that the elongation rate of E. coli cells during oscillatory hyperosmotic shock depended on the phase of the oscillatory cycle. During the phase when the medium osmolarity was being raised or lowered, the cells acutely shrank and swelled owing to osmosis (Fig. 2 B and C). Cell-wall width decreased upon each hyperosmotic shock and was only restored when the cells were reimmersed in LB (Fig. 2B), suggesting that turgor pressure was indeed reduced for the duration of each shock. Cell-wall length also underwent acute deformation during the phases of media exchange (Fig. 2C), leading to sharp peaks and valleys in the time-dependent cell-wall elongation rate (Fig. 2D).

During the phase when the cells were in LB, their cell walls elongated at the same rate as they did before the oscillatory shock, when they were also growing in LB (Fig. 2E, blue and gray bars, respectively). Conversely, during the phase when they were in concentrated media, their walls elongated at a slower rate (Fig. 2E, green bar). Even though the cells spent equal time in each medium, the cell-wall elongation rate averaged over the period of the entire oscillatory shock was not equal to the average of the elongation rates in the two media; rather, it was equal to the steady-state elongation rate in LB alone (Fig. 2E, red bar). This result is explained by the observation that the cell-wall elongation rate averaged over the phases of media exchange was higher than the steady-state elongation rate in LB (Fig. 2E, orange bar).

In contrast to the cell wall, the cytoplasm elongated at a nearly constant rate that was independent of the phase of the oscillatory cycle and that was equal to the steady-state elongation rate in LB (Fig. 2E and Fig. S6A). These data suggest that the cell wall and the cytoplasm can elongate independently during oscillatory shock. To examine this hypothesis in more detail, we calculated the effective population-averaged lengths, $\overline{l}$, of the cell wall and of the cytoplasm by integrating their average elongation rates over time (Fig. 2F and SI Materials and Methods). This calculation revealed that the cytoplasm shrank more than the cell wall upon each hyperosmotic shock and proceeded to elongate faster than the wall until the lengths of the two were equal. Thus, as in the single-shock experiments, the elongation of the cell wall was only retarded when the cell was plasmolyzed. Because the separation of the cell wall from the cytoplasm is well below the diffraction limit, we could not resolve this plasmolysis in single cells, which demonstrates the value of averaging the elongation rate over a population of cells.

All of the above behaviors were observed over the entire range of oscillation periods that we were able to apply (>60 s, Fig. S6B) and across a range of shock magnitudes (<100 mM). As a whole, these data suggest that the cell-wall elongation rate is independent of turgor pressure unless the cell is plasmolyzed, i.e., $P\le 0$. In addition, we propose that even during slight plasmolysis, in which the inner membrane recedes from the cell wall at the pole(s) of the cell, the cells continue to incorporate peptidoglycan into the lateral cell wall in an unextended state that makes only a partial contribution to elongation of the cell wall. A corollary to this proposal is that cell-wall biosynthesis must be independent of turgor pressure, which would explain why there is a nonzero cell-wall elongation rate during plasmolysis, and also why when pressure is re-established, the cell wall extends to the length that it would have attained had pressure never been depleted in the first place. This behavior is reminiscent of so-called “stored growth,” long observed in certain plant tissues (30) and more recently in unicellular algae (31). The growth rate of these organisms can be decreased by reducing their turgor pressure, but if pressure is reestablished, they quickly grow to the size that they would have attained had pressure never been reduced.

For shock magnitudes of 100–300 mM, cells undergo severe, visible plasmolysis during each cycle, and their average elongation rate across the oscillatory-shock cycle is lower than the steady-state rate in LB (Fig. S6B). To explain this decrease, we hypothesize that severe plasmolysis causes the inner membrane to recede from both the polar and lateral cell walls, yielding a reduced overall rate of incorporation of peptidoglycan into the cell wall.

MreB Speed Is Unaffected by Hyperosmotic Shock.

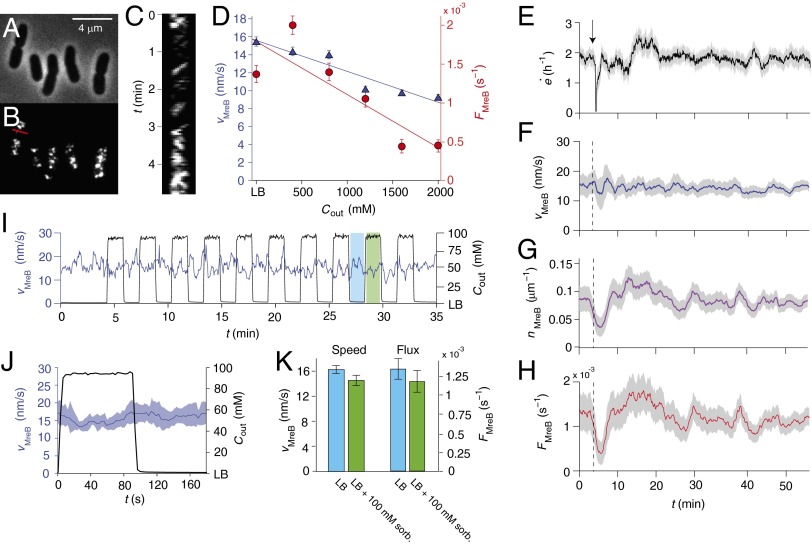
As a whole, our data suggest that cell-wall synthesis is the rate-limiting step in cell-wall expansion, and that synthesis is independent of pressure. Thus, we next sought to investigate the rate of synthesis under osmotic shock. Although it is not possible to measure this quantity directly on the minute time scale, we can infer it by tracking MreB (Fig. 3 A and B), a protein whose circumferential motion (Fig. 3C) is dependent on cell-wall synthesis in E. coli (19). To do this, we used total internal reflection fluorescence (TIRF) microscopy to make time-lapse images of a strain of E. coli that possesses an mreB-msfGFP sandwich fusion as the sole copy of mreB, and which complements the wild-type gene with respect to growth rate and cell morphology (23) (Fig. S7 and Table S1). We found that the steady-state ensemble-averaged speed of MreB puncta, $v_{\mathrm{MreB}}$, decreases moderately with increasing external osmolarity (Fig. 3D). However, the MreB flux, $F=n_{\mathrm{MreB}}{v}_{\mathrm{MreB}}$, where $n_{\mathrm{MreB}}$ is the the number of processive puncta per unit length of cell, decreases more severely (Fig. 3D), suggesting that this is the key variable that is correlated with cell elongation rate. Indeed, when E. coli cells were subjected to a 400 mM hyperosmotic shock, the ensemble-averaged speed of MreB puncta was unaffected (Fig. 3F), but the density of processive puncta and the MreB flux transiently increased beyond their original values before settling at a lower, steady-state value (Fig. 3 G and H). This behavior resembles the growth-rate response to 400 mM hyperosmotic shock (Figs. 1G and 3E), which suggests that it is MreB flux that determines this response.

Fig. 3.

Hyperosmotic shock does not affect MreB motion. (A) Phase images of E. coli cells possessing a GFP-MreB fusion protein as the sole copy of MreB. (B) TIRF images of the same cells. (C) Kymograph consisting of a montage of a one-pixel-wide region across the width of one cell. This slice is indicated by the red line in B. Diagonal stripes in the kymograph correspond to processive MreB puncta. (D) The dependence of steady-state, ensemble-averaged speed of processive MreB puncta (blue triangles) and the steady-state MreB flux (red circles) as a function of external osmolarity. The lines are linear best fits. Error bars indicate ±1 SE. The criteria for determining whether a punctum was processive are described in SI Materials and Methods. (E) The elongation rate during a 400 mM hyperosmotic shock (from LB to LB+400 mM sorbitol). The arrow (and dotted lines) indicates the time of the shock. The confidence intervals indicate ±1 SE. (F) The average MreB speed during the same shock. The confidence intervals indicate ±1 SE. (G) The average MreB density during the same shock. The confidence intervals indicate ±1 SE. (H) The MreB flux during the same shock. The confidence intervals indicate ±1 SE. (I) The average MreB speed and the concentration of sorbitol in the media during a 100 mM oscillatory hyperosmotic shock. The phases of low and high osmolarities are highlighted in blue and green, respectively. (J) The MreB speed and sorbitol concentration averaged over all 10 cycles of the oscillatory shock. The confidence intervals indicate ±1 SD of the ensemble-averaged MreB speed at each phase. (K) The average MreB speed and MreB flux as a function of the phase of the oscillatory shock. Error bars indicate ±1 SE.

In response to oscillatory hyperosmotic shock, the MreB speed and flux both exhibited a ∼10% reduction during the phases of elevated medium osmolarity (Fig. 3 I–K). It is unlikely that this modest reduction in flux can account for the drastic reduction in cell-wall elongation rate that we observe during oscillatory hyperosmotic shock (Fig. 2E). Rather, these data support the idea that it is minor plasmolysis that causes the reduction in elongation rate, and that cell-wall synthesis is largely unaffected by turgor pressure. This interpretation is corroborated by the fact that MreB speed, density, and flux are not significantly affected by 400 mM hypoosmotic shock (Fig. S3 B–D).

Discussion

To measure the fundamental dependence of E. coli growth on turgor pressure we monitored the single-cell elongation rate and MreB dynamics during osmotic shock. Collectively, our findings indicate that turgor pressure is not an essential driver of cell-wall expansion in this organism. First, although cell growth can be quenched by increasing medium osmolarity, elastic strain within the cell wall decreases only moderately with osmolarity. Second, elongation rate responds on slow time scales (>5 min) to large hyper- and hypoosmotic shocks (Fig. 1 and Fig. S3). Third, osmotic shock has little effect on MreB motion (Fig. 3). Fourth, although is it possible to slow cell-wall expansion by plasmolyzing the cell, cells can “store” growth such that when turgor pressure is reestablished the cell elongates to the length that it would have attained had plasmolysis not occurred (Fig. 2).

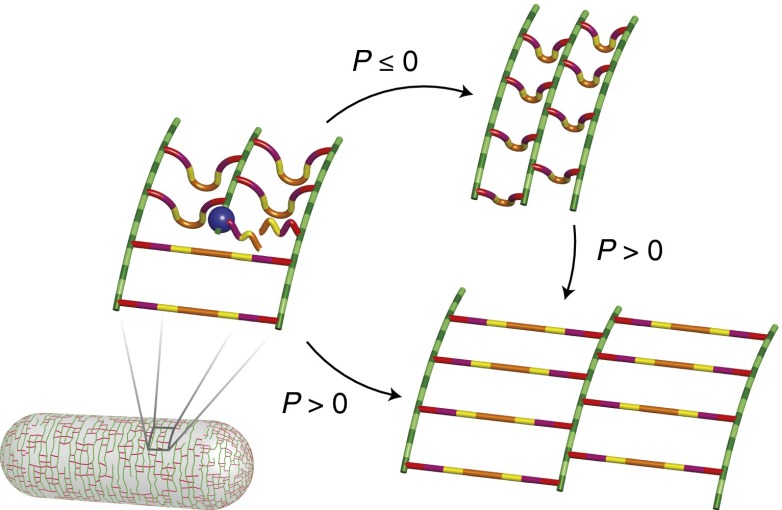
As a whole, these data are consistent with a model in which the rate of cell-wall synthesis is independent of turgor pressure and is the primary determinant of cell elongation rate. Based on our observation of stored growth, we propose that nascent peptidoglycan is inserted into the cell wall in an unextended state and that positive turgor pressure is required for extension (Fig. 4). Thus, during plasmolysis this material makes a smaller contribution to elongation than it does when the cell is turgid. However, once pressure is reestablished, this material is able to contribute its full potential to cell elongation. Hence, according to our model, turgor pressure does play a simple role whereby a positive value is required to stretch out newly synthesized, unextended peptidoglycan. Although the molecular organization of peptidoglycan is still a matter of debate, cryoelectron tomography suggests that glycan strands are oriented circumferentially, whereas polypeptides are oriented parallel to the long axis of the cell (3). According to our model, this would imply that growth can be “stored” in unextended polypeptide loops, although our conclusions do not rely on this being the case (Fig. 4).

Fig. 4.

Model of stored growth in E. coli. Green bars represent glycan strands and red bars represent peptide cross-links. The blue sphere represents the peptidoglycan synthetic machinery, which includes MreB. New glycan polymers are inserted such that cross-linking peptides buckle out of the plane of the cell wall. These cross-links are subsequently extended if turgor pressure is positive. During periods of plasmolysis, elongation is “stored” in these polypeptide loops, which become fully extended when positive turgor pressure is restored.

Our data contradict two theoretical studies that predict that bacterial elongation rate, peptidoglycan synthesis, and/or MreB speed scale directly with turgor pressure (12, 13). We also provide a rich dataset with which to test other mechanical models of bacterial growth (10, 11). Because elongation rate does not respond rapidly to changes in the osmolarity of the growth medium, it is unlikely that the steady-state dependence of elongation rate on medium osmolarity (6–9) is mediated directly by turgor pressure, although we cannot rule out a scenario in which turgor pressure is involved in a signaling cascade that modulates elongation rate over longer time scales. However, given the congruence between the responses of elongation rate and MreB flux to osmotic shock (Figs. 1G and 3C), we find it more plausible that cell-wall synthesis is sensitive to medium osmolarity independently of pressure.

The response of E. coli to osmotic shock contrasts with the wealth of evidence showing that plant cell elongation rate is directly tunable by turgor pressure (1, 2). However, E. coli shares with plants the capability to store growth upon depletion of turgor pressure (30, 31). In the case of E. coli, which has a very thin (∼3 nm) cell wall (3), it is easy to conceptualize a mechanism for stored growth that depends on insertion of unextended wall material (Fig. 4), whereas in plants, which have a much thicker cell wall (>100 nm) (32), the proposed mechanisms of storing growth are more speculative (31).

E. coli growth is evidently robust to changes in turgor pressure. This could be an important adaptation for an enteric bacterium, which may regularly face drastic changes in its osmotic environment during entry and exit from the intestine. Similar studies of other bacterial species will reveal whether the behavior we observe for E. coli is general. In particular, it will be interesting to examine Gram-positive bacteria to see whether their thicker cell wall (≥20 nm) (33) is sufficient to endow them with a more plant-like elongation-rate response to changes in turgor pressure.

Materials and Methods

Growth Media.

Concentrated growth medium was made by adding sorbitol (Sigma-Aldrich) to LB (10 g tryptone, 5 g yeast extract, and 5 g NaCl per liter H₂O), which has a base osmolality of 260 mmol/kg, as measured with a vapor pressure osmometer (Wescor Environmental). We used the osmometer to confirm that osmolarity scales linearly with osmolality across the range of concentrations used for this study, that is, $c=b\rho$, where c is the osmolarity, b is the osmolality, and ρ is the density of water.

Bacterial Strains.

All strains in used in this study are listed in Table S1. Strain NO34, which possesses an msfGFP-mreB sandwich fusion as the sole copy of mreB, complements wild-type E. coli MG1655 in both growth rate and cell morphology (23). Growth curves of these strains are shown in Fig. S7. The maximum growth rates and minimum doubling times during exponential phase are given in Table S1.

To measure growth curves, cells were cultured in LB to stationary phase overnight then back-diluted 1,000-fold into LB. The optical density was measured using an M200 plate reader (Tecan Group).

Time-Lapse Imaging of Bacteria During Osmotic Shock.

Before osmotic shock experiments, overnight cultures grown in LB were diluted 1,000-fold into LB concentrated with a determined amount of sorbitol (0–2 M) and then incubated at 37 °C until the cells were in midexponential phase. These cultures were then diluted 100-fold into prewarmed media that contained 10 μg/mL WGA, Alexa Fluor 488 conjugate (Life Technologies) and loaded into a microfluidic flow cell (CellASIC). To ensure the cells were at steady state, the flow cell was incubated for an additional 1 h in the microscope environmental chamber (HaisonTech), which was preheated to 37 °C, before the cells were imaged. Before loading cells into the imaging chamber of the flow cell, the chamber was primed with growth media using the ONIX microfluidic perfusion platform (CellASIC). While imaging, fresh media containing WGA was perfused through the flow cell. The cell-trapping mechanism used by the CellASIC microfluidic chips had no detrimental effect on the elongation or morphology of cells, compared with cells growing on agarose pads (Fig. S8) or liquid culture (Table S1).

During osmotic shock, the media in the flow cell was exchanged using the ONIX system. WGA was included in all perfusion media. To monitor medium osmolarity during osmotic shock, 0.5 μg/mL Alexa Fluor 647 carboxylic acid, succinimidyl ester dye (Life Technologies) was included with the concentrated medium as a tracer dye. The intensity of the tracer dye was monitored using Cy5 excitation, and the osmolarity was then calculated by calibrating the high and low osmolarities with the maximum and minimum fluorescence intensities, respectively.

To measure the elastic strain within the cell wall, cells were plasmolyzed using LB concentrated with 3 M sorbitol.

The steady-state measurements of MreB speed and flux shown in Fig. 3D were made on cells growing on agarose pads containing varying concentrations of sorbitol. Before experiments, overnight cultures grown in LB were diluted 1,000-fold into LB concentrated with a determined amount of sorbitol (0–2 M) and then incubated at 37 °C until the cells were in midexponential phase, when they were applied to the pads. The flux of MreB puncta measured from cells growing on pads was about two times higher than the flux calculated from cells growing in the microfluidic flow cell (compare Fig. 3 D and H), which we hypothesize is due to differences in sensitivity between the imaging conditions. We emphasize that the absolute value of the flux is not important for our argument.

For epifluorescence microscopy, time-lapse images were acquired using a Nikon Eclipse inverted microscope and an Andor DU885 EMCCD camera (Andor Technology). We imaged at an interval of 10 s. Phase and YFP epifluorescence images had signal-to-noise ratios of 21.3 ± 2.5 and 87.6 ± 9.9, respectively.

MreB was imaged using a custom TIRF microscope built with a Ti-E Eclipse stand (Nikon Instruments) (34) and a Plan Apo Lambda 100× DM (N.A. 1.45) (Nikon) objective lens. CUBE diode 405-nm and Sapphire OPSL 561-nm lasers (Coherent) were combined into an optical fiber and into a TIRF illuminator (Nikon) attached to the microscope stand for fluorescent excitation. Shuttering of the laser illumination was controlled by an acousto-optic tunable filter (AA optoelectronics) before the fiber coupler. Images were acquired with an iXon3+ 887 EMCCD (Andor Technology) camera, and synchronization between components was achieved using μManager (35) with a microcontroller (Arduino). Images were acquired every 3 s.

Cell and MreB tracking were performed using custom MATLAB (The MathWorks) routines (Fig. S4). A thorough description of the methods used in data analysis is given in SI Materials and Methods.