Flight–crash events in turbulence

Significance

Irreversibility is a fundamental aspect of the evolution of natural systems, and quantifying its manifestations is a challenge in any attempt to describe nonequilibrium systems. In the case of fluid turbulence, an emblematic example of a system very far from equilibrium, we show that the motion of a single fluid particle provides a clear manifestation of time irreversibility. Namely, we observe that fluid particles tend to lose kinetic energy faster than they gain it. This is best seen by the presence of rare “flight–crash” events, where fast moving particles suddenly decelerate into a region where fluid motion is slow. Remarkably, the statistical signature of these events establishes a quantitative relation between the degree of irreversibility and turbulence intensity.

Abstract

The statistical properties of turbulence differ in an essential way from those of systems in or near thermal equilibrium because of the flux of energy between vastly different scales at which energy is supplied and at which it is dissipated. We elucidate this difference by studying experimentally and numerically the fluctuations of the energy of a small fluid particle moving in a turbulent fluid. We demonstrate how the fundamental property of detailed balance is broken, so that the probabilities of forward and backward transitions are not equal for turbulence. In physical terms, we found that in a large set of flow configurations, fluid elements decelerate faster than accelerate, a feature known all too well from driving in dense traffic. The statistical signature of rare “flight–crash” events, associated with fast particle deceleration, provides a way to quantify irreversibility in a turbulent flow. Namely, we find that the third moment of the power fluctuations along a trajectory, nondimensionalized by the energy flux, displays a remarkable power law as a function of the Reynolds number, both in two and in three spatial dimensions. This establishes a relation between the irreversibility of the system and the range of active scales. We speculate that the breakdown of the detailed balance characterized here is a general feature of other systems very far from equilibrium, displaying a wide range of spatial scales.

In systems at thermal equilibrium, the probabilities of forward and backward transitions between any two states are equal, a property known as “detailed balance.” This fundamental property expresses time reversibility of equilibrium statistics (1). In the important class of nonequilibrium problems, where the dynamics of the system is coupled with a heat bath, the notion of detailed balance can be extended and fluctuation theorems successfully describe the behavior (2, 3). This class contains many experimental situations (4) where quantitative information on irreversibility was obtained (3). When a system driven by thermal noise is characterized by a probability current, the fluctuation–dissipation theorem and detailed balance was found to apply in a comoving reference frame (5).

In comparison, very little is known concerning the statistical properties of a small part embedded in a fluctuating, turbulent background. The fundamental notion of detailed balance is not expected to apply in such systems. Here we ask, what does the time irreversibility inherent to the large system imply for the statistical properties of small parts in the system and how do we measure the degree of irreversibility (6, 7) (or equivalently, how far is the system away from equilibrium) by monitoring a small part in the system? We focus here on fluid turbulence, a paradigm for ultimate far-from-equilibrium states, where irreversibility of fluctuations is a fundamental property (8, 9). We show that the simplest and most fundamental scalar quantity, namely, the kinetic energy of a fluid particle, enables a clear identification and quantification of the irreversibility of the turbulent flow.

The characteristic properties of turbulence rest on the vastly different scales: from the scale $l_F$, where the flow is forced and inertia dominates, to the scale $l_D$, where dissipation takes over. For a balance between forcing and dissipation in a statistically steady flow, energy is transferred through scales at an average rate ε, a phenomenon called “energy cascade.” In 3D flows, where $l_F\gg l_D$ (9, 10), energy cascades from large to small scales. In contrast, energy transfers from small to large scales in 2D flows, where $l_F\ll l_D$ (11, 12). The energy flux is ultimately the source of statistical irreversibility. It is important to understand that the fluctuations in turbulence are fundamentally different from those about thermal equilibrium (8). The energy flux through scales, ε, however, cannot in itself be a measure of irreversibility in the system because ε is a dimensional quantity, so it can be made arbitrarily large by changing the units even if the system is very close to equilibrium. Moreover, it can be expressed as a moment of velocity differences at a single time (10, 13) without any reference to the evolution of the flow.

As we demonstrate below, the irreversibility induced by the energy flux through spatial scales can be revealed and quantified by following the change of the kinetic energy of small fluid elements (particles). The kinetic energy per unit mass of the fluid is simply $E\left(t\right)=\left(1/2\right)V^2\left(t\right)$, where $\mathbf{V}\left(t\right)$ is the velocity of a given fluid element. It should be stressed that detecting irreversibility from the motion of a single particle requires going beyond velocity structure functions, defined as the moments of velocity differences along trajectories, $\mathbf{V}\left(t\right)-\mathbf{V}\left(0\right)$, whose statistical properties are invariant under the $t\to -t$ transformation (14).

The recent advances in our ability to reliably measure the trajectories of small tracer particles in well-controlled laboratory flows (15–18), as well as to simulate accurately the motion of particle tracers using the Navier–Stokes equation (16) allow us to investigate these fundamental issues. In this work, we restrict ourselves to statistically stationary and homogeneous flows. The results shown here were obtained from a variety of flow configurations in 2D and 3D, including both laboratory experiments and direct numerical simulations of the Navier–Stokes equations. The datasets contain a large number of trajectories, with at least ${10}^8$ data points in total, both in 2D and 3D (see Materials and Methods and SI Text for details).

Results

“Flight–Crash” Events.

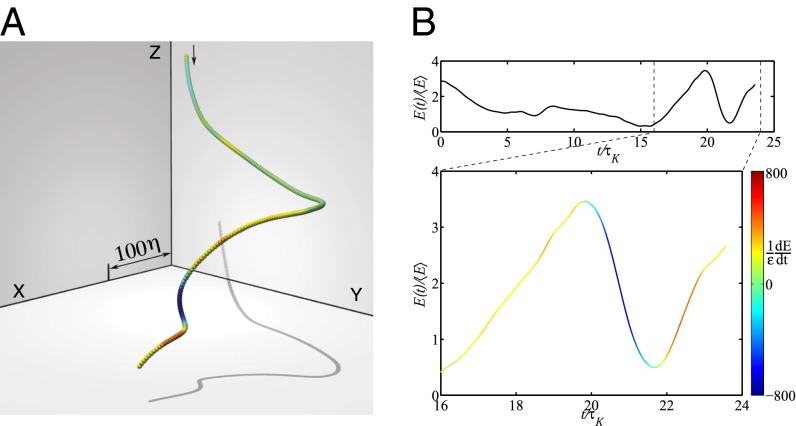
The phenomenon discussed here is illustrated in Fig. 1 A and B, which show the evolution of $E\left(t\right)$ along the trajectory of a fluid particle in a 3D laboratory water flow (17, 18). It illustrates that to build up large kinetic energy requires a longer time than to dissipate the same amount. This points to the occurrence of flight–crash like events, whereby a particle flies with a large velocity, before suddenly losing energy. This feature, which we also observed in numerical simulation of turbulent flows, is reminiscent of what occurs in very different systems, such as cars in traffic (19) or even fluctuations of stock values (20).

Fig. 1.

Asymmetry of the statistics of energy differences. (A) The trajectory of a fluid particle in a 3D laboratory flow at $R_{\lambda }=690$. The color coding refers to the instantaneous power $p\left(t\right)=\text{d}E/\text{d}t=\mathbf{a}\left(t\right)\cdot \mathbf{V}\left(t\right)$ acting on the fluid particle, showing that energy builds up slowly and dissipates quickly. The particle enters the observation volume from above and leaves from below. The scale bar is expressed in terms of the Kolmogorov scale η, which is the dissipation scale of this flow, $l_D=\eta =30\hspace{0.17em}\mathrm{\mu m}$. (B) The evolution of the kinetic energy $E\left(t\right)$ of the same particle as a function of time, in units of the Kolmogorov time ${\tau }_K$, the fastest time scale of the flow, characterizing the dynamics at scale $l_D$. B, Upper is for the entire trajectory, while Lower magnifies the period with strong energy change, i.e., high power fluctuations (same color coding as in A). The particle experiences higher values of negative p, compared with positive p, indicating that the particle loses kinetic energy more rapidly than gaining energy.

Statistics of Energy Difference.

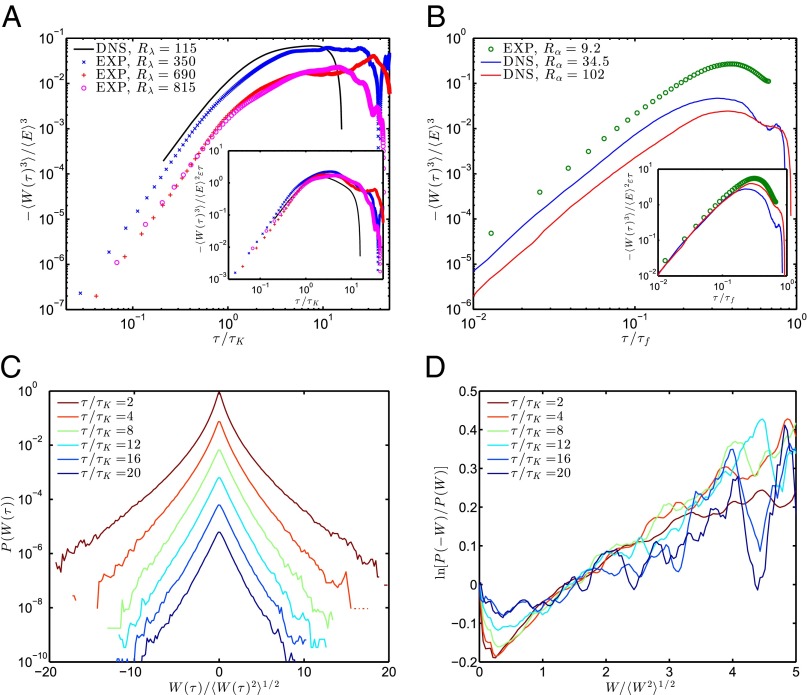
The statistics of the energy increments, $W\left(\tau \right)=E\left(t+\tau \right)-E\left(t\right)$, are sensitive to the flight-crash events. We stress that the moments of $W\left(\tau \right)$ cannot be expressed in terms of Lagrangian velocity structure functions, and notice that the kinetic energy $E\left(t\right)$ is not Galilean invariant, which we further discuss in SI Text. The asymmetry revealed by Fig. 1 implies that the distribution of $W\left(\tau \right)$ is skewed: Odd moments are expected to be negative for $\tau >0$. For stationary, homogeneous flows, the first moment vanishes, $\langle W\left(\tau \right)\rangle =0$. The first nonvanishing odd moment, $-\langle W^3\left(\tau \right)\rangle$, measured from both experiments and numerical simulations (18) of 3D turbulence is shown in Fig. 2A. In all these flows, $-\langle W^3\left(\tau \right)\rangle$ grows as ${\tau }^3$ at short times, then slower at intermediate times, and remains positive over the entire range of turbulence dynamical time scales. [Negative skewness of $u_x^2\left(t\right)-u_x^2\left(0\right)$, where $u_x$ is one velocity component of a tracer particle in a 3D turbulence flow, was also reported by Mordant (21).] Fig. 2B shows that the third moment of $W\left(\tau \right)$ in 2D is similar to those in 3D (Fig. 2A), i.e., it is independent of the difference in the direction of the energy flux in 2D and 3D. This demonstrates again that the energy flux ε by itself is not an appropriate measure of irreversibility and suggests the use of the dimensionless rate of change of the kinetic energy instead. A systematic statistical characterization of $W\left(\tau \right)$ can be formulated from its probability distribution function (PDF). Fig. 2C shows the PDF of $W\left(\tau \right)$ for several values of τ in the range ${\tau }_K\le \tau \le T$, where ${\tau }_K$ and T are the characteristic times at the dissipation scale $l_D$ and the forcing scale $l_F$, respectively. The PDF of $W\left(\tau \right)$, normalized by its variance, exhibits wide tails, the more so as the value of τ is smaller. This feature is possibly related to intermittency, a characteristic phenomenon in turbulent fluids.

Fig. 2.

(A) The third moment of energy increments $W\left(\tau \right)=E\left(t+\tau \right)-E\left(t\right)$ as a function of τ in 3D turbulence for different Reynolds numbers from both experiments (EXP) and direct numerical simulations (DNS). The quantity $-\langle W{\left(\tau \right)}^3\rangle$ grows like ${\tau }^3$ at short times. The curves obtained at different Reynolds numbers collapse once scaled using [3] (Inset). (B) The third moment of $W\left(\tau \right)$ from 2D turbulence experiments. Features similar to 3D turbulence are observed, i.e., $\langle W^3\left(\tau \right)\rangle$ is negative and nearly saturates when $\tau /{\tau }_f\sim 1$, where ${\tau }_f\sim {\left(l_F^2/\epsilon \right)}^{1/3}$ is the characteristic time corresponding to scale $l_F$ (SI Text). (C) PDFs of $W\left(\tau \right)$ at different values of τ, in the ${\tau }_K\le \tau \le T$ range, corresponding to 3D experimental flow at $R_{\lambda }=350$. The values of $W\left(\tau \right)$ are normalized by their rms values. For clarity, the PDFs have been shifted by a factor of 10 from each other. The PDF tails can be plausibly represented by exponentials. (D) The logarithm of the ratios of the probability of $-W$ and W as a function of W $\left(W>0\right)$ at different values of τ. The linear prediction of [1], which has been shown to apply in many systems in presence of several thermostats, does not simply apply for turbulence.

Could we understand the skewness of $W\left(\tau \right)$ in the framework of fluctuation theorems that have been established theoretically (22, 23), and verified experimentally (4)? For small systems in contact with thermostats, fluctuation theorems state that the probabilities of energy gaining and energy loss are related (2) by

$$\ln \left[\frac{P\left(-W\right)}{P\left(W\right)}\right]\propto W,$$ [1]

which, at a first glance, is also suggested by the shape of the tails of PDFs in Fig. 2C. Our measurements of $\ln \left[P\left(-W\right)/P\left(W\right)\right]$ at different values of time-lag τ, shown in Fig. 2D, however, shows a more complicated dependence on W than the simple linear law 1. This suggests that fluctuation theorems do not apply directly to tracer particles in turbulence. This we attribute to the properties of the forces acting on fluid particles, which are very different from the forces in usual thermodynamic systems (8).

Statistics of Power Fluctuations: Quantifying Detailed Balance Violations.

As we demonstrate that the results obtained in the general context of stochastic thermodynamics do not apply to a small fluid element carried by the fluid, the asymmetry observed for the distribution of the energy differences along a trajectory (Fig. 2C) points to a more fundamental aspect, namely the breakdown of time reversibility in the system. In fact, as we show in the following, the third moment of $W\left(\tau \right)$ allows us to quantify the irreversibility, and to relate it to the range of scales in the system.

Let us consider the rate of change of the kinetic energy following a tracer particle, i.e., the power $p={\lim }_{\tau \to 0}\left[W\left(\tau \right)/\tau \right]=\text{d}E/\text{d}t=\mathbf{V}\cdot \mathbf{a}$, with $\mathbf{a}=\text{d}\mathbf{V}/\text{d}t$ being the fluid acceleration. At thermal equilibrium, time reversibility is equivalent to detailed balance in the sense that the probability of energy gain $\left(p>0\right)$ is the same as the probability of energy loss $\left(p<0\right)$ for any particle with any velocity. Asymmetric (skewed) PDFs of p, as shown in Fig. 3 A and B, are therefore a signature that detailed balance is violated. [We note that the statistics of the power p may be affected by specific, nonuniversal aspects of the forcing, especially in 2D, in which the external forcing acts at small scales and is fast-changing (SI Text).] This violation can then be quantified by odd moments of the fluctuations of p, which change sign when reversing $t\to -t$, thus enabling to detect whether the movie of turbulence is playing backwards or forwards (9). Similar to $W\left(\tau \right)$, the first moment of p vanishes for stationary and homogeneous flows. The third moment, which can be measured reliably, is sufficient to quantify the violation of detailed balance.

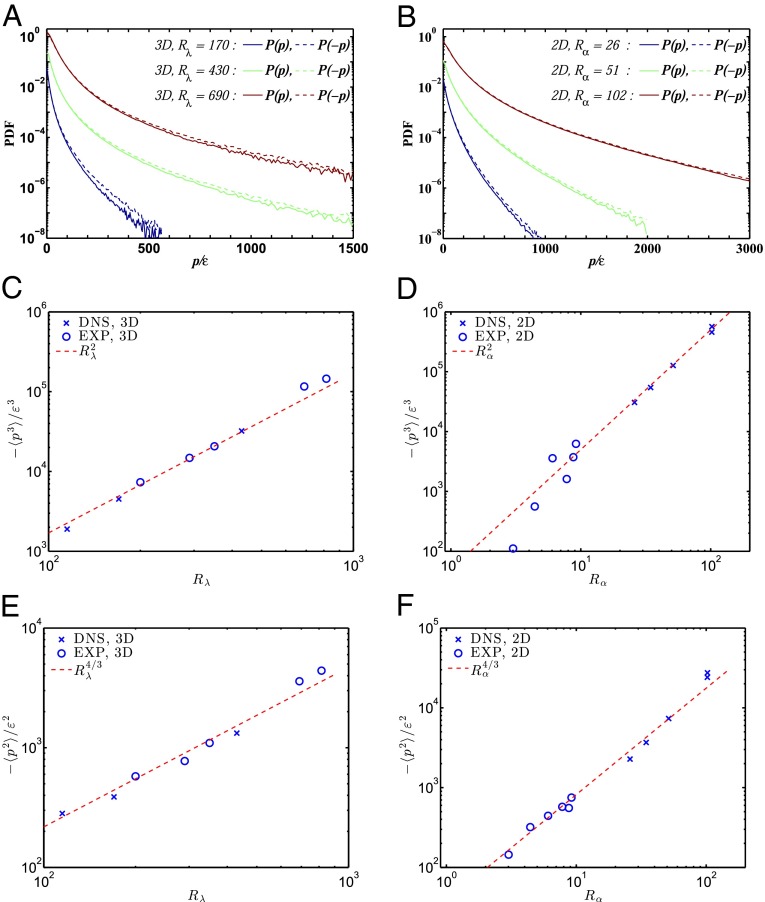
Fig. 3.

(A) The PDFs of $p/\epsilon$ at three different Reynolds numbers $R_{\lambda }=170$, 430, and 690 for 3D turbulence. For comparison, the PDFs of negative power $\left(p<0\right)$, shown by the dashed lines, are reflected around the vertical axis. The characteristic power is much larger than ε and increases with the Reynolds number. Moreover, large negative values of p are more frequent than large positive values, indicating that most of the violent energy exchange events that a fluid particle experiences are energy-loss events rather than energy gaining. Data at $R_{\lambda }=170$ and 430 are from DNSs and data at $R_{\lambda }=690$ are from experiments. (B) PDFs of $p/\epsilon$ from 2D turbulence simulations at $R_{\alpha }=26$, 51, and 102. Similar behavior as for 3D turbulence is observed. (C–F) Statistical properties of the instantaneous power p acting on fluid particles. (C) Variation of $-\langle p^3\rangle /{\epsilon }^3$ vs. $R_{\lambda }$ for 3D turbulence. Its increase is close to $R_{\lambda }^2$. (D) Variation of $-\langle p^3\rangle /{\epsilon }^3$ vs. $R_{\alpha }$ for 2D turbulence, which increases approximately as $R_{\alpha }^2$. (E and F) Variation of $\langle p^3\rangle /{\epsilon }^3$ for 3D and 2D turbulence, respectively. The variance increases rapidly with Reynolds numbers, close to $R_{\lambda }^{4/3}$ or $R_{\alpha }^{4/3}$ for 3D and 2D turbulence. This results in a skewness nearly independent of the Reynolds number: $\langle p^3\rangle /{\langle p^2\rangle }^{3/2}\approx -0.5$ in 3D and $\approx -0.20$ in 2D.

As already explained, a proper measure must be dimensionless. A natural choice is the dimensionless power $p/\epsilon$, whose third moment, Ir, defined as

$$Ir=-\langle p^3\rangle /{\epsilon }^3,$$ [2]

allows us to measure irreversibility. Fig. 3 C and D show that Ir increases with the Reynolds number in both 2D and 3D, hence with the separation of scales between forcing and dissipation. In 3D, it grows approximately as $Ir\propto R_{\lambda }^2$, where $R_{\lambda }\propto {\left(l_F/l_D\right)}^{2/3}$ is the Taylor-scale Reynolds number for 3D turbulence. For 2D turbulence in the energy cascade regime, i.e., $l_F\ll l_D$, we characterize the scale separation by the friction-based Reynolds number $R_{\alpha }\propto {\left(l_D/l_F\right)}^{2/3}$ (SI Text). The data from both experiments and numerics shown in Fig. 3D demonstrate that irreversibility grows also with this Reynolds number approximately as $Ir\propto R_{\alpha }^2$. The second moment, $\langle p^2\rangle /{\epsilon }^2$, grows with the Reynolds numbers as $R_{\alpha }^{4/3}$ and $R_{\lambda }^{4/3}$, as shown in Fig. 3 E and F. As a consequence, the skewness of the power fluctuations, defined as $s=\langle p^3\rangle /{\langle p^2\rangle }^{3/2}$, is approximately constant over the range of Reynolds numbers investigated in both 2D and 3D.

Thus, remarkably, the measure of irreversibility, Ir, directly accessible in laboratory flows, depends on the Reynolds number to a simple power, independent of the specificity of the forcing, and even more surprisingly, of the directions of the energy flux.

We note that the dependence of the moments $\langle {\left(p/\epsilon \right)}^n\rangle$ as $R_{\lambda }^{2n/3}$ or $R_{\alpha }^{2n/3}$ for $n=2$ and 3 does not extend to higher values of n, consistent with the observation that the PDFs of $p/\epsilon$ are not self-similar, and depend on the Reynolds number (SI Text).

Scaling of Power and Flight–Crash Events

The results documented in Figs. 2 and 3 establish a clear relation between the moments of the power, hence of the energy differences, and the Reynolds number. The aim of this section is to provide simple phenomenological arguments to interpret the dependence found in Fig. 3, which is observed both in 2D and 3D and seems universal.

First, let us note that the Lagrangian velocity difference does not have self-similar statistics, so it is reasonable to assume that there are events with different scaling exponents γ for the velocity change, $\delta V\left(\tau \right)\propto {\tau }^{\gamma }$. Different γ contribute different velocity moments. Landau–Obukhov phenomenology (14) suggests $\delta V\left(\tau \right)\simeq {\left(\epsilon \tau \right)}^{1/2}$, which physically corresponds to velocity diffusion under the action of random short-correlated forces. If particle acceleration (energy increase) would proceed in this way, one would expect $\langle p^2\rangle \propto \langle a^2\rangle \propto R_{\lambda }$. Our results of $\langle p^2\rangle \propto R_{\lambda }^{4/3}$ on power moments, as shown in Fig. 3, thus make it reasonable to assume that another type of events exists, where a fast particle takes flight and then sharply decelerates (by pressure gradient and/or viscous friction) to acquire the velocity of its neighbors. During such a flight, the particle travels a distance $\sim V\tau$ and the velocity difference across such distance can be estimated by the Kolmogorov estimate $\delta V\left(\tau \right)\simeq {\left(\epsilon V\tau \right)}^{1/3}$. This estimate rests on the assumption that the Eulerian field remains essentially frozen during the time τ. Note that this velocity change is much larger than the one suggested by Landau–Obukhov, ${\left(\epsilon V\tau \right)}^{1/3}/{\left(\epsilon \tau \right)}^{1/2}={\left(T/\tau \right)}^{1/6}$, thus such events must be rare. Therefore, it is unlikely that these rare flight–crash events dominate the Lagrangian structure functions $\langle {\left[\delta V\left(\tau \right)\right]}^n\rangle$, especially for small values of n. As we now demonstrate, however, the scaling of the power suggests that such events provide the main contribution to the moments of the energy changes and power, which are determined by the correlation between V and $\delta \mathbf{V}$. The flight and crash picture suggests for times in the inertial interval

$$W\left(\tau \right)\approx V\cdot \delta V\sim V^{4/3}{\left(\epsilon \tau \right)}^{1/3}.$$ [3]

This scaling for the energy change means that the Lagrangian quantity proportional to ε is the third-order structure function of the energy difference, $\langle W^3\left(\tau \right)\rangle \propto U_{rms}^3\left(\epsilon U_{rms}\tau \right)$. This suggests that the smooth scaling $\langle W^3\left(\tau \right)\rangle \propto {\tau }^3$ at $\tau \ll {\tau }_K$ turns into $\langle W^3\left(\tau \right)\rangle \propto \epsilon \tau$ at $\tau \gg {\tau }_K$. Accordingly, we normalize the third moment of W by $U_{rms}^4\epsilon \tau$, as shown in Fig. 2A, Inset. The very good collapse of the data in 3D gives support for the flight-crash picture discussed here. Using the same scaling in 2D leads to a very good collapse of the curves for very small τ. The difference between Fig. 2 A and B at longer times may be a manifestation of the very different physics occurring in 2D and 3D flows. The finite-time average power $W\left(\tau \right)/\tau$ behaves as $V\delta V/\tau \sim V{\left(V\epsilon \tau \right)}^{1/3}/\tau \sim \epsilon {\left(T/\tau \right)}^{2/3}$. It increases when τ decreases and saturates at $\tau \simeq {\tau }_K$, since $W\left(\tau \right)\propto \tau$ for $\tau \mathrm{\lesssim }{\tau }_K$. The moments of the instantaneous power can therefore be deduced from [3] using the saturation value $p\approx W\left({\tau }_K\right)/{\tau }_K\sim \epsilon {\left(T/{\tau }_K\right)}^{2/3}$, which leads to $\langle p^3\rangle \propto {\epsilon }^3{\left(T/{\tau }_K\right)}^2\propto {\epsilon }^3{R}_{\lambda }^2$ and $\langle p^2\rangle \propto {\epsilon }^2{R}_{\lambda }^{4/3}$ as observed in Fig. 3. The scaling provided by [3] also explains the systematic dependence of $\langle W^3\left(\tau \right)\rangle /{\langle E\rangle }^3$ as a function of the Reynolds number (SI Text).

Discussion

Turbulence is characterized by large fluctuations. Notoriously, the local energy dissipation rate shows strong spatial fluctuations, which are known to play a key role in the origin of intermittency, or fluctuations of other quantities of the turbulent flow (10). Much work has been devoted to the modeling of fluctuations of the local dissipation rate and of its coarse-grained generalization, especially in relation to devising approximate numerical schemes (13). Here we are interested in the related but different question of the exchange between a very small subsystem, a fluid particle, and the surrounding turbulent flow, in the spirit of work done for small systems in contact with thermostats (3). The comparison of our results with those described by stochastic thermodynamics, therefore, reveals the general features of systems very far from thermal equilibrium.

The main achievement of this work has been to document and quantify the intrinsic irreversibility of turbulent flows. This led us to define a quantity Ir, which increases as a power law when the Reynolds number increases, i.e., when the flow becomes more turbulent. Remarkably, this way of characterizing turbulent flows is insensitive to the direction of energy flux through spatial scales.

The observation of asymmetry in the time dependence of the kinetic energy of particle in a turbulent flows should be contrasted with the spatial asymmetry, observed in particular in the case of a passive scalar with an imposed gradient (24). In this case, the asymmetric, ramp-and-cliff structure results from a large scale forcing (the gradient), and persists all the way to very small scales. A weaker analogy has been documented in shear flows (25, 26). The phenomenon documented here is very different, as the temporal asymmetry is found both for direct and inverse cascades. It would be interesting to understand whether the possible connection between $\langle W^3\left(\tau \right)\rangle$ and the third-order Eulerian structure function point to any particular flow structures (27). We merely notice here that the sizes shown in Fig. 1A make any apparent relation with vortex tubes, observed many times before (15), unlikely.

Our results stress the main difference between the well-studied case of systems in contact with thermostats, and those involving a cascade through scales such as turbulence. In this context, our approach could shed new light on a variety of different problems, such as plasma turbulence (28), quantum turbulence (29), magnetohydrodynamics (30), and more generally, on any system that is irreversible and has a separation of scales. The investigation of such systems in the spirit of the present work is likely to lead to new concepts in the physics of the nonequilibrium.

Materials and Methods

We describe briefly the different turbulent flows that we analyzed in both 3D and 2D and in both physical experiments and numerical simulations. More details can be found in SI Text.

Experimental Setups.

The turbulent flows that we generated in laboratory experiments include the 3D von Kármán flows, 2D turbulence driven either electromagnetically or by surface ripples (Faraday waves).

von Kármán flows in 3D.

The 3D experiments were performed in a so-called von Kármán mixer, which generates high-Reynolds-number turbulent water flow between two counterrotating disks (15, 17). We measured 3D trajectories of tracer particles seeded in the flow using optical Lagrangian particle tracking (17, 18). The Reynolds number of the turbulence was in the $350\le R_{\lambda }\le 690$ range. The effects induced by the weak inhomogeneity of the flow at the center of the apparatus, where the measurements were carried out, can be shown to be small (SI Text).

Two-dimensional turbulence experiments.

Energy is injected into flows by driving horizontal vortices whose scale is much smaller than the size of the container. In electromagnetically driven turbulence such vortices are driven by the Lorenz force produced by the spatially varying vertical magnetic field and the electric current flowing across the fluid cell in electrolyte. In the Farady-wave-driven turbulence the vorticity is generated at the scale approximately at half of the wave period (31). The injected energy is then spread by the inverse energy cascade over a broad range of scales to form the Kolmogorov–Kraichnan spectrum. The 2D particle trajectories are tracked for a long time, up to 100 Lagrangian integral times (32).

Direct Numerical Simulations.

The numerical work is based on simulating the Navier–Stokes equations,

$${\partial }_t\mathbf{u}+\mathbf{u}\cdot \nabla \mathbf{u}=-\nabla P+\nu {\nabla }^2\mathbf{u}+\mathbf{f}-\alpha \mathbf{u},$$ [4]

where $\mathbf{u}\left(\mathbf{x},t\right)$ is the fluid velocity at location x and at time t. The velocity field is incompressible $\nabla \cdot \mathbf{u}=0$, a constraint which is imposed with the help of the pressure field P. The flow is forced by using an external field f, which varies at a characteristic scale $l_F$. The viscous term $\nu {\nabla }^2\mathbf{u}$ acts to dissipate energy. For 2D flows, a linear friction is introduced through the $-\alpha \mathbf{u}$ term ($\alpha =0$ in 3D), to prevent the accumulation of energy at scales larger than $l_D={\alpha }^{-3/2}{\epsilon }^{1/2}$.

The Lagrangian information is then obtained by integrating in time the equation of motion of fluid tracers

$$\frac{d\mathbf{X}}{dt}=\mathbf{V}\left(t\right)=\mathbf{u}\left(\mathbf{X},t\right),$$ [5]

in which the tracer velocity $\mathbf{V}\left(t\right)$ is the same as the fluid velocity u at position X and time t.

In all cases a statistically stationary flow was maintained by balancing the forcing and the dissipation terms. All the simulations discussed here were carried out in a periodic domain using standard pseudospectral methods.

In 3D, the simulations reported here used up to 384³ modes. The flow was forced at a scale $l_F$ comparable to the size of the domain, while energy was dissipated at the Kolmogorov scale η, $\eta =l_D={\left({\nu }^3/\epsilon \right)}^{1/4}$, which was the smallest scale resolved in the simulation. The turbulence Reynolds numbers were $R_{\lambda }=115$ and 170. Additionally, we used the flow field at $R_{\lambda }=430$ made available from the Johns Hopkins University database (33).

The simulations of 2D flows reported here were carried out with up to 8,192² modes. Forcing acted at a small scale $l_F$ only, and energy was damped by friction that acts at a scale $l_D$, comparable to the size of the system.