Abstract
DNA helicases are enzymes capable of unwinding double-stranded DNA (dsDNA) to provide the single-stranded DNA template required in many biological processes. Among these, UvrD, an essential DNA repair enzyme, has been shown to unwind dsDNA while moving 3′-5′ on one strand. Here, we use a single-molecule manipulation technique to monitor real-time changes in extension of a single, stretched, nicked dsDNA substrate as it is unwound by a single enzyme. This technique offers a means for measuring the rate, lifetime, and processivity of the enzymatic complex as a function of ATP, and for estimating the helicase step size. Strikingly, we observe a feature not seen in bulk assays: unwinding is preferentially followed by a slow, enzyme-translocation-limited rezipping of the separated strands rather than by dissociation of the enzymatic complex followed by quick rehybridization of the DNA strands. We address the mechanism underlying this phenomenon and propose a fully characterized model in which UvrD switches strands and translocates backwards on the other strand, allowing the DNA to reanneal in its wake.
Keywords: helicase, DNA replication, DNA repair, magnetic tweezers
Although helicases are essential molecular motors, their precise mechanism is only partially known. These motors translocate along DNA while stripping off one strand of the double helix (1, 2). Whereas a large number of helicases involved in DNA repair and recombination are either monomeric or dimeric, replicative helicases typically form processive, hexameric entities surrounding one or both strands. The process of separating the two strands of DNA is often described as the translocation of the enzyme on one strand, which defines the directionality of the process, whereas the displacement of the other strand is accomplished actively, if the helicase melts the base pairs, or, passively, if the helicase moves forward as the bases transiently unpair. Observing the activity of a single helicase unwinding a double helix yields valuable information on the enzymatic dynamics, as has been the case for other molecular motors such as kinesin and myosin (3).
UvrD (720 aa, molecular mass = 82 kDa), a member of the helicase SF1 superfamily (which includes PcrA and Rep), plays a crucial role in nucleotide excision repair and methyl-directed mismatch repair (4–8) and is required for the replication of several plasmids (9). It has been shown to initiate unwinding froma3′ end single-stranded DNA (ssDNA) tail, a gap, or a nick and to translocate along ssDNA in a 3′-5′ direction (10–12). The purpose of this study is to investigate the mechanochemistry of UvrD-catalyzed DNA unwinding at the single-molecule level, yielding more direct insight into its enzymatic activity by avoiding the inherent averaging of bulk assays. We present real-time measurements of the unwinding rate, lifetime, and number of base pairs unwound, as well as an estimate of the step size. In addition, we observe that an unwinding event can be followed by an enzyme-translocation-limited rehybridization of the opened strands. We propose that this rehybridization is due to the enzyme switching strands, and we fully characterize the rate constants of this model by using our data.
Materials and Methods
Substrate Preparation. Charomid DNA (13), a gift from O. Hyrien (Laboratoire de la Génétique Moléculaire, Ecole Normale Supérieure), is cut with ApaI and KpnI to produce a 11-kbp fragment. Eight hundred base pairs of DNA fragments multiply labeled with either biotin or digoxigenin are synthesized by PCR from the multiple cloning site of the Bluescript vector and cut respectively with ApaI and KpnI. The 11-kbp fragment is differentially end-labeled by ligating to each extremity the complementary 800-bp fragment. DNA is first mixed with streptavidin magnetic beads (diameter 4.5 μm, Dynal, Great Neck, NY) and incubated for 10 min. The bead–DNA construct is then incubated on an antidigoxigenin-coated glass surface previously incubated with tRNA (Sigma) to reduce nonspecific interactions. After the beads have sedimented, we use a gentle flow to eliminate untethered beads from the capillary.
Protein Purification. A full coding region of UvrD gene is prepared by PCR by using Escherichia coli chromosome DNA. The 2.2-kbp PCR product is cloned into pGEM-T easy vector, and the sequence of this insert is shown to be identical to the UvrD gene sequence (14). The UvrD gene is amplified again by PCR and then digested with NdeI and XhoI, and the 2.1-kb fragment is gel-purified and subcloned into NdeI/XhoI sites of the vector PET-15b. The constructed plasmid is further sequenced by MWG Biotech (Ebersberg, Germany). His-6-tagged E. coli UvrD helicase is expressed from pET-15b expression plasmid in E. coli strain BL21 (DE3) (15). The overexpressed protein is purified under native conditions by using chromatography on Ni2+-nitrilotriacetic acid columns (Qiagen, Valencia, CA), followed by FPLC size exclusion chromatography (Superdex 200, Pharmacia) and an ion-exchange chromatography (DEAE Sephadex A-50). Based on Sypro Orange-stained SDS/PAGE and electrospray mass spectrometry analyses, the purity of the UvrD preparation is determined to be >95%.
Single-Molecule Assay Conditions. Experiments are performed at 25°C in 20 mM Tris·HCl, 25 mM NaCl, 3 mM MgCl2, 0.1 mM EDTA, and 1 mM DTT. ATP (Amersham Pharmacia) is added to the final concentration indicated. The very low DNA concentration is impossible to determine accurately. We estimate that it is smaller than the DNA concentration in the bead–DNA solution, and greater than the concentration of beads tethered by a DNA molecule in the capillary, i.e., that 10-18 M < [DNA] < 10-15 M.
ATPase Bulk Assay. The ATPase activity is determined in a bulk assay by a measure of the radioactive 32Pi liberated during hydrolysis (16). Briefly, the measurement is carried out at 25°C in a reaction mixture containing 1.5 μM (nucleotide) heat-denatured HindIII-cut pGEM-7Zf linear DNA at the indicated concentration of ATP. The reactions are initiated by the addition of UvrD helicase into a 100-μl reaction mixture and stopped by pipetting 80 μl aliquots from the reaction mixture every 30 s into a hydrochloric solution of ammonium molybdate. The liberated radioactive 32Pi is extracted with a solution of 2-butanolbenzene-acetone-ammonium molybdate (750:750:15:1) saturated with water. An aliquot of the organic phase is counted in 6 ml of Aquasol.
Single-Molecule Measurements. Bead tracking and force measurements are performed on an inverted microscope as described (17). Briefly, a DNA molecule bound at one end to a glass surface and at the other to a small magnetic bead is stretched by the magnetic field gradient generated by small magnets placed above the sample. By optically tracking at video rate (25 Hz) the diffraction pattern around the bead, we measure its 3D position (x, y, and z). The uncertainties in the position are due to Brownian fluctuations. In the z direction, they reach the value of ≈1 nm2·Hz-1 (at a force F = 35 pN and for frequencies f > 2 Hz). The molecule extension L is obtained from the average mean height L = 〈z〉. To eliminate variations in 〈z〉 due to microscope drift, differential tracking with a second bead glued to the surface is performed. The bead's transverse fluctuations 〈δx2〉 allow for a determination of the stretching force by means of the equipartition theorem: F = kBT〈z〉/〈δx2〉 (kBT = 4 pN·nm at 25°C) (17). Here, F is measured with a 15% accuracy. Results are obtained at F = 35 pN except as otherwise mentioned. The magnets create a force field that varies on a millimeter scale. Because the tethered magnetic bead moves only by a few micrometers, the variation of F during an unwinding experiment is negligible. We detect nicked molecules by rotating the magnets and identifying the molecules that do not supercoil (18). We perform measurements only on singly nicked molecules, which we select by briefly stretching above 65 pN to melt the duplex (19). Molecules with more than one nick will break (if both strands are nicked), or lose a piece of ssDNA (if one strand is multiply nicked). Because the majority of molecules tested neither broke nor lost a significant piece of DNA, we conclude that the sample consists of molecules nicked at a single (but random) position.
Data Processing. The determination of the helicase unwinding rate requires measuring the elongation vs. time L(t). The number of base pairs unwound is given by: N(t) = [L(t) - L(0)]/δL(F), where δL(F) is the change in extension between double-stranded DNA (dsDNA) and ssDNA per base pair at force F. The local velocity vi of the helicase is determined as described (19) by fitting the data in an extension burst L(t) to a polygon {Li,ti} of i = 1,..., M vertices, and computing the local slope vi = (Li - Li-l)/(ti - ti-l). Data at F = 35 pN were collected over nine DNA molecules (436 bursts) at [ATP] = 500 μM. Data at 15, 40, 80, and 200 μM ATP were collected over respectively 76, 76, 99, and 175 bursts.
Results
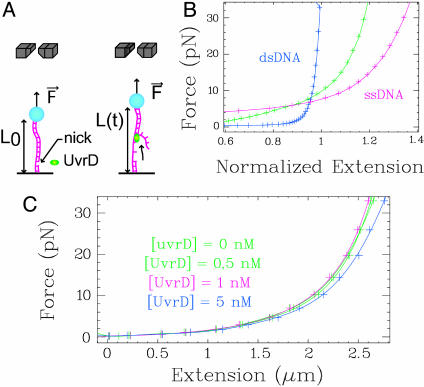
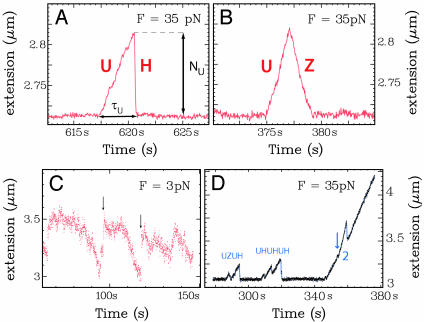
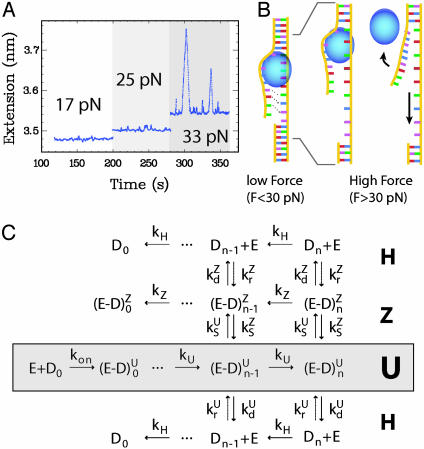
Monitoring Helicase Activity at the Level of a Single Enzymatic Complex. To monitor UvrD activity at the single-complex level, we specifically anchor a singly nicked dsDNA molecule at one end to a magnetic bead and at the other to a glass surface (Fig. 1A and Materials and Methods). Magnets placed above the sample control the vertical force F stretching the molecule (19). The difference in extension between stretched ssDNA and dsDNA allows us to monitor the unwinding activity (see Materials and Methods). At high force, ssDNA extends more than dsDNA (δL(F) ≈ 0.135 nm/bp at F = 35 pN) so that unwinding events result in an increase in L(t) (Fig. 1B). Below 5 pN, ssDNA is shorter than dsDNA, leading to a decrease in extension on unwinding. Therefore, the helicase works against the force below 5 pN and with the force above 5 pN. The binding of UvrD on the freed ssDNA does not affect its length within the range of concentrations used in the experiments in single enzymatic complex conditions ([UvrD] ≤ 1 nM << Kd ≈ 10 nM; refs. 20 and 21 and Fig. 1C). For [UvrD] < 1 nM (and F > 30 pN), the extension signal displays isolated bursts (Fig. 2A). They consist of a regular increase in extension as the DNA is unwound, followed by a much faster decrease when the enzyme dissociates from its substrate, thus allowing the strands to rehybridize quickly. These “UH” bursts (unwinding-rehybridization), are not observed in the absence of UvrD, ATP, or Mg2+ or when selecting a molecule having no nick (Fig. 7, which is published as supporting information on the PNAS web site). Because the timespan of an unwinding burst is 10- to 100-fold smaller than the time between two bursts, it is extremely unlikely that unwinding results from the simultaneous activity of multiple enzymatic complexes (18). Moreover, the simultaneous action of two complexes displays a characteristic doubling of the unwinding rate (sometimes observed at higher enzyme concentrations, Fig. 2D). From the slope of the increase in extension, we can deduce the unwinding rate, vU; from the burst height, we deduce the number of base pairs unwound, NU; and from its duration, we deduce the unwinding lifetime, τU (see Fig. 2 A and B for definitions). From the slope of the decreasing part of the burst, we can deduce the average DNA rehybridization rate: 〈vH〉 ≈ 2,300 bp/s, which is ATP-independent and similar to the rehybridization rate after a brief stretch above 65 pN of a nicked DNA molecule (see Materials and Methods). In all cases, unwinding proceeds uniformly and processively with no detectable pauses.
Fig. 1.
Experimental set-up. (A) Magnets (gray) exert an adjustable, constant force F on a bead tethered to the surface by a nicked DNA molecule. (B) Extension of a stretched dsDNA (blue), ssDNA (red), and a partially ds-ssDNA molecule (green) (normalized to the crystallographic length of the dsDNA). (C) Force–extension curves of ssDNA in the presence of increasing concentrations of UvrD ([ATP] = 500 μM). Within our working conditions ([UvrD] ≤ 1 nM), the change in extension of ssDNA is negligible.
Fig. 2.
Typical unwinding signals. At high forces, the extension of ssDNA is longer than dsDNA, and unwinding is observed as an increase in the molecule's extension (A and B): F = 35 pN; [UvrD] = 0.25 nM; [ATP] = 500 μM. (A) UH event (unwinding-rehybridization). (B) UZ event (unwinding-rezipping). (C) UvrD activity at F = 3 pN and [UvrD] = 50 nM. Unwinding is observed at low forces (F < 5 pN) as a decrease in the DNA's extension. Quick rehybridization (arrows) is still observed on dissociation of the enzyme. (D) Helicase activity observed at [UvrD] = 2 nM ([ATP] = 500 μM). At this UvrD concentration, there is enough binding of the enzyme to the ssDNA generated during an unwinding event to allow for successive rounds of unwinding, resulting in burst bunching. Notice also the simultaneous unwinding by two helicases. The arrow indicates when a second helicase has become active, doubling the unwinding rate. When one of the helicases dissociates, the rate of unwinding resumes its initial value.
Under the same conditions, we observe another type of burst (Fig. 2B), displaying a similar increase in extension due to unwinding, but followed by much slower reannealing. These events are denoted UZ: unwinding-rezipping. The rezipping rate vZ varies similarly with ATP concentration as the unwinding rate vU (see below). The decrease in the length of the molecule observed during rezipping events never goes below the dsDNA baseline length (although we sometimes observe more complicated burst patterns, e.g., UZU or UZH). These features suggest that the rezipping events consist of an enzyme translocation-limited closing of the two strands opened during unwinding. Another helicase, RecQ, was similarly studied and did not display any rezipping activity (data not shown).
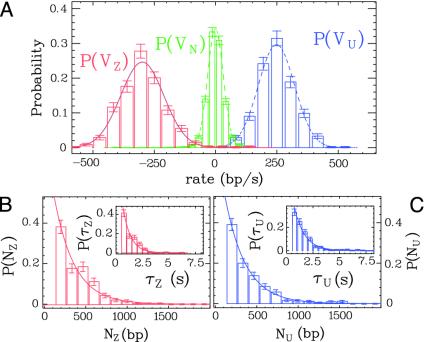
We define the rezipping rate vZ, lifetime τZ, and extent NZ as, respectively, the slope, duration, and height of the rezipping part of the burst. We observe that at [ATP] = 500 μM, the mean unwinding and rezipping rates vU and vZ follow Gaussian distributions of mean value 〈vU〉 = 248 ± 3 bp/s and 〈vZ〉 = -298 ± 3 bp/s and SDs σ(vU) = 74 bp/s and σ(vZ) = 88 bp/s, more than twice the width of the experimental noise distribution (Fig. 3A). This increased variability of the rate could result from sequence dependence of the rate or from enzyme to enzyme variability. The distribution of the number of base pairs unwound NU and rezipped NZ as well as the unwinding and rezipping lifetimes τU and τZ follow Poisson distributions of mean value 〈NU〉 = 240 ± 14 bp, 〈NZ〉 = 234 ± 13 bp, 〈τU〉 = 0.98 ± 0.05 s, and 〈τZ〉 = 0.73 ± 0.05 (Fig. 3 B and C).
Fig. 3.
Distributions of the unwinding and rezipping rates, lifetimes, and numbers of base pairs unwound at [ATP] = 500 μM. (A) The unwinding rate vU (blue curve), rezipping rate vZ (red curve), and the experimental noise vN between bursts (green curve) are fitted to Gaussian distributions (dashed curves) of mean value 〈vU〉 = 248 ± 3 bp/s, 〈vZ〉 ≈ -298 ± 3 bp/s and 〈vN〉 = -0.6 ± 0.7 bp/s and SD σ(vU) = 74 bp/s, σ(vZ) = 88 bp/s, and σ(vN) = 32 bp/s. (B) Number of base pairs rezipped NZ and rezipping lifetime τZ (Inset), fitted to Poisson distributions with mean value 〈NZ〉 = 234 ± 13 bp and 〈τZ〉 = 0.73 ± 0.05 s. UH and UZ bursts give similar values of 〈vU〉, 〈NU〉, and 〈τU〉.(C) Number of base pairs unwound NU and unwinding lifetime τU (Inset), fitted to Poisson distributions with mean value 〈NU〉= 240 ± 14 bp and 〈τU〉= 0.98 ± 0.05 s. The error bars on the histograms represent the statistical error in the bins.
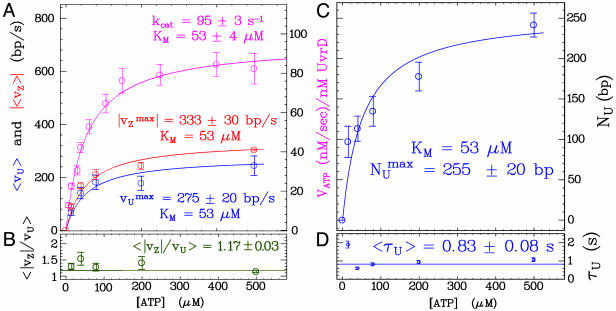
Helicase Activity at Various ATP Concentrations. By varying the ATP concentration, we observe that the Michaelis-Menten (MM) kinetics obtained in a bulk ATPase assay [〈VATP〉 = kcat[ATP]/(KM + [ATP]), with kcat = 95 ± 3s-1 and KM = 53 ± 4 μM] agree with the ATP dependence of vU and vZ (KM constrained to 53 μM, 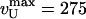 bp/s, and
bp/s, and 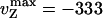 bp/s, Fig. 4A). This agreement constitutes a good control for our results. However, that the measured value of kcat is subject to the usual caveats of bulk measurements, namely the possible presence of inactive enzymes, means that the quoted value of that kcat is a lower bound. The unwinding lifetime 〈τU〉 = 0.83 ± 0.08 s is ATP-independent (Fig. 4D), a feature also observed for RecBCD (22, 23). This result suggests that UvrD's dissociation rate from ssDNA is not affected by its ATPase activity, even though the latter is stimulated by ssDNA binding. It is consistent with these observations that 〈NU〉 displays a MM kinetics similar to 〈vU〉 (KM constrained to 53 μM, and
bp/s, Fig. 4A). This agreement constitutes a good control for our results. However, that the measured value of kcat is subject to the usual caveats of bulk measurements, namely the possible presence of inactive enzymes, means that the quoted value of that kcat is a lower bound. The unwinding lifetime 〈τU〉 = 0.83 ± 0.08 s is ATP-independent (Fig. 4D), a feature also observed for RecBCD (22, 23). This result suggests that UvrD's dissociation rate from ssDNA is not affected by its ATPase activity, even though the latter is stimulated by ssDNA binding. It is consistent with these observations that 〈NU〉 displays a MM kinetics similar to 〈vU〉 (KM constrained to 53 μM, and 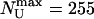 bp, Fig. 4C) with
bp, Fig. 4C) with 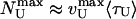 . The rate vZ follows the same MM kinetics as 〈vU〉, with 〈|vZ|/vU〉 = 1.17 ± 0.03 over the whole ATP concentration range (Fig. 4 A and B). This finding demonstrates that these slow rezipping (Z) events are limited by the ATP-dependent enzyme translocation, in contrast with the fast rehybridization events (H), whose rate is ATP independent.
. The rate vZ follows the same MM kinetics as 〈vU〉, with 〈|vZ|/vU〉 = 1.17 ± 0.03 over the whole ATP concentration range (Fig. 4 A and B). This finding demonstrates that these slow rezipping (Z) events are limited by the ATP-dependent enzyme translocation, in contrast with the fast rehybridization events (H), whose rate is ATP independent.
Fig. 4.
Rates, unwinding and rezipping extents and lifetimes as a function of ATP. (A) UvrD single-molecule unwinding rate 〈vU〉 (blue), rezipping rate 〈vZ〉 (red), and bulk ATP hydrolysis rate VATP (magenta) are fitted to the same MM kinetics. (B) The ratio 〈|vZ|/vU〉 is ATP-independent. The error on 〈vz〉/vu is only statistical. Because the value at 500 μM results from 288 points against typically 50 for the others, the associated error is much smaller and dominates the global mean value. (C) The mean unwinding extent NU follows the same MM kinetics as the unwinding rate. (D) The unwinding lifetime 〈τU〉 is ATP-independent. Each point is the average over histograms obtained on typically five DNA molecules.
Helicase Activity at Smaller Forces and Higher Enzymatic Concentration. At low concentrations of enzyme ([UvrD] < 1 nM), we observe isolated unwinding bursts only when F > 30 pN (Fig. 5A). However, by increasing the concentration of UvrD to 50 nM (>Kd = 10 nM), we can observe unwinding at very low forces (Fig. 2C). In this regime, individual events cannot be distinguished. This event bunching is due to the increased stability of the unwound strands against reannealing resulting from their coating by UvrD. It is therefore impossible to measure the number of base pairs unwound per event NU at such concentrations. However, the rate of unwinding is well defined and is very similar to the high force rate (≈200 ± 60 bp/s at [ATP] = 500 μM and [UvrD] = 50 nM). This rate is difficult to compute accurately because the kinetics of UvrD binding to the ssDNA generated in the wake of the complex is unknown. Thus, the calibration factor δL(F) cannot be determined. It is bound between its value for bare ssDNA and its equilibrium value at the studied UvrD concentration, which differ by 15%. It is nevertheless remarkable that vU varies by <20% between F = 3 and 35 pN because the enzyme works energetically downhill at high forces but uphill below 5 pN (recall that, for F < 5 pN, the molecule shortens as it is unwound; Fig. 1C). This result implies that our rate measurements on a single helicase at high forces can be extrapolated to zero force. Because the force does not affect the velocity, the enzyme rate-limiting step is associated neither with the enzyme's displacement nor with DNA opening.
Fig. 5.
(A) Single helicase activity is observed only above 30 pN. ([UvrD] ≈ 0.25 nM, [ATP] = 500 μM, a low-pass filter at 1 Hz was applied to the time trace for clarity). (B) Above 30 pN (Right), the separated strands behind the helicase are slightly mismatched in the stressed strand as compared with the free one. This mismatch inhibits rehybridization as long as the enzyme binds to the fork and thus hinders nucleation. When UvrD dissociates, reannealing can proceed from the seed provided by the fork. Below 30 pN, the kinetic barrier preventing reannealing behind the helicase is lowered so the strands are able to rehybridize behind the helicase, preventing any observation of an unwinding signal. (C) Kinetic scheme of UvrD activity. E refers to free enzyme, Dn to free DNA with n·δz bp unwound. 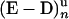 and
and 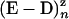 denote the UvrD–DNA complexes in U and Z states respectively, with n·δz bp unwound. Dashed arrows indicate events that are due to resumption of the enzymatic activity by the same enzyme or by another one bound to the ssDNA fraction. Note that kH corresponds to the rehybridization of 1 bp, in contrast with ku and kz, which correspond to steps of δz bp.
denote the UvrD–DNA complexes in U and Z states respectively, with n·δz bp unwound. Dashed arrows indicate events that are due to resumption of the enzymatic activity by the same enzyme or by another one bound to the ssDNA fraction. Note that kH corresponds to the rehybridization of 1 bp, in contrast with ku and kz, which correspond to steps of δz bp.
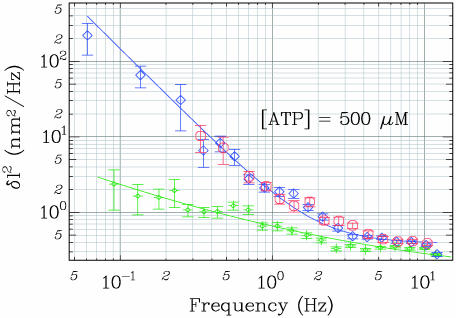
Stochastic Stepping of UvrD Along Its Substrate Increases the Noise Level. We have performed a Fourier analysis of the noise associated with the measurement of the molecule's extension. When a helicase is not actively unwinding the studied molecule, its extension remains constant (vU = 0). The fluctuations in extension are solely due to the Brownian fluctuations of the bead and are characterized by a frequency-independent spectrum (for frequencies f < 30 Hz at F = 35 pN). In contrast, during a burst of unwinding activity, the mean square fluctuations in extension δL2 = (L(t) - 〈vU〉t)2 are enhanced by the stochastic stepping of the enzyme. We use this increased noise to estimate the helicase step size δz, i.e., the number of bases opened per enzymatic cycle (24). In Fourier space, this extra noise increases at low frequencies as A/f2 (Fig. 6). The magnitude of A is related to the enzymatic rate 〈vU〉 and step size δz by A = δz〈vU〉/2π2, assuming that the duration of enzymatic cycles follows a Poisson distribution, i.e., that a single biochemical step limits the enzymatic turnover (25, 26). If there are two or more steps with comparable rate constants that limit the enzymatic turnover, then the model predicts that δz is a lower bound for the step size. The more rate-limiting steps, the more regular the cycle and the greater the step size required to produce a given amplitude of stochastic noise. Our data yield δz = 0.8 ± 0.15 nm corresponding to 6 ± 1.5 bp unwound per cycle, a value consistent with stop-flow estimates of ≈4–5 bp (27). A similar analysis of the rezipping data yields the same step size.
Fig. 6.
The average power spectra of unwinding (blue, n = 438) and rezipping activity (red, n = 291) are fitted to δl2 = δz〈vU〉/2π2f2 + b, leading to the same step size δz = 6 ± 1.5 bp. Experimental noise between activity bursts (green, n = 424) is shown for comparison.
Because of smaller processivity at low [ATP], we estimate δz only at saturating [ATP]. In principle, we cannot rule out that the step hereby estimated actually consists of a series of sequential smaller steps separated from the next series by a pause. The MM kinetics for the rate would require these pauses to be ATP dependent, which is very unlikely. The value of δz might also be overestimated due to variability of the rate with the sequence. Our method relies essentially on the same statistical principles used in a quenched flow estimate (27) and thus shares the same drawbacks.
Discussion
Strand Switching. To address the mechanism underlying the observations of UZ bursts, we can imagine three models. First, the enzyme might be able to switch polarity on the same strand from 3′-5′ to 5′-3′ in the course of its translocation. Second, when the complex dissociates, rehybridization of the two strands could be hindered by another enzyme that happens to be translocating 3′-5′ on the complementary strand. Third, the enzyme might switch strands in the course of unwinding and end up translocating on the complementary strand. Such a strand-switching mechanism could involve a partial or total release of the enzyme from its substrate. The first hypothesis is incompatible with previous results demonstrating that UvrD translocation occurs only with a 3′-5′ directionality (10). The second one is highly unlikely: at [UvrD] = Kd = 10 nM, the mean distance between two helicases bound to ssDNA is of the order of 20 nt because, at saturation, one monomer occupies 10 nt (28). When we reduce the UvrD concentration to our working conditions (0.25 nM), the mean distance l between monomers reaches l ≈ 20·10/0.25 = 800 nt. This distance is larger than the average number of base pairs unwound: 〈NU〉 ≈ 240 bp. Therefore, the probability for the fork to be blocked by an enzyme translocating on the displaced strand is very small. We deduce that UvrD switches strands in the course of its translocation, actively unwinding dsDNA as it moves 3′ to 5′ on one strand, and allowing passive rehybridization of the separated strands in its wake after it switches to moving 3′ to 5′ on the other (see details of the model in Fig. 5C). This strand-switching pathway is preferred to dissociation because 65% of the bursts observed at [ATP] = 500 μM are of this type. After a strand-switching transition, the enzyme can dissociate (UZH burst), switch strands a second time (UZU burst), or translocate back to its entry point. At this point, if the enzyme is bound to the nicked unstretched strand, it will dissociate (UZ burst with the Z part going back to the baseline as in Fig. 2B). Alternatively, if the enzyme is translocating back to its entry point on the intact stretched strand, it might possibly move further. This type of event produces a trace identical to the one resulting from a UZU event in which the second strand-switching transition (Z back to U) occurs right at the nick position (as in the first burst of Fig. 2D, UZUH).
The biological advantage of strand switching is not clear yet, but it is possible to form a conjecture. Recent experiments demonstrated that Srs2 (the ortholog of UvrD in Eukaryotes), in addition to its helicase activity, plays a regulatory role in homologous recombination. This regulation is mediated by the displacement of Rad51 recombinase from ssDNA (29, 30). Other helicases from T4 bacteriophage (gp41 and Dda) were also shown to displace streptavidin from biotinylated single-stranded oligonucleotides (31). If UvrD had to regulate the binding of proteins to DNA, displacing proteins along one strand and then along its complementary one might be an efficient mechanism to clear the DNA. In the following, we propose a new kinetic scheme to describe strand switching and fully characterize it by using our data.
Kinetic Scheme of UvrD Activity. Our single-molecule experiments allow us to deduce all of the rate constants defined in the reaction pathway (Fig. 5C) at [ATP] = 500 μM (Table 1). The rate constants ku and kz are simply computed from the rates of unwinding and rezipping by using the estimate for the step size: ku = 〈vU〉/δz = 41.3 ± 4 s-1, and similarly kz = 〈vZ〉/δz = 47.1 ± 5 s-1. The value of ku is approximately three times larger than quenched flow estimates (27, 32), a significant but not unusual difference when comparing single-molecule and bulk assays. The causes of this discrepancy still remain to be fully understood.
Table 1. Definitions and values (at [ATP] = 500 μM) of the rate constants of the proposed kinetic pathway.
| Reaction | Rate constant, s-1 |
|---|---|
| Unwinding | kU = 41.3 ± 4 |
| Strand switching from U state |
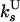 = 0.67 ± 0.07 = 0.67 ± 0.07 |
| Dissociation from U state |
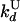 = 0.36 ± 0.04 = 0.36 ± 0.04 |
| Rezipping | kZ = 47.1 ± 5 |
| Strand switching from Z state |
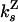 = 0.37 ± 0.2 = 0.37 ± 0.2 |
| Dissociation from Z state |
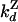 = 0.034 ± 0.02 = 0.034 ± 0.02 |
| Rehybridization | kH = 2,300 ± 200 |
| Rescue from H to U state |
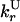 — — |
| Rescue from H to Z state |
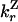 — — |
Let 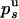 or
or 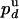 (
(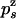 or
or 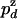 ) be the probabilities per cycle that the enzyme switches strands or dissociates in the course of an unwinding (rezipping) event. The processivity pu, defined as the probability per cycle to perform one enzymatic step forward (i.e., neither switching strand nor dissociating) is related to
) be the probabilities per cycle that the enzyme switches strands or dissociates in the course of an unwinding (rezipping) event. The processivity pu, defined as the probability per cycle to perform one enzymatic step forward (i.e., neither switching strand nor dissociating) is related to 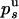 and
and 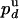 by
by 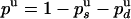 . But pu is also related to the mean number of enzymatic cycles performed during a burst of activity: 〈N〉 = 〈NU〉/δz = 240/6 = 40 ± 13 cycles, so pu = exp(-1/〈N〉) = 0.975 ± 0.009. Therefore,
. But pu is also related to the mean number of enzymatic cycles performed during a burst of activity: 〈N〉 = 〈NU〉/δz = 240/6 = 40 ± 13 cycles, so pu = exp(-1/〈N〉) = 0.975 ± 0.009. Therefore, 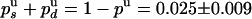 . On the other hand, the ratio of UZ to UH events (288/155) must be equal to the ratio of probabilities
. On the other hand, the ratio of UZ to UH events (288/155) must be equal to the ratio of probabilities 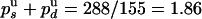 . We thus deduce
. We thus deduce 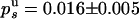 and
and 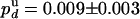 . Because the probabilities
. Because the probabilities 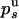 and
and 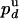 are related to the rate constants through
are related to the rate constants through 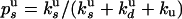 and
and 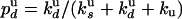 , we deduce
, we deduce 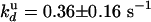 and
and 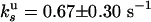 .
.
A similar analysis can be done for the rate constants on the rezipping (Z) pathway. It shows that the probability distribution of the number of base pairs rezipped (Nz) must be proportional to 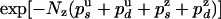 . Fitting the data for Nz to an exponential distribution yields
. Fitting the data for Nz to an exponential distribution yields 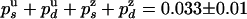 . Using the previous values of
. Using the previous values of 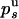 and
and 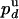 , we deduce that
, we deduce that 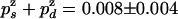 . From the ratio of UZH to UZU events (3/33), we obtain
. From the ratio of UZH to UZU events (3/33), we obtain 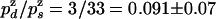 . This result allows us to compute
. This result allows us to compute 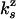 and
and 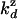 as previously done for
as previously done for 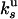 and
and 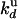 :
: 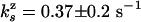 and
and 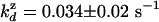 .
.
The small difference between vU and vZ shows that the rate of UvrD on DNA is only slightly affected by the enzyme having to open the strands or by the fork closing in its wake (Fig. 4B). These results directly suggest that the unwinding mechanism is active. Because we expect the velocity of UvrD on ssDNA to obey vU ≤ vssDNA ≤ vZ, our results imply that vssDNA ≈ 270 bp/s. We observe that the step size is the same for the U and Z events. Because 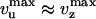 , it is reasonable to assume that the enzymatic efficiencies for unwinding, rezipping, and ssDNA translocation are similar. Thus, we estimate by using the bulk ATPase assay that UvrD consumes
, it is reasonable to assume that the enzymatic efficiencies for unwinding, rezipping, and ssDNA translocation are similar. Thus, we estimate by using the bulk ATPase assay that UvrD consumes 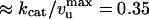 ATP/bp unwound. However, bulk ATPase consumption may not result solely from the enzyme's translocation. Therefore, the observed kcat may not reflect the ATP hydrolysis rate during translocation. Moreover, this estimate must be taken with caution because it is prone to the usual errors inherent in bulk estimates (presence of inactive enzymes, etc).
ATP/bp unwound. However, bulk ATPase consumption may not result solely from the enzyme's translocation. Therefore, the observed kcat may not reflect the ATP hydrolysis rate during translocation. Moreover, this estimate must be taken with caution because it is prone to the usual errors inherent in bulk estimates (presence of inactive enzymes, etc).
The Stretching Force Affects DNA Rehybridization in the Wake of the Complex. All helicase assays require a means to prevent the two DNA strands from rehybridizing in the wake of the enzymatic complex. Although in bulk assays this is usually done by using single-strand binding proteins, in our single-molecule experiment, the force F stretching the DNA substrate presents a very efficient way to solve this reannealing problem. In our assay, for the strands to rehybridize in the wake of the enzyme, a thermal fluctuation must provide the activation energy ΔEa required to match the separated unloaded strand with the stretched one. We estimate that activation energy to be: ΔEa ≈ N·F·δL(F), where N ≈ 10 (33) is the number of nucleotides covered by the helicase footprint and δL(F) is the overextension per base pair of stretched ssDNA in comparison with dsDNA (assuming that the distance between bases bound by the helicase is the same as in dsDNA). At F = 35 pN, δL(F) = 0.135 nm, so that Δ Ea ≈ 10 kBT, which reduces the rehybridization frequency by more than four orders of magnitude. The stretching force combined with the enzyme's footprint thus create a kinetic barrier that prevents reannealing during the timespan of an unwinding burst. This finding explains why we observe unwinding events only when F > 30 pN (Fig. 5 A and B). As the helicase dissociates, reannealing can proceed from the fork through successive matching of single base pairs. The kinetic barrier is thus drastically reduced, and rehybridization is fast.
At low forces (F < 30 pN), the tension is not sufficient to build a kinetic barrier that prevents reannealing. In this regime, it is possible to generate a kinetic barrier as usually done in bulk experiments, i.e. by coating the separated single strands with single-strand binding protein or with UvrD itself, which has a strong affinity for ssDNA (kd ≈ 10 nM for UvrD). Indeed, we are able to observe unwinding activity at F = 3 pN if we increase UvrD concentration above 10 nM (Fig. 2C).
However, at high enzymatic concentrations, the observed unwinding activity is not simply related to the UvrD concentration (because many enzymes may be bound and inactive). To overcome this limitation, stop-flow experiments have studied the activity of helicases prebound to short oligomers (20–30 bps long) and quickly mixed with ATP (27). In that situation, the helicase itself sets a kinetic barrier that hinders DNA reannealing, favoring the complete separation of the two DNA strands.
The use of specific experimental conditions to prevent reannealing of the separated strands is the most likely reason for the differences between single-molecule results and bulk data, namely the observation of single-molecule activity at subnanomolar enzymatic concentrations where none was reported in bulk assays, and the shift between the average number of base pairs unwound in the single-molecule assay (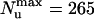 bp) compared with previous single-turnover experiments (45 bp; ref. 27). The force-generated lowering of the energy required to melt the DNA might also be another processivity-increasing factor.
bp) compared with previous single-turnover experiments (45 bp; ref. 27). The force-generated lowering of the energy required to melt the DNA might also be another processivity-increasing factor.
Although at this stage we cannot draw definite conclusions from these measurements about the oligomeric state of the complex, our data show that, under certain conditions, UvrD could be much more processive than assumed from its bulk in vitro behavior. It is also possible that the stretching force, besides preventing reannealing of the separated strands, helps the enzyme to plow through the DNA. This effect does not influence significantly the rate of unwinding but could affect the enzymatic processivity.
Supplementary Material
Acknowledgments
We thank T. M. Lohman and A. M. Pyle for critical discussions on the manuscript and G. Charvin and O. A. Saleh for a careful reading of the manuscript. We are grateful to J. F. Allemand for his help in improving the experimental set-up and to H. Q. Xu for his assistance in protein purification. This work was supported by grants from Association pour la Recherche sur le Cancer, Centre National de la Recherche Scientifique, Ecole Normale Supérieure, the Universities of Paris VI and Paris VII, and the European Mol Switch Project (IST-2001-38036).
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: ssDNA, single-stranded DNA; dsDNA, double-stranded DNA; MM, Michaelis-Menten.
References
- 1.Delagoutte, E. & Hippel, P. H. V. (2002) Q. Rev. Biophys. 35, 431-478. [DOI] [PubMed] [Google Scholar]
- 2.Delagoutte, E. & Hippel, P. H. V. (2003) Q. Rev. Biophys. 36, 1-69. [DOI] [PubMed] [Google Scholar]
- 3.Hua, W., Chung, J. & Gelles, J. (2002) Science 295, 844-848. [DOI] [PubMed] [Google Scholar]
- 4.Lohman, T. M. & Bjornson, K. P. (1996) Annu. Rev. Biochem. 65, 169-214. [DOI] [PubMed] [Google Scholar]
- 5.West, S. C. (1996) Cell 86, 177-180. [DOI] [PubMed] [Google Scholar]
- 6.Soultanas, P. & Wigley, D. (2001) Trends Biochem. Sci. 26, 47-54. [DOI] [PubMed] [Google Scholar]
- 7.Sancar, A. (1994) Science 266, 1954-1956. [DOI] [PubMed] [Google Scholar]
- 8.Yamaguchi, M., Dao, V. & Modrich, P. (1998) J. Biol. Chem. 273, 9197-9201. [DOI] [PubMed] [Google Scholar]
- 9.Bruand, C. & Ehrlich, S. D. (2000) Mol. Microbiol. 35, 204-210. [DOI] [PubMed] [Google Scholar]
- 10.Matson, S. W. (1986) J. Biol. Chem. 261, 10169-10175. [PubMed] [Google Scholar]
- 11.Runyon, G. T. & Lohman, T. M. (1989) J. Biol. Chem. 264, 17502-17512. [PubMed] [Google Scholar]
- 12.Brosh, R. M. J. & Matson, S. W. (1997) J. Biol. Chem. 272, 572-579. [DOI] [PubMed] [Google Scholar]
- 13.Saito, I. & Stark, G. R. (1986) Proc. Natl. Acad. Sci. USA 83, 8664-8668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Yamamoto, Y., Ogawa, T., Shinagawa, H., Matsuo, H. & Ogawa, H. (1986) J. Biochem (Tokyo) 99, 1579-1590. [DOI] [PubMed] [Google Scholar]
- 15.Xu, H. Q., Deprez, E., Zhang, A. H., Tauc, P., Ladjimi, M. M., Brochon, J. C., Auclair, C. & Xi, X. G. (2003) J. Biol. Chem. 278, 34925-34933. [DOI] [PubMed] [Google Scholar]
- 16.Avron, M. (1960) Biochim. Biophys. Acta 40, 257-261. [DOI] [PubMed] [Google Scholar]
- 17.Strick, T. R., Allemand, J. F., Bensimon, D. & Bensimon, A. (1996) Science 271, 1835-1837. [DOI] [PubMed] [Google Scholar]
- 18.Strick, T. R., Croquette, V. & Bensimon, D. (2000) Nature 404, 901-904. [DOI] [PubMed] [Google Scholar]
- 19.Maier, B., Bensimon, D. & Croquette, V. (2000) Proc. Natl. Acad. Sci. USA 97, 12002-12007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Mechanic, L. E., Latta, M. E. & Matson, S. W. (1999) J. Bacteriol. 181, 2519-2526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ali, J. A., Maluf, N. K. & Lohman, T. M. (1999) J. Mol. Biol. 293, 815-834. [DOI] [PubMed] [Google Scholar]
- 22.Bianco, P. R., Brewer, L. R., Corzett, M., Balhorn, R., Yeh, Y., Kowalczykowski, S. C. & Baskin, R. J. (2001) Nature 409, 374-378. [DOI] [PubMed] [Google Scholar]
- 23.Dohoney, K. M. & Gelles, J. (2001) Nature 409, 370-374. [DOI] [PubMed] [Google Scholar]
- 24.Svoboda, K., Mitra, P. P. & Block, S. M. (1994) Proc. Natl. Acad. Sci. USA 91, 11782-11786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Charvin, G., Bensimon, D. & Croquette, V. (2002) Single Mol. 3, 43-48. [Google Scholar]
- 26.Dekker, N. H., Rybenkov, V. V., Duguet, M., Crisona, N. J., Cozzarelli, N. R., Bensiomon, D. & Croquette, V. (2002) Proc. Nat. Acad. Sci. USA 99, 12126-12131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ali, J. A. & Lohman, T. M. (1997) Science 275, 377-380. [DOI] [PubMed] [Google Scholar]
- 28.Maluf, N. K. & Lohman, T. M. (2003) J. Mol. Biol. 325, 889-912. [DOI] [PubMed] [Google Scholar]
- 29.Veaute, X., Jeusset, J., Soustelle, C., Kowalczykowski, S. C., Cam, E. L. & Fabre, F. (2003) Nature 423, 309-312. [DOI] [PubMed] [Google Scholar]
- 30.Krejci, L., Komen, S. V., Li, Y., Villemain, J., Reddy, M. S., Klein, H., Ellenberger, T. & Sung, P. (2003) Nature 423, 305-309. [DOI] [PubMed] [Google Scholar]
- 31.Morris, P. D. & Raney, K. D. (1999) Biochemistry 38, 5164-5171. [DOI] [PubMed] [Google Scholar]
- 32.Maluf, N. K., Fisher, C. J. & Lohman, T. M. (2003) J. Mol. Biol. 325, 913-935. [DOI] [PubMed] [Google Scholar]
- 33.Runyon, G. T., Wong, I. & Lohman, T. M. (1993) Biochemistry 32, 602-612. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.