Abstract
Colocalization of proteins that are part of the same signal transduction pathway via compartmentalization, scaffold, or anchor proteins is an essential aspect of the signal transduction system in eukaryotic cells. If interaction must occur via free diffusion, then the spatial separation between the sources of the two interacting proteins and their degradation rates become primary determinants of the time required for interaction. To understand the role of such colocalization, we create a mathematical model of the diffusion based protein–protein interaction process. We assume that mRNAs, which serve as the sources of these proteins, are located at different positions in the cytoplasm. For large cells such as Drosophila oocytes we show that if the source mRNAs were at random locations in the cell rather than colocalized, the average rate of interactions would be extremely small, which suggests that localization is needed to facilitate protein interactions and not just to prevent cross-talk between different signaling modules.
Keywords: protein diffusion, protein mobility, intracellular reaction, protein localization
Interesting biological processes are not the result of the activity of a single protein. Instead, they result from controlled and coordinated activities of multiple proteins (1), which may or may not be synthesized from mRNA molecules that are close to each other. Recent experimental progress in mapping the organism-wide protein–protein interaction network has produced a surge of interest in functional inference based on connectivity structure of cellular proteins. The edges in these networks represent protein–protein interactions that have spatial and temporal dimensions. The existence of mutual binding sites is necessary for interactions; however, this is not sufficient, because the actual binding process requires diffusion that may be too slow for the lifetime of these interacting proteins. This is particularly true if the spatial volume of the cellular environment is relatively large and signaling proteins are in small numbers and/or have a short half-life.
For >80% of the yeast transcriptome, there is less than one mRNA transcript per cell (2), and for 95% of the human transcriptome there are 0.5–5 mRNA transcripts per cell (3). Because the rate of translation is proportional to the number of promoter sites and mRNA molecules, the small numbers of transcripts imply relatively infrequent translational events. It has been shown experimentally that in eukaryotic cells, stochasticity of transcriptional events propagates to the translational process and results in large variability in the number of proteins per cell even in a clonal population (4). Little theoretical work has been done to understand the consequences of stochastic fluctuation of protein concentration on protein–protein interactions, which form the basis of the majority of biological signaling pathways. In particular, very little is known about the dependence of protein interaction dynamics on the half-life and distance between the origins of interacting proteins. If proteins had an extremely long half-life, then protein interaction would be certain even in large cells such as Xenopus (average radius of 600 μm), Drosophila oocytes (average radius of 300 μm), or neuronal cells (length range of 1–5 mm). In fact, the half-lives of proteins in a living cell range from a few seconds to many days (5), and the protein abundance in yeast can range from <50 to >1 million molecules per cell (6).
It has been well documented that in eukaryotes, members of signaling pathways often are organized into multiprotein assemblies and localized via anchor and scaffold proteins (7, 8). In Drosophila and Xenopus oocytes, spatial and temporal control of protein synthesis during oogenesis and early embryogenesis underlie the establishment of polarity and subsequent patterning of the body axes (9, 10), and 75% of the yeast proteome is found in 22 distinct subcellular locations (11). It is commonly thought that this colocalization is an insulation mechanism that prevents “cross-talk” between signaling pathways. To verify this claim and to understand the role of colocalization and signal complex formation, we create a mathematical model of a free diffusion-based protein–protein interaction in the absence of colocalization of the interacting proteins or of their mRNA sources.
The aim of this study is to find the average rate of interactions between two protein species that were made from mRNA transcripts that are allowed to diffuse to a random position in the cytoplasm. This quantitative estimate of the interaction probabilities of freely diffusing proteins will help us understand the need for cellular localization and the relative importance of physical parameters such as diffusion coefficient, protein synthesis, and degradation rate. The outline of this article is as follows: first, we describe the model of diffusion-dependent protein–protein interaction; then we derive the expected rate of interactions when the point sources of proteins are located a certain distance from each other; we next verify this claim via simulation; then, approaching our key concern, we derive the expected rate of interactions when mRNA point sources can be located at random in a cell of radius R; finally, we discuss the implications of our result for understanding the need for localized accumulation of interacting proteins.
Description of the Model
We limit our discussions to freely diffusing signaling proteins such as protein kinase and phosphatase. We make the following assumptions in our model. (i) Ribosomes, RNases, and other factors involved in protein degradation and synthesis have long half-lives relative to the signaling proteins under consideration and occur in large copy numbers. (ii) Protein translation is constitutive, and the rate of protein degradation does not vary significantly over the cell. (iii) The mRNA transcripts serve as a point source for the proteins for which they code. (iv) mRNAs coding for freely diffusing cytoplasmic signaling proteins are located randomly in the cytoplasm (13). (v) The process of translation is such that the probability of proteins being made in the time interval (t, t + dt) is independent of the number of proteins made before time t. (vi) The process of degradation is such that the probability that a protein is degraded in the time interval (t, t + dt) is independent of the number of proteins degraded before time t.
Assumption i implies that protein synthesis and degradation activities are distributed uniformly throughout the cell. Assumption ii implies that the rate of translation, β, and the rate of degradation, δ, are time-independent. Assumption iii is justified as freely diffusing proteins are made from mRNAs that are not bound to endoplasmic reticulum and have multiple ribosomes on them; there can be ≥10 on average. This structure, known as the “polysome,” is rather large and diffuses little as a result (12). Assumptions v and vi imply that the process of protein degradation and synthesis satisfy the Markov assumption and form a pair of competing Poisson processes.
Fig. 1 shows the model of the protein interaction process that we use. As soon as a protein is translated it undergoes Brownian motion in the three-dimensional cellular environment. At any given time, there is a small constant probability that this protein may be degraded. If at any time two different types of proteins come close enough to each other for the first time, then we assume that interaction has taken place. Once a protein moving under Brownian motion has visited a point, it visits the neighborhood of this point many times; therefore it is sufficient to just consider the first time the two Brownian paths come within a small distance of each other. We do not explicitly model the mRNA movement, because mRNA is believed to be localized and this process involves many steps that are not well understood (14).
Fig. 1.
Model of protein interactions. Proteins are of two types: I and II. Protein of type I is translated from mRNA at rate β1, and that of type II is translated at rate β2. Protein of type I is degraded at rate δ1 and that of type II is degraded at rate δ2. The product of degradation is denoted by empty braces. As soon as a protein is made, it diffuses according to a three-dimensional Brownian process. If paths of interacting proteins come within distance ε of each other, then these proteins are considered to have interacted (ε is about a protein diameter).
Expected Rate of Interactions
Using the protein interaction model described in the previous section, we would like to derive the probability that two proteins that are synthesized at a certain distance apart from each other will ever interact before either one of them is degraded. Before we derive the probability of interaction, we note the changes that occur in the cellular environment from a perspective of a protein of type I, which is born at time t0. Because the protein degradation process is Markovian and the death rate is constant, this protein will have an exponentially distributed age, τ (15). As the system evolves, we must keep track of the positions of all the proteins of type II that were born before and during the time interval (t0, t0 + τ). Note that some of the proteins of type II that are born after time t0 could die before the time t0 + τ, whereas some could live past the time t0 + τ. The transience of the Brownian paths caused by random birth and death make this a complicated problem. From now on we refer to protein synthesis as a birth process and protein degradation as a death process. From the nature of the problem, it is clear that we must work with the sample paths of each individual protein rather than that of the population of the proteins of each type as a whole.
We denote the position of proteins j of type i by
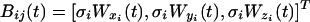 |
for i = 1, 2, which represents a three-dimensional nondrifting and unbiased Brownian motion, where the origins of each type of protein are at a distance r away from each other. Wi(t) is a one-dimensional standard Brownian motion such that for 0 ≤ s ≤ t the increment W(t) - W(s) have a Gaussian distribution with mean equal to 0 and variance equal to σ2(t - s) with diffusion parameter 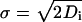 where Di is the diffusion coefficient of protein i. By nondrifting we mean that there are no external fields, and by unbiased we mean that the protein takes steps in every direction with the same probability and the step sizes in each direction have an identical distribution. Deriving the expected rate of pairs of Brownian trajectories that come within ε of each other is very hard analytically if we include the cell and the nuclear boundaries. Therefore, we neglect the boundaries and derive an estimate, which should provide a good first approximation to the real case, especially for large cells, or when half-life of protein is short.
where Di is the diffusion coefficient of protein i. By nondrifting we mean that there are no external fields, and by unbiased we mean that the protein takes steps in every direction with the same probability and the step sizes in each direction have an identical distribution. Deriving the expected rate of pairs of Brownian trajectories that come within ε of each other is very hard analytically if we include the cell and the nuclear boundaries. Therefore, we neglect the boundaries and derive an estimate, which should provide a good first approximation to the real case, especially for large cells, or when half-life of protein is short.
Let Xij(t) be the difference between position of protein i of type I and protein j of type II at time t. Because the difference of two Gaussian processes is another Gaussian process, we get that
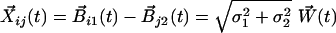 |
is also a Gaussian process with diffusion parameter
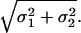 |
An important property of unbiased independent Brownian motion is that the process has spherical symmetry, which means that we only need to keep track of the magnitude of the difference of position. Letting Rij(t) = (1/σ)∥Xij(t)∥, we reduce the three-dimensional process, Xij(t), to a one-dimensional distance process. Protein interaction in terms of the Bessel process is illustrated in Fig. 2. We note that R(t) is a standard Bessel process and satisfies the Ito stochastic differential equation dR(t) = [dt/R(t)] + dW(t).
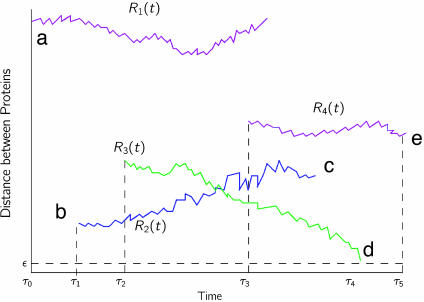
Fig. 2.
Illustration of the Bessel process that represents the three-dimensional problem of protein location as a one-dimensional problem of distance process. This figure describes events that can occur in the lifetime of a protein of type I that can interact only with another protein of type II. a, Protein P of type I is born at some time, τ0. As soon as it is born, it finds that there are certain proteins of type II that are alive. The time evolution of the distance is represented by R1(t). b, At time τ1, a protein of type II is born. Notice that distance r0, which is the initial distance between this newly born protein of type II and P, varies as P undergoes Brownian motion. Again, the time evolution of the distance between protein P and the protein of type II born at τ1 is represented by R2(t). c, Before this protein gets a chance to come close enough to P, it gets degraded. d, Protein of type II born at time τ2 is able to interact with P. Formally, we say that the Bessel process R3(t) is absorbed at ε. e, Protein of type II born at τ3 does not get enough time to interact with protein P, because P is degraded at time τ5.
The probability that the Bessel process, R(t), is in interval [r, r + dr] given that it started from r0 is given by p(r, r0, t)dr, where p(r, r0, t) is the transition density. If the diffusion parameter σ ≠ 1, then the probability shown above has to be scaled to p(r/σ, r0/σ, t)dr/σ. As shown in ref. 16, the transition density of the standard Bessel process is given by
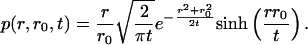 |
[1] |
Let fε(r, δ) denote the probability that the two proteins of different types, starting from distance r apart, will meet before either one of them is degraded. Formally, fε(r, δ) = P[τε < τδ|R(0) = r], where τε is the random time required for these proteins to diffuse to within a distance of ε of each other, and τδ is the minimum of their ages. Because the ages of each protein is exponentially distributed, τδ is exponentially distributed with parameter δ = δ1 + δ2.
It is a standard fact that for a process on (0, ∞) with generator
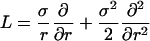 |
killed at a rate δ, the probability of reaching (0, ε), fε(r, δ), satisfies
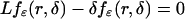 |
on (ε, ∞) and fε(ε, δ) = 1 (16). We show in Appendix a direct heuristic way to derive fε(r, δ) and show that for r > ε
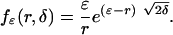 |
[2] |
If the diffusion parameter σ ≠ 1, then the probability that σR(t) starting at r with death rate δ ever comes within ε of the origin is fε(r/σ, δ). If M(t, r0) denotes the expected rate of interactions or ε meetings in time interval [0, t] of proteins born at different times in this interval with initial separation of r0 between their mRNA origins, then the mean is given by m(r0) = limt→∞[M(t, r0)/t]. Keeping in mind that we must consider both the cases in which protein of each type is born first, m(r0) is given by
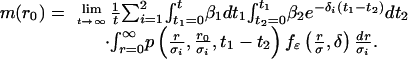 |
[3] |
The exponential term, e-δi(t1-t2), in the above equation is the probability that the protein born first is not degraded until after the time the protein of other type is born. The resulting equation for the mean rate of interactions is given by
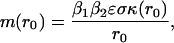 |
[4] |
where the term κ(r0)is given by
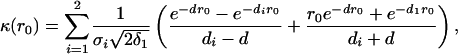 |
if δ1 ≠ δ2 and σ1 ≠ σ2. When δ1 = δ2 and σ1 = σ2,
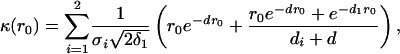 |
where 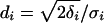 ,
, 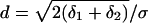 ,
, 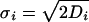 ,
, 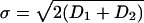 and Di is the diffusion coefficient of protein of type i. In the derivation of the above equation we used the assumption that the interaction distance, ε, is much smaller than the separation between the mRNA point sources, r0.
and Di is the diffusion coefficient of protein of type i. In the derivation of the above equation we used the assumption that the interaction distance, ε, is much smaller than the separation between the mRNA point sources, r0.
To verify Eq. 4 we simulated the interaction process with and without the cell boundary. The most important consideration when doing a discrete simulation of a continuous time process is the choice of an appropriate time step. Usually, the time step is chosen to be much smaller than the time scale of the most frequent events of interest, so that the probability of more than one event occurring during a single time step is negligible. Furthermore, to detect an interaction event, the distance traveled by a diffusing particle must be much smaller than the distance required for two proteins to interact. We used an adaptive step method for which time steps are chosen depending on the minimum of all pairs of distances between interacting particles.
By using a time step of 2 μs, interactions and births were counted after the elapse of a pre-steady-state time of 100 min, and then the simulation was run for an additional 1,000 min of real time. The reason for such a long simulation is that we are estimating a very small probability, and as a result a much longer run is needed to get a parameter estimate with a variance smaller than the estimate itself. Thirty-five simulations were done for each separation distance with point sources symmetric about the center of the cell.
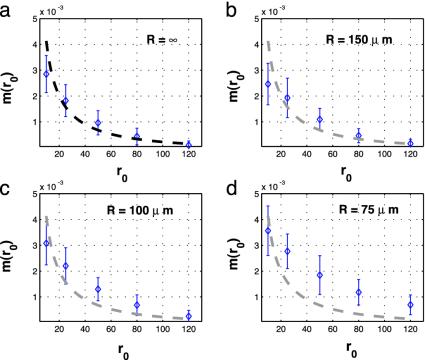
As can be seen in Fig. 3, for a cell radius of ≈100 μm (less than half the size of a Drosophila oocyte) the formula accurately predicts the average rate of interactions per protein lifetime found by simulations. The reason why the formula and the simulation do not agree well for r0 < 5 μm is that we made a simplification that ε << r0 in the derivation of Eq. 4. As a result, as r0 ceases to be large compared with ε, the estimate worsens. Furthermore, as the cell gets smaller (radius <100 μm), the estimation deteriorates as proteins live long enough to be able to travel longer than the diameter of the cell; interestingly they still don't “forget” where they were made and show a strong dependence on the initial separation.
Fig. 3.
The average rate of interactions as a function of distance between mRNAs. Thirty-five simulations were performed for each separation, with a protein synthesis rate of one per 3.5 min, a protein half-life of 15 min, and a diffusion coefficient of 1 μm2/s for both types. An interaction distance of 100 Å was used. (a) No boundary case. (b) Spherical cell with radius 150 μm. (c) Spherical cell with a radius of 100 μm. (d) Spherical cell with a radius of 75 μm. The error bars are at mean ±1 standard deviation. Heavy dashed lines represent the predicted value from Eq. 4, which assumes no cell boundary.
Expected Rate of Interactions for a Randomly Located Pair of Origins
Now that we know that the formula is a good approximation for cells with a radius ≥100 μm, we ask the question we initially set out to answer. Suppose that the mRNAs of each type of protein were not colocalized but diffused out from the nucleus into the cytoplasm at a random position (13) such that any location in the cytoplasm is equally likely; what would be the average rate of interactions over all possible distances between the point sources? Let R denote the radius of the cell (assumed to be spherical). For a large cell we can safely neglect the volume of the nucleus, because it would be quite small relative to the volume of the cell. Let r be the distance between two points picked uniformly in a cell of radius R, then it can be shown (17) that the probability that this distance lies in the interval [r, r + dr] is given by
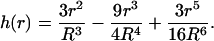 |
Thus, we can calculate the expected rate of interactions over all possible distances in [0, 2R] with n1 and n2 mRNAs of each type, respectively, as
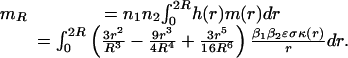 |
[5] |
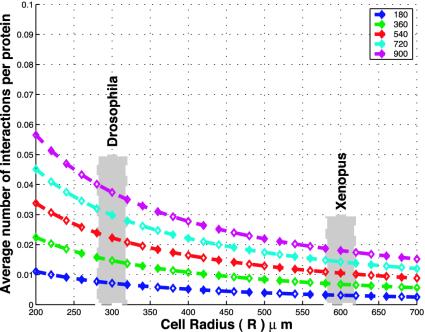
This integral was evaluated analytically, and a plot was made for several values of protein degradation rate and cell radii in the range of 200–600 μm by using a diffusion coefficient of 10-8 cm2/s (18–20) and four mRNA transcripts of each type (2, 3). Fig. 4 shows that the mean rate of interactions increases linearly with the half-life; however, even when the half-life is as large as 900 min (or 15 h) and there are four mRNAs of each type, the mean rate of interactions is <0.04. A value of 0.04 says that only 1 in 25 proteins ever interact with their intended partner before they are degraded.
Fig. 4.
Expected rate of interactions over all possible separations of mRNA sources as a function of half-life. The following parameters were used in Eq. 5: a protein synthesis rate (β1 and β2) of one per 2 min, number of mRNAs of type I and II (n1 and n2) of four each, a diffusion coefficient (D) of 10-8 cm2/s for both types, an interaction distance (ε) of 100 Å, and five values of half-life (δ), which are shown in the legend in minutes.
Discussion
Our goal in this article was to show that in a large cell, when proteins have a short half-life, there is an insignificant amount of cross-talk, because proteins would interact too few times to relay any significant signal. We approached this problem by modeling a protein interaction process without colocalization of mRNA point sources and have derived a relationship (Eq. 4) that estimates the expected rate of interactions between two freely diffusing proteins that are synthesized at separate locations from each other. The functional form of this equation, [β1β2εσκ(r0)]/r0, is intuitive: increases in birth rate (βi), the interaction distance (ε), and diffusion parameter (σ) increase the average rate of interactions, whereas the increase in distance between the mRNA origins decreases the mean rate of interactions. The parameter κ(r0) accounts for the transiency of paths and depends nonlinearly on the protein half-life and the distances between the sources, r0, of interacting proteins. The main result of this article is shown in Fig. 4, which clearly shows that, even for a large protein half-life of 15 h, only ≈1 in 25 proteins are expected to interact. Thus, we infer that colocalization is just as important for increasing the probability of interactions of intended signaling proteins as it is to suppress cross-talk between signaling pathways.
If the cellular boundary had been taken into consideration, it would not have been possible to obtain a closed-form formula for the mean rate of interactions. One of our assumptions is that proteins are constitutively expressed, but often transcription and translation are under tight regulatory control. Furthermore, for an interaction to result in an exchange of phosphate, for example, a protein must bind with its interacting partner in a lock-and-key type conformation; as a result, proteins must interact with each other many times before a collision with proper orientation and energy results in an actual reaction. The reasons described above imply that the mean rate of interactions in vivo most likely would agree well with the estimate shown in Fig. 4.
A signaling process having relay proteins with a short half-life gives the cell more control over its activity and range. Because of the short half-life, proteins won't diffuse too far and be involved in an unintended process, resulting in minimization of cross-talk between signaling modules. However, one can see in Fig. 4 that, even for modest distances between the mRNA origins, in large cells, for proteins with short half-lives, the mean rate of interactions per protein lifetime is low. If it were not for localization and signal complex formation, a significant proportion of proteins would die unproductively (i.e., without interacting) and a tremendous amount of energy would be wasted.
Even if the cellular environment were not crowded and did not contain spatial barriers (21–23), diffusion alone would not be sufficient for carrying out cellular processes at a significant rate in cells >50 μm in radius. The limitations of the short-range nature of diffusion may not afflict small secondary messengers (such as cAMP, inositol 1,4,5-trisphosphate, or Ca2+) (24), which can diffuse many times faster than proteins; however, the cell must use some mechanism to enrich the local concentration of short-lived interacting proteins. Anchor (8) and scaffold proteins (25) are some of the ways cells surmount the limitations of diffusion. Design of a reliable signaling system using intermediates that freely diffuse is a challenging engineering problem that evolution has solved by spatially constraining the positions of slowly diffusing intermediates while using faster diffusing intermediates (i.e., secondary messengers) to propagate signal over a larger distance. This design significantly increases the reliability and timing of individual signaling links within a signal transduction pathway, which otherwise would be plagued by undesirable large fluctuations in timing of time-critical cellular functions. The estimate of the average rate of protein interactions derived in this article shows clearly that, in large cells with a low number of mRNA transcripts (2, 3), unlocalized proteins with short half-lives most likely will not interact sufficiently nor rapidly enough to transmit a biologically meaningful signal. Thus, we are led to conclude that the role of localization is not only to prevent cross-talk between different signaling pathways but also to increase the probability of interactions of proteins that are within the same pathway.
Acknowledgments
N.N.B. thanks Daniel Gillespie, Dan Hershlag, Tobias Meyer, and the anonymous referees for critically reading the manuscript. This work was supported in part by National Institutes of Health Grant GM63817 (to Michael Levitt).
Appendix: Derivation of Probability of Interaction fε(r, δ)
Let f(r) ≡ fε(r, δ) be the probability that the standard three-dimensional Brownian motion starting at r with death rate δ comes within ε of the origin before death. Let dt denote the length of a small time interval, then in time dt the process has moved to f(r + dr). Because 1 - δdt is the probability of protein not being degraded in time dt, we have a recursive formulation using the mean value property of Brownian motion
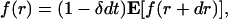 |
[6] |
where E [·] is the expectation operator. We do a second-order Taylor expansion of Eq. 6 and use the stochastic differential equation for dr, to get
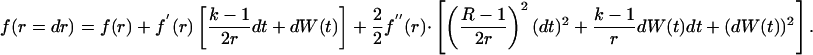 |
Because dt is small, (dt)2 ≈ 0 and dW(t) × dt ≈ 0; however, the variance term is significant because it is proportional to time and cannot be neglected. Noting that E(dW(t)2) = dt and E[dW(t)] = 0, we get the following second-order differential equation:
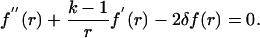 |
Using the boundary conditions f(ε) = 1 and f(∞) = 0, we can solve this equation (26) and find that the solution is (for three dimensions)
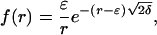 |
[7] |
where δ = δ1 + δ2.
References
- 1.Scott, J. D. & Pawson, T. (2000) Sci. Am. 282 (6), 72-79. [DOI] [PubMed] [Google Scholar]
- 2.Holstege, F. C., Jennings, E. G., Wyrick, J. J., Lee, T. I., Hengartner, C. J., Green, M. R., Golub, T. R., Lander, E. S. & Young, R. A. (1998) Cell 95, 717-728. [DOI] [PubMed] [Google Scholar]
- 3.Velculescu, V. E., Madden, S. L., Zhang, L., Lash, A. E., Yu, J., Rago, C., Lal, A., Wang, C. J., Beaudry, G. A., Ciriello, K. M., et al. (1999) Nat. Genet. 23, 387-388. [DOI] [PubMed] [Google Scholar]
- 4.Blake, W. J., Ern, M. K. A., Cantor, C. R. & Collins, J. J. (2003) Nature 422, 633-637. [DOI] [PubMed] [Google Scholar]
- 5.Varshavsky, A. (1996) Proc. Natl. Acad. Sci. USA 93, 12142-12149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ghaemmaghami, S., Huh, W.-K., Bower, K., Howson, R. W., Belle, A., Dephoure, N., O'Shea, E. K. & Weissman, J. S. (2003) Nature 425, 737-741. [DOI] [PubMed] [Google Scholar]
- 7.Garrington, T. P. & Johnson, G. L. (1999) Curr. Opin. Cell Biol. 11, 211-218. [DOI] [PubMed] [Google Scholar]
- 8.Pawson, T. & Scott, J. D. (1997) Science 278, 2075-2080. [DOI] [PubMed] [Google Scholar]
- 9.Johnstone, O. & Lasko, P. (2001) Annu. Rev. Genet. 35, 365-406. [DOI] [PubMed] [Google Scholar]
- 10.Kloc, M., Bilinski, S., Chan, A. P., Allen, L. H., Zearfoss, N. R. & Etkin, L. D. (2001) Int. Rev. Cytol. 203, 63-91. [DOI] [PubMed] [Google Scholar]
- 11.Huh, W.-K., Falvo, J. V., Gerke, L. C., Carroll, A. S., Howson, R. W., Weissman, J. S. & O'Shea, E. K. (2003) Nature 425, 686-691. [DOI] [PubMed] [Google Scholar]
- 12.Alberts, B., Johnson, A., Lewis, J., Raff, M., Roberts, K. & Walter, P. (2002) Molecular Biology of the Cell (Garland Science, New York).
- 13.Fusco, D., Accornero, N., Lavoie, B., Shenoy, S. M., Blanchard, J. M., Singer, R. H. & Bertrand, E. (2003) Curr. Biol. 13, 161-167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lipshitz, H. D. & Smibert, C. A. (2000) Curr. Opin. Genet. Dev. 10, 476-488. [DOI] [PubMed] [Google Scholar]
- 15.Karlin, S. & Taylor, H. M. (1975) A First Course in Stochastic Process (Academic, New York), 2nd Ed.
- 16.Ito, K. & McKean, H. P. (1996) Diffusion Processes and Their Simple Paths (Academic, New York).
- 17.Santalo, L. (1976) Integral Geometry and Geometric Probability (Addison–Wesley, Reading, MA).
- 18.Dayel, M. J., Hom, E. F. & Verkman, A. S. (1999) Biophys. J. 76, 2843-2851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gershon, N. D., Porter, K. R. & Trus, B. L. (1985) Proc. Natl. Acad. Sci. USA 82, 5030-5034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Jacobson, K. & Wojcieszyn, J. (1984) Proc. Natl. Acad. Sci. USA 81, 6747-6751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bray, D. (1998) Annu. Rev. Biophys. Biomol. Struct. 27, 59-75. [DOI] [PubMed] [Google Scholar]
- 22.Goodsell, D. S. (1998) The Machinery of Life (Springer, New York).
- 23.Weijer, C. J. (2003) Science 300, 96-100. [DOI] [PubMed] [Google Scholar]
- 24.Teruel, M. N. & Meyer, T. (2000) Cell 103, 181-184. [DOI] [PubMed] [Google Scholar]
- 25.Burack, W. R. & Shaw, A. S. (2000) Curr. Opin. Cell Biol. 12, 211-216. [DOI] [PubMed] [Google Scholar]
- 26.Abramowitz, M. & Stegun, I. A., eds. (1970) Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Table (Dover, New York).