Auditory-Filter Characteristics for Listeners With Real and Simulated Hearing Impairment

Abstract

Functional simulation of sensorineural hearing impairment is an important research tool that can elucidate the nature of hearing impairments and suggest or eliminate compensatory signal-processing schemes. The objective of the current study was to evaluate the capability of an audibility-based functional simulation of hearing loss to reproduce the auditory-filter characteristics of listeners with sensorineural hearing loss. The hearing-loss simulation used either threshold-elevating noise alone or a combination of threshold-elevating noise and multiband expansion to reproduce the audibility-based characteristics of the loss (including detection thresholds, dynamic range, and loudness recruitment). The hearing losses of 10 listeners with bilateral, mild-to-severe hearing loss were simulated in 10 corresponding groups of 3 age-matched normal-hearing listeners. Frequency selectivity was measured using a notched-noise masking paradigm at five probe frequencies in the range of 250 to 4000 Hz with a fixed probe level of either 70 dB SPL or 8 dB SL (whichever was greater) and probe duration of 200 ms. The hearing-loss simulation reproduced the absolute thresholds of individual hearing-impaired listeners with an average root-mean-squared (RMS) difference of 2.2 dB and the notched-noise masked thresholds with an RMS difference of 5.6 dB. A rounded-exponential model of the notched-noise data was used to estimate equivalent rectangular bandwidths and slopes of the auditory filters. For some subjects and probe frequencies, the simulations were accurate in reproducing the auditory-filter characteristics of the hearing-impaired listeners. In other cases, however, the simulations underestimated the magnitude of the auditory bandwidths for the hearing-impaired listeners, which suggests the possibility of suprathreshold deficits.

Introduction

Functional simulation of sensorineural hearing impairment is an important research tool that contributes to a more complete understanding of hearing impairment and to the development of more accurate models of hearing loss. These models can then lead to the design of novel and enhanced treatments of hearing loss since hearing-aid algorithms and other compensatory signal-processing schemes are ultimately based on such underlying models.

Hearing-loss simulation processes stimuli so that the sound that reaches the ear of the normal-hearing (NH) listener is transformed to achieve specific changes in auditory abilities that mimic those experienced by listeners with real hearing impairment. A successful hearing-loss simulation should be capable of reproducing in NH listeners the performance of hearing-impaired (HI) listeners on a wide range of psychoacoustic and speech-reception tasks. The current study investigates the ability of hearing-loss simulation to recreate the reduced frequency selectivity generally observed in hearing-impaired listeners.

Hearing-Loss Simulation

Several broad classes of techniques have been used to simulate cochlear hearing loss. One simulation approach involves the use of additive masking noise (e.g., Dubno & Schaefer, 1992; Florentine, Fastl, & Buss, 1988; Florentine, Reed, Rabinowitz, Durlach, & Braida, 1993; Milner, Braida, Durlach, & Levitt, 1984; Zurek & Delhorne, 1987) to reproduce the elevated thresholds, reduction in dynamic range, and loudness recruitment observed in sensorineural hearing loss. With a threshold-elevating noise (TN) simulation, signals can be delivered to listeners with real and simulated hearing loss at equivalent levels expressed both as sound-pressure level (SPL) and sensation level (SL; i.e., the level above hearing threshold in quiet for hearing-impaired listeners or in the presence of the noise simulation for normal-hearing listeners). Because of the levels of required masking noise, however, this simulation technique is limited to losses less than roughly 70 dB HL. A second technique, known as multiband amplitude expansion (MBE), employs level-dependent attenuation of the input signal to achieve elevated thresholds and recruitment (Duchnowski, 1989; Duchnowski & Zurek, 1995; Graf, 1997; Lum & Braida, 1997; Moore & Glasberg, 1993; Villchur, 1973, 1974). This method can thus be used to simulate impairments that are more severe than those that can be comfortably simulated using masking noise alone. The use of level-dependent attenuation, however, results in stimuli that may be presented at lower SPL to simulated-loss listeners compared to real-loss listeners (even though the SLs are equivalent for listeners with both real and simulated loss). Another approach to hearing-loss simulation has focused on the reproduction of specific aspects of the suprathreshold consequences of sensorineural loss. For example, the reduced frequency selectivity observed for HI listeners has been simulated through spectral smearing of signals applied to NH listeners and has been studied by itself (Baer & Moore, 1993; Moore, Glasberg, & Simpson, 1992; ter Keurs, Festen, & Plomp, 1992) as well as in combination with a multiband expansion simulation of loudness recruitment (Moore, Glasberg, & Vickers, 1995; Moore, Vickers, Glasberg, & Baer, 1997; Nejime & Moore, 1997).

The current research is concerned with the evaluation of one particular approach to hearing-loss simulation that employs the use of TN alone or in combination with MBE (TN/MBE) to reproduce the hearing thresholds of HI listeners (Desloge, Reed, Braida, Perez, & Delhorne, 2010, 2011a, 2011b) This approach to hearing-loss simulation is intended to mimic the effects of reduced audibility observed in HI listeners. These audibility effects are defined here to include elevated thresholds as well as the accompanying reduced dynamic range and loudness recruitment that are characteristic of sensorineural hearing loss.

Previous evaluations of this TN/MBE simulation indicate that it was successful in reproducing the speech-reception performance of HI listeners in steady-state and fluctuating backgrounds of noise for both unprocessed and amplified speech (Desloge et al., 2010). The TN/MBE simulation was also successful in reproducing the temporal masking patterns and reduced cochlear compression of listeners with sensorineural loss (Desloge et al., 2011b). Other temporal characteristics of hearing loss were not as well accounted for by the simulation, including amplitude-modulation detection (where the simulations often led to worse performance than observed in the HI listeners; Desloge et al., 2011a) and temporal integration for tone detection (where the simulation did not produce the reduced amounts of integration seen in cochlear loss; Desloge et al., 2011b). The goal of the current article was to extend the study of the TN/MBE simulation to include an assessment of its ability to reproduce the broadened auditory filters that are associated with cochlear hearing loss.

Frequency Selectivity in Cochlear Hearing Loss

Cochlear hearing loss is often accompanied by reduced frequency selectivity as evidenced by auditory filters that are broader than those associated with normal hearing (e.g., Bernstein & Oxenham, 2006; Carney & Nelson, 1983; Dubno & Dirks, 1989; Glasberg & Moore, 1986; Lutman, Gatehouse, & Worthington, 1991; Tyler, Hall, Glasberg, & Moore, 1984). Some of the broadened tuning observed in listeners with cochlear hearing loss may be attributable simply to the higher stimulus levels used in measurements obtained with HI compared to NH listeners. Dubno and Schaefer (1991), for example, examined the effects of background-noise level on the performance of NH listeners on several measures of frequency selectivity. Except for the critical ratio (which was constant over noise levels), the addition of broadband noise led to decreased frequency selectivity in terms of broader psychophysical tuning curves, broader auditory filters estimated from a notched-noise masking experiment, and elevated skirts of masking patterns obtained with narrow-band noise. Comparison of these NH data with results obtained by Dubno and Dirks (1989) for HI listeners suggests that although the effects of signal level and hearing threshold do not fully account for the reduced frequency selectivity observed in cochlear hearing loss, some of the deficits may arise from the higher stimulus levels at which HI listeners are typically tested. Similar conclusions have been reached in other investigations of signal-level effects on frequency selectivity in NH listeners (e.g., Carney & Nelson, 1983; Nelson, Chargo, Kopun, & Freyman, 1990; Nelson & Fortune, 1991; Florentine, 1992; Rosen & Baker, 1994).

Previous research has examined the ability of various types of hearing-loss simulations to reproduce the frequency selectivity of HI listeners. A summary of some of these previous studies is provided in Table 1 where each study is described in terms of method of hearing-loss simulation, psychoacoustic procedure and stimuli, number and ages of listeners, and a brief summary of results.

Table 1.

Summary of Studies of Frequency Selectivity Employing Hearing-Loss Simulation

Study	Simulation Method	Psychoacoustic Paradigm	Probe Characteristics	Masker Characteristics	Number and Age of Subjects	Summary of Findings
Florentine (1992)	Spectrally shaped broadband additive masking noise	Psychoacoustic tuning curves using simultaneous masking	500, 1000, 2000 Hz set at 10 dB SL	50-Hz narrow-band noise at 6 center frequencies around each probe frequency	4 HI: 19-44 years	Good correspondence between HI and SIM in some cases; in others, tuning less steep for HI
					2 NH: 20 and 25 years
Dubno and Schaefer (1992)	Spectrally shaped broadband additive masking noise	Notched-noise masking	800, 1200, 2000 Hz	9 symmetrical notches in a broadband noise around each probe frequency; 40 dB spectrum level	6 HI: 58-73 years	Mean difference of 6 dB between thresholds of HI and NH simulations; ERBs generally larger for HI
					18 NH: 18-38 years
Leek and Summers (1993)	Broadband noise at spectrum levels of 20 and 35 dB; applied to HI and NH	Notched-noise masking	500 and 2000 Hz	2 band-pass noises with width 0.4 times probe frequency; 10 symmetrical and 10 asymmetrical notches; 55 dB spectrum level	5 HI: 58-78 years	At 500 Hz, ERBs similar for HI and NH in both background noises; at 2000 Hz, ERBs larger for HI than NH in both background noises
					4 NH: 20-44 years
Sommers and Humes (1993)	Narrow-band masker centered around 2000 Hz to yield thresholds of 20 and 40 dB HL	Notched-noise masking	2000 Hz	2 800-Hz band-pass noises to create 7 symmetrical notches and 10 asymmetrical notches; 50 dB spectrum level	HI: 68-83 years	ERB increased with hearing level above 30 dB; ERB similar for HI and NH; greater filter asymmetry for HI
					NH: 25-33 years
Dubno and Schaefer (1995)	Spectrally shaped broadband additive masking noise applied to NH and HI	Notched-noise masking	800, 1200, 2000 Hz	9 symmetric notch widths for each signal frequency; notches created in broadband noise; spectrum level of 50 dB	4 HI: unknown ages	Critical ratios similar for HI and NH; notched-noise thresholds were on average 2-5 dB higher for HI across notch widths; larger differences for narrow compared to wider widths
					4 NH: unknown ages
Dubno and Schaefer (1995)	Spectrally shaped broadband additive masking noise applied to NH and HI	Narrow-band noise masking	11 tones in range of 630-4000 Hz	Narrow-band noise of 1100-1300 Hz with spectrum level of 60 dB	4 HI: unknown ages	Thresholds similar for HI and NH for frequencies within and below spectral range of masker but greater masking effects for HI at higher probe frequencies
					4 NH: unknown ages
Lum and Braida (2000)	Additive masking noise or multiband expansion to produce flat losses of 40 and 50 dB	Narrow-band noise masking	8 tones in range of 630-4000 Hz	Narrow-band noise centered around 1200 Hz; level of 63 dB SPL	4 NH: early 20s	Both simulations yielded similar results in producing thresholds for tones within passband of masker similar to NH without simulated loss but elevated thresholds above and below 1000 Hz in presence of simulations (similar to results of Dubno & Schaefer, 1991)
Lum and Braida (2000)	Additive masking noise or multiband expansion to produce flat losses of 40 and 50 dB	Psychoacoustic tuning curves using forward masking	1200 Hz at 20 dB SL	Pure tones in range of 600-1400 Hz	4 NH: early 20s	Both simulations produced similar results: broader tuning curves and shallower slopes than for NH without simulated loss (similar to results of Dubno & Schaefer, 1991)
Moore et al. (1992)	Spectral smearing	Notched-noise masking	1000 Hz	2 band-pass noises with width of 800 Hz; 7 symmetric notches and 10 asymmetrical notches; spectrum level of 50 dB	3 NH: unknown ages	Auditory filters with larger ERBs and shallower skirts than for NH without simulated loss

Note: HI = hearing-impaired; NH = normal-hearing; SIM = simulated-loss; ERB = equivalent rectangular bandwidth.

The predominant method of simulation employed in these studies is additive masking noise to achieve threshold elevation (Dubno & Schaefer, 1992, 1995; Florentine, 1992; Leek & Summers, 1993; Lum & Braida, 2000; Sommers & Humes, 1993); however, there are also examples of studies employing multiband expansion (Lum & Braida, 2000) and spectral smearing (Moore et al., 1992). The most common method for measuring auditory bandwidths is the use of the rounded-exponential (roex) filter model to estimate auditory-filter shape using data from notched-noise masking (Glasberg & Moore, 1990; Patterson, 1976). Other methods include the measurement of psychoacoustic tuning curves at a given probe frequency as a function of the spectral region of the masker and narrow-band masking to examine patterns of masking as a function of tone frequency for a given narrow-band of noise. Note that in many of the studies, the HI listeners were older than the NH listeners with simulated loss.

Results with additive-noise simulations and notched-noise masking procedures indicate that masked thresholds of HI listeners are on average 2 to 6 dB higher than NH listeners with simulated loss (Dubno & Schaefer, 1992, 1995) and that equivalent rectangular bandwidths were either similar for the two groups or larger in the case of real impairment (Dubno & Schaefer, 1992; Leek & Summers, 1993; Sommers & Humes, 1993). Additive-noise simulations conducted with psychoacoustic tuning curves indicated that the simulations produced broader tuning and shallower slopes than observed in NH listeners (Florentine, 1992; Lum & Braida, 2000) and that some HI listeners were better simulated than others (Florentine, 1992). In the case of the poorer simulations, tuning was less sharp for real compared to simulated hearing loss particularly in the region below the probe frequency.

In additive-noise simulations of narrow-band noise masking patterns, masked thresholds were similar for real and simulated hearing loss when the spectral composition of the masker overlapped with or was below the frequency of the probe, but showed greater masking effects for HI listeners at higher probe frequencies (Dubno & Schaefer, 1995). The only use of multiband expansion simulations occurred in the study of Lum and Braida (2000) who compared multiband expansion with an additive-noise masking simulation of flat hearing loss in measurements of psychoacoustic tuning curves and narrow-band noise masking patterns. Both simulations yielded similar patterns of results and were consistent with the measurements of Dubno and Schaefer (1991) on NH listeners as a function of background noise level. Specifically, both simulations yielded broader tuning and shallower slopes than for NH listeners in the psychoacoustic tuning curves and thresholds similar to NH within the passband of the narrow-band noise maskers but elevated thresholds for the simulations for frequencies above and below the passband.

Finally, a simulation designed to reproduce the broadened auditory filters, but not the reduced audibility, of cochlear hearing loss through spectral smearing (Moore et al., 1992) was successful in reproducing the auditory filters derived from notched-noise masking data in terms of broadened equivalent rectangular bandwidths (ERBs) and shallower slopes compared to NH listeners.

Goals of Current Study

The hearing-loss simulation employed in the current research was based on a combination of additive noise masking and multiband expansion and has been employed previously in studies of speech-reception in noise (Desloge et al., 2010), temporal modulation transfer functions (Desloge et al., 2011a), and temporal-masking functions (Desloge et al., 2011b). This method permits the specification of frequency-dependent threshold elevations associated with a given hearing loss as well as the effects of loudness recruitment. When the simulation is dominated by masking noise, signals are presented to HI and NH listeners at levels that are roughly equivalent in terms of SPL, SL, and loudness. When multiband expansion is combined with masking noise to simulate losses in excess of 70 dB HL, the simulation leads to signal presentation levels that are roughly equivalent in terms of SL and loudness for HI and NH listeners but are less for NH than HI listeners in terms of SPL. Some of the broadened tuning observed in listeners with cochlear hearing loss may be attributable simply to the higher stimulus levels used in measurements obtained with HI compared to NH listeners (e.g., Carney & Nelson, 1983; Dubno & Schaefer, 1991; Florentine, 1992; Hopkins & Moore, 2011; Nelson et al., 1990; Nelson & Fortune, 1991; Rosen, Baker, & Darling, 1998). Thus the simulation employed here provides greater control for the effects of level in comparisons between HI and NH listeners.

A constant-probe, variable-masker, notched-noise paradigm was used to explore auditory bandwidths in HI listeners over a broad range of probe frequencies and to compare their performance to that of age-matched NH listeners with simulated hearing loss. This paradigm was chosen based on the findings of Rosen et al. (1998), which demonstrate the advantages of this method over a variable-probe, fixed-masker paradigm in deriving auditory filter shapes. Among such advantages of the fixed-probe compared to fixed-masker paradigm are superior fits to a roex filter model, reduced variability among NH listeners, and greater correspondence to basilar-membrane vibration patterns.

The current study extends previous research in several ways. First, through the use of a simulation that combines additive masking noise and multiband expansion, we were able to simulate hearing losses greater than those that have been tested previously. Second, our studies involved simulations of individual hearing losses in NH listeners over the audiometric range of 125 to 8000. This approach contrasts with some previous studies that have simulated average hearing losses or used narrow-band noise to create threshold elevations in one particular frequency region. Finally, the measured loss of each individual HI listener was simulated in three NH listeners of roughly the same age. Although in some studies, hearing level rather than age appears to be the predominant factor in determining the ERB (e.g., Peters & Moore, 1992; Sommers & Humes, 1993), other studies have reported an increase in the size of the ERB with age (e.g., Glasberg, Moore, Patterson, & Nimmo-Smith, 1984; Lutman et al., 1991; Patterson, Nimmo-Smith, Weber, & Milroy, 1982). While the effects of age on frequency selectivity are not explicitly examined here, the use of age-matched simulations in the current study provides some control for possible effects of age in the notched-noise paradigm.

Method

Hearing-Loss Simulation Techniques

In the current study, hearing loss was simulated initially using additive threshold noise (TN) that was spectrally shaped to yield the desired threshold shifts. For severe threshold shifts (> 60-70 dB HL), however, the required amount of threshold noise could be unacceptably loud (i.e., > 80 dB SPL). In these cases, TN was combined with multiband expansion (MBE) to produce the desired threshold shifts. Each of these methods (TN and TN/MBE) is described below.

Simulation using Additive Threshold Noise (TN)

For this hearing-loss simulation technique, the desired frequency-dependent threshold shifts were obtained using spectrally shaped Gaussian threshold noise that was added to each stimulus prior to presentation to the listener (see top panel of Figure 1). The specific frequency-dependent noise necessary to simulate a particular hearing loss was derived as follows. The desired hearing thresholds were specified in terms of dB SPL at a minimum of six audiometric frequencies including 250, 500, 1000, 2000, 4000, and 8000 Hz. The 250 and 8000-Hz thresholds were extended to lower and higher frequencies, respectively, such that the threshold specification for the simulation covered frequencies ranging from 80 Hz to 12,500 Hz. Linear interpolation (in the log-frequency vs. dB-SPL domain) was then used to estimate thresholds at all third-octave-band center frequencies within this range. The spectrum level of the threshold-shifting noise, SpecLev(f_1/3-oct) in dB, was calculated at each third-octave frequency by subtracting the critical ratio, CR(f_1/3-oct) in dB (Hawkins & Stevens, 1950), which establishes the minimal signal-to-noise ratio at which a particular tone can be heard, from the desired threshold, THR(f_1/3-oct) in dB:

Figure 1.

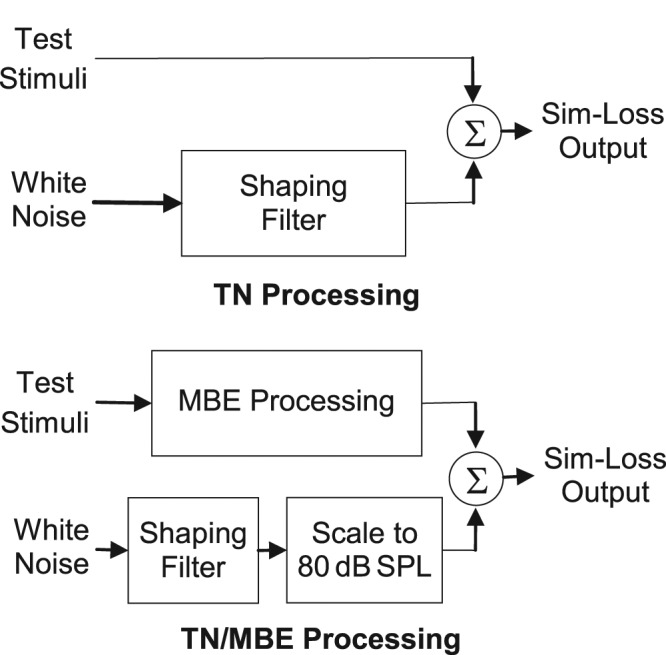
Panel on top: Block diagram of system used for hearing-loss simulation based on additive threshold noise (TN). Panel on bottom: Block diagram of system used for hearing-loss simulation based on a combination of additive threshold noise and multiband expansion (MBE) processing

Note: The upper path processes signal with MBE level-dependent gain while the lower path generates the threshold-shifting noise.

$$\text{SpecLev}({\text{f}}_{1/3\text{-oct}})=\text{THR}({\text{f}}_{1/3\text{-oct}})-\text{CR}({\text{f}}_{1/3\text{-oct}}).$$ (1)

The CR values employed in these computations (from Hawkins and Stevens, 1950, for NH listeners over a wide range of masking levels) were 17.75, 16.3, 17.25, 18.5, 19.25, 20.5, 22.5, 25.1, 26, and 27 dB at 125, 250, 500, 1000, 1500, 2000, 3000, 4000, 6000, and 8000 Hz, respectively. These CR values were extended and linearly interpolated (in the log-frequency vs. dB domain) to cover the third-octave-band frequencies ranging from 80 Hz to 12,500 Hz. Finally, these spectrum levels were used to determine the magnitude response of the filter required to transform white noise into additive threshold noise that yielded the threshold shift associated with the simulated loss. This magnitude response was inverse-Fourier-Transformed and Hanning-windowed to yield a 128-ms-duration finite-impulse-response shaping filter (indicated in the top panel of Figure 1) that was used to create the actual TN in the experiment.

Because of the matching threshold shift, the test stimuli were presented to HI and simulated-loss NH listeners at the same SPL and SL. Furthermore, because the additive threshold noise produces a growth of loudness similar to that experienced by HI listeners with the same threshold shift (e.g., Steinberg & Gardner, 1937), this method of simulating hearing loss simulated loudness recruitment as well.

Simulation using Additive Threshold Noise and Multiband Expansion (TN/MBE)

Multiband expansion (MBE) produced threshold shifts by attenuating the stimulus dynamically. This process involved passing the signal through a multiband filterbank, monitoring short-time band signal levels, and applying a level-dependent attenuation to each band signal (Duchnowski, 1989; Duchnowski & Zurek, 1995; Graf, 1997; Lum & Braida, 1997; Moore & Glasberg, 1993). The level-dependent attenuation used for hearing loss simulation was designed to yield the desired threshold shift as well as the loudness growth associated with sensorineural hearing loss. Specifically, MBE applied band attenuations that translated an input signal at the level of the simulated threshold so that it was presented at the listener’s actual hearing threshold. The degree of attenuation then decreased as input level increased above the simulated threshold until full recruitment was reached (defined here as 100 dB HL) and the attenuation was equal to 0 dB. For input levels above the full recruitment level, no attenuation was used.

TN and MBE were combined (bottom panel of Figure 1) in the following manner to produce a desired threshold shift. First, the wideband level, TN_lev, of the threshold noise required to yield a TN-only simulation of the desired loss was calculated. TN/MBE simulation was adopted only when TN_lev exceeded 80 dB SPL. In this case, the TN was attenuated by a frequency-independent factor of

$$\alpha ={\text{TN}}_{\text{lev}}-80\text{dB}$$ (2)

to yield a scaled TN with a wideband level of exactly 80 dB SPL. Given that the unscaled TN was designed to produce the desired threshold shifts of THR(f), the attenuated noise then yielded threshold shifts of up to α dB below the desired threshold shifts but not lower than the normal-hearing threshold of 0 dB SL:

$${\text{THR}}_{\text{αTN}}(\text{f})=\max \{0,\text{THR}(\text{f})-\alpha \}\text{dB}\text{SL}.$$ (3)

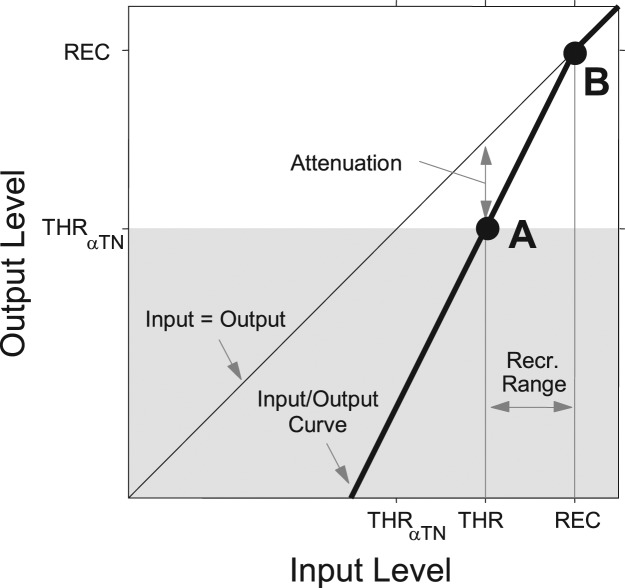
MBE was then used to re-create the remaining threshold shift necessary to restore the simulated thresholds to the desired levels. Figure 2 illustrates how the scaled TN and MBE were combined to yield the complete desired threshold shift in a particular frequency band. The solid line shows the mapping between input and output level. The MBE attenuation is equal to the vertical difference between this input/output mapping curve (thick solid line) and the input-equals-output curve (thin solid line) shown in the plot. At point A, the mapping attenuates inputs at a desired threshold of THR so that the corresponding output level is exactly equal to THR_αTN, that is, the hearing threshold in the presence of the scaled threshold noise. The MBE attenuation then decreases as input level increases until the level of full recruitment (REC) is reached at point B and no MBE attenuation occurs. In this way, MBE attenuates input sound levels that are below THR into output sound levels that are below THR_αTN and that are inaudible in the presence of the scaled-down threshold noise. MBE output levels corresponding to input levels above REC are not attenuated. For the current research, the full-recruitment level REC was always fixed at 100 dB HL.

Figure 2.

Example multiband expansion (MBE) input/output level mapping curve used to demonstrate how MBE processing is combined with additive threshold noise (TN) processing to yield the TN/MBE method of hearing-loss simulation

Note: Inputs at the desired hearing threshold (THR) are mapped to attenuated outputs at the actual hearing threshold (THRaTN), indicated by point A. Inputs at the full recruitment level (REC) are mapped unchanged to the outputs, indicated by point B. Intermediate inputs are mapped to outputs between these two extremes.

The specific MBE implementation used in this research was based on the work of Moore and Glasberg (1993). The input signal was first divided into 13 frequency bands using a fourth-order gammatone filterbank with center frequencies ranging from 100 to 5837 Hz and bandwidths in the range 106.5 to 1964 Hz. The band-pass filter impulse responses were time-aligned so that all impulse response peaks were coincident. The Hilbert Transform was computed and used to separate each band signal into an envelope (Hilbert-Transform-output magnitude low-pass filtered at 100 Hz) and fine-structure (Hilbert Transform output divided by the Hilbert-Transform-output magnitude) components. The input envelopes in each band were converted into output envelopes via the MBE input-to-output mapping described above. The output envelopes were combined with the input fine-structure and the inverse Hilbert Transform was applied to obtain output band signals. Finally, the output band signals were summed to form the output signal.

As shown in the block diagram (bottom panel of Figure 1), the input signal (upper path) was modified via MBE processing and added to spectrally shaped noise (lower path), which, as stated above, was scaled to a level of 80 dB SPL, for presentation to the listener. The scaling term α from Eq. 2 defines the relative contributions of TN and MBE to the combined TN/MBE simulation. Specifically, the threshold shifts obtained with the scaled TN, THR_αTN(f), were up to α dB lower than the desired threshold shift. This gap was then recovered using MBE processing.

Relative to the HI listeners, simulated-loss NH listeners using a TN/MBE simulation experienced stimuli at the equivalent SL but at an SPL that was as much as α dB lower.

Stimulus Generation

Experiments were controlled by a PC equipped with a high-quality, 24-bit PCI sound card (either LynxOne by LynxStudios or E-MU 0404 by Creative Professional). Stimulus signals (including the hearing-loss simulation, if present) were generated and played out using Matlab™; passed through a pair of Tucker-Davis (TDT) PA4 programmable attenuators and a TDT HB6 stereo headphone buffer, and presented to the listener in a soundproof booth via a pair of Sennheiser HD580 headphones. The system was calibrated to compensate for the HD580 frequency response over the range of 80 Hz to 12,500 Hz so that precise sound levels could be presented as measured at the eardrums of a KEMAR manikin. Peak output levels of approximately 117 dB SPL were attainable with this system.

The experimental stimuli were generated and adaptively modified using the AFC Software Package for Matlab™ provided by Stephan Ewert and developed at the University of Oldenburg, Germany. A monitor, keyboard, and mouse located within the sound-treated booth allowed interaction with the control PC.

Participants

The experimental protocol for testing human subjects was approved by the internal review board of the Massachusetts Institute of Technology. All testing was conducted in compliance with regulations and ethical guidelines on experimentation with human subjects. All listeners provided informed consent and were paid for their participation in the experiments.

Listeners with hearing impairment

Ten listeners with bilateral sensorineural hearing loss who were native speakers of American English participated in the study. Each listener was required to have had a recent clinical audiological examination (within 1 year of entry into the laboratory study) to verify that the hearing loss was of cochlear origin on the basis of air- and bone-conduction audiometry, tympanometry, speech-reception thresholds, and word-discrimination scores. On the listener’s first visit to the laboratory, informed consent was obtained and an audiogram was readministered for comparison with the listener’s most recent evaluation from an outside clinic. In all cases, good correspondence was obtained between these two audiograms.

The 10 HI listeners are the same listeners who participated in the study of Desloge et al. (2010). A subset of these listeners also participated in the studies of Desloge et al. (2011a, 2011b) using the same listener identifiers. Information is provided in Table 2, which contains data on sex, test ear, history/etiology, hearing-aid use, age, method used to simulate hearing loss, and, for TN/MBE simulations only, the broadband α term (Eq. 2) that represents the maximum attenuation provided by the MBE in any frequency band. The listeners (who ranged in age from 21 to 69 years) were selected to have bilateral losses that were roughly symmetrical. The audiometric thresholds of the listeners are provided in Table 1 of Desloge et al. (2010) and are consistent with laboratory-based measurements of their absolute-detection thresholds (described below and reported in Figure 3).

Table 2.

Description of Hearing-Impaired Subjects in Terms of Sex, Audiometric Thresholds in dB HL in Left and Right Ears at 6 Frequencies, Hearing-Aid (HA) Use, History/Etiology, and Age in Years

			Audiometric Thresholds in dB HL Specified for Frequencies in kHz
Subject	Sex	Ear	.25	.50	1.0	2.0	4.0	8.0	HA Use in Test Ear?	Etiology	Age	AM-SIM Group Age	Simulation Method
HI-1	M	*L	15	20	25	35	40	35	No	Hereditary	24	23.0	TN
		R	15	20	15	40	35	25
HI-2	M	L	30	35	45	55	55	60	Yes	Congenital?	21	20.3	TN
		*R	25	30	45	50	55	60
HI-3	M	L	25	25	25	30	55	75	No	Unknown/adult-onset	64	61.7	TN/MBE (α = 4)
		*R	25	35	30	30	40	75
HI-4	F	*L	10	30	45	60	60	80	Yes	Congenital	59	53.0	TN/MBE (α = 7)
		R	20	35	40	60	65	70
HI-5	F	*L	15	15	5	60	65	65	Yes	Early-childhood/measles	48	45.7	TN
		R	20	35	40	60	65	70
HI-6	F	*L	40	50	55	55	60	45	Yes	Unknown	55	55.3	TN
		R	40	50	55	60	70	90
HI-7	M	L	65	60	70	80	70	95	Yes	Hereditary/congenital	69	61	TN/MBE (α =13)
		*R	60	60	75	70	70	85
HI-8	M	L	55	65	65	65	70	90	Yes	Hereditary	68	64.0	TN/MBE (α = 10)
		*R	60	65	65	70	80	70
HI-9	F	L	85	95	110	110	110+	110+	Yes	Congenital	21	22.0	TN/MBE (α = 30)
		*R	50	65	75	75	100	95
HI-10	F	*L	50	35	30	20	15	95	Yes	Congenital	43	43	TN/MBE (α = 30)
		R	65	50	50	25	20	100

Note: For each subject, the test ear employed in the study is denoted by an asterisk and bold lettering. Also provided are the mean ages of the age-matched, simulated-loss (AM-SIM) group and the method used to simulate the hearing loss (threshold noise, TN, or threshold noise plus multiband expansion, TN/MBE) with the α factor (in dB) indicated for the TN/MBE simulations.

Figure 3.

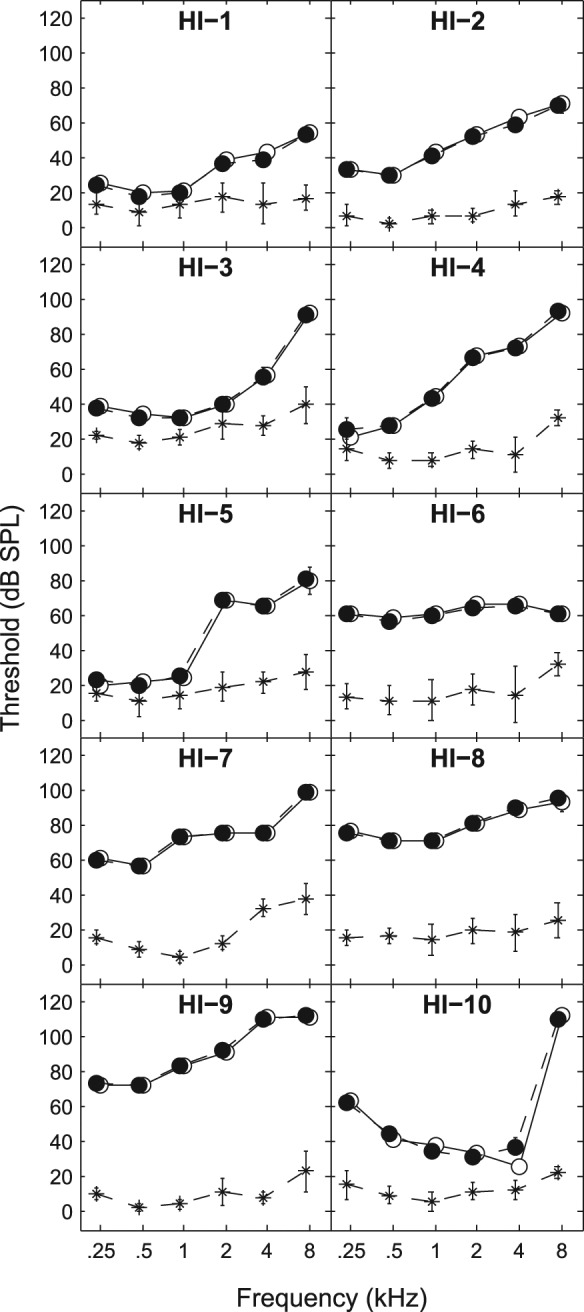
Threshold in dB SPL as a function of frequency for 500-ms tone stimuli

Note: In each subplot, absolute thresholds are shown for a given hearing-impaired (HI) listener (unfilled circles). For each HI listener, simulated-loss thresholds are averaged across the normal-hearing (NH) listeners in the age-matched, simulated-loss (AM-SIM) group (unfilled circles) Also shown are average quiet (without simulated loss) thresholds for the AM-SIM group (asterisks with error bars indicating ±1 standard deviation from the mean).

Audiometric thresholds across ears were within 20 dB of each other at each test frequency in all but two listeners. For HI-6, this symmetry criterion was relaxed at 8000 Hz. For HI-9, thresholds for the left ear were 30 to 35 dB greater than those in the right ear for frequencies between 250 and 2000 Hz (and left-ear thresholds were above the limits of the audiometer at frequencies greater than 2000 Hz). For each listener, a test ear was selected for monaural listening in the experiments (shown in Table 2). Typically, this was the ear with better average thresholds across test frequencies. Hearing losses ranged from mild/moderate to severe/profound across listeners. The audiometric configurations observed across the hearing losses of these listeners included (a) sloping high-frequency loss (HI-1, HI-2, HI-3, HI-4, HI-5), (b) relatively flat loss with no more than a 20-dB difference between adjacent audiometric frequencies (HI-6, HI-7, HI-8), (c) severe low-frequency loss advancing to profound high-frequency loss (HI-9), and (d) inverted cookie-bite loss characterized by near-normal thresholds in the midfrequency range and moderate loss at low and high frequencies (HI-10). All but two of the listeners (HI-1 and HI-3) were regular or occasional hearing-aid users at the time of entry into the study.

Listeners with normal hearing

Thirty NH listeners who were native speakers of English were recruited to participate in the hearing-loss simulation component of the study. Listeners provided informed consent and a clinical audiogram was then obtained to screen for normal hearing in at least one ear, defined as 25 dB HL or better at frequencies in the range of 250 to 4000 Hz and 30 dB HL at 8000 Hz. These criteria were chosen to be representative of normal hearing for listeners across the age range of 18 to 70 years who were selected as age-matched controls to each of the 10 HI listeners. These listeners’ ages were in the range of plus or minus 9 years relative to that of the given HI listener to whom they were assigned. The mean ages of the age-matched listeners with hearing-loss simulation (AM-SIM) associated with HI-1 through HI-10 are provided in Table 2. Also provided in Table 2 is the hearing-loss simulation method (TN or TN/MBE) used to simulate the corresponding HI listener’s loss. For each NH listener, a test ear was selected for conducting the experiment.

Two of these AM-SIM listeners (ages 56 and 62 years) also participated in the experiment without the use of hearing-loss simulation and are referred to as the NH group.

Absolute Threshold and Simulated-Loss Threshold Testing

Measurements of absolute-detection thresholds for pure tones were obtained for the test ear of each HI and NH listener without simulated hearing impairment at frequencies of 250, 500, 1000, 2000, 4000, and 8000 Hz. Thresholds at these frequencies were also measured for the AM-SIM listeners.

Threshold measurements were obtained using a three-interval, three-alternative, adaptive forced-choice procedure with trial-by-trial correct-answer feedback. Tones were presented with equal a priori probability in one of the three intervals and the listener’s task was to identify the interval containing the tone. Each interval was cued on the visual display during its 500-ms presentation period with a 500-ms interstimulus interval. Tones were windowed to have a 500-ms total duration with a 10-ms Hanning-window ramp on and off (yielding a 480-ms steady-state portion). During the experimental run, the level of the tone was adjusted adaptively using a one-up, two-down rule to estimate the stimulus level required for 70.7% correct (Levitt, 1971). The step size was 8 dB for the first two reversals, 4 dB for the next two reversals, and 2 dB for the remaining six reversals. The final masker level was estimated as the mean across the final six reversals. Listeners had unlimited response time and were provided with visual trial-by-trial feedback following each response.

When measuring thresholds for NH listeners with simulated hearing loss, each stimulus was processed by the hearing loss simulation immediately preceding each presentation. Threshold-elevating noise (presented to both ears) was initiated 500 ms before the first stimulus interval and terminated 50 ms after the final interval, for a total noise-onset time of 3050 ms per trial.

Thresholds were measured in blocks of 12 runs, with each block consisting of two 6-run subblocks where each subblock measured the 6 test frequencies in random order. The HI listeners typically completed two blocks of runs measuring thresholds in quiet. Each NH listener completed two blocks of runs measuring thresholds in quiet and another two blocks of runs measuring thresholds under the hearing-loss simulation. Thresholds were averaged across the two runs at each frequency under each type of listening condition.

Notched-Noise Masking

Auditory filter shapes were measured using the notched-noise method of simultaneous masking (Glasberg & Moore, 1990; Patterson, 1976). The masker level needed to mask a probe tone of frequency f_p was measured as a function of the width of a spectral notch between two band-pass maskers. One of the band-pass maskers was located in the frequency region below the probe tone and the other above the probe tone with either symmetric or asymmetric positioning around f_p. Testing was conducted using five values of f_p: 250, 500, 1000, 2000, and 4000 Hz. The lower and upper noise bands each had a bandwidth of 0.25* f_p. The spectral gap between the probe tone and the noise bands was proportional to f_p: Δ_L*f_p to the upper cutoff frequency of the lower band and Δ_U*f_p to the lower cutoff of the upper band. Therefore, the total notch width was (Δ_L+Δ_U)*f_p. The proportionality constants Δ_L and Δ_U took on values of 0.0, 0.1, 0.2, 0.3, and 0.4. Nine combinations of (Δ_L, Δ_U) were used for each f_p: 1: (0, 0), 2: (0.1, 0.1), 3: (0.2, 0.2), 4: (0.3, 0.3), 5: (0.4, 0.4), 6: (0.1, 0.3), 7: (0.3, 0.1), 8: (0.2, 0.4), and 9: (0.4, 0.2). For Condition 1, with a notch width of 0, a single band of noise with bandwidth 0.5*f_p was used. Conditions 2 through 5 consisted of symmetrical notches around f_p, Conditions 6 and 8 consisted of asymmetrical notches with the lower band closer to f_p, and Conditions 7 and 9 represented asymmetrical notches with the higher band closer to f_p.

Notched-noise functions were obtained by measuring the masker level required to mask a probe signal presented at a fixed level of either 70 dB SPL or 8 dB above the threshold of detection (whichever was greater) to ensure audibility of f_p. The probe signal was a gated tone of 200 ms total duration with 10-ms Hanning-window on/off ramps. The masker had a total duration of 220 ms with 10 ms Hanning-window on/off ramps. The probe tone was delayed by 10 ms so that it was centered temporally when added with the masker.

Thresholds were measured using a three-interval, three-alternative forced choice procedure with trial-by-trial correct-answer feedback to measure the level of the masker required for 70.7%-correct detection of the probe-tone frequency. The band-pass masker was presented in all three intervals and the probe was presented in one of these intervals (selected at random with equal a priori probability on each trial). The listener’s task was to identify which interval contained the probe tone. The intervals were cued visually on a computer screen. Each test run was initiated using a masker level of 38 dB SPL that was adjusted adaptively for subsequent presentations using a one-down, two-up rule: masker level was decreased after each incorrectly identified trial and increased after two successive correctly identified trials. The adaptive masker-level step size was 8 dB until the first reversal, 4 dB until the second reversal, and 2 dB for the remaining reversals. The measurement phase commenced when the step size reached 2 dB and lasted for 8 reversals. The final masker level at which the probe signal was just barely masked was estimated to be equal to the mean masker presentation level at the final 8 reversals. During the three-interval playback period, an additional masker was presented to the contralateral ear to assure that signal detection was based on the test ear alone. The contralateral masker was a band-pass noise centered about f_p with a bandwidth of 600 Hz for f_p = 250, 500, and 1000 Hz; a bandwidth of 800 Hz for f_p = 2000 Hz; and a bandwidth of 1000 Hz for f_p = 4000 Hz. The spectrum level of the contralateral masker was set at 40 dB below the level of the probe tone. For the AM-SIM listeners, signals to both the test and nontest ears were processed according to either the TN or TN/MBE hearing loss simulation prior to presentation, and the threshold noise was played continuously throughout the presentation of all three interval signals.

Two threshold measurements were obtained for each of the 45 experimental conditions (5 f_p*9 noises) for each HI and AM-SIM listener, with two exceptions. First, data were not obtained at f_p = 4000 Hz for HI-9 due to the severity of the loss. Second, one of the three AM-SIM listeners for HI-10 was able to complete only one replication for three of the probe frequencies (250, 2000, and 4000 Hz). For each of the two replications of the experiment, the conditions were presented in random order as follows. First, the order of the five probe frequencies was randomized and then the order of the nine noises. For each of the 45 conditions, a third measurement was obtained if the first two thresholds differed by more than 10 dB, and the outlier measurement was discarded (typically, the outlier was 10 or more dB worse than each of the other two measurements).

Results

Absolute Thresholds and Simulation Thresholds

The measured HI-listener and simulated-loss thresholds are shown in Figure 3, where threshold in dB SPL is plotted as a function of frequency. The HI-listener data points are the average of two measurements, while the AM-SIM group points are the average of six measurements (two measurements for each of the three listeners within a group). In addition to these two sets of data points, each panel also shows the average thresholds for each AM group without simulated loss. As with the simulated-loss data points, these data points are the average of six measurements (two per listener).

Averaged across all HI listeners the RMS differences between HI-listeners (unfilled symbols) and corresponding AM-SIM groups (filled symbols) were 0.9, 1.6, 1.5, 1.5, 4.3, and 1.5 dB at 250, 500, 1000, 2000, 4000, and 8000 Hz with an across frequency average of 2.2 dB. The large RMS difference at 4000 Hz arose due to a 12 dB discrepancy in threshold between HI-10 and the AM-SIM group at this frequency. This discrepancy in turn resulted from the steep increase (above 80 dB) in hearing threshold between 4 and 8 kHz for this HI listener. The energy of the TN in the frequency region around 8 kHz led to masking at 4 kHz.

Notched-Noise Measurements

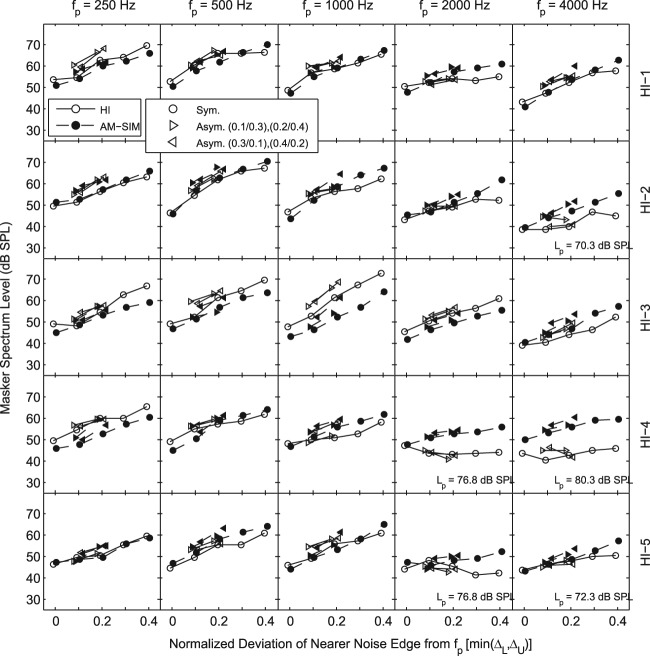
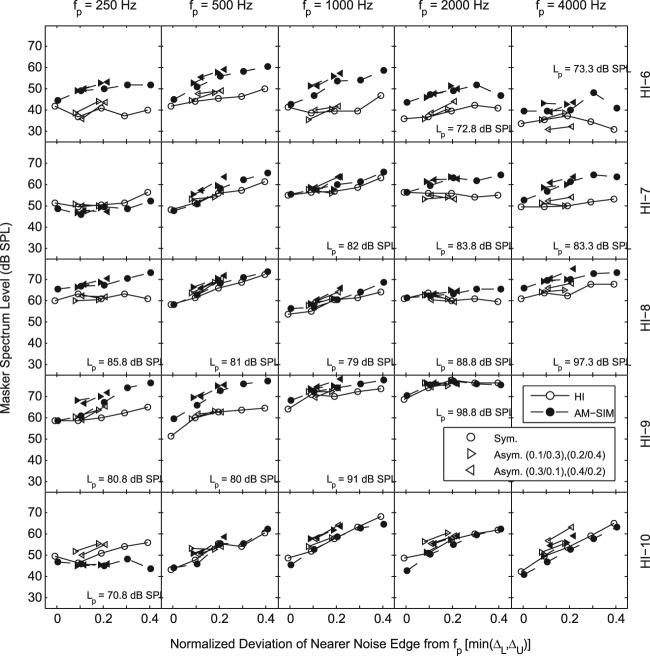
The notched-noise thresholds for each HI listener and the associated AM-SIM group are shown in each row of Figure 4 (HI-1 through HI-5) and Figure 5 (HI-6 through HI-10). Each column of Figures 4 and 5 shows results for one of the five probe frequencies. The masker spectrum level in dB SPL is plotted as a function of the normalized deviation of the nearer noise edge to the probe frequency: that is, min(Δ_L, Δ_U), where Δ_L, Δ_U are as defined above in Method. The probe signal level was equal to 70 dB SPL unless otherwise indicated in the figures. Many of the masking functions demonstrate the expected trend for lowest levels of the masker for a 0-Hz notch width and for an increase in masking level with an increase in the normalized notch width. Some functions, however, remain relatively flat and show little change in masker level with normalized notch width (e.g., HI-4 at 4000 Hz and HI-6 at 250 Hz). Average standard deviations across probe frequencies and noise conditions for each HI listener ranged from 1.1 (HI-3) to 2.2 (HI-10) dB with a mean of 1.5 dB. Average standard deviations for the corresponding AM-SIM groups (one group per HI listener) ranged from 2.1 to 4.0 dB with a mean of 3.4 dB.

Figure 4.

Masker spectrum level (in dB SPL) at threshold as a function of the normalized deviation of the nearer noise edge to the probe frequency [i.e., min(Δ_L,Δ_U)] for listeners HI-1 through HI-5

Each row corresponds to one hearing-impaired (HI) listener and each column corresponds to one probe frequency (f_p). Data are plotted for symmetric (circles) and asymmetric (triangles in two orientations) noise notches about the probe frequency. Unfilled symbols indicate HI-listener data and filled symbols indicate average data for the corresponding age-matched, simulated-loss (AM-SIM) group. Probe level (L_p) was 70 dB SPL unless otherwise indicated.

Figure 5.

The same as Figure 4 for listeners HI-6 through HI-10

To assess the ability of the hearing-loss simulations to reproduce the individual notched-noise thresholds of the HI listeners, the RMS threshold difference over the 9 data points at each probe frequency was computed between each HI listener and the corresponding average AM-SIM group (for a total of 49 comparisons due to missing data at 4000 Hz for HI-9). Across probe frequencies, the mean RMS difference was 5.6 dB and ranged from 5.3 dB at 500 Hz to 7.0 dB at 4000 Hz. A larger variation in mean RMS differences was observed across subjects, which ranged from 3.1 dB for HI-1 to 10.2 dB for HI-6. A histogram of the RMS differences is plotted in Figure 6, which demonstrates that 26 of the comparisons (53%) were within 4 dB and 34 of the comparisons (69%) were within 6 dB. Of the remaining 15 comparisons with RMS differences in excess of 6 dB, 5 are due to a single subject (HI-6) who performed worse than the matched AM-SIM listeners at all probe frequencies (Figure 6).

Figure 6.

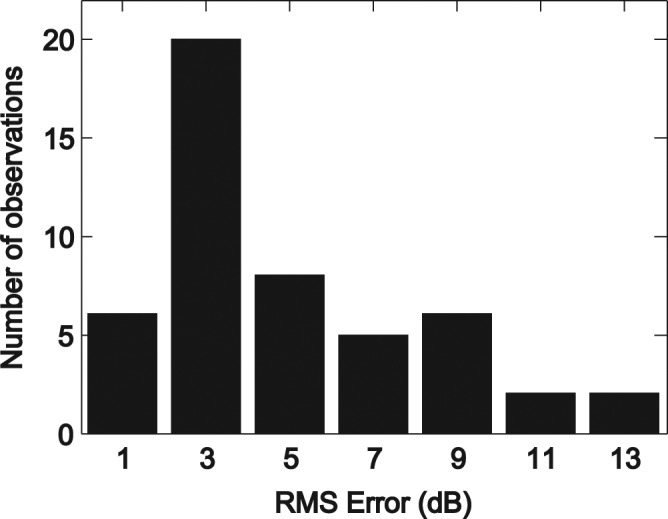
Histogram of root-mean-square (RMS) differences calculated for each probe frequency between hearing-impaired (HI) listener and corresponding age-matched, simulated-loss (AM-SIM) group data

Critical ratios for the HI and AM-SIM listeners at each probe frequency were calculated by subtracting the masker spectrum level (dB SPL) for the 0-Hz notch (i.e., no-notch) condition from the probe level (dB SPL) at that frequency. Figure 7 plots the AM-SIM versus HI critical ratio values. In the upper panel, the data points are identified by frequency and in the lower panel, these same data points are identified by subject. The partial correlation (controlling for probe frequency) between the two sets of critical ratio data (r = .541) was highly significant (p < .00007). Averaged across listeners, critical ratios at f_p = 250, 500, 1000, 2000, and 4000 Hz were 21.8, 23.8, 24.3, 27.8, and 32.6 dB, respectively, for the HI listeners and 22.4, 23.3, 24.9, 27.5, and 30.5 dB, respectively, for the AM-SIM groups. The values of the two groups are within 0.6 dB at all probe frequencies except for f_p = 4000 Hz, where the average HI critical ratio is 2.1 dB greater than the average AM-SIM critical ratio. The critical ratios for the NH group at the five probe frequencies were 23.2, 20.4, 22.7, 24.7, and 30.2, respectively, which were within 3.2 dB of the corresponding average HI and AM-SIM values.

Figure 7.

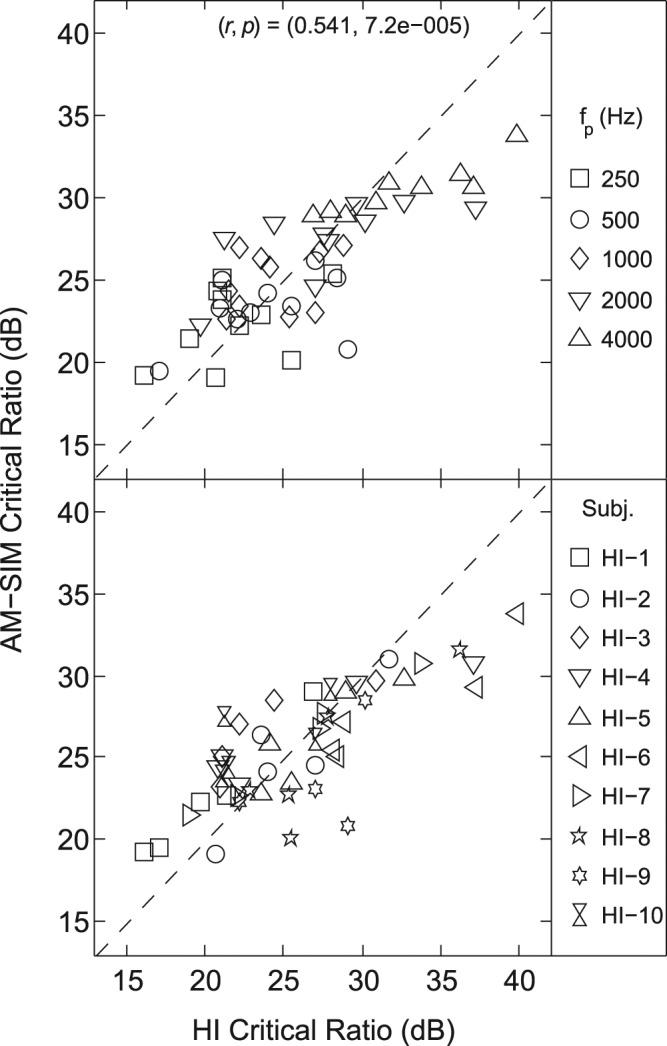
Age-matched, simulated-loss (AM-SIM) versus hearing-impaired (HI) critical ratio data

Both panels show the same data, which are identified by frequency in the top panel and by HI listener in the bottom panel. The correlation coefficient (r) and probability (p) of these data are indicated.

Fits to Rounded-Exponential Filter

The notched-noise data were also used to derive auditory filter shapes according to the method described by Rosen et al. (1998) and based on the rounded-exponential (roex) filter model of Patterson et al. (1982). The data were fit using the roex(p, r) filter defined as

$$\begin{array}{l}\text{W}(\text{g})=(1-\text{r})(1-{\text{p}}_1\text{g})\exp ({\text{p}}_1\text{g})+\text{r},\text{g}<0\\ =(1-\text{r})(1+{\text{p}}_{\text{u}}\text{g})\exp (-{\text{p}}_{\text{u}}\text{g})+\text{r},\text{g}\ge 0\end{array}$$ (4)

where g = (f-f_p)/ f_p, p_l and p_u define the slopes of the filter skirts below and above the center frequency, respectively, and r limits the filter dynamic range. Specifically, the filter W(g) can be used to predict thresholds for the nine notch conditions at a specific f_p. Optimal filter fits were obtained by iteratively adjusting the filter parameters p_l, p_u, and r to minimize the RMS difference between the predicted and actual thresholds. The fitting procedure incorporated a middle ear transformation, permitted variations in filter center frequency of up to 0.1*f_p, and altered the filter bandwidth with center frequency as described in Glasberg and Moore (1990). To ensure “reasonable” results, the fit parameters were restricted in terms of absolute slope (0 ≤ p_l, p_u ≤ 60), slope symmetry (0.1≤ p_u /p_l ≤ 10) and dynamic range (0 ≤ r < 1). Valid solutions were defined as solutions that converged within the restricted solution range and that did not converge to a boundary condition.

The iterative fitting procedure was applied to the threshold data for each HI and AM-SIM listener individually. Valid solutions were obtained for 37 of the 49 (HI-listener, f_p) combinations and for 140 of the 147 (AM-SIM-listener, f_p) combinations. Valid solutions were obtained for 6 of the remaining 12 HI-listener combinations and for 5 of the remaining 7 AM-SIM-listener combinations by eliminating at most one of the nine notch-condition threshold values from the fitting procedure. If the elimination of multiple, single notch-condition thresholds yielded valid solutions, then the solution with minimum error was selected. Solutions were not obtained for the HI listeners in 6 cases: HI-6 for f_p = 250 Hz, HI-4, HI-5, HI-7 and HI-8 for f_p = 2000 Hz, and HI-6 for f_p = 4000 Hz. Solutions were not obtained for the AM-SIM listeners in 2 cases, both for HI-10 for f_p = 250 Hz. The detailed results of the roex fits to the notched-noise data are provided in Appendices A to E. Individual fit data are provided for each HI subject and average fit data (using valid fits only) are provided for the corresponding AM-SIM group. The fits for each of the five probe frequencies are described in terms of the slope parameters of the filters, p_l and p_u; the ratio of these parameters, p_u/p_l; the dynamic range of the filter, r; the “efficiency” k, which is equal to the SNR at the filter output required to detect the probe signal with 70.7% accuracy; and estimates of Equivalent Rectangular Bandwidth (ERB) and the 3-dB-down filter bandwidths. The description of the results of the fitting procedure below is focused primarily on summarizing the derived auditory-filter characteristics using the ERB values and slope ratios. The remaining filter-fit parameters are provided in the appendices.

Figure 8 shows the ERB results for a given HI listener versus those for the corresponding AM-SIM group for the 43 conditions for which valid filter fits were obtained for both sets of listeners. The ERB values were first normalized by dividing by the probe frequency and then plotted on a log₁₀ scale. In the upper panel, the data points are identified by frequency and in the lower panel by HI listener. The partial correlation (controlling for probe frequency) between the two sets of normalized ERB data (r = .499) was highly significant (p < .0006). On average, ERBs at 250, 500, 1000, 2000, and 4000 Hz for these 43 conditions were 142, 145, 359, 658, and 2434 Hz, respectively, for the HI listeners and 116, 113, 279, 606, and 1361 Hz, respectively, for the AM-SIM listeners. By comparison, average ERBs for the NH group at the five probe frequencies were 68, 150, 298, 454, and 590 Hz, respectively. A one-way analysis of variance (ANOVA) was conducted on the normalized ERB values at each probe frequency with the main factor of listening group (HI vs. AM-SIM) including only cases where filter fits (and ERB values) could be obtained for the HI listener and at least one of the three AM-SIM listeners. The results of the ANOVAs (shown in Table 3) indicate no significant differences in ERB values between HI and AM-SIM listeners for probe frequencies of 250, 500, 1000, and 2000 Hz. At 4000 Hz, a significant group effect was observed with higher mean ERB values for HI (2434 Hz) compared to AM-SIM (1361 Hz) listeners.

Figure 8.

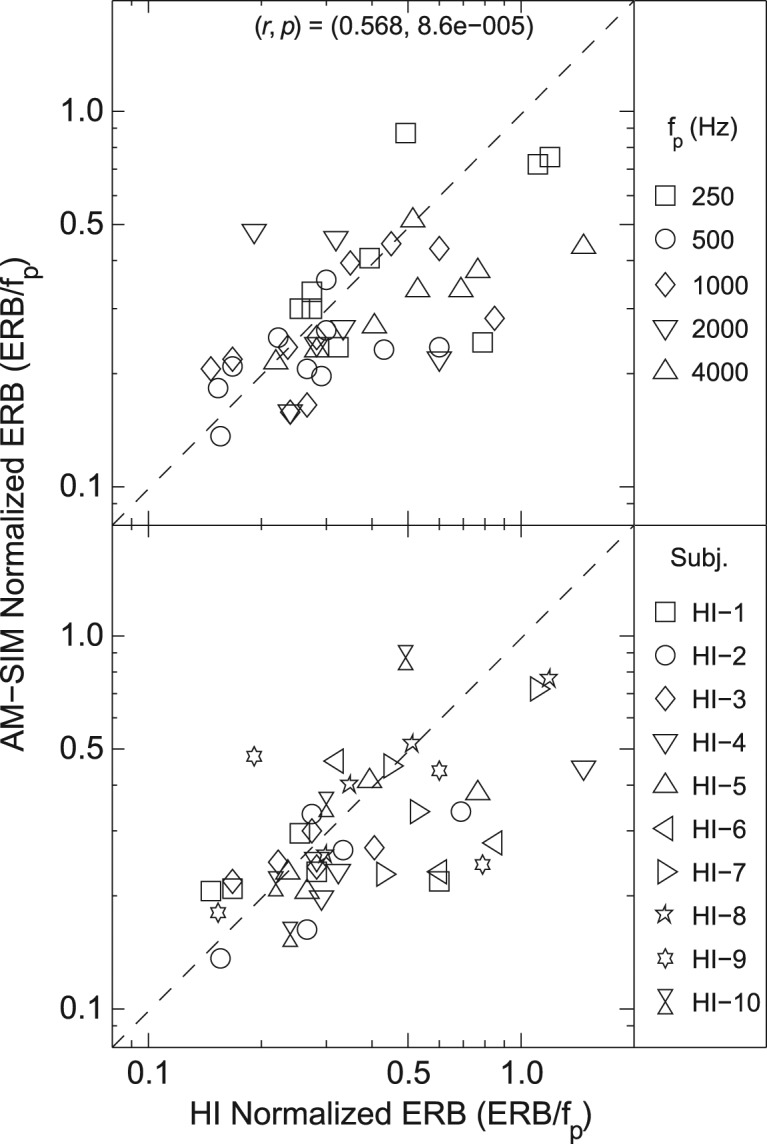
Equivalent rectangular bandwidth (ERB) normalized by probe frequency (f_p) for age matched, simulated-loss (AM-SIM) versus hearing-impaired (HI) results

Note: Both panels show the same data, which are identified by frequency in the top panel and by HI listener in the bottom panel. The correlation coefficient (r) and probability (p) of these data are indicated.

Table 3.

Results of One-Way Analyses of Variance With Main Effect of Group for Equivalent Rectangular Bandwidth (ERB) Values and for Slope Ratios p_u/p_l

		ERB		pu/pl
Probe Frequency	df	F	p value	F	p value
250	1, 32	1.30	.2627	0.04	.8461
500	1, 38	1.76	.1929	0.33	.5711
1000	1, 38	1.98	.1678	0.02	.8764
2000	1, 22	0.07	.787	0.41	.529
4000	1, 30	8.80	.0059*	0.01	.9239

Note: For each probe frequency and analysis, the degrees of freedom (df), F values, and probabilities (p) are provided. Significant effects are marked by an asterisk.

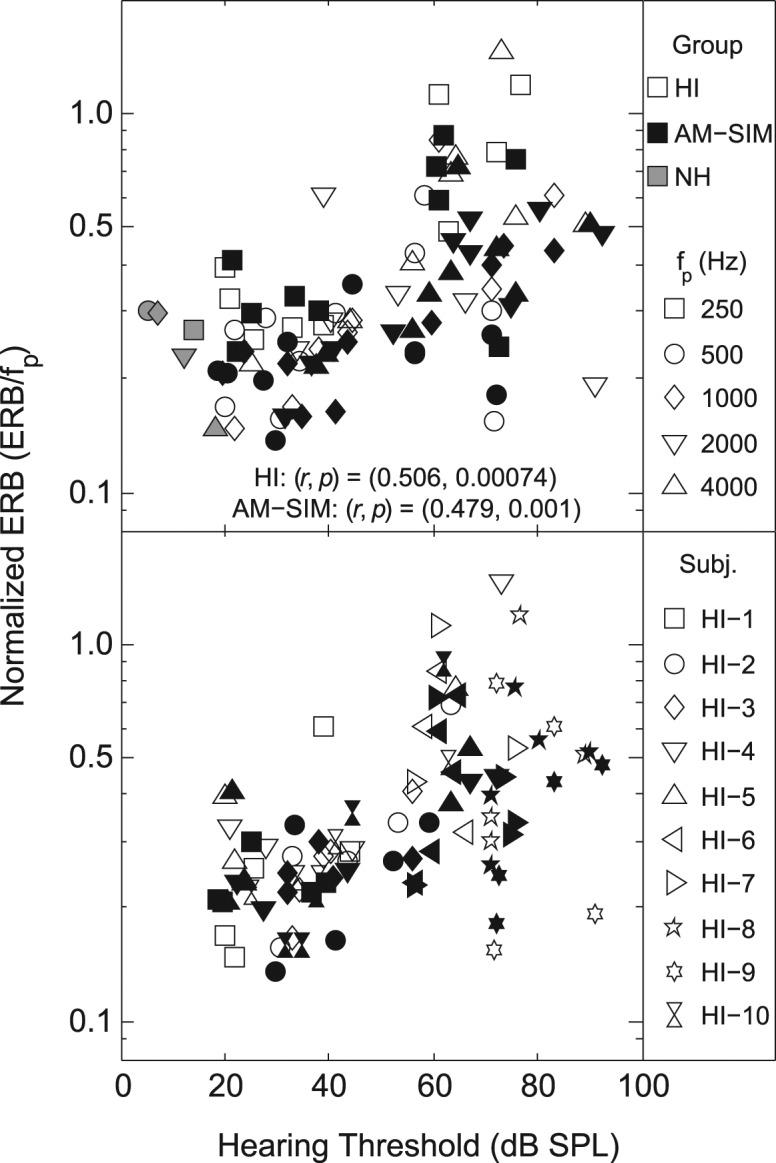
To examine the effects of hearing threshold level on the magnitude of the ERB, normalized ERB values were plotted versus the 500-ms threshold in dB SPL at f_p for the NH (top plot only), HI, and AM-SIM listeners (Figure 9). Data points include all conditions where fits were obtained for either HI or AM-SIM listeners. In the upper panel, the data points are identified by probe frequency and in the lower panel by HI listener. Partial correlations controlling for probe signal level and probe frequency were calculated for both the HI and AM-SIM groups between normalized ERB and hearing threshold. In the notched-noise experiment, signal level at a given probe frequency was set to the maximum of 70 dB SPL or 8 dB SL; thus, probe level increased with an increase in hearing threshold above 62 dB SPL. Because the ERB is known to increase with signal level (Rosen et al., 1998) as well as frequency, it was important to control for both of these effects in examining the relation between ERB and hearing threshold. The partial correlations for both the HI and AM-SIM listeners were moderate and significant r = .51, p < .0007 and r = .48, p < .001, respectively).

Figure 9.

Equivalent rectangular bandwidth (ERB) normalized by probe frequency (f_p) plotted as a function of probe-frequency hearing threshold (in dB SPL) for hearing-impaired (HI) and agematched, simulated-loss (AM-SIM) listeners

Note: Both panels show the same data, which are identified by frequency in the top panel and by HI listener in the bottom panel. The correlation coefficients (r) and probabilities (p) of these two data sets are indicated.

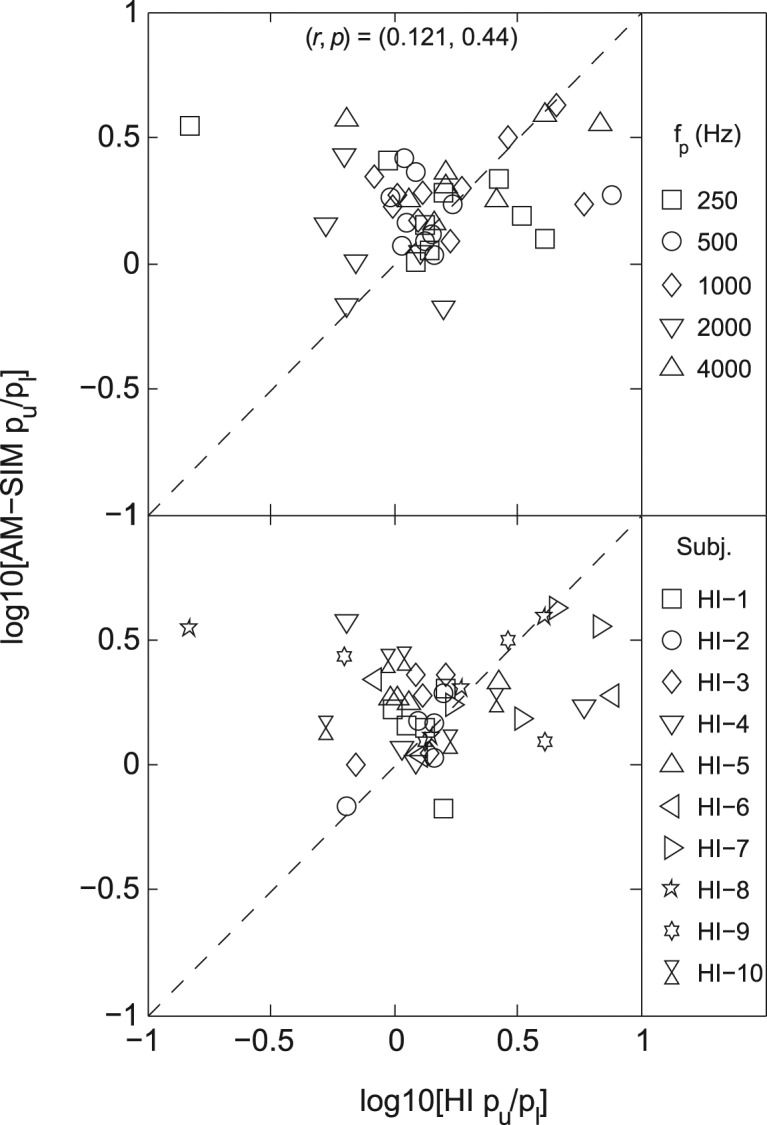
To investigate auditory filter symmetry, the ratios of the filter-fit slope parameters, p_u/p_l, were calculated for all filter fits. Figure 10 plots the log₁₀ values of these ratios for each HI listener versus the log₁₀ values for the corresponding AM-SIM group for the 43 conditions where fits were obtained for both sets of listeners. In the upper panel, the data points are identified by probe frequency and in the lower panel by HI listener. When viewing the plots of log10 (p_u/p_l), values greater than zero indicate steeper high-frequency slope in the filter fit while values less than zero indicate steeper low-frequency slope. The partial correlation (controlling for probe frequency) of log₁₀ (p_u/p_l) between the HI and AM-SIM listeners (r = .121) was not significant (p < .44). The average slope ratios at 250, 500, 1000, 2000, and 4000 Hz for these 43 conditions were 1.85, 1.91, 2.24, 0.90, and 2.51, respectively, for the HI listeners and 1.83, 1.66, 2.15, 1.26, and 2.57, respectively, for the AM-SIM listeners. For the NH listeners without simulated loss, the average ratios at the five probe frequencies were 1.33, 1.57, 1.68, 0.87, and 2.54, respectively. A one-way ANOVA, analogous to that performed on the ERB values, was conducted on the slope-ratio values (p_u/p_l) at each probe frequency to examine the main effect of group (HI vs. AM-SIM). The results of these ANOVAs (shown in Table 3) indicate no significant difference in p_u/p_l between HI and AM-SIM listeners for any probe frequency.

Figure 10.

Relationship of roex filter-fit slope ratios (p_u/p_l) for age-matched, simulated-loss (AMSIM) versus hearing-impaired (HI) listeners

Note: Slope ratios are transformed using a base-10 logarithm prior to plotting. Both panels show the same data, which are identified by frequency in the top panel and by HI listener in the bottom panel. The correlation coefficient (r) and probability (p) of these data are indicated.

Discussion

The effects of cochlear hearing loss can result in two major types of deficit in the perception of auditory signals. The first type of deficit arises from a reduction in audibility due to elevated thresholds, and the second type of deficit is defined as a degradation of auditory abilities beyond those associated with threshold elevation (also referred to as suprathreshold deficits). The hearing-loss simulation employed here was designed to reproduce effects associated with a reduction in audibility, including threshold elevation, reduced dynamic range, and loudness recruitment. Thus this research addressed the question of whether audibility-based effects are capable of explaining the reduced frequency selectivity observed in listeners with cochlear hearing impairment or whether this degraded performance must be ascribed to other, non-audibility-based suprathreshold factors.

The TN/MBE simulation employed here was shown to be capable of reproducing the pure-tone threshold elevations associated with the hearing losses of individual HI listeners to a high degree of accuracy (a mean RMS difference of 2.2 dB across all simulations). Its ability to reproduce the masked thresholds obtained in the notched-noise masking paradigm was also reasonably good (resulting in a mean RMS difference of 5.6 dB across all simulations) but not as accurate as in reproducing the audiometric hearing loss. The error associated with the notched-noise simulations is similar to that reported in previous studies of additive noise simulations of hearing loss in notched-noise test conditions. Dubno and Schaefer (1992), for example, reported a mean difference of 6.0 dB between masked thresholds for simulations and hearing-impaired listeners across notch widths and subjects, and Sommers and Humes (1993) reported a range of differences in masked thresholds of 0.18 to 7.91 dB across notch width and subjects. Humes, Espinoza-Varas, and Watson (1988) used a model based on additivity of masking in NH listeners to predict the notched-noise thresholds of HI listeners from the studies of Tyler et al. (1984) and Glasberg and Moore (1986). The deviations between observed HI thresholds and predicted results for noise-masked NH listeners were similar to those between data for listeners with real and simulated hearing loss.

Our results indicate some individual differences in the quality of the notched-noise simulations. The simulations produced poorer matches for HI-4, HI-6, HI-7, and HI-9 (mean RMS differences in the range 6-10 dB) than for the remaining six HI subjects (mean RMS differences less than 6 dB). In the cases of poor simulations, the fixed-level tone was masked by lower levels of the notched noise for the HI than for the AM-SIM listeners. The possible contribution of dead regions (Moore, Huss, Vickers, Glasberg, & Alcantara, 2000) at the probe frequency to the lowered notched-noise masking functions of the HI listeners can be assessed by examining performance at the zero-notch conditions (which can be used to estimate the critical ratio). In particular, thresholds for the masking noise that are 5 to 10 dB worse than those of the AM-SIM groups may be suggestive of dead regions at the given probe frequency. In the presence of dead regions where there are no functioning inner hair cells in the cochlea around a given probe frequency, thresholds are thought to be associated with the activation of functioning hair cells in other regions of the cochlea, which respond to high levels of presentation. This appears to be the case at 250 Hz for HI-8, 500 Hz for HI-9, 2000 Hz for HI-6 and HI-10, and 4000 Hz for HI-6. Across subjects and frequencies, estimates of the critical ratio obtained from the zero-notch condition at each probe frequency were generally well correlated between the HI and AM-SIM groups (see Figure 7) and were also similar in magnitude (within 1-2 dB of each other at each probe frequency). These values were roughly 2 dB larger than those of the NH group. For the highest observed critical ratios for HI listeners, however, there was a tendency for the AM-SIM values to be somewhat lower as can be observed in the upper right quadrant of Figure 7. These values are associated with measurements with probe tones of 2000 and 4000 Hz for subjects HI-4, HI-6, and HI-8 and with possible dead regions only for HI-6 at both of these frequencies.

The critical ratios measured here are several dB higher than those reported by Dubno and Schaefer (1992) for NH, HI, and simulated-loss listeners. These somewhat higher values may be related to the relatively high signal levels at which our measurements were obtained. In our procedures, the level of the tone had values ranging from 70 to 97 dB SPL across subjects and frequencies and the masker level was adjusted in threshold measurements. The resulting spectrum levels of these maskers were typically in the range of 45 to 60 dB SPL. Dubno and Schaefer (1992), on the other hand, employed a fixed-level noise with a spectrum level of 40 dB and varied the tonal level to measure threshold. Although the critical ratio is generally regarded as being insensitive to noise level, Reed and Bilger (1973) reported a systematic increase in the critical ratio with an increase in the spectrum level of the noise for test frequencies above 500 Hz. Thus the magnitude of the critical ratios observed in the current study is likely related to the relatively high signal and masker levels employed in the measurements.

The effectiveness of the hearing-loss simulations was also evaluated using the results of the roex model to estimate the bandwidths and shapes of the auditory filter as a function of probe frequency. Significant differences in ERB values between the HI and AM-SIM listeners were observed only for f_p = 4000 Hz. On average across the five test frequencies, however, ERBs were slightly larger for the HI listeners compared to the AM-SIM groups (by a mean factor of 1.3 across probe frequencies). A significant correlation, controlling for probe frequency, was observed between the normalized ERB values of the HI and AM-SIM listeners (see Figure 8); however, there were some cases (to the right of the dashed diagonal line in Figure 8) where the HI values were underestimated by the simulations. Estimates of auditory filter symmetry, as measured by the ratio p_u/p_l of the slopes of the upper and lower filter-fit skirts, indicated steeper slopes of the high-frequency compared to the low-frequency skirts of the filters in nearly all cases (with the exception of 2000 Hz for the HI and NH groups). Slope ratios, however, were not correlated between the HI and AM-SIM listeners (see Figure 10).

Consistent with previous studies that have found a correlation between ERB and hearing threshold (Dubno & Dirks, 1989; Sommers & Humes, 1993; Moore, Vickers, Plack, & Oxenham, 1999; Hopkins & Moore, 2011), our results also demonstrated ERBs that were positively and significantly correlated with hearing threshold. Furthermore, as observed by Hopkins and Moore (2011), these correlations remained significant even when controlling for the effects of stimulus level and probe frequency. Leek and Summers (1993) examined the relation between hearing threshold and ERB as a function of signal level. For a 500-Hz probe, there was no change in ERB with hearing threshold for either HI or masked-normal listeners; at 2000 Hz, however, an increase in ERB was observed only for HI listeners for threshold above 40 dB SPL, particularly at the highest signal levels.

The simulations were not entirely accurate in predicting the broadened auditory bandwidths for individual HI listeners at particular probe frequencies (see off-diagonal points in Figure 8). These failures occurred for each of the probe frequencies [e.g., 250 Hz (HI-1, HI-7, and HI-8); 500 Hz (HI-6); 1000 Hz (HI-6); 2000 Hz (HI-4); and 4000 Hz (HI-2 and HI-5)] and were more common for TN-alone simulations where the probe tone was near the minimal SL of 8 dB and thus associated with losses in excess of 62 dB HL. It appears that in these cases the HI listeners experienced more difficulty detecting the tone in the notched-noise maskers compared to the AM-SIM listeners in threshold-elevating noise. An additional difficulty in evaluating the simulations arose with the inability to fit the notched-noise data with the roex filter model for six of the 49 HI functions shown in Figure 4, including four with a probe frequency of 2000 Hz. By contrast, roex fits were obtained for the AM-SIM listeners in each of these six cases. The HI functions were atypical in that they showed no improvement in tone detectability with a widening of the masker notch even though performance was similar to that of the AM-SIM listeners for the zero-notch condition. In all but one of these functions, the probe level was at the minimum value of 8 dB SL. These results are indicative of extremely broad auditory bandwidths in which masking components remote from the center frequency were as (or more) effective in masking the tone as were in-band frequencies. These functions did not contribute to the analyses of ERB and slope ratios; nonetheless they did contribute to the RMS differences shown in Figure 6 and do detract from the effectiveness of the simulations.

Several possibilities may account for the observed inadequacies in the simulations. One possible explanation is that loudness recruitment near threshold was not accurately simulated: that is, the loudness of the notched-noise maskers grew more rapidly for the HI listeners than for the AM-SIM listeners making the maskers more effective at lower levels and resulting in increased estimates of ERB. This hypothesis could be examined in future research by using MBE-alone simulations to specify different recruiting functions. Another explanation might lie in suprathreshold factors related to aspects of cochlear damage that are not reproduced by the audibility-based simulations employed here. For example, some aspects of the hearing loss may have arisen from the loss of neuronal cells in the spiral ganglion, which do not contribute to audibility but may contribute to other suprathreshold effects (Kujawa & Liberman, 2009; Makary, Shin, Kujawa, Liberman, & Merchant, 2011). Alternately, the failures of the simulation (which typically occurred for hearing loss in excess of 62 dB HL) may be related to aspects of severe outer hair cell damage leading to a reduction or loss of the active cochlear-compression mechanism. Moore et al. (1999) demonstrated a tendency for an increase in ERB with a reduction in a psychoacoustic measure of cochlear compression in HI listeners, and Baker and Rosen (2002) found a weaker effect of level on filter shape in HI compared to NH listeners, also suggestive of a reduction in nonlinearity in cochlear hearing loss. These results lend support to the hypothesis that outer hair cell damage may contribute to widened auditory bandwidths.

Conclusion

The current study extends the use of TN/MBE simulations of hearing loss to auditory-filter characteristics to complement previous studies concerned with speech reception in noise (Desloge et al., 2010) and temporal processing (Desloge et al., 2011a, b). The simulations were more successful in reproducing the ERB values of certain HI listeners than others due primarily to greater masking effects in the notched-noise data of the more poorly fit HI listeners compared to their AM-SIM groups. For some HI listeners at certain probe frequencies, the data could not be fit with a roex model to estimate auditory-filter characteristics because there was no improvement in the detectability of the tone with increasing notch width of the masker. In the remaining cases where roex fits were obtained, the ERB values of the HI listeners were statistically equivalent to those of the AM-SIM listeners at four of the five probe frequencies and no statistical differences in filter symmetry were observed between the two groups at any probe frequency. Overall, the results suggest that audibility effects were capable of reproducing the auditory-filter characteristics for certain listeners and probe frequencies. In other cases, however, the auditory bandwidths of the HI listeners remained larger than those observed in the presence of the simulation, which suggests that suprathreshold effects may have played a role.

Future research will be concerned with continued refinement and extension of the functional model of hearing loss to improve its ability to reproduce the performance of HI listeners on speech and psychoacoustic tasks. A more accurate model of hearing loss will facilitate the design and evaluation of new hearing-aid algorithms.

Appendix

Appendix A.

Results of roex Filter Fit for Probe Frequency f_p = 250 Hz

Subject	pl	pu	pu/pl	r	k	ERB	BW-3dB
NH	13.7	18.2	1.3	−21.8	4.2	67.5	54.1
HI-1	14.5	19.3	1.3	−21.3	−0.4	63.7	51
AMSIM-1	12.6	17.8	1.4	−19.9	1	74.4	58.3
HI-2	12.9	20.3	1.6	−19.3	3.7	68.6	53.8
AMSIM-2	10.4	17.7	1.9	-70.6	1.1	82.9	68.1
HI-3	12.5	17.4	1.4	−166.7	5.8	68.6	57.5
AMSIM-3	16	16	1.1	−20.8	7.5	74.9	60
HI-4	12	14.7	1.2	−18.9	1.4	81.2	64.3
AMSIM-4	19.4	18.9	1	−69.1	9.1	58.5	45.6
HI-5	6.9	18.6	2.7	−165.8	6.3	98.6	82.8
AMSIM-5	7.7	15.2	2.2	−153.1	5.5	102.5	86.1
HI-6	—	—	—	—	—	—	—
AMSIM-6	17.7	12.3	0.9	−57	6.2	146.7	120.4
HI-7	1.8	5.7	3.3	−145.3	0.8	278.7	312.3
AMSIM-7	9.6	9.3	1.5	−102.3	6.6	181.1	173.8
HI-8	6.8	1	0.1	−78.8	4.5	297.6	479.5
AMSIM-8	4	12.5	3.5	−105	1.6	190.3	178.8
HI-9	2.8	11.4	4.1	−130.2	3.7	196.7	186.8
AMSIM-9	17.2	19.6	1.2	−70.5	5.6	61	50
HI-10	8.4	8	1	−145.7	3.6	122.1	102.3
AMSIM-10	2.8	7.3	2.6	−92.8	6.1	219.8	205.3

Note: Dash indicates that no valid roex fit was obtained. For normal-hearing (NH), hearing-impaired (HI), and corresponding age-matched, simulated-loss (AM-SIM) listeners, the following parameters are shown: upper and lower slope parameters p_l and p_u; slope-parameter ratio p_u/p_l; filter dynamic range r; efficiency term k; equivalent rectangular bandwidth (ERB); and 3-dB-down filter bandwidths (BW-3dB).

Appendix B.

Results of roex Filter Fit for Probe Frequency f_p = 500 Hz

Subject	pl	pu	pu/pl	r	k	ERB	BW-3dB
NH	12.4	19.2	1.6	−17.7	−1.5	150.4	114.5
HI-1	26.1	29.1	1.1	−19	−1.2	84.4	61.5
AMSIM-1	17.3	24.9	1.4	−21.9	−1.2	105	83.3
HI-2	22.5	32.5	1.4	−25	4.9	78.1	63
AMSIM-2	33.7	36.5	1.1	−27.2	5.6	68.2	54.8
HI-3	16.8	20.8	1.2	−23.5	0.2	111.6	90.5
AMSIM-3	12.7	29.5	2.3	−65.9	3.4	124.1	101.5
HI-4	17.8	19.1	1.1	−13.9	0.1	145.2	95
AMSIM-4	23.6	23.7	1.2	−23.4	5.6	98.9	79.2
HI-5	17.2	16.8	1	−17.4	4	133.7	100.5
AMSIM-5	17.3	30.1	1.8	−21.9	4	103.2	79.8
HI-6	3.5	26.6	7.7	−134.3	6.4	302	273.5
AMSIM-6	20.1	32.1	1.9	−21.5	6.2	117.3	93.3
HI-7	7.3	12.7	1.7	−148.5	0	215.6	181
AMSIM-7	15.5	26.5	1.7	−26.2	3	115.6	93.8
HI-8	12.4	17.7	1.4	−18.1	2.3	150.3	116
AMSIM-8	18	21.1	1.3	−19.1	2.8	129.6	98.8
HI-9	28.6	38.2	1.3	−17.7	11	77	52
AMSIM-9	22.7	26.9	1.2	−22	1.6	91.2	71.5
HI-10	14	15.4	1.1	−18.3	4.7	149.3	116
AMSIM-10	18.6	28.4	2.6	−66.7	8.4	177.1	164.7

Note: Dash indicates that no valid roex fit was obtained. For normal-hearing (NH), hearing-impaired (HI), and corresponding age-matched, simulated-loss (AM-SIM) listeners, the following parameters are shown: upper and lower slope parameters p_l and p_u; slope-parameter ratio p_u/p_l; filter dynamic range r; efficiency term k; equivalent rectangular bandwidth (ERB); and 3-dB-down filter bandwidths (BW-3dB).

Appendix C.

Results of roex Filter Fit for Probe Frequency f_p = 1000 Hz

Subject	pl	pu	pu/pl	r	k	ERB	BW-3dB
NH	12.3	20.9	1.7	−17.7	−2	298.9	225.5
HI-1	33.3	32.6	1	−18.6	0.1	147.7	104
AMSIM-1	17	29.1	1.7	−22.5	−1.4	207.6	165
HI-2	17	21.1	1.2	−15.3	−1	265.8	183
AMSIM-2	25.4	36.6	1.5	−28.6	4.6	164.3	132.3
HI-3	21.3	28	1.3	−29	0.1	167.5	138
AMSIM-3	14.1	26.8	1.9	−159	4.7	219.4	183.7
HI-4	8.2	48.6	5.9	−167.7	0.7	284.5	239
AMSIM-4	14.9	25.4	1.7	−17.8	−0.1	250.2	183.7
HI-5	19.6	20.1	1	−17.2	1	236.3	172
AMSIM-5	13.3	24.6	1.9	−119.4	2.2	234	195.7
HI-6	5	4.2	0.8	−140.7	5.9	851.3	740
AMSIM-6	21.8	25.7	2.2	−114.9	4.7	280.2	235.3
HI-7	5.4	24.6	4.6	−157.5	3.2	446.8	380
AMSIM-7	6.5	24.4	4.3	−151.5	2.7	445.6	377.7
HI-8	11.1	20.9	1.9	−13.9	1.6	346.4	241
AMSIM-8	8.5	17.1	2	−159.2	−0.4	395.3	332
HI-9	4.3	12.4	2.9	−145.9	−1.6	607.6	525
AMSIM-9	8.4	21.1	3.2	−55.3	−2.5	434.2	332
HI-10	13.3	22.5	1.7	−36	−1.7	239.9	200
AMSIM-10	25.6	31.1	1.2	−22.6	2.2	158.7	125

Note: Dash indicates that no valid roex fit was obtained. For normal-hearing (NH), hearing-impaired (HI), and corresponding age-matched, simulated-loss (AM-SIM) listeners, the following parameters are shown: upper and lower slope parameters p_l and p_u; slope-parameter ratio p_u/p_l; filter dynamic range r; efficiency term k; equivalent rectangular bandwidth (ERB); and 3-dB-down filter bandwidths (BW-3dB).

Appendix D.

Results of roex Filter Fit for Probe Frequency f_p = 2000 Hz

Subject	pl	pu	pu/pl	r	k	ERB	BW-3dB
NH	21.6	17.7	0.9	−21.2	−2.4	454.5	360
HI-1	5.3	8.5	1.6	−74.4	−12	1211.1	1026
AMSIM-1	24.6	16.3	0.7	−21.5	−3.9	437	345.3
HI-2	17.1	10.9	0.6	−17	−0.7	670.2	516
AMSIM-2	20.2	13.8	0.7	−78	−0.2	530.1	432
HI-3	17.3	12.2	0.7	−26.7	−3.6	566.6	470
AMSIM-3	18.1	18.2	1	−21.3	0.9	476.9	377.3
HI-4	—	—	—	—	—	—	—
AMSIM-4	15.7	7.5	0.5	−107	0.7	857.1	689.3
HI-5	—	—	—	—	—	—	—
AMSIM-5	11.8	8	0.8	−92.5	2.9	1054.6	902
HI-6	13.4	17.3	1.3	−15.1	10.4	638.1	458
AMSIM-6	17.4	8.8	1.1	−130.1	0.5	918.4	787.3
HI-7	—	—	—	—	—	—	—
AMSIM-7	22.9	13.8	0.7	−62.6	0.5	621.8	489.3
HI-8	—	—	—	—	—	—	—
AMSIM-8	10.1	7.8	1.2	−83.5	−2	1111.5	931.3
HI-9	33.9	21.3	0.6	−16.8	5.5	383.9	262
AMSIM-9	18.6	19	2.7	−61.1	−0.6	957.1	982
HI-10	24.7	13.1	0.5	−24.3	−4.5	479.7	392
AMSIM-10	25.4	34.9	1.4	−29.3	1.7	318	264

Note: Dash indicates that no valid roex fit was obtained. For normal-hearing (NH), hearing-impaired (HI), and corresponding age-matched, simulated-loss (AM-SIM) listeners, the following parameters are shown: upper and lower slope parameters p_l and p_u; slope-parameter ratio p_u/p_l; filter dynamic range r; efficiency term k; equivalent rectangular bandwidth (ERB); and 3-dB-down filter bandwidths (BW-3dB).

Appendix E.

Results of roex Filter Fit for Probe Frequency f_p = 4000 Hz

Subject	pl	pu	pu/pl	r	k	ERB	BW-3dB
NH	21.3	49.4	2.5	−25.2	1.8	589.9	472
HI-1	13	21.2	1.6	−16.8	−3.2	1136	844
AMSIM-1	13.8	27.4	2	−69.6	−1.4	927.7	765.3
HI-2	4.8	7	1.5	−148.5	1.2	2760.1	2356
AMSIM-2	11.3	16.8	1.5	−112.7	0.7	1346.4	1082.7
HI-3	7.9	12.9	1.6	−149.7	1	1627.5	1364
AMSIM-3	11.7	25.3	2.3	−67.8	1.1	1077.2	877.3
HI-4	2.4	1.6	0.6	−138.7	5.6	5844.5	7004
AMSIM-4	6.2	21.9	3.7	−107.6	0.3	1766.1	1512
HI-5	4.8	5.5	1.2	−91.2	−3.1	3061.5	2624
AMSIM-5	8.4	14.9	1.8	−112.9	−0.8	1515.6	1268
HI-6	—	—	—	—	—	—	—
AMSIM-6	4.2	8.9	2	−113.7	3.3	2915.9	2548
HI-7	6.2	42.1	6.8	−10	6.9	2124.6	1384
AMSIM-7	11.3	27.9	3.6	−109.2	1	1342.9	1068
HI-8	6.1	25	4.1	−11.9	6.8	2036.6	1464
AMSIM-8	6.4	25.4	3.9	−108.9	1.7	2049.7	1494.7
HI-9	—	—	—	—	—	—	—
AMSIM-9	—	—	—	—	—	—	—
HI-10	12.6	32.5	2.6	−161.6	−2.7	881.7	736
AMSIM-10	16	29.1	1.8	−67.4	−0.6	868.1	694.7

Note: Dash indicates that no valid roex fit was obtained. For normal-hearing (NH), hearing-impaired (HI), and corresponding age-matched, simulated-loss (AM-SIM) listeners, the following parameters are shown: upper and lower slope parameters p_l and p_u; slope-parameter ratio p_u/p_l; filter dynamic range r; efficiency term k; equivalent rectangular bandwidth (ERB); and 3-dB-down filter bandwidths (BW-3dB).