Application of the Iterative Helical Real-Space Reconstruction Method to Large Membranous Tubular Crystals of P-type ATPases

Abstract

Since the development of three-dimensional helical reconstruction methods in the 1960’s, advances in Fourier-Bessel methods have facilitated structure determination to near-atomic resolution. A recently developed iterative helical real-space reconstruction (IHRSR) method provides an alternative that uses single-particle analysis in conjunction with the imposition of helical symmetry. In this work, we have adapted the IHRSR algorithm to work with frozen-hydrated tubular crystals of P-type ATPases. In particular, we have implemented layer-line filtering to improve the signal-to-noise ratio, Wiener-filtering to compensate for the contrast transfer function, solvent flattening to improve reference reconstructions, out-of-plane tilt compensation to deal with flexibility in three dimensions, systematic calculation of Fourier shell correlations to track the progress of the refinement, and tools to control parameters as the refinement progresses. We have tested this procedure on datasets from Na⁺/K⁺-ATPase, rabbit skeletal Ca²⁺-ATPase and scallop Ca²⁺-ATPase in order to evaluate the potential for sub-nanometer resolution as well as the robustness in the presence of disorder. We found that Fourier-Bessel methods perform better for well-ordered samples of skeletal Ca²⁺-ATPase and Na⁺/K⁺-ATPase, although improvements to IHRSR are discussed that should reduce this disparity. On the other hand, IHRSR was very effective for scallop Ca²⁺-ATPase, which was too disordered to analyze by Fourier-Bessel methods.

1. INTRODUCTION

Methods for 3D image reconstruction from electron micrographs were developed in the 1960’s and 1970’s by Klug and colleagues (Klug, 1983). They recognized that a 3D structure could be determined from multiple views of an object at different orientations and used Fourier transforms as a convenient way to combine the corresponding data (Crowther et al., 1970). An alternative method employed a Fourier-Bessel transform to produce a 3D structure from a single view of an object with helical symmetry (Klug et al., 1958), with the first successful application being to the helical tail of the T4 bacteriophage (DeRosier and Klug, 1968). This helical application offered a great advantage over 2D crystallographic methods that required systematic tilting of the specimen to build up a 3D dataset (Henderson and Unwin, 1975). Basic steps in helical reconstruction were described by DeRosier and Moore (1970) and involve indexing of the layer lines that compose the Fourier transform, extracting amplitude and phase data from these layer lines, and correcting phase data for out-of-plane tilt. To improve the signal-to-noise ratio, data from multiple images were averaged after finding a common phase origin and Fourier-Bessel transformation was used to produce the 3D map. For these methods, data manipulations were done entirely in Fourier space.

Over the ensuing two decades, these methods became the standard in the field and were used on a wide variety of biological systems, including actin, tubulin, myosin, and bacterial flagella. Adaptations were made to the basic algorithm to maximize resolution for particular applications. Notable advances include an algorithm to account for bending in the plane of electron micrographs of helical objects by spline-fitting and real-space re-interpolation of curved actin filaments (Egelman, 1986) and automated processing of large datasets to extract high resolution (10 Å) data when only low resolution (25 Å) data were visible in the Fourier transforms from individual bacterial flagellar filaments (Morgan and DeRosier, 1992).

A substantial reworking of the original algorithms was undertaken by Toyoshima and Unwin (1990) in their work on membranous protein crystals of the nicotinic acetylcholine receptor. New procedures included interpolation of the image in real-space to ensure that layer-lines not only were aligned to the sampling lattice of the Fourier transform, but also fell at an integral number of reciprocal pixels. Also, real-space averaging of 3D maps was used to combine data from different helical symmetries. Further improvements were made by Beroukhim and Unwin (1997) analogous to the unbending procedures that had been developed for 2D crystals (Henderson et al., 1990). Helical unbending involved determination of precise orientational parameters from segments of the tubular crystals (i.e. in-plane bending & scale changes, and out-of-plane tilting & twist around the tube axis) based on comparison with a reference data set. Notable applications of these techniques include Ca²⁺-ATPase (Stokes et al., 1998, Xu et al., 2002) and bacterial flagella (Yonekura et al., 2003) at better than 10 Å resolution, and a recent structure of the acetylcholine receptor at 4 Å (Unwin, 2005). Finally, an iterative Fourier-Bessel algorithm was developed for reconstruction of helical structures with severe Bessel overlap (Wang and Nogales, 2005), and methods for combining data from different symmetry groups both by averaging real-space densities derived from 3D maps (Toyoshima and Unwin, 1990) and by averaging Fourier-Bessel coefficients (g_n,l(r)) prior to calculation of 3D maps (DeRosier et al., 1999).

Despite this tremendous progress, Fourier-Bessel reconstruction methods are limited in their ability to deal with flexible and disordered helical samples. In order to address these problems, a hybrid iterative helical real-space reconstruction (IHRSR) method was recently developed, which employs algorithms from single particle analysis in conjunction with real-space helical averaging, to overcome significant disorder in thin helical filaments like RecA (Egelman, 2000). This method divides images into small overlapping segments, whose relative orientations are determined by the standard single particle technique of projection matching (see Jiang and Ludtke, 2005, for a recent review). After using back projection to produce a 3D structure, helical symmetry is empirically determined and imposed on this structure prior to the subsequent round of refinement. Over the last few years, these methods have found wide application in helical assemblies, including F-actin (Galkin et al., 2003), RecA (VanLoock et al., 2003), and bacterial pilli (Mu et al., 2002).

In the current work, we have adapted and modified the original IHRSR methodology for use on large frozen-hydrated tubular crystals of P-type ATPases, with the goal of achieving 3D reconstructions at sub-nanometer resolution. Previously, we have encountered limitations in Fourier-Bessel reconstruction methods due to the presence of bending, variable symmetry, indexing ambiguity, and low signal-to-noise ratios (SNR). To overcome these problems, we have enhanced the IHRSR algorithm by implementing layer-line filtering to improve the SNR, Wiener-filtering to compensate for the contrast transfer function, solvent flattening to iteratively produce improved reference reconstructions, out-of-plane tilt to track short-range flexibility in three dimensions, automatic isolation of single molecules from the lattice to track refinement via Fourier Shell Correlation, as well as tools to control and track the refinement. The procedure has been tested on three distinct datasets that demonstrate its relative strengths and weaknesses.

2. METHODS

Tubular crystals of rabbit sarcoplasmic reticulum (SR) Ca²⁺-ATPase and duck Na⁺,K⁺-ATPase were prepared and imaged as previously reported (Xu et al., 2002 , Rice et al., 2001). Scallop SR Ca²⁺-ATPase was isolated and crystallized as described by Castellani et al. (1985). The resultant crystals were plunge-frozen in liquid ethane and imaged at 50,000x magnification on a Philips CM200 field-emission electron microscope (FEI Corp., Eindhoven, Netherlands) under low-dose conditions (~15 electrons/Ų) with an Oxford CT3500 (Gatan Corp., Pleasanton CA) cryo-holder. Images were taken on Kodak SO-163 (Rochester, NY) electron imaging film and push processed in full-strength D19 developer for 12 mins. Optical diffraction was used to identify good images, which were scanned at 14 μm intervals with a Zeiss SCAI densitometer (Intergraph Corp., Madison AL), resulting in an effective sampling size of 2.73 Å/pixel.

Computations were performed on dual-processor, 64-bit Opteron workstations running RedHat Fedora Core 3 version of the LINUX operating system. The image processing package SPIDER (Frank et al., 1996) was used for many of the steps of the refinement cycle with the addition of two independent programs written by Ed Egelman for the helical symmetry search of the asymmetric 3D volume and, subsequently for imposing this symmetry on this 3D volume (Egelman, 2000). The series of operations were controlled from a SPIDER script provided by Ed Egelman and modified to include the additional steps described in the Results. For the first round of refinement, we used an interactive version of the helical search program to manually look for the most likely helical parameters. Thereafter, the cycle could be run without user intervention. With our computer hardware, a single cycle including 600 subimages took 3 h; most of the time was spent on multireference alignment, which depends on the square of the subimage dimension and linearly on the number of subimages. A complete refinement typically took 3-4 days.

3. RESULTS

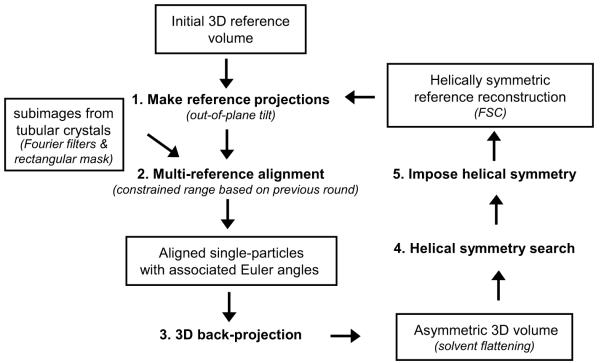
The eight basic steps of the original IHRSR algorithm developed by Egelman (2000) are illustrated in Fig. 1. To summarize, the input data is generated by cutting individual images of tubular crystals into a series of square subimages that typically overlap each other by ~90%. The refinement cycle then begins by comparing these subimages to a reference structure, which can be a 3D structure of a related helix, a low-resolution Fourier-Bessel reconstruction, or even a featureless cylinder of the same diameter. This comparison is done by generating projection images from the reference at all possible orientations about the tube axis (step 1), which are then used for multi-reference alignment of the input series of subimages (step 2). The Euler angles specifying the relative orientation of each subimage are determined by the orientation of the matching reference projection. These Euler angles are used for back-projection of the input subimages to generate an asymmetric 3D volume (step 3). A systematic search for the helical symmetry in this 3D volume is then conducted (step 4), followed by imposition of this symmetry on the volume (step 5) to generate a new reference for subsequent rounds of refinement. This cycle is iterated until convergence of the various parameters (Euler angles and helical symmetry) is achieved. In Fig. 1, the italicized comments in parentheses refer to additions that we made to this basic algorithm, each of which is described in detail below.

Figure 1.

Overview of the IHRSR cycle. 1) A series of 2D projections are calculated from a 3D reference model. 2) Tubular crystal segments (i.e. “single-particle” subimages) are aligned against the reference projections (i.e. multi-reference alignment). 3) Single-particle subimages are back-projected to form an initial asymmetric 3D volume. 4) A helical search is conducted on the asymmetric 3D volume to determine helical symmetry parameters. 5) Helical symmetry is imposed onto the 3D volume. 1) The helically symmetric 3D volume is then used as the new “reference” model for the next round, and the cycle is iterated until a stable reconstruction is obtained. Significant modifications to the original algorithm are italicized in brackets and are described in Table 1.

We have adapted the IHRSR reconstruction algorithm to helical crystals of three different P-type ATPases preserved in the frozen-hydrated state (Fig 2). The first dataset came from tubular crystals of Na⁺,K⁺-ATPase from the supraorbital glands of salt-adapted ducks, which were previously solved using Fourier-Bessel reconstruction methods as implemented by Beroukhim and Unwin (1997) to ~12 Å resolution (Rice et al., 2001). Recent efforts to improve this reconstruction failed to extend the resolution beyond ~10 Å, even after increasing the number of tubes and applying constraints such as solvent flattening. We hoped that the IHRSR algorithm would be successful where Fourier-Bessel methods were not. The second dataset came from well-ordered tubular crystals of rabbit SR Ca²⁺-ATPase, which are better ordered and have previously been solved to 6.5 Å resolution (Xu et al., 2002) using these same Fourier-Bessel methods. This sample offered a comparison to Na⁺/K⁺-ATPase to see how the algorithm responded to higher resolution data. The final dataset came from more disordered tubular crystals of scallop SR Ca²⁺-ATPase, which have previously only been studied at low resolution by Fourier-Bessel reconstruction of negatively stained crystals (Castellani et al., 1985). A low SNR has made it difficult to establish the helical symmetry of these scallop Ca²⁺-ATPase tubes and impossible to find a common phase origin for averaging data from multiple tubes. Ultimately, our goal is to use IHRSR to overcome the limitations of Fourier-Bessel reconstructions and thereby to resolve the secondary structural elements, in the case of Na⁺/K⁺-ATPase, and at least the domain organization, in the case of scallop Ca²⁺-ATPase.

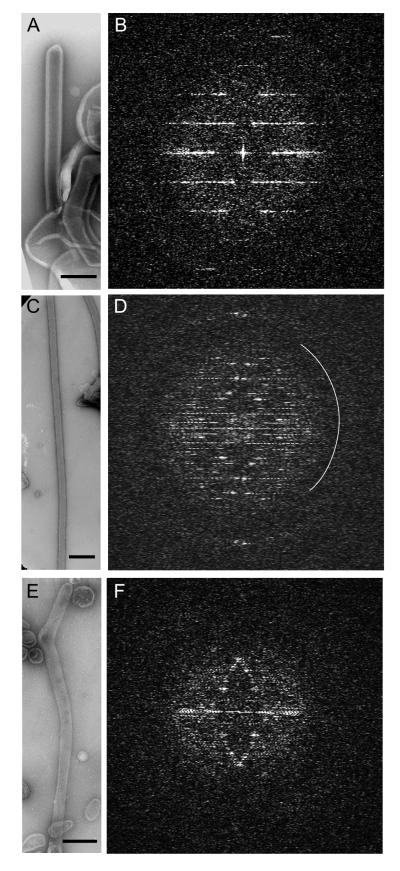
Figure 2.

Three different samples were used to develop and test the IHRSR algorithm. Na⁺/K⁺-ATPase from duck salt gland (a,b). Ca²⁺-ATPase from rabbit skeletal muscle (c,d). Ca²⁺-ATPase from scallop catch muscle (e,f). All three samples show layer lines and in the case of Na⁺/K⁺-ATPase and rabbit Ca²⁺-ATPase, these extend to 15 Å resolution. These high order reflections are near the second maximum in the CTF and the approximate position of the first CTF zero is shown by the white arc in (d). Note that the image of skeletal Ca²⁺-ATPase in (c) is at lower magnification and that this tube is much longer than the others. Scale bars correspond to 200 nm.

3.1 Na⁺,K⁺-ATPase Tubular Crystals

Compared to previous studies of skeletal SR Ca²⁺-ATPase (Xu et al., 2002) and nicotinic acetylcholine receptor (Toyoshima and Unwin, 1990), tubular crystals from Na⁺,K⁺-ATPase are relatively short (maximum of 300-400 nm, compare Figs. 2a and 2c), but still suitable for Fourier-Bessel methods. More problematic is that Na⁺/K⁺-ATPase tubes are wider (~800 Å) and therefore tend to adopt a larger number of helical symmetries. In previous work, we followed the conventional strategies of Fourier-Bessel reconstruction, increasing the numbers of tubular crystals in several symmetry groups and using real-space averaging in order to maximize the resolution. In contrast to Ca²⁺-ATPase where we were able to achieve 7 Å resolution with as few as 13 tubes (Stokes et al., 2005), a 12 Å structure of Na⁺/K⁺-ATPase required 27 tubes (Rice et al., 2001) and further increases in this number have not improved this resolution significantly (unpublished results). This suggests the presence of disorder such as short range bending or variable twist that cannot be compensated by Fourier-Bessel methods, but may be tractable by IHRSR.

Our first problem occurred in the search for helical symmetry during the initial round of refinement, which did not produce a clear minimum for the helical symmetry parameters Δφ and Δz. We hypothesized that this problem was due to the low SNR arising from the innately low contrast of frozen-hydrated, unstained samples and, in this case, from the rather thick ice required to fully embed these 800-Å thick tubes. We therefore implemented additional pre-processing steps devised to maximize the signal for initial cycles of this dataset. In particular, we implemented a filter to select data along the layer lines that characterize these helical samples (compare Figs. 3b and 3d), thus eliminating considerable background noise. This filter was applied to the Fourier transform of the original image prior to preparing the subimages for multireference alignment (Fourier filters in Fig. 1) and consisted of generous masks around all the strong layer-lines using the program MASKTRAN from the MRC image processing suite (Crowther et al., 1996). After applying this filter, a shallow, but discernable, minimum was obtained at the expected values of Δφ and Δz. This filter has the disadvantage of eliminating weaker layer lines that are not visible in raw images and is therefore only used during the initial stages of refinement until the reference becomes better determined. Thereafter, subimages from the original, non-layer-line-filtered images were used for further refinement of the orientation and helical symmetry.

Figure 3.

Subimages of Na⁺/K⁺-ATPase and their Fourier transforms after application of various Fourier filters. (a,b) Original images. (c,d) Layer line filtering. (e,f) Wiener filtering. (g,h) Both Wiener and layer line filtering.

In order to include data beyond ~20 Å resolution, data must be compensated for the CTF. The CTF oscillates periodically between +1 and −1, causing certain spatial frequencies to be dampened or even to contribute with inverted contrast (Erickson and Klug, 1971). Furthermore, differing defocus levels in individual images induce characteristic changes in the period of the CTF oscillation, requiring compensation prior to combining subimages into one large dataset. During initial rounds of refinement, we applied a low-pass Fourier filter to the input subimages, which limits data to the first band of the CTF, but this also limits resolution to 20-25 Å. For subsequent rounds we considered several alternative approaches for a more comprehensive solution. Ideally, the Fourier terms would simply be divided by the CTF, but this approach would lead to amplification of noise in regions where the CTF is close to zero and where the SNR is innately low. Another approach would be to restore the phases in the transform, which would prevent inclusion of data with inverted contrast, but do nothing about the dampened Fourier amplitudes both near the origin and at the nodes in the transform. The Wiener filter not only restores the phases, but also adjusts the amplitudes depending on the value of the CTF and the estimated SNR of the dataset: W(k) = CTF*(k) / (| CTF(k) | ² + 1/SNR) (where W(k) is the Wiener filter function and CTF*(k) is the complex conjugate of the CTF at the spatial frequency k) (Penczek et al., 1997). The value of the SNR effectively limits the maximum correction near the CTF nodes and we used a value of 2.0 for our samples (Fig. 3f).

Although the original IHRSR algorithm included translational and rotational alignment of subimages within the projection plane, it did not compensate for tilt of the tube out of this plane, which is a standard consideration for Fourier-Bessel reconstruction (DeRosier and Moore, 1970). Based on Fourier-Bessel analysis of these Na⁺/K⁺-ATPase tubes, this out-of-plane tilt is substantial and generally ranges between +/−5°. We have included a compensation in our IHRSR refinement by simply creating additional reference projections with the helical axis rotated out of the plane of the micrograph by +/−10° (step 1 in Fig. 1). Of course, this procedure substantially increases the number of reference projections and consequently slows the refinement cycle.

Solvent flattening is a constraint that is routinely applied to x-ray crystallographic refinement , and has recently also been used in conjunction with real-space averaging of Fourier-Bessel reconstructions (Yonekura and Toyoshima, 2000). Solvent flattening involves replacing densities within the solvent regions of an electron density map with a single, average value, thus removing the noise and improving the reference that will be used for the next round of refinement. We have implemented solvent flattening in the IHRSR refinement cycle by first isolating a single unit cell from the 3D reconstruction and then defining density thresholds that produce 150 and 200% of the molecular volume expected for Na⁺,K⁺-ATPase. A feathered mask is then applied to the map with a Gaussian falloff between the density threshholds corresponding to molecular volumes of 150% and 200%; a single, average density value was imposed outside this mask (solvent flattening in Fig. 1). This average density value depends on the radius and is determined from the mean radial density distribution, which is derived as the inverse Fourier transform of the equator (e.g., Toyoshima and Unwin, 1990, Yonekura and Toyoshima, 2000). Further constraints are applied to the map by setting density values to zero both in the center of the tube and beyond the outermost radius.

The subimages used for Na⁺/K⁺-ATPase are much larger than previous IHRSR applications, due to the larger diameter of these tubular crystals and the computational requirement for square subimages. We reasoned that this large dimension limited our ability to follow bending and twisting along the length of the tube. We therefore masked the subimages so that the image data only filled a third the height of the subimages (i.e., 360 pixels in width and 120 pixels in height; rectangular masks in Fig. 1). The remaining pixels were filled with a uniform background value. This masking reduced the SNR during projection matching and was therefore applied only after initial rounds of the refinement had created a well defined reference.

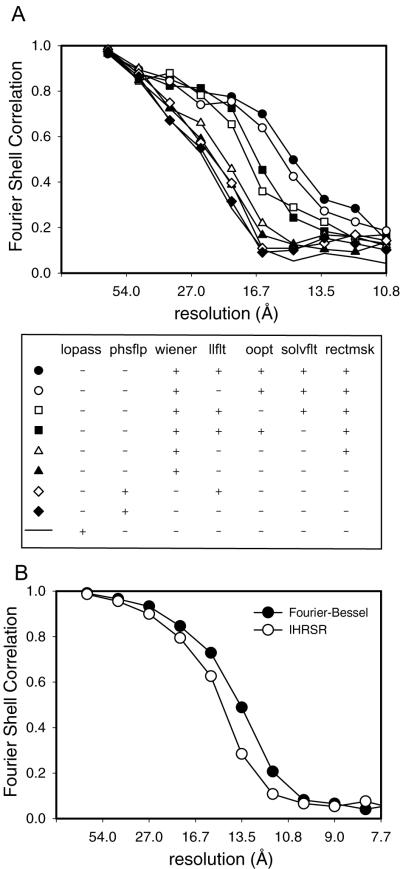
The effects of these various improvements were judged by the Fourier Shell Coefficient (FSC). Calculation of the FSC requires comparison of two data sets, which is generally done by splitting the data into two parts. In the current case, we have used a Fourier-Bessel average from 9 tubular crystals as a fixed reference for comparing the effects of the improved IHRSR algorithm applied to a single tubular crystal (Fig. 4). In order to prevent interference from the packing of molecules into a crystal lattice, we applied a mask to select a single molecule from each of the two data sets and, after alignment, calculated the FSC. This mask was loose-fitting and had gently tapered edges to avoid artifacts associated with alignment of the mask edges. It is clear from the FSC’s shown in Fig. 4, that Wiener filtering, out-of-plane tilt compensation (oopt), solvent-flattening (solvflt), and subimage masking (rectmsk) each make an incremental improvement to the resolution of the reconstruction.

Figure 4.

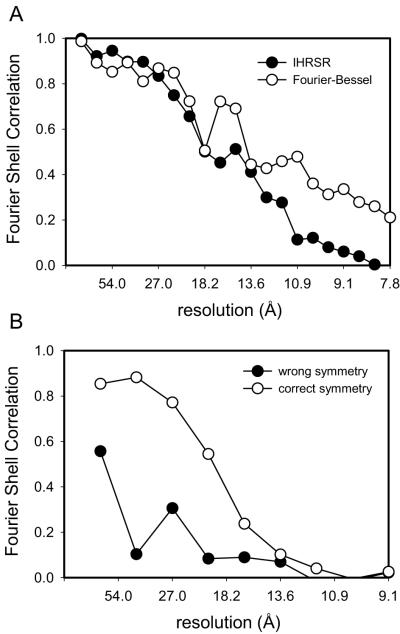
Fourier Shell Correlations of Na⁺,K⁺-ATPase reconstructions. (a) FSC of reconstructions resulting from the implementation of various modifications to the cycle; legend is shown directly below with columns corresponding to 1) low pass filter, 2) phase reversal, 3) Wiener filter, 4) layer line filter, 5) out-of-plane tilt correction, 6) solvent flattening, and 7) rectangular subimages. b) FSC of the final IHRSR reconstruction (open circles) versus previous Fourier-Bessel reconstruction of the same symmetry group dataset (filled circles).

A fundamental limit to all reconstructions is the accuracy with which the orientation of a given projection is determined. In IHRSR, this orientation is determined by projection matching and is constrained to the intervals at which the reference projections are calculated. The interval depends linearly on the resolution desired and on the dimension of the object being reconstructed, according to the Crowther formula: Δθ= d/D, where Δθ is the angular increment of projections, d is the resolution and D is the diameter of the object. Although initial refinement rounds can be done at a coarser increment, this increment should be decreased as the refinement progresses. However, after including out-of-plane tilt and attempting to extend the resolution by decreasing the angular increment, the number of reference projections included in the multireference alignment becomes computationally prohibitive. We have therefore implemented a tracking system for each individual subimage that defines a limited range for projection matching about the Euler angles determined in the previous refinement round (step 2 in Fig. 1). In a similar fashion, the tracking system includes both translational alignments of subimages and helical symmetry of reconstructions and allows all of these parameters to be more finely sampled as the refinement progresses. As a further convenience, parameters and refinement rates can be initialized at the beginning and adjusted depending on progress of the refinement, which should be judged by the FSC determined after splitting the data set in half.

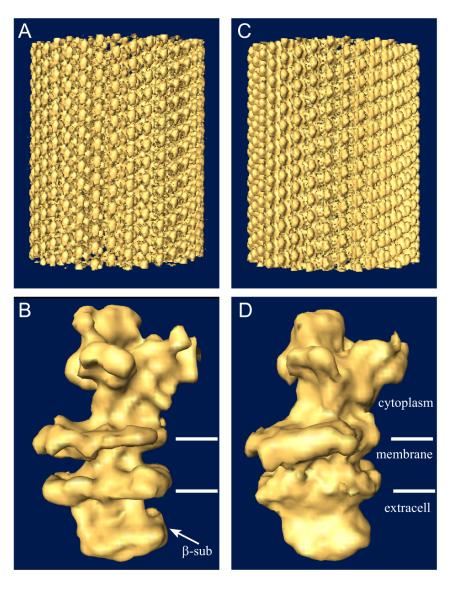
Finally, we applied this enhanced IHRSR algorithm to a larger data set of 9 Na⁺,K⁺-ATPase tubular crystals belonging to the −35,11 helical family (characterized by Bessel orders for the layer lines indexed as 1,0 and 0,1, respectively). This data set comprises ~7200 individual single-particle images with dimensions of 360×120 pixels. We estimated the resolution by comparing the resulting reconstruction with that obtained from 35 tubular crystals processed with Fourier-Bessel methods and combined with real-space averaging (Fig. 4b). Based on a cutoff of 0.5 in the FSC, the resolution of this reconstruction is 15.2 Å, compared to 13.8 Å resolution obtained from the same dataset using Fourier-Bessel methods. The features of the IHRSR reconstruction are also comparable to the Fourier-Bessel reconstructions (Fig. 5), with both the catalytic domains in the cytoplasm and the β-subunit on the extracellular side of the membrane clearly identifiable. However, the distribution of density normal to the membrane (i.e., radial density distribution of the tube) is different, with the transmembrane density notably weaker in the IHRSR reconstruction. This density distribution is determined by the equator in the Fourier transform, which is strongly affected by the CTF compensation at very low resolution. Thus, the gross differences in Figs. 5b and d are likely to reflect failure of the Wiener filter to fully restore equatorial data, particularly as it approaches the origin of the Fourier transform.

Figure 5.

Surface rendering of 3D reconstructions of Na⁺,K⁺-ATPase tubular crystals. (a,b) Reconstruction resulting from the IHRSR refinement shown both as an overview of the helical tube (a) and an isolated molecule (b). (c,d) Fourier-Bessel reference volume in comparable views.

3.2 Rabbit SR Ca²⁺-ATPase Tubular Crystals

Tubular crystals of rabbit SR Ca²⁺-ATPase are considerably longer (up to 10 μm) and thinner (~600 Å) with abundant straight sections of 0.5 - 1 μm (Fig. 2c). Furthermore, they are generally better ordered with layer lines frequently visible to 15 Å resolution in Fourier transforms (Fig. 2d). As with Na⁺/K⁺-ATPase, tube diameters are variable due to different helical symmetries, though the underlying 2D lattice is relatively constant. Previous work with these tubes established not only this helical symmetry, but also repeat length, out-of-plane tilt, and defocus of individual tubes from a variety of different data sets (e.g., Xu et al., 2002, Toyoshima et al., 1993, Zhang et al., 1998). We tested the improved IHRSR algorithm described above on one of these Ca²⁺-ATPase tubular crystals in order to compare the results with Fourier-Bessel methods. The size and overlap of the subimages represent parameters that need to be customized for a given data set. For skeletal Ca²⁺-ATPase tubes, we simply used the same size as for Na⁺/K⁺-ATPase tubes (despite the thinner diameter) and empirically determined the overlap as follows. Initially, a series of subimages with one-pixel shifts were made, and the number of consecutive subimages matching a given reference projection was noted. In this case, four consecutive subimages generally matched the same reference projection, indicating that a four-pixel shift could be used for creating the subimages to minimize redundancy, yet maximize angular sampling during back-projection.

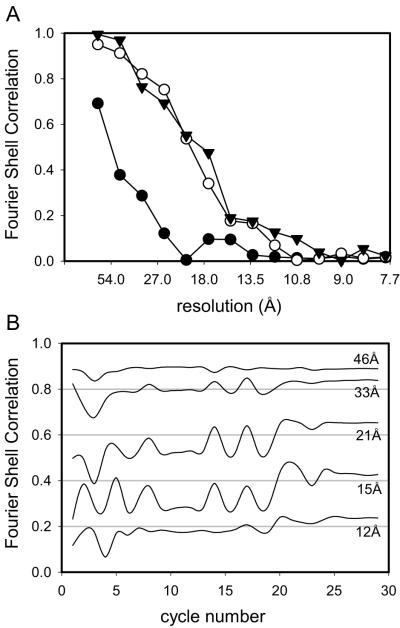
We ran the IHRSR algorithm on a single Ca²⁺-ATPase tube with the helical symmetry defined as −23, 7. This data set consisted of 635 subimages with dimensions of 360×120 pixels, a relative shift of 4 pixels, and comprising a total of ~1500 unit cells. Initially, we used a reference from a Fourier-Bessel reconstruction from 13 tubular crystals with the same helical symmetry and with an estimated resolution of ~7 Å (Stokes et al., 2005). We easily obtained a well-defined minimum at the expected helical parameters Δφ and Δz during the first round of refinement, even though we did not employ layer line filtering for this data set. The various filters, masks and corrections were gradually introduced over the first 30 cycles of IHRSR, which was allowed to run for a full 100 cycles. At this point Δφ and Δz no longer changed, indicating convergence of the refinement. A calculation of FSC relative to the reference reconstruction indicated a resolution of 14-15 Å (FSC of 0.5, Fig. 6a). A dip in the FSC at ~17 Å comes from the node of the CTF at this resolution (see Fig. 2d).

Figure 6.

Fourier Shell Correlation of a single rabbit Ca²⁺-ATPase tubular crystal. (a) Results of reconstructions determined by Fourier-Bessel (open circles) and IHRSR (filled circles) methods. (b) Results of IHRSR refinement starting with a reference model with an incorrect symmetry. Refinements were initiated by specifying either the correct (open circles) or incorrect (filled circles) helical symmetry. Thereafter, the symmetry was freely refined by the algorithm.

To test the sensitivity of IHRSR to the starting model, we also ran the cycle starting with a well defined reference with a different helical symmetry (−27, 7). In this case, the minimum in helical symmetry parameters was not clear, even after running several rounds of refinement without imposing symmetry parameters. We therefore ran two refinement cycles in which these symmetry parameters were initially constrained to correct and incorrect values and thereafter allowed to move with the refinement. Fig. 6b shows the FSC for these two refinements, illustrating the fact that IHRSR converged to a plausible structure only after using the correct symmetry parameters. For comparison we also produced a reconstruction from this same tube using advanced Fourier-Bessel methods described by Beroukhim and Unwin (1997). These methods also involve dividing the tube into subimages - though larger and not overlapping - and refining orientation parameters against a reference. We used the same reference for this refinement and calculated the FSC using the same mask and algorithm as for the IHRSR reconstruction. The FSC for the Fourier-Bessel reconstruction indicates a resolution of 11 Å (Fig. 6a), which is somewhat higher than for the IHRSR reconstruction, but may be biased somewhat by the way this data had been iteratively refined against this very same reference.

3.4 Scallop Ca²⁺-ATPase Tubular Crystals

Tubular crystals of scallop Ca²⁺-ATPase are relatively short and considerably less ordered than those from rabbit Ca²⁺-ATPase or Na⁺/K⁺-ATPase (Fig. 2). Layer lines are visible to only ~25 Å resolution and are often broadened in the direction of the helical axis. We were able to determine the helical indexing of several tubes, which differs from rabbit skeletal Ca²⁺-ATPase by having an additional set of layer lines that suggest a doubled unit cell. However, in attempting a Fourier-Bessel reconstruction, we were unable to find a common phase origin for averaging Fourier data from multiple tubes due to the innately low SNR. Nevertheless, we used the Fourier-Bessel method to calculate a 3D reconstruction from individual tubes and used these structures as a reference for the IHRSR algorithm. This algorithm was independently applied to two individual scallop Ca²⁺-ATPase tubes, which each contributed ~700 subimages with ~850 unit cells. Helical parameters could not be reliably ascertained after the first round of refinement, so we initially used values derived from the indexing of Fourier transforms, which were subsequently allowed to change over the course of the refinement. Similar to rabbit skeletal Ca²⁺-ATPase tubes, we tested the dependence of the algorithm on the starting model. In this case, we produced a Fourier-Bessel reconstruction using an alternative (incorrect) helical indexing (−29,4 instead of −31,4). Predictably, the helical symmetry search did not produce a well-defined minimum. Therefore we ran the refinement twice: once using the helical parameters for the incorrect symmetry (Δφ, Δz = 92.54°, 7.93 Å) and once using helical parameters for the correct symmetry (Δφ, Δz = 272.69°, 8.40 Å). These helical parameters were constrained for the first few rounds, and then allowed to move freely with the refinement. Although the alternative model converged to the expected structure when using the correct symmetry parameters, the refinement failed to converge to a plausible structure when using the incorrect parameters (Fig. 7a).

Figure 7.

Fourier Shell Correlation of scallop Ca²⁺-ATPase reconstructions. (a) FSC determined by comparing two independent IHRSR reconstructions of scallop Ca²⁺-ATPase. For the triangles, the correct helical symmetry was used to create the initial reference and to search for helical parameters throughout the refinement. For the circles, the reference was made with an incorrect symmetry and refinement proceeded near either the correct symmetry (open circles) or the incorrect symmetry (filled circles). (b) FSC plotted in resolution shells as a function of refinement round for a single tube. This plot facilitates tracking of the refinement and shows that the algorithm converged after ~25 rounds. This particular tube was refined with the correct symmetry and corresponds to the triangles in (a).

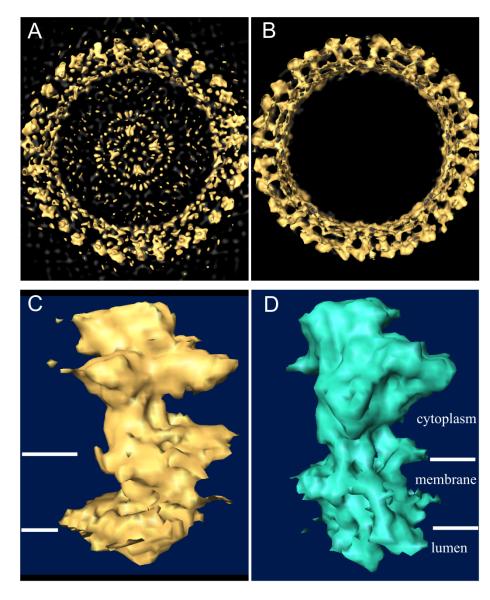
The improvement over the initial Fourier-Bessel reconstruction is demonstrated in Fig. 8, which shows an overview of an initial reference (Fig. 8a) compared with the corresponding final reconstruction (Fig. 8b). Also, the domain organization of scallop Ca²⁺-ATPase (Fig. 8c) appears similar to that of rabbit skeletal Ca²⁺-ATPase (Fig. 8d), though with some interesting variations that will be the subject of future research. The resolution was judged by FSC to be ~17 Å (Fig. 7a) by comparing reconstructions from the two scallop Ca²⁺-ATPase tubes which had been refined independently (starting models derived from Fourier-Bessel reconstructions from the respective tubes and data separated throughout the refinement). Fig. 7b illustrates the progress of the refinement of one of these scallop Ca²⁺-ATPase tubes, which converges after 25 rounds of refinement. To calculate this running FSC, subimages from the one tube were arbitrarily divided into two equal parts and used to create two interim reconstructions; each line in Fig. 7b corresponds to the correlation coefficient from one of the resolution shells.

Figure 8.

Surface rendering of scallop Ca²⁺-ATPase reconstruction. (a) View down the axis of the tube produced by Fourier-Bessel reconstruction of a single tubular crystal; this structure served as the reference for IHRSR. (b) View down the tube axis of the refined structure from a single tube. (c) Single molecule taken from the IHRSR reconstruction of scallop Ca²⁺-ATPase. (d) Single molecule taken from the Fourier-Bessel reconstruction of rabbit skeletal Ca²⁺-ATPase characterized in Fig. 6.

3.5 Computational Resources

The computational considerations required for our IHRSR application are more intense than previous applications, due primarily to the larger subimage dimension (defined by the tube diameter) and the greatly increased number of reference-projections for considering out-of-plane tilt and potential future consideration of twisting and stretching. In general, IHRSR is far more demanding than Fourier-Bessel reconstruction, which represents a trivial load on modern desktop computers. Although we have made a number of modifications to maximize computational efficiency, refinements generally take several days on dual-processor workstations. This processing time will increase as we add either more data or more reference projections in the attempt to improve the resolution. Thus, the use of distributed processing on a cluster is highly recommended, which fortunately is supported by the SPIDER image processing suite.

4. DISCUSSION

We have adapted the IHRSR method to work with wide tubular crystals of the membrane-embedded P-type ATPases. Compared to previous samples analyzed by this technique, our tubes present new challenges, arising from their much larger diameter, the presence of multiple helical symmetry families and a lower SNR. Our use of frozen-hydrated samples and our goal of subnanometer resolution required compensation for the CTF and for bending of the tubes in three dimensions. Our additions to the original IHRSR refinement algorithm include layer-line filtering, Wiener-filtering, solvent flattening, rectangular subimages, and out-of-plane tilt. In addition, we have implemented controls for refining the search of subimage orientation and for monitoring the progress of the refinement using FSC (summarized in Table I). The modified algorithm successfully determined structures from tubular crystals of Na⁺/K⁺-ATPase and Ca²⁺-ATPase from both rabbit and scallop SR. For the former two, the 15 Å resolution was only slightly worse than that obtained from Fourier-Bessel reconstructions using the same data. For scallop SR, the 17 Å resolution was excellent considering that Fourier-Bessel reconstruction was not possible and that only two tubes have so far been processed.

Table 1.

Overview of Improvements/Modifications to the Original IHRSR Algorithm.

Procedure	Implementation	Effect
Layer-line filtering	Mask layer lines in Fourier transform prior to creating subimages	Allowed refinement of helical symmetry parameters from noisy images of frozen- hydrated samples
Wiener filter	Applied to original image prior to creating subimages	Phase and amplitude compensation for CTF required for extending resolution beyond ~15 Å.
Out-of-plane tilt	Created additional projections from model prior to multireference alignment	Corrects for bending of tubular crystal out of the plane of the micrograph. Standard correction for Fourier-Bessel methods.
Solvent flattening	Molecular mask defined from the symmetrized structure and used to zero solvent densities	Refinement constraint that promotes convergence by improving the quality of the reference structure
Rectangular subimages	Rectangular mask applied to the square subimages required by SPIDER	Allows detection of shorter range disorder
Restricted multireference alignment	Euler angles from previous round of refinement used to restrict search range	Reduces computational load, thus allowing finer increments for orientational search
Refinement tracking	Molecule masked from the reconstruction and used for running FSC calculation	Provides feedback about refinement and allows intelligent adjustment of parameters as resolution increased

Fourier-Bessel and IHRSR reconstructions have complementary strengths and weaknesses, some of which can be seen in the current results. If a tubular crystal is well ordered, then Fourier data is concentrated in discrete locations and Fourier based analysis of relevant layer lines has the effect of filtering out a tremendous amount of noise that continues to contribute to IHRSR reconstructions. This can be seen in the noticeable difference between FSC’s for rabbit skeletal Ca²⁺-ATPase (Fig. 6a) and in the effects of layer line filtering on Na⁺/K⁺-ATPase images (Fig. 4). On the other hand, Fourier-Bessel reconstructions have limited ability to deal with disorder. Enhancements by Beroukhim and Unwin (1997) were designed to partially account for stretching and bending along the tubular axis, but these parameters were determined for relatively long segments (~1000 Å in length). The overlap of subimages for IHRSR is able to compensate considerably shorter range disorder. So far, we have implemented only bending disorder, but it would also be possible to account for stretching and twisting by including additional reference projections during multireference alignment. Indeed, stretching could be compensated by applying an appropriate re-interpolation and different twists could be segregated into subpopulations of subimages, both features that we plan to incorporate into future versions of our algorithm. On the other hand, flattening of these cylindrical structures is difficult to cope with. Given the large diameter of Na⁺/K⁺-ATPase tubes (800 Å) relative to a typical layer of ice on a frozen-hydrated sample support (1000-1500 Å), it is easy to imagine that such flattening may be the ultimate resolution limit for these particular samples.

The CTF is another area where IHRSR needs further development. Although the Wiener filter is in widespread use in single particle analysis (Penczek et al., 1997), it is less rigorous than the method used in previous Fourier-Bessel reconstructions (Beroukhim and Unwin, 1997), where a weighted average of amplitudes was obtained from a group of tubes with different defocus values, followed by full restoration using the aggregate CTF. Accurate CTF correction is particularly important for helical samples because the radial distribution of mass in the reconstruction is determined by the equatorial layer line which, in turn, is strongly affected by the diminishing CTF as it approaches the origin of the transform. Thus, incorrect compensation produces artifactual density gradients as one moves from one side of the membrane to the other (i.e., in the radial direction of the reconstruction, see Figs. 5 and 8). A similar strategy is currently in development for this IHRSR method, at least with respect to the low-resolution part of the equator.

Our results indicate that IHRSR is currently most effective when applied to relatively disordered tubular crystals and is less effective than Fourier-Bessel methods on relatively well ordered samples. In particular, resolutions produced by IHRSR on tubes from Na⁺/K⁺-ATPase and skeletal Ca²⁺-ATPase are somewhat lower than the corresponding Fourier-Bessel analyses. Thus, if layer lines are well defined enough to allow Fourier analysis and averaging of Fourier data from multiple tubes, then Fourier-Bessel reconstruction should be attempted. Nevertheless, the power of IHRSR is apparent in our results from scallop Ca²⁺-ATPase tubes. These samples have poorly defined layer lines and have proven intractable by Fourier-Bessel analysis, yet IHRSR was able to produce creditable reconstructions, even when the wrong helical indexing was applied to the initial reference volume.

A weakness of IHRSR is its inability to objectively determine helical parameters under certain conditions. In all cases, one must have some idea of the helical parameters, which can be readily deduced from the positions of layer lines in the Fourier transform and is used to define the neighborhood for searching the structure produced from the first round of refinement. For well ordered crystals with well defined starting references, we obtained clear minima for Δφ and Δz, but not for poorly ordered crystals with questionable starting references. One difference from previous work is that the one-start helix used for specifying the helical symmetry of our wide tubular crystals represents a high order layer line (Δz of 8 Å or less) with highly variable values for Δφ. Thus, closely related scallop Ca²⁺-ATPase symmetries of −29,4 and −31,4 produce values for Δφ that differ by ~180°. The corresponding minima in a search of Δφ and Δz are therefore far apart and separated by many local minima, making it impossible for the search algorithm to smoothly migrate from one symmetry to another. Although layer line filtering is effective in refinement of an established minimum, it is not able to distinguish one symmetry from another, especially given the absence of an objective reference for the initial determination of subimage orientation. Nevertheless, we have shown that refinements do not converge to a meaningful structure when using incorrect helical symmetry parameters. This would suggest a strategy of using convergence as a criterion for choosing amongst related symmetries for a given tube. Candidate symmetries could be deduced from even a few visible layer lines in the Fourier transform. Although it would be beneficial to include subimages from multiple tubes in a given refinement, it would not seem possible to include tubes with different symmetries, as they would produce innately different projection images and prevent the rational application of helical averaging (step 5, Fig. 1). Given the preponderance of different symmetries for our wide tubular crystals, we plan to set up separate refinements for each symmetry (which can include data from multiple tubes) and, upon conclusion, to mask individual molecules or unit cells from the separate reconstructions for alignment and averaging in real space.

In conclusion, Egelman and colleagues have previously demonstrated how the IHRSR algorithm can be used on a wide range of smaller, solid helices with relatively little knowledge of their helical symmetry (Egelman, 2000). We can now extend this principle to the large, hollow helices from membrane proteins in the frozen-hydrated state and, after implementation of our algorithmic improvements, have the prospect of extending the resolution well beyond 15 Å simply by increasing the number of tubular crystals included in the refinement.