Cooperative synchronized assemblies enhance orientation discrimination

Abstract

There is no clear link between the broad tuning of single neurons and the fine behavioral capabilities of orientation discrimination. We recorded from populations of cells in the cat visual cortex (area 17) to examine whether the joint activity of cells can support finer discrimination than found in individual responses. Analysis of joint firing yields a substantial advantage (i.e., cooperation) in fine-angle discrimination. This cooperation increases to more considerable levels as the population of an assembly is increased. The cooperation in a population of six cells provides encoding of orientation with an information advantage that is at least 2-fold in terms of requiring either fewer cells or less time than independent coding. This cooperation suggests that correlated or synchronized activity can increase information.

Traditionally, research in sensory cortex has sought to link sensory information with changes in the impulse rate of single neurons (1), under the presumption that the rate code is the primary signaling modality. The principle of a rate code has also been applied to a population of cells (2, 3), but concerns still arise about the ambiguities of rates, and the ability of a rate code to account for perceptual phenomena such as association, generalization, hyperacuity, and contextual modulation has been debated (2-8). Alternative theories of cortical function (4-8) require a reliable means of preserving the temporal information of impulses in a cortical network of unreliable synapses. Information-theoretic methods demonstrate the existence of links between the temporal structure of neural responses and sensory input (9-11), and mechanisms capable of generating predictable temporal patterns (e.g., bursts and oscillations) by means of intrinsic cellular properties and network interactions have been well documented (12-14). However, temporal information is relevant only when an appropriate decoding mechanism exists (15). Synchronization between neural assemblies provides one such mechanism for encoding, and possibly decoding, temporal structure because synchrony is dependent on temporal patterns (17-19) and is correlated with the orientation (17-19) and coherence (17, 18, 20) of visual stimuli.

We have previously shown (21) that the orientation selectivity of dependency (a numeric measure reflecting synchrony) between two cells is on average 35.5% narrower than the selectivity of their individual rate tuning. Similar results have been documented with other methods (19, 22). We also measured positive synergy (i.e., cooperation; information available only in the joint activity of the cells) among pairs of cells, at least for discriminating fine differences in orientation (21). The average bin width (4.6 ms) and discharge history (total time of 9.2 ms) of this analysis suggested that the cooperation results from correlated (or synchronous) activity. Traditionally, correlation among cells has been considered a limitation in the information capacity of population coding (23). However, because correlation (i.e., synchrony and cooperation) is deterministically stimulus-dependent, it can actually contribute information.

Here we explored the spatial characteristics of cooperative orientation discrimination across larger assemblies. We wished to discover how the relatively small amount of cooperation found among pairs of cells scaled with more cells. Because cooperation is a percentage, even if it held constant across a larger population, the amount of cooperative information would grow. Because we find an increase in cooperation vs. assembly size, this implies an even greater impact on cortical function.

Materials and Methods

Recording and Stimulation. Preparation, stimulation, and recording details are described elsewhere (21). Experimental procedures were performed under the guidelines established by the American Physiological Society and Vanderbilt University's Animal Care and Use Committee. We recorded with a 5 × 5 (400-μm spacing) Bionics multielectrode array (Bionics, Salt Lake City) from the area centralis of area 17 in three cats (22, 25, and 23 cells) anesthetized with propofol and N₂O and paralyzed with Pavulon. The array was pneumatically inserted to a maximum depth of 0.6 mm (exact depth varies because of the brain curvature and the insertion procedure). Two-second drifting sinusoid gratings (10° diameter) were displayed with the VSG2/4 controller board (Cambridge Research Systems, Rochester, U.K.) and a 21-inch Trinitron graphics display (Sony, Tokyo) with a frame rate of 120 Hz and a mean luminance of 73 cd·m^-2 at a distance of 0.5 m. Waveform classification and noise and artifact removal were performed with the Bionics classification software.

Data Analysis. Type analysis methods are described in detail elsewhere (21, 24). Briefly, the responses are broken down into discrete bins (optimized for each measurement between 2 and 6 ms) and assigned a letter depending on which cells fired within each bin. Probabilities are calculated for each letter and for each bin to form a type (estimated probability distribution):

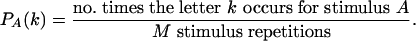1

Conditional probabilities are calculated for a letter occurring depending on the letters that occur in previous bins (D):

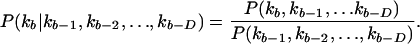2

We have found (21) that the Kullback-Leibler distance (KL distance) depends on previous firing history only as far as one previous bin (by using 2-6 ms for bin width). We also performed Markov analysis on this dataset and again find a Markov order of one to be reasonable. However, we are limited (21, 24) on how many previous bins (D) we can examine and cannot definitively say whether the KL distance depends on more discharge history (N cells, M stimulus repetitions):

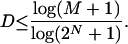3

We do find that as we increase the number of cells, we measure more cooperation with larger bins and that a Markov order of two provides greater KL distance for four cells than a Markov order of one, but we find there is no significant difference between the KL distances for D = 1 and D = 2 (90% confidence). The accumulated KL distance d(p∥q) between two types (P₁ and P₂) for bins 1 to B and for K possible letters from M stimulus repetitions and a Markov order D (the number of previous bins) is

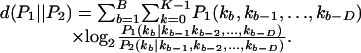4

One-half of the resistor average of the KL distances d(P₁∥P₂) and d(P₂∥P₁) (24) is actually used when we refer to KL distances.

The simplest example of the KL distance would be two responses that are represented by Poisson distributions of spikes differing only in the average rate. The spike probabilities would differ between the responses for each bin across time leading to a constant increase in accumulated KL distance that would not depend on the bin width used to characterize the responses. A second example would be two responses that differ in their temporal structure. The KL distance would show large increases in the bins where precise spike times differ between the responses. Last, from the perspective of joint coding among cells, the KL distance will increase when two responses differ in the number of synchronous events among the cells. The increase in KL distance occurs because there will be a difference in the probabilities of the letters that represent synchronous firing between the two responses.

The synergy is the ratio between the KL distance calculated by using an ensemble alphabet (including joint firing) and the sum of KL distances calculated for each cell (only two letters: the cell did or did not fire):

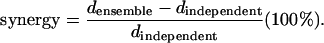5

When the synergy is positive, we refer to it as cooperation; when the synergy is zero, we refer to it as independent; and when the synergy is negative, we call it redundancy.

As we extend the KL distance and synergy to larger populations, we must consider the possibility of artifacts arising from the higher dimensionality of the data representation. To address this issue as well as to provide a more conservative definition of cooperation, we used a second baseline (beyond simple independence) against which the enhancement provided by population dependency was compared. This baseline was created by shuffling the trials of each cell to remove the short-term dependencies from direct neural interactions. The shuffled KL distance retains information from factors such as temporal synchronization by stimulus features (9-11, 21) as well as the same statistical structure (i.e., dimensionality) as our original ensemble KL distance measure. The difference between the ensemble KL distance and the shuffled ensemble KL distance thus provides a more conservative estimate of that information contributed by direct neural interaction, and the additional KL distance provided by the ensemble measure is not simply a result of the high dimensionality of the measurement itself.

Bootstrap analysis was used to make bias and confidence interval estimates, but does not guarantee accurate estimates for an insufficient number of samples (25). The KL distance and synergy estimates were made with M = 516 ± 33 stimulus repetitions, which falls above the limits for any bin-based, Markov-chain estimate with the dimensionality that we employ to represent our data (see Eq. 3 and refs. 24 and 26). This limit does not necessarily guarantee accurate KL distance estimates (24), but the bootstrapping analysis does suggest reliability in our estimates. Undersampling effects were mitigated by the application of the Krichevsky-Trofimov estimate (24, 27). There is no known methodology (e.g., bootstrapping) that can resolve these uncertainties within the restrictions of a limited data set. We therefore use the synergy as an upper limit and the distance between the shuffled and unshuffled KL analyses (i.e., the increase in distance gained by inclusion of short-term firing relationships) as a lower limit of the cooperative information.

The dependency is the accumulated zero Markov order KL distance (see above) between the original type and a forced-independent type that has been recalculated by assuming the cells are independent (24). The dependency quantifies how much the response varies based on the null hypothesis that if the cells in an assembly fire independently, the probability of all cells firing within the same bin should be equal to the product of the probabilities of each neuron firing within a bin (i.e., mutual exclusivity). We find the dependency to indicate synchronous or correlated firing by comparing our measurements with gravitational clustering (28) and cross-correlation analysis (19, 29). The latter measurements are, however, limited to calculations between pairs of cells, so any direct comparisons are not practical. The bias and confidence intervals for dependency are also calculated with the bootstrap method.

Results and Discussion

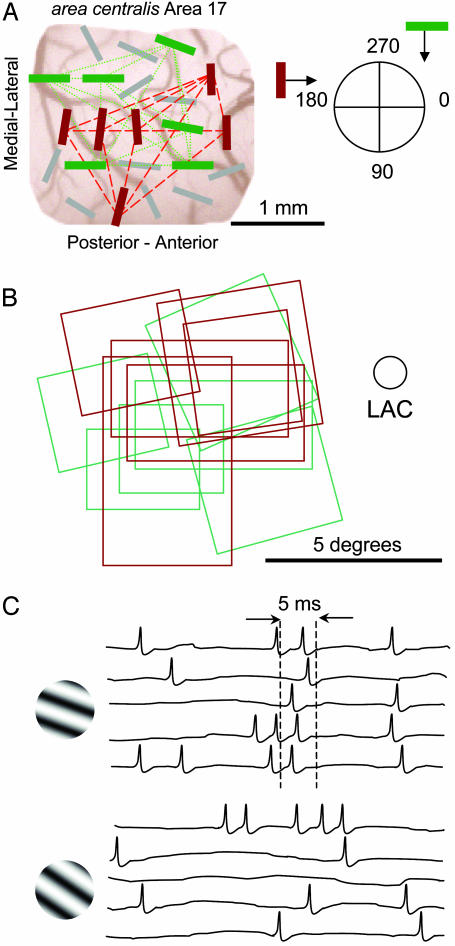
(Fig. 1A) shows the preferred orientations for a population of 22 cells recorded simultaneously in the primary visual cortex of a cat with a 5 × 5 electrode array. We first identified cell assemblies based on similarity of preferred orientation as well as synchronized firing, which was determined with both gravitational clustering (28) and cross-correlation (19, 29) analysis. Cells that had the same preferred orientation were usually synchronized. Of 96 pairs of cells with similar preferred orientations, 79 (82.3%) showed at least a moderate peak in their cross-correlogram (“effective connectivity”; refs. 19, 21, and 29). The high percentage is because of selecting cells with similar orientation (from 784 possible pairs) and measuring the synchrony when stimulating the cells with their preferred orientation. The green bars represent a synchronized assembly of six cells preferring 270° oriented gratings, whereas the red bars represent a second assembly from the same recording of six cells synchronized for 180° oriented gratings. Because the populations of cells were recorded at a shallow depth (0.6 mm) with low-impedance electrodes, the majority (20 of 24) of the cells analyzed for cooperation were complex. Fig. 1B displays the receptive field plots that correspond to the synchronized assemblies in Fig. 1 A by demonstrating synchronization among cells with both overlapping and discrete receptive fields. Fig. 1C shows a 100-ms sample of the responses of five cells from another recording, where the cells synchronize their responses within a window of 5 ms for a grating with the preferred orientation of 20°, but do not synchronize for a grating oriented at 34°.

Fig. 1.

(A) A map of a microelectrode array recording session (cortex viewed from above). The bars represent the preferred orientation (drifting in the direction of the arrow) of the cell recorded at each electrode location. The dashed and dotted lines represent moderate synchronization when activated by a drifting sinusoid grating at the preferred orientation (red: 180°; green: 270°). (B) Receptive field plots for the two assemblies described above (corresponding colors). LAC, left area centralis. (C) An example of 100-ms responses from another recording session from 5 cells to 20° (Upper) and 34° (Lower) orientated drifting gratings.

Quantifying Synchrony and Discrimination. Array recordings from three cats yielded six different six-cell assemblies for analysis. Each population was exposed to drifting sinusoidal gratings of fixed spatial frequency (0.5 cycle per degree), temporal frequency (2 Hz), and contrast (50%) with orientations varied in both large (10°) and small (2°) increments. Because we had no a priori assumptions regarding the form of group interactions, we performed type analysis (21, 24) on responses from each of the identified assemblies. Type analysis is a generalized information measure that makes almost no assumptions on the nature of the neural code (24) and yields the KL distance, synergy, and dependency (see Materials and Methods for details). The KL distance is a formal quantification, based on classification theory, of the difference between neural responses to two different stimuli. Each response is a single- or multineuron vector in time, and comparisons are calculated between responses to spatial stimulus variations (e.g., two different angles). The error in classifying the two responses with an optimal classifier is reduced proportionally by 2^{-KL distance}. The KL distance in effect represents a theoretical upper bound in performance (i.e., lower bound in error) for distinguishing responses. Because the KL distance for the responses to drifting gratings grows essentially linearly over time, we report KL distances as average rates. The synergy is the ratio between the (total) KL distance calculated from the joint (multineuron) firing within an assembly and the sum of the independent KL distances calculated for each cell individually, and thus represents the information advantage from simultaneous examination of the members of an assembly. The dependency is a probabilistic quantification of the interaction between the cells (e.g., correlated or synchronized firing). The dependency is also a function of time and is reported as an average rate. We use these quantitative measures to demonstrate how a synchronized assembly can encode finer differences in orientation than are discriminable on the basis of information available from the cells if they are analyzed individually. The relationship between these measures and population size was quantified by varying the number of cells used in the calculations from 1 to 6 (2 to 6 cells for synergy and dependency measurements).

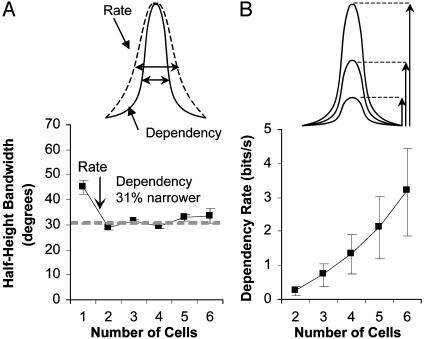
As found earlier (21), the selectivity of dependency with respect to orientation (i.e., bandwidth) is narrower than the rate tuning (Fig. 2A Upper). In addition, as the source for information is increased from two to four cells there is a growth in peak dependence that accelerates for larger assemblies (Fig. 2B Upper). The accelerated growth of average dependency (Fig. 2B Lower) is not surprising when considering the possible interactions among an assembly. For example, the dependency for two cells measures only one interaction, whereas the dependency of three cells considers the interaction between cell 1 and 2, cell 2 and 3, and cell 1 and 3 in addition to the simultaneous interaction among all three cells (24). It may also represent the disproportionate growth of the indirect influence from cells that are not directly recorded but communicate with the assembly members.

Fig. 2.

The dependency for an assembly is more selective for orientation than the firing rate (A Upper) and grows at an accelerated rate (B Upper). (A Lower) The half-height bandwidth of dependency vs. the number of cells (error bars are standard error). (B Lower) The dependency rate vs. the number of cells included in the calculation (error bars are the average of 90% confidence interval for estimates from 101 ± 7 stimulus repetitions).

We calculated the dependency for all possible combinations of pairs (n = 105), triplets (n = 140), quadruplets (n = 105), and quintuplets (n = 42) of cells for each of seven six-cell assemblies (Fig. 2 Lower). Fig. 2 A Lower shows that the dependency bandwidth (half-height) for larger numbers of cells is on average 31% narrower than the bandwidth for the average individual cell firing rate (n = 42). The slight increase in bandwidth with larger assemblies is likely because of sample restrictions. To construct assemblies with reasonable populations, we had to include cells with differences as great as 20° in preferred orientation, which would broaden the entropy-based (21) dependency merely from the influence of the aggregate activity of the assembly. The bandwidth accuracy is also experimentally limited to 10° increments. Fig. 2 A shows that the dependency of the larger assemblies is still highly selective for orientation, which is noteworthy given the increase in aggregate bandwidth of the population. Bandwidth of the individual cells is not necessarily a limiting factor in the amount of information that can be conveyed by populations of cells (30). However, presumably the bandwidth of the dependency (representative of the population of cells) would be suggestive of the information available from the neural dependencies.

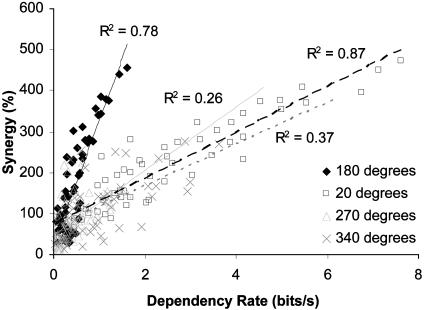
Synchrony and Cooperative Discrimination. The accelerated growth of dependency will not necessarily make a substantial contribution to KL distance (i.e., discrimination of orientation) and consequently guarantee cooperation (24). In other words, the absolute amount of dependency is less important than how it changes with different stimuli, which we demonstrated above. Because assemblies of cells that have a greater amount of dependency typically have a greater amount of cooperation (Fig. 3), our data suggest that dependency is indeed enhancing orientation discrimination. Each set of points in Fig. 3 represents the synergy and dependency for all of the associated subgroups (two to five cells) drawn from each six-cell assembly associated with a particular orientation range. Differences in the correlation slopes probably result from different assembly characteristics (e.g., firing rates, strength of synchrony, tuning bandwidths) that are currently unidentified.

Fig. 3.

Synergy and dependency rate cross-plotted for all possible two- to six-cell combinations for the four six-cell assemblies (preferred orientations given in the key). R² values were calculated for each set of data points with linear regression analysis.

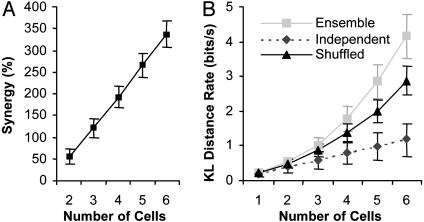
The contribution of dependency to discrimination is also reflected in Fig. 4A, which shows that the synergy, representing the fraction of the KL distance that is available only when examining the cells simultaneously, continues to grow as the number of cells increases. When combined with the algebraic growth of information from independent contributions, this yields (Fig. 4B) an accelerated increase in the total KL distance (for a 4° difference in orientation) with more cells. Because the increase in cooperation and KL distance measurements might be an artifact of the high dimensionality of the data representation, we used the shuffled KL distance as a second, more conservative, baseline (see Materials and Methods for details). Use of either the shuffled KL distance or the independent KL distance as a baseline qualitatively yields the same results for our data, with the difference between the ensemble KL distance and either baseline (e.g., synergy) increasing with a greater number of cells (Fig. 4B).

Fig. 4.

(A) Synergy vs. the number of cells (24 individual cells, 60 pairs, 80 triplets, 60 quadruplets, 24 quintuplets, and 4 sextuplets; error bars are average 90% confidence interval for estimates from 516 ± 33 stimulus repetitions). (B) The ensemble KL distance rate, shuffled ensemble KL distance rate, and the independent KL distance rate for a 4° variation from the preferred orientation vs. the number of cells (error bars are average 90% confidence interval for estimates).

Fig. 4B shows that for a 4° orientation difference the average KL distance rate for a single cell is only 0.20 bit/s. Even with 6-fold cells considered independently, the average KL distance rate for this same difference would be 1.18 bits/s (dashed line), which would reduce the error of classifying the responses by only ≈2.3 after 1 s. However, when considering the interactions among the six-cell assemblies, the average KL distance rate added is at least 1.28 bits/s (by using the shuffled KL distance), resulting in at least a 5.5-fold reduction in classification error after 1 s.

With cooperative coding, we find that six cells can achieve a level of discrimination that would require at least 12 cells when an independent coding scheme is used. We also can consider the advantage of cooperation in terms of time because the KL distance is integrated over time. For a 4° angular difference, a cooperative code across six cells can reach the same level of discrimination in less than half the time required by independent coding. The advantage with such a small population can be considered conservative, because the relationship of cooperation vs. population size suggests continued growth with assembly growth. However, the KL distance will be limited by the input information to the population and cannot accelerate indefinitely with respect to population size (31). The advantage in coding efficiency may also apply to discrimination with greater acuity rather than with smaller populations or shorter times. The hyperacuity found in behavioral orientation discrimination does suggest some form of population coding (32).

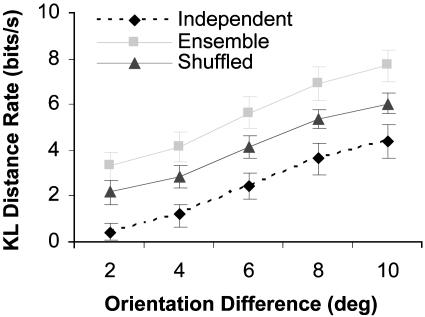
A Neural Mechanism for Hyperacuity. Fig. 5 shows how cooperation depends on angular difference. The independent KL distance rate for 2° approaches zero, suggesting that orientation differences of 2° cannot be discriminated (i.e., zero KL distance) by individual cells, but the ensemble (six cells) KL distance rate is still substantial. This implies that the orientation discrimination performance of humans cannot be accounted for by single cells (32), suggesting the brain takes advantage of some form of population code. The independent KL distance does not represent a true population gain because the discriminability of a population of independent cells is only as good as that of each individual cell (31). This does not mean that cooperation is the only way to achieve the same fidelity of orientation coding represented by our cooperative assembly (31). For example, populations that do not exhibit cooperation can take advantage of noise removal through averaging (2, 3). This will likely be less efficient than cooperation (using our independent KL distance as a comparison) because of the redundancy that results from integration (2, 33). As we move to coarser angles, where discrimination is more obvious from the rate code, assembly coding becomes more independent (21). Discrimination of coarser angles can be achieved whether the assembly is active or not.

Fig. 5.

Comparing ensemble KL distance to independent KL distance and shuffled ensemble KL distance (vs. the difference in orientation).

Fig. 5 also permits a comparison of the ensemble KL distance with the shuffled KL distance. Because the independent KL distance does not represent an actual population gain, comparing it with the ensemble KL distance can be ambiguous and misleading (31). The shuffled KL distance provides us with a more meaningful comparison because it allows us to identify directly how short-term neural interactions contribute to orientation discrimination. The results when comparing the ensemble KL distance with the shuffled KL distance or the independent KL distance, in our case, are qualitatively the same. The percentage gained by using the ensemble KL distance (e.g., synergy) increases as we test the coding limits of the single cells (i.e., smaller angle differences or more difficult orientation discrimination tasks). At least over the limited range of orientation differences (2-10°) that we investigated, the absolute KL distance contributed by joint analysis appears to increase only slightly (1.29 to 1.67 bits/s) relative to the total KL distance (3.32 to 7.70 bits/s). The cooperation, which is the percentage difference between the ensemble KL distance and the independent KL distance, therefore decreases as the orientation increment increases.

One question that could be raised is whether cells encode specifically for their preferred orientation. Theoretical population codes have examined those regions on the rate tuning curves of single cells with the greatest amount of Fisher information (i.e., the steepest slope) where the cells would not encode for their preferred orientation, but rather away from the peak of the tuning function (34). Our hypothesis is that the assemblies behave as filter-like structures where the stimulus that results in the greatest synchrony (Fig. 1C Upper) yields a signal that has the greatest chance of reaching the next layer in visual processing (6, 22). Stimuli that differ from this preferred feature (orientation) result in weaker synchronization across the assembly (Fig. 1C Lower) and smaller probabilities of their collective spikes being transmitted across synapses. In two cases our KL distances were calculated within 10° of the preferred orientation and for two additional cases, the KL distance analysis was performed in the region of the rate-tuning curves where their slopes were steepest. Whereas the cooperation was greater when analyzing near the preferred orientation, it was still substantial even away from the preferred orientation, implying that information from cooperation is useful for fine angular discrimination across a broad range of the rate tuning curves.

Our results do not conflict with alternative models of population codes that have sought to explain hyperacuity performance (2, 3, 35), but only demonstrate that there is considerable information available in the joint activity of cells that could provide a more efficient representation of visual information. The fact that we find a substantial effect within a limited sample of cells that have only moderate synchrony makes the results even more appealing. Because the analysis makes almost no assumptions about the nature of the code, we can definitively state only that the available information is from the point of view of an optimal classifier. However, the assumptions we make about temporal resolution and discharge history (ref. 20; see also Materials and Methods), along with the dependency and shuffling analysis, suggest that interspike intervals and synchrony between cells play a major role in producing this information about orientation. Our results provide a simple demonstration of the potential importance of considering simultaneous multiunit activity for understanding brain function. Even in the case of encoding elementary features such as orientation, there is a substantial amount of additional information available only from the dependencies that occur among a population of cells. Access to larger populations and use of more complex stimulus variations will likely yield even greater gains.

Independent Cells. Theoretical studies have revealed that in some cases, dependencies or correlation can enhance response discrimination (31, 36). However, past experimental studies have found that the information between cortical cells is mostly independent (33, 37). The discrepancy with our finding is most likely not an issue of cell proximities, because both here and in our earlier study on pairs (21) we found synergy in both nearby (recorded on the same single electrode) and widely separated (2 mm) cortical cells. The cooperation that we found is likely a result of selecting, from a larger population, cells with similar preferred orientations that are at least moderately synchronized and testing the small differences in orientation, where single cells fail to discriminate. For larger orientation differences, group activity approaches independence.

A more general issue about information-theoretic analysis of population coding is that the synergy measurement that is generally applied (e.g., Eq. 5) may not reliably represent cooperation, because by this definition both cooperative and noncooperative structures can appear to exhibit positive and negative synergy (cooperation and redundancy) (31). As mentioned above, the usual independent baseline is misleading. For example, the independent KL distance can grow indefinitely, whereas true population KL distances cannot grow indefinitely (limited by the input information) and will eventually reach an asymptote and appear to be redundant (31). When single cells cannot reliably encode a feature, we end up with a very small slope for the independent KL distance (e.g., Fig. 4B) and reveal large amounts of cooperation. If the individual cells can reliably encode a feature, the slope will be larger and reveal the population to be independent or redundant. Therefore, the traditional synergy measurement is highly dependent on the stimulus set, as well as the population size. By using our shuffled baseline (which will also be asymptotic vs. population size), we end up with a more suitable and definitive indication of the cooperation.

The Relevance of Synchrony. Whether the synchrony shown here can serve as a neural substrate for orientation discrimination and further visual processing depends primarily on two questions: (i) Can this joint information be used (i.e., is its detection physiologically plausible)? (ii) How is this cooperative information transmitted through the visual hierarchy to yield a percept? There has been much debate on the role of synchrony in perception (20, 38, 39). Most results demonstrating no apparent perceptual affects of synchrony have focused on temporally induced synchrony (38). Here we examine synchrony that is dependent instead on the spatial structure of the visual stimulus. Von der Malsburg (5) suggested that a resolution of 2-5 ms would be required to distinguish between synchronous and asynchronous activity. Our results do in fact fall within this level of temporal acuity (21). Synaptic unreliability might argue against the preservation of information on this temporal scale (2), but the mere fact that the synchronous activity is found on this, or even finer, time scales (38) proves this is not an obstacle for a coding system that is based on synchrony (40). Synaptic unreliability is overcome through coincident inputs (6), temporal integration and synaptic facilitation (12, 19), oscillations (7), and activity-dependent changes in integration times (21, 38, 41-43). These mechanisms can maintain and propagate synchrony throughout the visual hierarchy to form new synchronized assemblies at the perceptual level (4-7). Just as the distinction between temporal and rate coding depends on the definition of a time scale (11), we should note that the distinction between integration and synchrony is also blurred as a result of the time scale (an essential point because of the dynamic nature of time constants mentioned above) and might be considered more as a continuum (43). Synchrony might also inherently arise among a network to reliably propagate rate information (44).

Synchronized assemblies can remove the ambiguities of rates in independent cells (5, 7), and assemblies can dynamically integrate at various levels of the perceptual hierarchy to perform more complex filtering and feature detection for different sensory inputs (5). Our proposal for orientation discrimination is the simplest example of an assembly filter. Synchrony may also have implications for associations (4) and contextual modulations such as figure-ground discrimination (5), in addition to enhanced orientation discrimination. The fact that the presence of synchrony impedes rate coding and enhances temporal coding (2, 16), along with the correlation found with perceptually relevant features (17-22), suggests that synchrony does play some role in sensory perception. Deciphering exactly what that role is remains elusive.