Abstract
We investigated the effects of 10 hours of practice on variations of the N-Back task to investigate the processes underlying possible expansion of the focus of attention within working memory. Using subtractive logic, we showed that random access (i.e., Sternberg-like search) yielded a modest effect (a 50% increase in speed) whereas the processes of forward access (i.e., retrieval in order, as in a standard N-Back task) and updating (i.e., changing the contents of working memory) were executed about 5 times faster after extended practice. We additionally found that extended practice increased working memory capacity as measured by the size of the focus of attention for the forward-access task, but not for variations where probing was in random order. This suggests that working memory capacity may depend on the type of search process engaged, and that certain working-memory-related cognitive processes are more amenable to practice than others.
1. Introduction
Working memory (WM) is the workplace of the mind. It refers to a temporary memory buffer – lasting for only a few seconds – that passively stores and actively manipulates information (Baddeley & Hitch, 1974). WM is severely limited in its capacity (e.g, Miyake & Shah, 1999), and given this limit, the effectiveness of working memory depends on the efficient implementation of a set of general control operations that are likely involved in all aspects of cognition (e.g., Miyake et al., 2000). Thus, one would expect that working memory is associated both with very basic tasks of executive control and with higher-order tasks of fluid intelligence that presumably rely, at least in part, on these same processes. The literature bears this out. Working memory tasks have indeed been shown to correlate, on the one hand, with a host of tasks measuring different aspects of cognitive control, including Stroop, antisaccade tasks, flanker tasks, and dichotic listening tasks (for a review, see Engle, 2010) and, on the other hand, with tests of fluid intelligence (e.g., Conway et al., 2002; Engle, Kane, & Tuholski, 1999; Kyllonen, 1996; Salthouse & Pink, 2008). The latter correlation is quite respectable in size: In their meta-analysis, for instance, Ackerman, Beier and Boyle (2005) conclude that the average correlation between working memory capacity and markers of general fluid ability (g) is .36 (.48 after correcting for unreliability).
The central position of working memory in cognition makes it attractive for intervention. The hope is that extensive practice on WM tasks will improve scores on Gf measures (and presumably enhance Gf itself) (e.g., Dahlin, Nyberg, Backman, & Stigsdotter Neely, 2008, and Jaeggi, Buschkuehl, Jonides, and Perrig, 2008). Some have argued that WM training might alleviate attentional deficits seen in ADHD (Klingberg, Forsberg, & Westerberg, 2002), following stroke (Westerberg et al., 2007), or in general learning disability (Alloway & Alloway, 2009). Authors of these claims by and large conclude that WM training improves working memory performance and scores on Gf measures, although dissenting voices can be heard as well, mostly on methodological grounds (e.g., Shipstead et al., 2012).
Many training tasks and training regimes exist. For the present study, we examined a particular task, a modified version of the N-Back task, and investigated how its constituent processes change with extended practice. We did this for three reasons. First, the N-Back task, unlike classic WMC tasks such as Operation span (Turner & Engle, 1989), has readily decomposable constituent processes (viz., updating, one-step retrieval, and search; see below). Second, the N-Back task, unlike WMC tasks, includes an updating component, which has been shown to be related to Gf independently of WMC (Kane, Conway, Miura, & Colflesh, 2007). Third, the N-Back task and its close cousin, the running span task, also comprise a sizeable portion of the extant training literature (for review, see Shipstead et al., 2012).
In the N-Back task, participants indicate whether a given stimulus matches the stimulus shown N positions back. In our version of the task (Verhaeghen, Cerella, & Basak, 2004), single digits appear left-to-right in N columns on the screen, and participants indicate whether the current digit matches the one last shown in that same column. The columnized display serves to facilitate item-to-position binding; this minimizes the keeping-track demand as the task parameter N is increased, and puts more emphasis on the item-memory aspect of the task. We measured both accuracy and response latency as functions of N.
What mental operations serve this task? The starting point of our task analysis (see also Zhang, Verhaeghen, & Cerella, 2012) is Cowan's (2005) embedded-processes WM model posits a hierarchy of content availability within working memory, a two-tier structure composed of a small, capacity-limited zone of immediate access, labeled the focus of attention or inner store, and a larger, activated portion of long term memory, called the outer store (Verhaeghen et al., 2004). The outer store, where memory representations are available but not immediately accessible, has unlimited capacity, but suffers from interference and possibly decay. When the number of items exceeds the inner store's capacity, the subject may need to bring an item back into focus for processing (‘focus switching’). Depending on the task, the subject may also need to remove an item from the focus to the outer store (‘updating’, e.g., Oberauer, 2002). Our own recent work (Lange, Cerella, & Verhaeghen, 2011) has shown that there are two types of focus switching. Given a sequential series of study items, suppose that the memory set is subsequently probed item-by-item. If the test sequence is in the study order, item retrieval is highly efficient (we called this ‘one-step’ retrieval). If the probes are in any order other than forward, such as random or backward, an additional search process appears to be engaged within the outer store. This embedded-processes view of working memory serves as the starting point of our task analysis (see also Zhang, Verhaeghen, & Cerella, 2012). Our current experiment assesses how practice affects these two focus-switching processes and the updating process.
In the standard N-Back task, participants indicate whether a given stimulus matches the stimulus shown N positions back. In our version of the task (Verhaeghen, Cerella, & Basak, 2004), single digits appear left-to-right in N columns on the screen, and participants indicate whether the current digit matches the one last shown in that same column. The columnized display serves to facilitate item-to-position binding; this minimizes the keeping-track demand as the task parameter N is increased, and puts more emphasis on the item-memory aspect of the task. We measured both accuracy and response latency as functions of N.
We administered three modified N-Back tasks over ten sessions. Together, these tasks allow us, under the assumption of subtractive logic, to isolate the duration of the presumed component processes of the working memory system. The first task was the aforementioned N-Back procedure, with items presented in N columns and probed left-to-right (forward-updating condition). The second task resembled the first, but without the requirement to update the information for comparison. Subjects studied the first N items, presented at the top of each column, for comparison with all subsequent probes in their respective columns (forward-no-updating). The third condition likewise excluded updating, but probed the N items in random order (random-no-updating). This random condition contained two distinguishable probe types. Either the location of the current probe matched the location of its predecessor, referencing an item presumably still in the focus (non-switch probe), or these two locations differed, necessitating a focus switch plus a search process (focus-switch probe). In both forward-order conditions, all probes were necessarily focus-switches, but free of Lange and colleagues’ (2011) search process. In short, our three modified N-back tasks yield four trial types for examination: Random-no-updating switch trials, random-no-updating non-switch trials, forward-no-updating switch trials, and forward-with-updating switch trials.
Subtractive logic on probe latencies isolates the N-Back task's three subcomponents, as follows. (a) The duration of the one-step, forward focus-switch operation can be estimated directly from the forward conditions (forward-updating or, more cleanly, forward-no-updating). This duration is given by the difference between the response to probes in the N=1 condition, where no forward step is required, and probes in the N>1 conditions, where such steps are required. Here, we will use the difference between N=1 and N=2 as the simplest proxy of the step duration; in our previous work, we have found the forward probe RT from N=2 to N=5 to be reasonably constant, with near zero linear slope, making values of N>2 interchangeable for this analysis (e.g., Verhaeghen et al., 2004). (b) The duration of the search-based, random focus-switch operation can be estimated from the difference between the focus-switch and non-switch probes in the random condition. This difference should be computed from mismatch probes only, because non-switch match probes (where the same item simply repeats in the same column) likely benefit from repetition priming. (c) The duration of the updating process can be estimated from the difference between the two forward conditions. This cost could be constant, independent of N, but it is also possible that increasing memory load slows down the WM updating process.
Controversially, it is also possible that some (or all) of the effect of N-Back practice occurs not by a change in process duration, but by a change in the size of the focus. Using forward-order probes, Verhaeghen et al. (2004) concluded that with extended practice, the FoA expanded from one to four items. Conversely, Oberauer (2006), using random probes, found no such expansion. The divergence in results may be due to differences in how expansion is measured in an N-Back task. N-Back latencies usually show a step function, with the increment occurring at N=2, indicating that the FoA holds only one item (Garavan, 1998; McElree, 2001; Oberauer, 2002). Verhaeghen et al. (2004) found a shift in the step from N= 2 at the onset of practice to N=4 at the end of practice, and interpreted this as evidence for focus expansion. Oberauer (2006), in his random-probe design, calculated the difference between switch and non-switch trials; under this scheme, the range of N over which the difference is negligible delimits the size of the focus. The two approaches are distinct, but – we would argue – complementary. The Oberauer index provides the clearest indicator of cost-free access within the focus, but it is confounded with search and simply cannot be applied to forward-order probes. The Verhaeghen et al. index can be, but it is then confounded with increasing memory load.
Another reason for the discrepancy might be the processes embedded in the task. Verhaeghen et al. (2004) hypothesized that the inner store's capacity trades off with task-processing demands. If this is indeed the case, focus expansion may depend on the ease of focus switching – tasks involving an easy search process, such as our one-step forward process, may permit expansion, whereas harder search processes, such as a random-order search may monopolize too many resources to allow this expansion. If our conjecture has merit, we would expect expansion in the forward conditions (measured using the Verhaeghen et al. metric), but not in the random condition (measured using the Oberauer metric).
To our knowledge, no previous study has assessed practice effects on the four aspects of WM that are examined here (the size of the focus of attention, the search process, the one-step process, and the updating process). However, preceding work hints at possible outcomes. Both Garavan (1998) and Oberauer (2006) had participants practice for about ten hours on a random-order focus-switching task and were unable to eliminate the switch cost. However, both studies required updating. This updating requirement obscures what resisted extended practice – random switching, updating, or both. With regard to capacity changes, and as explicated above, Verhaeghen et al. (2004) found evidence for an expansion in the focus, while Oberauer (2006) did not.
2. Methods
2.1 Participants
Seven participants (four female) under the age of 35 were recruited from the student population in the School of Psychology at the Georgia Institute of Technology. Participants were compensated $15 per session.
2.2 Materials and procedure
In each trial for each of this study's three versions of the N-Back task (described above), there was first a study phase, followed by either a retrieval phase (random-no-updating and forward-no-updating conditions) or a retrieval-and-updating phase (forward-updating condition). In the study phase, participants were presented simultaneously with 1 to 5 numbers (digits 1 to 9), each in a separate column on the screen. Study time was determined by the participants; when ready, they advanced to the retrieval/updating phase by pressing the spacebar. Following encoding, retrieval/update probes were presented one at a time; they remained on the screen until a response was made. For matching probes, participants pressed the “1” key; for non-matching probes participants pressed the “3” key. For each study set of N stimuli, participants received 2N + 1 probe items. Across a task block, match/mismatch probes were approximately 50% of each. Mismatch stimuli were sampled at random from the stimulus set of 9 digits remaining after deleting the match stimulus, without regard to whether they occurred elsewhere in the current memory set or not. In the random-no-update condition, approximately 50% of the retrieval items occurred in the same location, that is, were non-switches. The sequence of N study items and 2N + 1 probes constituted one trial.
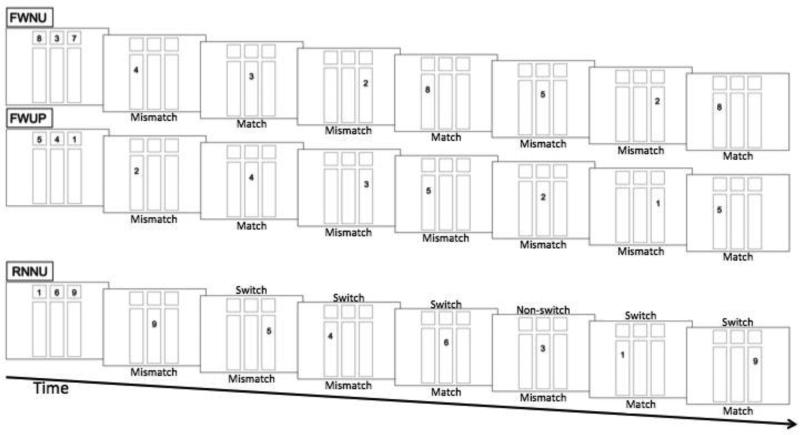
Three tasks were implemented (see Figure 1), all with an identical study phase. In the random-no-update task, participants evaluated whether each digit presented in the retrieval phase matched the digit originally presented at the top of the column. Switch probes were implemented by choosing a different column at random. The forward-no-update task was identical to the random no-updating task, except that probes appeared from left to right; they were still to be compared to the original digit for their column. The forward-update task replicated the task used by Verhaeghen et al. (2004). Probes proceeded in a left-to-right manner, but were now to be compared to the previous digit to appear in that column.
Figure 1.
Example 3-back tasks (RNNU – random access without updating; FWNU – forward access without updating; FWUP – forward access with updating) depicting encoding followed by 7 retrieval probes. Subjects match the probes to the elements presented in the same column during encoding for the first two conditions; they match it to the last seen element in the same column for the third condition. Presentation of retrieval probes is subject-paced.
In every session, participants completed 10 blocks of each task before starting the next task, with each block consisting of 2N +1 trials for each N, except for N = 1 which had 10 trials. Participants completed two blocks of trials for each N, scheduled in stepwise order from 1 to 5 and then 5 to 1 items. In the first session only, practice blocks (N = 3) preceded each task. Within each block, match/mismatch probes were equally likely. Mismatch stimuli were sampled at random from the stimulus set after deleting matches. For the random-no-update condition, N = 1 was omitted, yielding nine blocks. Participants completed two 1-hour sessions a day for 5 consecutive days, for a total of 10 sessions.
3. Results
Accuracy was uniformly high and close to ceiling (96% on average), and therefore not analyzed further. Only correct responses were analyzed.
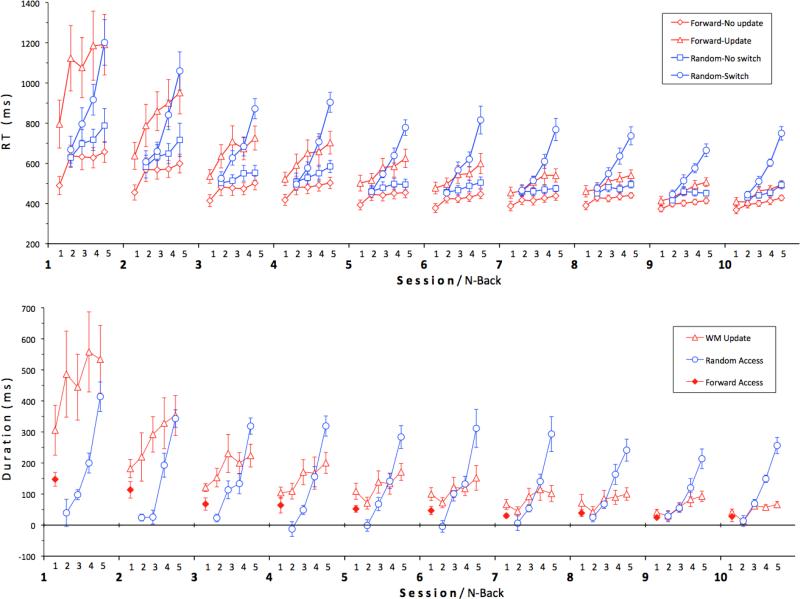
As explained above, some latency analyses are more interpretable using mismatch probes only. All analyses were conducted twice, once with mismatch probes, and once with all probes. Results from the mismatch data are reported here, and show the same pattern of results as the analysis of all probes. Figure 2 shows correct mismatch latencies to each probe type as a function of N within Session.
Figure 2.
Top panel: Average response times (and SE, denoted by error bars) in four N-Back trial types as a function of Session and N. Only correct mismatch-probe trials were included. Forward-No update is an N-Back task requiring only comparison of each stimulus with the corresponding item from the first N stimuli; Forward-Update requires continuous updating. The Random condition probes the first N items in random order, and has two trial types: Random-No Switch and Random-Switch. Random-No Switch refers to repeated probing of the same item; Random-Switch concerns the switch trials (i.e., the item currently probed is different from the item probed on the previous trial) in the same condition. Bottom panel: The duration of the three working memory processes as derived from the four conditions shown in the top panel. See text for details.
The first analysis included all four trial types (forward-updating; forward-no-updating; random-no-switch; random-focus-switch), all sessions (1–10), and four values of N (2-4, the range spanned in the random conditions). All main effects and all interactions were significant, smallest F(81, 486)=2.55, p<.001, ηp2=.30. The interactions provide the warrant for the planned contrasts previously outlined, designed to isolate the constituent task processes.
The duration of the one-step-forward focus-switch operation is estimated from the forward no-updating condition as the increment in RT from N=1 to N=2 (Figure 2). Over the course of practice, the step size shrank from 147ms to 28ms, a reduction to 19% of its original size. This decrease was significant, as attested by a significant N-by-session interaction, F(9, 54)=7.11, p<.001, ηp2=.54.
Characteristics of the random search process are estimated by differences between the focus-switch probes and non-switch probes in the random condition. Participants got faster with practice, F(9, 54)=20.62, p<.001, ηp2=.78; focus-switch probes took longer than non-switch probes, F(1, 6)=81.09, p<.000, ηp2=.93, and latency increased with N, F(3, 18)=60.29, p<.001, ηp2=.91. These main effects were qualified by interactions: The search process sped up over the course of practice, F(9, 54)=2.98, p<.01, ηp2=.33; the effect of N grew less pronounced over the course of practice, F(27, 162)=7.60, p<.001, ηp2=.56; the effect of N was larger in the focus-switching condition, F(3, 18)=90.26, p<.001, ηp2=.94; and the effect of N on the focus-switching process became smaller with practice, F(27, 162)=2.03, p<.01, ηp2=.25. Over the course of practice, search time (averaged over N) decreased from 188ms to 122ms, a reduction to 65% of its original size, and the slope of the search time over N decreased from 122ms/item to 81ms/item, a reduction to 66% of its original rate. Thus, practice made the search process more efficient.
The duration of the updating process is estimated as the difference between the forward-updating and forward-no-updating conditions. Participants got faster with practice, F(9, 54)=23.64, p<.001, ηp2=.80; the updating requirement increased latency, F(1, 6)=28.90, p<.01, ηp2=.83, and latency increased with N, F(4, 24)=30.32, p<.001, ηp2=.84. Again, these main effects were qualified by interactions: The updating process sped up over the course of practice, F(9, 54)=14.77, p<.001, ηp2=.71; the effect of N decreased over the course of practice, F(36, 216)=6.68, p<.001, ηp2=.53; the effect of N was greater in the updating condition, F(4, 24)=11.08, p<.001, ηp2=.64; and the effect of N on the updating process grew smaller as practice progressed, F(36, 216)=2.19, p<.001, ηp2=.27. Averaged over N, the time needed for updating decreased from 466 ms to 48 ms, a decrease to 10% of the original cost. The influence of N on updating decreased from 53ms/item to 10ms/item, a reduction to 18% of the original rate. The rate nonetheless remained significantly greater than zero after practice, as indicated by a significant trial type-by-N interaction in the final session, F(4, 24)=7.74, p<.001, ηp2=.56.
Finally, we turn to the question of focus expansion. In the forward no-updating condition, Session 1 yielded a step function with a clear discontinuity between N=1 and larger values of N, as verified by successive comparisons between different levels of N (with Bonferroni correction, one-tailed): RT at N=1 differed from RT at N=2, t(6)=6.62; RTs for Ns 2 and 3, and Ns 3 and 4 were statistically equivalent, t(6)=0.20 and 0.21, respectively; N=5 was elevated above N=4, t(6) = 3.20. The latter result is likely due to the visible dip at N=4, because RT at N=5 was not statistically different from RT at Ns 2 and 3. For Session 10, a significant main effect of N notwithstanding, F(4, 24)=8.12, p<.001, ηp2=.58, none of the successive contrasts were significant, largest t(6)=1.86. The Session 10 result suggests a gentle ramp (14ms/item) rather than a step function. We compared this ramp to that obtained in the random non-switch condition, which by definition exclusively contains non-switch probes. The two ramps did not differ, as verified by a non-significant task-by-N (2–5) interaction, F(3, 18)=0.91, ns, ηp2=.13. The results thus suggest that in the forward no-updating condition the focus of attention, initially able to hold only a single item, expanded over the course of practice to include 5 items.
Turning to the random-order condition, both Sessions 1 and 10 show significantly slower RTs for switch probes compared to non-switch probes, with effect size virtually unchanged, F(1, 6)=88.10, p<.001, ηp2=.94, and F(1, 6)=87.53, p<.001, ηp2=.94, respectively. Above, we noted the presence of a significant Session-by-Probe type-by-N interaction. This interaction emphatically does not signify an expansion: For both Session 1 and Session 10, the switch cost was not significant at N=2, t(6)=0.90 and 0.76, respectively. For Session 1, the cost was significant from N>3 upwards, while for Session 10, the cost was significant from N>2 upwards, signaling, if anything, focus shrinkage. The data show that in the random-order condition, the focus of attention is only able to hold a single item, even after extensive practice.
4. Discussion
In the present study, seven participants practiced three versions of an N-back task, with N varying from 1 to 5, for ten hours. The tasks were designed to isolate three working memory processes: the one-step-forward access process (when memory-set items are accessed in a strictly forward fashion), true memory search (locating random items in the memory set), and updating (transferring an in-focus item to working memory at large). We asked two questions: (a) Which of these processes benefit from extended practice; and (b) Does the focus of attention expand with extended practice?
Which processes benefit? The short answer is that all three processes became more efficient with practice. Subjects sped up in all conditions, and all analyses which isolated practice effects in specific processes were significant. Looking more closely, we found that the random-access process proved more resistant to change than the others. Search was performed 1.5 times faster after practice, while one-step forward access was 5.3 times faster, and updating 5.5 times faster. Moreover, while all three processes were highly sensitive to the memory load N at the beginning of practice, the load effect remained high at the end of practice only for search (search slopes of about 81ms/item), but was much reduced for both forward access (14 to 28ms/step, depending on estimation method) and updating (a slope of 10ms/item).
It surprised us that the updating and random search processes should behave so differently, updating improving markedly and search much more resistant to change. Other studies shed additional light on these fundamental components of working memory, notably suggesting that the two processes are independent. Ecker, Lewandowsky, Oberauer, & Chee, (2010) devised no fewer than eight variations on an N-back task, and tested them in a within-subjects design (N was fixed at 3 in their study). Four variations included an updating requirement and, orthogonally, four required random access. From these ensembles encoding (i.e., updating) and retrieval (i.e., search) were abstracted as latent factors at the individual subject level. Ecker et al. found that the two factors were independent (true for both latencies and accuracies), with proficiency in one unrelated to proficiency in the other – setting the stage for other differences in the two factors such as their responsiveness to practice as found here. Lange, Verhaeghen, & Cerella (2010), using two more variations on the N-back task, identified some of the content of the two processes. One of their tasks was similar to ours, requiring a match on item location together with item identity; the other task used probes without locations, to be matched to the memory set on identity only. Lange et al. concluded that in both conditions WM was searched first on item identity. If needed, location information was then ascertained, a processing step that added a constant amount to the search time. The memory model here is of a set of items each tagged, if necessary, with a location tag. This model of working-memory representations can be applied to our forward-updating condition. To perform an update subjects must first establish a WM entry defined by an item's identity, and then attach a location tag to this entry. Initially, the tagging process is likely highly sensitive to the number of locations that need tagging, but over the course of practice, near-perfect efficiency can, and did, emerge. Subjects in the random no-update condition, on the other hand, presumably perform a search on identity, followed by a location check. The random search process did improve in efficiency, but far less so. This model of items-plus-location-tags makes differences between item search and item tagging (as part of the updating process) more understandable.
What about the third process isolated here, forward access? Lange et al. (2011) argued that forward “search” across a memory set has a special status, being far more efficient than random search, a finding replicated here. The present data show furthermore that the forward-access process is eminently improvable: Practice effects were large, leading to near-perfect efficiency (14 ms/item).
Differences in process efficiency bring us to our second question: Are there conditions in which practice expands the FoA? Previous research findings diverge: Verhaeghen et al. (2004), using an RT increment measure, found evidence for focus expansion from an initial size of one item to a final size of four items in a forward-updating condition; Oberauer (2006), using switch/non-switch difference scores, found no expansion beyond a size of one in a random-updating condition.
We replicated and extended both of these results. First, our forward-updating condition replicated the Verhaeghen et al. result, with the step function initially observed becoming a shallow ramp after practice (In Verhaeghen et al., the ramp encompassed Ns 1-4, here it extended to N=5). Additionally, after practice, the forward-updating ramp was statistically indistinguishable from that of the non-switch random condition, where by definition no focus-switching takes place. This implies that in the forward condition there was no retrieval from the outer store – all memory items (up to five digits after extended practice) were held within the focus, and were just as accessible as non-switch items in the random condition.
Second, our random-no-updating condition replicated the result from Oberauer (2006), where focus-switch and non-switch latencies diverged throughout practice. Interestingly, in both studies the load functions for switch and non-switch probes diverged between Ns 1 and 2, suggesting a focus size ranging from one to two items. Oberauer suggested that this reflects a mixture of some trials governed by a one-item focus and others by a two-item focus. Beyond the divergence point, focus-switch costs increased linearly with memory load, signaling Lange and colleagues’ (2010) random-order search process. Thus, when random access was required, only one or perhaps two items were immediately accessible, even after extended practice.
Whether the FoA expands with practice then seems to depend on the type of memory access required by the task. Verhaeghen et al. (2004) proposed that the processing demand was the underlying determinant, with focus capacity trading off with processing demands (Kahneman, 1973; Barrouillet, Bernardin, & Camos, 2004). The results here support this proposal – expansion depended on the ease of the search process tapped by the task. A task enlisting an easy search process which ran with increasing efficiency as practice continued (the forward condition), led to an expansion of focus; a task requiring a more difficult search process that improved relatively little with practice (the random condition), showed no enlargement of the focus. Forward search processes improve with practice, allowing the focus of attention to expand for such tasks, whereas random search allows no such benefit.
Finally, our findings may have some bearing on WM training programs, although such programs typically involve experimenter-paced, adaptive-difficulty regimens (Shipstead, Redick, & Engle, 2012). We do note that it is unclear how, and to what extent, our modified, participant-paced N-back task format relates to a more traditional, experimenter-paced N-back task. In fact, a direct comparison is difficult to draw between our modified N-back and the traditional format. Our version is by necessity focused on reaction time, due to our specific aim to decompose reaction time into time needed for constituent processes. The standard N-back, in contrast, is experimenter-paced and the results are expressed in the accuracy domain. However, our design does allow for the examination of how individual processes drive performance in tasks that involve updating, forward, and random search processes. Based on our findings, programs focusing on WM updating through tasks such as N-Back may lead to larger and/or more generalizable benefits than programs focusing on search or retrieval from the outer store, such as WMC tasks. This prediction follows from our finding that, although both updating and WMC are related to Gf (Kane et al., 2007), the updating process benefits the most from repeated practice. This prediction invites further study: it is unclear whether WM updating as trained in the specific context of the N-Back task facilitates performance on Gf tests, and, conversely, whether gains in Gf due to WM training are tied to improved updating efficiency.
Highlights.
We examined whether the focus of attention can expand through extended practice.
Forward access, memory search, and updating working memory processes were trained.
Focus expansion depended on the ease of the search process tapped by the task.
Forward search improved more with practice, leading to focus expansion.
Random search improved little with practice, showing no focus expansion.
Acknowledgments
Supported by a grant from the National Institute of Aging, AG-16201.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
John M. Price, School of Psychology, Georgia Institute of Technology
Gregory J. H. Colflesh, School of Psychology, Georgia Institute of Technology
John Cerella, Department of Psychology, Syracuse University..
Paul Verhaeghen, School of Psychology, Georgia Institute of Technology.
References
- Ackerman PL, Beier ME, Boyle MO. Working memory and intelligence: Same or different constructs? Psychological Bulletin. 2005;131:30–60. doi: 10.1037/0033-2909.131.1.30. doi:10.1037/0033-2909.131.1.30. [DOI] [PubMed] [Google Scholar]
- Alloway TP, Alloway RG. The efficacy of working memory training in improving crystallized intelligence. Nature Precedings. 2009 < http://hdl.handle.net/10101/npre.2009.3697.1>.
- Baddeley A, Hitch GJ. Working memory. In: Bower GA, editor. Recent advances in learning and motivation. Academic Press; New York: 1974. pp. 47–89. [Google Scholar]
- Barrouillet P, Bernardin S, Camos V. Time constraints and resource sharing in adults’ working memory spans. Journal of Experimental Psychology: General. 2004;133:83–100. doi: 10.1037/0096-3445.133.1.83. doi:10.1037/0096-3445.133.1.83. [DOI] [PubMed] [Google Scholar]
- Cowan N. Working memory capacity. Psychology Press; Hove, East Sussex, UK: 2005. [Google Scholar]
- Dahlin E, Nyberg L, Bäckman L, Stigsdotter Neely A. Plasticity of executive functioning in young and older adults: Immediate training gains, transfer, and long-term maintenance. Psychology and Aging. 2008;23:720–730. doi: 10.1037/a0014296. doi:10.1037/a0014296. [DOI] [PubMed] [Google Scholar]
- Ecker UKH, Lewandowsky S, Oberauer K, Chee AEH. The components of working memory updating: An experimental decomposition and individual differences. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2010;36:170–189. doi: 10.1037/a0017891. doi:10.1037/a0017891. [DOI] [PubMed] [Google Scholar]
- Engle RW. Roll of working-memory capacity in cognitive control. Current Anthropology. 2010;51:17–26. doi:10.1086/650572. [Google Scholar]
- Garavan H. Serial attention within working memory. Memory & Cognition. 1998;26:263–276. doi: 10.3758/bf03201138. [DOI] [PubMed] [Google Scholar]
- Jaeggi SM, Buschkuehl M, Jonides J, Perrig WJ. Improving fluid intelligence with training on working memory. PNAS. 2008;105:6829–6833. doi: 10.1073/pnas.0801268105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kahneman D. Attention and effort. Prentice Hall; Englewood Cliffs, NJ: 1973. [Google Scholar]
- Kane MJ, Conway ARA, Miura TK, Colflesh JH. Working memory, attention control, and the N-back task: A question of construct validity. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2007;33:615–622. doi: 10.1037/0278-7393.33.3.615. doi:10.1037/0278-7393.33.3.615. [DOI] [PubMed] [Google Scholar]
- Klingberg T, Forssberg H, Westerberg H. Training of working memory in children with ADHD. Journal of Clinical and Experimental Neuropsychology. 2002;24:781–791. doi: 10.1076/jcen.24.6.781.8395. doi:10.1076/jcen.24.6.781.8395. [DOI] [PubMed] [Google Scholar]
- Lange EB, Cerella J, Verhaeghen P. Ease of access to list items in short-term memory depends on the order of the recognition probes. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2011;37:608–620. doi: 10.1037/a0022220. doi:10.1037/a0022220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lange EB, Verhaeghen P, Cerella J. Dual representation of item positions in verbal short-term memory: Evidence for two access modes. European Journal of Cognitive Psychology. 2010;22:463–479. doi: 10.1080/09541440903155658. doi:10.1080/09541440903155658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McElree B. Working memory and focal attention. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2001;27:817–835. doi:10.1037/0278-7393.27.3.817. [PMC free article] [PubMed] [Google Scholar]
- Oberauer K. Access to information in working memory: Exploring the focus of attention. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2002;28:411–421. doi:10.1037/0278-7393.28.3.411. [PubMed] [Google Scholar]
- Oberauer K. Is the focus of attention in working memory expanded through practice? Journal of Experimental Psychology: Learning, Memory, and Cognition. 2006;32:197–214. doi: 10.1037/0278-7393.32.2.197. doi:10.1037/0278-7393.32.2.197. [DOI] [PubMed] [Google Scholar]
- Shipstead Z, Redick TS, Engle RW. Is working memory training effective? Psychological Bulletin. 2012 doi: 10.1037/a0027473. doi:10.1037/a0027473. [DOI] [PubMed] [Google Scholar]
- Turner ML, Engle RW. Is working memory capacity task dependent? Journal of Memory and Language. 1989;28:127–154. doi:10.1016/0749-596X(89)90040-5. [Google Scholar]
- Verhaeghen P, Cerella J, Basak C. A working memory workout: How to expand the focus of serial attention from one to four items in 10 hours or less. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2004;30:1322–1337. doi: 10.1037/0278-7393.30.6.1322. doi:10.1037/0278-7393.30.6.1322. [DOI] [PubMed] [Google Scholar]
- Westerberg H, Jacobaeus H, Hirvikoski T, Clevberger P, Östensson M-L, Bartfai A, Klingberg T. Computerized working memory training after stroke – A pilot study. Brain Injury. 2007;21:21–29. doi: 10.1080/02699050601148726. doi:10.1080/02699050601148726. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Verhaeghen P, Cerella J. Working memory at work: How the updating process alters the nature of working memory transfer. Acta Psychologica. 2012;139:77–83. doi: 10.1016/j.actpsy.2011.10.012. doi:10.1016/j.actpsy.2011.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]