Conveying Tactile Feedback in Sensorized Hand Neuroprostheses Using a Biofidelic Model of Mechanotransduction

Abstract

One approach to conveying tactile feedback from sensorized neural prostheses is to characterize the neural signals that would normally be produced in an intact limb and reproduce them through electrical stimulation of the residual peripheral nerves. Toward this end, we have developed a model that accurately replicates the neural activity evoked by any dynamic stimulus in the three types of mechanoreceptive afferents that innervate the glabrous skin of the hand. The model takes as input the position of the stimulus as a function of time, along with its first (velocity), second (acceleration), and third (jerk) derivatives. This input is filtered and passed through an integrate-and-fire mechanism to generate a train of spikes as output. The major conclusion of this study is that the timing of individual spikes evoked in mechanoreceptive fibers innervating the hand can be accurately predicted by this model. We discuss how this model can be integrated in a sensorized prosthesis and show that the activity in a population of simulated afferents conveys information about the location, timing, and magnitude of contact between the hand and an object.

I. INTRODUCTION

Neural prostheses, such as cochlear, vestibular, and retinal implants sense the environment using artificial sensors, convert data from these sensors into neural signals, and apply a pattern of electrical stimulation to a neural epithelium designed to mimic the signals that would have been produced by the sensory environment if the native sensory transducers were still in place.

For the sense of touch, the hand is the principal sensory organ and feedback from the hand is critical in the dexterous manipulation of objects. The skin of the hand is innervated by a large number of receptors, each of which conveys different kinds of information. Some receptors convey information about form and texture, others about temperature, and still others signal potentially harmful mechanical, thermal, or chemical stimulation. In designing a sensorized neural prosthesis for upper arm amputees, appropriate signals must be conveyed to the nerve fibers innervating each of these types of receptors (or to the afferent targets of these receptors in the brain or spinal cord) if feedback is to be realistically conveyed to the user. Here, we describe a model that mimics the response of low-threshold mechanoreceptors (i.e., those that signal non-noxious deformation of the skin) to arbitrary dynamic stimuli presented to the surface of the skin. Using this model then, signals transduced by sensors located on a prosthesis can be converted into desired patterns of neural activity, which can then be effected in the peripheral nerve through electrical stimulation (Fig. 1). Preliminary versions of this paper have been presented in abbreviated form else-where [1],[2].

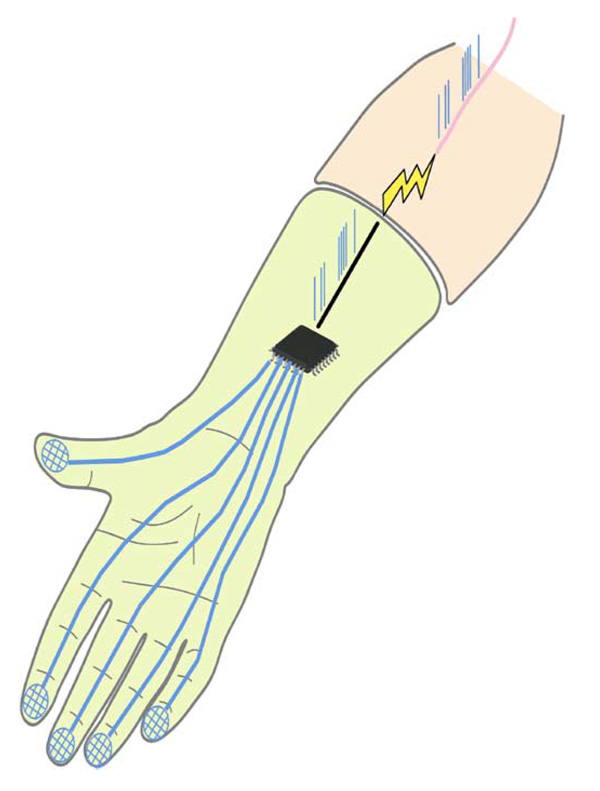
Fig. 1.

Diagram of a sensorized prosthetic limb. Force signals from sensors on the fingertips of the prosthesis are converted by using the model described here (and visually represented as a microchip) into the spike trains that would be evoked in the native limb by the stimulus. The spike trains are then effected into the residual nerve fibers through electrical stimulation.

II. MECHANORECEPTIVE AFFERENTS

The three types of mechanoreceptive fibers: 1) slowly adapting type 1 (SA1); 2) rapidly adapting (RA); and 3) Pacinian (PC) convey information about different aspects of the deformation produced at the surface of the skin (see [3] for a review): SA1 fibers respond to pressure and low-frequency vibrations and convey information about form and texture [4]. RA fibers respond to stimuli that brush against the skin and to oscillations at intermediate frequencies (20–100 Hz) and convey information about motion [5]. Pacinian fibers are exquisitely sensitive to higher frequency vibrations (their peak sensitivity is around 250–300 Hz) and are thought to convey information about distal events (as when sensing through a tool)[6] and the material properties of a surface [7].

A hallmark of afferent responses to dynamic stimuli is their repeatability. Repeated presentations of a dynamic stimulus evoke almost identical responses, suggesting that models can be developed to replicate this afferent activity.

In previous attempts to characterize the transduction process, not all aspects of afferent response properties were captured [8]–[11]. For instance, extant integrate-and-fire models account for the relationship between stimulus intensity and afferent responses, but cannot accurately predict the responses to stimuli other than sinusoids [8]–[10]. Other models that can be applied to spectrally complex stimuli do not exhibit important response properties of afferents, such as the stereotyped entrainment plateaus observed in the rate-intensity functions [11].

In developing a model of mechanotransduction, a critical question is what should constitute the input to the model. Specifically, what stimulus quantity determines the response of the afferent? We have previously shown that the stimulus quantity that drives the responses of SA1 and RA afferents when spatial patterns are statically indented into the skin is the strain experienced by the mechanoreceptor [12]. However, most stimuli are not static, and dynamic stimuli involve much more complex skin and receptor dynamics than do static stimuli. In this study, we then adopted a framework within which a variety of possible stimulus quantities and dynamics could be incorporated into the model.

The existing literature on mechanoreceptors offers hints as to the stimulus quantities that drive afferent responses and their associated nonlinearities. The three fiber types exhibit differential sensitivity to the instantaneous position (indentation depth), velocity, and acceleration of the stimulus [11]. Furthermore, different fibers, even within a given category, exhibit different stimulus noninearities: some fibers respond when the stimulating probe is indented beyond the resting level of the skin and do not respond to retractions (half-wave rectification) whereas others respond to indentations and retractions to the same degree (full-wave rectification)[1]. The model that will be described can incorporate the differential sensitivity of afferent fibers to stimulus position, velocity, acceleration, and jerk as well as the range of possible rectifying nonlinearities.

III. MODEL

We implemented an integrate-and-fire (IF) model with the ability to replicate the putative properties of all three types of mechanoreceptive afferents. The model was driven by four input variables—position and its first, second, and third derivatives (corresponding to velocity, acceleration, and jerk, respectively, see Fig. 2). Since the framework we adopted to estimate the model parameters only allows for linear transformations of the inputs, we separated each input into its positive and negative components (e.g., indentations and retractions in the case of position), allowing separate linear transformations on each component. This partition allowed us to account for full-wave, half-wave, or partial rectification of the input signal using appropriate linear transformations on each component.

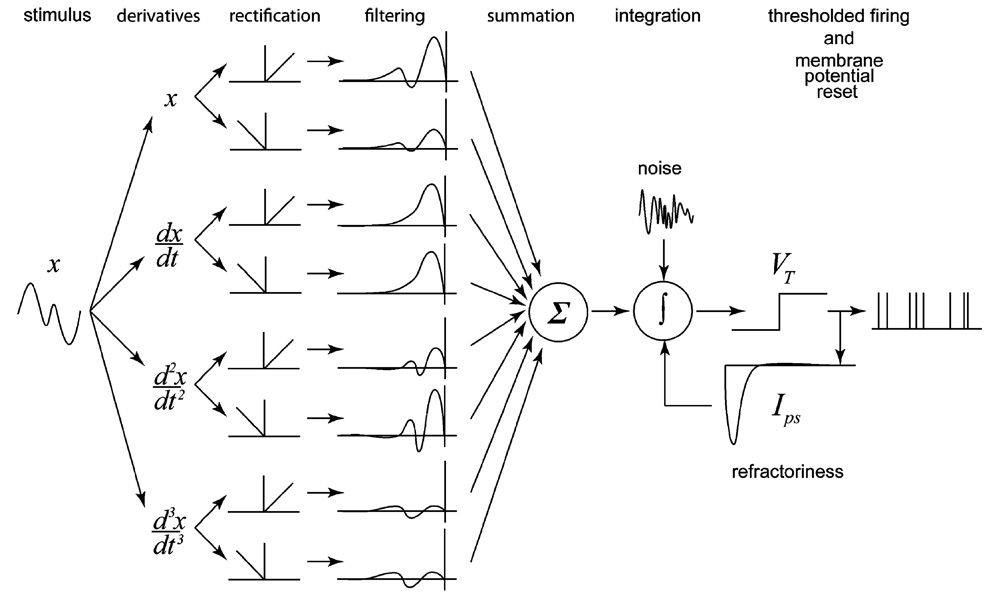
Fig. 2.

Diagram of the full leaky and noisy integrate-and-fire model used to predict afferent activity. The model comprises eight inputs, corresponding to the positive and negative components of position, velocity, acceleration, and jerk, each of which is passed through a linear prefilter. The summed output of the prefilters constitutes the input to the IF mechanism. When the membrane potential of the IF mechanism reaches threshold, a spike is produced and an inhibitory current is released to mimic refractoriness.

In the model, inputs are filtered separately then summed and converted into current to form the input to the IF mechanism. Noise is injected into the IF mechanism along with this input current. The IF mechanism has several parameters associated with it, namely, the membrane time constant (τ_m), reset potential (V₀ = 0), resting potential (V_r), and electrical threshold (V_T = 1). When the membrane potential reaches threshold (V_T), an action potential is produced, the membrane potential is reset (to V₀), and a postspike inhibitory current is injected into the neuron to place it into a refractory state.

The membrane potential V is given by

$$\text{dV}=\left(-\frac{(V-V_r)}{{\tau }_m}+I_{\text{in}}(t)+I_{\text{ps}}(t)\right)\text{dt}+W_t$$ (1)

where I_ps(t) is the (fitted) postspike inhibitory current, accumulated over all past spikes, W_t is Gaussian noise, and I_in(t), the input current, is given by (in the full model)

$$I_{\text{in}}(t)={\displaystyle \sum _{i=0}^3{H}_i^{+}(t)*y_i^{+}(t)+H_i^{-}(t)*y_i^{-}(t)}$$ (2)

where $y_i^{+}(t)y_i^{-}(t)$ are the positive and negative components of the ith derivative of position, respectively; $H_i^{+}(t)\text{and}{H}_i^{-}(t)$ are the corresponding linear filters; and * denotes the convolution operation. The filter associated with each input was allowed to vary independently in order to accommodate differential sensitivity across inputs.

The model was developed and tested on the responses of 5 SA1, 5 RA, and 5 PC fibers (recorded from two anesthetized Rhesus macaques) to a variety of vibratory stimuli, including diharmonic stimuli (superimposed sinusoids) and bandpass noise stimuli varying in amplitude and frequency content (for details, see [13]). Since the physical quantity that drives transduction is unknown, we evaluated models using combinations of position, velocity, acceleration, and jerk as inputs–a total of ten models. Models that included all of the inputs were at least as good as any model that comprised a subset of inputs. However, some simpler models were as good as the full model; different afferent types required different combinations of inputs. For the purposes of implementation in a neuroprosthesis, using all four inputs results in a generic model that can be parametrically adapted to different afferent types. The primary source of variability across cells was the type of rectification they effected on the inputs: Some neurons were full-wave rectifiers, others half-wave rectifiers, and many exhibited intermediate rectification. Interestingly, the shapes of the filters were similar across fibers of a given type and differed across fiber types. The discussion of the afferent sensitivity to different inputs and of the shape of the input filters falls outside the scope of this paper.

The difficulty in implementing an IF model to predict measured spiketimes lies in estimating the parameters of the model. In our case, the parameters include those defining the input filters, the parameter describing the noise, the IF parameters (τ_m and V_r), and the parameters defining the shape of the post-spike inhibitory current. Although these parameters can be estimated by using conventional optimization techniques, such as annealing [14], these methods do not guarantee convergence to a unique solution. Recently, Paninski and Pillow [15], [16] have pioneered a novel approach that does ensure convergence. Briefly, by assuming that the noise in the current driving the IF mechanism is Gaussian, the approach uses density propagation techniques to compute the probability of a spike at time t_j given a set of parameters

$$p(\text{spike at}{t}_j|\text{spike at}{t}_{j-1})={\displaystyle {\int }_{V\in C_j}G(V(t)|y,\theta )}$$ (3)

where C_j is the set of possible voltage trajectories during inter-spike interval j, bracketed by spike times t_j−1 and t_j. Specifically, C_j includes all of the trajectories where V (t_j−1) = V₀, V (t_j) = V_T) (V_T is the threshold potential), and V (t_j−1 < t < t_j) < V_T. G(V(t) | y, θ) is the Gaussian density function of the voltage trajectory over this interval, y is the stimulus, and θ represents the parameters of the IF model. The mean of G is the noiseless solution of (1) and its covariance is given by

$$\text{Cov}(t_p,t_q)=\frac{{\tau }_m}{2}(e^{-|t_q-t_p|/{\tau }_m}-e^{-|t_p+t_q|/{\tau }_m}).$$ (4)

The joint likelihood of the set of observed spikes evoked by the stimulus, given parameters θ, can then be obtained by multiplying the probabilities in (3) for all spikes. This likelihood function is convex in its parameters [13] and, thus, we can use standard optimization techniques to find the most likely set of parameters for the model, given the set of observed spikes.

IV. MODEL PERFORMANCE

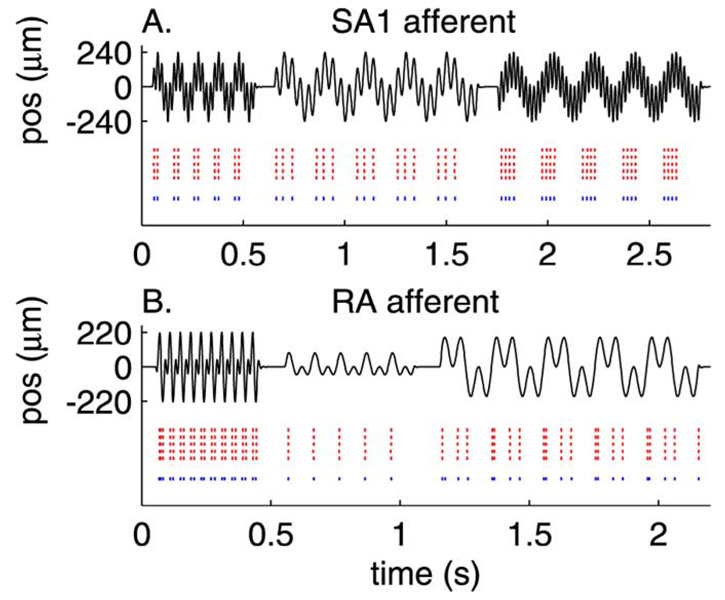
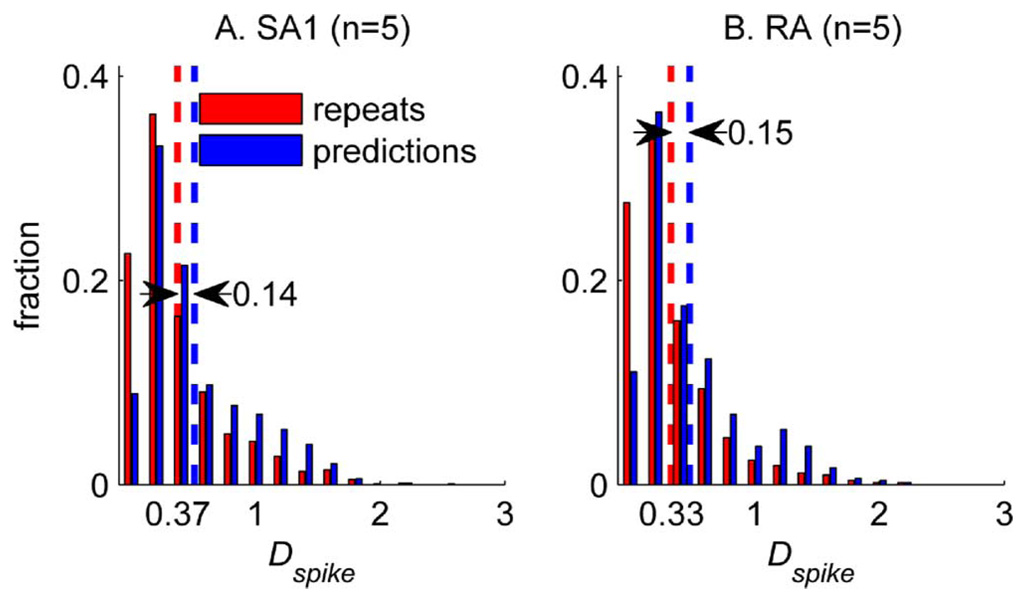
Fig. 3 shows the measured (red) and predicted (blue) spike trains evoked by three diharmonic stimuli for an SA1 [Fig. 3(a)] and an RA [Fig. 3(b)] fiber. The predicted spike trains are almost identical to their measured counterparts. Not only can the model predict almost flawlessly the individual spike times in the training set, but it can also yield good predictions of novel data (Fig. 4). To evaluate objectively the fits of the IF model, we calculated a measure of dissimilarity between the predicted and observed patterns of spikes evoked by the training set. This measure, called spike distance (D_spike), and proposed by Victor and Purpura [17], is an index of the cost required to change one spike train into another. D_spike increases as two spike trains become increasingly dissimilar; the more dissimilar the two trains are, the greater the cost (the cost associated with adding or subtracting one spike is 1, and the cost for shifting a spike by 1 ms is 0.25). To establish a baseline for D_spike, we computed D_spike for pairs of responses to the same stimuli in a given afferent. This baseline distribution of D_spike (pooled across stimuli for each afferent individually) establishes an upper bound for model performance because model predictions cannot be more similar to afferent responses than afferent responses are to themselves. As shown in Fig. 5 for the SA1 fiber from Fig. 3(a) and Fig. 4(a), the distribution of D_spike for repeats and for predictions overlapped considerably: the difference in mean between the two distributions is about 0.15. In other words, the predicted and actual spike trains differ by an average of 1 spike per 7, or the timing discrepancy between the two trains is less than 0.6 ms per spike.

Fig. 3.

Measured (red) and predicted (blue) spike trains evoked by three stimuli (black traces) for (A) and SA1 and (B) an RA afferent. Each row in the red raster plot shows the response evoked on each of the five presentations of the stimulus. The blue raster plot shows the spike trains predicted by the model with parameters estimated by using the same stimuli.

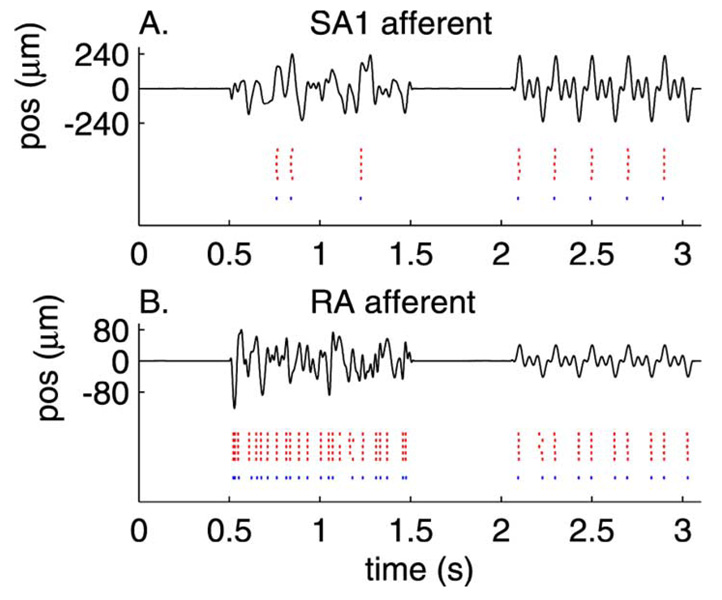
Fig. 4.

Measured and predicted spike trains evoked by two stimuli for (A) an SA1 and (B) an RA afferent (conventions as in Fig. 3). Parameters obtained from the training set were used to derive predictions to novel stimuli. Each row in the red raster plot shows the response evoked on each of five presentations of the stimulus. The blue raster plot shows the spike trains predicted by the model with parameters estimated by using the same stimuli.

Fig. 5.

Distribution of D_spike for pairs of measured responses to the same stimuli (red) and for predicted responses paired up with their measured counterparts (blue), pooled across stimuli for all of the SA1 and RA fibers. D_spike is an index of the cost required to change one spike train into another; the greater the difference between the two trains, the greater the cost. The cost associated with adding or subtracting one spike is 1, and the cost for shifting a spike by 1 ms is 0.25. Other values of the cost parameter yielded similar results.

V. IMPLEMENTATION

Given the biofidelic model proposed herein, the implementation of this approach to provide tactile feedback for an upper extremity neuroprosthesis is envisaged to require the following steps. First, arrays of stimulating microelectrodes would be implanted into the residual median and ulnar nerves of the amputated arm. Second, fibers stimulated by the electrodes would be classified according to fiber type and the projected field. To accomplish this, trains of electrical pulses would be delivered through each electrode in succession, and the amputee would report the elicited sensations. Classification of afferents based on subjective reports can be assumed to be accurate because the stimulation of SA1 afferents has been shown to elicit sensations of pressure and stimulation of RA afferents evokes sensations of flutter and stimulation of PC afferents sensations of vibration [18]. Stimulation of other types of fibers will produce other sensations (painful, thermal, etc.). Once fibers have been categorized by type, their projected field of sensation must be identified. This is achieved by having the amputee report where the sensations elicited by the electrical stimulation originate on the hand. The prosthetic sensors responsive to the afferent’s projected field will then be associated with that particular afferent. For instance, the responses of afferents whose receptive fields are located on the native index finger will be driven by the output of sensors on the index finger of the prosthesis.

The final step in implementing this strategy is to determine the parameters of a single electrical pulse that results in a single action potential in the stimulated fiber. Indeed, for the stimulation to be perceived as natural, trains of action potentials must be evoked with the temporal pattern specified by the biofidelic model. As human subjects can perceive a single action potential evoked in a single afferent fiber [18], we can assume that a liminal electrical pulse will produce a single action potential in the stimulated afferent. To evoke a train of action potential with a given temporal sequence in the fiber, a stimulator will deliver a train of liminal electrical pulses with the desired temporal structure (assuming that temporally adjacent pulses behave independently).

VI. RESULTS

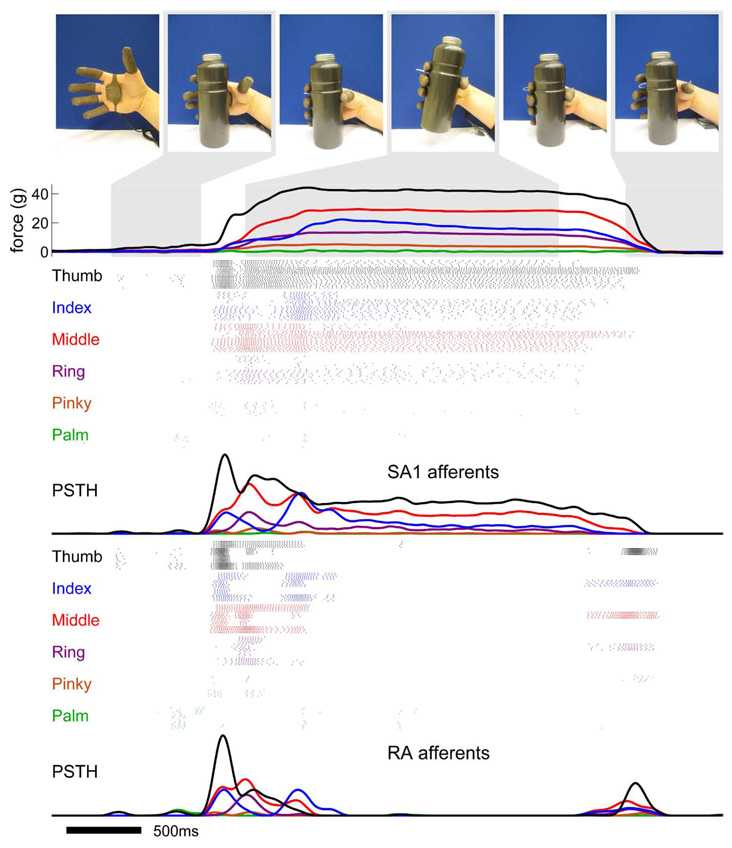
The functionality of the model as a tool for tactile feedback was tested by simulating the responses evoked in populations of afferents when objects are manipulated with a hand fitted with a sensorized glove (FingerTPS, PPS, Inc., Los Angeles, CA). At the top of Fig. 6, images are shown from a video sequence in which a water bottle is grasped, picked up, and then put down. The outputs of the glove’s force sensors on the fingertips and palm are converted to position signals, which are, in turn, used as inputs to five clones of four SA1 and four RA afferents at each location (for a total of 240 instantiations of the transduction model, 120 of each type). The bottom of Fig. 6 displays the sequences of action potentials generated by the biofidelic models along with the peristimulus spike histograms. In a real prosthesis, the output from each simulated afferent would be used to stimulate an afferent whose projected field is located in the vicinity of the sensor.

Fig. 6.

Illustration of the biofidelic approach to tactile feedback. A hand equipped with a sensorized glove grasps, picks up, and puts down a water bottle. Each colored trace shows the force exerted on a fingertip or on the palm as a function of time. The outputs of the force sensors on the digits and palm are used as inputs to five clones each of four SA1 and four RA afferents on each digit and on the palm, for a total of 240 simulated afferents. For the purposes of this simulation, we assumed that the force exerted on each digit was equally distributed across all of the stimulated receptors. The model is designed for more localized force sensors whose receptive fields are approximately the same size as that of mechanoreceptive afferents. Each group of colored rasters corresponds to the activity evoked in a population of afferents whose receptive fields are located on a single digit or on the palm (colors match those of the displacement traces). The peristimulus spike histograms are shown under the corresponding rasters showing the mean response across the population of SA1 and RA fibers. As can be seen from the figure, simulated SA1 and RA afferents produce qualitatively different responses during the manipulation of the bottle. SA1 afferents tend to respond throughout the contact period whereas RA afferents respond at the onset and offset of contact. Information about the location of contact on the hand, timing of contact, and force of contact are contained in the activity of the population of afferents.

As can be seen, the simulated afferent activity conveys rich dynamic information about the order in which digits contact the object, the time at which contact begins and ends, and the force exerted by each digit on the object. For example, the palm and pinky barely touch the object throughout the recording period, as is reflected in the weak neural activity originating from these regions. In addition, it can be seen that contact with the ring finger occurs later than contact with the thumb, as reflected in the later onsets of the SA1 and RA responses. Interestingly, SA1 and RA afferents produce robust responses not only when the object is first contacted but also when it is raised, signaling that the object is no longer supported by the table. RA afferents tend to respond at the onset of contact, during the initial elevation of the object, and at the offset of contact whereas SA1 afferents generally respond during the entire period when the hand is in contact with the object. Information about the timing of events may thus be more robustly conveyed by RA afferents. Finally, most of the force required to lift the object is shared between the thumb and middle finger, as reflected by the strong responses in these regions. SA1 afferents convey the most robust information about the magnitude of the force as their responses are more strongly modulated by this stimulation parameter than are their RA counterparts. Presumably, this simulated spatiotemporal pattern of activity would be intuitive and familiar if generated in the residual nerves of an amputee because the model faithfully replicates the dynamic pattern of activation that would normally be evoked in the nerves in the intact hand.

VII. CONCLUSION

The central conclusion of this study is that a simple IF model can capture the fine temporal structure of the firing patterns evoked in mechanoreceptive afferent fibers in a dynamic environment. In developing models of neural encoding for a neural prosthesis, the next step may be to incorporate into the model the spatial filtering caused by the skin [12]. We have previously developed a model that describes how a stimulus, impinging upon the surface of the skin, exerts forces at the surface of the skin which are then distributed within the skin as tissue strain. The effects of skin mechanics may be implemented by using a simple mapping between force and strain (based on the mechanical properties of the skin) and using the time-varying strain, along with its first, second, and third time derivatives, as inputs to the present model. Whether this nonlinear transformation reflecting skin mechanics should be effected in a prosthesis remains to be determined. This transformation will make the simulated activity more similar to that evoked in the native limb and, thus, more intuitively interpretable by the amputee. However, the spatial filtering of the skin reduces spatial acuity by redistributing forces exerted at the surface, so a prosthetic limb lacking this transformation will offer greater spatial resolution. Whether this mechanical filtering enhances the interpretability of afferent signals can be tested empirically.

Biographies

Sung Soo Kim received the B.S. and M.S. degrees in electrical engineering from Seoul National University, Seoul, in 1998 and 2000, respectively, and is currently pursuing the Ph.D. degree in neuroscience at The Johns Hopkins University, Baltimore, MD.

In Korea, he studied the design of control systems using neural networks. He studies the modeling of peripheral mechanoreceptors and the neural mechanisms of somatosensation and proprioception in the central nervous system.

Arun P. Sripati received the B.Tech degree in electrical and computer engineering from the Indian Institute of Technology, Bombay, India, in 1999, and the M.S.E and Ph.D. degrees in electrical and computer engineering from the Johns Hopkins University, Baltimore, MD, in 2002 and 2005, respectively.

Currently, he is a Postdoctoral Fellow at the Center for the Neural Basis of Cognition at Carnegie Mellon University, Pittsburgh, PA. His research interests include the neural basis of perception and object recognition.

R. Jacob Vogelstein (S’99–M’09) received the B.Sc. degree in bioelectrical engineering from Brown University, Providence, RI, in 2000 and the Ph.D. degree in biomedical engineering from Johns Hopkins University, Baltimore, MD, in 2007.

Currently, he is working on advanced neuroprostheses at the Johns Hopkins University, where he is with the Applied Physics Laboratory and the Department of Electrical and Computer Engineering. His work focuses on neuroprosthetic devices and brain-machine interfaces, and his research has been featured in publications ranging from IEEE journals to the BBC World News.

Dr. Vogelstein was inducted into the Tau Beta Pi and Sigma Xi honor societies in 1999, won the Brown University Engineering Department’s Outstanding Student Award in 2000, received a National Science Foundation Graduate Research Fellowship in 2002, and was awarded a Lawrence Hafstad Fellowship in 2008.

Robert S. Armiger received the B.S. degree in mechanical engineering from the Virginia Polytechnic Institute and State University, Blacksburg, in 2003 and the M.S. degree in biomedical engineering from The Johns Hopkins University, Baltimore, MD, in 2006.

He is with the Johns Hopkins University Applied Physics Laboratory, working in the fields of biomechanics and computer-assisted surgery as well as upper extremity prostheses and robotics.

Alexander F. Russell received the B.Sc degree in mechatronic engineering from the University of Cape Town, Cape Town, South Africa, in 2006 and is currently pursuing the Ph.D. degree in electrical and computer engineering at the Johns Hopkins University, Baltimore, MD.

His research interests include optimization methods for spiking neurons and biofidelic sensory encoding algorithms.

Dr. Russell was a recipient of the Klaus-Jurgen Bathé Scholarship, the Manuel and Luby Washkansky Postgraduate Scholarship from the University of Cape Town, and the Paul V. Renoff Fellowship from The Johns Hopkins University.

Sliman J. Bensmaia was born in Nice, France, in 1973. He received the B.Sc. degree in cognitive science from the University of Virginia, Charlottesville, in 1995, and the Ph.D. degree in cognitive psychology at the University of North Carolina at Chapel Hill in 2003.

He was then a Postdoctoral Fellow with Kenneth O. Johnson at the Krieger Mind/Brain Institute of The Johns Hopkins University, Baltimore, MD. Currently, he is an Assistant Professor in the Department of Organismal Biology and Anatomy at the University of Chicago, Chicago, IL, where he studies neural coding and the neural basis of perception in the somatosensory system. He combines neurophysiology with psychophysics and computational models to investigate the tactile processing of form, motion, texture, and vibration. The general approach, pioneered by Vernon Mountcastle, consists in measuring an aspect of perception on human subjects then recording the responses evoked in peripheral afferents and in cortical neurons in macaque monkeys.

Dr. Bensmaia received the Baughman award for innovative dissertations and is a member of the Society for Neuroscience and the American Physiological Society.