A novel approach to represent and compare RNA secondary structures

Abstract

Structural information is crucial in ribonucleic acid (RNA) analysis and functional annotation; nevertheless, how to include such structural data is still a debated problem. Dot-bracket notation is the most common and simple representation for RNA secondary structures but its simplicity leads also to ambiguity requiring further processing steps to dissolve. Here we present BEAR (Brand nEw Alphabet for RNA), a new context-aware structural encoding represented by a string of characters. Each character in BEAR encodes for a specific secondary structure element (loop, stem, bulge and internal loop) with specific length. Furthermore, exploiting this informative and yet simple encoding in multiple alignments of related RNAs, we captured how much structural variation is tolerated in RNA families and convert it into transition rates among secondary structure elements. This allowed us to compute a substitution matrix for secondary structure elements called MBR (Matrix of BEAR-encoded RNA secondary structures), of which we tested the ability in aligning RNA secondary structures. We propose BEAR and the MBR as powerful resources for the RNA secondary structure analysis, comparison and classification, motif finding and phylogeny.

INTRODUCTION

Ribonucleic acids (RNAs) are complex molecules that can fold, globally or locally, into intricate secondary and tertiary structures. In recent years, RNA molecules are revealing a new central (1), but not yet completely elucidated, role in regulation (2–4), especially in higher organisms (5). The genome contains a relatively well-established number of protein-coding genes and a still uncertain number of several classes of genes expressing non-coding transcripts (6,7). Their functions are often not directly associated with their sequence but in many cases are critically dependent upon their secondary and tertiary structures (8–12), and, accordingly, the need for developing instruments for their functional characterization is becoming more pressing. Sequence and structure comparison plays an important role in annotating ncRNAs and also in many other analyses such as RNA alignment and classification, sequence/structure recurrent motifs finding and phylogenetic inference. In particular, the secondary structure of RNA molecules is often more conserved than their primary sequence (13) and in the analysis of homologous RNAs the importance of secondary structure information increases with decreasing sequence identity (below 50–60%) (14). Hence, encoding the secondary structure in comparison tools is needed in order to exploit also structural information.

The most common encoding for the RNA secondary structure is the dot-bracket notation, consisting in a balanced parentheses string composed by a three-character alphabet {.,(,)}, that can be unambiguously converted in the RNA secondary structure. Its characters code for an unpaired base ‘.’, an open base pair (BP) ‘(’ and a closed BP ‘)’. Considering the simple information provided by a three-character alphabet, processing steps are required to map each nucleotide into the structural element it belongs to. In other words, this simple representation stores no direct information about the structural context of the nucleotide, which must be extracted by means of ad hoc post-processing procedures. Several approaches have been developed that use the dot-bracket notation to improve RNA secondary structure analysis and comparison. Among others, Sankoff's dynamic programming algorithm (15) was the first exhaustive method for structural RNA alignment but its high computational complexity (O(N^⁁6) in time and O(N^⁁4) in space) limits its usage in high-throughput settings. Lower complexity has been reached by different methods using different approaches: dynamic programming (16–18), formal grammars (19) and genetic algorithms (20,21). Moreover, other encodings were proposed to overcome the above-mentioned drawbacks of the dot-bracket notation, such as motif description (22,23) and tree-based encodings (24,25). By using a tree-based approach, the topology of the RNA secondary structure is encoded using a graph, instead of a string, increasing the information stored in the encoding but the algorithmic complexity of the comparison as well. The motif description approach, instead, often does not allow fast and automatic encoding procedures, requiring the user to choose the best descriptor. Hence, we argue that a new and more comprehensive approach to describe RNA secondary structure, that can be also applied to compare RNAs without increasing the algorithmic complexity, would be useful per se and also instrumental to complement other methods for RNA study and analysis.

In this work, we present a new encoding for RNA secondary structure called BEAR (Brand nEw Alphabet for RNA). Within a simple string of characters, the BEAR encoding allows one to store information about RNA secondary structure. BEAR unambiguously associates with each nucleotide in an RNA sequence its secondary structure. Differently from the dot-bracket notation described above, the assignment of each nucleotide to the secondary structure element (SSE) it belongs to allows one to discriminate nucleotides described with the same symbol (a dot or a bracket) but belonging to a different SSE. For instance, the BEAR encoding easily discerns unpaired nucleotides belonging to a loop and a bulge. These features allow one to compute appropriately the statistics upon the accepted variations in families of homologous RNAs and offer novel perspectives for methods analyzing the evolution of these complex molecules.

The development of a structural alphabet to encode secondary or tertiary structures into a string has been successfully applied also in the context of protein structure (26–29). The underlying idea is to encode fragments of the protein backbone using protein blocks (PBs), defined in terms of the phi and psi dihedral angles. This kind of structural encoding has found applications in binding site signature identification (30), structure prediction from sequence (31,32) or peptide design (33). It was shown that using PBs improves protein structure comparison in terms of time and accuracy (34).

In this perspective, we showed how, using our encoding, it is possible to extract information about ‘transition rates’ between RNA sub-structures with different length and type in related RNAs, obtaining a substitution matrix for SSEs. The definition of a substitution matrix for RNA SSEs allows the extension of the benefits of the new encoding also to methods for RNA global, local or multiple alignment, for the identification of recurring secondary structure patterns, for the application of a PSSM (position-specific scoring matrix) approach and in general to analyze RNA secondary structures based on statistical preferences. To support these ideas, we show the reliability and usefulness of the approach by performing pairwise global RNA alignments using the previously computed substitution matrix, obtaining, even with the simplest possible algorithm (an opportunely modified Needleman–Wunsch algorithm), an alignment accuracy comparable to the state-of-the-art methods, which are nevertheless associated with a higher computational complexity.

MATERIALS AND METHODS

Selection and folding of RNA families from the Rfam database

Rfam is a manually curated collection of RNA families (13); RNAs belonging to the same family share a similar secondary structure and generally also the same function. Families are populated starting from a set of manually curated RNAs, then alignment tools are used to increase the number of RNA sequences in the families. Finally, a multiple sequence alignment (called ‘seed’ alignment) is produced for each family along, for most families, with a consensus secondary structure.

First, we selected all Rfam (release 10.1) families annotated with a consensus secondary structure. Next, we selected all families with a multiple sequence alignment and reported per-column conservation. Then, we removed highly similar sequences (more than 50% sequence identity) from the data set by using BLASTClust (35) and filtered off all those families with less than five members remaining. The total number of Rfam families satisfying these criteria, which were used to analyze intra-family variations of SSEs, is reported in Supplementary Table S1 in the Supplementary materials.

To fold each Rfam RNA we used the RNAfold program, included in the Vienna package (36). We used as structural constraints for the folding the consensus secondary structure of all the positions annotated as highly conserved in the Rfam seed alignment. We argue that using this strategy we would be able to predict more reliable secondary structures and, at the same time, allowing sufficient freedom to the folding algorithm in order to capture variations between RNAs in the same family.

The BEAR encoding

In the BEAR encoding, different sets of characters are associated with the different RNA basic structures (loop, internal loop, stem and bulge). Let L, I, S and B denote the set of characters for loop, internal loop, stem and bulge respectively; for example, L is the alphabet of the loop-associated characters {L₁, L₂, …, L_n} defining loops with different length: L₃ would be a three-residue loop, L₄ a four-residue loop and so on. Similarly, the sets of characters describing stems and internal loops also contain length information (Figure 1A). We translated into the BEAR encoding both hairpin structures, from now on ‘non-branching structures’ (26) and ‘branching’ SSEs, e.g. the closing stem of a multi-loop. More in detail, a non-branching structure ‘NB’ is the maximal set of BPs (i,j) containing a loop, such that for all 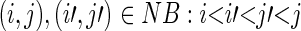; all sets of BPs not containing a loop are defined as branching. A different set of characters was used for branching and non-branching SSEs, since we observed differences in frequencies, transition rates and length distributions. Therefore, each L, I, S, B set of characters is defined as the union of characters associated with non-branching and branching structures (e.g. 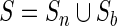where S_n and S_b indicate the set of characters for non-branching and branching stem structures, respectively). Then, the BEAR alphabet β is defined as .

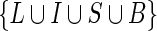Figure 1.

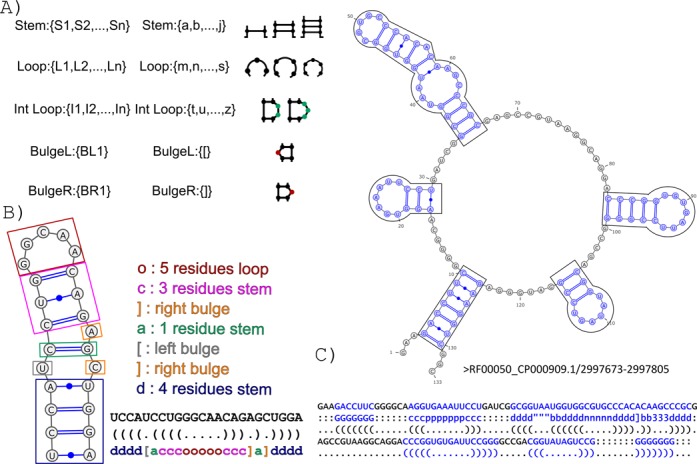
The BEAR encoding. (A) The BEAR structural alphabet. Different sets of characters are associated with the different RNA basic structures (loop, internal loop, stem and bulge on the right side of a stem, and bulge on the left side, denoted here as L, I, S,BL and BR, respectively), with different characters used for basic structures of different length. (B) RNA hairpin with the constituent substructures (loop, stem, bulges and internal loop) highlighted in different colors. On the top right, the BEAR characters corresponding to each substructure, shown with the same colors. On the bottom right, the hairpin RNA sequence is shown associated with its dot-bracket and its BEAR secondary structure descriptions. (C) Conversion into BEAR of an RNA secondary structure. An RNA secondary structure, extracted from Rfam, is shown, containing four non-branching structures depicted in boxes. The resulting BEAR conversion of the non-branching and branching structures is shown in blue below the secondary structure. A ‘:’ character is assigned to the remaining nucleotides that do not belong to non-branching or branching structures (reported in black).

Let s denote one of the possible RNA basic structures (loop, stem, internal loop and bulge) and l denote the length of s. Then, we define m(s, l) = c as the mapping function of every possible pair (s, l) to the corresponding BEAR character .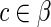

The translation from the dot-bracket representation into the BEAR encoding can be summarized in two steps (Figure 1):

1. identify RNA basic structures along with their length by scanning the string of dot-bracket characters;

2. translate, using the mapping function m, the information about length and structure type into a BEAR character.

The BEAR translation requires linear time, therefore its application even to large sets of RNAs is fast. The output string of BEAR characters has the same length of the nucleotide sequence. An example of the conversion of a secondary structure into BEAR is shown in Figure 1B. We did not translate into the BEAR encoding some branching SSEs not representable with the dot-bracket notation, such as pseudo-knots. Additionally, we used a special character, ‘:’, to describe nucleotides belonging to unpaired regions not belonging to loops, internal loops or bulges. As a consequence, the resulting encoding for RNA secondary structures will be a combination of BEAR-encoded structures separated by ‘:’ characters (see Figure 1C for an example).

In order to determine the cardinality of the alphabets, that is the maximal encoding length for stems, loops and internal loops, we calculated the distribution of the length of these RNA sub-structures in a selection of Rfam families (13) (Figure 2A). We used the value of the 95th percentile of each distribution as upper limit for the associated basic structure descriptor (stem: 10; loop: 16; internal loop 10; stem in a branching structure: 10; internal loop in a branching structure: 16). All the sub-structures with a length higher than the threshold were grouped and encoded using a sub-structure-specific character. The software that converts from the dot-bracket notation to BEAR encoding, taking as input the RNA sequence and secondary structure, is freely available at http://bioinformatica.uniroma2.it/BEAR/BEAR_Encoder.zip.

Figure 2.

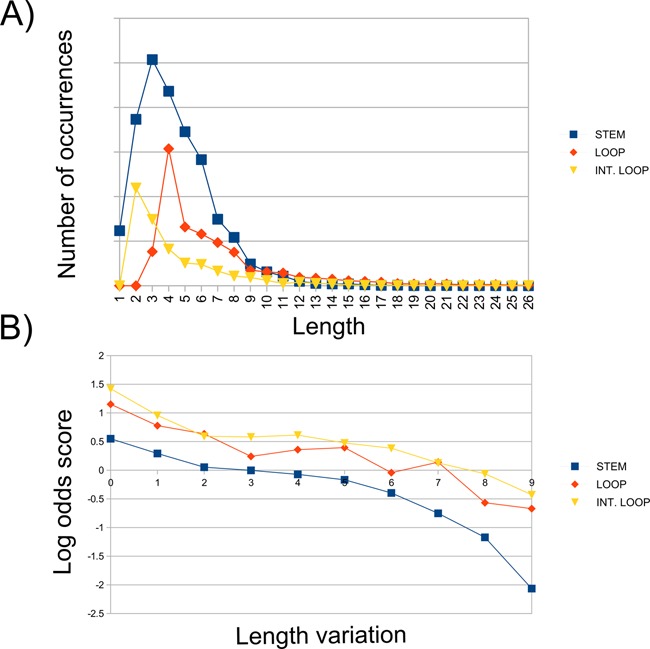
(A) Length distribution of stems, loops and internal loops detected in Rfam. (B) Inverse correlation between length variation and log-odds score. For each Rfam RNA, we extracted the length of stems, loops and interior loops, counted the number of transitions from an RNA sub-structure to another of the same type but with different length for each aligned RNA sequence pair in Rfam (e.g. from a stem of length 1 to a stem of length 2, from a stem of length 1 to a stem of length 3 and so on for all possible combinations) and grouped together transitions having the same length difference (e.g. transitions from a stem of length 1 to a stem of length 3, from a stem of length 2 to a stem of length 4, from a strand of length 3 to a strand of length 5 and so on were collected together in the same group containing all transitions of size 2). The frequency of each transition group was then computed as log-odd scores. The three distributions in the figure show the log-odds scores for any variation in size for stems (blue curve), loops (red) and internal loops (yellow), respectively, and highlight an inverse relationship between the length variation in each class of SSEs and its frequency in the data set of RNA alignments.

Substitution matrix of RNA SSEs

To build an SSEs substitution matrix, we started from a set of highly structured families reported by Meyer et al. in 2011 (37) in order to have a higher number of evidences for all the possible substitutions between RNA SSEs. In that work, a family is considered highly structured if all of its members have a high number of non-branching structures. To further increase the cardinality of the data set, we scanned Rfam looking for families having a number of non-branching structures similar to those used in the work of Meyer et al., which have seven non-branching structures on average, with a standard deviation of 2. Hence, we looked for Rfam families with a mean number of non-branching structures between 5 and 9 and whose mean number of BEAR characters, different from ‘:’, was higher than 67%. The list of Rfam families used to build the SSE substitution matrix is reported in the Supplementary materials (Supplementary Table S2). Each RNA in the selected RNA families was folded as described, and its secondary structure converted into the BEAR encoding. Then, we mapped every BEAR character to its corresponding nucleotide in the multiple sequence alignment, obtaining a multiple BEAR alignment for each family. We used the same approach employed by Dayhoff (38) to compute a substitution matrix for the BEAR characters. We computed the observed frequency of substitution of BEAR characters in the multiple sequence alignments and computed the substitution matrix as follows:

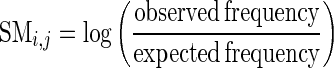Here, the observed frequency is the number of pairs of BEAR characters found in the alignment over the total number of pairs and the expected frequency is the product of the frequency of each member of the pair. From now on we refer to the substitution matrix of BEAR characters as MBR (Matrix of BEAR-encoded RNA secondary structures). A pseudo-count of 1 is used to initialize the observed pairs in order to avoid taking the logarithm of zero when there are no counts for a specific pair of characters in the alignments. The full pipeline is summarized in Figure 3.

Figure 3.

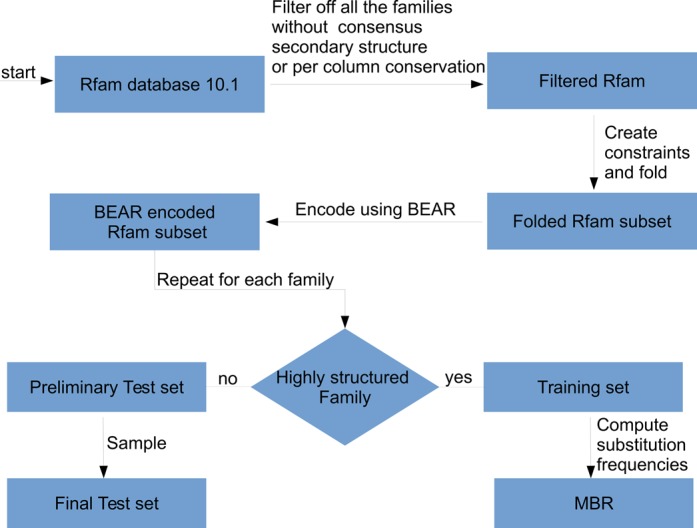
MBR construction and testing pipeline. We started from Rfam 10.1, selecting families for which a consensus structure and a per-column conservation is reported. Conserved positions in the Rfam multiple alignments were used to select structural constraints that guided RNAfold. The resulting secondary structures for each member of the Rfam families were converted into BEAR. A set of Rfam families having high density of SSEs was used to compute SSEs substitution frequencies and build the MBR (the training set). From the remaining families, pairwise alignments were randomly sampled and used to test the ability of MBR in reconstructing the alignment.

To test the MBR performance in capturing secondary structure similarities, we created additional control matrices, each one associated with a different information content. The ‘positive diagonal’ matrix assigns a positive score to identical aligned BEAR characters and a negative score to all other substitutions. The ‘positive group’ matrix assigns a positive score to substitutions between characters encoding for the same RNA secondary structure type (e.g. all stems), disregarding possible differences in length, and a negative score elsewhere. Finally, two randomized versions of the MBR were generated, one having shuffled rows and the other by shuffling the entire matrix.

Structural alignment algorithm

We employed the Needleman–Wunsch algorithm (39) to test the usefulness of BEAR encoding combined with the MBR. The Needleman–Wunsch algorithm performs the global alignment of two sequences, requiring O(nm) time, where n and m represent the length of the input sequences. In our case, the input sequences are the BEAR encodings of two RNAs, thus only structural information is used to compute the alignment. Consequently, we modified the algorithm in order to let it take as input BEAR encodings along with nucleotide sequences.

Test data sets and algorithms

We built four different data sets to test the performance of our implementation of the Needleman–Wunsch algorithm based on the BEAR encoding and the MBR. We retrieved known RNA secondary structures from the RNA STRAND (40) and RNAspa data sets (41). RNA STRAND integrates information about known RNA secondary structure of any type and from different organisms retrieved from several public databases. Instead, RNAspa data set is a collection of curated secondary structures from Rfam.

Data sets of curated sequence alignments were retrieved from RNASTAR (42) and BRAliBase II (14). BRAliBase II is a collection of RNA alignment data sets proposed for benchmarking of alignment algorithms. Among the available data sets supplied by BRAliBase, we selected the data set 2 since it is the only one that includes pairwise alignments. RNASTAR includes refined Rfam alignments that were manually curated using structural information from the PDB (Protein Data Bank) (43). Since these curated data sets of alignments do not provide secondary structure annotation, we combined together structural data sets and secondary structure data sets to obtain a collection of curated alignments of known RNA structures. In particular, we used RNA STRAND secondary structure for RNASTAR alignments, RNAspa secondary structure for BRAliBase alignments and finally the remaining RNAs in RNAspa for Rfam alignments (Supplementary Table S3 in the Supplementary materials reports the number of RNAs and alignments in each data set).

Moreover, we randomly selected pairwise alignments from the RNA families, filtered and folded as described above (excluding those used to compute the substitution matrix), to create a fourth additional data set called RRS (Rfam Random Sampling).

We compared the results obtained using the Needleman–Wunsch + MBR with those obtained using other six alignment methods, namely a sequence-only version of the Needleman–Wunsch, as implemented in the ‘needle’ tool from the EMBOSS package (44), LocARNA (18), RNASTraT (25), RNAdistance and RNAforester (both included in Vienna package) and gardenia (24).

We used the sum-of-pairs score (SPS) (14) as a measure to evaluate the performances of the alignment methods. SPS is defined as the number of ‘correct pairs’ (pairs found in the reference alignment) over the total number of ‘predicted pairs’ (pairs found in the alignment computed by one of the tested algorithms), and it can be considered as a measure of the sensitivity of a pairwise alignment method. An SPS score of 0 indicates two completely different alignments; conversely, a score of 1 indicates an identical alignment.

Including sequence information into the structural alignment algorithm

A sequence similarity contribution can be included into the Needleman–Wunsch scoring function, by including sequence information in the function that fills in the dynamic programming matrix. In particular, we add a new term when moving from cell i-1,j-1 to i,j:

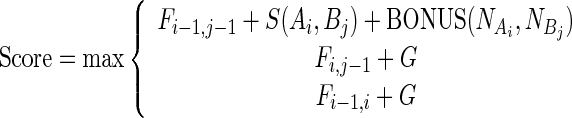where 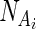and 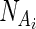identify the nucleotides associated with BEAR character in A_i and B_j, respectively. BONUS is a function assigning a positive score if N_A and N_B are identical:

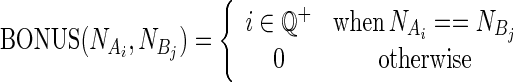where i can be any positive rational number. The higher the ‘bonus’, the more the sequence will influence the alignment. Different values for the i parameter were tested (Supplementary Figure S1), and the one leading to better alignment accuracy in all tested data sets was chosen.

Secondary structure recovery and structural distance

In order to verify the ability of MBR to recover secondary structure information, that is to say the ability of the method to correctly align conserved secondary structures, we computed the structural conservation index (SCI) (45) of the resulting pairwise alignments. SCI is defined as the ratio between the consensus minimum free energy (MFE) of the consensus alignment normalized by the average MFE or the single sequences:

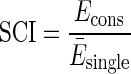We used RNAalifold in the Vienna package to compute the MFE for the consensus alignment and RNAfold for the individual sequences. Generally, SCI ranges from 0 to 1, where 0 indicates lack of structural conservation and 1 perfect structure conservation. The presence of compensatory mutations is interpreted as ‘bonus’ by the algorithm computing the consensus energy, in some cases leading to an SCI higher than 1. Other important factors influencing the SCI are the length of the alignments and non-compatible BPs.

Finally, we tested whether the MBR can be used to estimate the structural distance between two BEAR-encoded RNA secondary structures. We introduced a distance score based on the BEAR characters, defined as the weighted sum of the aligned pairs substitution scores, when both characters belong to a stem structure:

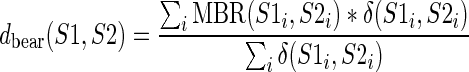where S1 and S2 are a pair of BEAR-encoded RNAs, 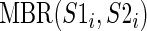is the MBR substitution score of the BEAR character in position i of each RNA and 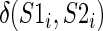is a function returning 1 if S1_i and S2_i belong to a stem structure; 0 otherwise. This score ranges from negative to positive values with no upper or lower limits. The lower the score, the more different are the structures compared, while positive values indicate similar structures. A score equal of 0 indicates that the two structures do not share sub-structures. We computed the Pearson correlation coefficient between this distance score and all distances computed by RNAdistance (namely weighted tree, weighted string, full tree, full string, HIT (Homeomorphically Irreducible Tree) tree and HIT string) and with that of RNAforester. As comparison, we also computed the Pearson correlation between the RNAdistance distances and the BP distance, defined as the fraction of BPs not shared by the two structures and reported in (45) to be a good measure of RNA structural distance.

RESULTS

Overview

We developed a new structure-aware encoding called BEAR for RNA secondary structure allowing the mapping of each nucleotide to the secondary structure it belongs to. Using this encoding, we analyzed the distribution and conservation of RNA SSEs in multiple alignments extracted from Rfam. By doing so, we highlighted regularities in the pattern of substitution rates between BEAR-encoded structure elements and showed that a substitution matrix that captures transition rates between SSEs (loop, stem, bulge and internal loop) can be computed. The MBR (Matrix of BEAR-encoded RNA secondary structures) represents tolerated changes in SSEs in related RNAs. We tested the approach analyzing the contribution of the MBR matrix in calculating RNA secondary structure alignments using a simple variant of the Needleman–Wunsch algorithm and obtained on different data sets results comparable to those obtained by other state-of-the-art methods (listed in the Materials and Methods section) which are computationally more complex. We propose that the BEAR encoding and the MBR matrix can be the basis for several kinds of RNA analyses (e.g. comparative, evolutionary and functional) and can additionally be included into the available more sophisticated methods and help them improving their performances.

The BEAR encoding

We developed a new encoding for the RNA secondary structure called BEAR. The BEAR encoding not only stores information about the ‘paired’ or ‘unpaired’ status of a nucleotide but also takes into account the SSE to which the nucleotide belongs. As a consequence, the BEAR encoding is a structure-aware representation. In BEAR, we introduce an alphabet in which each nucleotide is represented by a character that carries information about the length and type of the structural element the nucleotide belongs to (see the Materials and Methods section and Figure 1). With this new encoding, for example, an unpaired nucleotide in a loop and an unpaired nucleotide in a bulge are represented with different characters, making it possible and immediate to discriminate among them.

Analysis of secondary structure variation in subsets of the Rfam database

The Rfam database (13) classifies non-coding RNAs in families whose members possess a similar secondary structure, suggesting evolutionary relationships and similar functions. Rfam provides a consensus secondary structure for each family. We chose to use this information as a structural constraint to guide the secondary structure folding, as described in the Materials and Methods section.

After folding all the RNAs surviving a redundancy reduction in all Rfam families selected using criteria described in the the Materials and Methods section, we translated all the secondary structures into BEAR encoding. Then, we looked for trends in SSE types and sizes, and their variation within families. Since Rfam stores families of structurally related RNAs, likely to be functionally related and homologous, we ran quantitative analysis on Rfam in order to find global rules shared among RNAs that could help in the characterization of their secondary structures with the aim of measuring in statistical terms how these structural elements differ in related RNAs.

We focused on the distributions of the length of the secondary structure basic elements defined in the BEAR algorithm, namely loops, stems, bulges and interior loops. First, we extracted information about the length of stems, loops and interior loops, for every RNA in Rfam (Figure 2A). Then, we counted the number of transitions from an RNA sub-structure to another of the same type but with different length for each aligned RNA sequence pair in Rfam (e.g. from a stem of length 1 to a stem of length 3, in all combinations found). The results of this analysis (Figure 2B) highlight an inverse relationship between the length variation in each class of SSEs and its frequency in the data set of RNA alignments. This relation is somehow expected (i.e. related RNAs are more likely to contain similar SSEs having comparable size), but has never been exploited so far to gain a better performance in an RNA alignment. These observations suggest that within an RNA family, extension or shortening of sub-structures is tolerated to a certain extent, and the larger the length variation, the smaller is its observed frequency. On the other hand, transitions from one type of SSE to a different one (e.g. from a stem to a loop, from a loop to an interior loop and so on) can occur but are more rarely observed (Supplementary Table S4).

MBR substitution matrix

The results described in the previous paragraph proved the possibility of extracting general information about RNA structure variation in related RNA families that can be used to compare RNA secondary structures, by calculating the frequency of transitions from an RNA structure to another. Computing such kind of transition frequencies between SSEs would allow the creation of a structural substitution matrix, similar in principle to those that are broadly used to compute DNA/RNA and protein sequence alignments, but based in this case on variations not at the primary but at the secondary structure level. Similar approaches have been successfully applied on proteins. With reference to this, the work of Ku and Hu (46) is particularly interesting because, after encoding the protein secondary structure as fragments of the protein backbone defined in terms of phi and psi dihedral angles, they computed a substitution matrix of protein structural elements, called TRISUM, using a self-training strategy.

We created a substitution matrix called MBR (Matrix of BEAR-encoded RNA) using a subset of Rfam families; in particular, we chose those families characterized by a high number of SSEs (Supplementary Table S2). Members of the selected families were folded using a constrained approach as described in the Materials and Methods section. We used the new BEAR codification to determine transition rates among secondary sub-structures belonging to the same or to different RNA structural elements aligned in the same family of homologous sequences. The MBR is computed, following the classic Dayhoff approach (28), as log-odds scores, by normalizing the observed frequency of transition between two elements by the expected transition frequency, obtained as the product of the frequencies of the two elements in the data set. Substitution frequencies were computed in MBR for all BEAR characters representing different structural elements (stems, loops, bulges and interior loops) and their lengths, for all branching and non-branching structures. A color-coded representation of the MBR is shown in Figure 4. The full MBR is available in the Supplementary materials.

Figure 4.

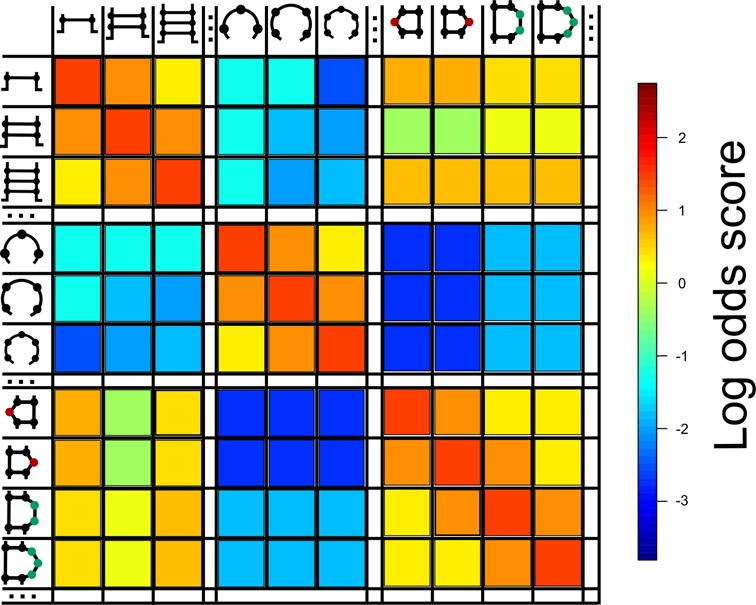
Graphical representation of the MBR. This figure shows a subset of rows/columns of the MBR matrix, using a color-coding to show substitution rate patterns: color scale represents log-odds scores from lower (blue) to higher (red). Rows and columns are elements of RNA secondary structure of different length and every cell stores the log-odds value for the substitution of one element with another element. The cells in the principal diagonal always have the highest value in the respective row and column. Substitutions between elements belonging to the same group (i.e. stems, loops and interior loops) display higher log-odds values than substitutions between elements belonging to different groups. The ‘…’ notation indicates that some rows/columns were omitted from the graphical matrix representation.

Using the MBR to align RNA structures

As stated before, the substitution frequencies in MBR capture the type and amount of structural variation that structurally similar, homologous and/or functionally related RNAs can tolerate. Therefore, among other applications, MBR rates can be used to align the SSEs of two related RNAs encoded using the BEAR representation, in a similar way in which amino acid or nucleotide substitution matrices are used to align two protein or RNA primary sequences. This approach can improve many RNA analyses such as clustering, phylogeny and sequence alignments. We decided to test the reliability of the information obtained with the BEAR encoding by performing pairwise RNA structural alignments. As described in the the Materials and Methods section, we decided to employ the simplest way to align strings of characters and used a modified version of the Needleman–Wunsch algorithm capable to handle the MBR to obtain a global alignment of two BEAR-encoded RNAs. In order to check the consistency of the proposed encoding and associated substitution matrix, we created four different control matrices: (i) a ‘positive diagonal’ matrix (all identical BEAR characters are given the same positive score, which is identical and negative for all other character pairs); (ii) a ‘positive group’ matrix (all BEAR characters denoting the same type of SSE, e.g. a stem, are given the same positive score, which is identical and negative for character pairs belonging to different groups); (iii) an MBR with randomized rows; (iv) an MBR with randomized rows and columns. The performances of these control matrices were compared to that of the full MBR. The purpose of the first two control matrices was to show the increase of the performances with the increase of the structural information carried by the matrix. Specifically, using the positive diagonal matrix, two equal BEAR characters are preferentially paired with respect to other characters, while the pairing of different BEAR characters is penalized. Using the positive group matrix, all the characters encoding for the same RNA sub-structure, even if they belong to SSEs of different length, are preferentially paired; the pairing between groups of SSEs is penalized (i.e. the association of residues belonging with stems of different length is positively scored, while a pairing between a residue in a stem and a residue in a loop is penalized). We expected this matrix to perform better than the positive diagonal matrix.

The two randomized matrices were intended to confirm the consistency of the scores in the MBR: by randomizing the scores in the MBR we added different degrees of disorder depending on the type of randomization. We tested the four control matrices and the full MBR on a data set created by sampling the Rfam database by randomly extracting pairwise alignments from the seed multiple alignment of randomly selected families (excluding those used to calculate the MBR), denoted from now on RRS (Rfam Random Sampling). Figure 5 shows the results of the test, measured as the fraction of aligned nucleotides in the reference alignment that are correctly aligned by the tested algorithm (SPS). As expected, the performance of the positive group matrix (second bar in the plot) is higher than that obtained with the positive diagonal matrix (first bar), because of the higher level of information. By contrast, the randomized matrices show poorer performances; in particular, the per-row-randomized MBR (third bar) performs better than the entirely randomized MBR (fourth bar), supporting the consistency of the scores in the MBR original matrix.

Figure 5.

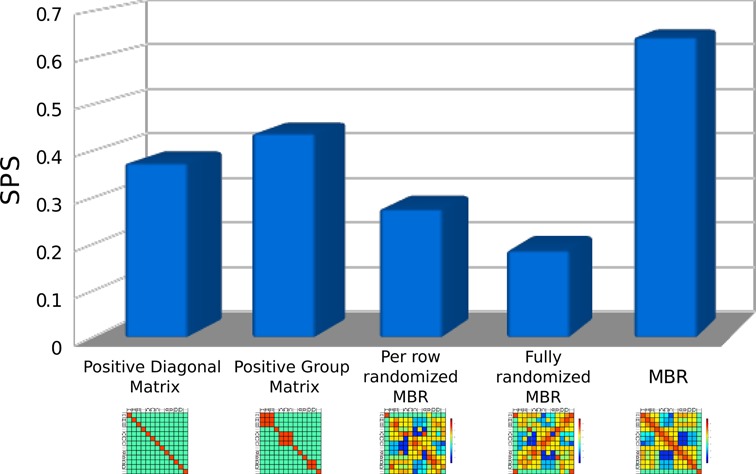
Alignment performances using different types of matrices. The MBR and four other different matrices are used to align the structures of pairs of RNAs sampled from Rfam using an implementation of the Needleman–Wunsch algorithm able to receive as input the BEAR encoding. ‘Positive diagonal’ is a matrix where a positive score is assigned to identical characters, and a negative score everywhere else. ‘Positive group’ is a matrix where a positive score is assigned between elements of the same type of RNA SS, and a negative one everywhere else. ‘Per row randomized MBR’ and ‘Fully randomized MBR’ are matrices built using randomized values of the MBR. More details can be found in the main text. The fifth column shows the performance of the MBR matrix, without the sequence BONUS. Sum-of-pairs (SPS), which is the fraction of correctly aligned nucleotide pairs, is used as quality measure.

Comparison with other methods for the pairwise RNA alignment on data sets with curated structure information

To assess the contribution of reliable secondary structures in correctly aligning RNAs, we created three additional data sets where alignments were curated using structural knowledge. By cross-referencing RNA secondary structure repositories and curated alignments, we created three RNA alignment data sets in which the alignments were manually curated and/or revised, and the RNA secondary structures were experimentally determined or manually curated as well. We also included the above-mentioned RRS data set that we used to test the different types of matrix.

We compared our results with those from other five RNA structure-based alignment algorithms, namely LocARNA (18), RNAStrAT (25), gardenia (24), RNAforester and RNAdistance, and with those from the sequence-based Needleman–Wunsch algorithm (‘needle’). Despite all the methods (except ‘needle’) use structural information to compute the alignments, they are based on different approaches. In particular, gardenia, RNASTraT, RNAdistance and RNAforester use a tree-based approach, while LocARNA works by folding and aligning simultaneously the input sequences. All the algorithms (except ‘needle’) were fed with the curated secondary structures or (in the case of RSS) with the sequence folded using conservation constraints. In the case of LocARNA, these input structures are only used to compute the partition function from which the algorithm computes the best consensus structure for the input sequences. In this aspect, LocARNA behaves differently from the other tested methods. By using only primary sequence information, ‘needle's’ results helped us in discriminating the sequence and structural contribution in reconstructing the alignment. Nevertheless, even in cases where two RNAs share a very similar secondary structure and a less similar sequence, which can frequently happen since the secondary structure evolves more slowly than the primary (9), yet the primary sequence can help in obtaining a better alignment, especially in unstructured regions. For this reason, our algorithm can additionally use a numeric ‘bonus’ to include primary sequence information by favoring the alignment of identical nucleotides, without increasing the algorithm complexity. To find the optimal value for this ‘bonus’, we tested all the data sets varying the bonus weight from 0 to 1.1 (Supplementary Figure S1) and checked how it affects the alignment accuracy. When performances increase as the ‘bonus’, sequence information has a positive contribution on the alignment. Even if the optimal ‘bonus’ varies in the different tested data sets, we selected the value (0.1) that offers the best overall accuracy, and used it for all the following tests.

Figure 6A shows the comparison of the performances of the five programs on the above-mentioned data sets, measured as the fraction of aligned nucleotides in the reference alignment that are correctly aligned by each method. In general, the alignments obtained using the Needleman–Wunsch algorithm on the BEAR encoding using the MBR are of similar quality, in some instances better than those of the other considered methods. Results clearly show that the performances strictly depend on the characteristic of the data set used. The BRAliBase data set contains only transfer RNAs, which are known to have a more conserved secondary than primary structure (47) and, as a consequence, all the programs except ‘needle’ show approximately the same good performances. The RNAspa and RNA STRAND data sets contain different types of RNAs but show the same trend as before. The low performance of gardenia on the RNA STRAND data set is likely due to non-canonical secondary structures stored in RNASTAR database that we used to annotate RNAs in RNA STRAND. For example, some RNAs stored in the RNASTAR database do not follow the general constraints assumed by many algorithms such as hairpins missing the loop, and gardenia seems negatively affected by such inconsistencies, as opposed to the other tested algorithms.

Figure 6.

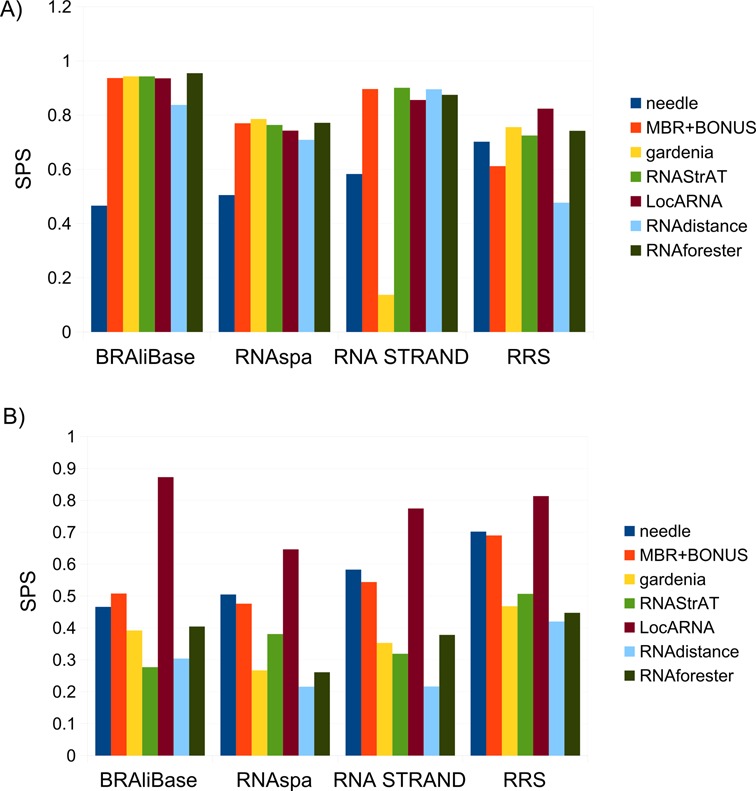
(A) Alignment performance of the seven tested methods on the four different data sets. We evaluated seven different alignment methods, from left to right: a sequence-based Needleman–Wunsch (needle), our modified Needleman–Wunsch using the MBR including the sequence BONUS (MBR+BONUS), then gardenia, RNAStrAT, LocARNA, RNAdistance and RNAforester. All methods were tested on the four employed data sets; (B) Alignment performance of the five tested methods when secondary structures are predicted using RNAfold.

RRS shows different characteristic when compared with the other data sets. In particular, there is little difference between the performances of ‘needle’ over the structural methods. There are two main reasons that can explain this result: first, Rfam contains multiple sequence alignments calculated using only primary sequence information; second, this is the only data set with no curated secondary structures. The results from RNAspa and RNA STRAND support the two previous hypotheses considering that both use Rfam alignments but ‘needle’ has lower performances than the other methods, suggesting that not all the Rfam alignments rely on the secondary structure and that it is sometimes difficult to correctly fold Rfam family members even when using conservation constraints. In contrast, RNAspa integrates Rfam with curated secondary structures, and RNA STRAND also takes advantage of curated secondary structures as well as curated Rfam alignments using known RNA 3D structures extracted from the PDB.

These results imply that structural information alone, or augmented using little primary sequence information, is sufficient for correctly aligning RNAs and that the BEAR encoding and the resulting MBR matrix are able to capture structural similarities between RNAs. As expected, when the RNA secondary structure is predicted de novo (using RNAfold) we witnessed a general performance drop for all structure-based methods (Figure 6A), which often are less accurate than the ‘needle’ sequence alignments. Hence, predicted secondary structures supply wrong information leading to poor alignments. LocARNA seems less affected by imprecise secondary structures, likely because it computes a consensus folding structure for the two input sequences while aligning them. In other words, LocARNA does not use the same structures used by other methods, even if these structures were provided to the algorithm.

To further prove the importance of secondary structure information in obtaining correct alignments, we tested the alignment accuracy at different levels of sequence identity. We merged the BRAliBase, RNA STRAND and RNAspa data sets and divided the resulting data set into sequence identity bins, by computing the sequence identity of the reference alignments. All the sequences having less than 50% identity were grouped together into one bin. Results (Figure 7) show that our approach and RNAforester provide the best performances when the identity is smaller than or equal to 50%. On the contrary, LocARNA is the most accurate when identity is higher than 50%. Likely, the main reason of the LocARNA alignment accuracy decrease at low sequence identity is that the lower the identity, the less reliable are the structures computed by LocARNA during the folding and aligning step. On the same lines, we verified whether the alignment accuracy is dependent on how similar in length are the two input sequences. We first computed the correlation between the length of the input sequences and that of their curated alignment, to assess how much heterogeneous in length are the sequences in the alignments in our data sets. In particular, given two aligned sequences, we verified that there is no correlation (Pearson r = 0.05) between the absolute difference of their lengths and the difference between the length of their alignment and that of the longer sequence, indicating that the input sequences length difference is not related to how much ‘complex’ the alignment is. Then, we computed, for all the tested methods, the average alignment SPS at different levels of size difference between the two input sequences (Table 1), observing, for our method, no correlation (Pearson r = −0.05), meaning that the reconstructed alignment accuracy does not depend on how similar the length of the RNAs is. In contrast, for all the other tested methods, the more similar in size are the input sequences, the more accurate is the reconstructed alignment compared to the reference one.

Figure 7.

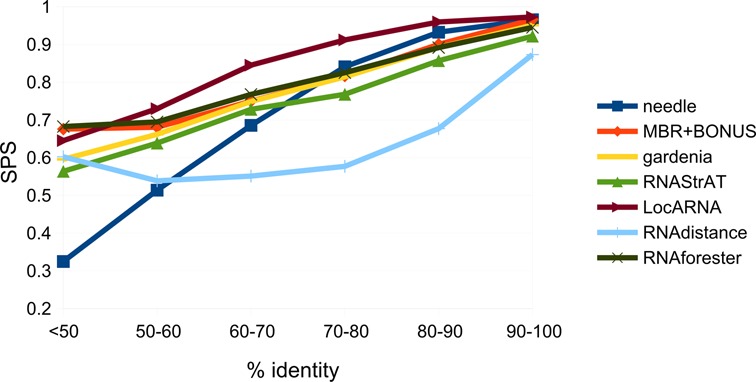
Alignment performance at different levels of sequence identity. The curated reference alignments were divided into bins at different levels of sequence identity, and the alignment accuracy (evaluated as SPS) is reported for each bin for all the employed alignment algorithms. All alignments having identity lower than 50% were grouped in the same bin.

Table 1.

Pearson correlation between alignment SPS and length difference of the input sequences

	Pearson correlation
needle	−0.37
MBR+BONUS	−0.05
gardenia	−0.42
RNAStrAT	−0.10
LocARNA	−0.58
RNAdistance	0.13
RNAforester	−0.13

Ultimately, in order to compute the structural accuracy of each method, that is to say how well each method is able to capture structural information within the sequences and exploit it for a correct alignment, we computed the SCI. SCI is defined as the ratio between the MFE of the ‘consensus’ alignment and the mean MFE of the input sequences. An SCI close to 1 means that the alignment captured the structural characteristics of the input sequences. We divided the reference alignments from the RNAspa, RNA STRAND and BRAliBase data sets into sequence identity bins and then computed the mean SCI score for each bin (Figure 8), first for the reference alignments (the light green curve) and then for each of the tested methods. Results show how, in general, all the methods are equally able to recover secondary structure information and that, even with a coarse implementation of the Needleman–Wunsch algorithm, our method shows results comparable to those of the state-of-the-art. As expected, SCI scores obtained when the sequence identity is low are higher than those computed at high sequence identity, indicating a stronger structural influence. LocARNA and gardenia show a different trend compared with other methods because their SCI scores are in some cases higher than the SCI of the reference alignments. In the case of gardenia, this is likely due to random fluctuations caused by a smaller number of alignments in each bin compared to other methods, given the already discussed problems with non-canonical secondary structures. In the case of LocARNA, the SCI calculation is likely biased by its approach for computing alignments. Indeed, align-and-fold approach explores the partition function matrix looking for the best common secondary structure for the two input sequences and therefore leads to the maximization of the numerator of the SCI score function. As a consequence, with low sequence identity the SCI score is always higher than 1 and also higher than the reference; with higher sequence identity the score returns lower than the reference score.

Figure 8.

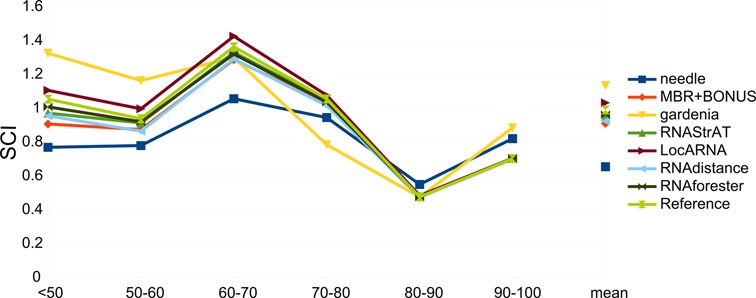
Structural conservation index (SCI) at different levels of sequence identity. All the data sets annotated with secondary structure information were divided into sequence identity bins, and the mean SCI score for each bin is reported for all tested methods.

Using BEAR and the MBR as a measure of RNA structural distance

The BEAR encoding and the MBR can capture tolerated structural divergence between related RNAs. As such, it can in principle be used for evaluating the structural distance between RNAs. We introduced a distance measure based on the BEAR characters, defined as the weighted sum of the aligned pairs substitution scores. This score can be either positive, indicating two structures having similar structural elements that in the MBR have high substitution scores, or negative, indicating structures with low scoring elements substitutions. Then, we computed the Pearson correlation coefficient between this metric and all distances computed by RNAdistance (namely weighted tree, weighted string, full tree, full string, HIT tree, HIT string) and with that of RNAforester. As comparison, we also computed the Pearson correlation between the RNAdistance distances and the BP distance, defined as the number of base pairs not shared by the two structures and reported in (45) to be a good measure of RNA structural distance (Supplementary Figure S2). Results show that the distance based on BEAR is highly correlated with the BP distance, but these two metrics show little correlation between all the distances computed using RNAdistance and RNAforester. Among different metric measuring conservation of RNA secondary structure, BP distance is one of the most accurate (45). Hence, the high correlation between BP metric and BEAR metric suggests the reliability and the potential of the latter. Indeed, BP distance simply counts the number of brackets facing each other in the alignments while BEAR metric is also able to quantify how similar are the structural elements whose brackets belongs to. These results suggest that BEAR- and MBR-based distances can provide good estimates of structural similarity and divergence.

DISCUSSION

The issue of taking into account secondary structure in RNA alignments is a pressing one, given the higher divergence rates of RNA sequence with respect to its structure. This problem was approached before, with different degrees of success, by a number of usually complex algorithms. These methods, additionally, are in general not based on models of RNA structural evolution and cannot be extended to large-scale analysis. The BEAR encoding and the MBR, on the other hand, represent a way to capture, in a rigorous and quantitative form, how structural variation is tolerated in functionally related RNAs. By means of testing the MBR to align RNAs we demonstrated the efficacy of the approach that, even with a very simple implementation and using little sequence information, can already provide accurate structural alignments. Our algorithm has the smallest complexity and fastest running time of all the tested methods (Table 2). From this starting point, more accurate algorithms can be developed, as well as other algorithms to compute, for example, local or multiple alignments. The simplicity and effectiveness of the MBR approach make it suitable for large-scale applications, such as finding the more structurally similar RNA in large collections of RNAs given a query. Tasks such as classification of RNAs into families are also approachable. A major focus is certainly to identify recurring patterns of local secondary structures, in order to characterize collections of un-annotated RNAs. For example, recent techniques to detect protein–RNA interactions, such as CLIP-seq or PAR-clip (48,49), often highlight large numbers of RNAs sharing the same function (i.e. binding the same protein partner), but the identification of the interaction motif, which can be encoded (partially or totally) in the structure, is often non-trivial.

Table 2.

Computational complexity and running times of the tested algorithms

	Computational complexity	Running time (s)
		BRAliBase	RNAspa	RNA STRAND	RRS
needle	O(n∧2)	1.2	19.8	32.6	105.9
MBR+BONUS	O(n∧2)	0.4	4.1	1.7	12.6
gardenia	O(n∧4)	1.2	36.4	20.8a	327.1
RNAStrAT	O(n∧4)	2.3	630.2	1498.3	11403.4
LocARNA	O(n∧2(n∧2+m∧2))	2.2	166.5	64.5	982.3
RNAdistance	O(n∧3)	1.2	19.9	32.7	109.7
RNAforester	O(|F1|*|F2|*deg(F1)*deg(F2)*(deg(F1)+deg(F2))b	3.3	1460	2654	2 days

For each data set, the running time (computed on a Intel® Core™ i7–2600K CPU @3.40 GHz with 16GB RAM) is reported in seconds employed to process the whole data set. The modified Needleman–Wunsch algorithm that can take as an input BEAR strings and can use the MBR as a substitution matrix was implemented in Java.

^aAn output alignment was produced for only 70% of the total input.

^b|Fi| is the number of nodes in the forest Fi; deg(Fi) is the degree of Fi.

Finally, the BEAR encoding is not only suitable for substitution matrix-like approaches but computational linguistics techniques could be applied to it as well. Such kind of approaches could not be applied to secondary structure described using the dot-bracket notation or a tree-based representation, while it perfectly fits into an informative string of characters like in BEAR. The final goal is to find signal and stretches of characters that could be used to classify and annotate RNAs.

We provide a novel way to tackle all these issues, by releasing to the scientific community the MBR (in the Supplementary materials) and the software to compute the BEAR encoding given the secondary structure (available upon request) that can be the basis for the development of new methods but that can also be seamlessly integrated in existing methods to help them improve their performances.

AVAILABILITY

The program that encodes RNA secondary structure using the BEAR alphabet can be freely downloaded at http://bioinformatica.uniroma2.it/BEAR/BEAR_Encoder.zip.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Programmi di Ricerca di rilevante Interesse Nazionale (PRIN) 2010 [prot. 20108XYHJS_006 to M.H.C.]. Funding for open access charge: Epigenomics Flagship Project (EPIGEN) MIUR-CNR.

Conflict of interest statement. None declared.