Understanding Classrooms through Social Network Analysis: A Primer for Social Network Analysis in Education Research

The authors introduce basic concepts in SNA, along with methods for data collection, data processing, data analysis, and conduct analyses of a study relationship network. Also covered are generative processes that create observed study networks and practical issues, such as the unique aspects of human subjects review for network studies.

Abstract

Social interactions between students are a major and underexplored part of undergraduate education. Understanding how learning relationships form in undergraduate classrooms, as well as the impacts these relationships have on learning outcomes, can inform educators in unique ways and improve educational reform. Social network analysis (SNA) provides the necessary tool kit for investigating questions involving relational data. We introduce basic concepts in SNA, along with methods for data collection, data processing, and data analysis, using a previously collected example study on an undergraduate biology classroom as a tutorial. We conduct descriptive analyses of the structure of the network of costudying relationships. We explore generative processes that create observed study networks between students and also test for an association between network position and success on exams. We also cover practical issues, such as the unique aspects of human subjects review for network studies. Our aims are to convince readers that using SNA in classroom environments allows rich and informative analyses to take place and to provide some initial tools for doing so, in the process inspiring future educational studies incorporating relational data.

INTRODUCTION

Social relationships are a major aspect of the undergraduate experience. While groups on campus exist to facilitate social interactions, the classroom is a principle domain wherein working relationships form between students. These relationships, and the larger networks they create, have significant effects on student behavior. Network analysis can inform our understanding of student network formation in classrooms and the types of impacts these networks have on students. This set of theoretical and methodological approaches can help to answer questions about pedagogy, equity, learning, and educational policy and organization.

Social networks have been successfully used to test and create paradigms in diverse fields. These include, broadly, the social sciences (Borgatti et al., 2009), human disease (Morris, 2004; Barabási et al., 2011), scientific collaboration (Newman, 2001; West et al., 2010), social contagion (Christakis and Fowler, 2013), and many others. Network analysis entails two broad classes of hypotheses: those that seek to understand what influences the formation of relational ties in a given population (e.g., having the same major, having relational partners in common), and those that consider the influence that the structure of ties has on shaping outcomes, at either the individual level (e.g., grade point average [GPA] or socioeconomic status) or the population level (e.g., graduation rates or retention in science, technology, engineering, and mathematics [STEM] disciplines). A growing volume of research on social influences at the postsecondary level exists, examining outcomes such as overall GPA and academic performance (Sacerdote, 2001; Zimmerman, 2003; Hoel et al., 2005; Foster, 2006; Stinebrickner and Stinebrickner, 2006; Lyle, 2007; Carrell et al., 2008; Fletcher and Tienda, 2008; Brunello et al., 2010), cheating (Carrell et al., 2008), drug and alcohol use (Duncan et al., 2005; DeSimone, 2007; Wilson, 2007), and job choice (Marmaros and Sacerdote, 2002; De Giorgi et al., 2009). The impacts are often significant, perhaps not surprisingly; this research has many implications, including the importance that randomly determined relationships such as roommate or lab partner can have on undergraduates’ behavioral choices and, consequently, their college experiences.

One key direction for education researchers is to study network formation within classrooms, in order to elucidate how the realized networks affect learning outcomes. Network analysis can give a baseline understanding of classroom network norms and illuminate major aspects of undergraduate learning. Educators interested in changing curriculum, introducing new teaching methods, promoting social equity in student interactions, or fostering connections between classrooms and communities can obtain a more nuanced understanding of the social impacts different pedagogical strategies may have. For example, we know active learning is effective in college classrooms (Hake, 1998; O’Sullivan and Copper, 2003; Freeman et al., 2007; Haak et al., 2011), but the full set of causal pathways is unclear. Perhaps one important change introduced by active learning is the facilitation of student networks to be stronger, less centralized, or structured in some other new way to maximize student learning. Social network analysis (SNA) can help us assess these types of hypotheses.

Recent research in physics education has found that a student's position within communication and interaction networks is correlated with his or her performance (Bruun and Brewe, 2013). An informal learning environment was found to be facilitative in mixing physics students of diverse backgrounds (Fenichel and Schweingruber, 2010; Brewe et al., 2012). However, these exciting initial steps into network analysis in STEM education still leave many hypotheses to explore, and SNA provides a diverse array of tools to explore them.

The goal of this paper is to enable and encourage researchers interested in biology education, and education research more generally, to perform analyses that use relational data and consider the importance of learning relationships to undergraduate education. In doing so, we first introduce some of the many basic concepts and terms in SNA. We outline methods and concerns for data collection, including the importance of gaining approval from your local institutional review board (IRB). We briefly discuss a straightforward way to organize data for analysis, before performing a brief analysis of a classroom network along three avenues: descriptive analysis of the network, exploration of network evolution, and analysis of network position as a predictor of individual outcomes. This paper is aimed at serving as an initial primer for education researchers rather than as a research paper or a comprehensive guide. For the latter, see Further Resources, where we provide a list of additional resources.

INTRODUCTION TO THE CASE STUDY

In introducing network analysis, we draw our example from a subset of a 10-wk introductory biology course with 187 students who saw the course to completion as an example. Each student in this course attended either a morning or afternoon 1-h lecture of ∼90 students four times a week and attended one of eight student labs of ∼24 students each, which met once a week for 3 h and 20 min. This course used a heavy regimen of active learning, including a significant amount of guided student–student interaction in both lecture and lab. The total percentage of active-learning activities used in this lecture course was greater than 65% of classroom time, including audience response–device questions. The data we collected included who students studied with for the first three exams, all of their class grades, the lecture and lab sections to which they belonged, and general demographic information from the registrar.

Network Concepts

In this section, we lay out some of the foundations of SNA and introduce concepts and measurements commonly seen in network studies.

Social Network Basics.

SNA aims to understand the determinants, structure, and consequences of relationships between actors. In other words, SNA helps us to understand how relationships form, what kinds of relational structures emerge from the building blocks of individual relationships between pairs of actors, and what, if any, the impacts are of these relationships on actors. Actors, also called nodes, can be individuals, organizations, websites, or any entity that can be connected to other entities. A group of actors and the connections between them make up a network.

The importance of relationships and emergent structures formed by relationships makes SNA different from other research paradigms, which often focus solely on the attributes of actors. For example, traditional analyses may separate students into groups based on their attributes and search for disproportional outcomes based on those attributes. A social network perspective would focus instead on how individuals may have similar network positions due to shared attributes. These similar network positions may present the same social influences on both individuals, and these social influences may be an important part of the causal chain to the shared outcome. In situations in which a presence or absence of social support is suspected to be important to outcomes of interest, such as formal learning within a classroom, the SNA paradigm is appealing.

Network Types.

One way to categorize networks is by the number of types of actors they contain. Networks that consist of only one type of actor (e.g., students) are referred to as unipartite (or sometimes monopartite or one-mode). While not discussed in detail here, bipartite (or sometimes two-mode) networks are also possible, linking actors with the groups to which they belong. For example, a bipartite network could link scholars to papers they authored or students to classes they took, differing from a unipartite network, which would link author to author or student to student.

Networks can also be categorized by the nature of the ties they contain. For example, if ties between actors are inherently bidirectional, the network would be referred to as undirected. A network of students studying with one another is an example of an undirected network; if student A studies with student B, then we can be certain that student B also studied with student A, creating an undirected tie. If the relational interest of a network has an associated direction, such as student perceptions of one another, then it is referred to as a directed network; if student A perceives student B as smart, it does not imply that student B perceives student A as smart; without the latter, we would have one directed tie from A to B.

Ties can also be binary or valued. Binary ties represent whether or not a relation exists, while valued ties include additional quantitative information about the relation. For example, a binary network of student study relations would indicate whether or not student A studied with student B, while a valued network would include the number of hours they studied together. Binary networks are simpler to collect and analyze. Valued networks include a trade-off of more information in the data versus increased analytical and methodological complexity. Using the example of a study network, the added complexity of valued networks would allow an investigation regarding a threshold number of study hours necessary for a peer impact on learning gains, while a binary network would treat any amount of study time with a peer equally.

Network Data Collection.

Collecting network data requires deciding on a time frame for the relationships of interest. Real-world networks are rarely static; ties form, break, strengthen and weaken over time. At any given time, however, a network takes on a given cross-sectional realization. Network data collection (and subsequent analyses) can be categorized, then, by whether it considers a static network, a cross-sectional realization of an implicitly dynamic network, or an explicitly dynamic network. The last of these may take the form of multiple cross-sectional snapshots or of some form of continuous data collection. Measuring and analyzing dynamic networks introduces a host of new challenges. Because the set of actors in a classroom population is mostly static for a definite period of time (i.e., a semester or quarter), while the relational ties among them may change over that period, all three options are feasible in this setting. The type of collection should, of course, be driven by the research question at hand. For example, our interest in the evolution of study networks inspired a longitudinal network collection design. Examining the impact of network ties on subsequent classroom performance, on the other hand, could be done with a single network collection.

Beyond considering the time frame of collection, it is also important to consider how to sample from a population. Egocentric studies focus on a sample of individuals (called “egos”) and the local social environment surrounding them without explicitly attempting to “connect the dots” in the network further. Typically, respondents are asked about the number and nature of their relationships and the attributes of their relational partners (called “alters”). In some fields, the term “egocentric data collection” implies that individual identifiers for relational partners are not collected, while in other fields this is not part of the definition. By either definition, egocentric studies tend to be easier to implement than other methods, both in terms of data collection and ethics and human subjects review. Egocentric data are excellent first descriptors of a sample and, in many situations, may be the only form of data available. A wide range of important hypotheses can be tested using egocentric data, although questions about larger network structure cannot. Asking a sample of college freshmen to list friends and provide demographic information about each friend listed would represent egocentric network collection.

At the other end of the spectrum, census networks, sometimes referred to as whole networks, collect data from an entire bounded population of actors, including identifiable information about the respondents’ relational partners. These alters are then identified among the set of respondents, yielding a complete picture of the network. This results in more potential hypotheses to be tested, due to the added ability to look at network structures. In our classroom study, we asked students to list other students in that same classroom with whom they studied; this is an example of a census network whose population is bounded within a single classroom.

High-quality census networks are rare, due to the exhaustive nature of the data collection, as well as the need for bounding a population in a reasonable way. It is worth noting that census networks may lack information on potentially influential relations with actors who are not a part of the population of interest; for example, important interactions between students and teaching assistants will be absent in a census network interested in student–student interactions, as would any students outside the class with whom students in the class studied. In the case of longitudinal studies, an added challenge arises—handling students who withdraw from the class or who join after the first round of data collection has been conducted. Census data collection also presents a nonresponse risk, which may result in a partial network. Nonresponse is more acute in complete network studies than other kinds of data collection because many of the commonly used analytical methods for complete networks consider the entire network structure as an interactive system and assume that it has been completely observed. Educational environments such as classrooms are fairly well bounded and have unique and important cultures between relatively few actors; they are thus prime candidates for census data collection, although the above issues must still be attended to.

Network Level Concepts and Measures.

Network analysis entails numerous concepts and measurements absent in more standard types of data analyses. Perhaps the most basic measurement in network analysis is network density. The density of a network is a measurement of how many links are observed in a whole network divided by the total number of links that could exist if every actor were connected to every other actor. These measurements are frequently small but vary by the type and size of the network. Density measurements are often hard to interpret without comparable data from other similar networks.

Density is a global metric that simply indicates how many ties are present. A long list of network concepts are further concerned with the patterns of who is connected with whom. One pervasive concept in the latter realm is homophily (McPherson et al., 2001), a propensity for similar actors to be disproportionately connected in a relation of interest. If we are interested in who studies with whom, and males disproportionately studied with other males and females with other females, this would exemplify some level of homophily by gender. Likewise, we could see homophily by ethnicity, GPA, office-hours attendance, or any other characteristic that can be the same or similar between two students. Understanding and researching homophily in classroom and educational networks may be central for several reasons. For example, two reasonable hypotheses are that relationships of social support in classrooms are more likely to be seen between students with similar backgrounds and that having sufficient social support is important for STEM retention. Testing these hypotheses by looking for homophily in networks with relation to STEM retention would provide valuable information regarding the lower STEM retention rates of underrepresented groups. Confirming these hypotheses, then, would inform improved classroom behavioral strategies for educators to emphasize.

Finding a pattern of homophily for certain research questions is interesting on its own. Note, however, that a pattern of homophily can emerge from multiple processes. Two examples of these are social selection and social influence. Social selection occurs when a relationship is more likely to occur due to two actors having the same attributes, while social influence occurs when individuals change their attributes to match those of their relational partners, due to influence from those partners. As an example, we can imagine a hypothetical college class in which a network of study partners reveals that students who received “A's” disproportionately studied with other students receiving “A’s.” If “A”-level students seek out other “A”-level students to study with, this would be social selection; if studying with an A-level student helps raise other students’ grades, this would be social influence. Depending on the goals of a study, disentangling between these two possibilities may or may not be of interest. Doing so is most straightforward when one has longitudinal data, so that event sequences can be determined (e.g., whether student X became an “A” student before or after studying with student Y).

Analyzing ties between two individuals independently, such as in studies of homophily, falls into the category of dyad-level analysis. When one has a census network, however, analysis at higher levels such as triads is possible. Triads have received considerable interest in network theory (Granovetter, 1973; Krackhardt, 1999) due to their operational significance. Triads are any set of three nodes and offer interesting structural dynamics, such as one node brokering the formation of a tie between two other nodes, or one node acting as a conduit of information from one node to the other. One version of classifying triads in an undirected network (commonly called the undirected Davis-Leinhardt triad census) is shown in Figure 1.

Figure 1.

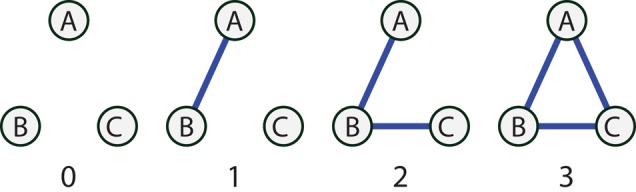
Davis and Leinhardt triad classifications for undirected networks.

In a study network, a class exhibiting many complete triads may indicate a strong culture of group study compared with a class that exhibits comparatively few complete triads. One way to examine this would be a triad census—a simple count of how many different triad types exist in a network. Another way to measure this would be to look at transitivity, a value representing the likelihood of student A being tied to C, given that A is tied to B and B is tied to C. Transitivity is a simple, local measure of a more general set of concepts related to clustering or cohesion, which may extend to much larger groups beyond size three.

In directed networks, transitivity can take on a different meaning, pointing to a distinct pair of theoretical concepts. When three actors are linked by a directed chain of the form A→B→C, then there are two types of relationships that can close the triad: either A→C or C→A (or, of course, both). The first option creates a structure called a transitive triad, and the latter a cyclical triad. For many types of relationships (i.e., those involving giving of goods or esteem), a preponderance of transitive triads is considered an indicator of hierarchy (with A always giving and C always receiving), while a preponderance of cyclical triads is an indicator of egalitarianism (with everyone giving and everyone receiving). If asking students about their ideal study partners, the presence of transitive triads would reflect a system wherein students agree on an implicit ranking of best partners, presumably based on levels of knowledge and/or helpfulness. Cyclic triads (as well as other longer cycles) would be more likely to appear if students believed that other factors mattered instead or as well; for instance, that it is most useful to study with someone from a different lab group or with a different learning style so as to maximize the breadth of knowledge.

Actor-Level Variables.

Nodes within a network also have their own set of measurements. These include the exogenously defined attributes with which we are generally familiar (e.g., age, race, major), but they also include measures of position of nodes in the network. Within the latter, a widely considered cluster of interrelated metrics revolves around the concept of centrality. Several ways of measuring centrality have been proposed, including degree (Nieminen, 1974), closeness (Sabidussi, 1966), betweenness (Freeman, 1977), and eigenvector centrality (Bonacich, 1987). Degree centrality represents the total number of connections a node has. In networks in which relations are directional, this includes measures of indegree and outdegree, or the number of edges pointing to or away from an actor, respectively. Degree centrality is often useful for examining the equity or inequity in the number of ties between individuals and can be done by looking at the degree distribution, which shows the distribution of degrees over an entire network. Betweenness centrality focuses on whether actors serve as bridges in the shortest paths between two actors. Actors with high betweenness centrality have a high probability of existing as a link on the shortest path (geodesic) between any two actors in a network. If one were to look at an airport network (airports connected by flights), airports serving as main hubs, such as Chicago O’Hare and London Heathrow, would have high betweenness, as they connect many cities with no direct flights between them. Closeness centrality focuses on how close one actor is to other actors on average, measured along geodesics. It is important to keep in mind that closeness centrality is poorly suited for disconnected networks (networks in which many actors have zero ties or groups of actors have no connection to other groups). Eigenvector centrality places importance on being connected to other well-connected individuals; having well-connected neighbors gives a higher eigenvector centrality than having the same number of neighbors who are less well connected. Easily the most famous metric based upon eigenvector centrality is the PageRank algorithm used by Google (Page et al., 1999). Because the interpretation of what centrality is actually measuring depends on the metric selected and the type of network at hand, careful consideration is advised before selecting one or more types of centrality for one's study.

Network Methods: Data Collection

In this section, we provide guidance for collecting network data from classrooms. Our discussion is based on existing literature as well as personal experience from our previously described network study.

Both relational and nodal attribute data can be collected using surveys. Designing an effective survey is a more challenging task than often anticipated. There are excellent resources available for writing and facilitating survey questions (Fink, 2003; Denzin and Lincoln, 2005). This section highlights some of the issues unique to surveys for educational network data.

Survey fatigue, and its resulting problems with data quality (Porter et al., 2004), can be an issue for any form of survey research; however, for network studies, it can be especially challenging, given that students are reporting not only on themselves but also on each of their relational partners. For our project, we avoided overuse of surveys in several ways. Routine administrative information such as lab section, lecture section, student major, course grades, and exam grades was easily collected from instructor databases. Data about student demographics, educational background, and standardized testing were obtained through a request to our university's registrar's office (with accompanying human subjects approval).

We strongly suggest pilot studies with your survey, as scheduling a single high-value data collection as the first use of a survey instrument can be risky. The delay in waiting for the next term or the next class for a more vetted collection is worthwhile. Data processing time and effort can be greatly reduced by streamlined data collection, and analysis will be strengthened by iterative improvement of survey questions. With adequate design preparation, brief surveys can easily collect relational data. It is important to keep questions clear and compact. Guidance into the form of the data can make data collected from both closed- and open-ended questions much simpler to clear and process (Wasserman et al., 1990; Scott and Carrington, 2011).

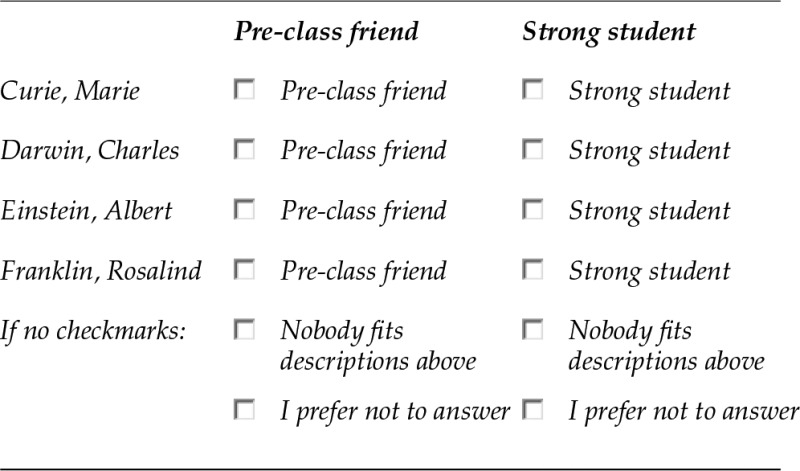
Relational data collected in a closed-ended format such as lists, drop-down menus, or autocomplete forms can limit errors that come with open-ended data collection and are often easier to process. While these streamline student choices, they also come with a downside: they can introduce name confusions (e.g., in our class, nine students share the same first name) and are most problematic when students use nicknames. List data should always allow for both a “Nobody” answer choice and a default “I prefer not to answer” answer choice. An example of data collection with a closed list is shown below:

Question 11: We are interested in learning how in-class study networks form in large undergraduate classes. Over the next few pages is a class roster with two checkboxes next to each student—one which says “Pre-class friend” and one which says “Strong student”. For each student, evaluate whether they fit the description for each box (immediately below this paragraph), and check the box if they do.

Pre-class friend: A student that you would consider a friend from BEFORE the term of this class. If you have met someone in this class that you would consider a friend now but not before this class, do not list them as a pre-class friend.

Strong student: A student you believe is good at understanding class material.

If you are not exactly sure of a name, mark your best guess. The next question in this survey will allow you to write in a name if you don't see one or aren't sure.

***Please know that your response is completely confidential. All names will be immediately re-coded so we will have no idea who studied with whom. This information will never be used for any class purpose, grading purpose, or anything else before the end of the class. Also, please note that students that you list will not know that you listed them in this survey, and you will not know if anyone listed you.***

The number of possible choices given to subjects is an area of intense interest to survey writers in other fields (Couper et al., 2004). Limiting respondents to a given number of answers has a variety of purposes; e.g., in egocentric studies in which a respondent will be asked many questions about each partner, it can help to limit respondent fatigue. For census network data, this is not an issue because we will not need to ask students a long list of questions about the attributes of their alters; we will have that information from the alters themselves, who are also students in the class. It can also help avoid a subject with a broad definition of friendship or collaboration from dominating the data set. We chose to avoid limits on numbers of student nominations, which have the potential to induce subjects to enter data to fill up their perceived quota. In our experience, individual student responses are typically few; no student listed so many friends or study partners that it drowned out other signals significantly.

Open-ended data collection should also include a means for students to indicate that no choices fit the question, to differentiate between nonrespondents and null answers. The largest source of respondent error in open-ended data is again name confusion between students. However, errors can be minimized by providing concise instructions for student-answer formatting. For one of our projects, one example of an open-ended relational survey question was:

We are interested in how networks form in classes. Please list first and last names if possible. If this is not possible, last initials or any description of that person would be appreciated (ie: “they are in the same lab as me”, “really tall” or “sits in the second row”).

If no one fits one of these descriptions, simply write “none.”

***Your response is completely confidential. All names will be re-coded so we will have no idea who listed whom. This information will never be used for any class purpose, grading purpose, or anything else before the end of the class. Also, please note that students that you list will not know you listed them in this survey, and you will not know if anyone listed you.***

There are no right or wrong answers for this. We will ask you similar questions a few times this term. These data are incredibly valuable, so we truly appreciate your answers!

Please list any people in the class that you know are strong with class material. If you do not list anybody, please type either “No one fits description” OR “I prefer not to answer”. (separate multiple students with a comma, like “Jane Doe, John Doe”).

Finally, it may be appropriate in smaller classes, communities with less online capability, or in particularly well-funded studies to collect relational data by interviews. This brings along greater privacy concerns but may be necessary for some hypotheses. Open-ended questions allow for greater breadth of data collection but come with intrinsic complexity in processing. For example, a valued network describing the amount of respect that students have for various faculty might be best collected in a private interview. In this format, the interviewer could more thoroughly describe “respect” by using repeated and individualized questioning to ascertain the amount of respect a student has for each faculty member.

Timing of Survey Administration

Timing of survey questions throughout a class is important. For classroom descriptions consisting of a single network, data should be collected at the earliest possible time that all students have had the experiences desired in the research study. This limits the loss of data due to students forgetting particular ties, dropping or switching classes, or failing to complete the assignment as submission rates inevitably drop toward the end of the term. For longitudinal studies involving several collections, relational data can be collected either at regular intervals or around important classroom events. In either case, we strongly suggest implanting relational survey questions in already existing assignments, if permitted, to maximize data collection rates.

For our project, we collected data throughout the 10-wk term of an introductory biology course. We surveyed for student study partnerships after each exam, spread at semiregular intervals throughout the term (weeks 3, 5, 8, and 10). It will come as no surprise to instructors that attempts to administer an additional, nongraded survey gave lower response rates from already overworked and overscheduled undergraduates. Instead, we appended ungraded survey questions to existing graded online assignments. Depending on your research question, it may be appropriate to repeat some collections to allow for redundancy or for longitudinal analyses. Friendships, for example, are subjectively defined and temporal (Galaskiewicz and Wasserman, 1993). In some of our projects, we ask students for friendship relational data at both the beginning and end of the term as an internal measure of this natural volatility.

Given high response rates, anecdotal accounts of student study groupings that corroborated with the relational data, and limited extra work placed on students to provide data, we have a high level of confidence in the efficacy of our data collection methods, and others interested in network research with similar populations may also find these methods effective.

IRB and Consent

Data used solely for curricular improvement and not for generalizable research often do not require consent, but any use of the data for generalizable research does (Martin and Inwood, 2012). Social network data include the unique issue of one individual reporting on others in some form or other, even if it is only on the presence of a shared relationship. They also often describe vulnerable populations; this can be especially true for educational network research, when researchers are often also acting as instructors or supervisors to the student subjects and are thus in a position of authority. This may create the impression in students’ minds that research participation is linked to student assessment. Because of this, early and frequent conversations with your local human subjects division are useful, illuminating, and should take priority (Oakes, 2002).

The nature of network data not only allows subjects to report information on other subjects but may allow recognizability of even anonymized data (called deductive disclosure), especially in small networks. This makes larger data sets typically safer for subjects. It also means that some network data fields must be stripped of information (Martin and Inwood, 2012). A relatively common example is in networks of mixed ethnicity in which one ethnic group is extremely small. In these cases, ethnicities may need to be identified by random identifiers rather than specific names. In many scenarios, researchers must plan on anonymizing or removing identifiers on data (Johnson, 2008). Your IRB will determine the best fit of plan for any given population of subjects.

Obtaining consent makes networks exciting and problematic at the same time. Complete inclusion of all subjects gives fascinating power to network statistics. Incomplete networks are far less compelling. More so than simpler unstructured data, networks may hinge on a small group of centralized actors in a community. The twin goals of subject protection and data set completion may compete (Johnson, 2008).

In our experience, conversations with IRB advisors led to an understanding of opt-in and opt-out procedures. For example, a standard opt-in procedure would use an individual not involved with the course to talk students through a consent script, answer questions, and retrieve signed consent forms from consenting subjects. An opt-out procedure would provide the same opportunities for student information and questions but ask subjects to opt out by signing a centrally located and easily accessible form kept confidential from researchers until after the research is completed. While the opt-in procedures are more common and foreground subject protection, they tend to omit data with a bias toward underserved and less successful populations. For this reason, we used an opt-out procedure, which commonly leads to higher rates of data return. Balancing research goals and appropriate protection of subject rights and privacy is critical (Johnson, 2008). By minimizing the risk to our subjects via confidential network collection, the use of an opt-out procedure was justified.

Data Management

Matrices are a powerful way to store and represent social network data. Common practice is to use a combination of matrices, one (or more) containing nodal attributes (see Table 1) and one (or more) containing relational data. A common form for the latter is called a sociomatrix or adjacency matrix (see Table 2); another is as an edgelist, a two-column matrix with each row identifying a pair of nodes in a relationship. For our study, we compiled several sociomatrices taken longitudinally at key points in the class, as well as one matrix with data of interest about our students.

Table 1.

Example of nodal attributes held in a matrix

	Gender	Major	Lab section	Grade
Marie	1	Chemistry	2	3.5
Charles	0	Theology	1	2.6
Rosalind	1	Biophysics	4	3.8
Linus	0	Biochemistry	5	4.0
Albert	0	Physics	5	3.3
Barbara	1	Botany	1	3.1
Greg	0	Pre-major	3	3.0

Table 2.

Example of a small sociomatrix

	Marie	Charles	Rosalind	Linus	Albert	Barbara	Greg
Marie	–	0	1	0	1	0	1
Charles	0	–	0	1	0	0	0
Rosalind	0	0	–	0	0	0	0
Linus	0	0	0	–	0	0	0
Albert	1	0	0	0	–	0	0
Barbara	0	0	0	1	0	–	0
Greg	0	0	0	0	0	0	–

A unipartite sociomatrix will always be square, with as many rows and columns as there are respondents. For undirected networks, the sociomatrix will be symmetric along the main diagonal; for undirected, the upper and lower triangles will instead store different information. Matrices for binary networks will be filled with 1s and 0s, indicating the existence of a tie or not, respectively. In cases of nonbinary ties (e.g., how many hours each student studied together) the numbers within the matrix may exceed one. The matrix storing nodal attribute information need not be square; it will have a row for each respondent and a column for each attribute measured.

It is important to understand the value of keeping rows of attribute data linkable to, and in the same order as, sociomatrices—this will ensure the relational data of a student are paired properly to his or her other data. The linkage can be done through unique names; more typically it will be done using unique study IDs.

The amount of effort and time spent cleaning the data will depend on how the data were collected and the classroom population. For this reason, it is advisable to plan the amount and means of collecting data around your ability to process them. Recently, we collected a large relational data set via open-ended survey online. To process these data into sociomatrices we created a program capable of doing more than 50% of the processing (Butler, 2013), leaving the rest to simple data entry. For data collected using a prepopulated computerized list, it may even be possible for all data processing to be automated.

Data Analysis

Many different questions can be addressed with SNA, and there are nearly as many different SNA tools as there are questions. As an example, we will look at the change in student study networks over the span of two exams from our previously described study. Our main interest in these analyses will be how study networks form in a classroom and the impacts these networks have on students. To generate testable hypotheses, we will first perform exploratory data analysis, taking advantage of sociographs. These informative network visualizations offer an abundance of qualitative information and are a distinguishing feature of SNA. It is important to note that, while SNA lends itself well to exploratory analyses, it is often judicious to have a priori hypotheses before beginning data collection. The exploratory data analysis embedded below is used to provide a more complete tutorial rather than to model how research incorporating relational data must be performed.

Starting Analyses

Most familiar statistical methods require observations to be independent. In SNA, not only are the data dependent among observations, but we are fundamentally interested in that dependence as our core question. For these reasons, the methods must deal with dependence. As a result, analyses may occasionally seem different from familiar methods, while at other times they can seem familiar but have subtle differences with important implications. This point should be kept in mind while reading about or performing any analysis with dependent data.

There are a number of proprietary software packages available for performing SNA, and interested investigators should weigh the pros and cons of each for their own purposes before choosing which to use. We use the statnet suite of packages (Handcock et al., 2008; Hunter et al., 2008) in R, primarily its constituent packages network and sna (Butts, 2008). R is an open-source statistical and graphical programming language in which many tools for SNA have been, and continue to be, developed. The learning curve is steeper than for most other software packages, but it comes with arguably the most complex statistical capabilities for SNA. Other network analysis packages available in R are RSiena (Ripley et al., 2011), and igraph (Csardi and Nepusz, 2006). Other software packages commonly used for analysis for academic purposes include UCINet (Borgatti et al., 1999), Pajek (Batagelj and Mrvar, 1998), NodeXL (Smith et al., 2009; Hansen et al., 2010), and Gephi (Bastian et al., 2009).

We include R code for step-by-step instructions for our analysis in the Supplemental Material for those interested in using statnet for analyses. The Supplemental Material also includes instructions for accessing a mock data set to use with the included code, as confidentiality needs and corresponding IRB agreements do not allow us to share the original data.

Exploratory Data Analysis

In performing SNA, visualizing the network is often the first step taken. Using sociographs, with nodal attributes represented by different colors, shapes, and sizes, we will be able to begin qualitatively assessing a priori hypotheses and deriving new hypotheses. We hypothesize that students who are in the same lab are more likely to study together, due to their increased interaction. We also think students with fewer study partners, and thus less group support in the class, are less likely to perform well in the class.

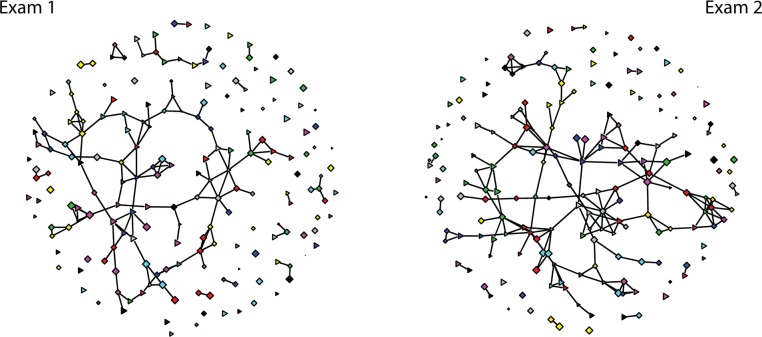
Figure 2 contains two sociographs visualizing the study networks for the first and second exam. Each shape represents a student, and a line between two shapes represents a study relationship. In these graphs, each color represents a different lab section, shape represents gender, and the size of each shape corresponds to how well the student performed in the class.

Figure 2.

Sociographs representing study networks for the first and second exam. Male students are represented as triangles and females as diamonds. The color of each node corresponds to the lab section each student was in. Edges (lines) between nodes in the networks represent a study partnership for the first and second exam, respectively.

While no statistical significance can be drawn from sociographs, we can qualitatively assess our hypotheses. Judging by the clustering of colors, it seems as though same-lab study partnerships were rarer in the first exam than the second exam, for which several same-color clusters exist. This provides valuable visual evidence, but more rigorous statistical methods are important, particularly if policy depends on results.

There does not seem to be any strong visual evidence for an association between classroom performance and number of study partners. If this were true, we would see isolated nodes (those with zero ties) and nodes with few connections to be smaller on average than well-connected nodes. Visually, it is hard discern whether this is the case, and more rigorous tests can help us test this hypothesis. We first explore structural changes in study networks between the first two exams before statistically testing for an association between test scores and social studying.

Network Changes over Time

We can compare the study networks from the first and second exams using network measures such as density, triad censuses, and transitivity. These measurements allow us to assess whether the number of study partnerships are increasing or decreasing and whether any changes affect larger network structures such as triads.

Examining Table 3, a few things become clear. First, 34 more study partnerships exist in the second exam compared with the first, a 22.5% increase in network density. This increase in study partnerships does not distinguish between students moving from studying alone to studying with other students and students who have study partners adopting more study partners. One way to gain a better understanding of the increase in overall study partnerships is to look at the degree distribution for the first two exams, seen in Table 4.

Table 3.

General measurements taken from study networks of the first two exams

Measure	First exam study network	Second exam study network
Edges	151	185
Density	0.00868	0.01064
Triad (0)	1,044,790	1,038,672
Triad (1)	27,407	33,384
Triad (2)	216	326
Triad (3)	32	63
Transitivity	0.3077	0.3670

Table 4.

Degree distribution from the study networks of the first two exams

	Degree
	0	1	2	3	4	5	6	7	8	9
First	57	45	32	34	8	7	4	0	0	0
Second	51	43	24	33	17	12	1	3	2	1

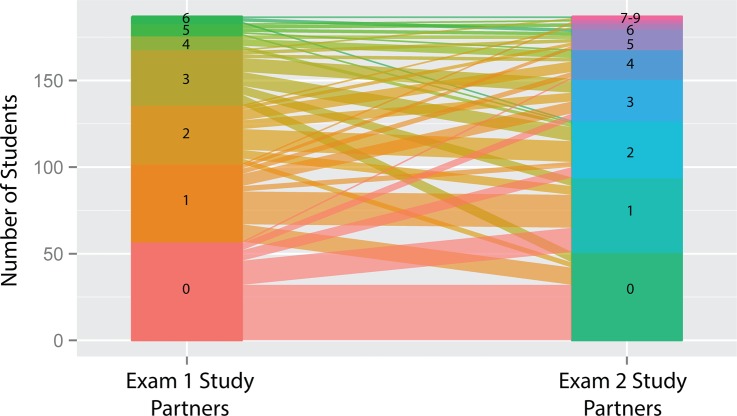
There are fewer students without study partners on the second exam, several students exhibiting extreme sociality in their study habits, and an overall trend toward more students with upwards of five study partners. Unfortunately, the degree distribution does not completely illuminate the social mobility of students between the first and second exam. One way to view general trends is to use a parallel coordinate plot using the degree data from the first and second study networks.

The plot in Figure 3 seems to indicate that the overall increase in study partnerships is not dominated by a few individuals and is instead an outcome of an overall class increase in social study habits. While we see many isolated students studying alone on the first and second exam, we also find many branching off and studying socially in the second exam. At the same rate, many students studied with partners in the first exam and become isolated on the second.

Figure 3.

A parallel coordinate plot tracking changes in number of study partners from the first and second exam. The number of students whose number of study partners changes from exam 1 to exam 2 is denoted by the line widths.

Not only are there more overall connections, but we see higher transitivity and a trend toward complete triads. This increase in both measures indicates how students find their new study partners; they become more likely to study with their study partner's study partner, resulting in more group studying.

Ties as Predictors of Performance

Understanding study group formation and evolution is both interesting and important, but we are not limited to questions focused on network formation. As educators, we are inherently interested in what drives student learning and the kinds of environments that maximize the process. We can start addressing this broad question by integrating student performance data with network data.

As an example, we will test for an association between exam scores and both degree centrality and betweenness centrality. Studying with more students (indicated by degree centrality) and being embedded centrally in the larger classroom study network (indicated by betweenness centrality) may be a better strategy than studying alone or only with socially disconnected students. If we think of each edge in the study network as representing class material being discussed in a bidirectional manner, then more social students may have a leg up on those who are not grappling with class material with peers.

Owing to the dependent nature of centrality measures, testing for an association between network position and exam performance is not completely straightforward. One way around the dependence assumption is to use a permutation correlation test. The general idea is to create a distribution of correlations from our data by randomly sampling values from one variable and matching them to another. In effect, we will assign each student in the study network a randomly selected exam score from the scores in the class 100,000 times. This creates a null distribution of correlation coefficients (ρ) for the correlation between exam score and centrality measure for the set of exam scores found in our data, as seen in Table 5. We can then test the null hypothesis that ρ = 0 using this created distribution.

Table 5.

Results from a permutation correlation test between degree and betweenness centrality and student exam performance

Centrality measure	Exama	Correlation	Pr (ρ ≥ obs)
Degree centrality	Exam 1	0.072	0.164
	Exam 2	0.212	0.001
Betweenness centrality	Exam 1	0.031	0.337
	Exam 2	0.117	0.048

^aSignificance is seen between both types of centrality for the second exam, but not the first.

With a one-tailed test, we see no significant correlation for either centrality measure for the first exam but find a significant correlation between both betweenness centrality and degree centrality and exam performance on the second exam. With our understanding of how students changed their studying patterns between the first and second exam, this finding is rather interesting. Given the opportunity to revise their network positions after some experience in the course, we find a social influence on exam performance.

Because we are unable to control for student effort (a measure notoriously hard to capture), we are unable to discern whether study effort confounds our finding and makes causality vague. Regardless, the association is interesting and exemplifies the sort of direction researchers can take with SNA.

More Complex Models of Network Formation

The methods we present here only scratch the surface of those available and largely focus on fairly descriptive techniques. A variety of approaches exists to explore the structure of networks, to infer the processes generating those structures, and to quantify the relationships among those structures and the flow of entities on them, with a recent trend away from description and toward more inferential models. For instance, past decades saw great interest in specific models for network structure (e.g., the “small-world” model) and their implications (Watts and Strogatz, 1998). A host of methods exist for identifying endogenous clusters in networks (e.g., study groups) that are not reducible to exogenous attributes like major or lab group; these have evolved over the decades from more descriptive approaches to those involving an underlying statistical model (Hoff et al., 2002). Recently, more general approaches for specifying competing models of network structure within the framework and performing model selection based on maximum likelihood have become feasible. These include actor-oriented models, implemented in the RSiena package (Snijders, 1996), and exponential-family random graph models, implemented in statnet (Wasserman and Pattison, 1996; Hunter et al., 2008). One recent text that covers all of these and more, using examples from both biology and social science and with a statistical orientation, is Statistical Analysis of Network Data by Kolaczyk (2009).

FUTURE DIRECTIONS

Within education research, we are just beginning to explore the kinds of questions that can benefit from these methods. Correlating student performance (on any number of measures) to network position is one clear area of research possibility. Specific experiments in pedagogical strategies or tactics, beyond having effects on student learning, may be assessable by differential effects on student network formation. For example, three groups of students could be required to perform a classroom task either by working alone, by working in pairs, or by working in larger groups. Differential outcomes might include grade results, future self-efficacy, or understanding of scientific complexity. The outcomes could be correlated with significant differences in the emergent network structures, strength of ties, and number of ties that emerge in a network of studying partnerships. Controlled experimentation with social constraints and network data would provide insight on advantages or disadvantages of intentional social structuring of class work.

Educational networks are not exclusive to students; relational data between teachers, teacher educators, and school administrators may reveal how best teaching practices spread and explain institutional discrepancies in advancing science education.

Beyond correlational studies, major questions of equity and student peer perceptions will be a good fit for directed network analysis. Conceivably, network analysis can be used to describe the structure of seemingly ethereal concepts such as reputation, charisma, and teaching ability through the social assessment of peers and stakeholders. With a better understanding of the formation and importance of classroom networks, instructors may wish to understand how their teaching fosters or hinders these networks, potentially as part of formative assessment. Reducing the achievement gaps along many demographic lines is likely to involve social engineering at some granular level, and the success or failure of interventions represents rich opportunities for network assessment.

SUMMARY

In this primer, we have analyzed two study networks from a single classroom. We have discussed collection of both nodal and relational data, and we specifically focused on keeping surveys brief and simple to process. We transitioned these data to a sociomatrix form for use with SNA software in a statistical package. We analyzed and interpreted these data by visualizing network data with sociographs, looking at some basic network measurements, and testing for associations between network position and a nodal attribute. Data were interpreted both as a description of a single network and as a longitudinal time lapse of community change. For this project, data collection required a single field of data from the institution registrar and a single survey question asked longitudinally on just two occasions. With a relatively small investment in data collection we can rigorously assess hypotheses about interactions within our educational environments.

It bears repeating: this primer is intended as a first introduction to the power and complexity of educational research aims that might benefit from SNA. Your specific research question will determine which parts of these methods are most useful, and deeper resources in SNA are widely available.

In short, networks are a relatively simple but powerful way of looking at the small and vital communities in every school and college. Empirical research of undergraduate learning communities is sparse, and instructors are thus limited to anecdotal evidence to inform decisions that may impact student relations. We hope this primer helps to guide educational researchers into a growing field that can help investigate classroom-scale hypotheses, and ultimately inform for better instruction.

FURTHER RESOURCES

For readers whose interest in SNA has been piqued, there are numerous resources to use in learning more. We provide some of our favorites here:

Carolan, Brian V. Social Network Analysis and Education: Theory, Methods & Applications. Los Angeles: Sage, 2013.

Kolaczyk, Eric D. Statistical Analysis of Network Data: Methods and Models. Springer Series in Statistics. New York: Springer, 2009.

Lusher, Dean, Johan Koskinen, and Garry Robbins. Exponential Random Graph Models for Social Networks: Theory, Methods, and Applications. Structural Analysis in the Social Sciences 35. Cambridge, UK: Cambridge University Press, 2012.

Prell, Christina. Social Network Analysis: History, Theory & Methodology. Los Angeles: Sage, 2012.

Scott, John, and Peter J. Carrington. The Sage Handbook of Social Network Analysis. London: Sage, 2011.

Wasserman, Stanley, and Katherine Faust. Social Network Analysis: Methods And Applications. Structural Analysis in the Social Sciences 8. Cambridge, UK: Cambridge University Press, 1994.

Other resources include the journals Social Network Analysis and Connections, both published by the International Network for Social Network Analysis; the SOCNET listserv; and the annual Sunbelt social networks conference.