The Use of Normal Tissue Complication Probability (NTCP) Models in the Clinic

Abstract

The QUANTEC (quantitative analysis of normal tissue effects in the clinic) review summarizes the currently-available three dimensional dose/volume/outcome data to update and refine the normal tissue dose/volume tolerance guidelines provided by the classic “Emami” paper (IJROBP 21:109, 1991). A “clinician’s view” on using the QUANTEC information in a responsible manner is presented along with a description of the most commonly-used normal tissue complication probability (NTCP) models. A summary of organ-specific dose/volume/outcome data, based on the QUANTEC reviews, is included.

Introduction

Historically, radiation therapy (RT) fields/doses were selected empirically, based largely on experience. Physicians relied on clinical intuition to select field sizes/doses. They understood that these empiric guidelines were imprecise, and did not fully reflect the underlying anatomy, physiology, and dosimetry.

A great promise of three dimensional (3D) treatment planning was quantitative correlates of doses/volumes with clinical outcomes. This promise was partly delivered. When 3D dosimetric information became widely available, guidelines were needed to help physicians predict the relative safety of proposed treatment plans, though only limited data were available. In 1991, investigators pooled their clinical experience, judgment, and information regarding partial organ tolerance doses, and produced the “Emami paper” (1). While “Emami” is often criticized, the paper clearly stated the uncertainties and limitations in its recommendations, and it is widely admired for addressing a clinical need.

During the last 17 years, numerous studies reported associations between dosimetric parameters and normal tissue outcomes. The QUANTEC (quantitative analysis of normal tissue effects in the clinic) articles summarize the available data to update/refine the estimates provided by “Emami”. A central goal of QUANTEC, is to summarize this information in a clinically useful manner.

We hope the information will improve patient care by providing clinicians and treatment planners with tools to estimate “optimal/acceptable” 3D dose distributions. We hope that (at least some of) the summary tables, graphs, and models presented will be reproduced, and posted in resident workrooms, dosimetry planning areas, and physician offices, as is currently done with the “Emami” tables.

The information provided by QUANTEC is not ideal, and care must be taken to apply it correctly in the clinic. We herein present a “clinician’s view” on using the QUANTEC information in a responsible manner, highlighting the diverse type of limitations of the presented data.

1) Limitations inherent in extracting data from the literature

The information presented is largely extracted from publications. Since different investigators often present information differently (e.g., actuarial vs. crude complication rates), pooling data from multiple studies may be inaccurate. Summary tables are often included to help the reader better understand the primary data.

2) Limitations of Predictive Models

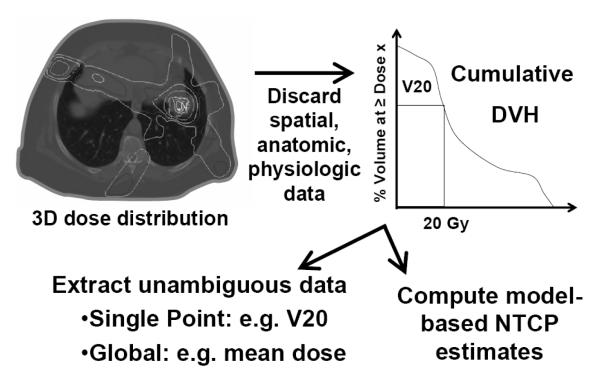
Some studies use models to estimate the complication risk. Care should be taken when applying models, especially when clinical dose/volume parameters are beyond the range of data used to generate the model/parameters. Models and dose/volume recommendations are only as good as the data available. Typically, they are based on dose-volume histograms (DVH’s). DVH’s are not ideal representations of the 3D doses as they discard all organ-specific spatial information (and hence assume all regions are of equal functional importance), and often do not consider fraction size variations. They are usually based on a single planning computed tomography (CT) scan that does not account for anatomic variations during therapy (Figure 1). Inter-institutional/physician differences in image segmentation, dose calculation, patient populations, and preferred beam arrangements may limit model exportability. Before introducing a predictive model into a clinical practice, it is prudent to assess if its predictions “make sense” in regard to that clinic’s treatment plans and experience.

Figure 1.

A 3D dose distribution is reduced to a 2D DVH by discarding all spatial, anatomic and physiologic data. The 2D graph is then further reduced to a single value of merit, such as the mean dose, the percent of the organ receiving ≥20 Gy (V20), or a model-based NTCP (Normal tissue complication probability).

3) Evolving fractionation schedules

RT-induced normal tissue responses are fraction size dependent. Throughout the QUANTEC reviews, this variable is acknowledged and, where possible, considered by making adjustments for fraction size based on the linear quadratic (LQ) model. Nevertheless, α/β ratios are uncertain. Particular care must be taken when QUANTEC information is applied to stereotactic RT, where the fraction size is much different than that in the cited literature. For very novel fractionations, even the validity of the LQ model is questioned (2).

Even when the prescribed tumor dose is “conventionally” fractionated, the fraction size seen by the normal tissue may have varied over time. When “Emami” was published, most external RT was delivered with opposing fields, and shrinking field techniques —the normal tissue was irradiated with a fairly uniform fraction size. Modern techniques often utilize multiple beams (+/− concurrent boosts); the volume of normal tissue exposed to low doses is often increased and the dose is delivered at fraction sizes ranging from ≈ zero to the prescription dose.

4) Combined Modality Therapy

Use of sequential/concurrent chemotherapy/RT is increasing for many tumors. Concurrent chemotherapy is typically believed to exacerbate the severity of normal tissue reactions, but data quantifying this is often lacking. Even when such data are available, the chemotherapy doses, schedules and agents—which may influence outcomes—are in evolution.

5) Host factors

Host-factors (e.g., chronic liver disease, genetic, life-style) may affect dose-response relationships and are partly responsible for the shallowness of these relationships in the patient population. It is likely that incorporating these factors, when they are known, will produce better models/correlations/predictors of toxicity.

6) Balancing the risks to different organs

Different morbidities vary in their clinical significance. Grade 2 toxicity has a different clinical meaning for the esophagus than for the rectum. Further, different patients may have different levels of acceptance for injuries. When comparing competing treatment plans, there is usually a tradeoff; e.g., should we accept a certain dose to the lung or to the esophagus? For most cases, modern treatments will redistribute, not eliminate, the dose to normal tissue. The fundamental problem of treatment planning is how to balance exposure of one organ against that of another. Unfortunately, there is no objective way to do this.

Investigators have considered the risks to multiple organs, and computed the probability of uncomplicated tumor control (3-5). Others have attempted to incorporate the relative importance of different toxicities, by considering their impact on patients’ quality of life. This approach generates a global figure of merit such as the “quality of life adjusted tumor control probability” (6, 7). The utility of this approach, while conceptually attractive, is not clear.

7) Follow-up duration

If dose-effect relationships for a late complication are derived from a patient population with very poor prognosis, they may be limited by lack of long-term follow-up, and not applicable to patients with a better prognosis (e.g., applying brain toxicity from patients with high grade glioma to patients with low-grade tumors).

The risk of normal tissue complication occurs in the context of a patient’s expected longevity. RT is an effective anti-cancer therapy, and can provide good palliation for patients with recurrent/metastatic/incurable disease. In these settings, concern for late normal tissue reaction often should not limit the application of RT. For example, re-irradiation of the whole brain for recurrent brain metastases to cumulative doses well above tolerance can provide palliation for these challenging cases (8-10) where concern about late toxicity may be unnecessary. Similarly, RT for locally advanced lung cancers may routinely exceed the normal dose limits for lung and heart. In these instances, there typically are no good alternative therapies available. Withholding thoracic RT due to the risk of pericarditis, or pneumonitis, may not be therapeutically rational.

These concerns are most applicable to recently-trained radiation oncologists who are accustomed to utilizing 3D dosimetric information for most of their clinical decisions. They may be uncomfortable in clinical settings where large RT fields need to be applied without 3D dosimetry in order to provide palliative effect. It is the physician’s responsibility to tell dosimetrists/physicists when it is appropriate to proceed with treatment without a formal 3D dose/volume assessment and/or suspend the conventional departmental dose/volume guidelines.

8) Relating “whole treatment” DVH’s with acute toxicities

For some organs, a relevant acute toxicity may occur during the course of RT (i.e. prior to the delivery of the entire RT course). Relating the incidence of such acute events to a DVH that reflects the whole treatment course may be somewhat illogical. It might be preferable to try to relate acute events to the dose delivered prior to symptom onset (or even to doses received a number of days prior to symptom onset- if there is a known latency time).

If a consistent set of treatment fields is used throughout the entire course of treatment (e.g. no field reductions), the “whole course” DVH might be a reasonable surrogate for the 3D doses delivered prior to acute symptom onset. Therefore, in these situations, it still might be a reasonable to relate the risk of acute events to a DVH that reflects the whole treatment course.

However, field arrangements often change during therapy, thus altering the dose/volume parameters for the target organ (e.g., initial AP-PA fields plus a subsequent off-cord boost). In these situations, the “whole course” DVH is less likely to be a reasonable surrogate for the 3D doses delivered prior to the acute toxicity. Thus, some dose/volume/outcomes analyses for acute endpoints that consider the “whole course” DVH may be suspect.

Further complicating the issue is the fact that the duration of symptoms (that may also influence the scoring of toxicity), may be affected by RT dose delivered after the onset of symptoms. In this regard, the “whole course” DVH may indeed be reasonable to consider in dose/volume/outcomes analyses.

A similar concern may apply for analyses of late effects. If a late toxicity results from a severe acute toxicity occurring during the course of RT, relating that late event to the “whole course” DVH may also be suboptimal.

9) Tumor coverage versus normal tissue risk

For most curative patients, a marginal miss is more serious than a normal tissue complication. For many tumors, recurrences are difficult to manage, cause severe morbidity, and usually result in mortality. Target coverage should generally not be compromised to reduce the normal tissue risks. This is exemplified by the experience from Israel in treating orbital lymphomas. In 24 tumors treated in 23 patients, intra-orbital recurrence was seen in 4/12 (33%) of the tumors treated with conformal fields (including the radiographically-defined gross tumor with margin), vs. none of the 12 tumors treated with conventional whole-orbit techniques (11). Similarly, Washington University noted a higher relapse rate in lung cancers closer to the spinal cord; perhaps reflecting compromised GTV coverage due to spinal cord protection. ([12], and personal communication J Deasy, 2008). The use of improved diagnostic imaging, and improved immobilization and image guidance during RT, may facilitate a more “realistic” PTV margin to be applied safely.

10) Applicability to children

In the young, a mosaic of tissues develop at different rates and temporal sequences. In adults, the same tissues are in a steady state with relatively-slow cell renewal kinetics. The vulnerability of tissues to RT typically increases during the periods of rapid proliferation. Consequently, generalizing data from adult to pediatric populations is problematic and requires caution. Ideally, specific data from investigations on children should be used to predict risks in this population.

11) Understanding the Basics of NTCP models

Despite these caveats, model-based risk estimates are a reality. Physicians routinely use models, in their broadest sense, to make treatment decisions. Use of metrics such as the mean lung dose, and cord maximum dose to estimate risks are ‘models’, albeit simple ones. We present a primer regarding the basic principles of NTCP models.

Generally, NTCP models attempt to reduce complicated dosimetric and anatomic information to a single risk measure. Most models fall into one of three categories: DVH-reduction models, tissue architecture models, and multiple-metric (‘multi-metric’) models.

a. DVH-reduction models

While most applications of DVH reduction models are to non-uniform dose distributions, they are based on estimated complication probability under uniform irradiation. A dose-response for uniform irradiation is described by a mathematical function with at least two parameters, e.g.: TD50 which denotes the dose for 50% complication probability, and m, which is inversely proportional to the slope at the steepest part of the response curve. For a patient cohort with diverse radiosensitivities, the response curve is shallower (larger m) than for a biologically similar population receiving the same treatment (13). Various S-shaped functions are used to fit dose-response data, including the probit function used by Lyman (below).

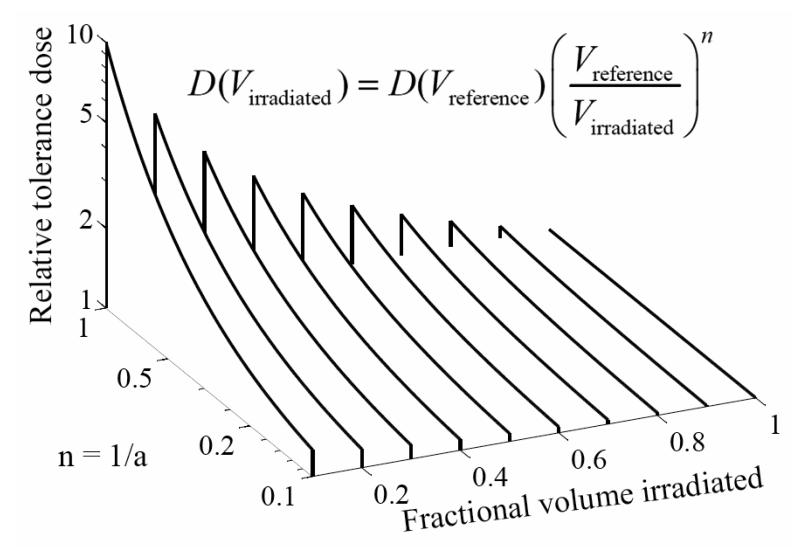
To account for the dose heterogeneity typical of parallel opposed beam irradiation (“partial organ uniform irradiation”), Jolles (14) described tissue tolerance as a power-law of the fractional volume irradiated:

$$D\left(V_{\text{irradiated}}\right)=D\left(V_{\text{reference}}\right){\left(\frac{V_{\text{reference}}}{V_{\text{irradiated}}}\right)}^n,$$ [1]

Here V_reference is the ‘reference volume,’ V_irradiated is the uniformly irradiated volume. D is the corresponding tolerance doses, representing a chosen level on the dose-response curve, such as TD50. The parameter “n,” controls the ‘volume effect.’

Lyman (15) used this power law model to define the risks associated with partial organ volume uniform irradiation. From Eq. 1, decreasing the irradiated volume fraction shifts the dose-response curve (TD50) to higher doses by a factor of the irradiated fractional volume raised to the power “negative n”. The effect of different n values on tolerance dose is shown in Figure 2.

Figure 2.

As the (idealized) irradiated organ fraction decreases, the tolerance dose (D) increases, more so for larger values of n, or smaller values of a (=1/n). V_Reference represents the reference volume (usually the full organ volume), and V_Irradiated represents the volume irradiated.

For example, if the “n” parameter equals 1 then the TD50 of irradiation for one half the volume is expected to increase by a factor of 2 while if the “n” parameter is 0.5, TD50 for irradiation of one half the volume would increase by a factor of the square root of 2.

To generalize this to clinically realistic, heterogeneous dose distributions, a summary statistic—the generalized equivalent uniform dose (gEUD)—is often introduced (16, 17). The gEUD is the dose that, if given uniformly to the entire organ, is believed to yield the same complication rate as the true dose distribution. The gEUD is computed by summing over all voxels in the organ:

$$\mathrm{gEUD}={\left[\frac{1}{N_{\text{Voxels}}}\left(d_1^{1∕n}+d_2^{1∕n}+\dots +d_{N_{\text{Voxels}}}^{1∕n}\right)\right]}^n.$$ [2]

Here N_Voxels is the number of equi-volume voxels, and d_i is the dose to the i^th voxel. The gEUD equation is consistent with the power-law assumption. Together, the gEUD equation and the Lyman assumptions are often referred to as the Lyman-Kutcher-Burman (LKB) model (15, 17-19).

Note that some analyses use the parameter “n,” and some use the parameter “a,” equal to 1/n. Both are shown in Figure 2. When “n” is small (“a” large) changes in irradiated volume make only a modest change in relative tolerance while as “n” gets larger (“a” smaller), the tolerance dose depends strongly on the irradiated volume fraction.

b. ‘Serial’ vs. ‘Parallel’ complication endpoints

There have been efforts to devise mechanistic models that ascribe the volume dependence of some complications to disruption of the organ’s functional “architecture” by RT (20-22).

In ‘parallel’ complications, sub-volumes of the organ function relatively independently. Sufficiently small portions of the organ can be damaged without clinical effect; the complication is observed only after more than a “critical volume” is damaged. Parallel complications have large volume effects, and for this reason they are often likened to LKB models with n ≈ 1 (as is found in analyses of liver, lung and kidney complications). More detailed models exist, including models employing the concept of a ‘functional reserve,’ representing a hypothesized fraction of organ function which can be lost before a complication is likely (22).

In contrast, ‘serial’ complications occur when even a small portion of the organ suffers damage. Here, “n” is small, (e.g., ≈ 0.1 for late rectal bleeding). Serial complications are most affected by the hottest portion of the DVH. More detailed models exist for this type of endpoint as well, including models that make explicit the size of small sub-units, all of which need to be preserved to avoid a complication (22).

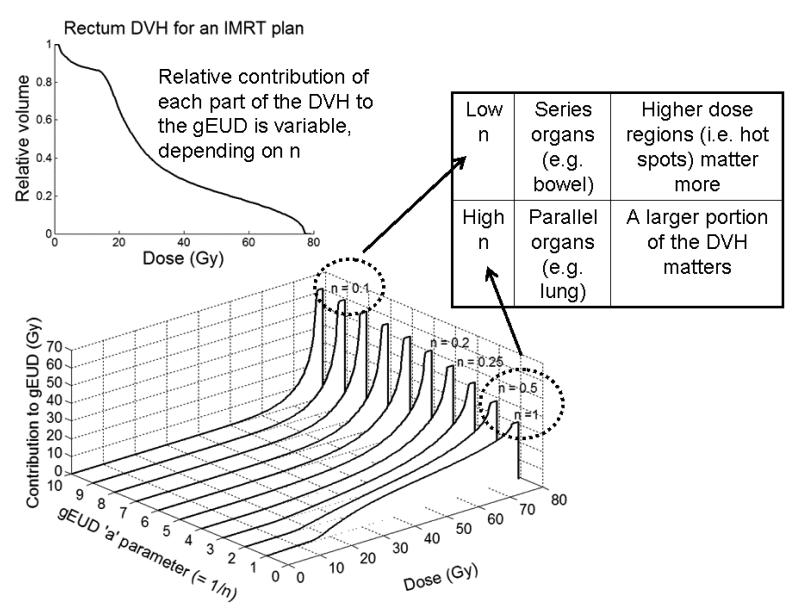
Figure 3 shows how different parts of an example DVH contribute to the overall gEUD as “n” varies. Note that: 1) the lowest value of “n” results in the highest gEUD corresponding to the hottest point on the DVH (more appropriate for serial-like endpoints), and 2) the lower dose bins contribute more when “n” approaches 1 (more appropriate for parallel-like endpoints).

Figure 3. The volume-effect parameter.

The effect of changing the ‘n’ parameter (= 1/a) in the Lyman model with the generalized equivalent uniform dose equation to compute NTCP is shown. Starting with a (real) rectal DVH computed for an IMRT prostate patient plan (upper left), the DVH is first transformed into a single number by the generalized equivalent uniform dose equation that weights dose values exponentially. The lower figure shows the cumulative contribution of each part of the DVH to the overall gEUD for all bins below the given dose value. As one can see, if a is set to 1 (rightmost curve), gEUD would equal the mean dose (e.g., for parallel organs), and many voxels with doses as low as 20-30 Gy contribute significantly to the gEUD, and therefore may increase the final NTCP value (although contributions are proportional to dose, so higher dose still does contribute more for the same volume). As ‘n’ decreases, the value of gEUD is a determined mainly by the highest dose voxels (e.g., for series organs). Typical clinical values for late rectal bleeding are ~n = 0.1. Unfortunately, investigators sometimes report a (especially when discussing the gEUD) and other-times use n, where n=1/a.

c. Multi-metric Models

Clinicians frequently estimate complication risk via a single DVH point based on a statistically-significant dose/volume cut-point reported in one or more studies. An example is the often-used V20 (% of lung receiving >20 Gy) as a predictor of radiation pneumonitis (23). However, such single “volume threshold” rules are overly simple, and often easily manipulated by the treatment planner, or by the optimization software. Optimizing based on such a threshold may introduce a ‘kink’ in one part of the DVH to achieve a desired “threshold value”, while inadequately constraining the rest. An infinite number of very different dose distributions (some likely with very different risks) can have the same V20. The same is true for any DVH-reduction scheme, including the LKB models; markedly different-looking DVH’s can yield the same NTCP. However, models that consider a larger fraction of the DVH are less-easily manipulated (and may be more radiobiologically logical) than are the threshold models that consider only one point on the DVH. Nonetheless, reports correlating single DVH point thresholds to toxicity are common and are often included in the QUANTEC reviews.

The more robust multi-metric approach selects several univariate-significant dosimetric features of the dose distribution (e.g., multiple V_dose values) as well as medical variables and use multivariate analysis together with sophisticated statistical methods or “machine learning” algorithms to pick out the most significant combinations (24). In-depth discussions of this topic can be found in reviews elsewhere (25-28).

Summary

A major goal of this IJROBP issue is to provide practical clinical guidance for physicians and treatment planners. The information presented is not perfect, as evidenced by the multiple caveats above. The lack of good predictors is somewhat unsettling. Nevertheless, the QUANTEC papers present a valuable review. Over time, with the help of new studies guided by new physical, statistical and biological technologies, we hope to be able to update this information so that patient care can be continually improved.

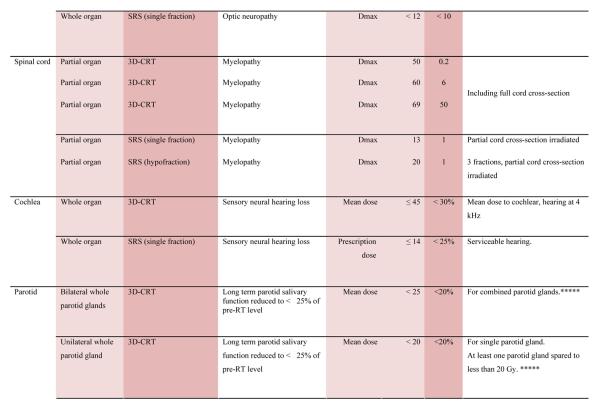
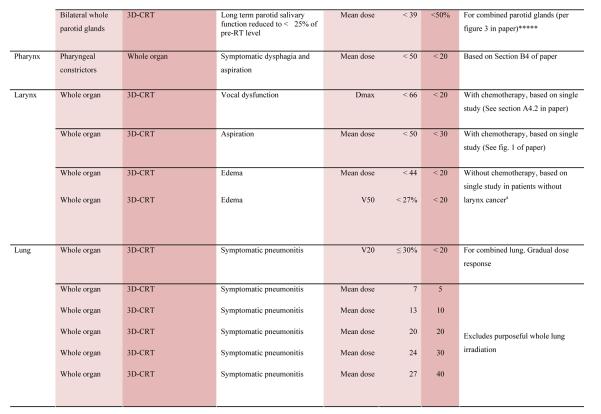
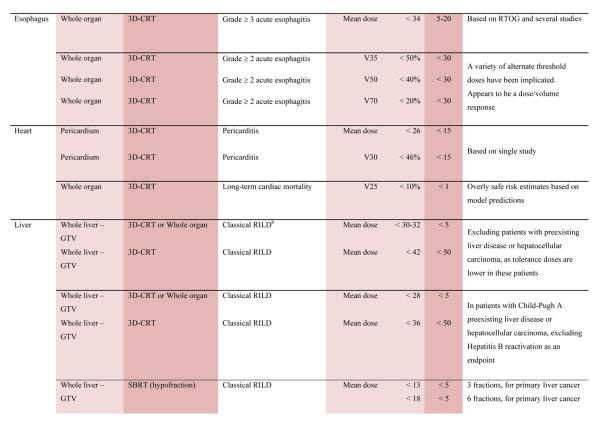
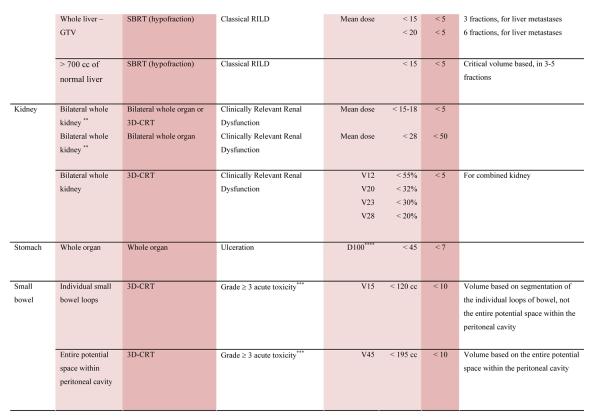
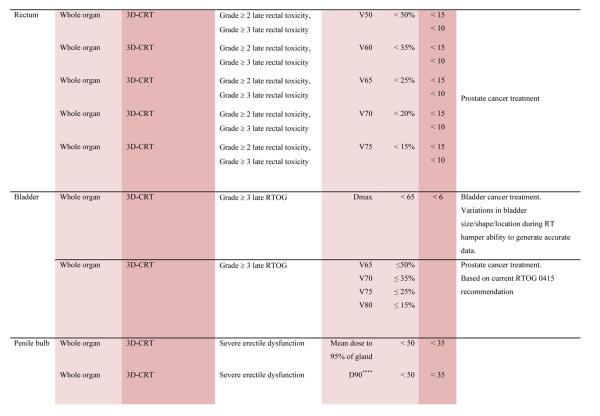
With the multiple caveats outlined above in mind, a limited summary of available organ-specific dose/volume/outcome data is provided in the appendix. This is not meant to replace the detailed information provided in the individual organ-specific reviews. Treatment planners and physicians are encouraged to read the individual papers to understand the origin, certainty, and nuances that apply to the dose/volume/outcome data provided in the summary table. In general, the dose/volume/outcome data provided in the summary table are associated with generally-regarded clinically-acceptable rates of injury; i.e. low rates for severe injury (e.g. brain necrosis), and higher rates of less severe endpoints (e.g. erectile dysfunction). Thus, these are dose/volume parameters that might be widely applied in clinical practice. Obviously many clinical situations require treatments that exceed the dose/volume values shown. Where practical, some dose response data are included as well. Further, most of the data in the table is based on conventionally-fractionated radiation using conventional techniques, and may or may not be applicable in other settings.

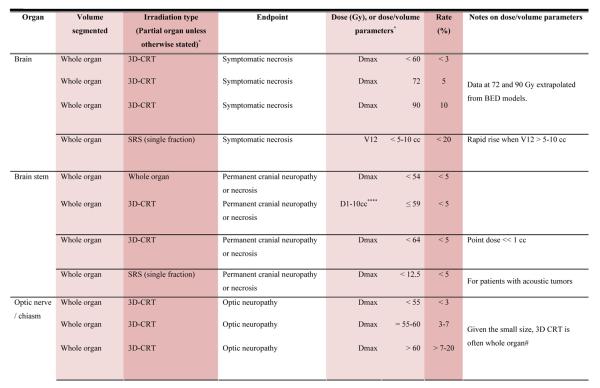
QUANTEC Summary Table.

Approximate Dose/Volume/Outcome Data for Several Organs Following Conventional Fractionation (Unless Otherwise Noted)^{^}

^{^}All data are estimated from the literature summarized in the QUANTEC reviews (unless otherwise noted). Clinically, these data should be applied with caution. Clinicians are strongly advised to use the individual QUANTEC articles to check the applicability of these limits to the clinical situation at hand. They largely do not reflect modern IMRT.

^*all at standard fractionation (i.e. 1.8 -2.0 Gy per daily fraction) unless otherwise noted.

^**non-TBI

^***with combined chemotherapy

^****Dx = minimum dose received by the “hottest” x% (or x cc’s) of the organ

^*****Severe xerostomia is related to additional factors including the doses to the submandibular glands.

^aEstimated by Dr. Eisbruch

^bClassic RT-induced liver disease (RILD) involves anicteric hepatomegaly and ascites, typically occurring between 2 weeks to 3 months after therapy. Classic RILD also involves elevated alkaline phosphatase (more than twice the upper limit of normal or baseline value).

^#For optic nerve, the cases of neuropathy in the 55-60 Gy range received ~59 Gy (see optic nerve paper for details). Excludes patients with pituitary tumors where the tolerance may be reduced.