Abstract
Researchers routinely use historical control data (HCD) when analyzing rodent carcinogenicity data obtained in a particular study. Although the concurrent control group is considered to be the most relevant group to compare with the dose groups, the HCD provides a broader perspective to assist in understanding the significance of the current study. The HCD is used to provide information about the incidences of spontaneous tumors and malignant systemic disorders such as lymphoma and leukemia. This paper presents some possible ways of incorporating the HCD when analyzing data from a rodent cancer bioassay. Specifically, exploratory (informal) and formal statistical procedures for analyzing such data are reviewed. The boxplot is presented as an exploratory tool that describes the current data in the context of the distribution of the HCD. It will also identify potential outliers that would not be otherwise be flagged using standard methods such as the mean, standard deviation and range. The various options for the statistical analysis of HCD presented here do not necessarily represent standard practice.
Keywords: boxplot, IQR, lower quartile, median, range, upper quartile, historical control data
Introduction
Two-year rodent toxicology and carcinogenesis bioassays are conducted by government agencies, private companies and research institutes to identify toxic and carcinogenic compounds that are potentially hazardous to human health through exposure to pharmaceuticals, nutraceuticals, food, water or other environmental sources. When analyzing the tumor incidences in treatment (or dose) groups, the most appropriate control for comparison is the concurrent control group. The evaluation of the tumor incidences in the treatment groups relative to the concurrent control group is traditionally based on established statistical methods such as the Poly-3 trend test (Bailer and Portier, 1988; Bieler and Williams, 1993). This test, which adjusts for survival, allows one to determine the statistical significance of the tumor incidence within a treatment group and also helps to determine if there is a statistically significant trend across dose groups within a study.
To assess if the tumor responses in the current study are unusual in comparison to what is known historically about the lesion among control animals, it is customary for researchers to compare the responses in the current study with the tumor incidences in control groups from previous studies. “Historical control data” (HCD) is the term used for this compilation of data from previous studies. Thus the HCD can be used to determine if the tumor incidence in the concurrent control group or dual control groups are consistent with the tumor incidence in the historical control groups. Comparison of the tumor incidence rates in treated groups with both concurrent control groups and HCD can, along with other study data such as the incidence of other lesions of similar cell lineage, help to determine biological relevance.
HCD is helpful in interpreting the tumor incidences in a variety of situations, such as: rare tumors, common tumors (e.g. pituitary pars distalis adenomas in male and female rats), tumors with highly variable incidence rates (e.g., pancreatic islet cell tumors in male rats or thyroid C-cell adenomas in male and female rats), a tumor that has a marginal increase in incidence relative to concurrent controls, or if there are unexpected increases or decreases of tumor incidences in study control animals; Baldrick 2005; Eiben and Bomhard 1999; Haseman et al. 1990; http://ntp.niehs.nih.gov/ntpweb; http://www.criver.com/sitecollectiondocuments/rm_rm_r_survival_wistar_han_rats_compilation_data.pdf).
Comparison of the tumor incidence data from the current study with HCD can be performed in two different ways. One may use an exploratory (informal) analysis of the data or take a more formal statistical approach to the analysis. Although these procedures provide a statistical evaluation of the data, one should weigh this information along with other biological/toxicological information when making a final assessment regarding a chemical.
Exploratory (Informal) Statistical Analysis of Tumor Incidence
For a given lesion, a common informal method of using HCD is to provide the mean, standard deviation and range of tumor incidence from a historical control database or published literature. Usually, for a given species, strain, sex and vehicle, two different sets of means, standard deviations and ranges are provided: one set that is specific to the route of exposure and another set that combines all routes. In some situations, statistical inferences based on the range of the distribution alone may provide misleading results. As the number of studies increases, the range of the distribution increases so that the range of historical control rates may be too high to be useful. Also summary statistics such as the mean, the standard deviation and the range can be affected by one anomalous study in the historical control database.
For example, consider the incidence of hepatoblastoma in male B6C3F1 mice. In the NTP's database for the 29 studies conducted during the period 09/13/99 to 02/10/04 (based on NTP-2000 diet) there were 48 male mice out of 1447 diagnosed with hepatoblastoma (Table 1) (http://ntp.niehs.nih.gov/ntpweb). These studies had a mean of 3.31%, a standard deviation of 6.47% and a range of 0% to 34% for all routes and vehicles. However, the 34% incidence (17 out of 50 mice) was found in only one oral study with water as the vehicle. The next largest incidence was 8% (4 out of 50 mice). Without this “unusually” large incidence, the range would have been 0-8%. Thus the range quadrupled as a consequence of one study. Other examples include hepatocellular and adrenal cortex adenomas in female F344 rats. In the NTP's database for the 27 studies (all routes and vehicles) conducted during the period 08/16/99 to 01/22/04 (based on NTP-2000 diet) there were 16 out of 1350 female rats diagnosed with hepatocellular adenoma (mean 1.19%; standard deviation 2.62%; range 0% to 12%) and there were 24 female rats out of 1346 diagnosed with adrenal cortex adenoma (mean 1.78%; standard deviation 3.39%; range 0% to 16%) (http://ntp.niehs.nih.gov/ntpweb). The 12% incidence (6 out of 50) of hepatocellular adenoma was found in one skin study with ethanol as the vehicle. The range, without this outlier is 0% to 4%. Thus the range tripled as a consequence of this one study. The 16% incidence (8 out of 50 rats) of adrenal cortex adenoma was found in only one inhalation study (vehicle air). The next largest incidence was 6%. Without this one outlier the range would have been 0% to 6%. Thus the range more than doubled as a consequence of one study.
These examples emphasize that range uses only the two end points of the entire distribution of the HCD and the intervening data are not considered. Consequently, comparison with the historical control range may result in overlooking a potential effect because the current study tumor incidences are “within” the historical range. Therefore, when comparing the current study data with the historical control range, the potential effect that outliers may have on the range should be considered along with all other relevant biological and toxicological data. When outliers are identified, they are not to be discounted, but considered along with other relevant data to determine the significance of any potential treatment-related effect in dosed groups.
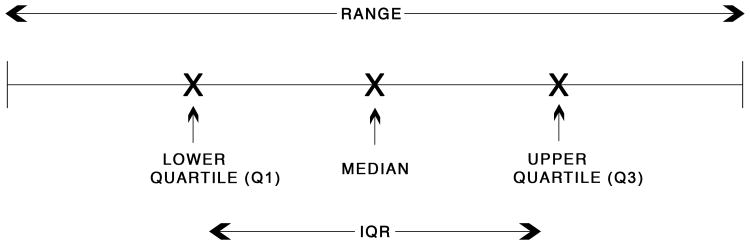
Since the range, mean and standard deviation can be influenced by a single study, if there are a sufficient number of studies available, one could also report the median and interquartile range (IQR) of the HCD, which are not influenced by extreme data points (Figure 1). The median is the mid point of all values sorted from smallest to largest. The range is the difference between the minimum and maximum values. The IQR is a measure of statistical dispersion and is equal to the difference between the upper and lower quartiles (75th and 25th percentiles), which are usually denoted as Q3 and Q1, respectively (Dawson and Trapp, 2004) (Figure 1). The lower quartile is the median of the first half of the data sorted from smallest to largest. The upper quartile is the median of the second half of the data sorted from smallest to largest. In the above hepatoblastoma example, the 34% rate does not contribute to the IQR, but it does contribute to the range. The IQR for this example would be 6% (0% to 6%) compared to the range which is 34% (0% to 34%). In this example if the maximum data point were anywhere beyond 8% the IQR and median would not change but the mean, standard deviation and range would increase, illustrating the robustness of the IQR and median.
Figure 1.
Schematic drawing of the interquartile range (IQR). The median is the mid point of all HCD values sorted from smallest to largest and the range is the difference between the minimum and maximum HCD values. The IQR is the difference between the upper and lower quartiles (75th and 25th percentiles). The lower quartile (Q1) is the median of the first half of the data sorted from smallest to largest. The upper quartile (Q3) is the median of the second half of the data sorted from smallest to largest.
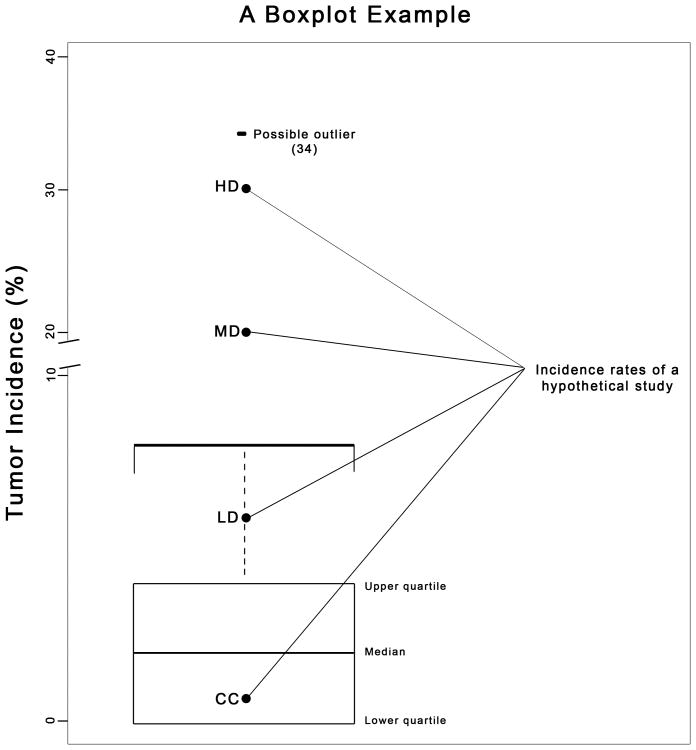
The IQR can be used to build a boxplot, which is a simple graphical way to summarize the distribution of the HCD and is most informative when there are 15 or more studies to assess (Benjamini, 1988; Dawson and Trapp, 2004). The boxplot depicts groups of numerical historical control data through their five-number summaries: the smallest observation, lower quartile (Q1), median (Q2), upper quartile (Q3) and largest observation (Figure 2). It consists of a vertical box, capturing the middle 50% of the data, with the bottom of the box representing Q1 (lower quartile) and the top of the box representing Q3 (upper quartile). The median of the distribution is a horizontal line inside the box. The IQR is the height of the box. From the top of the box a vertical line segment is drawn (known as a “whisker”). This line extends to the largest value in the data not exceeding Q3 + 1.5 IQR. All data points (34% in this example) beyond this value are regarded as unusually large observations (potential outliers). Similarly a whisker below the lower end of the box may also be drawn. This line segment extends to the smallest value in the data not less than Q1 – 1.5 IQR. Thus all observations that go below this point are regarded as unusually small observations (potential outliers). Note, as in Figure 2, that if no data exists within the interval (Q1 – 1.5 IQR, Q1) then there will be no whisker at the lower end of the distribution (and hence no “low” outliers). Similarly, if no data exists within the interval (Q3, Q3 + 1.5 IQR) then there will be no whisker at the higher end of the distribution (and hence no “high” outliers).
Figure 2.
The historical control data from Table 1 was used to construct this boxplot. A boxplot can be used to graphically summarize the distribution of study data and concurrent control with regard to historical control data. The IQR is the height of the box with the bottom of the box representing the lower quartile (Q1) of the HCD and the top of the box representing the upper quartile (Q3) of the HCD. The median of the HCD is a horizontal line inside the box. The “whisker is a hatched line that extends from the top of the box to the largest value in the HCD data, not exceeding Q3 + 1.5 IQR. In this example, the potential HCD outlier of 34% is indicated. Superimposed on the boxplot are hypothetical examples of concurrent control (CC) and study data consisting of low dose (LD), mid dose (MD) and high dose (HD) groups. The presence of a possible outlier (34%) results in data from the MD and HD groups falling within the HCD range. Without this outlier, this data would be outside of the upper range of the HCD.
On a boxplot of the HCD, one may mark the tumor rates in the concurrent control (CC), low dose (LD), medium dose (MD) and high dose (HD) groups (Figure 2). Such a plot would clearly display the current experimental data in the context of the distribution of historical controls. For instance, if HD falls outside the upper whisker of the boxplot, while CC is within the box or whiskers of the distribution, then one may conclude that there is a possible treatment effect observed in the current data. The evidence of a potential treatment effect is stronger if the CC falls within the box. Due to potential differences in survival rates between dose groups and control groups, we recommend that the boxplot be constructed using the Poly-3 survival adjusted tumor incidence rates (Bailer and Portier, 1988) rather than the raw incidence rates.
The data from Table 1 demonstrates that commonly used measures such as the mean, standard deviation and range can be highly affected by extreme data, whereas the median and IQR do not change. In this example, for illustration purposes, if the highest data point of 34 were increased to 70 then the range and standard deviation would almost double and the mean would increase by 40% (3.31 to 4.5). However, the robust measures such as Q1, median, Q3 and the IQR would be unaffected.
Formal statistical analysis of tumor incidence
Another approach to analyzing the concurrent data using information from historical controls would be to apply formal statistical methods. Over the past two decades several attempts have been made by statisticians to develop a statistical procedure for analyzing concurrent experimental data by formally making use of the HCD (Tarone, 1982; Dempster et al., 1983; Hoel, 1983; Hoel and Yanagawa, 1986; Tamura and Young, 1986 and 1987; Prentice et al., 1992; Ibrahim and Ryan, 1996; Ibrahim et al., 1998; Dunson and Dinse, 2001). Each of these methods has strengths and limitations. For instance, Tarone (1982) treats tumor incidence as a binomial proportion and accounts for the extra binomial variation among historical studies using a probability distribution called the beta distribution. While this model seems reasonable and intuitive, the method does not take into consideration that not all animals survive to the end of the study. The statistical methodology of Ibrahim and Ryan (1996) assumes that tumors are lethal and cause instantaneous death, while Ibrahim et al. (1998) assume that the tumors are non-lethal. Both of these assumptions are extreme and may not be true in practice. Dunson and Dinse (2001) overcame the above deficiencies by using a Bayesian methodology which does not make any of the above assumptions regarding the tumor. However, their method requires carefully chosen values for some of the statistical parameters in the model, termed “prior parameters”. From a practical point of view, it may be difficult to choose values for such prior parameters of the statistical model as it requires the toxicologist and pathologist to have a sound understanding of the underlying statistical model and the impact of the prior parameters on the data. Similarly, the statistician would require an understanding of the underlying biological/toxicological mechanisms when choosing the prior parameters.
Recently, Peddada et al., (2007) have proposed a non-parametric statistical method, which overcomes the above deficiencies. This methodology can be modified to compare the dose group with concurrent control and historical controls separately, thus resulting in a pair of p-values rather than one single p-value. It can also be modified to compare the concurrent control with historical controls. From a “weight of evidence” point of view the three p-values may be useful in understanding the significance of the current data. No distributional assumptions are made by this methodology regarding tumor incidences or tumor lethality. Similar to the Poly-3 trend test (Bailer and Portier, 1988; Portier and Bailer, 1989), it uses the Poly-3 correction to the sample size to account for differences in survival rates among dose groups. Such survival adjustments cannot be made without having survival times for individual animals. These data are usually not publicly available for the historical controls and it would be useful to report this information as a part of the HCD. If survival adjustments are not made then there is a potential for bias due to survival differences.
Summary
While the concurrent control group provides the most relevant control data for determining treatment-related effects in a study, evaluation of HCD may be useful in certain situations. These include the interpretation of rare tumors, high-incidence tumors, tumors with a highly variable incidence, tumors with a marginal increase in incidence relative to concurrent controls, or when there are unexpected increases or decreases of tumor incidences in study control animals. All of the statistical approaches described here (exploratory and formal) may be used in combination to evaluate the HCD and to determine its appropriateness for comparison to a set of test data. However, HCD should be used as one of many sources of information that can add to the “weight of evidence” approach when assessing the potential carcinogenic effect of a compound. Other data to consider may be the incidences of other lesions of similar cell lineage, body weight, survival, time of tumor onset, if the tumor occurs in both species or both sexes, if there is a positive dose-related response or if there are bilateral lesions in paired organs. The goal of using HCD is to gain additional information that may aid in the overall evaluation of a carcinogenicity study. The various statistical tools that are available to evaluate HCD should be considered and discussed in the context of sound biological principles. For further comments on statistical approaches, one may refer to the US FDA CDER (2001) guidance for industry document.
Supplementary Material
Acknowledgments
The authors wish to thank Ms. Elizabeth Ney of NIEHS for preparation of the IQR and boxplot figures, and members of the Society of Toxicologic Pathology Historical Control Data Working Group for helpful discussion and review. This research was supported [in part] by the Intramural Research Program of the NIH, National Institute of Environmental Health Sciences [Z01 ES101744-04].
Abbreviations
- HCD
historical control data
- NTP
National Toxicology Program
- IQR
interquartile range
- Q1
lower quartile
- Q2
median
- Q3
upper quartile
- F344
Fischer 344
- CC
concurrent control
- LD
low dose
- MD
medium dose
- HD
high dose
- FDA
Food and Drug Administration
Footnotes
This is an opinion paper submitted to the Regulatory Forum and does not constitute an official position of the Society of Toxicologic Pathology or the Journal “Toxicologic Pathology”. All opinions, positions or ideas expressed within this paper are entirely those of the authors who take full responsibility for them.
References
- Bailer AJ, Portier CJ. Effects of treatment-induced mortality and tumor-induced mortality on tests for carcinogenicity in small samples. Biometrics. 1988;44:417–31. [PubMed] [Google Scholar]
- Baldrick P. Carcinogenicity evaluation: comparison of tumor data from dual control groups in the Sprague-Dawley rat. Toxicol Pathol. 2005;33:283–91. doi: 10.1080/019262390908371. [DOI] [PubMed] [Google Scholar]
- Benjamini Y. Opening the box of a boxplot. The American Statistician. 1988;42:257–262. [Google Scholar]
- Bieler GS, Williams RL. Ratio estimates, the delta method, and quantal response tests for increased carcinogenicity. Biometrics. 1993;49:793–801. [PubMed] [Google Scholar]
- Dawson B, Trapp R. Basic and clinical biostatistics. 4th McGraw-Hill Medical publishers; 2004. [Google Scholar]
- Dempster AP, Selwyn MR, Weeks BJ. Combining historical and randomized controls for assessing trends in proportions. J Amer Stat Assoc. 1983;78:221–7. [Google Scholar]
- Dunson DB, Dinse GE. Bayesian incidence analysis of animal tumorigenicity data. Appl Stat. 2001;50:125–41. [Google Scholar]
- Eiben R, Bomhard EM. Trends in mortality, body weights and tumor incidences of Wistar rats over 20 years. Exp Toxicol Pathol. 1999;51:523–36. doi: 10.1016/S0940-2993(99)80133-X. [DOI] [PubMed] [Google Scholar]
- Haseman JK, Arnold J, Eustis SL. Tumor incidences in Fischer 344 rats: NTP historical data. In: Boorman, Eustis, Elwell, Montgomery, MacKenzie, editors. Pathology of the Fischer Rat Reference and Atlas. Academic Press, Inc; San Diego, California: 1990. pp. 555–564. [Google Scholar]
- Hoel DG. Conditional two sample tests with historical controls. In: Sen PK, editor. Contributions to Statistics. North-Holland Publishing Company; Amsterdam, Netherlands: 1983. [Google Scholar]
- Hoel DG, Yanagawa T. Incorporating historical controls in testing for a trend in proportions. J Amer Stat Assoc. 1986;81(396):1095–9. [Google Scholar]
- Ibrahim JG, Ryan LM. Use of historical controls in time-adjusted trend tests for carcinogenicity. Biometrics. 1996;52(4):1478–85. [PubMed] [Google Scholar]
- Ibrahim JG, Ryan LM, Chen M. Using Historical Controls to Adjust for Covariates in Trend Tests for Binary Data. J Amer Stat Assoc. 1998;93:1282–93. [Google Scholar]
- Peddada S, Dinse G, Kissling G. Incorporating Historical Control Data When Comparing Tumor Incidence Rates. J Amer Stat Assoc. 2007;102:1212–20. doi: 10.1198/016214506000001356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Portier CJ, Bailer AJ. Testing for increased carcinogenicity using survival‐adjusted quantal response test. Fundam Appl Toxicol. 1989;12(4):731–37. doi: 10.1016/0272-0590(89)90004-3. [DOI] [PubMed] [Google Scholar]
- Prentice RL, Smythe RT, Krewski D, Mason M. On the use of historical control data to estimate dose response trends in quantal bioassay. Biometrics. 1992;48(2):459–78. [PubMed] [Google Scholar]
- Tamura RN, Young SS. The incorporation of historical information in tests of proportions: simulation study of Tarone's procedure. Biometrics. 1986;42(2):343–9. [PubMed] [Google Scholar]
- Tamura RN, Young SS. A stabilized moment estimator for the beta-binomial distribution. Biometrics. 1987;43(4):813–24. [PubMed] [Google Scholar]
- Tarone RE. The use of historical control information in testing for a trend in proportions. Biometrics. 1982;38(1):215–20. [PubMed] [Google Scholar]
- US FDA CDER. Guidance for Industry: Statistical Aspects of the Design, Analysis and Interpretation of Chronic Rodent Carcinogenicity Studies of Pharmaceuticals. (Section C) 2001 doi: 10.1081/BIP-100101980. Available at Web site http://www.fda.gov/cder/guidance/815dft.htm. [DOI] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.