Adaptively Constrained Convex Optimization for Accurate Fiber Orientation Estimation with High Order Spherical Harmonics

Abstract

Diffusion imaging data from the Human Connectome Project (HCP) provides a great opportunity to map the whole brain white matter connectivity to unprecedented resolution in vivo. In this paper we develop a novel method for accurately reconstruct fiber orientation distribution from cutting-edge diffusion data by solving the spherical deconvolution problem as a constrained convex optimization problem. With a set of adaptively selected constraints, our method allows the use of high order spherical harmonics to reliably resolve crossing fibers with small separation angles. In our experiments, we demonstrate on simulated data that our algorithm outperforms a popular spherical deconvolution method in resolving fiber crossings. We also successfully applied our method to the multi-shell and diffusion spectrum imaging (DSI) data from HCP to demonstrate its ability in using state-of-the-art diffusion data to study complicated fiber structures.

1 Introduction

With the advance of diffusion weighted MR imaging techniques from the Human Connectome Project (HCP) [1, 2], large scale datasets acquired using sophisticated sampling schemes are becoming publicly available. This provides unprecedented opportunities for mapping the white matter fiber structure with higher spatial and angular resolutions. The vast amount of data, however, also poses significant challenges for data analysis algorithms that have focused mostly on conventional, single-shell acquisition schemes. In this work, we propose a novel method for analyzing diffusion images with arbitrary acquisition schemes by accurately reconstructing the fiber orientation distribution (FOD). We demonstrate our method can achieve superior angular resolution and resolve fiber structures on both simulated and in vivo data from the HCP.

The diffusion tensor model is practically the most popular method for studying major fiber bundles with diffusion imaging data [3]. For the mapping of whole brain connectivity, however, the tensor model is vastly insufficient as complicated fiber crossings occur frequently throughout the brain. To overcome this difficulty, various techniques for high angular resolution diffusion imaging (HARDI) were developed [4–9]. By representing the FOD with spherical harmonics, the spherical deconvolution model has demonstrated great potential in efficiently resolving complicated fiber crossings [6, 9]. The ill-posedness of the deconvolution problem, however, has hindered the use of high order spherical harmonics to resolve fibers with small separation angles. To improve numerical stability, Laplacian or Tiknohov regularizations [7, 9] were incorporated, but these models are limited to single-shell acquisition schemes and only partially overcome the difficulty.

In this work we propose a new method for FOD estimation from data acquired with general sampling schemes, which enables us to seamlessly process HCP data collected with either the multi-shell or DSI schemes [10] illustrated in Fig. 1. At the core of our method is a constrained convex optimization problem for spherical deconvolution with adaptively chosen constraints. By adaptively selecting a minimal set of uniformly distributed constraints, our method can easily use high order spherical harmonics to reconstruct crossing fibers with very small separation angles. In our experiments, we demonstrate on simulated data that our method outperforms a previous method [9] in reliably resolving fibers with small crossing angles. We also apply it to data from the HCP to demonstrate its generality in processing cutting-edge diffusion imaging data.

Fig. 1.

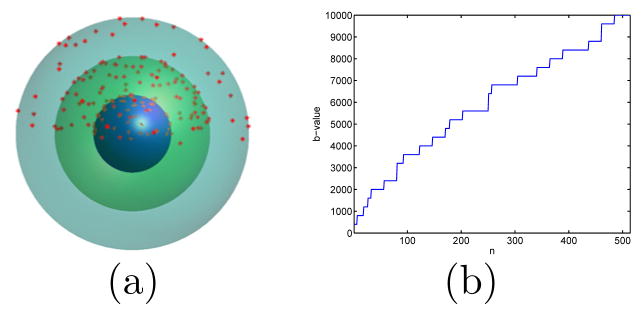
An illustration of the two acquisition schemes from the HCP. (a) The multi-shell sampling scheme with 270 directions distributed over three shells with b=1000,2000,3000 s/mm². (b) The DSI sampling scheme has 514 directions with b-values increasing from 400 to 10,000 s/mm².

The rest of the paper is organized as follows. In section 2, we formulate the spherical deconvolution problem in the general setting of analyzing data from arbitrary acquisition schemes. The adaptively constrained convex optimization approach is then developed in section 3. Experimental results are presented in section 4. Finally conclusions are made in section 5.

2 Spherical Deconvolution Model

In this section, we develop the spherical deconvolution model for FOD reconstruction from general acquisition schemes. At each voxel, the diffusion signal at the b-value b_i and the direction u_i is denoted as s(b_i, u_i)(i = 1, ···, N). Let S denote the unit sphere, and f : S → ℝ⁺ the FOD. Given the single fiber response function k(b, u, w) for a fiber in the direction w, the diffusion signal is expressed as the convolution of the FOD and the kernel:

$$s(b,u)={\int }_{S}f(w)k(b,u,w)dw+n(b,u)$$ (1)

where n is noise. Instead of estimating the kernel directly from the data [6], which is difficult for general acquisition schemes such as DSI, we follow the single tensor model and represent the kernel parametrically as:

$$k(b,u,w)=e^{-b({\lambda }_2+({\lambda }_1-{\lambda }_2){(u·w)}^2)}.$$ (2)

where the only parameters λ₁ ≫ λ₂ = λ₃ are the eigenvalues of the tensor model. These parameters can be either chosen from previous literature or computed easily from the data.

For efficient computation, the FOD is represented with the spherical harmonics up to the order L as:

$$f(w)=\sum _{l,m}{x}_l^m{Y}_l^m(w)\forall w\in S$$ (3)

where $Y_l^m$ is the m-th real spherical harmonics at the order l = 0, 2, ···, L, and $x_l^m$ is the coefficient for the basis $Y_l^m$. Note that only even order spherical harmonics are used because the FOD is symmetric on the sphere. From a signal processing perspective, high order spherical harmonics are needed if we want to accurately represent or reconstruct crossing fibers with really small separation angles. Due to numerical difficulties, typically spherical harmonics up to the order of eight were used in previous work [6, 9], which limits their capability in reliably resolving fiber crossing of small angles.

Using the Funk-Hecke theorem, we can express the diffusion signal as

$$\begin{array}{l}s(b,u)=\underset{S}{\int }\sum _{l,m}{x}_l^m{Y}_l^m(w)e^{-b({\lambda }_2+({\lambda }_1-{\lambda }_2){(u·w)}^2)}dw+n(b,u)\\ =\sum _{l,m}{Y}_l^m(u)G_l(b,{\lambda }_1,{\lambda }_2)x_l^m+n(b,u)\end{array}$$ (4)

with G_l(b, λ₁, λ₂) defined as:

$$G_l(b,{\lambda }_1,{\lambda }_2)=2\pi \underset{-1}{\overset{1}{\int }}{P}_l(t)e^{-b{\lambda }_2-b({\lambda }_1-{\lambda }_2)t^2}dt$$ (5)

where P_l is the Legendre polynomial of degree l.

Let s denote the vector of diffusion signals s(b_i, u_i) sampled at a discrete set of points (b_i, u_i)(i = 1, ···, N). For simplicity, we denote $Y_l^m$ and $x_l^m$ by Y_j and x_j, respectively, with $j=m+\frac{l^2+l+2}{2}$. Given the maximum order L of spherical 2 harmonics used, the total number of basis functions is J = (L + 1)(L + 2)/2. Let x = [x₁, ···, x_j, ···, x_J] be the vector of coefficients for the FOD, we can write (4) in matrix form as:

$$\underset{\_}{s}=A\underset{\_}{x}+\underset{\_}{n}$$ (6)

where n denotes the vector of noise, and A = B · G is the entry-wise product of two matrices B and G defined as follows:

$$B=\left(\begin{array}{cccc}{Y}_1(u_1)& Y_2(u_1)& \cdots & Y_J(u_1)\\ Y_1(u_2)& Y_2(u_2)& \cdots & Y_J(u_2)\\ \cdots & \cdots & \cdots & \cdots \\ Y_1(u_N)& Y_2(u_N)& \cdots & Y_J(u_N)\end{array}\right)G=\left(\begin{array}{cccccc}{G}_0(b_1)& G_2(b_1)& \cdots & G_2(b_1)& \cdots & G_L(b_1)\\ G_0(b_2)& G_2(b_2)& \cdots & G_2(b_2)& \cdots & G_L(b_2)\\ & & & \cdots & & \\ G_0(b_N)& G_2(b_N)& \cdots & G_2(b_N)& \cdots & G_L(b_N)\end{array}\right).$$

For each order l, the element G_l(b_i) = G_l(b_i, λ₁, λ₂) is repeated 2l + 1 times on the i-th row.

3 Adaptively Constrained Convex Optimization

In this section, we develop a novel approach for FOD estimation by solving the spherical deconvolution problem as a constrained convex optimization problem. The key idea is the adaptive selection of the set of constraints for every voxel to avoid overly constrain the solution and affect reconstruction accuracy. The constraint we impose on FOD reconstruction is motivated by its non-negativity condition. With the spherical harmonics representation up to a fixed order, however, it is impossible to completely eliminate negative values in the FOD. It is thus critical to limit the negative components to the minimal extent and ensure major fiber directions are captured. To achieve this goal, our strategy is to constraint the FOD to be non-negative on a minimal set of uniformly distributed points on the sphere.

With a remeshing algorithm [11], we build a collection of constraint sets = {V₁, V₂, ···, } with varying number of points on the sphere, where each member $V_Q=\{v_Q^1,v_Q^2,\cdots ,v_Q^Q\}$ is a set of Q uniformly distributed points on the hemisphere of the unit sphere. With the spherical harmonics representation, the requirement that f should be non-negative on V_Q can be expressed as:

$$C_Q\underset{\_}{x}\ge 0$$ (7)

where C_Q is a matrix of size Q × J defined as

$$C_Q=\left(\begin{array}{cccc}{Y}_1(v_Q^1)& Y_2(v_Q^1)& \cdots & Y_J(v_Q^1)\\ Y_1(v_Q^2)& Y_2(v_Q^2)& \cdots & Y_J(v_Q^2)\\ \cdots & \cdots & \cdots & \cdots \\ Y_1(v_Q^Q)& Y_2(v_Q^Q)& \cdots & Y_J(v_Q^Q)\end{array}\right).$$

Given a specific constraint set V_Q(Q = 1, 2, ···), the spherical deconvolution problem for FOD reconstruction can be formulated as a constrained convex optimization problem:

$$min{\Vert \underset{\_}{s}-A\underset{\_}{x}\Vert }^2\mathrm{s}.\mathrm{t}.C_Q\underset{\_}{x}\ge 0$$ (8)

Because this problem is convex, global minimum can always be found numerically with software packages such as cvx [12]. With the FOD being non-negative on a set of uniformly distributed points, we ensure that large negative components will not occur and most of the energy of the FOD are contributed by physically meaningful, i.e., positive, components. Because the complexities of fiber crossings are spatially varying across the brain, the number of active constraints in (8) could be different as a result. Thus it is also unreasonable to fix the number of constraints. To overcome this difficulty, we adaptively search through the constraint collection at every voxel to find the smallest Q such that the solution satisfies:

$$\frac{{\int }_{f(w)>0}\mathit{fdw}}{{\int }_{f(w)<0}\mid f\mid dw}>\delta .$$ (9)

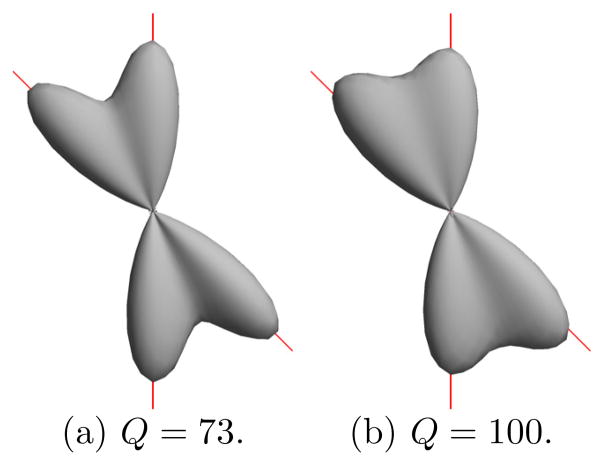
This condition measures how successful the reconstructed FOD is able to focus its energy on positive components. For example, if we pick δ = 25, we ensure more than 95% of the L1 energy of the FOD are from positive components. As a demonstration, we show in Fig. 2 the FOD reconstruction results of two fibers using simulated diffusion data from 60 directions with b=1000 s/mm². The maximum order of spherical harmonics used here is L = 8. The result in Fig. 2(a) is obtained from adaptively determined constraints, where Q = 73, and the result in Fig. 2(b) is obtained by fixing Q = 100. We can see the overly constrained solution is less sharp and one of its peaks is obviously misaligned with the true fiber direction.

Fig. 2.

FOD reconstruction from simulated diffusion data. The true fiber directions are plotted as red lines.

For practical implementation, there is no need to start the search from Q = 1. Given a maximum order L, we can pick a constraint set from experience and start the search there. For L = 8, we typically start the search at Q = 60 and the reconstruction of the FOD in Fig. 2(a) took less than one second.

4 Experimental Results

In this section, we present experimental results to demonstrate our method on both simulated and in vivo data from the HCP. In our experience, the FOD reconstruction results from our method are very robust to the selection of the parameters in the kernel. For all experiments, we thus fix the parameters for the kernel as λ₁ = 0.0017 and λ₂ = 0.0003 following the literature [9], and the threshold in (9) as δ = 25.

4.1 Simulated Data

In the first experiment, we compare with the spherical deconvolution method in [9] on simulated data. For two fibers with a crossing angle of 30°, we follow the multi-tensor model to simulate the diffusion data from a single-shell acquisition scheme of 81 directions with b = 3000 s/mm². Rician noise was added to obtain a signal to noise ratio of 20. For every parameter selection from both methods, the experiments were run 100 times to obtain the mean and standard deviation of the FOD. For the spherical deconvolution method in [9], the results with the maximum order L = 8 and L = 16 are plotted in Fig. 3(a) and (b). At the order of L = 8, we chose the same regularization parameter 0.006 as in [9]. We can see that the reconstructed FOD at this order cannot resolve the fiber crossing. When the order was increased to L = 16, its result became highly oscillatory even though we increased the regularization parameter to 0.02. With our adaptively constrained optimization method, such oscillations were successfully suppressed and accurate results were obtained as shown in Fig. 3(c). This demonstrates the superior ability of our method in resolving fiber crossings at small angles with data from single-shell acquisition schemes.

Fig. 3.

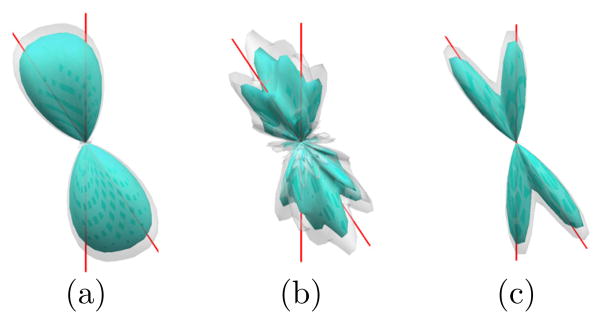
A comparison of 100 runs of FOD reconstruction results from simulated diffusion data. The cyan surface is the mean FOD and the shaded surface is mean plus two standard deviation of the FOD from 100 runs. Red lines indicate true fiber directions. (a) Method in [9]: L = 8. (b) Method in [9]: L = 16. (c) Our method: L = 16.

4.2 Multi-shell Data from HCP

In the second experiment, we applied our method to the diffusion data of a subject from the HCP that was acquired with a multi-shell sampling scheme as illustrated in Fig. 1(a). The reconstructed FODs of an ROI on an axial slice, which is shown in Fig. 4(b), in the right thalamus with L = 8 and L = 16 are plotted in Fig. 4(a) and (c). All FODs are color-coded with the directions. The reconstructed FODs are consistent with known anatomical knowledge that various fibers cross the thalamus to reach different cortical regions. The top-right corner of the ROI touches the cortical spinal tract that goes from inferior to the superior part of the brain. At this location, the FOD reconstructed with our method in both Fig. 4(a) and (c) has only one major fiber direction, which is consistent with the orientation of the cortical-spinal tract. By comparing the results in Fig. 4(a) and (c), especially regions highlighted by the dashed lines, we can clearly see that our method successfully uses high order spherical harmonics to achieve better angular resolution of crossing fibers than results reconstructed with low order spherical harmonics.

Fig. 4.

FOD reconstruction results from multi-shell diffusion data of the HCP.

4.3 DSI Data from HCP

In the third experiment, we applied our method for FOD reconstruction using DSI data of a subject from the HCP. As illustrated in Fig. 1(b), the diffusion data was acquired at 514 points in the q-space with b-values ranging from 400 to 10000 s/mm². For an ROI on a coronal slice shown in Fig. 5(b) that has crossing fibers possibly from the corpus callosum, cortical spinal tract, and superior longitudinal fasciculus, we applied our method with L = 8 and L = 16 to compute the FODs. The reconstructed FODs are plotted in Fig. 5(a) and (c). As a demonstration, we highlighted two FODs with dashed lines in Fig. 5(a) and (c). It clearly shows the power of our method in using high order spherical harmonics to resolve crossing fibers with small separation angles.

Fig. 5.

FOD reconstruction results from DSI data of the HCP.

5 Conclusions

In this paper we developed a novel approach for the accurate reconstruction of FODs from arbitrarily sampled diffusion imaging data. By solving the spherical deconvolution as an adaptively constrained convex optimization problem, our method can robustly use high order spherical harmonics to resolve complicated fiber crossings. We demonstrated the power of our method on HCP data from both the multi-shell and DSI acquisition schemes. For future work, we will integrate our method with tractography algorithms and investigate its application in studying whole brain connectivity.