In Vivo Radiofrequency Heating in Swine in a 3T (123.2 MHz) Birdcage Whole-Body Coil

Abstract

Purpose

To study in vivo radiofrequency (RF) heating produced due to power deposition from a 3T (Larmour frequency = 123.2 MHz), birdcage, whole-body coil.

Methods

The RF heating was simulated in a digital swine by solving the mechanistic generic bioheat transfer model (GBHTM) and the conventional, empirical Pennes bioheat transfer equation for the following two cases: (1) when the porcine head was in the isocenter, and (2) when the porcine trunk was in the isocenter. The simulation results were validated by making direct fluoroptic temperature measurements in the skin, brain, simulated hot regions, and rectum of ten swine (Case 1, N= 5, mean animal weight = 84.03 ± 6.85 kg, Whole-body average SAR = 2.65 ± 0.22 W/kg; Case 2, N= 5, mean animal weight = 81.59 ± 6.23 kg, Whole-body average SAR = 2.77 ± 0.26 W/kg) during one hour of exposure to a turbo spin echo sequence.

Results

The GBHTM simulated the RF heating more accurately compared to the Pennes equation. In vivo temperatures exceeded safe temperature thresholds with allowable SAR exposures. Hot regions may be produced deep inside the body, away from the skin.

Conclusion

SAR exposures to produce safe temperature thresholds may need re-investigation.

INTRODUCTION

Excessive, non-uniform in vivo radiofrequency (RF) heating of the body during an MRI session is a ‘grave’ safety concern. To mitigate this concern, the International Electrotechnical Commission (IEC) has recommended safe absolute temperature and temperature change thresholds that should not be exceeded during a session (maximum core and local temperature ≤ 40 °C and maximum core temperature change ≤ 1 °C in the First Level mode) (1). Since it is difficult to determine local temperatures non-invasively, and unpleasant/time-consuming to measure core temperatures for every scan, values for specific absorption rates (SAR) were determined to satisfy the temperature guidelines. These SAR values were computed using simple thermal models (e.g., Pennes model or simpler models) with several physiologically unrealistic assumptions and no MRI-relevant experimental validations (1–4). New, physiologically more realistic, validated bioheat models are needed to better understand in vivo heating and accurately compute SARs to keep temperatures below safe thresholds (5).

The IEC recommends the maximum whole-body average SAR of 4 W/kg in the First Level mode for a volume transmit body coil application. The maximum allowable deposition of RF energy is 4 W/kg * 60 min = 240 W.min/kg. No limits are recommended for local SAR values. The maximum allowable local SAR in the body for a surface coil application is 20 W/kg to satisfy the safe local temperature thresholds (1). RF energy is deposited non-uniformly in the body during an MRI scan. The energy distribution is a function of the coil used to deposit the energy, tissue geometry, and the distribution of tissue electromagnetic properties. Resultant RF heating is a function of the distribution of thermal properties, thermal mass, surface area, blood flow, clothing, other thermo-physiologic responses (e.g., sweating), room temperature, room air flow, and room humidity. Non-uniform in vivo distribution of the RF energy and heating makes it necessary to appropriately define global and local limits for the SAR to avoid heating beyond specified safe temperature limits and improve safety.

The maximum allowable whole-body average SAR of 4 W/kg was determined primarily by implementing the two-node model of Drs. Adair and Berglund of the US Air Force Research Laboratory. The model was developed to simulate average core and skin temperature changes in healthy volunteers during exercise due to a uniformly distributed heat load (3,4,6). To validate the model for predicting core temperature change in MRI applications, experiments were performed on two healthy, awake volunteers. The researchers were surprised to note that, contrary to the prediction of their model of a plateaued core temperature change, the core temperature of the volunteers kept increasing during the RF power deposition with a 1.5T, birdcage whole-body coil. They recommended “more human experiments and development of better more complex models” to accurately simulate the core as well as local temperature changes.

Another model that has often been used to determine the maximum allowable whole-body average SAR is Pennes bioheat transfer equation (BHTE) (1,2,7). The Pennes BHTE overestimates the SAR needed to produce a given temperature change in deep tissue. This is so because the conventional implementation of this model does not allow the blood temperature to change as a result of the heat exchange between the blood and surrounding tissue. Further, the Pennes equilibration constant is set to zero, which is an inverse measure of the effectiveness of the energy exchange between the blood and surrounding tissue (Pennes equilibration constant = 0 for 100% ideal heat exchange, Pennes equilibration constant = 1 for 0% ideal heat exchange). The simplifications result in overestimation of the cooling effects of the blood and thus underestimation of the resultant heating in deep tissue for a given power. The conventional Pennes BHTE has been criticized by several researchers due to its unrealistic assumption of constant blood temperature and several improvements have been proposed (8–24). Also, there exists no experimental validation of the results of this model for MRI applications.

The IEC does not provide any restrictions for the local SAR deposition for volume coils. However, assuming that the local SAR deposition may be regulated on modern MR scanners as per the local SAR limits developed for surface coil applications; once again, these local SAR limits were determined by simulating the Pennes BHTE. Thus, as discussed above, these local SAR limits may be overestimated for deep tissues.

There is little data available related to the RF heating due to power deposition with a 3T volume transmit body coil. Boss et al. measured skin temperature changes of 0.88 °C in human volunteers due to the whole-body average SAR exposure of 1.60 W/kg for ~6.75 min and 2.85 W/kg for an additional 4.25 min (i.e., total exposure of ~10 min) (25). More experimental data are needed to develop and validate new bioheat transfer models, and to better understand in vivo heating.

Realizing the limitations of the current thermal models and dearth of available experimental data, the International Commission on Non-Ionizing Radiation Protection (ICNIRP) recommends “further investigation to define more precisely the spatial deposition of RF energy during an MR procedure and the corresponding temperature fields in the human body using a three-dimensional bio-heat transfer model, including modeling of the pregnant woman and fetus” to improve MRI safety (5).

This preliminary investigation simulates RF heating in a digital pig placed in a 3T volume transmit body coil, by solving the new mechanistic generic bioheat transfer model (GBHTM). Next, direct fluoroptic temperature measurements are made in ten swine to validate the GBHTM results. Finally, the GBHTM simulation results and direct fluoroptic measurements are compared to the predictions of the ‘gold standard’, conventional, empirical Pennes BHTE. The investigation was performed to better understand the non-homogeneous RF heating in a 3T whole-body scanner.

METHODS

This section presents justification for using swine as an animal model, development of a digital swine model and details of the electromagnetic and thermal simulations to determine the RF heating, experimental design to validate the simulations, and statistical analyses.

Swine as an Animal Model

Pigs are thermo-physiologically similar but conservative animal models of humans. A pig has human-comparable thermal mass, surface area, water loss through skin over and below its critical hot environmental temperature (7–16 g m⁻² h⁻¹ for swine and 6–10 g m⁻² h⁻¹ for humans), metabolic energy per unit surface area (52.2 Wm⁻² for swine and 50.5 Wm⁻² for humans), cardiac output, cardiac rate, respiratory volume, respiratory rate, electromagnetic and thermal properties, and thermoregulatory mechanisms (e.g., swine, like humans, do not pant, etc.) (26–30). The critical hot environmental temperature limit for a pig (36 °C for a newborn, 30 °C for a mature) is comparable to but lower than that of a human (37 °C for a newborn, 43 °C for a mature), making it a thermo-physiologically conservative model of a human (31).

In addition, swine do not sweat actively. However, the passive water loss thorough swine and human skin is comparable. The inability of swine to actively sweat allows obtaining more conservative estimates of the RF heating. This is especially important since temperature thresholds of sweating are not well understood in mammals in health and disease. Clothing and coil arrangements can further reduce the effectiveness of sweating in removing energy through the skin because of the reduced evaporation.

Next, as mentioned above, RF heating is a function of the RF coil, tissue geometry, tissue type, blood flow, and the physiological status of the biological model. Porcine and human body geometries differ from one another (e.g., swine skull is 2–5 times thicker than a human skull; swine brain mass is ~7 times lighter than that of a human brain; swine trunk is largely cylindrical compared to a human trunk, which is largely elliptical; swine and human limbs are significantly different from one another; etc.). Large differences in porcine and human body geometries will result in significantly different RF exposure levels and RF heating in swine compared to that in humans.

Digital Swine Model to Simulate RF Heating

A digital swine model was developed by using computed tomography to acquire 1.5 mm isotropic, whole-body anatomic images of a ~73.61 kg euthanized pig. The images were segmented in six tissue types- skin, fat, muscle, bone, lungs, and internal air- using MIMICS software (Materialise, Belgium). Appropriate electromagnetic and thermal properties were assigned to the tissues. The digital pig had a mass of ~73.95 kg. The segmented swine model was exported to appropriate softwares to compute electromagnetic field and associated RF heating.

Simulations to Study RF Heating

In vivo RF heating produced due to the power deposition from a 3T birdcage body coil was simulated by solving the GBHTM and the conventional Pennes BHTE (In Vivo Temperatures, LLC, Roseville, MN, USA) (2,13,32). No thermoregulatory input (e.g., temperature based perfusion change) was included in the simulations. The GBHTM was chosen because it was derived based on the conservation of energy and allows blood to change its temperature based on the thermal interaction between the blood and the surrounding heated tissue. This permits better estimation of the heating. The conventional Pennes BHTE was chosen because it had been used to simulate in vivo RF heating and determine safe SAR limits by the regulatory agencies (1,33).

Traditionally, the Pennes BHTE has been a point of contention and a source of confusion. This is because the lack of a formal derivation of the Pennes BHTE makes it difficult to interpret the Pennes’ variables, parameters, and results in terms of the underlying physiology. For example, thermodynamically the blood temperature in the Pennes BHTE can be defined in at least four different ways: (1) local, point-wise true blood temperature; (2) blood velocity weighted blood vessel area averaged blood temperature; (3) blood vessel area averaged blood temperature; and (4) perfused tissue volume averaged blood temperature. Assuming blood temperature as the point-wise true temperature or the velocity weighted temperature makes the Pennes BHTE physically invalid. Assuming blood temperature as the area averaged or volume averaged temperature renders physically invalid the traditional conception of the Pennes perfusion term as a blood flow term. Any extension of the Pennes BHTE (e.g., modeling Pennes blood temperature without a mechanistic derivation) is expected to suffer from similar shortcomings.

Next, comparing the GBHTM and Pennes BHTE theoretically, the GBHTM has been shown to be a mechanistic, generalized derivation of the Pennes model. The GBHTM presented exact mathematical relations between Pennes empirical variables and parameters, and the underlying physiology; and explained implicit and explicit assumptions of the Pennes BHTE. The GBHTM reduces to the form of the Pennes BHTE in the limiting case of infinite blood flow (13). Hence, to appropriately implement the Pennes BHTE, the GBHTM was simulated with infinite blood flow. All other parameters and variables were kept the same between the GBHTM and the Pennes BHTE. In other words, the GBHTM simulations presented here consider variations in the tissue and blood temperatures, while the Pennes BHTE simulations consider variations in the tissue temperatures alone and keep the blood temperature constant.

RF heating was simulated for the following two cases: (1) when the porcine head was in the isocenter of a 3T volume transmit birdcage body coil (Larmor frequency ~ 123.2 MHz), and (2), when the porcine trunk was in the isocenter of the coil. The two cases were chosen as typical examples to study the RF heating because head and body scans are regularly performed with body transmit coils. The 3T (~123.2 MHz) body coil was modeled as a 32 channel, high pass, 50 cm long, 60 cm internal diameter (ID) birdcage coil shielded with a 120 cm long and 65 cm ID faraday cage in REMCOM finite difference time domain software (XFdtd, Remcom, State College, Pennsylvania, USA). The local SAR distribution (a necessary input to the GBHTM and Pennes BHTE to compute the associated heating) in swine was obtained by importing the digital pig in the REMCOM’s XFdtd software and solving Maxwell's equations with the digital pig appropriately placed in the 3T body coil.

Experimental Design to Validate Simulations

The animal experiment protocol for this study was approved by the Institutional Animal Care and Usage Committee (IACUC) of the University.

RF heating was measured as a function of time in ten swine due to the RF power deposition from a 3T birdcage, volume transmit body coil using fluoroptic probes (Luxtron Corporation, model m3300 and 3000). The RF heating was produced by implementing a turbo spin echo (TSE) sequence in a 3T scanner. The appropriate amount of power to be deposited was determined by measuring the weight of the pig before the pig was placed in the scanner. The power, as reported by the scanner, was adjusted by adjusting the flip angle of the TSE sequence to obtain necessary whole-body average SAR exposure. The whole-body average SAR was computed by dividing the RF power from the weight. The RF power was deposited for ~62 minutes by running two ~31 min long TSE sequences contiguously. Temperatures were measured for approximately one hour before the RF power deposition (pre-RF region), for approximately one hour during the RF power deposition (RF region), and for approximately 30 minutes after the RF power deposition (post-RF region). The pre-RF region temperatures were recorded to characterize the approximate linear drop of in vivo temperatures in animals due to anesthesia. The RF power was deposited for an hour to produce reliably measurable temperature changes. The post-RF region temperatures were recorded to compare the thermal responses in the post-RF region to the thermal responses in the pre-RF region.

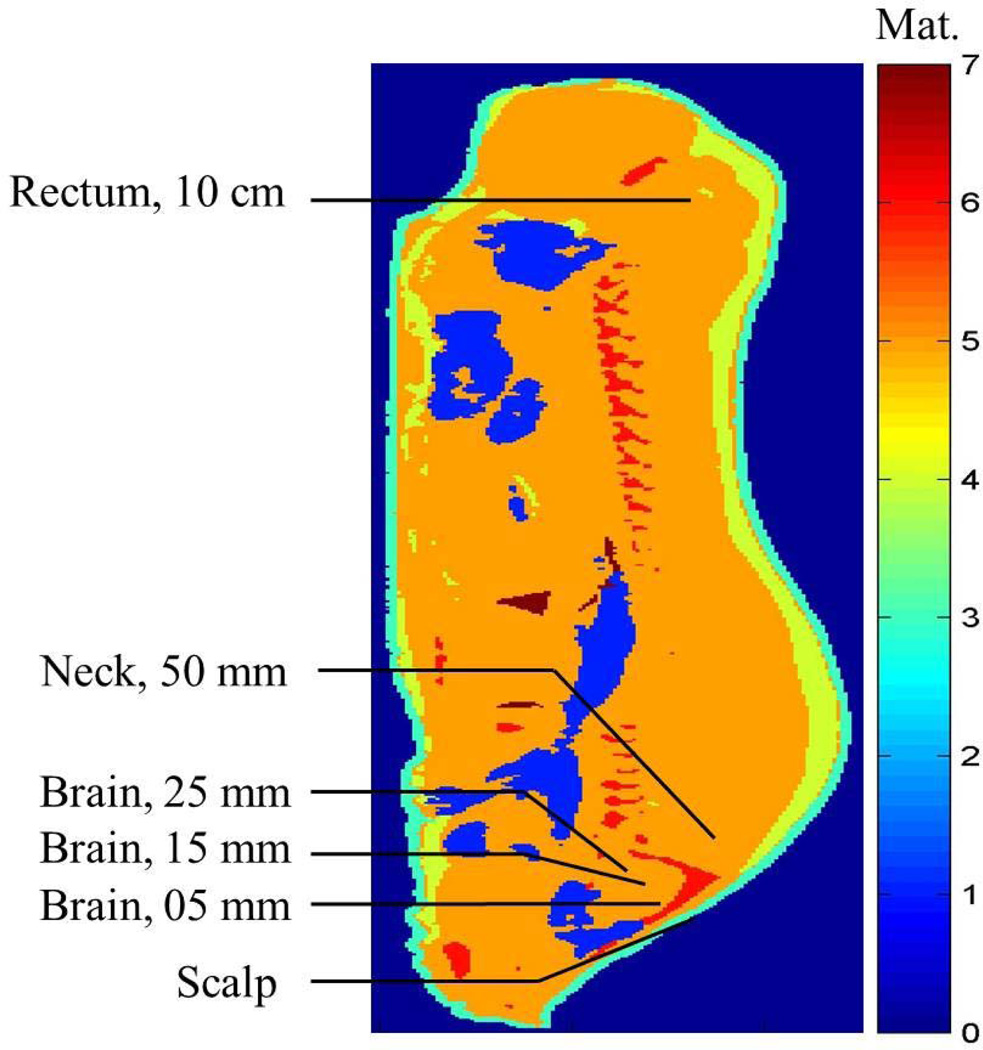
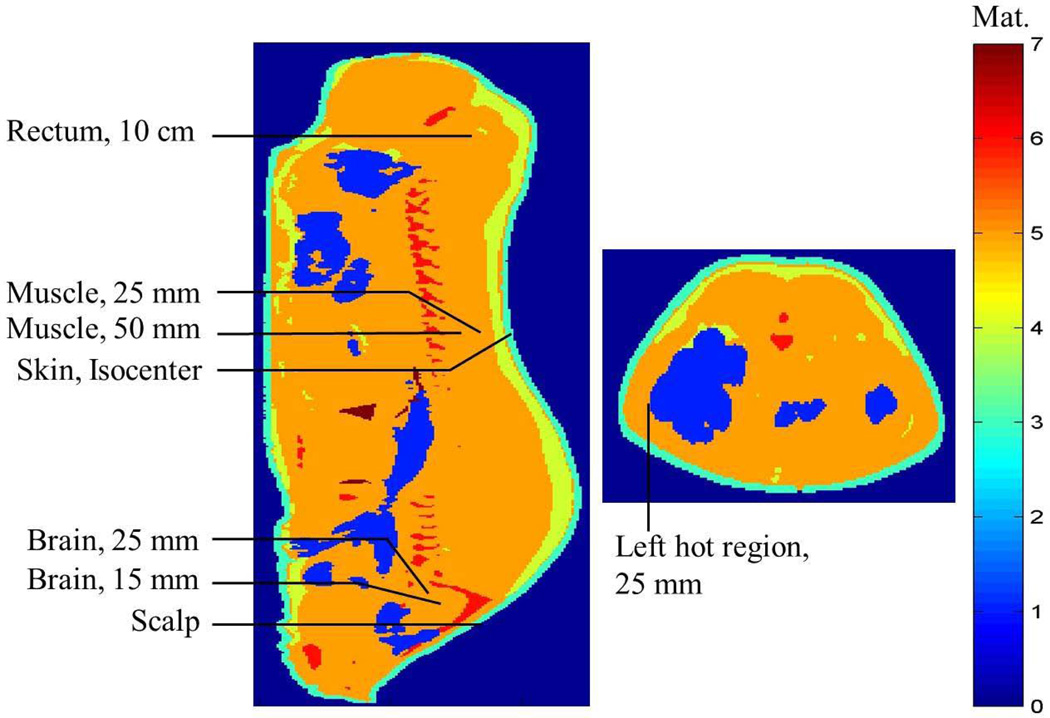
Regarding the placement of the fluoroptic probes to measure the RF heating, for case 1 (when the porcine head was in the isocenter of the body coil, N= 5, mean animal weight = 84.03 kg, SD = 6.85 kg), the fluoroptic probes were placed in the subcutaneous layer of the scalp; 5, 10, 15, 20, and 25 mm deep in the brain after the dura; 5 cm deep and 4.5 cm proximal from the end of the skull, 5 mm lateral to the midline in a simulated hot region; and 10 cm deep in the rectum (Figure 1). For case 2 (when the porcine body was in the isocenter of the 3T coil, N= 5, mean animal weight = 81.59 kg, SD = 6.23 kg), the fluoroptic probes were placed in the sub-cutaneous layer of the scalp; 15 mm and 25 mm deep in the brain after the dura; in the subcutaneous layer of the skin in the plane of the isocenter, 5 mm lateral to the midline; 25 mm and 50 mm deep in the plane of the isocenter, 5 mm lateral to the midline in a simulated hot region; 25 mm deep in the plane of the isocenter on the left hand side (LHS) of the body closest to the MR table in another simulated hot region; and 10 cm deep in the rectum (Figure 2).

FIG. 1.

Approximate fluoroptic probe locations in the sagittal plane 5 mm lateral to the central plane in the digital swine model when the swine head was placed in the isocenter of a 3T birdcage body coil. Material (Mat.) 0¼external air, 1¼internal air, 2¼blood (not shown), 3¼skin, 4¼fat, 5¼muscle, 6¼bone, 7¼lungs.)

FIG. 2.

Approximate fluoroptic probe locations in the sagittal plane 5 mm lateral to the central plane (left) and central axial plane (right) in the digital swine model when the swine trunk was placed in the isocenter of a 3T birdcage body coil. Material (Mat.) 0¼external air, 1¼internal air, 2¼blood (not shown), 3¼skin, 4¼fat, 5¼muscle, 6¼bone, 7¼lungs.

The total of 10 swine was used for the experiments. Five swine were used when the swine head was placed in the isocenter of the 3T coil (Case 1). Five additional swine were used when the swine trunk center was placed in the isocenter of the 3T coil (Case 2). The number of animals was chosen as N=5 for each case since according to the statistical power analysis a minimum number of N=4 animals was required to detect a temperature change >0.3°C with >95% power and P<0.01 (two-sided). The room temperature and humidity, end tidal CO₂, and the % inspired/expired anesthetic agent Isoflurane were monitored continuously to keep the animals stable, and recorded manually every 30 min.

Each animal was rested for at least 3 days after its arrival to the animal facility to avoid anxiety, and was fasted for 12 hours before the induction of anesthesia to avoid complications (34). Water was provided ad libitum during fasting. For the experiment, first the animal was immobilized and sedated using 5–10 mg/kg Telazol (Tiletamine HCL + Zolzepam HCL). This was followed by intubation. The animal was kept anesthetized during the experiment (~5 hrs) using 1.5–2.5% isoflurane in 50%–50% air-O₂. Respiratory rate was set to 12–13 cycles/min using a ventilator (Ohmeda 7000). Minute volume was set between 7–8 l/min. Saline (0.9% NaCl) was provided through an ear vein at the rate of ~0.4–0.6 l/hr to keep the animal hydrated during the experiment. Afterwards, a ~18 gauge (~1.27 mm diameter) hole was drilled into the skull perpendicular to the plane of the skull. The hole was located ~45 mm distal from the back of the skull and ~5 mm lateral to the midline between the ears. The dura was punctured using an 18 gauge (1.27 mm diameter) catheter. Next, the animal was placed inside a 3T scanner and the fluoroptic probes were slipped through the dura into the brain at the above mentioned depths. A piece of cotton gauge was put in the hole to keep the fluoroptic probes stationary and stop cerebral spinal fluid (CSF) from leaking. One fluoroptic probe was placed 10 cm deep in the rectum to measure the core temperature. Other fluoroptic probes were placed using 18 gauge (1.27 mm diameter) catheters of suitable lengths at predetermined locations: scalp, skin, and in simulated hot regions. After the probe placements, the power deposition was adjusted and the temperatures were recorded during the pre-RF region, RF region, and post-RF region. At the end of the experiment, the animal was euthanized using a pharmaceutical grade saturated KCl solution.

Statistical Analyses

Mean temperature curves (per location), pairwise difference curves, and pointwise 95% confidence bands were estimated by fitting a functional linear mixed-effects ANOVA model (35) to the data, where location was treated as a fixed effect, and each pig was modeled as a random effect nested within location. The resulting estimated curves and confidence bands were then smoothed using cubic B-splines (36). All confidence intervals were adjusted for multiple comparisons. This statistical modeling accounts fully for the uncertainty in the measurements. Modeling a pig as a random effect nested within each location accounts for variation among pigs.

RESULTS

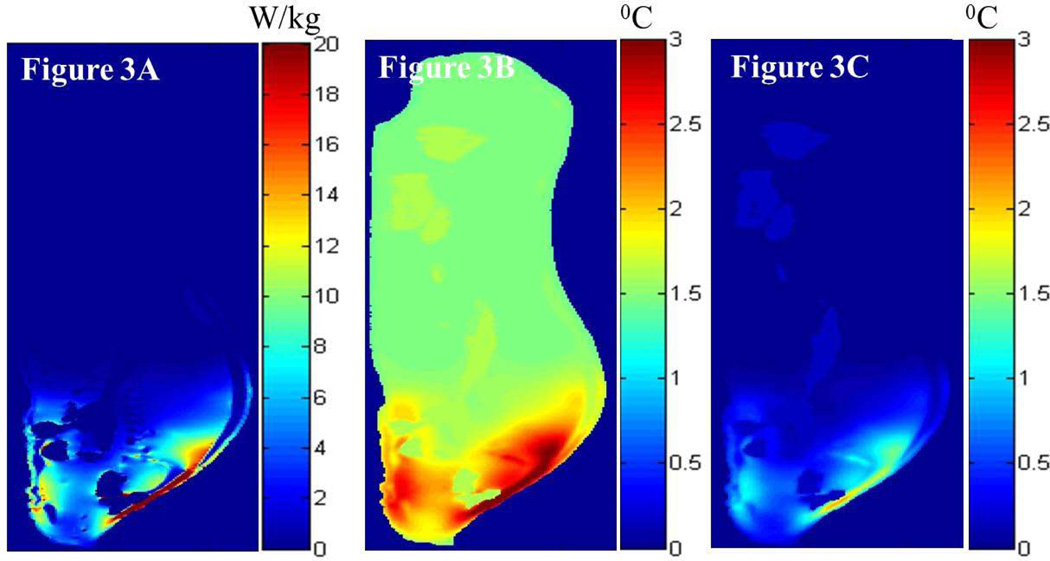
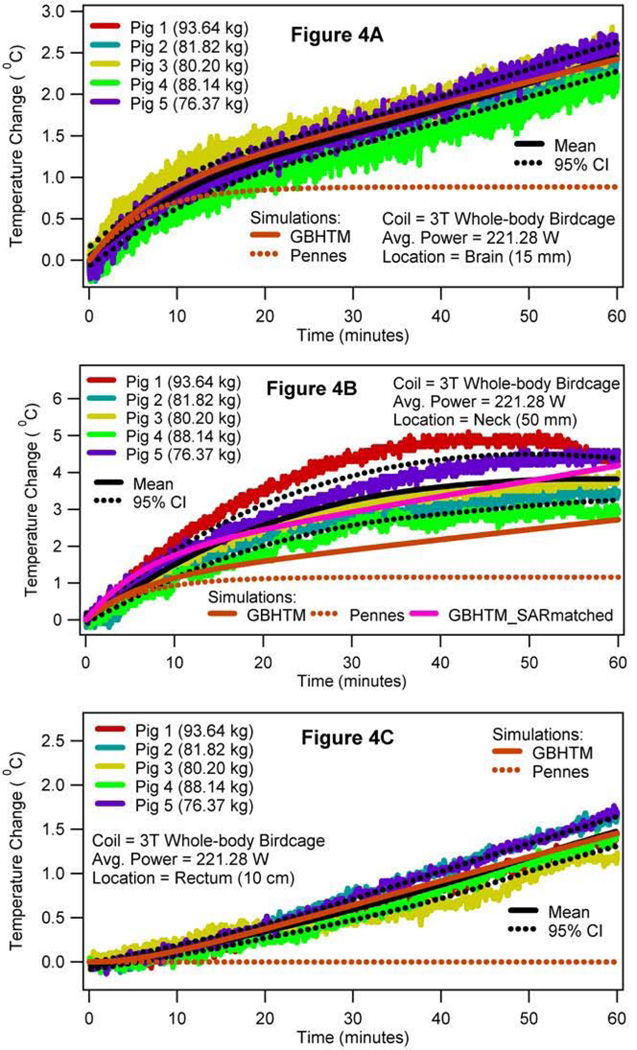
Figure 3 presents the simulated local SAR, and the associated simulated RF heating in the sagittal plane 5 mm lateral to the central plane of the digital pig, when the porcine head was placed in the isocenter of the 3T volume transmit birdcage coil (i.e., case 1). More specifically, Figure 3A presents the local SAR distribution in the sagittal plane due to the RF power deposition from the 3T coil for the whole-body average SAR of 2.65 W/kg. Figures 3B and 3C present the RF heating at the end of the RF deposition simulated using the GBHTM and Pennes BHTE, respectively. Figure 4 presents the measured and simulated local temperature change 15 mm deep in the brain (top figure), 50 mm deep in the neck in a simulated hot region (middle figure), and 10 cm deep in the rectum (bottom figure) (whole-body average SAR = 2.65 W/kg, SD = 0.22 W/kg). Estimated mean curves and 95% confidence bands are also presented. It is shown that the GBHTM simulated the measured RF heating more accurately compared to the conventional Pennes BHTE. The Pennes model underestimated the RF heating. Next, the measured brain temperature approached 1.1 °C (SD = 0.13 °C) within 15 minutes of the RF power deposition. The measured temperature change in the neck during this time approached 2.1°C (SD = 0.51 °C). The measured rectal temperature change during this time was 0.25 °C (SD = 0.11 °C), which was comparable to the standard deviation of the fluoroptic probes (~0.10–0.20 °C).

FIG. 3.

Simulated local SAR distribution (a) and associated temperature changes simulated using the GBHTM (b) and Pennes BHTE (c) in the sagittal plane 5 mm lateral to the central plane at the end of the heating, when the swine head was placed in the isocenter of a 3T birdcage body coil (case 1).

FIG. 4.

RF power induced temperature changes 15 mm deep in the brain after the dura (a), 50 mm deep in the neck (b), and 10 cm deep in the rectum (c) when the swine head was placed in the isocenter of a 3T birdcage body coil (case 1).

Table 1 presents the measured whole-body average SAR and the associated temperature changes when the porcine head was placed in the isocenter of the 3T coil for all five animals (case 1). The mean whole-body average SAR of 2.65 W/kg produced the mean temperature change of ~2.47 °C 15 mm deep in the brain after the dura (SD = 0.14 °C), 3.79 °C 50 mm deep in the neck (SD = 0.61 °C) and 1.48 °C 10 cm deep in the rectum (SD = 0.13 °C) at the end of the hour long RF heating (also, refer to Figure 4). The brain temperature changes were comparable to one another. The brain temperature change, the neck temperature change, and the rectal temperature change were significantly different from one another.

Table 1.

Measured whole-body average SAR and the associated temperature changes at the end of the heating, when the porcine head was placed in the isocenter of a 3T birdcage body coil (i.e., case 1).

No.	Weight (kg)	SAR (W/kg)	Scalp (°C)	Brain (5mm) (°C)	Brain (10mm) (°C)	Brain (15mm) (°C)	Brain (20mm) (°C)	Brain (25mm) (°C)	Neck (°C)	Rectum (°C)
1	93.64	2.37	4.01	2.48	2.45	2.47	2.52	2.40	4.38	1.40
2	81.82	2.72	3.78	2.52	2.41	2.45	2.58	2.40	3.40	1.60
3	80.20	2.76	5.51	2.80	2.59	2.57	2.56	2.30	3.75	1.50
4	88.14	2.48	4.18	2.34	2.30	2.24	2.32	2.30	3.02	1.30
5	76.37	2.92	3.68	2.83	2.60	2.61	2.49	2.60	4.42	1.60

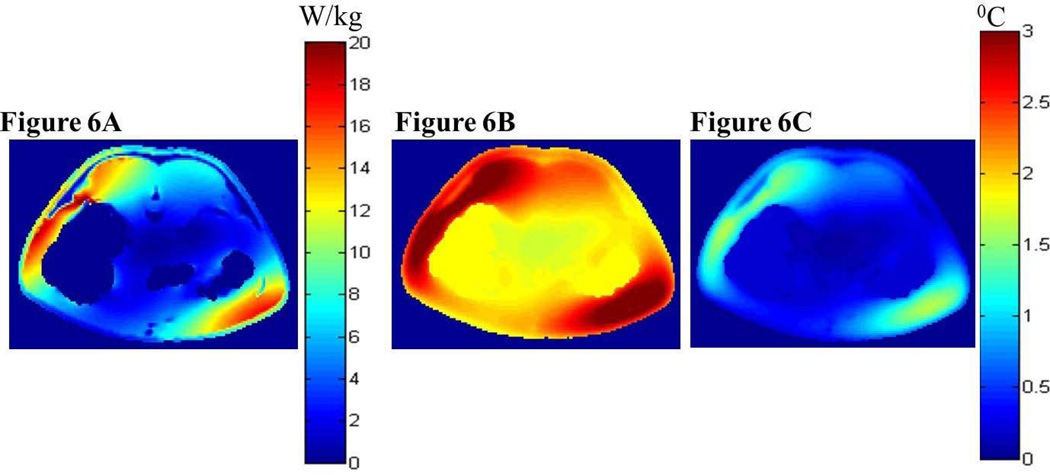
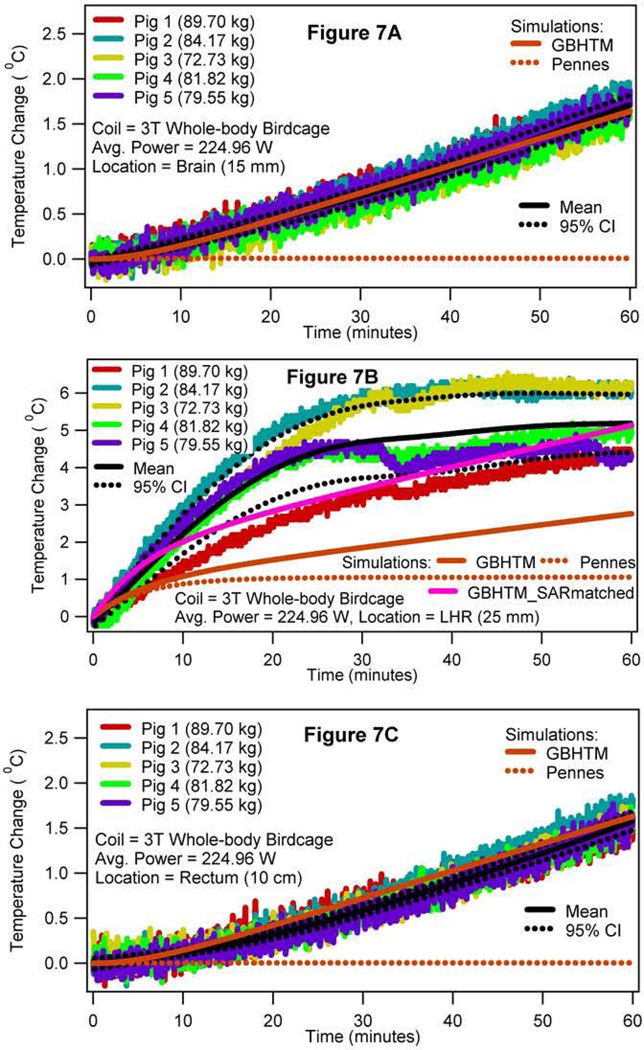
Figures 5 and 6 present the simulated local SAR and the associated temperature changes in the sagittal plane 5 mm lateral to the central plane and the central axial plane, respectively, of the digital pig when the porcine trunk was placed in the isocenter of the 3T volume coil (i.e., case 2). More specifically, Figures 5A and 6A present the local SAR distribution in the sagittal and axial planes due to the RF power deposition from the 3T coil for the whole-body average SAR of 2.77 W/kg, respectively. Figures 5B and 6B present the associated local temperature change distribution in the sagittal and axial planes at the end of the RF deposition simulated using the GBHTM, respectively. Figures 5C and 6C present the local temperature change distribution in the sagittal and axial planes at the end of the RF deposition simulated using the Pennes BHTE, respectively. Figure 7 presents the measured and simulated local temperature changes 15 mm deep in the brain (top figure), 25 mm deep in the plane of the isocenter on the left hand side (LHS) of the body closest to the MR table (middle figure), and 10 cm deep in the rectum (bottom figure) (whole-body average SAR = 2.77 W/kg, SD = 0.26 W/kg). Estimated mean curves and 95% confidence bands are also presented. It is shown that the GBHTM simulated the measured RF heating more accurately compared to the conventional Pennes BHTE. The Pennes model underestimated the RF heating. Next, the measured left hot region temperature change approached 3.2 °C (SD = 0.69 °C) within 15 minutes of the RF power deposition. The measured temperature change at 15 mm deep in the brain after the dura during this time was 0.28 °C (SD = 0.08 °C). The measured rectal temperature change during this time was 0.24 °C (SD = 0.10 °C). The measured brain and rectal temperature changes were comparable to the standard deviation of the fluoroptic probes (~0.10–0.20 °C).

FIG. 5.

Simulated local SAR distribution (a) and associated temperature changes simulated using the GBHTM (b) and Pennes BHTE (c) in the sagittal plane 5 mm lateral to the central plane at the end of the heating when the swine trunk was placed in the isocenter of a 3T birdcage body coil (case 2).

FIG. 6.

Simulated local SAR distribution (a) and associated temperature changes simulated using the GBHTM (b) and Pennes BHTE (c) in the central axial plane at the end of the heating when the swine trunk was placed in the isocenter of a 3T birdcage body coil (case 2).

FIG. 7.

RF power induced temperature changes 15 mm deep in the brain after the dura (a), 25 mm deep in the left hot region (b), and 10 cm deep in the rectum (c) when the swine trunk was placed in the isocenter of a 3T birdcage body coil (case 2).

Table 2 presents the measured whole-body average SAR and the associated temperature changes when the porcine trunk was placed in the isocenter of the 3T coil for all five animals (case 2). The mean whole-body average SAR of 2.77 W/kg produced the mean temperature change of ~1.76 °C 15 mm deep in the brain after the dura (SD = 0.09 °C), 5.16 °C 25 mm deep in the plane of the isocenter on the left hand side of the body closest to the MR table (SD = 0.94 °C, simulated left hot region), and 1.60 °C in the rectum (SD = 0.13 °C) at the end of the hour long RF heating (also, refer to Figure 7). The brain temperature changes were comparable to each other. The brain temperature change, the left hot region temperature change, and the rectal temperature change were significantly different from one another.

Table 2.

Measured whole-body average SAR and the associated temperature changes at the end of the heating, when the porcine trunk was placed in the isocenter of a 3T birdcage body coil (i.e., case 2).

No.	Weight (kg)	SAR (W/kg)	Scalp (°C)	Brain (15mm) (°C)	Brain (25mm) (°C)	Skin (°C)	Isocen. (25 mm) (°C)	Isocen. (50mm) (°C)	LHS (°C)	Rectum (°C)
1	89.70	2.54	1.27	1.86	1.77	4.90	5.30	4.50	4.30	1.51
2	84.17	2.83	0.96	1.86	1.97	3.60	3.70	2.70	6.00	1.82
3	72.73	3.14	1.31	1.74	1.80	3.10	4.24	2.97	6.29	1.51
4	81.82	2.51	1.04	1.65	1.40	3.90	3.80	3.20	4.90	1.53
5	79.55	2.82	1.00	1.71	1.70	4.00	3.60	3.00	4.30	1.62

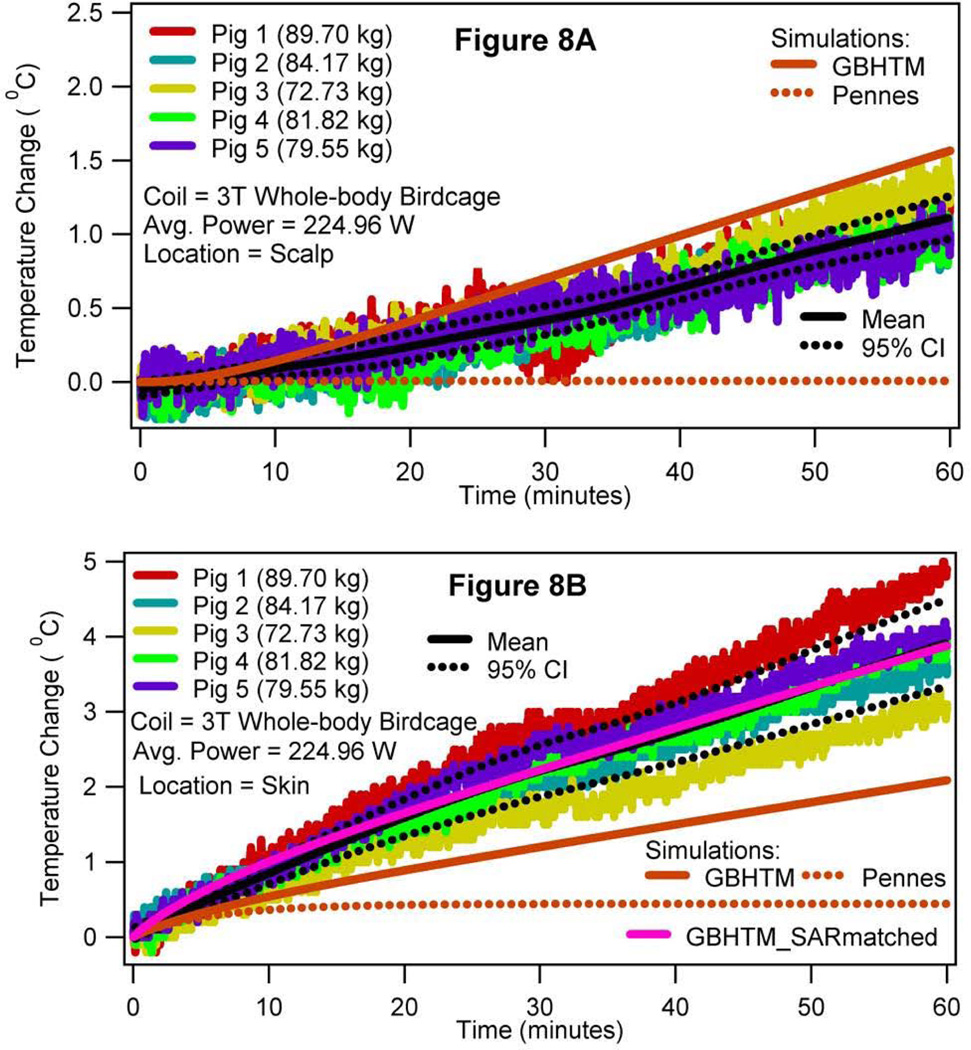
Figure 8 presents the measured and simulated temperature changes at the scalp (top figure) and in the subcutaneous layer of the skin in the plane of the isocenter, 5 mm lateral to the midline (bottom figure), when the porcine trunk was in the isocenter. The two skin temperature changes were significantly different from each other.

Figure 8.

RF power induced temperature changes in the subcutaneous layer of the scalp (a) and in the subcutaneous layer of the skin in the plane of the isocenter (b) when the swine trunk was placed in the isocenter of a 3T birdcage body coil (case 2).

DISCUSSION

Several important observations were made regarding in vivo heating produced due to the RF power deposition from a 3T volume transmit birdcage body coil. First, the new mechanistic GBHTM simulated in vivo RF heating more accurately compared to the conventional Pennes BHTE. The Pennes BHTE underestimated the RF heating (Figures 3–8). This was so because the GBHTM allowed the blood temperature to vary as per conservation of energy. However, the Pennes BHTE did not allow the blood temperature to vary. Keeping the blood temperature artificially and non-physiologically constant at the baseline core temperature made the Pennes BHTE overestimate the blood-tissue heat transfer rate and consequently underestimate the temperature rise. The predictions of the GBHTM and Pennes BHTE will converge if the thermal capacity of the blood is infinite for an RF heating application. In other words, the two simulations will converge if the spatial and temporal blood temperature variation due to the thermal interaction between a heated tissue and blood is close to zero. The observation suggests that it may be prudent to use the GBHTM simulations to redefine the ‘safe’ whole-body average SAR exposure vs time thresholds to keep in vivo temperatures below defined safety thresholds.

Next, the GBHTM underestimated the RF heating in hot regions (in neck in case1, as shown in Figure 4B; in left hot region and skin in case 2, as shown in Figures 7B and 8B, respectively). This was so because the local SAR in hot regions was underestimated. As mentioned before, local in vivo SAR distribution is a function of the RF coil geometry, RF coil operation, animal placement with in the coil, animal geometry, and animal tissue properties. Exact details of the 3T RF coil geometry (e.g., placement of rungs, capacitors, etc.) and operation (e.g., 2 port vs 4 port operation, port locations, patient table location, etc.) are proprietary information and are unknown to us. In addition, slightly off-center placement of an animal during the experiment may bring parts of the animal closer to the coil, resulting in higher local SAR and thus heating. The effect of the uncertainty in fluoroptic probe placement in measuring RF heating in hot regions is expected to be minimal due to relatively large size of the hot regions (Figures 3, 5, 6). Underestimated local SAR resulted in underestimated local temperatures in hot regions - this was verified by matching the measured and simulated local SARs and simulating heating using the GBHTM in the neck for case 1 (Figure 4B, GBHTM_SARmatched curve) and in the left hot region (Figure 7B, GBHTM_SARmatched curve) and skin (Figure 8B, GBHTM_SARmatched curve) in case 2. The local SAR was measured using the initial slope of the local experimental temperature response. The difference in the behavior between the measured and predicted temperature responses in Figures 4B (i.e., plateauing measurements vs continuously rising GBHTM_SARmatched curve), 7B (i.e., plateauing measurements vs continuously rising GBHTM_SARmatched curve), and 8A (i.e., overestimation by the GBHTM curve) originates due to the absence of thermoregulatory inputs in our thermal models. Appropriate overall consideration of the blood-tissue heat transfer rate mechanism was apparent from the good agreement found between the measured RF heating and the RF heating simulated using the GBHTM, away from the hot regions.

Second, safe in vivo temperature change thresholds were exceeded with allowable whole-body average SAR values. This was expected because the maximum allowable whole-body average SAR exposure values for the normal and first level modes were determined using the two-node model of Drs Adair and Berglund, which was unable to account for the non-homogeneous distribution of RF power, and the conventional Pennes bioheat model, which overestimated the thermal interaction between the blood and tissue. This suggests that new whole-body average SAR values vs time thresholds may be needed to keep in vivo temperatures and temperature changes within safe temperature thresholds.

Third, the brain temperature change in case 1 and the local temperature change in the left hot region in case 2 exceeded safe temperature thresholds within 15 minutes of RF power deposition with insignificant changes in rectal temperatures (Figures 3, 4A, 4C for case 1; Figures 5, 6, 7B, and 7C for case 2; Tables 1–2). This suggests that rectal temperature change measurement is necessary but not sufficient for determining whether an MRI study is safe. Local SAR distribution as well as heating must be determined with sufficient accuracy to verify compliance with the temperature guidelines and improve patient safety.

Fourth, thermal hot regions were simulated, as well as measured, deep inside the body, away from the skin and its thermal receptors. This suggests that the absence of a patient thermal sensation may not be interpreted as the absence of excessive, local in vivo heating. Excessive, local in vivo heating away from the skin and its thermal receptors can not be consciously ‘felt’ by a person, which could prevent a patient/technician/clinician from responding until it is too late to avoid redness, burning, etc. Again, validated tools must be developed to accurately determine in vivo RF heating in thermoregulatorily healthy, thermoregulatorily challenged, thermoregulatorily compromised, and pregnant subjects to make MRI thermal incident free.

Fifth, the RF power induced temperature changes away from the skin were not significantly different from one another for a location and swine placement inside the 3T body coil. This was apparent from the nearly overlapping measured temperature changes in the brain, hot regions, and rectum for cases 1 and 2 (Figures 4, 7). Nearly overlapping temperature changes were measured because swine of comparable weight and geometry received comparable local RF power distribution for a given placement inside the body coil and whole-body RF power deposition. Comparable RF power distribution resulted in comparable in vivo heating in healthy, anesthetized swine. This suggests that the effect of subject-to-subject variability on the in vivo RF heating may be insignificant for a given coil, RF power, weight range, geometry, subject placement, and physiological state. This further implies that validated simulation tools may be developed to keep in vivo temperatures and temperature changes within safe thresholds for a given coil, subject placement, RF power, weight range, geometry, and physiological state. It should be noted, however, that the local dielectric contrast and blood flow distributions may vary among subjects. Thus, the effect of this variation on the heating needs to be carefully investigated in humans.

Sixth, the skin temperature changes varied significantly from one location to another (Figure 8) for a given placement of swine inside the body coil. This was so because the RF power distribution varied over the skin. In addition, mammals can alter skin blood flow to transport energy (37–40). The observation suggests that the skin temperature change is an unreliable indicator of in vivo heating.

Seventh and finally, the near-linear rectal temperature rise, shown in figures 4C (case 1) and 7C (case 2), indicates that the rate of RF energy deposition was higher than what swine could get rid of. Plateauing local temperature rise, shown in figures 4B (case 1) and 7B (case 2), indicates that the thermoregulatory ability of the swine may be functional.

Comparing the present study with previous studies, the core temperature change simulated by the GBHTM (Case 1, ~1.61 °C for 159.0 W.min/kg; Case 2, 1.70 °C for 166.2 W.min/kg) and measured using fluoroptic probes (Case 1, ~1.48±0.13 °C for 159.0 W.min/kg; Case 2, 1.60±0.13 °C for 166.2 W.min/kg) was comparable to the core temperature change predicted by the two-node model (~1.3–1.7 °C for 160 W.min/kg) for a similar amount of RF energy deposition (4). Barber et al. measured the core temperature change of 1.26–1.80 °C/hr and the subcutaneous skin temperature change of up to ~6.3 °C/hr in sheep exposed to the whole-body average SAR of 4 W/kg in 1.5T (41). Shuman et al. measured an average deep tissue in vivo temperature change of 4.2 °C/hr in dogs exposed to the whole-body average SAR of 4 W/kg in 1.5T. The temperature increase in deeper tissue was found to be greater than the temperature increase in superficial tissue (42). Kido et al. measured a mean temperature change of 0.5 °C in the axilla due to the whole-body average SAR exposure of 0.8 W/kg for 17 min. in 1.5T (i.e., mean temperature change rate of 8.82 °C/hr at the whole-body average SAR of 4 W/kg) (43). Shellock et al. measured a scrotal skin temperature change of 0.2–3.2 °C due to the whole-body average SAR exposure of 0.56–0.84 W/kg for 23 min in 1.5T (44). Shellock et al. measured an insignificant change in the rectal temperature and a change of up to 7.5 °C in the skin temperature due to the whole-body average SAR exposure of 2.7–4.0 W/kg for 30 min in 1.5T (45). Adair et al. measured a rectal temperature change of 0.1 °C and a skin temperature change of 2.5 °C due to the whole-body average SAR exposure of 1.19 W/kg for 30 min in 1.5T (4). Shellock et al. measured a mean tympanic membrane temperature change of 0.4 °C and a mean skin temperature change of −0.5–3.6 °C due to the whole-body average SAR of 6 W/kg for 16 min in 1.5T (46). Boss et al. measured a skin temperature change of 0.88 °C due to the whole-body average SAR exposure of 3.2 W/kg for 10 min in 3.0T (25). All of these values are comparable to the data presented here for the rectal temperature change. No comparison could be made for the hot spot temperatures because hot spot temperatures have not been measured before.

Regarding the effect of the experimental setup on the RF heating measurements, the RF heating is expected to be similar in intubated and freely breathing, thermally unstressed swine. This is because the respiratory rate and lung volume were maintained at normal physiological values during the experiments. The anesthesia, however, may lower the observed RF induced temperature change in swine. This is so because Isoflurane is a known vasodilator. Vasodilation may bring warmer blood from the inside of a mammal to the surface, resulting in an increase in the rate of energy transfer from the skin to the ambient environment, lowering the RF induced temperature change. It should be noted, however, that the RF induced rectal temperature rise measured and simulated in this study was comparable to the temperature change predicted by the two-node model, which was developed for exercising Marines, for comparable RF energy deposition.

Regarding the limitations of the present study, the RF power distribution from a coil depends on the geometry and electrical properties of an imaged tissue. The resulting in vivo temperature distribution depends on the geometry, thermal properties, blood-tissue heat transfer, blood flow, clothing, and ambient conditions. The differences in the geometry, spatial distribution of electrical and thermal properties, and spatial distribution of the blood flow in humans and swine prohibit direct extrapolation of our results to humans. Further, anesthesia changes thermoregulatory thresholds and blood flow distribution in mammals (26). This would affect in vivo temperature response induced by an RF power distribution. Nevertheless, thermo-physiologically conservative animal models (e.g., porcine) with human comparable thermal mass are useful in studying RF heating and its unknown thermo-physiologic effects. The comparable core temperature changes predicted by the two-node model and simulated as well as measured in the present study for the same energy input buttresses this point. Human volunteers with appropriate physiology and fresh, perfused cadaver models are required to characterize the spatial and temporal distributions of RF heating and develop appropriate thermal and anatomical models for predicting RF heating in MRI applications. Simulations using validated thermal and anatomical models may offer a convenient way to predict RF heating and design safer, more flexible MRI protocols and systems in the future.

CONCLUSIONS

The new, mechanistic generic bioheat transfer model (GBHTM) accurately simulated the in vivo temperatures produced due to the RF power deposition from a 3T, birdcage volume transmit body coil. The empirical, conventional Pennes bioheat equation underestimated the heating. Safe temperature change thresholds were exceeded within allowable whole-body average SAR exposures. Rectal and skin temperature changes were found to be insufficient for determining temperature changes in hot regions, and thus, in concluding a thermally safe MRI scan. Safe SAR exposures to produce safe temperature thresholds may need re-investigation.