Abstract
Three-dimensional shape-based descriptors have been widely used in object recognition and database retrieval. In the current work, we present a novel method called compact Shape-DNA (cShape-DNA) to describe the shape of a triangular surface mesh. While the original Shape-DNA technique provides an effective and isometric-invariant descriptor for surface shapes, the number of eigenvalues used is typically large. To further reduce the space and time consumptions, especially for large-scale database applications, it is of great interest to find a more compact way to describe an arbitrary surface shape. In the present approach, the standard Shape-DNA is first computed from the given mesh and then processed by surface area-based normalization and line subtraction. The proposed cShape-DNA descriptor is composed of some low frequencies of the discrete Fourier transform of the processed Shape-DNA. Several experiments are shown to illustrate the effectiveness and efficiency of the cShape-DNA method on 3D shape analysis, particularly on shape comparison and classification.
1 Introduction
With rapid generation and increasingly availability of digital models in recent years, surface shape analysis has become one of the most important tasks in computer graphics community [1]. Some popular applications are shape comparison, classification and retrieval. The problem of rigid shape comparison and retrieval has been well studied and a large number of methods and tools have been developed [2, 3]. How to efficiently and accurately retrieve non-rigid (deformable) shapes from large databases, however, still remains a challenging problem, which inspires researchers to find good descriptors for non-rigid surface shapes. The existing methods on non-rigid shape descriptors can be roughly classified into two categories: global methods and local methods. Global methods use some global and isometric-invariant properties of shapes while local methods use local features of shapes as shape descriptors. We refer the readers to [4, 5, 6, 7] for more details on these descriptors. The present paper is focused on the global methods and a new global and compact descriptor is proposed to efficiently describe shapes. Among the work on non-rigid shape description using global features, spectral-based methods have gained a lot of attention due to its representing simplicity and computational efficiency [8], and have been studied both theoretically [9] and computationally [10]. For a detailed survey of spectrum-based mesh processing and shape description, the readers are referred to [11].
Thanks to the property of isometric invariance, the Laplace-Beltrami (L-B) operator on a manifold has become one of the most popular operators for non-rigid shape analysis in such applications as matching [12], recognition [13, 14, 15], retrieving [16, 17, 18], segmentation [19] and registration [20]. In particular, the eigenvalues and eigenfunctions of the L-B operator play important roles in describing shapes for shape-based retrieving and mesh segmentation. Xu [21] proposed several schemes for discretizing the L-B operator on triangular meshes and established the convergence under various conditions. Brandman [22] approximated the eigenvalues of the L-B operator by solving an eigenvalue problem in a bounded domain, discretized into a Cartesian grid. Rong et al. [23] used the eigenvalues and eigenfunctions of the L-B operator for mesh deformation. Wu et al. [6] proposed a symmetric mean-value L-B operator and used it as a descriptor in 3D non-rigid shape comparison. Shi et al.[24] presented a surface reconstruction method based on the eigen-projection and boundary reformation of the L-B operator. Ruggeri et al. [3] describeda method of matching 3D shapes based on the critical points of the eigenfunctions corresponding to some small eigenvalues of the L-B operator. As the eigenvalues are often computed on a mesh, a discrete approximation of the true underlying manifold, Dey et al. [25] studied the convergence and stability of eigenvalues to the true spectrum of the manifold. In addition to the traditional use for surface shapes, the L-B operator has been used for the recognition, retrieval and matching of images as well. Some early work dealing with those topics can be found in [26] and [27], in which the images are treated as Riemannian manifolds and the L-B or weighted L-B operators are applied to the manifold for characterizing the images.
From the perspective of signal processing, the eigen-decomposition of the L-B operator can be thought of as an frequency analysis of the shape: the eigenvalues correspond to the frequency values and the eigenfunctions correspond to the signals of the associated frequencies. The Shape-DNA [28, 29, 30, 31] consists of the N smallest eigenvalues of the L-B operator and is often used as a shape descriptor for measuring the similarity between different shapes by using the Euclidean (L2) distance between the Shape-DNA vectors. The property of isometric invariance derived from the L-B operator is one of the most important advantages of the Shape-DNA method, which makes it well suited for comparing non-rigid shapes. However, it is unclear as to what number of eigenvalues, i.e. N, should be used to form the Shape-DNA [32]. Reuter et al. used 20 eigenvalues for shape retrieval in [12] and 11 eigenvalues in [33]. In [34], the authors mentioned that 500 eigenvalues had to be computed for extracting important information from Dirichlet eigenvalues. However, in [35], the authors reported that 10 to 15 eigenvalues were enough for shape retrieving. In view of signal processing, more eigenvalues contains more information of detail and can describe the shape more accurately, but in the meantime, more time and space have to be used for computing, storing and comparing the Shape-DNAs. In this paper, we use at most 100 eigenvalues in the Shape-DNAs and our experiments show that the first 100 eigenvalues are typically enough for describing shapes in the database we used for testing.
Motivated by the Shape-DNA technique, we present a novel shape descriptor, called compact Shape-DNA (cShape-DNA), for analyzing the shape of a triangular surface mesh. The proposed method is a combination of the original Shape-DNA and discrete Fourier transformation (DFT), which encodes most of the shape information into only a small number of feature values and inherits all the advantages of the original Shape-DNA, including the isometric invariance. The time for computing the cShape-DNA is close to that of the original Shape-DNA, but the proposed shape descriptor requires smaller space for storing the cShape-DNA and less time for shape comparison, which makes the cShape-DNA a good candidate for fast shape retrieval especially in very large database applications.
The remainder of this paper is organized as follows. In Section 2, we introduce the cShape-DNA and the algorithmic detail. The comparison between the cShape-DNA and the original Shape-DNA for shape comparison and classification is made in Section 3. The impact of choosing different parameters and some other factors, such as noise and quality of the surface meshes, is also discussed in Section 3. The conclusion is given in Section 4.
2 Method
In this section, we first briefly review the original Shape-DNA and its computational procedure for a triangular surface mesh. We then elaborate on the detail of the proposed cShape-DNA.
2.1 The Original Shape-DNA
Generally speaking, the Laplace-Beltrami (L-B) operator is the Laplace operator on a Riemannian manifold. It is defined as the divergence of the gradient of a function f which is defined on the manifold [36, 37]:
| (1) |
The eigenvalue problem of the L-B operator has the following form:
| (2) |
The solutions λi and fi for i = 0, 1, … are called the eigenvalues and eigenfunctions of the L-B operator, respectively.
Let be a triangular surface mesh in with a set of vertices: The eigenvalues of the L-B operator on can be numerically computed by solving the following generalized eigenvalue problem:
| (3) |
where λ and f are considered unknown with being a vector of scalar function values f(v) defined on the vertices of . The calculations of the NV × NV matrices, A and B, are detailed below. The obtained λ’s and f’s are the eigenvalues and the eigenfunctions of the L-B operator on respectively, and the N smallest eigenvalues are known as the Shape-DNA of [29, 30].
The matrices A and B in Eq. (3) can be formulated when solving the partial differential equation in Eq. (2) with the finite element method (FEM), in which linear or higher order elements may be used. Although using quadratic or cubic elements typically yields better computational accuracy, the time cost for solving the corresponding FEM problem is much more expensive. After testing hundreds of mesh models taken from the McGill database [38], we choose to adopt the linear elements in our method because it yields almost identical Shape-DNAs to those obtained using quadratic or cubic elements but consumes much less time. With the linear finite element method, the matrices A and B take the following form when is a closed mesh [33]:
| (4) |
| (5) |
where t1 and t2 are the two triangles adjacent to edge vivj, ti| is the area of triangle ti, αij and βij are the angles opposite to vivj in t1 and t2 respectively, and N(i) is the index set of the vertices adjacent to vi.
The eigenvalues of the L-B operator is discrete and can be sorted in an increasing order: λ0 ≤ λ1 λ2 ≤ …. The first eigenvalue λ0 is always 0 when is closed.
The Shape-DNA should be normalized to guarantee scale-invariance, as the independence of an object’s size is one of the desired properties for a shape descriptor. Several methods of normalizing the Shape-DNA have been presented in [29]. Generally speaking, the values in a Shape-DNA are divided or multiplied with a constant number, which can simply be the first non-zero eigenvalue or the surface area of the given mesh. According to Weyl’s law [39], another interesting property of the Shape-DNA is that, for any 2–manifold in R3, the values of the Shape-DNA always distribute around a straight line determined only by the shape of the model (for examples, see Fig.1 (a)). For this reason, the normalization of the Shape-DNA can also be performed by considering the slope of the fitting line of the eigenvalues. In the present paper, a Shape-DNA is normalized by multiplying the eigenvalues with the surface area of the corresponding surface model. The normalized ShapeDNAs of some models are shown in Fig. 1 (b), where we can see that the normalized Shape-DNAs are distributed around a common straight line.
Figure 1.
(a) The Shape-DNAs (N = 100) of the bimba (red), cube (green) and sphere (blue) models, showing that each Shape-DNA is distributed roughly along a straight line determined only by the corresponding model. (b) After multiplying (a) with the surface areas of the corresponding models, the normalized Shape-DNAs are distributed around a common straight line of a slope about 4π.
2.2 Meshes with Boundary or Non-manifold Vertices
For meshes containing boundary or non-manifold vertices, we extend the coefficient matrices in (4) and (5) in the following ways. With the Neumann boundary condition, we have:
| (6) |
| (7) |
where T(ij) is the set of triangles which contains vivj as an edge, and χ(ij) is the set of angles in T(ij) which are opposite to edge vivj. Note that the number of triangles in T(ij) may be one (for boundary vertices), two (for inner vertices) or more (for non-manifold vertices). With the Dirichlet boundary condition, we assume the function values on the boundary and non-manifold vertices to be zero. Therefore, the unknowns are defined only on all inner and manifold vertices (denoted by VI). The calculations of the elements in A and B are similar to those in Equations (4) and (5), except that the vertices vi and vj are restricted to VI instead of V.
Both Neumann and Dirichlet boundary conditions described above have been implemented and tested on meshes with boundary or non-manifold vertices. The computed eigenvalues and eigenfunctions are identical to the results of the executable code provided by Reuter et al. on their website. According to [34], Neumann spectra can detect significant geometric features better than Dirichlet spectra and are less sensitive to mesh discretization and data loss. We thus always use Neumann boundary conditions for computing the raw Shape-DNA in the rest of this paper unless otherwise specified.
2.3 The Compact Shape-DNA
For a given surface mesh, we first compute the original Shape-DNA (i.e., some selected eigenvalues λk) and then normalize it by multiplying the eigenvalues with the surface area of the mesh. According to Wyel’s law [39], the sequence of eigenvalues λk is in the same order as when k goes to infinite. In other words, the normalized Shape-DNA of a shape can be approximated by a straight line given roughly by L(x) = 4πx. The main idea of the modified Shape-DNA is to model the fluctuation of the normalized eigenvalues about this straight line in a more compact way to represent and distinguish between different shapes. By denoting the values in the normalized Shape-DNA as , we the normalized Shape-DNA by the line, L(x) = 4πx, as follows:
| (8) |
Fig.2 (a-d) show respectively the bimba surface model, the original Shape-DNA, the normalized Shape-DNA by multiplying (b) with the surface area of the model, and the subtracted Shape-DNA as in Eq. 8. Then we apply discrete Fourier transform (DFT) to the N-vector . The DFT coefficients {Λi} are computed as follows:
| (9) |
where The DFT coefficients are complex numbers which encode the magnitudes and phases of the corresponding signals, namely, the normalized and subtracted Shape-DNA .
Figure 2.
(a) The bimba model. (b) The original Shape-DNA. (c) The normalized Shape-DNA by multiplying (b) with the surface area of the model. (d) The subtracted Shape-DNA as in Eq. 8. (e) The magnitudes of the circularly shifted DFT coefficients of (d). Please note that, due to the circular shifting, “low frequencies” are located around 50 but not 0 along the horizontal axis. (f) The cShape-DNA, given as some cropped low frequencies of the DFT in (e).
Due to the periodicity of DFT, low frequencies of the normalized Shape-DNA reside in the beginning and ending of the vector . Fig.2 (e) shows the magnitudes of the DFT coefficients, where the low frequencies have been circularly shifted to the center of the domain. Please note that the DFT coefficients are dominated by low frequencies. This phenomenon has been observed in all other models we have tested. A common technique in signal compression is by cropping high frequencies of an input signal. With the vector after shifting denoted by . Then we keep the 2M + 1 values around the center (i.e., ) and set the other frequencies as 0, where M is a user-specified parameter which controls the data compression ratio and restoration accuracy. We call the non-zeros in the vector the compact Shape-DNA (or cShape-DNA), with the following form:
| (10) |
Fig.2 (f) shows the cropped frequencies of the DFT of the normalized and subtracted Shape-DNA. These cropped frequencies (or cShape-DNA) define a compact shape descriptor of the original bimba surface model.
3 Experiments
In this section, we show some experiments to demonstrate the power of the proposed cShape-DNA on shape description. First, we compare the accuracy of cShape-DNA and the original Shape-DNA on shape comparison and shape classification in Section 3.1. We then discuss the impact of the parameter M on the accuracy of shape description in Section 3.2. Finally, we show the robustness of the proposed shape descriptor to geometric noise and mesh quality in Section 3.3.
3.1 Shape Comparison and Classification
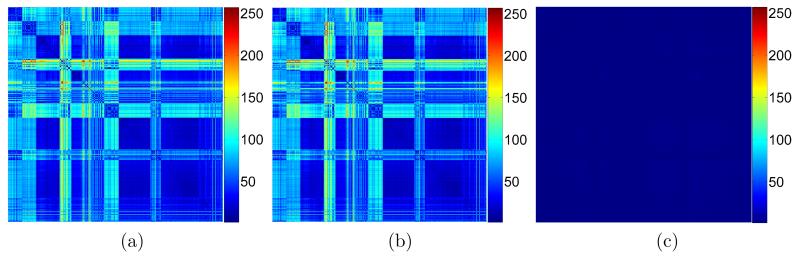
To show the capability of the proposed shape descriptor on shape comparison and classification, we consider in our experiments the McGill database [38], which contains 458 surface models. Each model in the database is first used as input to compute its normalized Shape-DNA (with N = 100) and cShape-DNA (with M = 16) vectors. The dissimilarity of any two models are measured as the Euclidean distance between the corresponding Shape-DNAs or cShape-DNAs, resulting in two 458 × 458 matrices (one for Shape-DNA and the other for cShape-DNA). Note that the dissimilarity values computed using Shape-DNAs and cShape-DNAs are often different, which makes it unreasonable to directly compare the two distance matrices. However, if we scale the values in each matrix into the same range, say [0, 255], each value in the scaled matrices can be considered as a relative dissimilarity (across the database) between two models, and the direct comparison between the two matrices becomes possible. Fig.3 (a) and (b) show the two scaled matrices, where the element values lie in the range of [0, 255]. The colors from blue to red correspond to high to low similarities between two models respectively. By computing the difference between the two scaled matrices, as shown in Fig.3 (c), we can see that the two scaled matrices are almost identical with a mean value of 0.68 and a standard deviation of 0.69, meaning that the proposed cShape-DNA can achieve the same accuracy as the normalized Shape-DNA on measuring dissimilarity of models, but the size of the proposed shape descriptor is only 1/3 (i.e., 2M + 1) of that of the original shape descriptor in [29, 30].
Figure 3.
(a) The scaled distance matrix of the McGill database generated by the Shape-DNA (N = 100)). (b) The scaled distance matrix of the McGill database generated by the cShape-DNA (M = 16). Note that the size of the cShape-DNA descriptor is only 1/3 (i.e., 2M + 1) of that of the original shape descriptor (i.e., N = 100). (c) The difference matrix (absolute substraction) of (a) and (b). Note that all the values in the matrices are scaled to [0, 255]. The mean and standard deviation of (c) are 0.68 and 0.69 respectively.
To demonstrate the power of cShape-DNA on shape classification, we compute the normalized Shape-DNAs (with N = 100) and cShape-DNAs (with M = 16) for several models and project them onto a 2D plane using the multi-dimensional scaling (MDS) method (see [40]). A variety of models are considered here, including animation models (CM, CS, D1, D2), medical objects (B, L), molecular models (M1, M2, M3, M4), articulated models (A1, A2, A3, A4, A5), and a few simple models (S1, S2, S3, C, E). The “CM” is generated using the marching cubes method on the “cow” object, and the “CS” is the optimized mesh using a quality improvement method [41] on the “CM” model. The “D1” model is the “dancer” object having 24, 998 vertices, and is refined to generate the “D2” model with 99, 992 vertices. Two medical objects are included in this study: the “brain” model (or “B”) and the “lung” model (or “L”). We also consider four molecular shapes: “M1” to “M4” standing for the molecules 1BPD, 2BPG, 2CJW, and domain A of 2CJW, all taken from the Protein Data Bank (http://www.rcsb.org/pdb/). The surface meshes are generated by using the surface modeling method described in [42]. The “M1” and “M2” are similar in shape but one is deformed from the other. The “M4” is a sub-domain of “M3”, but both are different from “M1” and “M2”. In addition, three versions of a unit spherical surface mesh are investigated: “S1”, “S2” and “S3” with different numbers (roughly 2K, 10K and 40K respectively) of vertices. These models have similar but not identical shapes because they are the representation of the unit sphere with different discretization levels. Finally, we consider five isometric deformations of the “armadillo” model (A1 to A5) and two other simple models (“C” for “cube” and “E” for “eight”) in this experiment.
Fig.4 (a) and (b) show the MDS plots for these models based on the normalized Shape-DNA (N = 100) and cShape-DNAs (M = 16) vectors. We can see that the clustering result of cShape-DNA is almost the same as that of the normalized Shape-DNA. To see how the discriminative power of the proposed method is affected by the size of the shape descriptor (i.e., 2M + 1), we plot the MDS results with different values of M. As shown in Fig.4 (c)-(f), when M decreases from 8, 4, 2 to 1 meaning that the sizes of the corresponding cShape-DNAs are 17, 9, 5 and 3 respectively, we can see that the shape-clustering results do become worse. However, even when M = 1, one can still separate different shapes well and meanwhile observe high similarity scores between isometric models.
Figure 4.
(a) 2D MDS plots of the normalized Shape-DNA. (b-f) 2D MDS plots of the proposed cShape-DNA with M = 16, 8, 4, 2 and 1 respectively. Please note that the size of the cShape-DNA descriptor is only 2M + 1, as compared to N = 100 or the size of the normalized Shape-DNA descriptor.
To see the performance of the normalized Shape-DNA in shape classification with smaller descriptors, we plot in Fig.5 (a)-(e) the 2D MDS results of the normalized Shape-DNAs with the first 33, 17, 9, 5, and 3 eigenvalues, corresponding to M = 16, 8, 4, 2, 1 respectively as shown in Fig. 4. We can see that the classification results are much different from that of the normalized Shape-DNA with 100 eigenvalues. For example, when N = 3, it is hard to distinguish between the cube (C) and sphere ((S1 to S3) or the brain (B) and lungs (L), as can be seen in Fig.5 (e). By comparison, the proposed cShape-DNA method can still discriminate these models when a 3-vector descriptor is used (see Fig.4 (f)). This experiment shows that the normalized Shape-DNA method performs worse than the proposed cShape-DNA method in shape comparison or classification when the same size of descriptors are used. Another related shape descriptor, presented in [13], is the F 1 feature vector and defined as , where {λi} are the eigenvalues of the L-B operator. The 2D MDS plots corresponding to the feature vectors (N = 100) are shown in Fig.5 (f). We can see that the discriminative power of the F 1 feature vector is worse than the proposed cShape-DNA method.
Figure 5.
(a-e) 2D MDS plots of the normalized Shape-DNA with different numbers of feature values (eigenvalues): (a) N = 33, (b) N = 17, (c) N = 9, (d) N = 5 and (e) N = 3. One can compare the results with those in Fig. 4 (b-f) generated by the cShape-DNA method. (f) The MDS plots of the F1 feature vectors described in [40].
3.2 The Parameter M
In this subsection, we investigate how the parameter M affects the accuracy of similarity measurement in the cShape-DNA method. Here, we compute the distance (similarity) matrices between any pair of models in the McGill database based on the cShape-DNA with different M values (M = 8, 4, 2, 1), as shown in Fig.6 (a)-(d). Visually these matrices do not look too much different from each other. To quantitatively assess the influence of the parameter M, the four matrices in Fig.6 (a)-(d) are compared with the distance matrix, seen in Fig.3(a), based on the normalized Shape-DNA (N = 100) and the difference matrices are plotted in Fig.6 (e)-(h). Note that the values in Fig.6 (a)-(d) have been scaled to [0, 255]. The mean values in the difference matrices are 1.3, 2.3, 4.8 and 6.0 respectively, and the standard deviations are 1.1, 1.8, 3.1 and 3.8 respectively. We can see that, when M decreases, the discriminating power of the cShape-DNA gradually becomes worse too. In practice, we hope to use as small vectors as possible to describe a shape without much loss of accuracy. The experiments shown here provide some hints on how small M could be in order to achieve acceptable result on measuring shape similarity. In real-world applications, however, the best value for the parameter M to be used really depends on the shapes under investigation, as different shapes may contain different spectral distributions. Another factor to be considered is the balance between accuracy and efficiency of shape description that the user may decide.
Figure 6.
(a-d) The distance matrices are generated by the cShape-DNA with M = 8, 4, 2, 1 respectively. (e-h) The corresponding difference matrices by comparing (a-d) with the distance matrix based on the Shape-DNA (see Fig. 3(a)). The mean values in the difference matrices (from (e) to (h)) are 1.3, 2.3, 4.8 and 6.0 respectively and the standard deviations are 1.1, 1.8, 3.1 and 3.8 respectively. Please note that the size of the cShape-DNA descriptor is only 2M + 1, as compared to N = 100 or the size of the normalized Shape-DNA descriptor.
3.3 Sensitivities to Model Noise and Mesh Quality
The present shape descriptor takes a surface mesh (typically a triangular mesh) as input. It is interesting to see how the proposed method is sensitive to model noise and mesh angle quality, which are two common issues in a given mesh. Similar analysis on other shape descriptors had been investigated in [34, 43]. In all experiments shown below unless otherwise specified, N = 100 and M = 16 are considered for the normalized Shape-DNA and cShape-DNA descriptors respectively.
First, five different levels of noise are added to each model in the McGill databases in the following way. Each vertex in a model is disturbed with a random noise up to a maximum distance of λ × L along the outward normal direction at that vertex, where L is the average edge length of the original model and λ is the noise level chosen as 0.5, 1.0, 2.0, 4.0 or 10.0. The normalized Shape-DNA and cShape-DNA are computed for each noisy model, yielding ten distance matrices (two for each noise level). After being scaled to [0, 255], the ten matrices are then compared with the corresponding distance matrix of the noise-free models in the database (see Fig. 3(a) or (b)). The resulting difference matrices are illustrated in Fig. 7 (a) to (e) for the normalized Shape-DNA method and Fig. 7 (g) to (j) for the proposed cShape-DNA method. From the difference matrices and the means and standard deviations given in Fig. 7, we can conclude that the noise does affect shape comparison to some extent. However, the proposed cShape-DNA descriptor gives very close results to those by the normalized Shape-DNA descriptor. The above observation is further demonstrated in Fig. 8. We first compute the normalized Shape-DNAs of the noisy models (with three noise levels 0.5, 1.0 and 10.0) in the McGill database, resulting in three 458-dimensional vectors. The differences between the three vectors and the normalized Shape-DNAs of the noise-free model in the databases are computed and plotted in Fig. 8 (a) after normalizing the values to [0, 1]. The plot in Fig. 8 (b) is generated the same way except that the cShape-DNA is used instead of the normalized Shape-DNA. From the curves, we can see the influence of noise on the computed shape descriptors.
Figure 7.
(a-e) The difference matrices based on the normalized Shape-DNA with different levels of noise: (a) λ = 0.5, (b) λ = 1.0, (c) λ = 2.0, (d) λ = 4.0, and (e) λ = 10.0. (f-j) The difference matrices based on the cShape-DNA with different levels of noise: (f) λ = 0.5, (g) λ = 1.0, (h) λ = 2.0, (i) λ = 4.0, and (j) λ = 10.0. The mean values in (a-e) are 4.3, 8.5, 11.8, 12.3 and 24.9, and in (f-j) the mean values are 4.6, 9.0, 12.2, 12.4, 24.9 respectively. The standard deviations in (a-e) are 5.5, 9.1, 12.0, 11.5 and 23.7, and in (f-i) the standard deviations are 5.5, 9.1, 12.1, 11.5, 23.7 respectively.
Figure 8.
(a) The difference between the normalized Shape-DNAs of the original models and three versions of noisy models ( λ = 0.5, 1.0 and 10.0) in the McGill database. (b) The difference between the cShape-DNAs of the original models and three versions of noisy models ( λ = 0.5, 1.0 and 10.0) in the McGill database.
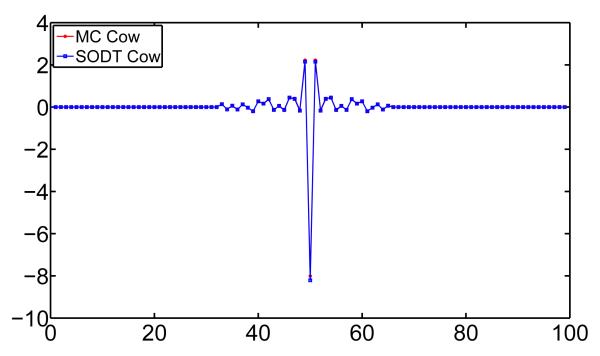
To see how mesh quality affects the cShape-DNA descriptor, we compute the cShape-DNA for the “CM” and the “CS” models. The“CM” model is generated using the marching cube method and hence the mesh quality is low. The “CS” is the optimized mesh using a quality improvement method [41] on the “CM” model. The cShape-DNAs of these two models are shown in Fig. 9 and it can be seen from the figure that the two spectra are almost identical, which means that the cShape-DNA is very robust to mesh quality. This observation confirms that the cShape-DNA, similar to the original shape-DNA, is a shape descriptor that depends heavily on the shape (up to isometry) but little on the parametrization of the surface [29].
Figure 9.
The cShape-DNAs of the original cow model (red) generated using the marching cube method and the smoothed model (blue) with improved mesh quality.
4 Conclusion
In the present paper, we proposed a new shape descriptor, called compact Shape-DNA (or cShape-DNA), based on the original Shape-DNA method. Numerous experiments have shown that the capability of cShape-DNA on shape comparison and classification is as good as that of the original Shape-DNA, while the size of the cShape-DNA could be much smaller than that of the original Shape-DNA. The reduced size of the descriptor is important for saving space in storing the feature vectors of a shape and for saving time as well in comparing the similarity between two meshes. The proposed method is expected to be useful in shape retrieval from very large databases, especially when shapes with isometric deformations are being retrieved. Experiments also show that, similar to the original Shape-DNA, the proposed cShape-DNA is very robust to mesh angle quality but sensitive to high levels of geometric noise on a surface shape.
Highlights of A Compact Shape Descriptor for Triangular Surface Meshes.
A compact Shape-DNA is presented to describe the shape of a triangular surface mesh.
Compact Shape-DNA is composed of low frequencies of DFT of processed Shape-DNA.
The method reduces up to 97% space and time consumptions compared to Shape-DNA.
Acknowledgments
Dr. Gao was partly supported by SinoProbe-09-01, the National Natural Science Foundation of China (Number 41304083), the Fundamental Research Funds for the Central Universities of China. Dr. Yu was supported in part by an NIH Award (Number R15HL103497) from the National Heart, Lung, and Blood Institute (NHLBI).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Osada Robert, Funkhouser Thomas, Chazelle Bernard, Dobkin David. Shape distributions. ACM Transactions on Graphics. 2002;21(4):807–832. [Google Scholar]
- [2].Shilane Philip, Min Patrick, Kazhdan Michael, Funkhouser Thomas. The princeton shape benchmark. IEEE Proceedings of Shape Modeling Applications. 2004:167–178. [Google Scholar]
- [3].Ruggeri Mauro R., Patanè Giuseppe, Spagnuolo Michela, Saupe Dietmar. Spectral-driven isometry-invariant matching of 3D shapes. International Journal Of Computer Vision. 2010;89(2-3):248–265. [Google Scholar]
- [4].Sun Jian, Ovsjanikov Maks, Guibas Leonidas. A concise and provably informative multi-scale signature based on heat diffusion. Computer Graphics Forum. 2009;28(5):1383–1392. [Google Scholar]
- [5].Ovsjanikov Maks, Mérigot Quentin, Mémoli Facundo, Guibas Leonidas. One point isometric matching with the heat kernel. Computer Graphics Forum. 2010;29(5):1555–1564. [Google Scholar]
- [6].Wu Huaiyu, Zha Hongbin, Luo Tao, Wang Xulei, Ma Songde. Global and local isometry-invariant descriptor for 3D shape comparison and partial matching; 23rd IEEE Conference on Computer Vision and Pattern Recognition (CVPR); San Francisco, CA, USA. 2010.pp. 438–445. [Google Scholar]
- [7].Lian Zhouhui, Godil Afzal, Bustos Benjamin, Daoudi Mohamed, Hermans Jeroen, Kawamura Shun, Kurita Yukinori, Lavou Guillaume, Van Nguyen Hien, Ohbuchi Ryutarou, Ohkita Yuki, Ohishi Yuya, Porikli Fatih, Reuter Martin, Sipiran Ivan, Smeets Dirk, Suetens Paul, Tabia Hedi, Vandermeulen Dirk. A comparison of methods for non-rigid 3d shape retrieval. Pattern Recognition. 2013;46(1):449–461. [Google Scholar]
- [8].Lai Zhaoqiang, Hu Jiaxi, Liu Chang, Taimouri Vahid, Pai Darshan, Zhu Jiong, Xu Jianrong, Hua Jing. Intra-patient supine-prone colon registration in CT colonography using shape spectrum; 13th International Conference on Medical Image Computing and Computer-Assisted Intervention; China Natl Convent Ctr, Beijing, PEOPLES R CHINA. 2010; pp. 332–339. [DOI] [PubMed] [Google Scholar]
- [9].Mémoli Facundo. A spectral notion of Gromov-Wasserstein distance and related methods. Applied and Computational Harmonic Analysis. 2011;30(3):363–401. [Google Scholar]
- [10].Bronstein Alexander M., Bronstein Michael M., Kimmel Ron, Mahmoudi Mona, Sapiro Guillermo. A Gromov-Hausdor framework with diffusion geometry for topologically-robust non-rigid shape matching. International Journal of Computer Vision. 2010;89(2-3):266–286. [Google Scholar]
- [11].Zhang Hao, van Kaick Oliver, Dyer Ramsay. Spectral mesh processing. Computer Graphics Forum. 2010;29(6):1865–1894. [Google Scholar]
- [12].Niethammer Marc, Reuter Martin, Wolter Franz-Erich, Bouix Sylvain, Peinecke Niklas, Koo Min-Seong, Shenton Martha E. Global medical shape analysis using the Laplace-Beltrami spectrum. Medical Image Computing and Computer-Assisted Intervention-MICCAI 2007, PT 1. 2007:850–857. doi: 10.1007/978-3-540-75757-3_103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Khabou Mohamed A., Hermi Lotfi, Rhouma Mohamed Ben Haj. Shape recognition using eigenvalues of the Dirichlet Laplacian. Pattern recognition. 2007;40(1):141–153. [Google Scholar]
- [14].Rhouma Mohamed Ben Haj, Khabou Mohamed Ali, Hermi Lotfi. Advances in Imaging and Electron Physics. Vol. 167. Elsevier Academic Press Inc; 2011. Shape Recognition Based on Eigenvalues of the Laplacian. [Google Scholar]
- [15].Bernardis Elena, Konukoglu Ender, Ou Yangming, Metaxas Dimitris N., Desjardins Benoit, Pohl Kilian M. Temporal shape analysis via the spectral signature. Medical Image Computing and Computer-Assisted Intervention-MICCAI 2012, Pt 2. 2012:49–56. doi: 10.1007/978-3-642-33418-4_7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Bronstein Alexander M., Bronstein Michael M., Kimmel Ron. Topology-invariant similarity of nonrigid shapes. International Journal Of Computer Vision. 2009;81(3):281–301. [Google Scholar]
- [17].Bronstein Alexander M., Bronstein Michael M., Guibas Leonidas J., Ovsjanikov Maks. Shape Google: Geometric words and expressions for invariant shape retrieval. ACM Transactions on Graphics. 2011;30(1):1. [Google Scholar]
- [18].Gurijala Krishna Chaitanya, Wang Lei, Kaufman Arie. Cumulative heat diffusion using volume gradient operator for volume analysis. IEEE Transactions on Visualization and Computer Graphics. 2012;18(12):2069–2077. doi: 10.1109/TVCG.2012.210. [DOI] [PubMed] [Google Scholar]
- [19].Raviv Dan, Bronstein Alexander M., Bronstein Michael M., Kimmel Ron. Full and partial symmetries of non-rigid shapes. International Journal Of Computer Vision. 2010;89(1):18–39. [Google Scholar]
- [20].Reuter Martin. Hierarchical shape segmentation and registration via topological features of Laplace-Beltrami eigenfunctions. International Journal of Computer Vision. 2010;89(2-3):287–308. [Google Scholar]
- [21].Xu Guoliang. Discrete Laplace-Beltrami operators and their convergence. Computer Aided Geometric Design. 2004;21(8):767–784. [Google Scholar]
- [22].Brandman Jeremy. A level-set method for computing the eigenvalues of elliptic operators defined on compact hypersurfaces. Journal Of Scientific Computing. 2008;37(3):282–315. [Google Scholar]
- [23].Rong Guodong, Cao Yan, Guo Xiaohu. Spectral mesh deformation. The Visual Computer. 2008;24(7-9):787–796. [Google Scholar]
- [24].Shi Yonggang, Lai Rongjie, Morra Jonathan H., Dinov Ivo, Thompson Paul M., Toga Arthur W. Robust surface reconstruction via Laplace-Beltrami eigen-projection and boundary deformation. IEEE Transactions on Medical Imaging. 2010;29(12):2009–2022. doi: 10.1109/TMI.2010.2057441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Dey Tamal K., Ranjan Pawas, Wang Yusu. Convergence, stability, and discrete approximation of Laplace spectra. The Twenty-First Annual Acm-Siam Symposium On Discrete Algorithms. 2010:650–663. [Google Scholar]
- [26].Peinecke Niklas, Wolter Franz-Erich, Reuter Martin. Laplace spectra as fingerprints for image recognition. Computer-Aided Design. 2007;39(6):460–476. [Google Scholar]
- [27].Peinecke Niklas, Wolter Franz-Erich. Mass density Laplace-spectra for image recognition; Proceedings of the 2007 International Conference on Cyberworlds (NASAGEM). IEEE; 2007.pp. 409–416. [Google Scholar]
- [28].Wolter FE, Peinecke N, Reuter M. Verfahren zur charakterisierung von objekten / a method for the characterization of objects (surfaces, solids and images) US Patent US2009/0169050 A1. 2009 Jul;
- [29].Reuter Martin, Wolter Franz-Erich, Peinecke Niklas. Laplace-Beltrami spectra as Shape-DNA of surfaces and solids. Computer-Aided Design. 2006;38(4):342–366. [Google Scholar]
- [30].Reuter Martin, Niethammer Marc, Wolter Franz-Erich, Bouix Sylvain, Shenton Martha. Global medical shape analysis using the volumetric Laplace spectrum; 2007 International Conference On Cyberworlds; 2007; pp. 417–426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Wolter Franz-Erich, Blanke Philipp, Thielhelm Hannes, Vais Alexander. Modelling, Simulation and Software Concepts for Scientific-Technological Problems. Springer; 2011. Computational differential geometry contributions of the welfenlab to grk 615; pp. 211–235. [Google Scholar]
- [32].Marini Simone, Patané Giuseppe, Spagnuolo Michela, Falcidieno Bianca. Spectral feature selection for shape characterization and classification. The Visual Computer. 2011;27(11):1005–1019. [Google Scholar]
- [33].Reuter Martin, Biasotti Silvia, Giorgi Daniela, Patanè Giuseppe, Spagnuolo Michela. Discrete Laplace-Beltrami operators for shape analysis and segmentation. Computers & Graphics. 2009;33(3):381–390. [Google Scholar]
- [34].Reuter Martin, Wolter Franz-Erich, Shenton Martha, Niethammer Marc. Laplace-Beltrami eigenvalues and topological features of eigenfunctions for statistical shape analysis. Computer-Aided Design. 2009;41(10):739–755. doi: 10.1016/j.cad.2009.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Lian Zhouhui, Godil Afzal, Bustos Benjamin, Daoudi Mohamed, Hermans Jeroen, Kawamura Shun, Kurita Yukinori, Lavouè Guillaume, Van Nguyen Hien, Ohbuchi Ryutarou, Ohkita Yuki, Ohishi Yuya, Porikli Fatih, Reuter Martin, Sipiran Ivan, Smeets Dirk, Suetens Paul, Tabia Hedi, Vandermeulen Dirk. SHREC11 track: shape retrieval on non-rigid 3D watertight meshes; Proceedings of the 4th Eurographics conference on 3D Object Retrieval; 2011.pp. 79–88. [Google Scholar]
- [36].Chavel Isaac. Eigenvalues in Riemannian geometry. Vol. 115. Academic press; 1984. [Google Scholar]
- [37].Rosenberg Steven. The Laplacian on a Riemannian manifold: an introduction to analysis on manifolds. Cambridge University Press; 1997. [Google Scholar]
- [38].Zhang Juan, Siddiqi Kaleem, Macrini Diego, Shokoufandeh Ali, Dickinson Sven. Retrieving articulated 3-D models using medial surfaces and their graph spectra. Energy minimization methods in computer vision and pattern recognition. 2005:285–300. [Google Scholar]
- [39].Weyl Hermann. Das asymptotische verteilungsgesetz der eigenwerte linearer partieller differential-gleichungen. Mathematische Annalen. 1912;71(4):441–479. [Google Scholar]
- [40].Cox Trevor F., Cox Michael A. A. Multidimensional scaling. Vol. 88. CRC Press; 2001. [Google Scholar]
- [41].Gao Zhanheng, Yu Zeyun, Holst Michael. Feature-preserving surface mesh smoothing via suboptimal Delaunay triangulation. Graphical Models. 2013;75(1):23–38. doi: 10.1016/j.gmod.2012.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Zeyun Yu. A list-based method for fast generation of molecular surfaces. Proceedings of the 31st Intl Conf. of IEEE Engineering in Medicine and Biology Society. 2009:5909–5912. doi: 10.1109/IEMBS.2009.5334843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Gao Wenhua, Lai Rongjie, Shi Yonggang, Dinov Ivo, Toga Arthur W. A narrow-band approach for approximating the Laplace-Beltrami spectrum of 3D shapes. International Conference on Numerical Analysis and Applied Mathematics. 2010:1010–1013. [Google Scholar]