Combining surface and fiber geometry: an integrated approach to brain morphology

Abstract

Despite the fact that several theories link cortical development and function to the development of white matter and its geometrical structure, the relationship between gray and white matter morphology has not been widely researched. In this paper, we propose a novel framework for investigating this relationship. Given a set of fiber tracts which connect to a particular cortical region, the key idea is to compute two scalar fields that represent geometrical characteristics of the white matter and of the surface of the cortical region. The distributions of these scalar values are then linked via Mutual Information, which results in a quantitative marker that can be used in the study of normal and pathological brain structure and development. We apply this framework to a population study on autism spectrum disorder in children.

1 Introduction

The shape of brain structures is an important feature thought to reflect various neurodevelopmental processes, which makes it of particular interest in neuroscience. A large body of neuroimaging literature has been devoted to studying the geometry of the brain’s cortical surface, in terms of measures such as curvature, area, thickness, gyrification (e.g., [1]). However, the relationship between gray and white matter morphology has not been extensively studied, despite the fact that several theories link cortical development and function to the development of white matter and its geometrical structure (e.g., [2]). In fact, most in vivo neuroimaging investigations of white matter have focused on voxel-based diffusion tensor imaging (DTI) measures such as fractional anisotropy (FA), mean, radial and axial diffusivities. As this type of information is of very different nature (i.e. non-geometrical), it is not clear how to combine such DTI-based findings on the white matter (WM), with morphological findings in the gray matter (GM).

Possibly as a result of this discrepancy, the problem of mapping white matter properties onto cortical geometry has not been widely investigated. In [3], tractography information is used to help determine corresponding points on the cortical surface of different subjects. More recently, [4] define correspondence between WM tracts and GM locations by extending the tract in a straight line from the tip of the tract to the boundary of the cortex. This approach is rather heuristic, and does not take into account the complex cerebral cortex structure which often causes axons to bend when they enter the gray matter.

In this paper, we introduce a novel framework to associate geometrical information from the white matter and the cortical surface without such severe restrictions. To quantify cortical surface geometry, standard features from the differential geometry of surfaces exist and have been widely used in the medical image community. Such features include functions of the surface’s principal curvatures, e.g. the mean and Gaussian curvatures, or the shape index and curvedness [1]. However, a lot less work has been done on the geometry of white matter fibers. In the diffusion MRI community, the sub-voxel geometry of fibers has been defined based for example on the diffusion-weighted signal, e.g. [5], or based on neighborhood regularization, e.g. [6]. However, for the purposes of the present work, we need larger scale macrostructural white matter geometry features, i.e. in features that span more than a single voxel. A method that provides such features is that of [7], where fiber geometry is computed based on the differential geometry of curve sets. By measuring the variation of a curve’s tangent vector in all directions orthogonal to the curve, this method provides a quantitative measure of fiber dispersion, or spread.

While it may be self-evident that the geometry of the white matter and that of the gray matter must somehow be related, it is not currently known whether a precise relationship actually exists, or what its formulation is. One could attempt to provide an explicit model for this relationship via formulas linking cortical folding with the spread and curvature of white matter fibers. However, such an approach would require extensive knowledge of brain tissue biomechanics and is essentially impossible with current neuroimaging technology.

In this work, we propose a simpler approach based on information theory. Given a set of fiber tracts which connect to a particular cortical region of interest (ROI), we first compute a scalar field over the fiber tracts, and separately a second scalar field over the cortical region. These two scalar fields represent a geometric characteristic of the white matter and of the gray matter, respectively. Then, we capture the relationship between them through the Mutual Information function. This type of approach is general, in that it can be applied with any scalar characteristics of the gray and the white matter. It also avoids the need to specify one-to-one correspondences between individual fibers and specific points on the cortex, as such correspondences are inherently unstable and depend on various parameters and tractography algorithm specifics.

We illustrate our approach with a small-scale study on autism. We focused our experiments specifically on the pars orbitalis region of the inferior frontal gyrus (IFG), a region that has been involved in semantic processing of language. We chose this region as the IFG and the pars orbitalis have been previously implicated in autism (e.g., [8]) and other neurodevelopmental disorders.

2 Methods

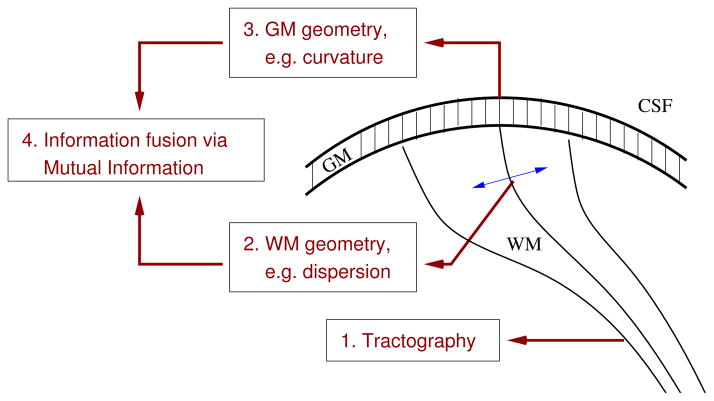
Our approach is summarized with the following four steps:

1. Perform tractography to define the white matter tracts of interest.

2. Compute the geometry of these tracts.

3. Compute the geometry of the cortical regions they connect to.

4. Quantify the relationship between the geometry of white matter and that of gray matter.

As detailed below, Step 1) is performed with the multi-fiber tracking algorithm of [9], and is used as in [7]. Step 2) implements the geometry method of [7], while steps 3) and 4) are the contribution of the present paper, and are described in more detail. Fig. 1 summarizes these steps.

Fig. 1.

A schematic illustration of the four steps in our pipeline.

2.1 Geometry computation (steps 1–3)

Following the work of [7], we first computed whole-brain tractography using the HARDI multi-fiber tractography method of [9]. This tractography algorithm is robust to partial volume effects and to complex fiber configurations. The next step was done with the help of FreeSurfer (http://surfer.nmr.mgh.harvard.edu), a freely available software tool. We extracted the interhemispheric tracts connecting the pars orbitalis area of the inferior frontal gyrus of both hemispheres, using the FreeSurfer cortical parcellation of these areas as extraction masks.

Once the tracts were extracted, we computed the Total Dispersion (T D) measure of [7]. Given a set of curves that represent white matter fibers, and a tangent vector E_T at each point along each curve, we measure the rate of change of E_T in 20 directions uniformly distributed on the unit circle, in the plane orthogonal to E_T. At each point along each curve, this samples the “dispersion distribution function” (DDF) of [7], a function that represents the amount of fibre dispersion in each direction orthogonal to the fibre. The T D measure at each point is then defined as the average value of the DDF. As the DDF can be computed at a variety of spatial scales [7], we used an empirically selected scale parameter value S = 10mm.

In addition to performing cortical surface parcellation, the FreeSurfer tool also extracts the GM/WM boundary surface. This surface is represented as a mesh, with the principal curvatures calculated at each vertex. At each vertex in the pars orbitalis cortical region, we computed the mean curvature Cm, defined as the mean of the surface’s two principal curvatures κ₁ and κ₂. Note that while the FreeSurfer parcellation was registered to the diffusion MRI space to allow for cortical ROIs to be used as extraction masks for the tractography, all surface curvature computations are performed in the original FreeSurfer space, to avoid the introduction of registration artifacts.

As an illustration, we show in Fig. 2 the fibers connecting to the pars orbitalis region in the right hemisphere, colored by the T D value at each point. Note the ‘bottleneck’ with low T D (yellow/red), and the fibers’ dispersion towards the cortex (green/blue). We overlay these fibers onto a volume representing the mean curvature of the GM/WM boundary surface. To create this visualization, the mean curvature values were rasterized into a 3D volume with the mri surf2vol utility (part of the FreeSurfer toolkit). The resulting volume was then registered to the diffusion MRI space (which gives a thickness to the surface as a byproduct). As an anatomical reference, we also show the fibers over the T1 image.

Fig. 2.

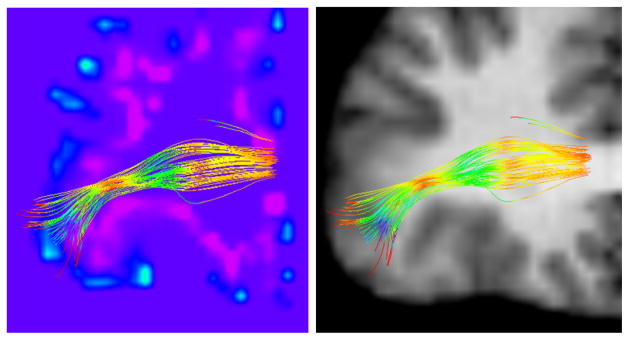
A zoom-in on an anterior coronal view of the right hemisphere with fibers connecting the pars orbitalis. The fibers are colored by TD, such that low TD values are indicated with red/yellow, and high values with green/blue. Please keep in mind that fiber dispersion is a 3D phenomenon. Left: a volume rendering of the mean curvature of the GM/WM boundary surface, such that blue/purple intensities denote the curvature sign and magnitude. Right: the T1 image, shown for anatomical reference.

2.2 Fusion of WM and GM geometry information via Mutual Information (step 4)

The above preprocessing steps give, at each point along the fiber tract of interest, a scalar quantifying the dispersion of the tract at that point. In addition, at each point on the cortical surface ROI, we have a scalar quantifying the mean curvature (or possibly another feature) of the surface at that point. The probability density functions (pdf) of these values can then be estimated, and the relationship between them captured via a quantity known as Mutual Information (MI) [10]. The MI between two random variables measures the amount of information they share. The higher the MI value, the more ‘dependent’ the variables are, i.e. the more knowledge we gain of one by knowing the value of the other. MI should not be confused with the correlation between two variables, which measures the strength of the linear relationship between them. MI is much more general, as it does not assume any particular form for the relationship between the two variables. MI has been widely used in medical imaging, in particular for image registration (e.g., [11]). Here, the use of MI allows us to combine information between geometrical measures on the white matter and on the gray matter.

The Mutual Information of two continuous random variables X and Y is defined as follows [10]:

$$M(X;Y)={\int }_Y{\int }_{X}p(x,y)log\left(\frac{p(x,y)}{p(x)p(y)}\right)\mathit{dxdy},$$ (1)

where p(x, y) is the joint probability density function of X and Y, and p(x) and p(y) are their respective marginal probability densities. In our implementation, to compute M we used the MILCA estimator [12], which is available online. This is a robust estimator which does not require a priori knowledge of the joint density of the two variables. This is in contrast to MI computations typical to the image registration literature, which usually require explicit correspondence between two images to compute their pixel-based joint density. In our work, we do not compute MI between two images. Rather, we use kernel density estimation [13] to compute one probability density estimate for Cm over the cortical area and another one for T D over the connecting white matter tract. We treat these two density estimates as two one-dimensional signals, and we then use the method of [12] to compute MI between them. Because of this, explicit pointwise correspondence between white matter and cortical locations is not required.

3 Experiments

3.1 Subjects and Data Acquisition

We illustrate our method with a small-scale study on autism. Autism has been characterized as a disorder in which the brain undergoes an early period of overgrowth, from birth to approximately age 4. This early period of excessive growth is thought to be followed by abnormally slow or even arrested growth [14]. Based on this knowledge, we hypothesize that our MI based measure will reveal a difference in the trajectory of brain development with age. Of course, the main purpose of this study is to illustrate the method, and not to make any conclusive clinical claims about autism. The study is only preliminary, as it uses a relatively small number of subjects, and is focused on a single cortical region.

Diffusion and structural MRI data were acquired from 15 healthy male controls (HC, age range: 6.4 – 13.9 years, mean: 10.3, std dev: 2.4) and 14 male autism spectrum disorder patients (ASD, age range: 6.4 – 13.3 years, mean: 10.0, std dev: 2.1).

All imaging was performed using a Siemens 3T Verio^™ scanner with a 32 channel head coil. Structural images were acquired on all subjects using an MP-RAGE imaging sequence (TR/TE/TI = 19s/2.54ms/.9s, 0.8mm in plane resolution, 0.9mm slice thickness). In addition, A HARDI acquisition was also performed using a monopolar Stejskal-Tanner diffusion weighted spin-echo, echo-planar imaging sequence with the following parameters: TR/TE=14.8s/110ms, b=3000s/mm², 2mm isotropic resolution, and 64 gradient directions as well as two b0 images. The DW-MRI images for both acquisitions of each subject were then filtered using a joint linear minimum mean squared error filter for removal of Rician noise. Eddy Current Correction was then performed using registration of each DWI volume to the unweighted b0 image.

3.2 Results

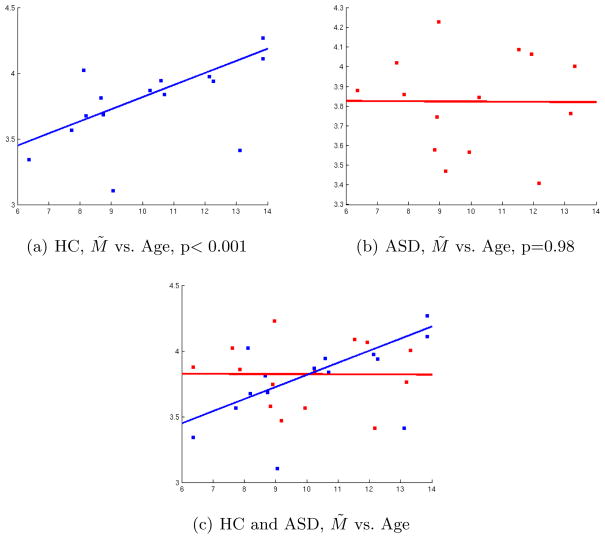
To test our hypothesis, we computed the correlations between subject age and M̃ ≡ M (Cm, T D). The correlations in the left hemisphere were not significant, so we focus on the right hemisphere. In the HC group, we obtained a significant Pearson correlation coefficient (p=0.0403). However, due to the presence of apparent outliers, we also computed the correlation using a robust linear regression method, as implemented with the ‘robustfit’ Matlab routine. This robust correlation was more significant (p=0.00022). As for the ASD group, we did not obtain a significant correlation (p=0.95 for the Pearson correlation, p=0.98 for the robust correlation), which may indicate a pathology-based alteration of the normal course of brain development. These results are shown in Fig. 3, and appear to fall in line with the notion that autism may be characterized by early brain overgrowth (till about age 4), followed by a reduced or arrested brain growth [14]. Our regression results suggest that at age 6, ASD children have a higher M̃ value than healthy controls. This value doesn’t appear to change at later age in ASD children, while there is a steady change in healthy controls. Again, this study is based on a single cortical region (previously implicated in ASD), thus a more global analysis is needed prior to making strong clinical claims. Nevertheless, our results illustrate potential applications of the method.

Fig. 3.

Correlation in the Right hemisphere between Age (x-axis) and M̃ = M (Cm, T D). Top row: Control (HC) subjects (Left). ASD subjects (Right). Bottom row: Both groups shown in the same plot. The lines indicate the fit obtained by robust correlation for each group, with the corresponding p-values indicated.

4 Summary and Discussion

We introduced the motivation and groundwork for a novel analysis of the relationship between white matter geometry and cortical surface geometry. This relationship could be informative in many contexts in neuroscience, such as the study of neurodevelopment or the progression of atrophy in neurodegenerative diseases. Our proposed approach is relatively simple, yet we showed it holds a potential for discovering pathology-based differences. Our preliminary results suggest that normal age-related changes in the brain may be altered by ASD pathology. It is particularly interesting that in controls, we find significant correlations in the right hemisphere (as opposed to the left), as previous work on lateralization has implicated the right hemisphere in autism (e.g., [15]).

The basic framework described in this paper can be extended in several ways. First of all, metrics other than Mutual Information can be used, such as kernel-based methods [16]. Methods based on machine learning can also be applied to ‘learn’ the relationship between the two types of geometry. In future work, we will perform an investigation over a parcellation of the entire cerebral cortex, which will then be incorporated into a network analysis framework in order to detect global patterns of change. Finally, a promising application area of our methods lies in longitudinal studies.