Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2014 Jun 3.
Published in final edited form as: Microcirculation. 2009 Jan 31;16(3):213–219. doi: 10.1080/10739680802527404

Glycocalyx volume measurements: a critical review of tracer dilution methods for its measurement

CC Michel 1, FE Curry 2
PMCID: PMC4041983  NIHMSID: NIHMS271464  PMID: 19184776

Abstract

A clinical measure of endothelial glycocalyx structure would have great potential importance because lesions of the glycocalyx may be the first changes to occur in diabetes and in a wide range of vascular diseases. A method recently described by Nieuwdorp et al [15, 16] for estimating the volume of the luminal glycocalyx of the entire human vascular system would seem to be the first attempt to develop a measure of this kind. It is based on the tracer dilution principle and this review considers the principles and conditions that underlie this method and the extent to which the conditions appear to have been fulfilled in this case. Our analysis raises two questions about (a) the estimation of the concentration of the tracer (dextran 40) at zero time and (b) the estimation of plasma volume, both of which can be answered by changes in experimental protocol. A third question, concerning the partition coefficient of the tracer between plasma and the fluid within the glycocalyx, cannot be answered at the present time and until it has been resolved, glycocalyx volume cannot be estimated from the dilution of a macromolecular tracer.

Introduction

The glycocalyx (ECL) is the thin layer of membrane glycoproteins and other macromolecules that separates the lipid bi-layers of endothelial cell membranes from the circulating plasma. Over the past 30 years, increasing evidence has bolstered the idea that this layer acts as a barrier to plasma macromolecules, responsible for the ultrafiltration properties that characterize microvascular walls in most tissues [14, 20]. In addition it appears to have important anticoagulant properties and there is evidence that various membrane bound enzymes as well as some endothelial flow sensors are located here. Because changes in glycocalyx structure might precipitate a cascade of changes in normal vascular function, it is reasonable to speculate that lesions of the glycocalyx might be fundamental to a range of cardiovascular diseases. A method for measuring the properties of the endothelial glycocalyx of human subjects could therefore be of great importance to clinical investigation.

Consequently, it was with great interest that we read the paper by Nieuwdorp et al [15] describing a method for estimating the volume of the entire endothelial glycocalyx (VECL) in healthy volunteers. Here they report that a reduction of glycocalyx volume occurred during an acute period of hyperglycemia. In a second paper, Nieuwdorp et al [16] describe lower values of glycocalyx volume in patients with Type 1 diabetes mellitus than they had seen earlier in healthy subjects. Furthermore, those patients with microalbuminuria had even lower values of glycocalyx volume than those without it.

The importance of these reports ultimately depends on the validity of the method of measurement. Unfortunately the method is described rather briefly, raising several questions for which we have been unable to gain satisfactory answers. Recent publications by the same group, emphasize the reproducibility of the values they measure for glycocalyx volume (VECL) in individual subjects but they do not address the questions of how these estimates relate to the real VECL [17]. Because it is important to have an accurate clinical measure of glycocalyx structure, we are raising these questions in the hope that either the principles of the method may be clarified or that an alternative measure may be developed.

Principles of the Method

The method is based on the difference between the volume of distribution of neutral dextran 40 (D40) and the plasma volume. Whereas plasma macromolecules such as serum albumin and fibrinogen appear to be excluded from the most peripheral region of the lumen of living microvessels adjacent to the endothelium (where the glycocalyx is located), D40 has been observed to fill the entire lumen of microvessels right up to the lipid bilayers of the endothelial cell membranes [20]. From this, it is argued that the volume of distribution of D40 should correspond to the volume of the plasma plus the volume of the glycocalyx. Plasma volume is estimated independently from the volume of distribution of labeled red cells, so the volume of the glycocalyx can be calculated by subtracting the plasma volume from the distribution volume of D40 and plasma.

The method makes two assumptions that are fundamental to the use of a volume of distribution of a tracer solute to estimate the fluid volumes within a structure such as the glycocalyx. These assumptions are: (a) that initial volume of distribution of D40 in the plasma and the glycocalyx fluid can be calculated from a value for total dextran concentration in plasma at zero time estimated by backward extrapolation of the curve relating dextran concentrations of plasma samples taken at known times after the infusion of the dextran; (b) that the partition coefficient for D40 between plasma and glycocalyx fluid is 1.0. At present, the justification for both of these assumptions is questionable. A further criticism of the method, which has important implications, is the estimation of the plasma volume from the circulating red cell volume and the haematocrit. We shall consider first, the assumptions underlying the elementary theory of the volume dilution technique.

Principles of volume-dilution and the use of D40 dilution to estimate glycocalyx volume

The method is a simple application of mass conservation. If m g or moles of solute are dissolved in the water of a compartment of unknown volume, V, and when well mixed throughout the compartment has a concentration, C, then:

V=m/C (1)

V calculated from equation 1 should be equal to the volume of water in the compartment, providing that the following conditions are fulfilled: (i) all the solute molecules are retained in the compartment at the time C is determined; (ii) that solute does not combine with structures in the compartment; (iii) the solute molecules are the same size as water molecules; (iv) at equilibrium, the solute molecules are at the same concentration in all regions of the compartment.

Condition (i) and the calculation of initial volume of distribution

In the estimation of VECL, D40 is infused into the circulation and it is assumed that it distributes itself rapidly throughout the intravascular space including the fluid filled spaces within the ECL. The first blood sample is taken 5 min after the end of the D40 infusion and subsequent samples are taken at 7, 10, 15, 20 and 30 mins and plasma concentration of dextran estimated from the increase in glucose concentration after hydrolyzation of the dextran polymers. Between the onset of the D40 infusion and 5 min after its cessation when the first blood sample was taken, some D40 left the intravascular space and entered the interstitium so infringing condition (i) that solute molecules should be contained within the compartment. To adjust for this potential error, the authors use the time honored method of plotting values of D40 concentration in plasma samples against the time at which the samples were taken at known times after the end of the infusion of D40 into the circulation. The curve describing the fall in concentration with time is then extrapolated back to zero time when the concentration is believed to represent that which would have existed had all the D40 been distributed uniformly throughout the blood before any D40 had left the circulation. They have then used this concentration at zero time in equation 1 to estimate the initial volume of distribution of D40. The back-extrapolation procedure, however, is valid only if the clearance of D40 from the circulation is the same between the injection of D40 into the blood and the collection of the first sample as it is over the period between this first sample and subsequent samples. On the limited evidence available to us, there are strong grounds for questioning this assumption of back-extrapolation is valid here.

Nieuwdorp et al [15, 16, 17] used commercial Rheomacrodex as their source of D40. Rheomacrodex is a mixture of dextrans of different molecular weights with a mean value of 40KDa. Between 20% and 25% of many samples of Rheomacrodex consist of polymers with molecular weights between 7KDa and 20KDa. No details are given by Nieuwdorp et al [15, 16] to suggest that the low molecular weight components were removed by ultrafiltration or chromatography from the samples of Rheomacrodex that they used. If their failure to mention this means that they did not use dextrans within a very narrow band of molecular weight, the consequences are quite serious. Whereas dextran polymers with a molecular weight of 40KDa have a molecular radius of 4.9 nm and would leave the circulation very slowly, dextran polymers with molecular weights in the range of 7KDa to 20 KDa have smaller molecular radii (1.5 – 3.0 nm) and can leave the circulation within a few minutes [2, 12]. Therefore if a mixture of dextrans is injected, most of the small molecular components will escape from the circulation within the first few minutes and leave the larger molecules to exchange more slowly at later times. Since Nieuwdorp et al [15, 16] determined plasma dextran concentrations from the number of glucose residues of all polymers, the clearance of dextran from the plasma before the first blood sample was taken at 5 mins cannot be assumed to be the same as its clearance from the plasma at later times. Unless the dextran molecules that were being cleared from the plasma were of the same molecular weight and size and had the same permeability through vascular endothelium, the backward extrapolation method of obtaining a concentration at zero time, cannot be justified.

Experimental evidence demonstrating the rapid clearance of the low molecular weight fractions of Rheomacrodex was reported many years ago by Arturson and Wallenius [2] and Arturson [1]. Fig 1 is based on Arturson's paper [1] and it is seen that 6 minutes after Rheomacodex injection, most of the low molecular weight dextran fractions have left the circulation. These fractions leaving the circulation constitute between 20% and 30% of the total dextran concentration in the initial sample of Rheomacrodex. Figure 2 shows these same data in terms of the total plasma concentration of dextrans of all molecular weights (which is what Nieuwdorp et al were measuring) plotted against time. It is seen that the rapid fall in concentration over the first 6 minutes is followed by a much slower decline, indicating that backward extrapolation of a curve based on the samples taken between 5 mins and 30 mins would give a value at zero time that is significantly below the true initial concentration.

Figure 1.

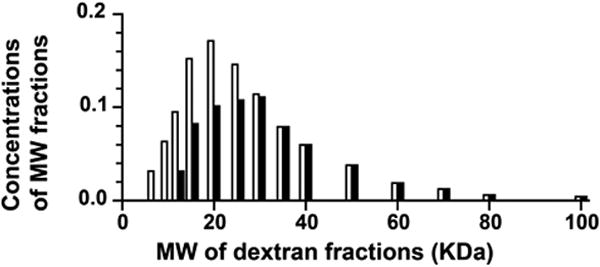
Figure 1

Open in a new tab

The concentration of dextrans of different molecular weights in Rheomacrodex expressed as fractions of the total dextran concentration initially present in the sample in plasma and at 6 mins after their injection into the circulation of seven human subjects. (Redrawn From Arturson, G. Glomerular permeability to dextrans. In Crone C. & Lassen NA eds. Capillary Permeability. Alfred Benzon Symposium II. Munksgaard. 1970).

Figure 2.

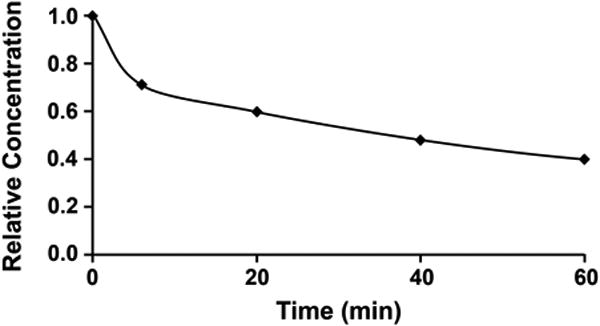
Figure 2

Open in a new tab

Plasma concentration of total dextran during the first hour after intravenous injection of Rheomacrodex. (Calculated from data of Arturson G., Glomerular permeability to dextrans. In Crone C. & Lassen NA eds. Capillary Permeability. Alfred Benzon Symposium II. Munksgaard. 1970.

The consequences of this error for estimates of VECL can be considerable. If an exponential curve is fitted to the data the 6, 20, 40 and 60 min points in Figure 2 and extrapolated back to zero time, the intercept indicates the initial concentration to be 75.1% of its actual value. This means that use of this intercept value to estimate the initial volume of distribution of Rheomacrodex would yield a value that was 1/0.751 = 1.33 times larger than its true value.

Applying this factor to the work of Nieuwdorp et al [15] we find that their reported mean values of 4.7 liters for the initial volume of distribution of D40 would correspond to an actual value of 3.53 liters. Since Nieuwdorp et al estimated plasma volume as having a mean value of 3 liters, VECL calculated from the difference between VD40 and plasma volume is reduced from 1.7 liters (= 4.7 – 3.0) to 0.53 liters (= 3.53 – 3.0). Because the estimates of VECL can be influenced by errors in the estimation of plasma volume as well as errors in the initial volume of distribution of D40, we shall consider a potential error here before going on to examine the applicability of the other conditions of the dilution – volume technique.

Estimation of plasma volume

Nieuwdorp et al [15, 16, 17] estimated the plasma volume of their subjects from the distribution volume of circulating labeled red cells and the haematocrit of blood taken by venepucture. This is surprising since it has been known for more than 60 years that estimates of plasma volume made in this way are 15-20% less than estimates of plasma volume made from the distribution volume of a plasma marker such as serum albumin (labeled with either Evans Blue or RISA) or fibrinogen [5]. Furthermore, the rationale for using D40 as a marker of ECL volume arises from the observations of Vink and Duling [20] that serum albumin and fibrinogen are excluded from the glycocalyx region of capillaries in vivo whereas D40 is able to enter this region.

In a major review, Lawson [13] compared estimates plasma volume that were made from the volume of distribution of labeled red cells and the haematocrit with those made from the initial volume of distribution of Evans Blue labeled albumin and showed that larger values were derived in studies using labeled albumin. The most convincing set of data that he reviews are those of Chaplin et al [5], who had carried out both measurements simultaneously in 28 human subjects. These showed that plasma volume was 18% greater when estimated by Evans Blue than when calculated from the circulating red cell volume and the large vessel haematocrit. This imples that if Nieuwdorp et al were to estimate plasma volume using labeled albumin or fibrinogen, its mean value would be 18% greater than the figure they report i.e. it would be increased from 3.0 to 3.54 liters. This “corrected” figure is approximately the same as the adjusted value for the volume of distribution of D40. It implies that VECL has a value close to zero. Obviously this cannot be so if the original observations of Vink and Duling [20] are correct. A possible explanation of this discrepancy emerges when we consider the assumptions underlying the other conditions of the dilution-volume method.

Conditions (ii), (iii) and (iv) and the partition coefficient of solute between plasma and glycocalyx water

Calculations of volumes of body compartments from the volumes of distribution assume that when a known amount of identifiable solute is added to plasma, it will all remain in solution (condition ii) and will distribute itself evenly throughout some fractional volume of the body fluids reaching equilibrium when its concentration is the same in all parts of that volume including the sample of plasma used for estimation of its concentration (condition iv). In the absence of evidence to suggest that significant amounts of any of the constituent polymers of D40 bind to elements in the plasma, the glycocalyx or matrix molecules of the interstitium. We can conclude that it is reasonable to assume condition (ii) applies.

The component molecules of D40, however, are all many times greater in size than water (assumption iii) and as a consequence one cannot assume condition (iv) applies. The equilibrium concentrations of D40 molecules in ECL water and plasma may be expected to differ considerably because the ECL is a molecular matrix and the water within it is held in spaces with comparable dimensions to those of the component D40 molecules. Consequently, the centers of the dextran molecules cannot enter a film of water surrounding each of matrix macromolecules. The thickness of this film is equal to that of the molecular radius of the dextran molecule and within a matrix like that ECL is likely to constitute a significant fraction of the volume of water (see for example, Wiig et al [21], Curry [6] and earlier references cited by these authors). This phenomenon of steric exclusion is illustrated in Figure 3.

Figure 3.

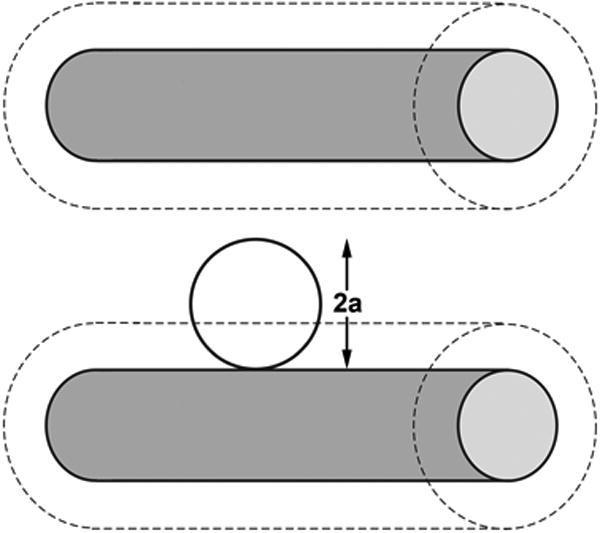
Figure 3

Open in a new tab

Diagram to illustrate steric exclusion of the centre of a spherical molecule from the water surrounding two cylindrical molecules (shaded) acting as components of a molecular matrix such as the glycocalyx. Because the centre of the spherical molecule cannot approach the matrix molecule closer than its own radius (a), it is excluded from region of water surrounding the matrix molecule of thickness = a shown by the outer dashed cylinders.

The difference between the equilibrium concentrations of a solute in two compartments is described by the partition coefficient, λ. Referring to the concentration in the two compartments as CP and CE:

λ=CECP (2)

To appreciate the importance of λ in estimating volumes of distribution let us consider the very simple case of the distribution of a macromolecule, A, between the plasma and the fluid within the ECL when the macromolecule does not enter any other compartment. If we add M moles of A to the plasma (which has a volume = VP) and A distributes itself only between the plasma and the fluid in the ECL (volume = VECL), at a later time:

M=CA(P)VP+CA(ECL)VECL (3)

where CA(P) and CA(ECL) are the concentrations of A in VP and VECL respectively. Since, from equation 2, at equilibrium, CA(ECL) = CA(P)λ, it follows that:

M=CA(P)VP+CA(ECL)VECL=CA(P)Vp+λCA(p)VECL=CA(P)(VP+λVECL) (4)

The procedure followed by Nieuwdorp et al is to divide M (which is known) by CA(P) (which can be measured) and assume that this ratio is the sum of the plasma volume and the VECL. Rearrangement of equation 4, however, reveals this interpretation is valid only if λ = 1, since:

M/CA(P)=V(P)+λVECL (5)

Obviously the validity of the estimates of the initial volume of distribution of D40 depends critically on the extent to which λ for D40 between ECL fluid and plasma deviates from unity. The value of λ is determined by the dimensions of the water filled spaces within the ECL, which are a function of its structure, and the dimensions of the probe molecule, which in this case is D40. We have estimated the maximum width of the entrances into the water filled spaces of the ECL from the plasma and used this value to assess values of λ for possible ECL structures. These calculations, which are summarized in the appendix to this paper, indicate that D40 has a value of λ between 0.01 and 0.05 for the more reasonable ECL structures. If λ for D40 is assumed to have a value 1.0 when its real value is 0.01, 1.5 liters of fluid within the ECL would be estimated as 15ml. Such a volume is too small to appear as a significant difference between estimates of the initial volume of distribution of D40 and the plasma volume. This would be consistent with our earlier conclusion that by estimating plasma volume from the initial volume of distribution of albumin or fibrinogen might reduce the apparent ECL volume to zero.

This discussion leads us to conclude that the volume of fluid within the glycocalyx can only be estimated from the initial volume of distribution of a tracer if the partition coefficient of the tracer between the glycocalyx fluid and the plasma is known. At present there are no measurements of this nor is it possible to calculate what its value might be until the detailed structure of the glycocalyx has been determined.

Discussion

Earlier we emphasized the importance of having a clinical measure of glycocalyx structure that could be shown to be valid. Although Nieuwdorp et al [15, 16] have shown their estimates of glycocalyx volume are reproducible in different individuals, the arguments presented in this short paper indicate that there are critical questions to be answered about their method before the numbers gained from it can be regarded as a valid measure of either the volume of the glycocalyx or the volume of water within it.

First, in estimating the volume of distribution of D40 in the plasma, the determination of the concentration of D40 at zero time by back extrapolation to zero time of the relation between plasma concentrations at later times, is only justifiable if it can be shown that the dextran molecules that leave the circulation immediately after infusion at the same rate as dextran molecules are cleared at later times. We have argued that it is unlikely to be so if the commercial samples of Rheomacrodex that were used in this study contain fractions that have molecular weights of less than 30 KDa. The best way to check this would be follow Arturson's example [1] and estimate the concentrations of the different molecular weight fractions of dextrans in Rheomacrodex after it has been added to (and suitably diluted in) plasma in vitro, and compare the distribution of these concentrations with those in samples of plasma taken from human subjects 5, 10, 15, 20 and 30 mins after Rheomacrodex had been infused into the circulation. Alternatively, a single molecular fraction of D40 (or a very narrow band of MW) could be prepared and infused into the subjects, with subsequent checks on the MW distribution in the plasma to be sure that low MW fractions have not developed on dilution of the sample.

Second, we have also questioned the plasma volume measurements that Nieuwdorp et al [15, 16] have used based on the distribution volume of circulating red cells and the haematocrit of blood taken by venepuncture. These problems are compounded by the evidence that plasma and red cells have different distribution patterns within the microvasculature [8, 18]. We suggest that these problems can be easily rectified by measuring the initial volume of distribution of either serum albumin or fibrinogen since both of these molecules appeared to be initially excluded from the glycocalyx in the studies of Vink and Duling [20].

Third, we have pointed out that if the volume of distribution of a macromolecule such as D40 is to be used to estimate the volume of the plasma plus the fluid within the glycocalyx, it is necessary to know the partition coefficient of D40 between the glycocalyx fluid and the plasma. We have argued that its value is likely to be small so that the error in ignoring it may be very large indeed. It can be argued on more general grounds that a molecule that can distribute itself fairly rapidly between the plasma and glycocalyx fluid but leave the circulation relatively slowly will have an ECL: plasma partition coefficient that is very much less than one. Once a molecule has entered the glycocalyx fluid it has only to pass through the clefts between the endothelial cells to leave the vascular system and these are 20 nm wide and would only hinder the movements of the largest molecules significantly. Because the glycocalyx is the principal component of the endothelial barrier to macromolecules, macromolecules will be excluded from large volumes of fluid within it meaning that their partition coefficients between this fluid and the plasma will be considerably less than one. This leads us to conclude that the volume of fluid within the glycocalyx cannot be determined from the volume dilution principle when the tracer is a macromolecule partition coefficient with an unknown partition coefficient between ECL fluid and plasma. Furthermore, since the partition coefficient is likely to change with alterations in glycocalyx structure, it would seem that such a method could have only very limited clinical application.

Finally, we would like to add that although the measurements of Nieuwdorp et al [15, 16, 17] may not represent values of ECL volume, the changes in these values are of considerable potential interest. It would be very interesting indeed to know what the measurements do reflect but this can only emerge from a more rigorous examination of the method than has been published so far.

Supplementary Material

Supp App Fig S1

Appendix Figure A1. Diagram to illustrate steric plus electrostatic charge exclusion in a matrix. Radius of solute molecules (= a; radius of matrix molecules = r ; D is the Debye length (the range of electrostatic influence) and this is ∼ 1.0 nm in solutions the ionic strength of plasma. Figure A1A shows a neutral solute molecule (grey scale) adjacent to a charged matrix molecule of radius r (solid back). The centre of the neutral solute molecule is excluded from a region of solution of radius r+a (heavy broken line distance a surrounding the matrix molecule but with no effect of the electrostatic exclusion zone a distance D (=1nm) surrounding the matrix (inner broken line). Figure A1B shows the case where negatively charged solutes (light hatched) are excluded by both steric and electrostatic charge (similar charge density on both solute and matrix). The center of the charged solute is excluded from a region of solution of radius r+a+2D(dot and dash line). The space available to 2 negatively charged solute molecules (ds) between matrix molecules that are a distance d apart when the matrix molecules also carry a negative charge is ds = d − 2(r+a+2D) whereas the space available to water and small solutes (a close to zero) = d − 2r.

Supp App Fig S2

Appendix Figure A2. Four examples of possible structures for which λ has been calculated. Figs A2A and A2C represent the glycocalyx as a series of cylindrical molecular chains, which arise from trans-membrane proteins in the luminal endothelial cell membrane. In figures A2B and A2D the cylindrical chains link globular proteins (represented by spheres). In Figures 1A and 1B the chains are based on a square array, the diagonal of which is 11.2 nm (note the cylinders are further apart in A2C because the diagonal is measured between the spheres. In FiguresA 2C and A2D the chains arise from equilateral triangles of side length 11.2 nm. Calculations suggest that highest values of the partition coefficient (λ) between plasma and the fluid within the glycocalyx occur with variants of Figure A2D when λ may have a value as high as 0.4 and there is no cross linking. Cross-linking between the chains (shown as solid connecting lines) reduces λ to less than 0.05. For Figures A1 A and A1C all values for λ are less than 0.05.

Acknowledgments

We thank Joyce Lenz for the preparation of the Figures.

The work in FEC's laboratory is supported by NIH grant HL 44485.

Appendix

Estimation of the maximum width of the entrances between the plasma and the water filled spaces within the ECL available to a spherical macromolecule

The Stokes Einstein radii (aES) of dextran molecules can be calculated from their diffusion coefficients in aqueous solutions and have been widely used (See for example [9, 10, 11, 12]. For D40, aES has a value of 4.9 nm. The maximum diameter of the entrance from the plasma into the ECL that is available to a neutral molecule of this size can be estimated from the known molecular properties of serum albumin, a negatively charged macromolecule, which is almost completely excluded from the ECL [20]. This is possible because in addition to steric exclusion, which affects both charged and uncharged molecules, the effects of a charged matrix in excluding a molecule of the same charge is determined by the Debye length. In aqueous solutions of the ionic strength of mammalian plasma, the Debye length has a value of 1.0 nm. (for discussion of this approach see [6]). For a negatively charged albumin molecule to be excluded from entering a negatively charged matrix, the portals of the matrix can be no more than 4 nm larger than the diameter of the albumin molecule (which is 7.1 nm). The 4 nm is made up of 2 nm linked to effects of the net negative charge on each side of the albumin molecule and a further 2 nm associated with the negative charge on each side of the entrance to the matrix. This means that the opening is no more than 7.1 + 4 = 11.1 nm. This phenomenon is illustrated in general terms in Appendix Figure 1.

Since D40 has a molecular diameter of 4.9 × 2 = 9.8 nm, the center of a D40 molecule is excluded from over 88% of the entrance region. Water molecules by contrast (diameter 3 nm) are able to occupy 97% of the entrance region. Thus the concentration of D40 within the matrix must be considerably less than its concentration in the plasma.

In these calculations we have used the Stokes Einstein radii as molecular radii for serum albumin and D40. The Stokes Einstein radius of a molecule is the radius of a sphere that faces the same friction resistance to diffusion through an aqueous solution as the molecule. Studies of rotational diffusion coefficients of serum albumin suggested that it was ellipsoidal rather than spherical with axes of 14.4 × 4.4 × 3.2 nm [7] i.e. its Stokes Einstein diameter is approximately half long as its major axis. Models based on its chemical [3] and crystallographic structure suggest that it is more spherical in shape [4]. More recently Sugio et al [19] have indicated that human serum albumin is roughly heart shaped with dimensions of 8 × 8 × 3 nm. From this it seems reasonable to take the Stokes Einstein diameter of 7.1 nm.

Estimation of λ for a series of possible matrix structures

If a molecule can enter the matrix, the value of λ is determined by the dimensions of the molecule and the spacing between the component matrix molecules of the ECL. We have explored what λ might be for simple hypothetical structures based on the ECL being a matrix of cylindrical molecules or cylindrical chain molecules linking larger globular molecules (see Appendix Fig. A2).

Four representative structures are shown below. For all structures composed of cylindrical molecules separated by 11.2 nm. λ for a molecule of diameter 9.8 nm has a value of 0.05 or less. If the entrances to the water filled spaces within the ECL are guarded by large globular molecules set on relatively small diameter (e.g. 1 nm) cylindrical molecules, λ may rise to 0.1 or more. Further increases in λ can be achieved theoretically by increasing the ratio of the diameters of the gatekeeper globular molecules to those of the cylindrical chains and increasing the length of the latter. Structures such as these are unlikely to be stable as the chains lengthen, unless there is some cross-linking between the cylindrical chains. The cross-links, however, increase the degree of exclusion of a probe molecule and consequently lower the value of λ. The most likely structures would appear to have λ values of no more 0.05 for molecule with a Stokes Einstein radius of 4.9 nm

References

  • 1.Arturson G. Glomerular permeability to dextrans. In: Crone C, Lassen NA, editors. Capillary Permeability: Proceeding of the Alfred Benzon Symposium II. Munksgaard; Copenhagen: 1970. pp. 520–530. [Google Scholar]
  • 2.Arturson G, Wallenius G. The intravascular persistence of dextrans of different molecular sizes in normal humans. Scand J Lab Clin Invest. 1964;16:76–81. doi: 10.3109/00365516409060485. [DOI] [PubMed] [Google Scholar]
  • 3.Brown JR. Structural origins of mammalian albumin. Fed Proc. 1976;35:2141–2144. [PubMed] [Google Scholar]
  • 4.Carter DC, He XM. The structure of human serum albumin. Science. 1990;249:302–303. doi: 10.1126/science.2374930. [DOI] [PubMed] [Google Scholar]
  • 5.Chaplin H, Mollison PL, Vetter H. The body/venous hematocrit ratio: its constancy over a wide hematocrit range. J Clin Invest. 1953;32:1309–1316. doi: 10.1172/JCI102859. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Curry FE. Mechanics and thermodynamics of transcapillary exchange. In: Renkin EM, Michel CC, editors. Handbook of Physiology Section 2. Vol. 4. American Physiological Society; Washington DC: 1984. pp. 309–373. [Google Scholar]
  • 7.Edsall JT. Configuration of certain protein molecules. An inquiry concerning the present state of our knowledge. J Polymer Sci. 1954;12:253–280. [Google Scholar]
  • 8.Eppihimer MJ, Lipowsky HH. (1994) Leukocyte sequestration in the microvasculature in normal and low flow states. Am J Physiol. 1994 Sep;267(3 Pt 2):H1122–34. doi: 10.1152/ajpheart.1994.267.3.H1122. [DOI] [PubMed] [Google Scholar]
  • 9.Garlick DG, Renkin EM. Transport of large molecules from plasma to interstitial fluid and lymph in dogs. Am J Physiol. 1970;219:1595–1605. doi: 10.1152/ajplegacy.1970.219.6.1595. [DOI] [PubMed] [Google Scholar]
  • 10.Granath KA. Solution properties of branched dextrans. J Colloid Sci. 1958;13:308–328. [Google Scholar]
  • 11.Granath KA, Kvist BE. Molecular weight distribution analysis by gel chromatography on Sephadex. J Chromatog. 1967;28:69–81. doi: 10.1016/s0021-9673(01)85930-6. [DOI] [PubMed] [Google Scholar]
  • 12.Grotte G. Passage of dextran molecules across the blood-lymph barrier. Acta Chir Scand Suppl. 1956;211:1–84. [PubMed] [Google Scholar]
  • 13.Lawson HC. The volume of blood – a critical examination of methods for its measurement. In: Hamilton WF, Dow P, editors. Handbook of Physiology Section 2. Vol. 1. American Physiological Society; Washington DC: 1962. pp. 23–49. [Google Scholar]
  • 14.Michel CC, Curry FE. Microvascular Permeability. Physiol Rev. 1999;79:703–761. doi: 10.1152/physrev.1999.79.3.703. [DOI] [PubMed] [Google Scholar]
  • 15.Nieuwdorp M, van Haeften TW, Gouverneur MCLG, Mooij HL, van Lieshout MHP, Levi M, Meijers JCM, Holleman F, Hoekstra JBL, Vink H, Kastelein, Stroes ESG. Loss of endothelial glycocalyx during acute hyperglycemia coincides with endothelial dysfunction and coagulation activation in vivo. Diabetes. 2006a;55:480–486. doi: 10.2337/diabetes.55.02.06.db05-1103. [DOI] [PubMed] [Google Scholar]
  • 16.Nieuwdorp M, Mooij HL, Kroon J, Atasever B, Spaan JAE, Ince C, Holleman F, Diamant M, Heine RJ, Hoekstra JBL, Kastelein JJP, Stoes ESG, Vink H. Endothelial glycocalyx damage coincides with microalbuminaemia in Type 1 diabetes. Diabetes. 2006b;55:1127–1132. doi: 10.2337/diabetes.55.04.06.db05-1619. [DOI] [PubMed] [Google Scholar]
  • 17.Nieuwdorp M, Meuwese MC, Mooij HL, Ince C, Broekhuizen LN, Kastelein JJP, Stroes ESG, Vink H. Measuring endothelial glycocalyx dimensions in humans: a potential novel tool to monitor vascular vulnerability. J Appl Physiol. 2008;104:845–852. doi: 10.1152/japplphysiol.00440.2007. [DOI] [PubMed] [Google Scholar]
  • 18.Pries AR, Ley K, Gaehtgens P. Generalization of the Fahraeus principle for microvessel networks. Am J Physiol. 1986;251:H1324–32. doi: 10.1152/ajpheart.1986.251.6.H1324. [DOI] [PubMed] [Google Scholar]
  • 19.Sugio S, Kashima A, Mochizuki S, Noda M, Kobayashi K. Crystal structure of human serum albumin. Protein Engineering. 1999;12:439–446. doi: 10.1093/protein/12.6.439. [DOI] [PubMed] [Google Scholar]
  • 20.Vink H, Duling BR. Capillary endothelial surface layer selectively reduces plasma solute distribution volume. Am J Physiol Heart Circ Physiol. 2000;278:H285–H289. doi: 10.1152/ajpheart.2000.278.1.H285. [DOI] [PubMed] [Google Scholar]
  • 21.Wiig H, Gyenge C, Iversen PO, Gullberg D, Tenstad O. The role of extracellular matrix in tissue distribution of macromolecules in normal and pathological tissues: potential therapeutic consequences. Microcirculation. 2008;15:283–296. doi: 10.1080/10739680701671105. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supp App Fig S1

Appendix Figure A1. Diagram to illustrate steric plus electrostatic charge exclusion in a matrix. Radius of solute molecules (= a; radius of matrix molecules = r ; D is the Debye length (the range of electrostatic influence) and this is ∼ 1.0 nm in solutions the ionic strength of plasma. Figure A1A shows a neutral solute molecule (grey scale) adjacent to a charged matrix molecule of radius r (solid back). The centre of the neutral solute molecule is excluded from a region of solution of radius r+a (heavy broken line distance a surrounding the matrix molecule but with no effect of the electrostatic exclusion zone a distance D (=1nm) surrounding the matrix (inner broken line). Figure A1B shows the case where negatively charged solutes (light hatched) are excluded by both steric and electrostatic charge (similar charge density on both solute and matrix). The center of the charged solute is excluded from a region of solution of radius r+a+2D(dot and dash line). The space available to 2 negatively charged solute molecules (ds) between matrix molecules that are a distance d apart when the matrix molecules also carry a negative charge is ds = d − 2(r+a+2D) whereas the space available to water and small solutes (a close to zero) = d − 2r.

NIHMS271464-supplement-Supp_App_Fig_S1.tif (725KB, tif)
Supp App Fig S2

Appendix Figure A2. Four examples of possible structures for which λ has been calculated. Figs A2A and A2C represent the glycocalyx as a series of cylindrical molecular chains, which arise from trans-membrane proteins in the luminal endothelial cell membrane. In figures A2B and A2D the cylindrical chains link globular proteins (represented by spheres). In Figures 1A and 1B the chains are based on a square array, the diagonal of which is 11.2 nm (note the cylinders are further apart in A2C because the diagonal is measured between the spheres. In FiguresA 2C and A2D the chains arise from equilateral triangles of side length 11.2 nm. Calculations suggest that highest values of the partition coefficient (λ) between plasma and the fluid within the glycocalyx occur with variants of Figure A2D when λ may have a value as high as 0.4 and there is no cross linking. Cross-linking between the chains (shown as solid connecting lines) reduces λ to less than 0.05. For Figures A1 A and A1C all values for λ are less than 0.05.

NIHMS271464-supplement-Supp_App_Fig_S2.tif (964.1KB, tif)

RESOURCES