Asymptotic SNR of Scalar and Vector Minimum-Variance Beamformers for Neuromagnetic Source Reconstruction

Abstract

To reconstruct neuromagnetic sources, the minimum-variance beamformer has been extended to incorporate the three-dimensional vector nature of the sources, and two types of extensions—the scalar- and vector-type extensions—have been proposed. This paper discusses the asymptotic signal-to-noise ratio (SNR) of the outputs of these two types of beamformers. We first show that these two types of beamformers give exactly the same output power and output SNR if the beamformer pointing direction is optimized. We then compare the output SNR of the beamformer with optimum direction to that of the conventional vector beamformer formulation where the beamformer pointing direction is not optimized. The comparison shows that the beamformer with optimum direction gives an output SNR superior to that of the conventional vector beamformer. Numerical examples validating the results of the analysis are presented.

I. Introduction

The Search for efficient algorithms for reconstructing spatio-temporal brain activities from neuromagnetic measurements has attracted great interest [1]. One promising algorithm is the minimum-variance beamformer, which was originally developed in the field of array signal processing such as in radar, sonar, and seismic exploration, and has been successfully applied to neuromagnetic source reconstruction problems [2]-[4]. However, the minimum-variance beamformer in its original form [5] cannot be directly applied to neuromagnetic source reconstruction. This is because the neural source distribution is an electrophysiological current distribution, which is a three-dimensional (3-D) vector quantity, so the method should be extended to incorporate the 3-D vector nature of the sources.

So far, two types of extensions of the minimum variance beamformer that incorporate source orientation have been proposed in the literature. One extension, called the scalar-type beamformer, uses a beamformer weight that depends not only on the location but also on the direction of a source [6]. The other type of extension, called the vector-type beamformer, uses a set of three weights where each weight detects one component in the three orthogonal directions [7], [8]. A previous study [9] showed that the scalar-type beamformer can attain twofold better output SNR compared to the vector formulation.

In this paper, we show that the scalar and the vector formulations give exactly the same asymptotic output SNR if the beamformer pointing direction is chosen to maximize the beamformer outputs. We then analyze the performance of this beamformer with optimum pointing direction, and compare its performance to that of the conventional vector beamformer formulation where the beamformer pointing direction is not optimized. A theoretical analysis is given for an isolated source and for two closely located sources. The results of the analysis show that significant SNR degradation can arise in the conventional formulation, and numerical experiments validate these results.

Following a brief review on the two types of extensions in Section II, this paper presents our theoretical analysis in Sections III–V. Section VI presents numerical examples that illustrate the results of our analysis. Throughout this paper, plain italics indicate scalars, lower-case boldface italics indicate vectors, and upper-case boldface italics indicate matrices. The eigenvalues are numbered in decreasing order.

II. Scalar and Vector Minimum-Variance Beamformer Formulations

A. Definitions

We define the magnetic field measured by the mth detector coil at time t as b_m(t), and a column vector b(t) = [b₁(t), b₂(t), …, b_M(t)]^T as a set of measured data where M is the total number of sensor coils and superscript T indicates the matrix transpose. The spatial location is represented by a 3-D vector r:r. The second-order moment matrix of the measurement is denoted R, i.e., R = 〈b(t)b^T(t)〉, where 〈· 〉 indicates the ensemble average, which is replaced with the time average over a certain time window in practice. When 〈 b(t)〉 ≈ 0 holds, R is also equal to the covariance matrix of the measurement. The source magnitude is denoted s(r,t). The source orientation is defined as a 3-D column vector η(r) = [η_x(r), η_y(r),η_z(r)]^T whose ζ component (where ζ equals x,y, or z) is equal to the cosine of the angle between the direction of the source and the ζ direction. The 3-D source vector is expressed as [s_x(r,t), s_y(r,t), s_z(r,t)]^T = s(r, t)[η_x(r), η_y(r), η_z(r)]^T.

We define $l_m^{\zeta }\left(\mathit{r}\right)$ as the output of the mth sensor. The output is induced by the unit-magnitude source located at r and pointing in the ζ direction. The column vector l_ζ(r) is defined as ${\mathit{l}}_{\zeta }\left(\mathit{r}\right)={\left[l_1^{\zeta }\right(\mathit{r}),l_2^{\zeta }(\mathit{r}),\dots ,l_M^{\zeta }(\mathit{r}\left)\right]}^T$. The array response matrix, which represents the sensitivity of the whole sensor array at r, is defined as L(r) = [l_x(r),l_y(r),l_z(r)]. The array response vector in the direction η is defined as l(r,η), where l(r,η) = L(r)η(r). The array response matrix L(r) and the array response vector l(r,η) are often, respectively, called the lead field matrix and the lead field vector in the field of the biomagnetic imaging.

B. Scalar-Type Minimum-Variance Beamformer

We focus on the technique referred to as the minimum-variance beamformer [5] for reconstructing neuromagnetic sources. Since the neuromagnetic source is a 3-D vector quantity, the original minimum-variance beamformer formulation should be extended to incorporate the 3-D vector nature of sources. Two types of extensions have been proposed. The scalar extension derives the weight w(r) by minimizing w^T(r)Rw(r) under the constraint of l^T(r,η)w(r) = 1. The explicit form of the weight is expressed as

$$\mathit{w}\left(\mathit{r}\right)=\frac{{\mathit{R}}^{-1}\mathit{l}(\mathit{r},\eta )}{{\mathit{l}}^T\left(r,\eta \right){\mathit{R}}^{-1}\mathit{l}\left(r,\eta \right)}.$$ (1)

Note that the weight in (1) depends not only on the spatial location r but also on the direction η, and therefore the information regarding the source orientation is needed to calculate w(r).

Using the weight in (1), the output source power (the power of the reconstructed source) is obtained from

$$\langle \widehat{s}{(\mathit{r},t)}^2\rangle =\frac{1}{{\mathit{l}}^T\left(r,\eta \right){\mathit{R}}^{-1}\mathit{l}\left(r,\eta \right)}.$$ (2)

We also define the value Z_S such that

$$Z_S\left(\mathit{r}\right)=\frac{\langle \widehat{s}{(\mathit{r},t)}^2\rangle }{{\sigma }_0^2{\mid \mid \mathit{w}\left(\mathit{r}\right)\mid \mid }^2}=\frac{{\mathit{l}}^T\left(r,\eta \right){\mathit{R}}^{-1}\mathit{l}\left(r,\eta \right)}{{\sigma }_0^2\left[{\mathit{l}}^T\right(r,\eta \left){\mathit{R}}^{-2}\mathit{l}\right(r,\eta \left)\right]}$$ (3)

where ${\sigma }_0^2$ is the variance of the input noise. Because the square of the weight norm ||w(r)||² is the white noise power gain, as is shown in Appendix I, Z_S(r) is equal to the reconstructed source power divided by the reconstructed noise power, and this value is customarily called the output SNR¹. It should be noted that the expression similar to (3) has been reported in the fields of power spectrum estimation [10] and of antenna-array processing [11].

C. Vector-Type Minimum-Variance Beamformer

The other type of extension, called the vector-type beamformer, allows simultaneous estimation of the source orientation as well as the source magnitude. It uses a set of three weight vectors, w_x(r), w_y(r), and w_z(r), which estimate the x,y, and z components of a source current vector. (Note that any of three orthogonal directions can be used, instead of the x,y, and z directions.) A set of weights for a vector-extended minimum-variance beamformer is derived using the optimization [7], [8]

$$\min \mathrm{tr}\left\{{\mathit{W}}^T\right(\mathit{r}\left)\mathit{RW}\right(\mathit{r}\left)\right\}\text{subject to}{\mathit{L}}^T\left(\mathit{r}\right)\mathit{W}\left(\mathit{r}\right)=\mathit{I}$$ (4)

where W(r) is a weight matrix defined as W(r) = [w_x(r), w_y(r), w_z(r)]; I is the identity matrix; and tr{·} indicates the trace operation. The resultant weight matrix is given by [8]

$$\mathit{W}\left(\mathit{r}\right)={\mathit{R}}^{-1}\mathit{L}\left(\mathit{r}\right){\left[{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-1}\mathit{L}\right(\mathit{r}\left)\right]}^{-1}.$$ (5)

Using this weight matrix, the x, y, and z components of the source current vector are estimated from

$${\left[{\widehat{s}}_x\right(\mathit{r},t),{\widehat{s}}_y(\mathit{r},t),{\widehat{s}}_z(\mathit{r},t\left)\right]}^T={\mathit{W}}^T\left(\mathit{r}\right)\mathit{b}\left(t\right)$$ (6)

where ${\widehat{s}}_{\zeta }(\mathit{r},t)$ is the ζ component (ζ = x,y, or z) of the estimated source vector. The output source power is conventionally given by [8]

$$\begin{array}{cc}\hfill \langle \widehat{s}{(\mathit{r},t)}^2\rangle =& \langle {\mid \mid \left[{\widehat{s}}_x\right(\mathit{r},t),{\widehat{s}}_y(\mathit{r},t),{\widehat{s}}_z(\mathit{r},t\left)\right]\mid \mid }^2\rangle \hfill \\ \hfill =& \mathrm{tr}\left\{{\mathit{W}}^T\right(\mathit{r}\left)\mathit{RW}\right(\mathit{r}\left)\right\}=\mathrm{tr}\left\{{\left[{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-1}\mathit{L}\right(\mathit{r}\left)\right]}^{-1}\right\}.\hfill \end{array}$$ (7)

When using the above equation, the white-noise power gain is given tr{W^T(r)W(r)} by, as is shown in Appendix I. Thus, the output SNR corresponding to the output power in (7), Z_v, is expressed in [9]

$$\begin{array}{cc}\hfill Z_V\left(\mathit{r}\right)=& \frac{\mathrm{tr}\left\{{\mathit{W}}^T\right(\mathit{r}\left)\mathit{RW}\right(\mathit{r}\left)\right\}}{{\sigma }_0^2\mathrm{tr}\left\{{\mathit{W}}^T\right(\mathit{r}\left)\mathit{W}\right(\mathit{r}\left)\right\}}\hfill \\ \hfill =& \frac{\mathrm{tr}\left\{{\left[{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-1}\mathit{L}\right(\mathit{r}\left)\right]}^{-1}\right\}}{{\sigma }_0^2({\mid \mid {\mathit{w}}_x\left(\mathit{r}\right)\mid \mid }^2+{\mid \mid {\mathit{w}}_y\left(\mathit{r}\right)\mid \mid }^2+{\mid \mid {\mathit{w}}_z\left(\mathit{r}\right)\mid \mid }^2)}.\hfill \end{array}$$ (8)

III. Equivalence of the Two Types of Beamformers Under the Optimum Pointing Orientation

This section shows that the scalar-type beamformer in (1) and the vector-type beamformer in (5) give exactly the same outputs if the beamformer orientation is optimized. As mentioned previously, the scalar-type beamformer requires the determination of the source orientation η at each spatial location r. One way to determine the optimum orientation at each r is to choose the orientation that gives the maximum power output, i.e., η is determined by using

$$\underset{\eta }{\max }\frac{1}{{\mathit{l}}^T\left(r,\eta \right){\mathit{R}}^{-1}\mathit{l}(\mathit{r},\eta )}={\left(\underset{\eta }{\min }\left[{\eta }^T{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-1}\mathit{L}\right(\mathit{r}\left)\eta \right]\right)}^{-1}.$$ (9)

We define the eigenvalues and eigenvectors of the 3×3 matrix L^T(r)R⁻¹L(r) as λ_j and u_j, where j = 1, 2, and 3. We assume that the eigenvalues are numbered in decreasing order. It is well known, based on the Rayleigh-Ritz formula, that η giving the minimum of [η^TL^T(r)R⁻¹L(r)η] is equal to u₃, which is the eigenvector corresponding to the minimum eigenvalue of L^T(r)R⁻¹L(r) [12], [13]. The maximum output source power is then expressed as

$$\langle \widehat{s}{(\mathit{r},t)}^2\rangle ={\left[{\mathit{u}}_3^T{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-1}\mathit{L}\right(\mathit{r}\left){\mathit{u}}_3\right]}^{-1}=\frac{1}{{\lambda }_3}.$$ (10)

We define this value of the output power as S_opt, namely, S_opt = 1/λ₃.

We next show that the vector beamformer also attains S_opt by maximizing the beamformer output. For the vector-type beamformer, the output source power in the η direction is expressed as $\langle {\mid \mid \left[{\widehat{s}}_x\right(\mathit{r},t),{\widehat{s}}_y(\mathit{r},t),{\widehat{s}}_z(\mathit{r},t\left)\right]\eta \mid \mid }^2\rangle$. Using (5), the maximization of the output power leads to

$$\underset{\eta }{\max }\langle {\mid \mid \left[{\widehat{s}}_x\right(\mathit{r},t),{\widehat{s}}_y(\mathit{r},t),{\widehat{s}}_z(\mathit{r},t\left)\right]\eta \mid \mid }^2\rangle =\underset{\eta }{\max }{\eta }^T{\left[{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-1}\mathit{L}\right(\mathit{r}\left)\right]}^{-1}\eta .$$ (11)

Because the relationship

$${\left[{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-1}\mathit{L}\right(\mathit{r}\left)\right]}^{-1}=\sum _{j=1}^3\frac{1}{{\lambda }_j}{\mathit{u}}_j{\mathit{u}}_j^T$$

holds, the optimum η obtained in maximizing the right-hand side of (11) is equal to the eigenvector corresponding to the maximum eigenvalue of the matrix [L^T(r)R⁻¹L(r)]⁻¹, which is equal to 1/λ₃. Accordingly, we obtain the optimum direction as the eigenvector corresponding to 1/λ₃, i.e., η = u₃. Thus, the output power is expressed as

$$\underset{\eta }{\max }\langle {\mid \mid \left[{\widehat{s}}_x\right(\mathit{r},t),{\widehat{s}}_y(\mathit{r},t),{\widehat{s}}_z(\mathit{r},t\left)\right]\eta \mid \mid }^2\rangle ={\mathit{u}}_3^T\left[\sum _{j=1}^3\frac{1}{{\lambda }_j}{\mathit{u}}_j{\mathit{u}}_j^T\right]{\mathit{u}}_3=\frac{1}{{\lambda }_3}=S_{\mathrm{opt}}.$$ (12)

This equation indicates that either type of beamformer formulation attains S_opt when the beamformer pointing direction is set to the direction that gives the maximum output.

We then show that the scalar and vector beamformer formulations also give exactly the same output SNRs (the Z values) when the beamformer pointing direction is optimized. In the scalar beamformer formulation, the output SNR maximized with respect to η is defined as $Z_S^{\mathrm{opt}}\left(\mathit{r}\right)$, which is obtained by

$$\begin{array}{cc}\hfill Z_S^{\mathrm{opt}}\left(\mathit{r}\right)=& \underset{\eta }{\max }\frac{{\mathit{l}}^T\left(r,\eta \right){\mathit{R}}^{-1}\mathit{l}\left(r,\eta \right)}{{\sigma }_0^2\left[{\mathit{l}}^T\right(r,\eta \left){\mathit{R}}^{-2}\mathit{l}\right(r,\eta \left)\right]}\hfill \\ \hfill =& \frac{1}{{\sigma }_0^2}{\left(\underset{\eta }{\min }\frac{{\eta }^T\left[{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-2}\mathit{L}\right(\mathit{r}\left)\right]\eta }{{\eta }^T\left[{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-1}\mathit{L}\right(\mathit{r}\left)\right]\eta }\right)}^{-1}.\hfill \end{array}$$ (13)

We define the generalized eigenvalues and eigenvectors of [L^T(r)R⁻²L(r)] in the metric [L^T(r)R⁻¹L(r)] as γ_j and ν_j, i.e., γ_j and ν_j satisfy

$$\left[{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-2}\mathit{L}\right(\mathit{r}\left)\right]{\nu }_j={\gamma }_j\left[{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-1}\mathit{L}\right(\mathit{r}\left)\right]{\nu }_j$$ (14)

where j = 1, 2, and 3. Then, it is shown in Appendix II (and in [14]) that the optimum η in (13) is given as ν₃, which is the eigenvector corresponding to the minimum eigenvalue of (14), and thus $Z_S^{\mathrm{opt}}\left(\mathit{r}\right)$ is expressed as

$$Z_S^{\mathrm{opt}}\left(\mathit{r}\right)=\frac{1}{\left({\sigma }_0^2{\gamma }_3\right)}.$$ (15)

Because the matrix [L^T(r)R⁻¹L(r)] is invertible, the generalized eigenproblem in (14) can be changed to the following conventional eigenproblem:

$${\left[{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-1}\mathit{L}\right(\mathit{r}\left)\right]}^{-1}\left[{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-2}\mathit{L}\right(\mathit{r}\left)\right]{\nu }_j={\gamma }_j{\nu }_j$$ (16)

and γ₃ can also be obtained as the minimum eigenvalue of (16).

In the vector beamformer formulation, the output SNR maximized with respect to η is defined as $Z_V^{\mathrm{opt}}\left(\mathit{r}\right)$, which is obtained by using

$$\begin{array}{cc}\hfill Z_V^{\mathrm{opt}}\left(\mathit{r}\right)=& \underset{\eta }{\max }\frac{\langle {\mid \mid \left[{\widehat{s}}_x\right(\mathit{r},t),{\widehat{s}}_y(\mathit{r},t),{\widehat{s}}_z(\mathit{r},t\left)\right]\eta \mid \mid }^2\rangle }{{\sigma }_0^2{\mid \mid \mathit{W}\left(\mathit{r}\right)\eta \mid \mid }^2}\hfill \\ \hfill =& \frac{1}{{\sigma }_0^2}{\left(\underset{\eta }{\min }\frac{{\eta }^T\Omega \eta }{{\eta }^T{\left[{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-1}\mathit{L}\right(\mathit{r}\left)\right]}^{-1}\eta }\right)}^{-1}\hfill \end{array}$$ (17)

where

$$\Omega ={\left[{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-1}\mathit{L}\right(\mathit{r}\left)\right]}^{-1}\left[{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-2}\mathit{L}\right(\mathit{r}\left)\right]\times {\left[{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-1}\mathit{L}\right(\mathit{r}\left)\right]}^{-1}.$$

We define the generalized eigenvalues and eigenvectors of Ω in the metric [L^T(r)R⁻¹L(r)]⁻¹ as ${\gamma }_j^{\prime }$ and ${\nu }_j^{\prime }$, i.e., ${\gamma }_j^{\prime }$ and ${\nu }_j^{\prime }$ satisfy

$$\Omega {\nu }_j^{\prime }={\gamma }_j^{\prime }{\left[{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-1}\mathit{L}\right(\mathit{r}\left)\right]}^{-1}{\nu }_j^{\prime }.$$ (18)

The optimum η in (17) is equal to ${\nu }_3^{\prime }$, and $Z_V^{\mathrm{opt}}\left(\mathit{r}\right)$ is expressed as $Z_V^{\mathrm{opt}}\left(\mathit{r}\right)=1∕\left({\sigma }_0^2{\gamma }_3^{\prime }\right)$. It is easy to see that the generalized eigenproblem in (18) can be changed to the conventional eigenproblem

$$\left[{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-2}\mathit{L}\right(\mathit{r}\left)\right]{\left[{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-1}\mathit{L}\right(\mathit{r}\left)\right]}^{-1}{\nu }_j^{\prime }={\gamma }_j^{\prime }{\nu }_j^{\prime }$$ (19)

and ${\gamma }_3^{\prime }$ is obtained as the minimum eigenvalue in (19).

Comparing the matrix in (19) with that in (16), one can see that both of these matrices consist of the product of the same two matrices [L^T(r)R⁻¹L(r)]⁻¹, and [L^T(r)R⁻²L(r)], and only the order of multiplication differs. Therefore, the eigenvalue ${\gamma }_j^{\prime }$ in (19) is equal to γ_j in (16) [12], and $Z_V^{\mathrm{opt}}\left(\mathit{r}\right)$ is rewritten as

$$Z_V^{\mathrm{opt}}\left(\mathit{r}\right)=\frac{1}{\left({\sigma }_0^2{\gamma }_3\right)}.$$ (20)

Because $Z_V^{\mathrm{opt}}\left(\mathit{r}\right)$ is exactly the same as $Z_S^{\mathrm{opt}}\left(\mathit{r}\right)$, it can be concluded that the scalar and the vector formulations can attain the same output SNR when the direction that gives the maximum SNR is chosen. We denote this output SNR obtained with the optimum beamformer direction as Z_opt, namely, $Z_{\mathrm{opt}}=1∕\left({\sigma }_0^2{\gamma }_3\right)$.

IV. Asymptotic Output SNR of Beamformers With Optimum Orientation

In Section III, we show that when the beamformer pointing direction is optimized, both the vector and the scalar beamformer formulations attain the output SNR Z_opt. In this section, we derive the explicit form of Z_opt. Here, we omit the notations of t and r for simplicity unless any confusion arises. We define for later use the generalized cosine between two column vectors a₁ and a₂ in the metric C as ${\cos }^2({\mathit{a}}_1,{\mathit{a}}_2\mid \mathit{C})={\left({\mathit{a}}_1^T{\mathit{Ca}}_2\right)}^2∕\left[\right({\mathit{a}}_1^T{\mathit{Ca}}_1\left)\right({\mathit{a}}_2^T{\mathit{Ca}}_2\left)\right]$. When C is equal to the identity matrix, this cosine is simply denoted cos²(a₁,a₂).

We first assume the simplest case where a single source whose orientation is equal to η₁ exists at r₁, and define the lead field vector for this single source as f, such that f = L(r₁)η₁. The power of the source is defined as ${\sigma }_1^2$. The power of the input noise is again denoted ${\sigma }_0^2$. The covariance matrix and its inverse are then expressed as

$$\mathit{R}={\sigma }_0^2\mathit{I}+{\sigma }_1^2{ff}^T$$ (21)

(where σ₀ is again the power of the input noise) and

$${\mathit{R}}^{-1}=\frac{1}{{\sigma }_0^2}\left(\mathit{I}-\frac{\alpha }{1+\alpha }\frac{{ff}^T}{{\mid \mid \mathit{f}\mid \mid }^2}\right)=\frac{1}{{\sigma }_0^2}\left(\mathit{I}-\xi \frac{{ff}^T}{{\mid \mid \mathit{f}\mid \mid }^2}\right)$$ (22)

where $\alpha =({\sigma }_1^2∕{\sigma }_0^2){\mid \mid \mathit{f}\mid \mid }^2$ and ξ = α(1+α). This α is sometimes referred to as the input power SNR [15]. This α is usually much greater than 1 for large sensor arrays such as those used in recent neuromagnetic measurements, and ξ is approximately equal to 1. (Numerical examples of these values are given in Section VI.)

In the scalar beamformer formulation, when the beamformer pointing direction is set to η, the output SNR Z_S is expressed, using (3), as

$$\begin{array}{cc}\hfill Z_S\left({\mathit{r}}_1\right)=& \frac{1}{{\sigma }_0^2}\frac{{\eta }^T\left[{\mathit{L}}^T\right({\mathit{r}}_1\left){\mathit{R}}^{-1}\mathit{L}\right({\mathit{r}}_1\left)\right]\eta }{{\eta }^T\left[{\mathit{L}}^T\right({\mathit{r}}_1\left){\mathit{R}}^{-2}\mathit{L}\right({\mathit{r}}_1\left)\right]\eta }\hfill \\ \hfill =& \frac{[1-\xi \cos (\eta ,{\eta }_1\mid {\mathit{L}}^T\mathit{L}\left)\right]}{[1-(2\xi -{\xi }^2\left){\cos }^2\right(\eta ,{\eta }_1\mid {\mathit{L}}^T\mathit{L}\left)\right]}.\hfill \end{array}$$ (23)

It can be seen that Z_S(r₁) reaches its maximum when η = η₁. Setting η equal to η₁ in (23), Z_opt(r₁) is expressed as

$$Z_{\mathrm{opt}}\left({\mathit{r}}_1\right)=\frac{1-\xi }{1-(2\xi -{\xi }^2)}=1+\alpha =1+\left(\frac{{\sigma }_1^2}{{\sigma }_0^2}\right){\mid \mid \mathit{f}\mid \mid }^2.$$ (24)

Thus, the input SNR and the output SNR are equal and there is no SNR degradation in the beamformer reconstruction.

We next analyze a case where two sources exist. The locations of the sources are denoted r₁ and r₂, and their orientations are denoted η₁ and η₂. We define the lead field vectors for the two sources as f and g, such that f = L(r₁)η₁ and g = L(r₂)η₂. Here, we define the spatial correlation [16] between the two sources as cos²(f,g), which is nearly equal to 1 when the two sources create similar lead field vectors, but is nearly equal to zero when their lead field vectors are very different. We define the power of the first source as ${\sigma }_1^2$, and that of the second source as ${\sigma }_2^2$. The covariance matrix is then expressed as

$$\mathit{R}={\sigma }_0^2\mathit{I}+{\sigma }_1^2{ff}^T+{\sigma }_2^2{gg}^T.$$ (25)

We define β as $\beta =({\sigma }_2^2∕{\sigma }_0^2){\mid \mid \mathit{g}\mid \mid }^2$ and ν as ν = β/(1+β). Generally, the relationship β >> 1 holds for a large sensor array and the value of ν is very close to 1. (Numerical examples of these values are presented in Section VI.) As shown in Appendix III, it is straightforward to derive Z_opt(r₁), as follows:

$$Z_{\mathrm{opt}}\left({\mathit{r}}_1\right)=1+\left(\frac{{\sigma }_1^2}{{\sigma }_0^2}\right){\mid \mid \mathit{f}\mid \mid }^2[1-\nu {\cos }^2(\mathit{f},\mathit{g}\left)\right].$$ (26)

Equation (26) shows that the output SNR is directly affected by the spatial correlation, and only when the relationship cos²(f,g) = 0 holds, the input SNR is preserved in the beamformer reconstruction process.

V. Asymptotic Output SNR of Vector Beamformer without Orientation Optimization

In Section IV, we derived the explicit form of Z_opt, which is the output SNR attained either by the scalar or the vector beamformer formulations when the beamformer pointing direction is optimized. On the other hand, as mentioned in Section II-C, the vector beamformer conventionally does not optimize the beamformer pointing direction, and (8) is used for calculating the output SNR. In this section, we derive the explicit form of the output SNR when (8) is used.

We first assume a case where a single source exists, and use the expression in (22) for the inverse of the covariance matrix. We use the three orthogonal directions u₁, u₂, and u₃ (where u_j (j = 1, 2, 3) is the three eigenvectors of L^T(r)R⁻¹L(r)) to calculate the weight matrix W, and define l_j such that l_j = Lu_j(j = 1, 2, 3). Then, the output power obtained using (7) is denoted S_conv(r), which can be expressed as

$$\begin{array}{cc}\hfill S_{\mathrm{conv}}\left({\mathit{r}}_1\right)=& \mathrm{tr}\left\{{\left[{\mathit{L}}^T\right({\mathit{r}}_1\left){\mathit{R}}^{-1}\mathit{L}\right({\mathit{r}}_1\left)\right]}^{-1}\right\}\hfill \\ \hfill =& \sum _{j=1}^3\frac{1}{{\lambda }_j}\hfill \\ \hfill =& \sum _{j=1}^3\frac{{\sigma }_0^2}{{\mid \mid {\mathit{l}}_j\mid \mid }^2[1-\xi {\cos }^2({\mathit{u}}_j,{\eta }_1\mid {\mathit{L}}^T\mathit{L}\left)\right]}.\hfill \end{array}$$ (27)

Let us define the output SNR obtained using (8) as Z_conv(r). The denominator in (8) can be expressed as

$$\begin{array}{cc}\hfill \mathrm{tr}\left\{{\mathit{W}}^T\mathit{W}\right\}=& \sum _{j=1}^3{\mathit{u}}_j^T{\Omega u}_j\hfill \\ \hfill =& \sum _{j=1}^3\frac{{\sigma }_0^2[1-(2\xi -{\xi }^2\left){\cos }^2\right({\mathit{u}}_j,{\eta }_1\mid {\mathit{L}}^T\mathit{L}\left)\right]}{{\mid \mid {\mathit{l}}_j\mid \mid }^2{[1-\xi {\cos }^2({\mathit{u}}_j,{\eta }_1\mid {\mathit{L}}^T\mathit{L}\left)\right]}^2}\hfill \end{array}$$ (28)

where we use the relationship

$$\begin{array}{cc}\hfill {\mathit{u}}_j^T\Omega {\mathit{u}}_j=& {\mathit{u}}_j^T{\left[{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-1}\mathit{L}\right(\mathit{r}\left)\right]}^{-1}\left[{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-2}\mathit{L}\right(\mathit{r}\left)\right]\times {\left[{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-1}\mathit{L}\right(\mathit{r}\left)\right]}^{-1}{\mathit{u}}_j\hfill \\ \hfill =& {\mathit{u}}_j^T\left[\sum _{i=1}^3\frac{1}{{\lambda }_i}{\mathit{u}}_i{\mathit{u}}_i^T\right]\left[{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-2}\mathit{L}\right(\mathit{r}\left)\right]\times \left[\sum _{i=1}^3\frac{1}{{\lambda }_i}{\mathit{u}}_i{\mathit{u}}_i^T\right]{\mathit{u}}_j\hfill \\ \hfill =& \frac{{\mathit{u}}_j^T\left[{\mathit{L}}^T\right(\mathit{r}\left){\mathit{R}}^{-2}\mathit{L}\right(\mathit{r}\left)\right]{\mathit{u}}_j}{{\lambda }_j^2}\hfill \\ \hfill =& \frac{{\mathit{l}}_j^T{\mathit{R}}^{-2}{\mathit{l}}_j}{{\lambda }_j^2}=\frac{\left[{\mathit{l}}_j^T{\mathit{R}}^{-2}\right]{\mathit{l}}_j}{{\left[{\mathit{l}}_j^T{\mathit{R}}^{-1}{\mathit{l}}_j\right]}^2}.\hfill \end{array}$$ (29)

Assuming cos²(u_j,η₁|L^TL) << 1 where j = 1, 2, and substituting (27) and (28) into (8), we finally obtain

$$Z_{\mathrm{conv}}\left({\mathit{r}}_1\right)=\frac{\frac{1}{{\mid \mid {\mathit{l}}_1\mid \mid }^2}+\frac{1}{{\mid \mid {\mathit{l}}_2\mid \mid }^2}+\frac{1}{{\mid \mid {\mathit{l}}_3\mid \mid }^2[1-\xi {\cos }^2({\mathit{u}}_3,{\eta }_1\mid {\mathit{L}}^T\mathit{L}\left)\right]}}{\frac{1}{{\mid \mid {\mathit{l}}_1\mid \mid }^2}+\frac{1}{{\mid \mid {\mathit{l}}_2\mid \mid }^2}+\frac{1-(2\xi -{\xi }^2){\cos }^2({\mathit{u}}_3,{\eta }_1\mid {\mathit{L}}^T\mathit{L})}{{\mid \mid {\mathit{l}}_3\mid \mid }^2{[1-\xi {\cos }^2({\mathit{u}}_3,{\eta }_1\mid {\mathit{L}}^T\mathit{L}\left)\right]}^2}}.$$ (30)

Assuming that ${\mid \mid {\mathit{l}}_1\mid \mid }^2\approx {\mid \mid {\mathit{l}}_2\mid \mid }^2\approx {\mid \mid {\mathit{l}}_3\mid \mid }^2$, and using the relationship, u₃ = η₁, Z_conv(r₁) is finally expressed as

$$\begin{array}{cc}\hfill Z_{\mathrm{conv}}\left({\mathit{r}}_1\right)=& \frac{2+\frac{1}{(1-\xi )}}{2+\frac{1-(2\xi -{\xi }^2)}{(1-\xi )}}\hfill \\ \hfill =& 1+\frac{1}{3}\alpha =1+\frac{1}{3}\left(\frac{{\sigma }_1^2}{{\sigma }_0^2}\right){\mid \mid \mathit{f}\mid \mid }^2.\hfill \end{array}$$ (31)

This equation indicates that Z_conv(r₁) is one third of the input SNR. This is in contrast to Z_opt(r₁), where the input SNR is preserved.

When the spherically symmetric homogeneous conductor model [17] is used for the forward calculation, the source current vector is expressed in the two tangential components. As a result, the lead field matrix L(r) is an M × 2 matrix, and L^T(r)R⁻¹L(r) is a 2 × 2 matrix. In such cases, it is easy to show that (31) changes to

$$Z_{\mathrm{conv}}\left({\mathit{r}}_1\right)=1+\frac{1}{2}\left(\frac{{\sigma }_1^2}{{\sigma }_0^2}\right){\mid \mid \mathit{f}\mid \mid }^2.$$ (32)

The above equation indicates that Z_conv(r₁) is half of the input SNR. This result is in accordance with that obtained by Vrba and Robinson [9], who assumed a special source-sensor configuration where a single source exists directly below the center of a rotationally-symmetric sensor array.

By further assuming the use of the spherically symmetric homogeneous conductor model, we can next derive an expression for Z_conv(r₁) when two sources exist. We use the same notations defined in Section IV. After some lengthy calculations, (a part of which is shown in Appendix III), we finally obtain

$$Z_{\mathrm{conv}}\left(r_1\right)=\frac{1+{\epsilon }_1}{1+{\epsilon }_2}\cdot \left(1+\frac{{\sigma }_1^2}{{\sigma }_0^2}{\mid \mid \mathit{f}\mid \mid }^2[1-\nu {\cos }^2(f,g\left)\right]\right)$$ (33)

where

$${\epsilon }_1=\frac{[1-\nu {\cos }^2(f,g\left)\right]}{[1-\nu {\cos }^2({\mathit{l}}_1,\mathit{g}\left)\right]+\alpha H({\mathit{l}}_1,\mathit{f},\mathit{g})}$$ (34)

and where we have (35), as shown at the bottom of the page. The definition of H(l₁, f, g) is given in (47). In deriving (33)-(35), we use several appropriate approximations such as l₂ ≈ f or ||l₁|| ≈ ||l₂||. However, it is not straightforward to evaluate ε₁ and ε₂ using (34) and (35). In Section VI, we numerically determine these values and show that ε₁ is much smaller than 1 but is considerably larger than 1 in typical neuromagnetic measurement conditions.

VI. Numerical Examples

Numerical examples are presented here to illustrate several results of the analysis in Sections II–V. A sensor alignment of the 148-sensor array from Magnes 2500™ (4D Neuroimaging Inc., San Diego) whole-head neuromagnetometer was used. The coordinate origin was set at the center of the sensor coil located at the center of the coil array. The x direction was defined as that from the posterior to the anterior; the y direction was defined as that from the right to the left hemispheres; and z direction was defined as that perpendicular to the surface of the coil at the origin.

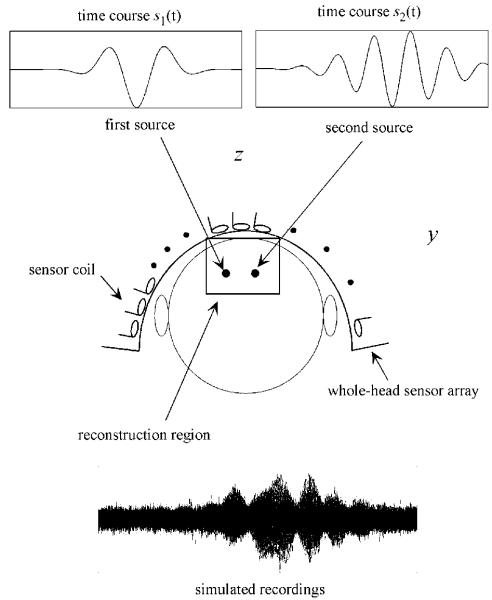
Two point sources were assumed to exist at (0, −0.8, −6) and (0, 0.8, −6) cm, i.e., they were 1.6 cm apart and located 6 cm below the center of the sensor array on the plane x = 0. The source-sensor configuration and the coordinate system are illustrated in Fig. 1. The simulated time courses assigned to the first and the second sources, s₁(t) and s₂(t), are also shown in Fig. 1. The cross correlation coefficient between these two time courses is approximately equal to 0.086, and they are nearly orthogonal to each other. The amplitudes of s₁(t) and s₂(t) are adjusted to have the relationship ${\sigma }_1^2={\sigma }_2^2$, i.e., the two sources have equal powers.

Fig. 1.

Coordinate system and source-sensor configuration used in the numerical experiments. The coordinate origin was set at the center of the sensor coil located at the center of the array. The plane at x = 0 cm is shown. The two point sources, shown by the small filled circles, were located on the line (x = 0; z = −6) cm. The time courses assigned to the two sources are shown in the two upper panels.

The lead field vectors of the sensor array for these sources, f and g, were calculated by using the spherically homogeneous conductor model with its center set at (0,0, −11). The simulated magnetic recording b(t) is calculated using b(t) = s₁(t) f + s₂(t)g. Simulated sensor noise uncorrelated among sensor channels was added so that the ratio between the average power of the signal magnetic field 〈||b||²〉/M to the noise power ${\sigma }_0^2$ is equal to 1. Here, M is the total number of

$${\epsilon }_2=\frac{[1-\nu {\cos }^2(f,g\left)\right][1-\nu {\cos }^2({\mathit{l}}_1,\mathit{g}\left)\right]+{\alpha }^2{[1-\nu {\cos }^2(f,g\left)\right]}^2\mathit{H}({\mathit{l}}_1,f,g)}{{\left[\right[1-\nu {\cos }^2({\mathit{l}}_1,\mathit{g})]+\alpha \mathit{H}({\mathit{l}}_1,f,g\left)\right]}^2}$$ (35)

sensors and it is equal to 148 in our numerical experiments. Typical simulated recording with this SNR is shown in the lower panel in Fig. 1.

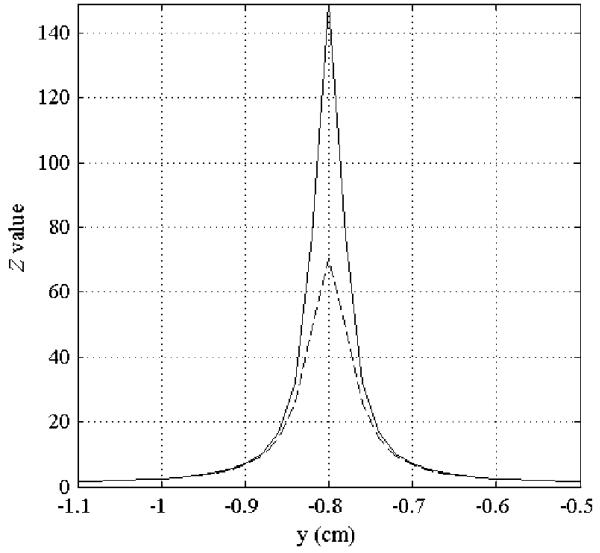
First, we simulated a case where a single source exists. We assigned the time course s₁(t) to the first source, but we set the second-source time course to zero, i.e., s₂(t). In this case, the input SNR for the first source, α, is equal to M (148) and ξ results in 0.998. The cross sections of the reconstructed first source along the line (x =0; z = −6 ) are shown in Fig. 2. Here, the reconstruction with Z_opt is shown by the solid line, and that with Z_conv is shown by the broken line. The peak value of Z_opt is equal to 147.5, and that of Z_conv is equal to 70.5. These results show that the peak from Z_opt is nearly twice as high as the peak from Z_conv, and this is in accordance with the results in Section V.

Fig. 2.

Cross-sectional view of the reconstructed first source along the line (x = 0; z = −6)cm for the single-source experiments. The solid line shows Z_opt and the broken line shows Z_conv. The SNR of the simulated data $\langle {\mid \mid \mathit{b}\mid \mid }^2\rangle ∕\left(M{\sigma }_0^2\right)$ was set to 1, resulting in α equal to 148.

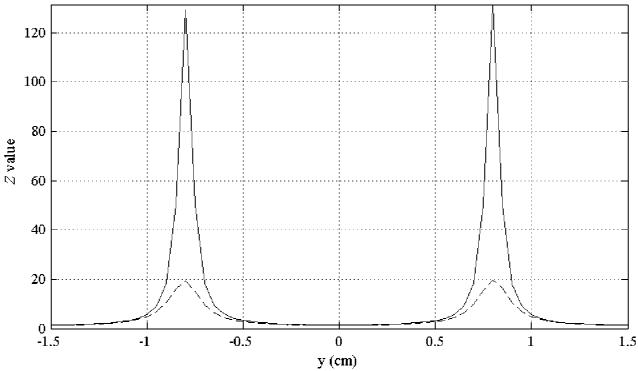
We then simulated a case where the two sources are both active by assigning the time courses s₁ and s₂(t), shown in Fig. 1, to the first and the second sources. The orientation of the two sources were set equal to (0.91, 0.42) and (0.91, −0.42). The spatial correlation represented by is nearly equal to zero in this case (cos²(f, g) = 0.02). Simulated sensor noise was added so that the ratio $\langle {\mid \mid \mathit{b}\mid \mid }^2\rangle ∕\left(M{\sigma }_0^2\right)$ is equal to one. The input SNRs for the first and second sources, α and β, are both equal to 131, and the values of ξ and ν are both equal to 0.992. The cross sections of the reconstructed results along the line (x = 0; z = −6) cm are shown in Fig. 3. The reconstruction with Z_opt is shown by the solid line, and that with Z_conv is shown by the broken line.

Fig. 3.

Cross-sectional view of the reconstruction results along the line (x = 0; z = −6) cm for the experiments where the two sources are both active. The solid line shows Z_opt and the broken line shows Z_conv. The SNR of the simulated data $\langle {\mid \mid \mathit{b}\mid \mid }^2\rangle ∕\left(M{\sigma }_0^2\right)$ was set to 1, and this results in both α and β equal to 131. The source orientations of the two sources were set to (0.91, 0.42) and (0.91, −0.42), resulting in cos²(f,g) ≈ 0.

The peak intensities of Z_opt were found to be 131 for the first and the second sources, and those of Z_conv were found to be 19. Thus, the peak-intensity ratio of Z_conv to Z_opt is calculated to be Z_conv/Z_opt = 19/131.5 ≈ 0.14. On the other hand, since the values of ε₁ and ε₂ in this case are 0.047 and 6.04, respectively, the SNR reduction factor (1+ε₁)/(1+ε₂) in (33) is approximately equal to 1/7 ≈ 0.13. Therefore, the intensity reduction of Z_conv can be well explained by the factor (1+ε₁)/(1+ε₂), and these results clearly validate (33).

VII. Conclusion

In conclusion, this paper proves that the scalar and vector minimum-variance beamformer formulations give exactly the same output power and output SNR, if the beamformer pointing direction is optimized. We then compare the theoretical output SNR of a beamformer with optimum pointing direction to the output from the conventional vector beamformer formulation without an optimized pointing direction. The comparison shows significant SNR degradation with the conventional vector beamformer formulation.

The primary purpose of this paper was to show that both the scalar and vector types of beamformers potentially attain the same SNR performances, although the conventional way of formulating the vector beamformer can cause significant SNR degradation. However, it is not within the scope of this paper to discuss the superiority of one of the two formulations over the other. This is because the quality of the source reconstruction results are determined not only by the asymptotic SNR but also by various factors such as spatial resolution, source correlation or the influence from background physiological noise. Therefore, To determine the superiority, a thorough investigation would be required, not only of the theoretical SNR but also of other performance measures including the spatial resolution and the robustness to various causes of errors such as mentioned above. Such investigations are currently being conducted with results to be published in the near future.

Biographies

Kensuke Sekihara (M’88) received the M.S. and Ph.D. degrees from Tokyo Institute of Technology, Tokyo, Japan, in 1976 and 1987, respectively.

From 1976 to 2000, he was with the Central Research Laboratory, Hitachi, Ltd., Tokyo, Japan. He was a Visiting Research Scientist at Stanford University, Stanford, CA, from 1985 to 1986, and at Basic Development, Siemens Medical Engineering, Erlangen, Germany, from 1991 to 1992. From 1996 to 2000, he worked with the “Mind Articulation” research project sponsored by the Japan Science and Technology Corporation. He is currently a Professor at the Tokyo Metropolitan Institute of Technology. His research interests include the neuromagnetic source reconstruction and statistical signal processing, especially its application to functional neuroimaging.

Dr. Sekihara is a member of the IEEE Medicine and Biology Society and the IEEE Signal Processing Society.

Srikantan S. Nagarajan received the Bachelor’s degree in electrical engineering from the University of Madras, Madras, India, and the Master’s and Ph.D. degrees from the Department of Biomedical Engineering, Case Western Reserve University, Cleveland, OH, in 1993 and 1995, respectively.

From 1995-1998, he was a post-doctoral Fellow at the Keck Center for Integrative Neuroscience, University of California at San Francisco (UCSF). In 1999, he was a Research Scientist at Scientific Learning Corporation, Berkeley, CA and an Adjunct Assistant Professor in the Department of Otolaryngology, UCSF. From 2000 to 2002, he was an Assistant Professor in the Department of Bioengineering, University of Utah, Salt Lake City. Currently, he is the Director of the Biomagnetic Imaging Laboratory and an Assistant Professor in Residence in the Department of Radiology, UCSF. His research interests in neural engineering include multimodal and multiscale functional brain imaging using functional magnetic resonance imaging, magnetoencephalography, electroencephalography, systems and computational neuroscience, and neuro-rehabilitation.

David Poeppel received the B.S. and Ph.D. degrees in cognitive neuroscience from Massachusetts Institute of Technology, Cambridge, in 1990 and 1995, respectively.

He is currently an Associate Professor in the Departments of Linguistics and Biology, University of Maryland at College Park. His research uses the functional neuroimaging methods magnetoencephalography, electroencephalography, positron emission tomography, and functional magnetic resonance imaging to investigate the neural basis of speech and language processing.

Alac Marantz received the B.A. degree in psycholinguistics from Oberlin College, Oberlin, OH, in 1978 and the Ph.D. degree in linguistics from the Massachusetts Institute of Technology (MIT), Cambridge, MA, in 1981.

He joined the faculty of MIT in 1990, where he is currently the Kenan Sahin Distinguished Professor of Linguistics and Head of the Department of Linguistics and Philosophy. His research interests include the syntax and morphology of natural languages, linguistic universals, and the neurobiology of language. He is currently involved in revising morphological theory within linguistics and in exploring magnetoencephalography techniques to uncover how the brain process language.

Appendix I

This Appendix shows that the white-noise power gain is equal to ||w(r)||² for the scalar beamformer and it is equal to tr{W^T(r)W(r)} for the conventional vector beamformer. We assume that the additive noise n(t) is contained in the measurement, i.e., the measurement b(t) is expressed as $\mathit{b}\left(t\right)={\Sigma }_{j=1}^Q\mathit{l}({\mathit{r}}_j,{\eta }_j)s({\mathit{r}}_j,t)+\mathit{n}\left(t\right)$, where Q is the number of sources. We assume that n(t) is the white Gaussian noise uncorrelated among sensor channels. The variance of the noise is denoted ${\sigma }_0^2$. Then, the output noise for the scalar beamformer is expressed as w(r)n(t). The variance of the output noise is, thus, equal to

$$\langle {\mid \mid \mathit{w}\left(\mathit{r}\right)\mathit{n}\left(t\right)\mid \mid }^2\rangle ={\mathit{w}}^T\left(\mathit{r}\right)\langle \mathit{n}\left(t\right){\mathit{n}}^T\left(t\right)\rangle \mathit{w}\left(\mathit{r}\right)={\sigma }_0^2{\mid \mid \mathit{w}\left(\mathit{r}\right)\mid \mid }^2.$$ (36)

For the vector beamformer, using (6), the output noise is expressed as W^T(r)n(t). Therefore, the variance of the output noise is expressed as

$$\begin{array}{cc}\hfill \langle {\mid \mid {\mathit{W}}^T\left(\mathit{r}\right)\mathit{n}\left(t\right)\mid \mid }^2\rangle =& \mathrm{tr}\left\{{\mathit{W}}^T\right(\mathit{r})\langle \mathit{n}(t\left){\mathit{n}}^T\right(t)\rangle \mathit{W}(\mathit{r}\left)\right\}\hfill \\ \hfill =& {\sigma }_0^2\mathrm{tr}\left\{{\mathit{W}}^T\right(\mathit{r}\left)\mathit{W}\right(\mathit{r}\left)\right\}\hfill \end{array}$$ (37)

where tr{ · } indicates the trace operation.

Appendix II

We define A and B as M × M positive definite matrices, and x as an M × 1 column vector. This Appendix shows that

$$\underset{\mathit{x}}{\min }=\frac{{\mathit{x}}^T\mathit{Ax}}{{\mathit{x}}^T\mathit{Bx}}=\frac{{\mathit{x}}_{\min }^T{\mathit{Ax}}_{\min }}{{\mathit{x}}_{\min }^T{\mathit{Bx}}_{\min }}={\kappa }_{\min }$$ (38)

where κ_min and x_min are the minimum eigenvalue and its corresponding eigenvector of the following generalized eigen problem:

$$\mathit{Ax}=\kappa \mathit{Bx}.$$ (39)

Since the value of the ratio (x^TAx)/(x^TBx) is not affected by the norm of x, we set the norm of x so as to satisfy the relationship x^TBx = 1. Then, the minimization problem in (38) is rewritten as

$$\underset{\mathit{x}}{\min }{\mathit{x}}^T\mathit{Ax}\text{subject to}{\mathit{x}}^T\mathit{Bx}=1.$$ (40)

We change this constrained minimization problem to an unconstrained minimization problem by introducing the Lagrange multiplier κ, i.e., we define the function Φ(x,κ) such that

$$\Phi (\mathit{x},\kappa )={\mathit{x}}^T\mathit{Ax}-\kappa ({\mathit{x}}^T\mathit{Bx}-1).$$ (41)

The minimization in (40) is equivalent to minimizing Φ(x, κ). To obtain the minimum of Φ(x, κ), we calculate the derivatives

$$\begin{array}{cc}\hfill \frac{\partial \Phi (\mathit{x},\kappa )}{\partial \mathit{x}}=& \mathit{Ax}-\kappa \mathit{Bx},\hfill \\ \hfill \frac{\partial \Phi (\mathit{x},\kappa )}{\partial \kappa }=& {\mathit{x}}^T\mathit{Bx}-1.\hfill \end{array}$$ (42)

By setting these derivatives to zero, we can derive the relationships, Ax = κBx and κ = x^TAx. Therefore, the minimum value of x^TAx is equal to κ_min, which is the minimum eigenvalue of Ax = κBx, and x that attains this minimum value is equal to the eigenvector x_min.

Appendix III

This Appendix provides several supplementary formulae that are the basis of the analysis for the two-source case in Sections IV and V. We define the lead field vector for the first source as f and its power as ${\sigma }_1^2$. The lead field vector for the second source is defined as g and its power as ${\sigma }_2^2$. The power of the input noise is denoted ${\sigma }_0^2$. When two sources exist, the covariance matrix is expressed as (25). Its inverse is expressed as

$${\mathit{R}}^{-1}=\frac{1}{{\sigma }_0^2}\left({\mathit{D}}^{-1}-{\mathit{D}}^{-1}{ff}^T{\mathit{D}}^{-1}\frac{\left(\frac{{\sigma }_1^2}{{\sigma }_0^2}\right)}{1+\alpha }\right)$$ (43)

where $\mathit{D}=\mathit{I}+({\sigma }_2^2∕{\sigma }_0^2){\mathit{gg}}^T$; ${\mathit{D}}^{-1}=\mathit{I}-\nu \left({\mathit{gg}}^T\right)∕{\mid \mid \mathit{g}\mid \mid }^2$; $\alpha =({\sigma }_1^2∕{\sigma }_0^2){\mid \mid \mathit{f}\mid \mid }^2$; ν = β/(1+ β); and $\beta =({\sigma }_2^2∕{\sigma }_0^2){\mid \mid \mathit{g}\mid \mid }^2$. Using (43), we can obtain the following equations:

$${\mathit{l}}^T{\mathit{R}}^{-1}\mathit{l}=\frac{{\mid \mid \mathit{l}\mid \mid }^2}{\Gamma }\left(\right[1-\nu {\cos }^2(\mathit{l},\mathit{g})]+\alpha \mathit{H}(l,f,g\left)\right)$$ (44)

and

$${\mathit{l}}^T{\mathit{R}}^{-2}\mathit{l}=\frac{{\mid \mid \mathit{l}\mid \mid }^2}{{\Gamma }^2}\left(\right[1-\nu {\cos }^2\left(l,g\right)]+{\alpha }^2[1-\nu {\cos }^2(\mathit{f},\mathit{g})\left]\mathit{H}\right(l,f,g\left)\right)$$ (45)

where

$$\Gamma ={\sigma }_0^2+{\sigma }_1^2{\mid \mid \mathit{f}\mid \mid }^2[1-\nu {\cos }^2(f,g\left)\right]$$ (46)

and

$$\mathit{H}\left(l,f,g\right)=1-{\cos }^2\left(l,f\right)-\nu {\cos }^2\left(f,g\right)-\nu {\cos }^2\left(l,g\right)+2\nu \cos \left(l,f\right)\cos \left(l,g\right)\cos \left(f,g\right).$$ (47)

Note that l(= l(r,η) is an arbitrary lead field vector, andH(l,f,g) = 0 when l = f.

Using (44) and (45), the output SNR for the scalar beamformer is expressed as

$$Z_S\left(\mathit{r}\right)=\frac{{\mathit{l}}^T{\mathit{R}}^{-1}\mathit{l}}{{\sigma }_0^2\left[{\mathit{l}}^T{\mathit{R}}^{-2}\mathit{l}\right]}=\frac{\Gamma }{{\sigma }_0^2}\cdot \frac{[1-\nu {\cos }^2(l,g\left)\right]+\alpha H\left(l,f,g\right)}{[1-\nu {\cos }^2(l,g\left)\right]+{\alpha }^2[1-\nu {\cos }^2(f,g\left)\right]H\left(l,f,g\right)}.$$ (48)

The optimum output SNR is obtained using this equation by setting l equal to f, and it results in (26). To derive (33), we choose the two orthogonal directions as the directions u₁, and u₂, which are the eigenvectors of L^T(r)R⁻¹L(r) when the spherical homogeneous conductor is used. We then calculate the numerator and the denominator of (8). The numerator can be expressed as

$$\begin{array}{cc}\hfill \langle \widehat{s}{\left({\mathit{r}}_1\right)}^2\rangle =& \sum _{j=1}^2\frac{1}{{\mathit{l}}_j^T{\mathit{R}}^{-1}{\mathit{l}}_j}\hfill \\ \hfill =& \sum _{j=1}^2\frac{{\sigma }_0^2+{\sigma }_1^2{\mid \mid \mathit{f}\mid \mid }^2[1-\nu {\cos }^2(f,g\left)\right]}{{\mid \mid l_j\mid \mid }^2\left(\right[1-\nu {\cos }^2({\mathit{l}}_j,\mathit{g})]+\alpha \mathit{H}({\mathit{l}}_j,f,g\left)\right)}\hfill \end{array}$$ (49)

$$\mathrm{tr}\left\{{\mathit{W}}^T\mathit{W}\right\}=\sum _{j=1}^2\frac{{\mathit{l}}_j{\mathit{R}}^{-2}{\mathit{l}}_j}{{\left[{\mathit{l}}_j{\mathit{R}}^{-1}{\mathit{l}}_j\right]}^2}=\sum _{j=1}^2\frac{\left(\right[1-\nu {\cos }^2\left(l_j,g\right)]+{\alpha }^2[1-\nu {\cos }^2\left(f,g\right)\left]\mathit{H}\right({\mathit{l}}_j,f,g\left)\right)}{{\mid \mid {\mathit{l}}_j\mid \mid }^2{\left(\right[1-\nu {\cos }^2({\mathit{l}}_j,\mathit{g})]+\alpha H({\mathit{l}}_j,f,g\left)\right)}^2}$$ (50)

and the denominator can be expressed as in (50), shown at the top of the page. We assume that the beamformer can correctly detect the source orientation at r₁ and thus l₂ is equal to f. We also assume that the norm of the lead field vector is similar between the two tangential directions, i.e., ||l₁|| ≈ ||l₂||. Using these appropriate approximations, we can derive (33) from (49) and (50).