Abstract
Deep brain stimulation (DBS) is an established therapy for movement disorders, but the fundamental mechanisms by which DBS has its effects remain unknown. Computational models can provide insights into the mechanisms of DBS, but to be useful, the models must have sufficient detail to predict accurately the electric fields produced by DBS. We used a finite element method model of the Medtronic 3387 electrode array, coupled to cable models of myelinated axons, to quantify how interpolation errors, electrode geometry, and the electrode-tissue interface affect calculation of electrical potentials and stimulation thresholds for populations of model nerve fibers. Convergence of the potentials was not a sufficient criterion for ensuring the same degree of accuracy in subsequent determination of stimulation thresholds, because the accuracy of the stimulation thresholds depended on the order of the elements. Simplifying the 3387 electrode array by ignoring the inactive contacts and extending the terminated end of the shaft had position dependent effects on the potentials and excitation thresholds, and these simplifications may impact correlations between DBS parameters and clinical outcomes. When the current density in the bulk tissue is uniform, the effect of the electrode-tissue interface impedance could be approximated by filtering the potentials calculated with a static lumped electrical equivalent circuit. Further, for typical DBS parameters during voltage-regulated stimulation, it was valid to approximate the electrode as an ideal polarized electrode with a nonlinear capacitance. Validation of these computational considerations enables accurate modeling of the electric field produced by DBS.
Index Terms: Computational modeling, deep brain stimulation, electric field, finite element method, neural engineering
I. Introduction
Deep brain stimulation (DBS) is an established therapy for treating neurological disorders, where high frequency (typically 100–200 Hz) electrical pulses are delivered to specific regions of the brain. DBS is effective in treating Parkinson’s disease and essential tremor [1, 2], and may be a promising therapy for epilepsy and psychiatric disorders [3, 4]. However, the mechanisms by which DBS relieves symptoms are still unknown.
Determining the mechanisms of DBS requires a quantitative understanding of how altering DBS parameters affects the response of neural elements within the central nervous system (e.g., excitation [5], inhibition [5], blocking [6]). Studying the effects of DBS on neural activation using experiments alone is impractical because the parameter space of DBS is vast. For example, tens of thousands of combinations of pulsewidth, frequency, and amplitude are available in implanted pulse generators, such as the Medtronic Soletra Model 7426 (Medtronic Inc, Minneapolis, MN); and there are multiple electrode configurations and anatomical targets [7]. Further, there is a lack of understanding of what neural elements are being affected and whether these effects are local or distributed throughout the targeted neural network. Thus, computational models are important tools to study DBS.
To be useful, computational models must have sufficient detail to predict accurately the electric fields produced by DBS. The most detailed computational models of DBS are patient-specific finite element method (FEM) models: the geometry of brain structures is defined by individual brain images, and the conductivities of each brain region are determined using diffusion-tensor magnetic resonance imaging [8, 9]. Comparisons between patient-specific models and experimental data show that the electrode-tissue interface (ETI) impedance and heterogeneities and anisotropies in tissue conductivity affect the distribution of electric potentials, and these features are important when modeling DBS [8, 9].
In addition, there are a number of approximations typically used when modeling DBS, and in many instances these approximations have not been validated. For example, one common assumption is that convergence of the potentials is a sufficient criterion for ensuring accurate determination of neural activation thresholds [5, 10, 11]. However, determination of activation thresholds requires calculation of the second difference of the potentials, which is subject to interpolation errors that depend on the size and order of the FEM elements [12]. Another common assumption is that the platinum-iridium (PtIr) electrode can be approximated as an ideal polarized electrode with capacitance independent of the applied stimulus [9, 13–15]. However, charge transfer at the ETI is both capacitive and Faradaic [16], and the capacitance of the ETI varies with the applied stimulus [17].
The goal of this study was to determine the impact of several common simplifications on the electrical potentials and neural stimulation thresholds calculated with numerical models of DBS. We used a spatiotemporal model of a four-contact clinical DBS electrode to address the following questions: (1) How does the accuracy of calculation of the potentials and thresholds depend on FEM mesh parameters? (2) What effects do ignoring the inactive contacts and extending the terminated end of the shaft have on the potentials and thresholds? (3) What effects does simplifying the representation of the ETI with a lumped circuit representation have on the potentials and thresholds? And, (4) what effects does approximating the DBS contact with an ideal polarized electrode with a constant capacitance have on the potentials and thresholds? The results delineate the level of detail required in computational models of the electric fields produced by DBS to make accurate calculations of the neural response to DBS.
II. Methods
A. FEM Model
We constructed an FEM model of the Model 3387 electrode array (Medtronic Inc, Minneapolis, MN) in COMSOL Multiphysics v3.4 (COMSOL Inc., Burlington, MA) that consisted of four annular contacts on an insulating shaft surrounded by homogeneous tissue (Fig 1) representing a medium of infinite extent. Cylindrical annular contacts were 1.5 mm in height, 1.27 mm in diameter, 0.15 mm in thickness, spaced 1.5 mm apart, and had a conductivity of 9.5 × 106 S/m. Brain tissue can be approximated as primarily resistive for typical stimulation parameters used in DBS [18], so the permittivity of the tissue was ignored. Grey matter was modeled as a 60 mm × 60 mm × 60 mm cube with an isotropic conductivity of 0.2 S/m [19], and white matter perpendicular (parallel) to the electrode was modeled as a 120 mm × 40 mm × 40 mm (40 mm × 40 mm × 120 mm) with an anisotropic conductivity of 0.1 S/m and 0.9 S/m transverse and longitudinal to the long axis of the prism, respectively [20].
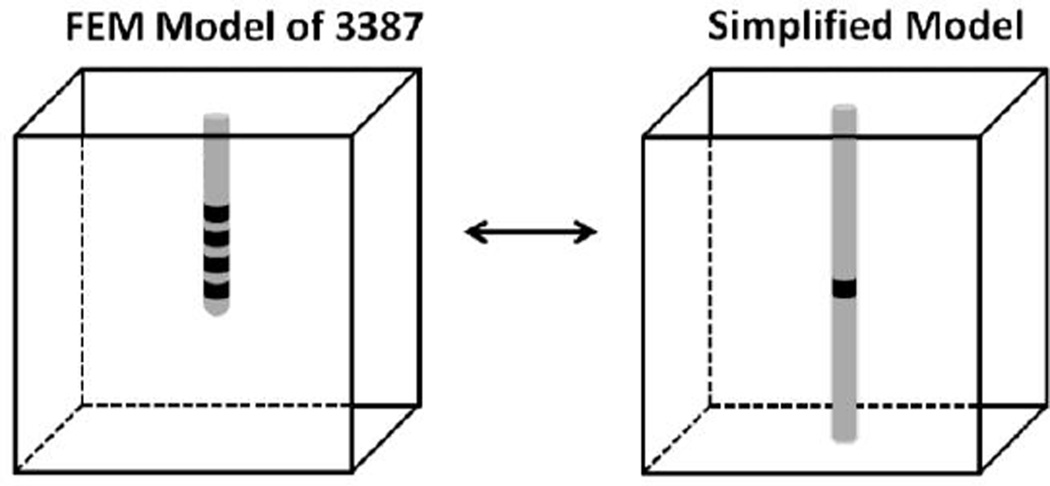
Fig. 1.
The Model 3387 array was simplified by removing the inactive electrodes and extending the terminated end of the shaft.
Monopolar voltage-regulated stimulation was modeled by applying potentials of 1 V and 0 V (Dirichlet boundary conditions) on the surface of the stimulation electrode and outer surface of the tissue volume, respectively. The electrode shaft was assumed to be perfectly insulating and was modeled as a boundary layer with zero normal current density (Neumann boundary condition), except where the Dirichlet conditions were applied. At internal boundaries, the normal current density exiting/entering the surface of the electrodes was set equal to normal current density entering/exiting the adjoining tissue region (continuity).
The FEM model was discretized into a graded mesh of Lagrange tetrahedral elements, where the mesh density was greatest near the electrode surface, using a Delaunay triangulation algorithm. The potential distribution was calculated by solving Laplace’s equation (Equation 1), where ∇ is the divergence operator, σ is the conductivity and is the current density; and the current was calculated by integrating the current density (Equation 2) on the surface of the electrode, where is the electric field.
| (1) |
| (2) |
A convergence analysis was conducted to assess the effect of mesh parameters, including the number and order of elements, on the accuracy of the potentials and stimulation thresholds. The FEM model was initially solved using a coarse mesh, for elements of a set order, and the mesh was refined (i.e., the elements were split into smaller elements) until no further refinement was possible under the memory constraints (8 GB) of our work station. Error (δ) was defined as the root mean square deviation (RMSD) in the measured quantity (x) ± 1 standard deviation (SD), expressed as a percent relative to x after the mesh was refined:
| (3) |
where k denotes the number of refinements. A δ of 5 % was chosen as the value which all errors should fall below. In addition, we verified that the model was large enough to behave as an infinite medium by doubling the model volume and verifying that the lumped resistance of the model, the potentials, and the stimulation thresholds had a δ of < 5 %.
All subsequent results (except for those in our convergence analyses) were obtained using the maximum number of cubic elements possible: ~ 1.3 million cubic elements using 8 GB of memory. Mesh refinement from ~ 727,000 to ~1.3 million cubic elements and doubling the volume with ~ 1.3 million cubic elements yielded δ in the potentials and stimulation thresholds of < 1 % in the isotropic case and < 2 % in the anisotropic case.
B. Population model of myelinated axons
The NEURON simulation environment [21] was used to implement cable models of myelinated axons oriented parallel and perpendicular to the electrode axis. Axons were 2.5 µm in diameter, 15 mm in length, and the myelin was assumed to be perfectly insulating. Nodes of Ranvier contained a parallel combination of a nonlinear sodium conductance (1.445 S/cm2), a linear leakage conductance (0.128 S/cm2), and a membrane capacitance (2.5 µF/cm2) [22], as these conductances and capacitance are sufficient for predicting activation thresholds [23]. Model parameters reflected a mammalian axon at 37° C [24].
Based on predicted volumes of tissue activated with the Model 3387 for typical DBS parameters, neural elements are expected to be between ~0.9–2.9 mm from the surface of the electrode [8]. To span this range, populations of 100 axons were uniformly distributed in an annulus around the electrode with inner and outer radii of 1 mm and 4 mm, respectively. Uniform distributions of coordinates were randomly picked using a Latin Hypercube Sampling design, and the coordinates were uniformly mapped to the annular volume in Cartesian coordinates using a coordinate transformation. Analyses were conducted on 3 independent populations of 100 model axons to ensure that the results were not dependent on the particular population. This left a 0.365 mm thick annular region immediately adjacent to the electrode that was intended to represent the space occupied by the glial scar. The scar thickness fell within the range of reported experimental values: 0–1 mm [25, 26], and since we focused on evaluating mesh parameters, electrode geometry, and the ETI, the scar had the same conductivity as the surrounding brain tissue.
For cases when the ETI was approximated as linear (see below), we used the interpolated potentials (between grid points) to stimulate the axon populations with a 100 µs monophasic rectangular pulse. Because of linearity, the potentials at a given stimulus amplitude were calculated by multiplying the 1V solution by a scalar. The stimulation voltage threshold for each fiber was calculated using a bisection algorithm (relative error < 1 %), and we constructed input-output curves of the activated population fraction as a function of the stimulation amplitude.
C. Simplifying the representation of the electrode
A number of published models have used a simplified model of the 3387 array (Fig 1) to study the effects of electrode geometry [27, 28] and the ETI [14] on DBS. The simplified geometry requires (1) ignoring the inactive electrodes (those that do not deliver charge) and replacing them with insulating boundary conditions, and (2) extending the terminating end of the insulating shaft so that it terminates on the bottom boundary of the tissue box. The simplified model of the 3387 is used in our analyses, so we quantified the effects of these simplifications.
D. Representation of the electrode-tissue interface
A simplified (Fig 1) axisymmetric FEM model of the 3387 array was constructed in MATLAB (v2008b, The Mathworks, Natick, MA) to study the filtering effects of a nonlinear ETI. The FEM model was discretized into a graded mesh of 40,000 bi-linear quadrilateral elements, which was enough to ensure that mesh refinement and doubling the volume of the model altered potentials and stimulation thresholds < 1 %.
We modeled the ETI using a thin-layer approximation [29, 30], given by the following Robin boundary condition:
| (4) |
| (5) |
where is the surface unit normal vector, rf is the distributed Faradaic resistance, cdl is the distributed double-layer capacitance, Φstim is the applied potential on the electrode surface, ΦD is the potential at the boundary between the compact and diffuse layers [31], and η is the overpotential, which is the potential difference between Φstim and the open-circuit (equilibrium) potential (Φoc). Although Φoc is non-zero for PtIr electrodes in brain tissue [17], it was ignored (Φoc = 0 V) to simplify the analysis of the FEM model.
We first conducted a sensitivity analysis to determine if the ETI could be ignored for typical DBS parameters, and subsequently, we determined whether the DBS electrode could be approximated as an ideal polarized electrode (rf = infinity). Typical DBS parameters include pulsewidths (PWs) between 60–210 µs and amplitudes between 1–5 V [7]. Within this parameter range, rf varies between 40–290 Ω-cm2 and cdl varies between 12–47 µF/cm2 [17]. Therefore, stimulation thresholds of parallel and perpendicular fibers were calculated for PWs between 50–200 µs at each of the four bounds of the ETI parameter space: (rf, cdl) = (40, 12), (40, 47), (290, 12), and (290, 47).
Next, the FEM model with a constant rf and cdl (i.e., a linear model) was used to test the assumption that the distributed boundary of the ETI can be approximated with equivalent lumped circuit values [14]. The time-varying potentials of the axisymmetric FEM model with the ETI (the spatiotemporal model) were compared to the potentials of the FEM model with no ETI (the static model) filtered by a three-element Randles equivalent circuit with a lumped access resistance, Ra, Faradaic resistance, Rf, and double layer capacitance, Cdl. Ra was calculated by taking the reciprocal of the current per applied volt in the static FEM model, Rf was calculated by dividing rf by the electrode area (1.905π mm2), and Cdl was calculated by multiplying cdl by the electrode area.
Finally, we constructed a nonlinear model of the ETI with rf and cdl that varied with ΦD. The initial values in the nonlinear case were the values of cdl and rf in the linear case. The nonlinear form of cdl was taken from the Gouy-Chapman-Stern model, which models the cdl as the series combination of an electrostatic capacitance, the Helmholtz capacitance (cH), and a diffusive capacitance (cD) [31].
| (6) |
| (7) |
cH = 45 µF/cm2, k1 = 31 µF/cm2, and k2 = 1.2 V−1 in (6) and (7) were calculated by fitting (6) to measured cdl values of the 3387 electrode array in brain tissue [17]. The nonlinear form of rf was derived by implicitly differentiating the Bulter-Volmer Equation (Bard and Faulkner, 2000), taking the reciprocal, and adding a constant term to account for the effect of diffusion:
| (8) |
Jo = 1 × 10−4 A/cm2 is the exchange current density, α = ½ and β = 37.44 V−1 are constants derived from first principles [31], and rmin = 40 Ω-cm2 is the minimum rf at η = infinity. Jo and rmin were calculated by fitting (8) to measured rf values of the 3387 electrode array in brain tissue [17].
Nonlinear systems of equations were linearized using the Newton-Raphson method, and linear systems were solved using the built-in MATLAB solver. Time integration was carried out using the implicit trapezoidal method [12]. The derivation of the governing equations and details of the implementation of the FEM are provided in the Appendix. At each mesh node, the RMSD in the waveforms of potential versus time between the linear and nonlinear cases was compared to determine if the nonlinear impedance of the ETI could be approximated as constant for typical DBS parameters.
III. RESULTS
We used FEM models of the Medtronic 3387 electrode, coupled with cable models of myelinated axons, to quantify how commonly used simplifications of numerical models of DBS affect the calculation of the potentials and stimulation thresholds.
A. Number and order of FEM mesh elements
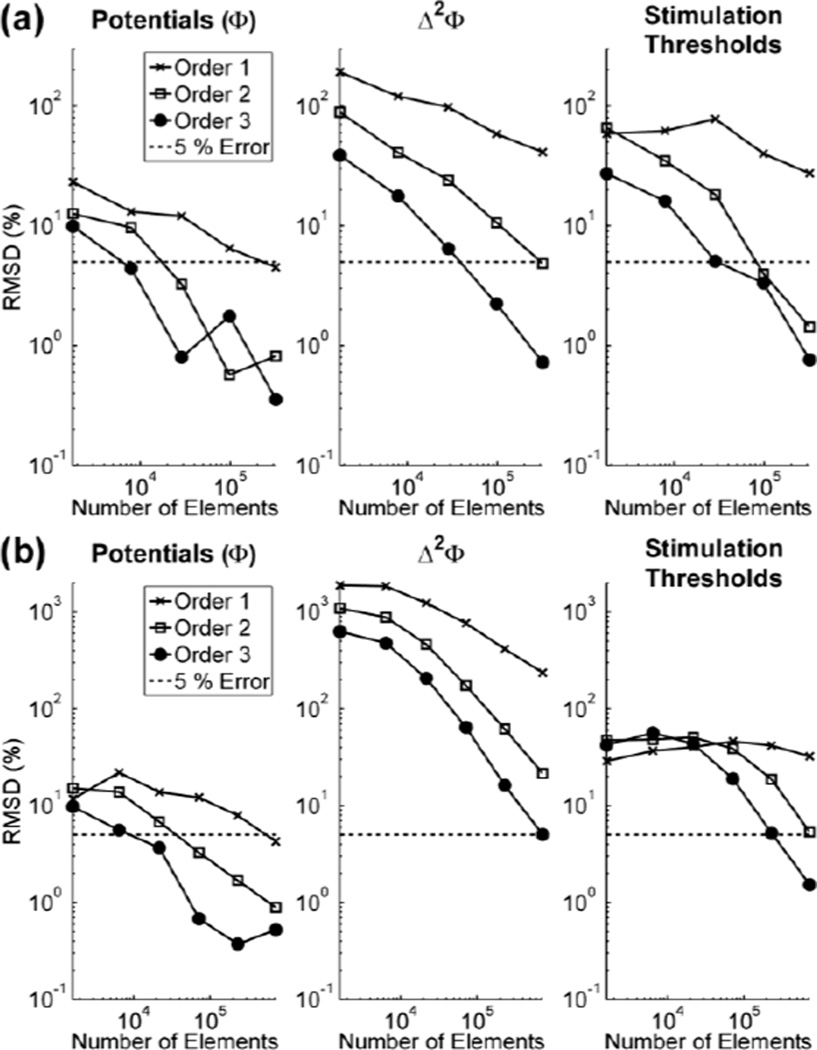
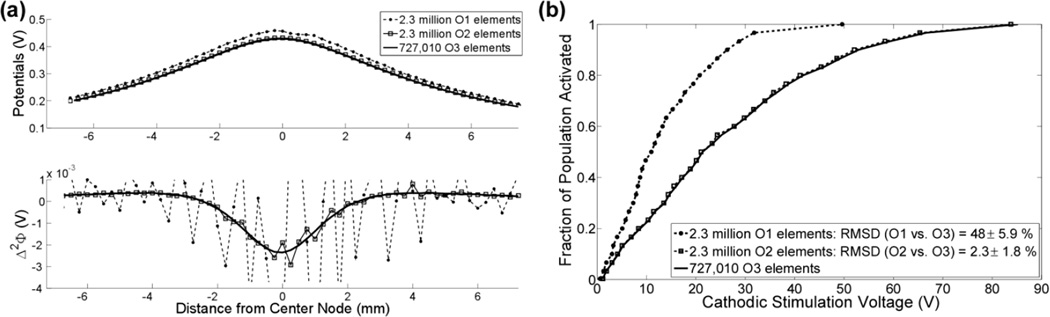
We quantified the error (3) in the potentials, the second difference of the potentials (Δ2Φ) between 3 consecutive nodes, which is proportional to the source driving membrane polarization [32], and stimulation thresholds to determine whether convergence of the potentials is a sufficient criterion for ensuring subsequent small errors in Δ2Φ and stimulation thresholds. In an isotropic medium, 320,000 first order (O1), 29,000 second order (O2), and 8,000 third order (O3) were sufficient for ensuring the error in the interpolated potentials was < 5 % but were not sufficient for calculating Δ2Φ and stimulation thresholds with an error of < 5 %. With these mesh parameters, the errors in Δ2Φ were 41 ± 16 %, 24 ± 14 %, and 18 ± 10 %, respectively; and the errors in the stimulation thresholds were 19 ± 13 %, 14 ± 12 %, and 13 ± 8 %, respectively (Fig 2a). At least 320,000 O2 and 98,000 O3 elements were required for calculating Δ2Φ with sufficient accuracy that the error in the stimulation thresholds was < 5 % (Fig 2a), while no number of O1 elements within the maximum number of elements tested (~ 2.3 million) was sufficient for calculating the stimulation thresholds to within 5 % accuracy.
Fig. 2.
Effects of the number and order of finite elements on potentials, Δ▫Φ, and stimulation thresholds in an (a) isotropic and (b) anisotropic media. Note: Δ▫Φ reflects the second difference of the potentials taken between 3 consecutive nodes of Ranvier in the modeled axon.
In an anisotropic medium, 727,000 O1, 72,000 O2, and 22,000 O3 elements were sufficient for calculating the potentials with an error of < 5 % but not sufficient for calculating Δ2Φ and the stimulation thresholds with an error of < 5 %. For this number of elements, the errors in Δ2Φ were 236 ± 79 %, 174 ± 151 %, and 207 ± 177 %, respectively; and the errors in the stimulation thresholds were 32 ± 16 %, 40 ± 28 %, and 44 ± 44 %, respectively (Fig 2b). 2.3 million O2 and 727,000 O3 elements were sufficient for calculating Δ2Φ with enough accuracy that the error in the stimulation thresholds was < 5 % (Fig 2b). Therefore, in both the isotropic and anisotropic cases, convergence of the potentials was not sufficient for calculating the stimulation thresholds to the same accuracy.
B. Volume of the FEM model
Doubling the volume of the isotropic model (60 × 60 × 60 mm3) increased Ra by 0.6 %, which corresponded to an RMSD of 3.2 ± 0.4 %, 3.0 ± 1.9 %, and 0.4 ± 0.2 % in Φ, Δ2Φ, and the stimulation thresholds, respectively. Doubling the volume of the anisotropic model (120 × 40 × 40 mm3) increased Ra by 0.5 %, which corresponded to an RMSD of 5.3 ± 0.7 %, 1.9 ± 2.2 %, and 0.6 ± 0.5 % in Φ, Δ2Φ, and the stimulation thresholds, respectively. Thus, the volume was large enough that the errors in Ra and the stimulation thresholds were < 5 %.
C. Simplifying the representation of the electrode
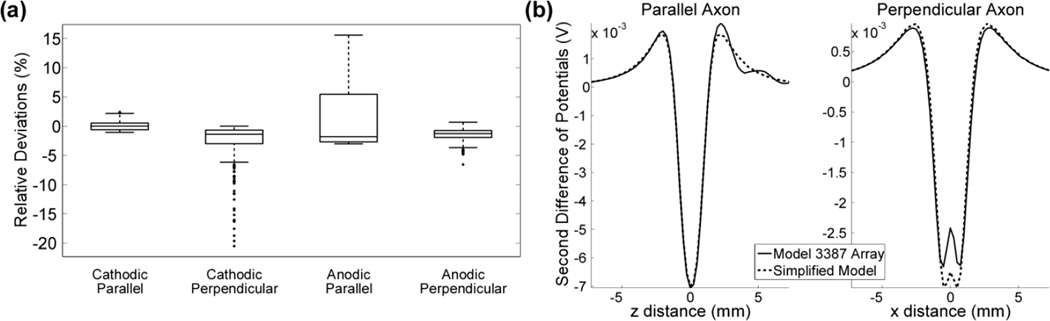
We quantified the RMSD of the stimulation threshold voltages to determine the effect of removing the inactive electrodes and extending the terminated end of the electrode shaft. Removing the inactive electrode contacts altered cathodic stimulation thresholds by −17 to +2.3 %, with an RMSD of 0.9 ± 2.3 %, and anodic stimulation thresholds by −6.3 to +13 %, with an RMSD of 2.3 ± 3.0 %. Extending the distal end of the shaft altered cathodic stimulation thresholds by −10 to +2.1 %, with an RMSD of 0.6 ± 1.2 %, and anodic stimulation thresholds by −2.9 to + 6.1 %, with an RMSD of 0.9 ± 1.3 %. Applying both simplifications produced cathodic stimulation threshold errors between −17 and + 2.5 %, with an RMSD of 1.5 ± 2.4 %, and anodic stimulation threshold errors between −6.2 and +18 %, with an RMSD of 3.2 ± 4.2 % (Fig 3a). Thus, removing the inactive electrodes had the greatest effect on the stimulation thresholds.
Fig. 3.
Effect of simplifying the representation of the Medtronic 3387 array. (a) Distributions of relative deviations in the stimulation thresholds between the simplified model and the 3387 electrode array. Outliers (greater than 1.5 times the interquartile range) are denoted by solid dots. (b) Δ2Φ generated by the 3387 array and the simplified model for representative parallel (left) and perpendicular (right) axons located <1.6 mm from the electrode surface.
The effect of geometric simplifications of the electrode on thresholds was dependent on the polarity of stimulation as well as the orientation of the axons. Across the 3 populations of 100 fibers, anodic stimulation threshold voltages in 78 (26 %) of the 300 parallel fibers increased > 5 % when using the simplified model of the 3387 array (Fig 3a). These 78 parallel fibers were the elements closest (< 1.6 mm) to the electrode surface. Similar to the parallel case, cathodic stimulation thresholds in the 30 closest (10 %) perpendicular fibers increased > 5 % (Fig 3a). Inspection of the potentials showed that the inactive electrodes had an effect on the distribution of potentials near the electrode shaft. Parallel to the electrode, the presence of the inactive contacts increased the magnitude of the secondary lobes of Δ2Φ (virtual anodes / cathodes), and perpendicular to the electrode, the presence of the inactive contacts decreased the magnitude of the primary lobe of Δ2Φ (Fig 3b).
Overall, the RMSD of the stimulation thresholds was < 5 % in all cases, except for anodic stimulation of parallel fibers, where the RMSD was > 5 %. Therefore, unless quantifying the activation of parallel neural elements < 1.6 mm from the electrode surface during anodic stimulation, the simplified representation of the 3387 array was sufficient.
D. Representation of the electrode-tissue interface
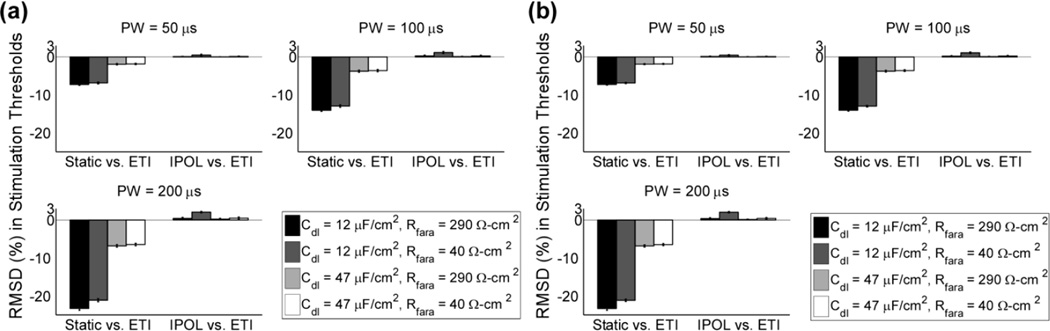
We analyzed the dependence of threshold voltages on cdl and rf to determine if the ETI could be ignored for typical DBS parameters. Ignoring the ETI altered the RMSD of the stimulation thresholds for parallel and perpendicular fibers between 2 and 7 % for a PW = 50 µs, between 4 and 14 % for a PW = 100 µs, and between 7 and 23 % for a PW = 200 µs (Fig 4). For each combination of cdl and rf, further increasing rf to infinity increased the RMSD of the stimulation thresholds with increasing PW, but the largest RMSD was 2.1 ± 0.2 % (Fig 4). Therefore, for typical DBS parameters, the ETI has a marked effect on the stimulation thresholds, but the ETI can be simplified by setting rf to infinity (i.e., the DBS electrode could be approximated as an ideal polarized electrode).
Fig. 4.
The effect of the ETI impedance on the threshold voltages to activate a population of model axons. (a) The RMSD of the stimulation threshold voltages for a population of parallel fibers at different PWs. Relative errors were calculated for two cases: between the linear and static models with and without the ETI, respectively (Static vs. ETI), and between the linear model with a constant rf and cdl and a corresponding ideal polarized electrode (IPOL) model with only a constant rf (IPOL vs. ETI). (b) As in a, but for perpendicular fibers.
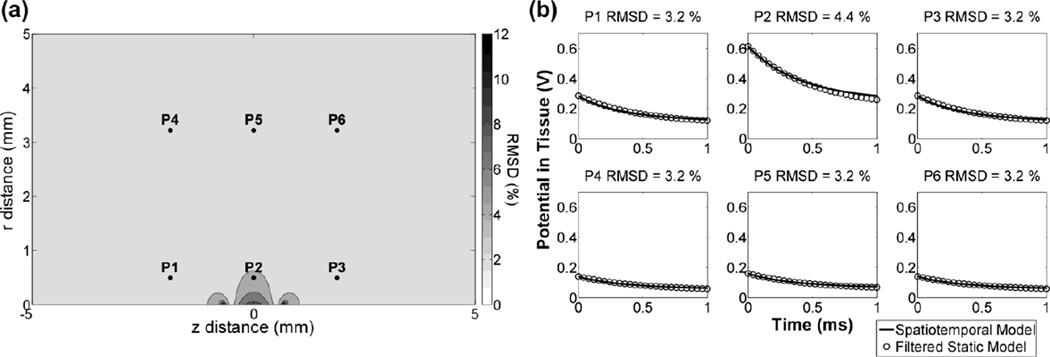
At each mesh node, we compared the waveforms of potential versus time between the axisymmetric spatiotemporal FEM model and the static FEM model filtered by a 3-element Randles equivalent circuit of lumped Ra, Rf, and Cdl. For PW = 1 ms, the RMSD between the waveforms of the two models at all mesh nodes ranged from 3 – 12 %. The largest errors occurred within 0.1 mm of the electrode surface and declined to a minimum value 0.6 mm from the electrode surface (Fig 5). The RMSD at all points within the region where axons were seeded was < 5 %, so the spatiotemporal FEM model can be simplified using the filtered static model.
Fig. 5.
The distributed ETI impedance can be approximated by filtering the static potentials with a lumped equivalent circuit. (a) The RMSD in the waveforms of the potential versus time (0–1 ms) at each node between the spatiotemporal and filtered static models. The electrode contact is centered at z = 0 mm (with respect to the electrode center) and the semi-infinite domain extends in the r direction (with respect to the electrode surface). (b) Tissue potentials vs. time at the six locations shown in a.
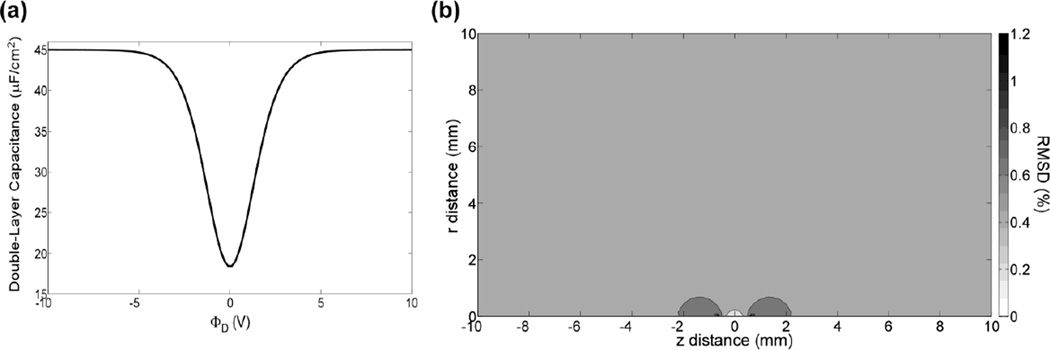
The cdl varies as a function of the applied potential for typical stimulation amplitudes [17, 31] but is often approximated as constant. Because the RMSD of the stimulation threshold voltages was < 5 % when rf changed from 40 Ω-cm to infinity, we approximated the 3387 array as an ideal polarized electrode and compared waveforms of potential versus time at the mesh nodes when cdl was linear and nonlinear (Fig 6a). For a PW = 210 µs, the RMSD in the waveforms between the linear and nonlinear models ranged from 0.3–1.2 % (Fig 7b), 0.2–0.7 %, and 0.2–0.4 % at stimulus amplitudes of 1 V, 3 V, and 5 V, respectively. In all cases, the largest errors were located near the electrode surface. In addition, at 1 V, 3 V, and 5 V, the RMSD in the waveforms between the two models was < 5 % across all mesh nodes for PWs up to 560 µs, 780 µs, and 1000 µs, respectively. Therefore, for typical stimulation parameters, although the cdl varies nonlinearly with the applied potential, it varied slowly enough with time that it could be approximated as quasi-static. That is, the nonlinear cdl at a given applied potential can be approximated by evaluating (6) at the beginning of each phase of the rectangular stimulation pulse and keeping cdl constant throughout the duration of each phase.
Fig. 6.
The effect of a nonlinear cdl on the potentials. (a) The relationship between cdl and the potential at the boundary between the compact and diffuse layers (ΦD) (b) The RMSD in the waveforms of potential versus time (PW = 210 µs) at all mesh nodes between the linear and nonlinear models when the nonlinear cdl changed most drastically (Φstim = 1 V). The electrode contact is centered at z = 0 mm and the semi-infinite domain extends in the r direction.
Fig. 7.
Interpolation of the potentials with O1 and O2 elements creates discontinuities in Δ2Φ and errors in stimulation thresholds. (a) The interpolated potentials and corresponding Δ2Φ across a representative fiber in an anisotropic media. (b) Input-output curves of the fraction of perpendicular axons activated versus the cathodic stimulation voltage for the mesh parameters in part a. The RMSD of the stimulation thresholds between the case and O3 elements is shown in the legend.
IV. DISCUSSION
We quantified the effect of model simplifications on the electrical potentials and excitation thresholds in FEM models of DBS. The results yielded four important conclusions. One, convergence of Δ2Φ, regardless of the element order, should be used to assess numerical accuracy when coupling numerical volume conductor models with cable-based models of neural elements, and cubic or greater elements should be used to avoid discontinuities in the calculation of Δ2Φ. Two, simplifying the 3387 array by ignoring the inactive contacts and extending the terminated end of the shaft has position dependent effects on the potentials and excitation thresholds, and these effects may impact correlations between DBS parameters and clinical outcomes. Three, when the current density in the bulk tissue is approximately uniform, the effect of the ETI impedance can be approximated by filtering the static model of the DBS electrode with lumped parameter electrical equivalent circuit. And four, for typical DBS parameters during voltage-regulated stimulation, the PtIr electrode contact can be approximated as an ideal polarized electrode with a nonlinear double-layer capacitance, and if the applied potential on the electrode surface is constant, the double-layer capacitance at a given applied potential can be treated as quasi-static.
A. The effect of interpolation on electric potentials and neural activation
A frequently used criterion for assessing the accuracy of solutions in FEM models of DBS is convergence of the potentials. Elements of any order (≥ 1) can be used to interpolate potentials without discontinuities, but unless O3 or greater elements are used, discontinuities arise when calculating Δ2Φ, which lead to errors in activation thresholds that exceed the errors in the potentials (Fig 2, Fig 7). This explains why, for example, (much) greater than 30 times as many (O1) O2 elements were required to reach the same accuracy in Δ2Φ as the potentials, while only 10 times as many O3 elements were required to reach the same accuracy in Δ2Φ (Fig 2a). Therefore, O3 or greater elements should be used to avoid discontinuities when calculating Δ2Φ in FEM models of DBS, and convergence of Δ2Φ should be used to assess numerical accuracy of the solution.
Using higher order elements comes at the expense of increased computational time, as the computational cost of using an element of order P is proportional to NPd+1 [33], where N is the number of elements and d is the number of dimensions. In our 3D model, it took 10 times as many O2 elements as O3 elements to reach the same accuracy in Δ2Φ. Because solving 10 times as many O2 elements took ~ 50 % longer, O3 elements were more efficient at calculating Δ2Φ. However, O3 elements are not necessarily the most efficient choice in all cases.
The rate of convergence for increasing element order is exponential in regions where the solution is smooth, so O4 or greater elements could be potentially more efficient far from the electrode [34]. However, in regions where the solution is not smooth, for example, where heterogeneous electrical properties create large gradients in the potentials, [35], increasing element order has only an algebraic rate of convergence and using a greater number of lower order elements is preferred [34]. Large gradients in the potentials are certainly expected in patient-specific models of the brain, which include inhomogeneous and anisotropic tissue electrical properties; therefore, a mixed method [36], where O1–O3 elements are used near to electrode, where the potentials are not smooth, and O4 or greater elements are used far from the electrode, where the potentials are smooth, is expected to be the most computationally efficient choice of mesh parameters.
B. Simplifying the representation of the electrode
The Medtronic 3387 electrode array is axially symmetric; therefore, when the surrounding tissue is also axially symmetric, a two-dimensional geometry can be used to represent the electrode. In addition, previous studies have proposed simplifying the 3387 array by ignoring the inactive electrode contacts and extending the terminated end of the shaft [13, 14, 27, 28]. Removing the inactive electrodes and extending the terminated end of the shaft had position dependent effects on the potentials (Fig 3a), and the effect of the former was more pronounced.
The inhomogeneities created by the highly conductive inactive contacts generated local short circuits adjacent to the tissue that had two effects on the potential. First, the inactive electrodes increased the magnitude of the “virtual cathodes” in Δ2Φ by flattening the potential distribution along the electrode shaft, and second, the inactive electrodes decreased the magnitude of the primary cathode in Δ2Φ by shunting current longitudinally along the electrode shaft (Fig 3b). In our computational model, these shaping effects extended up to 1.6 mm from the electrode surface. Since the spatial extent of this effect is expected to depend on a number of factors, including the geometry of the electrodes and the electrical properties of the surrounding tissue, and since the closest neural elements activated during DBS are certainly expected to lie within millimeters of the electrode surface [8], the effects of simplifying the electrode geometry should be confirmed before using a simplified model to make correlations between stimulation parameters and clinical outcomes.
C. Representation of the electrode-tissue interface
Different representations of the ETI have been used in previous studies analyzing the filtering effects of the ETI [14, 30, 37]. Although these studies agree that the effects of the ETI cannot be ignored during typical stimulation parameters, it is important to establish what level of detail is appropriate for modeling the ETI.
One question the results addressed is whether the PtIr electrode can be modeled as an ideal polarized electrode [14]. For typical stimulation parameters, the charge injected per pulse does not exceed the reversible charge injection capacity of PtIr [16, 38], so irreversible charge transfer occurs at a slow rate and can be ignored. However, reversible charge transfer with PtIr can include both capacitive and Faradaic pathways [16]. Our results showed that DBS electrode could be approximated as an ideal polarized electrode during voltage-regulated stimulation (Fig 4), but this was not because the Faradaic current was small compared to the capacitive current, but rather, because the charging of the ETI was insensitive to changes in the Faradaic current.
For example, for any combination of rf and cdl, increasing rf from its minimum value to infinity had a much smaller effect than increasing cdl from its minimum to maximum value (Fig 4). This can be explained qualitatively by examining the time constant (τ) of an equivalent Randles circuit of the DBS electrode:
| (9) |
τ is proportional to Cdl and the parallel combination of Ra and Rf. Because τ is only proportional to Rf when Rf << Ra, and Rf is greater than or equal to Ra for a PtIr electrode in brain tissue [17], τ is more sensitive to changes in Cdl. However, one should use caution when approximating the PtIr electrode as an ideal polarized electrode when Rf << Ra, or during current-regulated stimulation, because in both cases τ is directly proportional to both Cdl and Rf.
We also addressed the nonlinear dependence of rf and cdl on the electrode potential [17]. For voltage-regulated stimulation, the nonlinear rf can be ignored and the nonlinear cdl, despite its nonlinear dependence on ΦD (Fig 6a), varies slowly enough in time that for typical stimulation parameters it can be approximated as quasi-static, where the constant value is determined using (6). Prior work modeled a nonlinear ETI with an rf and cdl that varied with both frequency and amplitude, and assessed how the ETI impedance affects on the electrode surface [30]. Our work builds on this prior work by evaluating the impact of a nonlinear rf and cdl on activation thresholds for voltage-regulated stimulation and addressing the level of detail required for capturing these effects.
D. Representing effects of the ETI impedance
In FEM models of electrical stimulation, the ETI can be represented with a distributed boundary condition [29, 30] or with lumped circuit values [14]. Using the product of separate spatial and temporal solutions, where the static model solved the potential distribution in space and the Randles circuit solved the decay of the potentials over time, was indeed accurate. In other words, was approximately spherically uniform in the regions where the axons were seeded, so the rate of decay of in the bulk tissue could be described with a single equivalent time constant. However, heterogeneities in the tissue conductivity, such as cysts filled with cerebral-spinal fluid [39] or encapsulation tissue [13], can alter in the bulk tissue. In cases where is not (spherically or elliptically) uniform, the charging of the ETI cannot be described with a single τ [40], and such cases may require explicit representation of the ETI in time-dependent models.
E. Model Limitations
Two limitations in this study bear consideration. The first limitation is using a simplified (SW) model of a mammalian nerve fiber with perfectly insulating myelin, rather than a more detailed (MRG) axon model that better replicates the excitability of a mammalian nerve fiber [41]. Although the SW model does not reproduce the depolarizing after-potential and after-hyperpolarization [41], which account for the increased excitability of the axon following an action potential, it does reproduce conduction velocities [22], strength-duration and strength-distance relationships observed in mammalian fibers [42], and is much less computationally demanding than the MRG model.
The SW and MRG models have a single and double cable structure, respectively, but both have source terms (on the right-hand side of the cable equation) that are dependent on Δ2Φ. To analyze the effect of interpolation error on modeled MRG axons, additional simulation were conducted. 4832 O1, O2, and O3 elements yielded errors in the stimulation thresholds of 45 ± 23 %, 18 ± 13 %, and 5 ± 4 %, respectively. Therefore, the same qualitative trends observed with the SW model are expected to carry over in more detailed models of neural elements.
The second limitation is not accounting for the low conductivity of the glial scar, which has the effect of increasing Ra by as much as 800 Ω and thereby influencing stimulation thresholds [13]. Clinical measurements of DBS electrode impedances typically range from 500–1500 Ω. Our computational model had an Ra of 650 Ω and an ETI impedance that ranged between ~430–4,700 Ω for 10–1000 Hz, so the total impedance of the electrode fell within the range of clinical impedances. Yet, Ra was underestimated, which would have an impact on the charging of the ETI for voltage-regulated stimulation (Equation 9). Increasing Ra would increase τ, which would cause the ETI to charge more slowly, so our results should be interpreted as the maximum possible error.
IV. CONCLUSION
We quantified how interpolation error, electrode geometry, and the representation of the ETI affected the electric fields produced by DBS. The choices of mesh parameters, the representation of the inactive electrodes, and the nonlinear electrical properties of the ETI all had a marked effect on the calculated potentials and thresholds. Previous studies looking at computational models of DBS have shown that representations of the ETI [14], the glial scar [13], and anisotropies and inhomogeneities in the electrical properties of the brain tissue [8, 9, 39, 43] are critical for accurate predictions of clinical data. Further, previous studies have shown that uncertainty in the electrical properties of brain tissue [44] and their dispersive nature [37] can have an impact on calculated potentials. Our work builds on these previous studies by delineating the mesh parameters and level of detail in the electrode geometry and ETI required to accurately calculate stimulation thresholds.
Computational models are not only useful for understanding the mechanisms of DBS but also for studying the neural origins of biological signals that can be used to provide closed-loop control of DBS [45]. Models of closed-loop DBS require accurate predictions of the neural elements activated and their subsequent neural response. Interpolation errors and simplifications of the electrode array and ETI can certainly affect predicted stimulation thresholds and also the recorded neural signal. For example, representation of the ETI is important for capturing the (low pass) filtering effects of the ETI on the recorded signal. Therefore, the results have a broader impact on computational models used to study in vivo sensing and control for DBS.
Acknowledgements
This work was supported by a Ruth L. Kirschstein F31 NS079105 Predoctoral Fellowship and by Grant R01 NS040894 from the National Institute of Neurological Disorders and Stroke of the National Institutes of Health.
Biographies

Bryan Howell (M’2013) was born in McAllen, Texas in 1986. He received the B.S. degree in biomedical engineering in 2009 from The University of Michigan, Ann Arbor, and he is currently pursuing the Ph.D. degree in biomedical engineering at Duke University in Durham, North Carolina.
He is presently a graduate research assistant in Dr. Warren M. Grill’s Neural Prostheses Laboratory at Duke University. His research interests include computational neuroscience, the fundamentals of electrode design, and model-based design of electrodes to increase the efficiency and selectivity of deep brain stimulation.
In 2012, Mr. Howell was awarded an F31 Ruth L. Kirschstein Predoctoral Fellowship from the NIH.

Sagar Naik was born in Mumbai, India in 1991 and raised in Spartanburg, South Carolina. He received his BSE degree in biomedical engineering from Duke University, Durham, North Carolina, in 2013.
From 2011–2013 he performed research in the Duke Institute for Brain Sciences and the Pratt School of Engineering. His work involves computer modeling and stimulation of axons in deep brain stimulation and looks to improve methods for selective activation of different elements of the nervous system elements.

Warren M. Grill received the B.S. degree in biomedical engineering with honors in 1989 from Boston University and the Ph.D. in biomedical engineering in 1995 from Case Western Reserve University, Cleveland, OH.
He is the Addy Distinguished Professor of Biomedical Engineering at Duke University, Durham, NC, USA, with secondary appointments in Electrical and Computer Engineering, Neurobiology, and Surgery. His research interests are in neural engineering and neural prostheses and include design and testing of electrodes and stimulation techniques, the electrical properties of tissues and cells, and computational neuroscience with applications to restoration of bladder function, treatment of movement disorders with deep brain stimulation, and electrical stimulation for treatment of pain.
He is Co-Founder, Director, and Chief Scientific Officer of NDI Medical, a medical device incubator, Director and Chief Scientific Advisor at SPR Therapeutics, which has developed a novel therapy for treating pain, and Co-Founder, Director, and Chief Scientific Officer of DBI, which has developed a novel approach to brain stimulation for neurological disorders.
In 2008 received the Capers & Marion McDonald Award for Excellence in Teaching and Research at Duke University, in 2009 was inducted into the Bass Society of Fellows at Duke for excellence in teaching and research, and in 2013 was given the award for Outstanding Postdoctoral Mentor at Duke. He was elected as a Fellow of the American Institute of Medical and Biological Engineering in 2007 and as a Fellow of the Biomedical Engineering Society in 2011.
Dr. Grill serves as a Consultant to the Neurological Devices Panel of the Medical Devices Advisory Committee, Center for Devices and Radiological Health, U.S. Food and Drug Administration, and on the editorial boards of Brain Stimulation and Journal of Neural Engineering.
Appendix
The weak form (Equation A.1) of (1) was obtained by multiplying both sides of (1) by a weighting function (w), integrating over the domain Ω and its boundary Γ, and using the divergence theorem to represent the volume integral of the divergence of over Ω as the flux of over its boundary Γ.
| (A.1) |
Where σ is a conductivity tensor, ΓETI is the boundary of the ETI, ρ is the radial distance, and ρe is the radius of the electrode and its shaft.
We used the Galerkin method to approximate solutions of the boundary-value problem based on its weak formulation. The solution and weighting spaces were discretized using 4-node quadrilateral elements with bilinear shape functions shown below:
| (A.2) |
| (A.3) |
Where, the superscript h denotes an approximation, neqns is the number of shape functions on the quadrilateral element, ζ and η are the variables, z and ρ, mapped onto the bi-unit square domain, and da and ca are arbitrary constants. Application of (A.2) to (A.1) yielded the following system of equations:
| (A.4) |
| (A.5) |
| (A.6) |
| (A.7) |
| (A.8) |
Where, K is the stiffness matrix; and M, H, and F are sparse matrices that contain components arising from the ETI. M contains contributions from the non-Faradaic, capacitive current, and H and F contain contributions from the Faradaic, resistive current. (A.5)–(A.8) was linearized using the Newton-Raphson (NR) method, which yielded:
| (A.9) |
| (A.10) |
| (A.11) |
| (A.12) |
| (A.13) |
| (A.14) |
| (A.15) |
Where, the superscript i denotes the iteration number in the NR method. Note, (A.5) has no dependence on tissue potentials being solved for, so it remained unchanged. However, (A.6)–(A.8) were dependent on the potentials, so they were differentiated with respects to the degrees of freedom. Differentiation of (A.6)–(A.8) yielded:
| (A.16) |
| (A.17) |
| (A.18) |
Contributor Information
Bryan Howell, Biomedical Engineering Department, Duke University, Durham, NC, 27708 USA (bryan.howell@duke.edu).
Sagar Naik, Alumnus of the Biomedical Engineering Department, Duke University, Durham, NC 27708 USA.
Warren M. Grill, Departments of Biomedical Engineering, Electrical and Computer Engineering, Neurobiology, and Surgery, Duke University, Durham, NC 27708 USA (warren.grill@duke.edu)
REFERENCES
- 1.Limousin P, et al. Multicentre European study of thalamic stimulation in parkinsonian and essential tremor. J Neurol Neurosurg Psychiatry. 1999 Mar;66:289–296. doi: 10.1136/jnnp.66.3.289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Montgomery EB., Jr Deep brain stimulation reduces symptoms of Parkinson disease. Cleve Clin J Med. 1999 Jan;66:9–11. doi: 10.3949/ccjm.66.1.9. [DOI] [PubMed] [Google Scholar]
- 3.Kuhn J, et al. Deep brain stimulation for psychiatric disorders. Dtsch Arztebl Int. 2010 Feb;107:105–113. doi: 10.3238/arztebl.2010.0105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mayberg HS, et al. Deep Brain Stimulation for Treatment-Resistant Depression. Neuron. 2005;45:651–660. doi: 10.1016/j.neuron.2005.02.014. [DOI] [PubMed] [Google Scholar]
- 5.McIntyre CC, et al. Cellular effects of deep brain stimulation: model-based analysis of activation and inhibition. J Neurophysiol. 2004 Apr;91:1457–1469. doi: 10.1152/jn.00989.2003. [DOI] [PubMed] [Google Scholar]
- 6.Beurrier C, et al. High-frequency stimulation produces a transient blockade of voltage-gated currents in subthalamic neurons. Journal of neurophysiology. 2001;85:1351–1356. doi: 10.1152/jn.2001.85.4.1351. [DOI] [PubMed] [Google Scholar]
- 7.Kuncel AM, Grill WM. Selection of stimulus parameters for deep brain stimulation. Clinical Neurophysiology. 2004;115:2431–2441. doi: 10.1016/j.clinph.2004.05.031. [DOI] [PubMed] [Google Scholar]
- 8.Butson CR, et al. Patient-specific analysis of the volume of tissue activated during deep brain stimulation. Neuroimage. 2007;34:661–670. doi: 10.1016/j.neuroimage.2006.09.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chaturvedi A, et al. Patient-specific models of deep brain stimulation: influence of field model complexity on neural activation predictions. Brain Stimul. 2010 Apr;3:65–67. doi: 10.1016/j.brs.2010.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sotiropoulos SN, Steinmetz PN. Assessing the direct effects of deep brain stimulation using embedded axon models. Journal of Neural Engineering. 2007;4:107. doi: 10.1088/1741-2560/4/2/011. [DOI] [PubMed] [Google Scholar]
- 11.Wei XF, Grill WM. Analysis of high-perimeter planar electrodes for efficient neural stimulation. Front Neuroeng. 2009;2:15. doi: 10.3389/neuro.16.015.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hughes TJR. The Finite Element Method. 2000 [Google Scholar]
- 13.Butson CR, et al. Sources and effects of electrode impedance during deep brain stimulation. Clin Neurophysiol. 2006 Feb;117:447–454. doi: 10.1016/j.clinph.2005.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Butson CR, McIntyre CC. Tissue and electrode capacitance reduce neural activation volumes during deep brain stimulation. Clin Neurophysiol. 2005 Oct;116:2490–2500. doi: 10.1016/j.clinph.2005.06.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Yousif N, et al. The peri-electrode space is a significant element of the electrode–brain interface in deep brain stimulation: A computational study. Brain Research Bulletin. 2007;74:361–368. doi: 10.1016/j.brainresbull.2007.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Merrill DR, et al. Electrical stimulation of excitable tissue: design of efficacious and safe protocols. J Neurosci Methods. 2005 Feb 15;141:171–198. doi: 10.1016/j.jneumeth.2004.10.020. [DOI] [PubMed] [Google Scholar]
- 17.Wei XF, Grill WM. Impedance characteristics of deep brain stimulation electrodes in vitro and in vivo. J Neural Eng. 2009 Aug;6:046008. doi: 10.1088/1741-2560/6/4/046008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bossetti CA, et al. Analysis of the quasi-static approximation for calculating potentials generated by neural stimulation. J Neural Eng. 2008 Mar;5:44–53. doi: 10.1088/1741-2560/5/1/005. [DOI] [PubMed] [Google Scholar]
- 19.Gabriel C, et al. Electrical conductivity of tissue at frequencies below 1 MHz. Phys Med Biol. 2009 Aug 21;54:4863–4878. doi: 10.1088/0031-9155/54/16/002. [DOI] [PubMed] [Google Scholar]
- 20.Nicholson PW. Specific impedance of cerebral white matter. Exp Neurol. 1965 Dec;13:386–401. doi: 10.1016/0014-4886(65)90126-3. [DOI] [PubMed] [Google Scholar]
- 21.Carnevale NT, Hines ML. The NEURON Book. Cambridge: 1997. [Google Scholar]
- 22.Sweeney J, et al. Modeling of mammalian myelinated nerve for functional neuromuscular stimulation; IEEE 9th Annual Conference of the Engineering in Medicine and Biology Society; 1987. pp. 1577–1578. [Google Scholar]
- 23.Schwarz J, et al. Action potentials and membrane currents in the human node of Ranvier. [1995/06/01];Pflügers Archiv. 1995 430:283–292. doi: 10.1007/BF00374660. [DOI] [PubMed] [Google Scholar]
- 24.Chiu S, et al. A quantitative description of membrane currents in rabbit myelinated nerve. The Journal of Physiology. 1979;292:149–166. doi: 10.1113/jphysiol.1979.sp012843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Haberler C, et al. No tissue damage by chronic deep brain stimulation in Parkinson's disease. Ann Neurol. 2000 Sep;48:372–376. [PubMed] [Google Scholar]
- 26.Moss J, et al. Electron microscopy of tissue adherent to explanted electrodes in dystonia and Parkinson's disease. Brain. 2004 Dec;127:2755–2763. doi: 10.1093/brain/awh292. [DOI] [PubMed] [Google Scholar]
- 27.Butson CR, McIntyre CC. Role of electrode design on the volume of tissue activated during deep brain stimulation. J Neural Eng. 2006 Mar;3:1–8. doi: 10.1088/1741-2560/3/1/001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wei XF, Grill WM. Current density distributions, field distributions and impedance analysis of segmented deep brain stimulation electrodes. J Neural Eng. 2005 Dec;2:139–147. doi: 10.1088/1741-2560/2/4/010. [DOI] [PubMed] [Google Scholar]
- 29.Behrend MR, et al. Dynamic current density of the disk electrode double-layer. IEEE Trans Biomed Eng. 2008 Mar;55:1056–1062. doi: 10.1109/TBME.2008.915723. [DOI] [PubMed] [Google Scholar]
- 30.Cantrell DR, et al. Incorporation of the electrode-electrolyte interface into finite-element models of metal microelectrodes. J Neural Eng. 2008 Mar;5:54–67. doi: 10.1088/1741-2560/5/1/006. [DOI] [PubMed] [Google Scholar]
- 31.Bard AJ, Faulkner LR. Electrochemical Methods - Fundamentals and Applications. 2nd ed. Wiley: 2000. [Google Scholar]
- 32.Rattay F. Analysis of Models for External Stimulation of Axons. Biomedical Engineering, IEEE Transactions on. 1986;BME 33:974–977. doi: 10.1109/TBME.1986.325670. [DOI] [PubMed] [Google Scholar]
- 33.Dong S, Karniadakis GE. P-refinement and P-threads. Computer methods in applied mechanics and engineering. 2003;192:2191–2201. [Google Scholar]
- 34.Babuska I, et al. The p-version of the finite element method. SIAM journal on numerical analysis. 1981;18:515–545. [Google Scholar]
- 35.Grill WM, Jr, Mortimer JT. Modeling the effects of electric fields on nerve fibers: influence of tissue electrical properties. doi: 10.1109/10.775401. 19990921 DCOM- 19990921. [DOI] [PubMed] [Google Scholar]
- 36.Babuška I, Suri M. The p and h-p versions of the finite element method, basic principles and properties. SIAM review. 1994;36:578–632. [Google Scholar]
- 37.Grant PF, Lowery MM. Effect of Dispersive Conductivity and Permittivity in Volume Conductor Models of Deep Brain Stimulation. Biomedical Engineering, IEEE Transactions on. 2010;57:2386–2393. doi: 10.1109/TBME.2010.2055054. [DOI] [PubMed] [Google Scholar]
- 38.Rose TL, Robblee LS. Electrical stimulation with Pt electrodes. VIII. Electrochemically safe charge injection limits with 0.2 ms pulses. IEEE Trans Biomed Eng. 1990 Nov;37:1118–1120. doi: 10.1109/10.61038. [DOI] [PubMed] [Google Scholar]
- 39.Astrom M, et al. The effect of cystic cavities on deep brain stimulation in the basal ganglia: a simulation-based study. J Neural Eng. 2006 Jun;3:132–138. doi: 10.1088/1741-2560/3/2/007. [DOI] [PubMed] [Google Scholar]
- 40.Oldham KB. The RC time “constant” at a disk electrode. Electrochemistry Communications. 2004;6:210–214. [Google Scholar]
- 41.McIntyre CC, et al. Modeling the excitability of mammalian nerve fibers: influence of afterpotentials on the recovery cycle. Journal of Neurophysiology. 2002;87:995–1006. doi: 10.1152/jn.00353.2001. [DOI] [PubMed] [Google Scholar]
- 42.Kuhn A, et al. A model for transcutaneous current stimulation: simulations and experiments. [3/1/2009];Medical & Biological Engineering & Computing. 2009 47:279–289. doi: 10.1007/s11517-008-0422-z. [DOI] [PubMed] [Google Scholar]
- 43.Åström M, et al. Influence of heterogeneous and anisotropic tissue conductivity on electric field distribution in deep brain stimulation. Medical & biological engineering & computing. 2012;50:23–32. doi: 10.1007/s11517-011-0842-z. [DOI] [PubMed] [Google Scholar]
- 44.Schmidt C, et al. Influence of Uncertainties in the Material Properties of Brain Tissue on the Probabilistic Volume of Tissue Activated. 2013 doi: 10.1109/TBME.2012.2235835. [DOI] [PubMed] [Google Scholar]
- 45.Kent AR, Grill WM. Neural origin of evoked potentials during deep brain stimulation. Journal of neurophysiology. 2013 doi: 10.1152/jn.00074.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]