Developmental improvements in dynamic control of fingertip forces last throughout childhood and into adolescence

Abstract

While it is clear that the development of dexterous manipulation in children exhibits dramatic improvements over an extended period, it is difficult to separate musculoskeletal from neural contributors to these important functional gains. This is in part due to the inability of current methods to disambiguate improvements in hand strength from gains in finger dexterity (i.e., the dynamic control of fingertip force vectors at low magnitudes). We adapted our novel instrumentation to evaluate finger dexterity in 130 typically developing children between the ages of 4 and 16 yr. We find that finger dexterity continues to develop well into late adolescence and musculoskeletal growth and strength are poorly correlated with the improvements in dexterity. Importantly, because these behavioral results seem to mirror the known timelines of neuroanatomical development up to adolescence, we speculate that they reflect the functional benefits of such continual neural maturation. This novel perspective now enables the systematic study of the functional roles of specific neuroanatomical structures and their connectivity, maturity, and plasticity. Moreover, the temporal dynamics of the fingertip force vectors shows improvements in stability that provide a novel way to look at the maturation of finger control. From a clinical perspective, our results provide a practical means to chart functional development of dexterous manipulation in typically developing children and could be adapted for clinical use and for use in children with developmental disorders.

dynamic control of fingertip force magnitude and direction is essential for manipulation of small, deformable, and fragile objects (Birznieks et al. 2001; Johansson and Flanagan 2009; Murray et al. 1994; Valero-Cuevas et al. 2003). The dramatic improvement of manipulation ability during development requires improvements in both fundamental sensorimotor capabilities [e.g., muscle strength, individuation of finger forces (Schieber and Santello 2004; Zatsiorsky et al. 2000)] and task-related capabilities [e.g., control of variability (Deutsch and Newell 2001, 2002; Forssberg et al. 1991), adaptation to friction (Forssberg et al. 1995), predictive scaling of forces (Forssberg et al. 1992; Gordon et al. 1991, 1992)]. Prior developmental studies have focused on complex motor planning and sequencing tasks (Jebsen et al. 1969; Moberg 1958; Poole et al. 2005; Taylor et al. 1973), combined arm and hand movements (Mathiowetz et al. 1986; Taylor et al. 1973; Tiffin and Asher 1948), or cognitive tests of visual processing and spatial transformations (Murray et al. 1990). However, they show minimal change in the adolescent years and, importantly, do not have sufficient resolution to clarify the specific timelines of developmental changes.

Here we focus on the development of dynamic control of fingertip forces to produce and stabilize dynamic dexterous manipulation. We characterize the development of dexterous manipulation at low force levels in children by adapting the strength-dexterity (SD) test (Valero-Cuevas et al. 2003). The test quantifies the ability to dynamically control fingertip force magnitude and direction during compression of a variety of springs, where the spring becomes increasingly unstable as it is compressed (Mosier et al. 2011; Valero-Cuevas et al. 2003; Venkadesan et al. 2007). A prior version of this test was shown to capture the development of a unique trait of dynamic fingertip force coordination using a three-finger grasp in typically developing children through adolescence (Vollmer et al. 2010). However, because it contained many springs it was time consuming and required testing over a large range of force magnitudes (0–80 N) rather than just focusing on low force magnitudes. Importantly, that study did show that the steepest gradient of improvement in dexterity happens with slender (i.e., unstable) springs that require low force magnitudes, i.e., <3 N (Fig. 1). This study, therefore, focuses on quantifying the developmental improvements in dynamic control of fingertip forces involving high instability and low magnitude. This domain of sensorimotor function is of particular interest because it has been shown to engage the cortical sensory-motor networks for manipulation more intensely than during manipulation with larger forces (Ehrsson et al. 2001). Moreover, the development of manipulation has largely been attributed to the neuroanatomical development in projection and association white matter tracts [such as the corticospinal tracts (CSTs)] that undergo significant changes in microstructure, myelination, and synaptogenesis throughout childhood and continuing into adolescence (Asato et al. 2010; Colby et al. 2011; Giedd et al. 1999; Lebel and Beaulieu 2011; Lebel et al. 2008; Paus et al. 1999; Sowell et al. 1999b). Thus we hypothesize that behavioral improvements in dynamic dexterous manipulation at low forces will follow a timeline similar to those neurodevelopmental changes that last into adolescence.

Fig. 1.

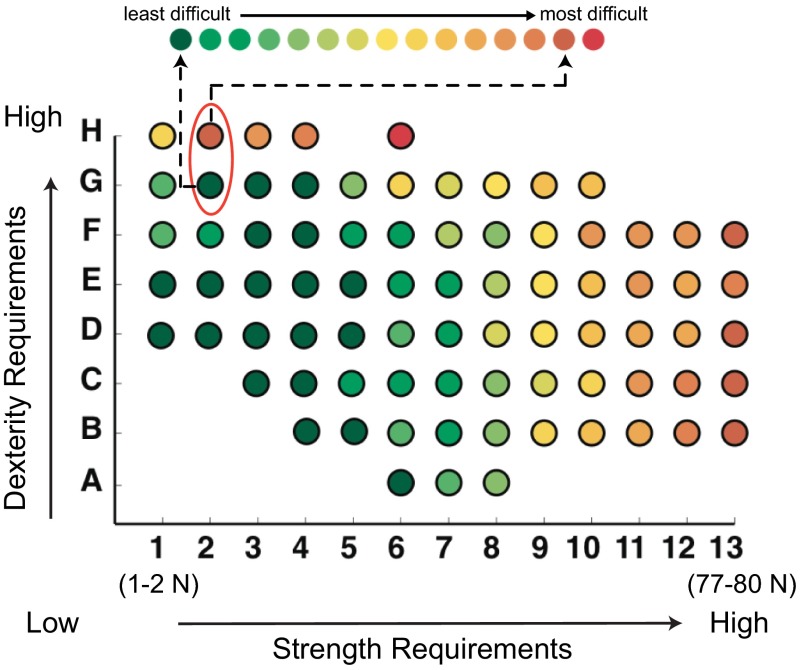
The strength-dexterity plane (Valero-Cuevas et al. 2003) describes the difficulty of compressing springs with different material and geometric properties along 2 functional axes. Compression springs have increasing strength requirements along the x-axis (they become increasingly stiffer) and increasing dexterity requirements along the y-axis (they are more slender, unstable, and prone to buckling). The results from Vollmer et al. (2010), color-coded for difficulty, demonstrate a large gradient of difficulty in children when they go from item G2 to item H2. This implies that higher-resolution measurements in this region of high dexterity and low force magnitudes could provide the best characterization of developmental changes in dexterity. The strength requirement in column 2 is only between 2.2 and 2.7 N. This served as the motivation, and design guidelines, for the present study.

MATERIALS AND METHODS

One hundred thirty children (4–16 yr; 76 girls, 54 boys) participated in this study. Ethical approval was obtained from the Regional Ethical Committee, Stockholm, Sweden and the University of Southern California, and all subjects and parents gave informed consent for participation in this study.

Instrumentation for dexterity measurement.

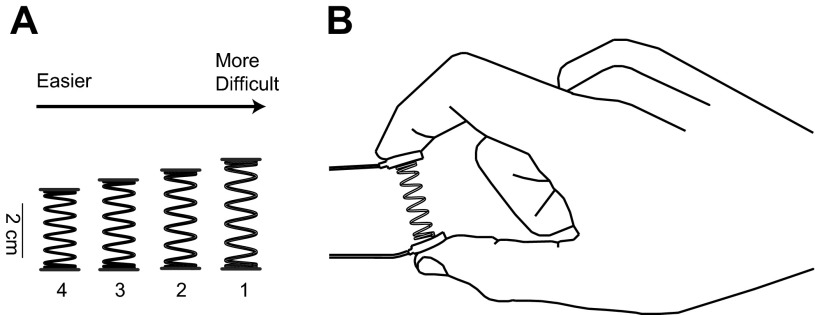
The physical characteristics of the springs define how stiff, compliant, stable, or prone to buckling they are—and therefore also define the necessary fingertip force vector magnitude and dynamical control of fingertip force vector direction. We used four custom-made springs (Century Springs, Los Angeles, CA) that required low force (<3 N) for complete compression and had the same stiffness (k = 0.8581 N/cm) and diameter (Table 1, Fig. 2) but, however, were prone to buckling and instabilities. The main reason for having more than one spring was to accommodate very small hands, if necessary. Given the nonlinear relationship between spring geometry and level of instability, the shorter springs were naturally easier to compress (Valero-Cuevas et al. 2003)—but therefore also more appropriate for very young children who also have smaller hands and less mature sensorimotor abilities. The low stiffness of the four springs was chosen to provide higher resolution in dexterity at the low levels of force magnitude identified from Vollmer et al. (2010) (Fig. 1). The following criteria were used: <4 N of force at full compression (Ehrsson et al. 2001) and free length between 3 and 4 cm. The springs were tested for linearity of their force vs. displacement with a stepwise loading protocol in a high-precision computer-controlled manufacturing machine instrumented with force sensors. Pilot studies confirmed that the properties of the custom-made springs would cover the dexterity range for the ages of 4–16 yr.

Table 1.

Spring specifications of experimental setup

	Spring 1	Spring 2	Spring 3	Spring 4
Free length, cm	3.96	3.60	3.24	2.90
Solid length, cm	0.69	0.69	0.69	0.69
Force range, N	0–2.84	0–2.5	0–2.19	0–1.89

The 4 springs used had the same stiffness (k = 0.8581 N/cm), but different lengths and forces were required for full compression of the springs.

Fig. 2.

Strength-dexterity setup demonstrating the 4 springs and the hardware for force data capture. A: springs were custom made such that the spring stiffness was the same (k = 0.86 N/cm) across all 4 springs. The lengths of the springs varied from 2.90 to 3.96 cm, while the maximal force required for compression of the springs remained below 3 N of force. Compression load cells were mounted on custom ABS plastic endcaps with double-sided tape. B: an example compression and hold at the maximal compression force; the miniature load cells are mounted on either side of the spring.

Two miniature compression load cells (ELB4-10, Measurement Specialties, Hampton, VA) were mounted on the spring endcaps (Fig. 2). The load cells were connected to a signal conditioner, which interfaced with an USB-DAQ (Measurement Computing, Norton, MA). The data were sampled at 400 Hz with a custom-written MATLAB program (MathWorks, Natick, MA), and a deadweight calibration procedure was used for conversion from voltage to force.

Experimental procedure.

The subjects were seated at a table with their dominant forearm supported in a midprone position. Children used the index finger and the thumb of their dominant hand to compress the spring as far as possible and maintain a sustained compression. After a brief familiarization with all springs and the task, the springs were presented in order, starting with the shortest and easiest (i.e., spring 4, 3, 2, or 1) to identify the first spring the subject could not compress fully. This spring was identified as their test spring. The subjects were then asked to compress their test spring as much as they could without causing the spring to buckle and maintain the pressure for a few seconds. The springs became more unstable the more they were compressed, requiring better dynamic control of fingertip force vector magnitude and direction by the subject to avoid buckling of the spring. The springs were long and slender, so that compressing them fully was quite difficult (Fig. 2). Test trials allowed the children to identify the boundary of compression beyond which the spring would buckle, i.e., this force level identified the greatest level of dynamic instability they could control with their fingertips. They were then asked to compress the spring to at least that point and maintain that level of compression for at least 3 s (Fig. 2). At least three successful maximal compression holds were collected per subject. This portion of the test took ∼5 min to complete.

In addition to the SD test, we measured 1) fine motor skill using Subtest One for Fine Manual Control of the Bruininks-Oseretsky Test of Motor Proficiency, Second Edition (BOT-2). The summed raw scores of the subtest were used to confirm handedness and typical fine motor development in the population. We also measured 2) maximal pinch strength with the index finger and the thumb of the dominant hand, using a tip-to-tip pinch with a pinch gauge (B&L Engineering, Tustin, CA). The children were verbally encouraged to do their best, i.e., get the highest score on the pinch gauge (Häger-Ross and Rösblad 2002). We collected at least two attempts from each child and used the maximal of the two for our analysis.

Hand anthropometric data were obtained for 92 of our subjects. The dominant hand was photographed in three positions, dorsal, palmar, and radial view, according to the protocol of Santos et al. (Santos 2007). Anthropometric data were extracted for multiple hand and finger dimensions as part of a different study. For this study we only utilized the thumb length, index finger length, and hand length, since these parameters have been shown to correlate with grip strength (Häger-Ross and Rösblad 2002).

Data reduction and analysis of sustained compression.

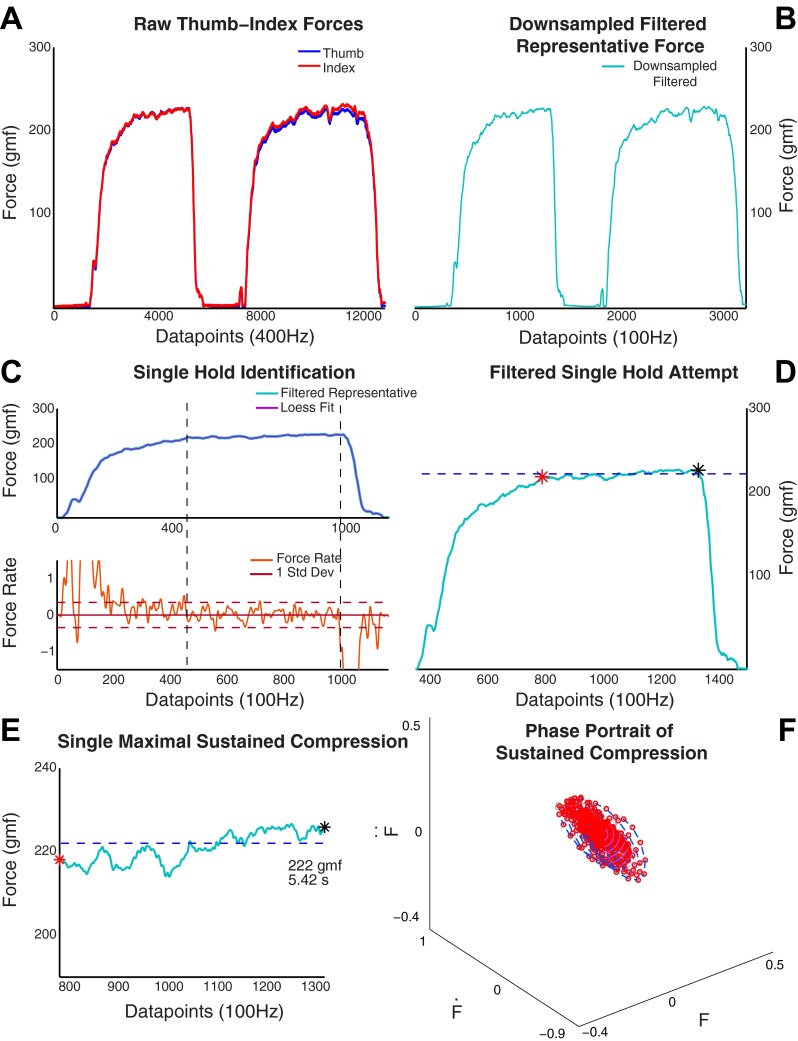
A representative force time series was created based on an average of the measured index finger and thumb force time series (Fig. 3A) with a custom program in MATLAB (MathWorks). The representative force was downsampled to 100 Hz and low-pass filtered at 25 Hz while maintaining phase (Butterworth, filtfilt) (Fig. 3B). We identified the sustained compression phases based on the compression force magnitude and rate of change (i.e., first time derivative of force) given the variability in force seen in this dynamic compression and stabilization of the spring. To facilitate this in the presence of high-frequency dynamic changes in the force, we used a loess smoother with a span of 10% before the force rate was computed. We defined a sustained compression phase as the period of time for which the force rate was bounded within 1 standard deviation of the mean force rate during each hold attempt (Fig. 3C). The start was identified when the rate was close to zero and the end when the rate went out of bounds and the force dropped toward baseline (Fig. 3C). As in Venkadesan et al. (2007), the mean of the representative force during the sustained compression force (Fig. 3, D and E) was calculated for all the hold attempts for each subject.

Fig. 3.

Data processing. A: an illustrative example of the force traces measured shows the forces from both the thumb and index finger at 400 Hz. Note that in a dynamical situation the index finger and thumb forces will not be equal and opposite at all times. A mean of the 2 forces at each time point was used to create a representative force. gmf, Gram force. B: this representative force was downsampled to 100 Hz and filtered at 25 Hz with a 2nd-order Butterworth filter. For each of the hold attempts (2 are seen in A and B) a loess filter was applied to the representative force and a force derivative was computed. C: both the force magnitude (top) and the force derivative (bottom) were used for identification of the start and end of the maximal sustained compression force. D and E: the single hold attempt and its mean are seen in its location in the time trace (D), and a magnified version (E) shows the force trace and its mean during the 5 s the maximal sustained compression force was maintained. F: the maximal sustained compression force was converted into a phase portrait (see Fig. 6) to quantify the amount of dispersion during the sustained compression period. F, Ḟ, F̈, force and its first 2 derivatives.

One aim was to develop a method that provided resolution over a large range to be able to include children with poor dexterity, e.g., children with neurodevelopmental disabilities. This was achieved by creating an unidimensional Dexterity Score that allowed us to combine performance levels across all test springs, including the fully compressed springs. For each subject a dexterity score was computed by summing the maximal force of each spring (i.e., 4, 3, 2) they could compress to solid length (i.e., when they could compress fully) plus the maximal sustained compression force they achieved in their test spring, normalized to that maximally possible sum of forces over the four springs (Eq. 1). That is, they earned a full score for each spring below their test spring, plus the compression they could achieve in their test spring. In addition, the springs were registered with each other by removing the dead bands of force in the springs, i.e., the region in the beginning and end of the range, which was noninformative. Consequently, and based on the complete data set, the informative/working regions for the springs were 33–124 gram force (gmf) for spring 3, 34–175 gmf for spring 2, and 51–286 gmf for spring 1. For example, children who were able to compress spring 2 beyond 175 gmf were also able to at least produce 51 gmf on spring 1. For most children in our study (n = 127), spring 1 or 2 was used as the test spring (3 children of age 4–5 yr used spring 3).

$$\text{Dexterity\hspace{0.17em}Score}=\frac{{\displaystyle {\sum }_{i=1}^n{\text{Spr}}_{\text{l}}-{\text{Db}}_{\text{l}}-{\text{Db}}_{\text{h}}}}{{\displaystyle {\sum }_{k\text{=1}}^{\text{4}}{\text{MaxSpr}}_k}}\times 100$$ (1)

where Spr = test spring used, MaxSpr = maximal force on that spring, n = test spring (1–3), k = spring (1–4), Db = dead band, l = low, and h = high.

Additional dynamical analysis.

We plotted the phase portraits of the fingertip forces to characterize the dynamics of how children control the dexterity device during the sustained compression. Phase portraits are a standard tool in studying dynamical systems. They consist of a plot of trajectories in the state space—in this case the fingertip forces vs. their derivatives. This reveals dynamical characteristics such as whether an attractor, a repellor, or a limit cycle is present for the fingertip forces, as well as the strength of those characteristics (Hirsch et al. 2004). In this case we plotted the state space of F vs. Ḟ vs. F̈, where F is force, Ḟ is force rate (velocity), and F̈ is change in force rate (acceleration) (Fig. 3F). The dynamics of the phase portrait during the hold phase was quantified by the dispersion of the Euclidean distance from the origin (i.e., 0,0,0) per unit time. The Euclidean distance was calculated on the sustained compression force after removing any trends and normalizing to the mean. The dispersion captures the amount traversed in this state space in 1 s, i.e., how much the operating point traveled in the state space during a given time of compression. Greater dispersion is an indication of a weaker attractor, i.e., a weaker neuromuscular controller enforcing the constant sustained compression.

Statistical analysis.

The independent variable of interest was age, while the dependent variables were 1) the mean compression of the three maximal sustained compressions in gmf, 2) the highest maximal sustained compression in gmf, 3) normalized dexterity score for the mean of the three maximal holds (nondimensional), 4) phase portrait dynamics during maximal sustained compression (dispersion, nondimensional), 5) pinch strength in kilograms, and 6) anthropometrics in millimeters. To test for the effect of age, we performed one-way ANOVAs with age as the independent variable [age binned into increments of 2 yr vs. mean compression for individual springs (Fig. 4) and age ranges in increments of 3 yr vs. phase portrait dynamics (see Fig. 6)]. To evaluate the influence of age and sex on performance we performed a two-way ANOVA with age and sex as the independent variables [age binned into increments of 2 yr and sex vs. dexterity score (Fig. 5)]. Linear regression models were created to evaluate shared variances 1) between pinch strength and maximal sustained compression, pinch strength = α × maximal compression + β, and 2) between hand and finger lengths and maximal sustained compression, sustained compression = α × hand length + β × index finger length + γ × thumb length + δ. A regression model based on a Fourier robust fit was created to evaluate the developmental growth curve of performance on the dexterity score: dexterity score = a0 + a1 × cos(age × w) + b1 × sin(age × w). We used a Fourier robust fit because initial analyses showed it to be superior to other nonlinear modes such as exponential and sigmoid functions.

Fig. 4.

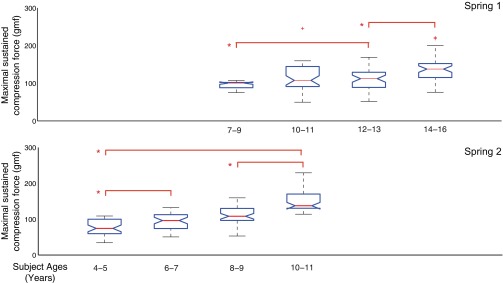
Mean compression force. Box plots show the median force that children were able to sustain for spring 1 (top) or spring 2 (bottom). Children (n = 127) used either spring 1 or spring 2 as their test spring. x-Axis: children's ages. y-Axis: force in gmf (0–300 gmf). Significant differences, indicated with an asterisk, are based on P < 0.05 and show changes throughout childhood and adolescence.

Fig. 6.

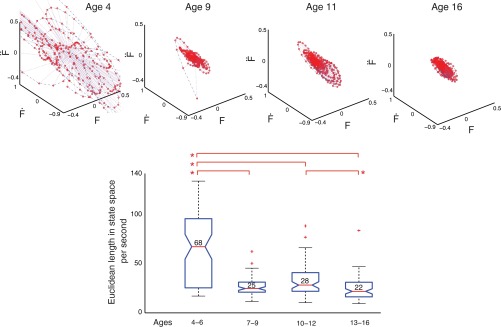
Dynamical analysis. Top: phase portraits of force during the maximal sustained compression for representative children for each age range. They show improvements in the ability to control the level of sustained force across childhood and adolescence. Note that, by convention, each coordinate axis has different units as they are force (F) and its first 2 derivatives (Ḟ, F̈), respectively. Bottom: quantification of the dispersion in the phase plots for all children, as per the Euclidean length in the phase portrait. Median values that are significantly different across age bins are indicated by asterisks (P < 0.05).

Fig. 5.

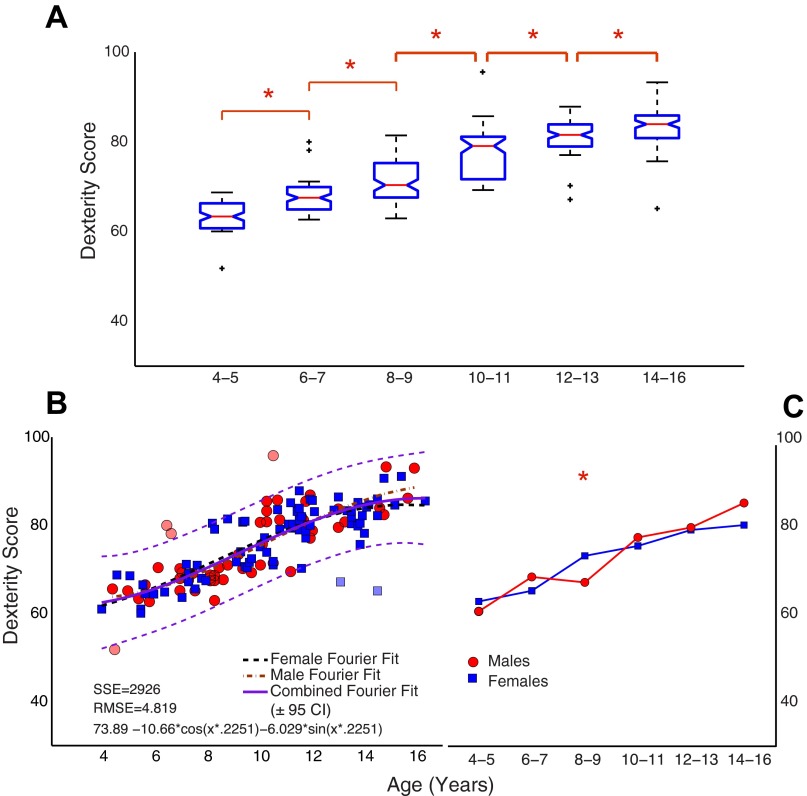
Normalized dexterity score throughout childhood and adolescence. The dexterity score was computed as a weighted average based on the mean hold force on the test spring and normalized to the maximal possible value (see Eq. 1). A: boxplots show changes across the age range. B: a regression line (±95% prediction bounds) based on a Fourier robust fit is shown in green/magenta, respectively. Outliers have been indicated in both A (as +) and B (as lighter-shaded data points). Data in B are colored by sex (blue, girls; red, boys), and individual regression lines are shown for each. Significant differences, indicated by asterisks based on P < 0.05, are seen in adjacent age bins across childhood and adolescence (A). The interaction between age and sex is shown in C along with significant age bins. SSE, sum of squared residuals; RMSE, root mean squared error; CI, confidence interval.

RESULTS

Age-related performance as per mean compression from springs 1 and 2.

In this analysis we only considered the 127 of 130 children who used spring 1 or 2 as their test spring. All 130 children managed to fully compress spring 4, and all but 3 children were able to fully compress spring 3. Not being able to fully compress both springs 3 and 4 is indicative of an uncommonly low level of dexterity, inability to follow the instructions, or having a very small hand. The children who managed to fully compress spring 2 were then “graduated” to using spring 1 as their test spring (n = 69, 7–16 yr), while spring 2 was the test spring for children who did not manage to fully compress it (n = 58, 4–11 yr; two 13-yr-old children who were unable to fully compress spring 2 were detected as outliers because they seemed distracted and unwilling to follow the instructions even though spring 2 was well within the capabilities of their younger peers). Figure 4 shows that the mean compression during the hold phase captured significant age-related development of dexterity in their age range for both spring 1 and spring 2, respectively (P < 0.05).

Age- and sex-related performance as per unidimensional dexterity score.

Figure 5A shows significant age-related changes (P < 0.0001) in the unidimensional dexterity score across the whole age span investigated. Post hoc multiple-comparison tests show that its main features include significant improvements across all the age bins and, importantly, also in late adolescence (cf. 12–13 yr and 14–16 yr). In Fig. 5B the developmental trajectory is represented by a Fourier robust fit with a shallower slope in late adolescence. The sum of squared (SSE) residuals of 2,926 and the root mean squared error (RMSE) of 4.819 (nondimensional units) were lowest for the Fourier robust fit compared with other exponential and sigmoid functions. Importantly, the shape of the Fourier robust fit allowed us to demonstrate faster developmental improvements early on, and slower improvements in late adolescence. While significant main effects were not seen between boys and girls (P = 0.85), there was a significant interaction between age and sex (P < 0.01; Fig. 5C). Individual one-way ANOVAs with a Bonferroni correction for multiple comparisons revealed a significant difference (P < 0.003) between boys and girls in the age bin at 8–9 yr, with girls showing a higher dexterity score (74.73 ± 6 vs. 68.39 ± 2.74; Fig. 5C).

Relationship between strength and dexterity.

Linear regressions of maximal sustained compression vs. pinch strength during the hold phase produced low r² values for both spring 1 (r² = 0.18, slope = 0.023, P < 0.005) and spring 2 (r² = 0.185, slope = 0.01, P < 0.001). This shows a weak association between dexterity and hand strength.

Changes in force dynamics during hold phase.

Figure 6 shows box plots of median values of dispersion of the phase portraits and representative phase portraits from children at each of the age groups (4–6, 7–9, 10–12, 13–16 yr). The dispersion is largest for the younger age group, with the greatest reduction seen in early childhood from 4–6 yr to 7–9 yr. While the age bin at 7–9 yr appears to have lower dispersion than the 10- to 12-yr-olds, this is not statistically significant. There are slight but significant reductions (P < 0.05) in late adolescence (from 10–12 to 13–16 yr). These changes in the dispersion of the phase portraits reflect the emergence of an increasingly stronger attractor (i.e., neuromuscular controller) at these low force magnitudes (i.e., tighter control on fluctuations of force magnitude and its derivatives). This strengthening of the attractor may be a contributor to the improved performance in controlling the spring prone to buckling.

Relationship between hand anthropometrics and dexterity.

The adjusted coefficients of determination (R²) for the multiple regression model of dexterity (maximal sustained compression) as a function of hand, index finger, and thumb lengths were 0.19 (spring 1) and 0.32 (spring 2). In the older children using spring 1 dexterous manipulation is not highly correlated to hand size, given that the combined variance in hand and finger lengths only accounts for 19% of performance. However, in the younger children who used spring 2 one can argue that there is a weak correlation that can account for ∼30% of variance in dexterity performance.

DISCUSSION

We demonstrate improvements in dexterity lasting into late adolescence that were previously not easily quantifiable beyond late childhood. These behavioral results mirror the timelines of neuroanatomical development well into adolescence—suggesting a causal relationship between the development of certain neural networks and pathways and the functional improvements. The temporal dynamics of the control of fingertip force vectors also show dramatic improvements particularly in early years that provide a novel way to look at the development of neural control of instabilities during dexterous manipulation. Moreover, demonstrating such long-lasting development extends the age ranges for which therapeutic interventions can be particularly fruitful. The new technique also provides a practical means to chart functional development of dexterous manipulation in typically developing children, and could be developed into a clinical instrument for use in children with neurodevelopmental disabilities.

The increased sensitivity of this technique, compared with the previous versions of the SD test (Vollmer et al. 2010), was made possible by focusing on the control of instabilities for low force magnitudes and adding miniature load cells to measure the dynamic regulation of fingertip forces during spring compression. We also changed from a three-finger grip to a “tip-to-tip” precision grip between the thumb and index finger to specifically focus on the neural control of precision manipulation. The thumb and index finger are the two most individuated digits (Edin et al. 1992; Häger-Ross and Schieber 2000) and thus mitigate the confounds of neuroanatomical enslavement (Schieber and Santello 2004; Zatsiorsky et al. 2000). Moreover, the simplified protocol lasted only a few minutes.

Progression of behavioral improvements and dynamics.

We found that the development of dexterous manipulation abilities showed improvements in increasing mean compression force, dexterity score, and tighter phase portraits of force. Both the mean compression force for individual springs and the normalized dexterity score showed changes in dexterous manipulation performance; therefore, it is unlikely that the changes we report are a function of the unidimensional scale that combines data from our two most difficult springs. In contrast with Vollmer et al. (2010), where boys had an overall steeper slope for SD test vs. age, our results show no main effect of sex, but there was a significant interaction between sex and age. The difference between the two studies may in part be due to the higher force magnitudes used in the Vollmer study (0–80 N) compared with the present study (<3 N). Interestingly, in the present study girls had a significantly higher dexterity score in the 8–9 yr age bin only. This was the same age at which the slopes of the SD test scores intercepted in the study by Vollmer et al. (2010). It is important not to overestimate the observed sex differences, since both studies have a cross-sectional design and longitudinal studies would be required in order to see whether there is a decrease in the development trajectory of boys in the actual age range, i.e., 8–9 yr. It would not be surprising if there is a difference in the development of dexterity between boys and girls, since there are noticeable sex differences in the developmental trajectories of the brain gray and white matter architecture (Giedd et al. 1999; Schmithorst et al. 2008).

The greater amount of dispersion of the phase portraits strongly suggests a weaker attractor in younger children. By contrast, the lowest dispersion in adolescent children suggests they have developed a stronger attractor able to further postpone bifurcation of the spring prone to buckling (i.e., compress the spring further) while demonstrating tighter control on force fluctuations. This dynamics of control shows the greatest change in the initial years, possibly related to the largest changes seen in the internal capsule density (Paus et al. 1999) or peripheral conduction times that mature by 3–5 yr (Müller et al. 1994). The timelines as observed by the dexterity score are different from that observed by the change in dispersion in the phase space. The dexterity score shows a continual improvement with a shallower slope in adolescence, while the dispersion mainly reaches stability in childhood. It is possible that this mismatch between the improvements in dispersion and dexterity score reflect different mechanisms involved in control of dexterous manipulation tasks. Grasping behaviors in grip and lift tasks show most improvements by ∼6–7 yr of age (Forssberg et al. 1991), presumably secondary to development of models for motor learning and adaptation as well with neural maturation. The long timescales of development and learning during childhood and adolescence can be considered as an evolving and changing attractor landscape in a developing body and neural controller, which helps to reinforce and change motor behavior (Newell et al. 2001).

Improvements in manipulation skills will depend on motor learning and consolidation as the child uses the newfound fingertip skills in everyday life (Franklin and Wolpert 2011; Johansson and Flanagan 2009; Wolpert et al. 2011). The process of controlling the direction of the fingertip forces during manipulation of unstable objects can be conceptualized as an internal model of the object and task constraints against which new incoming sensory information is compared (see Holmström et al. 2011a, 2011b). Maintaining the forces within stability limits involves a bilateral cortical network including the precentral gyri, the postcentral gyrus, and the cerebellum (Holmström et al. 2011a). The performance of this online adapting system is likely strongly dependent on the speed, e.g., afferent and efferent transmission between the periphery and cortical networks such as the CST, as well as the speed of the central processing in the network comparing sensory information with the internal model and generating accurate motor commands.

Neuroanatomical correlates of dexterous manipulation.

While we did not measure the neuroanatomical correlates of dexterous manipulation, it is important to discuss our results in the context of known timelines of neural development. Neural control of dexterous manipulation is attributed to a distributed network including the CST (Armand et al. 1994; Lemon et al. 2004a, 2004b) and its monosynaptic connections (Muir and Lemon 1983). The shape of the curve of developmental change in the dexterity score (Fig. 5) corresponds with the timelines of exponential change in the fractional anisotropy (FA) of the CST in the internal capsule (Lebel et al. 2008). Therefore, we extracted the data for the FA from Lebel et al. (2008) and performed a regression between dexterity score and FA and found a clear linear relationship (Fig. 7; r² = 0.99). A higher FA, which reflects larger and more myelinated nerve fibers organized in parallel bundles, can be regarded as a proxy for faster-conducting nerve fibers that are sustainable against fatigue, i.e., having a greater information and/or control bandwidth, and could therefore contribute to improved behavior and dynamics. The mean FA of the CST is correlated with hand function in children with unilateral cerebral palsy (Holmström et al. 2011b). While the development of CST is probably mainly genetically determined, environmental factors also seem to influence its development. In typically developing children intensive training during childhood, i.e., playing the piano before 11 yr of age, is shown to enhance FA of the CST in the internal capsule (Bengtsson et al. 2005). It remains to be shown whether early motor training in disabled children can influence the development of CST in a similar way, and thereby improve hand motor function. While the focus of our study was to elaborate on the timelines of development of dexterity during childhood and adolescence, in a parallel study comparing younger and older adults we report that the young adults in fact do perform better than the 16-yr-olds (Dayanidhi 2012), which is of significance given that the exponential change in the FA proceeds until young adulthood.

Fig. 7.

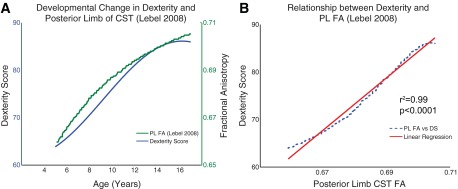
Association between behavioral and neuroanatomical development. A: developmental changes in dexterity score from this study compared with neuroanatomical connectivity as per fractional anisotropy (FA) of the corticospinal tract (CST) in the posterior limb (PL) of the internal capsule (data extracted from Lebel et al. 2008). B: linear regression of the dexterity score (DS) vs. fractional anisotropy shows an r² value = 0.99. These behavioral results are the first to mirror the known timelines of neuroanatomical development throughout childhood and adolescence, and they begin to reveal the functional benefits of such neural maturation.

In parallel with the development of the ascending and descending pathways between brain and hand, there are striking developmental processes taking place in the brain gray and white matter during childhood up to adolescence, e.g., expansion of the white matter and pruning of the cortical gray matter (Asato et al. 2010; Giedd et al. 1999; Lebel and Beaulieu 2011; Lebel et al. 2008; Martin et al. 2007; Paus et al. 1999). We (Ehrsson et al. 2001) demonstrated earlier that there is a greater activity in the fronto-parietal sensorimotor areas during the control of smaller forces than larger forces, with control of larger forces associated with increased activity in the M1 region. Fronto-parietal regions demonstrate significant developmental changes in the adolescent years (Asato et al. 2010; Lebel et al. 2008; Sowell et al. 1999b), and the pruning of the gray matter occurs later in the frontal and parietal areas (Sowell et al. 1999a) than in the M1. Although the associations between the development of cortical neural networks, including ascending and descending pathways on one hand, and the dexterity measured by this new method are only indicative and speculative, they are of both scientific and clinical interest.

Associated changes in pinch strength and anthropometrics.

A previous study (Vollmer et al. 2010) found that motor development showed strong covariation of maximal grip force and dexterity (r² = 0.61). In the present study, designed to test dexterity only at low force magnitudes (1.5–3 N), linear regression of pinch strength vs. mean compression force produced very low r² values. This suggests that the maximal pinch force capacity of the individual was not a dominant contributor to dexterity. Thus this study enabled us to focus on the maturation of the neuromuscular controller, and not hand strength.

The age-related increase of the raw and normalized dexterity scores could be a result of a more advantageous relation between the finger size of the children and the length of the spring, in addition to improved sensorimotor functions. Therefore we performed a multiple regression between hand anthropometrics and maximal sustained compression, which shows that the developmental changes in hand size and pinch strength are not strongly associated with improvements in dexterous manipulation capabilities. For spring 2 used in the younger children there seems to be a modest correlation with hand size. This is to be expected to a certain extent, given that these children do have the smallest hands to fit the size of our objects. In contrast, the older children tested with spring 1 show very low correlations with hand, thumb, and index finger lengths. This result also suggests that children were not improving their dexterity score by simply cocontracting the fingers and making them stiffer. This parallels the study by Venkadesan et al. (2007), where hand strength did not correlate strongly with dexterity, and showed that success in this unstable manipulation task depends on sensorimotor processing, later revealed to involve context-sensitive cortical networks (Holmström et al. 2011a; Mosier et al. 2011). Therefore this study likely reflects the development of sensorimotor control, and not changes in strength and hand anthropometrics, even though hand strength is highly correlated with anatomical growth and development, specifically with height, weight, and hand length from 4 to 16 yr of age (Häger-Ross and Rösblad 2002).

Clinical and scientific implications.

Our finding of continuous development into adolescence also suggests that the window of opportunity for rehabilitation in children with neurodevelopmental disabilities is longer, assuming that the plasticity, i.e., “critical period,” of the involved sensorimotor system remains high during this period (Armand et al. 1997; Martin et al. 2007). This interpretation is supported by findings in these children showing improvements in hand function with intense practice even in their adolescent years (Bonnier et al. 2006; Eliasson et al. 2006; Gordon et al. 2007; Kuhtz-Buschbeck et al. 2000). Pilot studies indicate that it is feasible for children with minor impairments, e.g., development coordination disorder and milder forms of cerebral palsy, while it needs to be adapted for more severe forms of disability in which children cannot independently move thumb and index finger. Although the principle of the method could be used for clinical testing, it is far too early to know whether it is possible, and in that case a long development process. Finally, this measurement paradigm may allow one to potentially train children at the “right challenge level” (Plautz et al. 2000) and serve as an intervention paradigm to understand and promote gains in sensorimotor capabilities for dynamic manipulation.

GRANTS

This work was supported in part by National Science Foundation (NSF) Grant EFRI-COPN 0237258, National Institute on Disability and Rehabilitation Research Grant RERC 84-133E2008-8, National Institutes of Health Grants R21-HD-048566, R01-AR-050520, and R01-AR-052345, a Wenner-Gren Foundation Fellowship to visit the Karolinska Institute to F. J. Valero-Cuevas, Foundation Olle Engkvist Byggmästare, Swedish Brain Foundation, Foundation Frimurarna Barnhuset, Swedish Research Council (5925), Swedish Foundation for Strategic Research, VINNOVA, and the Strategic Neuroscience Program at Karolinska Institutet to H. Forssberg.

DISCLOSURES

F. J. Valero-Cuevas holds US Patent No. 6,537,075 on some of the technology used but has no active or pending licensing agreements with any commercial entity.

AUTHOR CONTRIBUTIONS

Author contributions: S.D., Å.H., F.J.V.-C., and H.F. conception and design of research; S.D., Å.H., F.J.V.-C., and H.F. performed experiments; S.D., Å.H., F.J.V.-C., and H.F. analyzed data; S.D., Å.H., F.J.V.-C., and H.F. interpreted results of experiments; S.D., Å.H., F.J.V.-C., and H.F. prepared figures; S.D., Å.H., F.J.V.-C., and H.F. drafted manuscript; S.D., Å.H., F.J.V.-C., and H.F. edited and revised manuscript; S.D., Å.H., F.J.V.-C., and H.F. approved final version of manuscript.