Calculation of ion currents across the inner membrane of functionally intact mitochondria

Abstract

Mitochondrial ion transport systems play a central role in cell physiology. Rates of Ca²⁺ and K⁺ transport across the inner mitochondrial membrane have been derived from the measurement of ion accumulation over time within functional isolated mitochondria or mitochondria of cultured cells. Alternatively, the electrical currents generated by ionic flux have been directly measured in purified and swollen mitochondrial samples (mitoplasts) or reconstituted channels, and typically range from 1 pA to several 100s pA. However, the direct electrophysiological approach necessarily requires extensive processing of the mitochondria prior to measurement, which can only be performed on isolated mitoplasts. To compare rates of mitochondrial ion transport measured in electrophysiological experiments to those measured in intact mitochondria and cells, we converted published rates of mitochondrial ion uptake into units of ionic current. We estimate that for monovalent ions, uptake by intact mitochondria at the rate of 1 nmol ∙ mg⁻¹ protein ∙ min⁻¹ is equivalent to 0.2 fA of current per whole single mitochondrion (0.4 fA for divalent ions). In intact mitochondria, estimated rates of electrogenic cation uptake are limited to 1–100 fA of integral current per single mitochondrion. These estimates are orders of magnitude lower than the currents through mitochondrial channels directly measured via patch-clamp or artificial lipid bilayer approaches.

Introduction

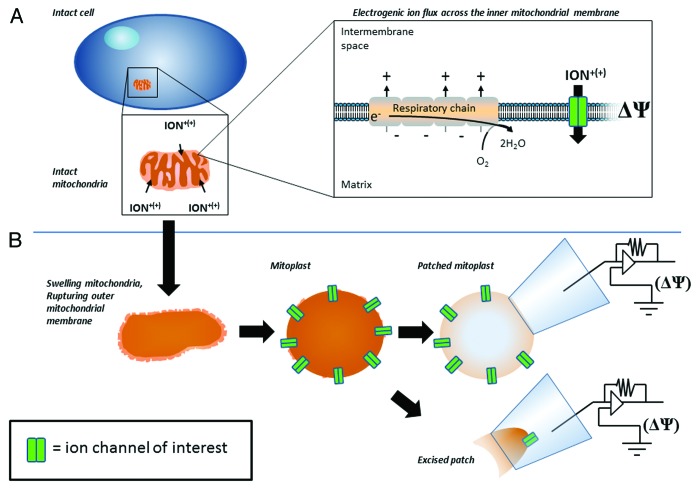
It is well established that mitochondria possess an elaborate system of ion transport. This ion transport has been studied in great detail at the level of isolated mitochondria, and more recently in intact cells. Key ions transported by mitochondria include K⁺, Na⁺, and Ca²⁺. Experiments involving isolated mitochondria established that mitochondrial Ca²⁺ and K⁺ uptake is an electrogenic process, meaning that the driving force for the transport of these ions is provided by the mitochondrial membrane potential (ΔΨ; Fig. 1). The mitochondrial ΔΨ is generated and maintained by the mitochondrial respiratory chain (reviewed in ref. 1). More recent studies employing patch-clamp of mitochondrial membranes, and electrophysiological studies using reconstituted mitochondrial components in artificial bilayers (BLM), generated substantial experimental evidence for the presence of ion-selective channels in the mitochondrial inner membrane.^2-4 Presently, it is well accepted that mitochondrial uptake of Ca²⁺ and K⁺ observed in intact cells and isolated mitochondria likely occurs through specific ion channels.^5,6 However, it is reasonable to expect the kinetics of the channel observed in electrophysiological experiments to reflect the kinetics of the channel in the native system. For example, studies of the voltage-gated ion channels responsible for generating action potentials in cell membranes demonstrate that the kinetics of the channel activity in model patch-clamp experiments is fully consistent with the role of these channels in generating the action potentials observed in vivo.^7,8 Unfortunately, it is not possible to make such a direct comparison in experiments aimed at studying mitochondrial ion transport. Studying a mitochondrial channel of interest requires one to first disintegrate the cell and isolate the mitochondria. Next, in order for the patch pipette to access the mitochondrial inner membrane, the mitochondria must be swollen to rupture the outer mitochondrial membrane. These manipulations raise the obvious issue of whether, or how closely, the channel activity observed with patch-clamp corresponds to the in vivo situation. The matter is further complicated by the fact that, unlike studying action potentials, which can be easily detected in live cells, it is not as straightforward to experimentally measure the activities of the mitochondrial ion transport system. However, although it is technically impossible to directly measure ionic current in functional individual mitochondria, it is possible to estimate the values of these currents based on the measurements of the total number of ions transported into the mitochondria in experiments involving large mitochondrial populations. Here, we mathematically transform published rates of ion accumulation into the expected values of ionic currents in intact mitochondria. We estimate that ionic currents in intact mitochondria are several orders of magnitude less than the currents directly measured in electrophysiological experiments performed at the level of purified mitochondrial inner membranes. This raises important questions about how mitochondrial channels (or other transporting systems) function and are regulated under physiological conditions of the intact organelle.

Figure 1. General overview of the 2 methods used to quantify mitochondrial ion transport, compared in the present report. Both methods begin with rupturing the intact cell to obtain mitochondria. (A) The method using intact mitochondria. Determining mitochondrial ion uptake involves isolating intact mitochondria and measuring the total amount of ions transported into the organelle after a given amount of time. In intact mitochondria, the electrogenic uptake of ions is dependent upon the driving force of the mitochondrial membrane potential (ΔΨ), which is established by the activity of the respiratory chain. (B) The direct method of measuring mitochondrial ion flux across the inner mitochondrial membrane. This method involves first swelling, and rupturing the outer mitochondrial membrane. The patch pipette can either be attached to the resulting mitoplast, or a portion of the mitoplast can be excised for direct measures of ionic currents generated by ionic flux through channel of interest. It is important to highlight that the voltage applied via the patch pipette is analogous to the ΔΨ in intact mitochondria, in that it provides the driving force for ionic uptake.

Results

The past several decades have seen mounting data published from measurements of ion transport in intact mitochondria and also the characterization of mitochondrial ion channels. The values used in our calculations are representative of those frequently reported in the literature for Ca²⁺, K⁺, and Na⁺. The values used for the rates of ion uptake in intact mitochondria can be found in references 1,9,10, while the typical values of ion current observed in patch-clamp experiments can be found in references 3,4,11.

How can rates of the mitochondrial ion transport be compared among methodologies?: Determination of the conversion factor

Most of the experiments measuring ion transport in intact mitochondria have been performed by measuring the integral uptake of ions by large populations of the isolated organelles. In these experiments, ionic uptake is measured in freshly isolated intact mitochondria, placed into a physiological solution, and energized by addition of substrates for the respiratory chain (i.e., oxidative phosphorylation). Traditionally, the rates of ion flux in intact mitochondria are reported in units of nmol ∙ mg⁻¹ protein ∙ min⁻¹;³ that is, a quantity of ions (in nmol) transported across the mitochondrial inner membrane per minute by the mitochondria of the amount of 1 mg of protein. This value reflects the total ionic uptake by all the mitochondria present in the recording cuvette. Conversely, patch-clamp experiments directly measuring ion transport are performed either at the level of a single, swollen mitochondrion (mitoplast), or single-channel excised patch-clamp in which a portion of the mitochondrial inner membrane is removed and patched (Fig. 1). To perform these experiments, mitochondria are first isolated and re-suspended in a low osmotic solution. This causes the mitochondria to swell and rupture the outer membrane, leaving vesicles of the inner membrane (mitoplasts). Though destructive, this maneuver is essential in order for the patch-clamp pipette to reach the mitochondrial inner membrane to perform direct ion current measurements. Due to the nature of these electrophysiological measurements, the results of experiments employing the approach are expressed as electrical current (usually picoamperes, pA) generated by the ionic flux across the reconstituted mitochondrial membrane or ion channel.³

The electrogenic (i.e., ΔΨ-dependent) mechanism of mitochondrial ion uptake is well established for Ca²⁺ and K⁺ flux through the Ca²⁺ uniporter and mitochondrial K⁺ channels, respectively. Indeed, while concentration gradients undoubtedly drive movement of ions, it should be noted that [Ca²⁺] in vivo, for example, is similar between the cytosolic and matrix compartments (i.e., 100–300 nM) at rest.^12,13 Thus, accumulation of free Ca²⁺ in the mitochondrial matrix requires ΔΨ as a driving force. Because mitochondrial ion flux is electrogenic, the uptake of ions by the mitochondria will generate an ionic current in direct proportion to the number of ions transported. With this idea in mind, we performed calculations to estimate the current (pA) expected to exist in intact mitochondria during active ionic uptake.

Calculations were performed with the following rationale: (1) Previous studies provide a relatively precise estimate of the number of mitochondria per one mg of protein in the mitochondrial isolation preparation. This number is estimated to be in the range of 7 to 9 billion mitochondria per 1 mg protein (Table 1).^14,15

Table 1. Literature estimates of mitochondrial content in tissues.

References	Source of isolated mitochondria	Estimated mitochondria per mg
Estabrook and Holowinsky. J Biophys Biochem Cyto., 9(1): 19–28, 1961; citations 4,5 within	rat liver	7.2 ∙ 109
Schwerzmann, et al. J Cell Biol. 102: 97–103, 1986	rat liver	7 to 9 ∙ 109

(2) Standard physical constants necessary for the calculations are as follows: Avogadro’s number (1 mol of molecules = 6 ∙ 10²³); 1 coulomb = 10⁻⁵ mol of charge (this is the inverse of the Faraday constant); current is expressed in units of amperes (A), where 1 A = 1 Q ∙ 1 s⁻¹. Thus, the flux of 10⁻⁵ mol ∙ sec⁻¹ is equivalent to 1 A of current for monovalent, and 0.5 ∙ 10⁻⁵ moles ∙ s⁻¹ for divalent ions. Because one divalent ion carries 2 charges, half the number of divalent ions would generate the same current.

(3) The basic conversion coefficient used to re-calculate nmol ∙ mg⁻¹ protein ∙ min⁻¹ into pA ∙ mitochondrion⁻¹ can be determined using the above mentioned constants and relationships. For simplicity, we use the value of 8 ∙ 10⁹ mitochondria per 1 mg protein. 10⁻⁹ mol ∙ mg⁻¹ protein ∙ min⁻¹ is equivalent to 10⁻⁹ ∙ (8 ∙ 10⁹)⁻¹ = 0.1 ∙ 10⁻¹⁸ = 10⁻¹⁹ mol ∙ min⁻¹ of charge flux per single mitochondrion. Because 10⁻¹⁹ mol ∙ min⁻¹ is equivalent to 0.02 ∙ 10⁻¹⁹ mol ∙ sec⁻¹ of ion flux per single mitochondrion, or 2 ∙ 10⁻²¹ mol ∙ sec⁻¹, we will consider that 2 ∙ 10⁻²¹ mol ∙ sec⁻¹ is the ionic flow through a single mitochondrion. If we then consider that 10⁻⁵ mol ∙ sec⁻¹ is 1 A, then 2 ∙ 10⁻²¹ ∙ (10⁻⁵)⁻¹ = 2 ∙ 10⁻¹⁶ A is the amperic flux through a single mitochondrion equivalent to 1 nmol ∙ mg⁻¹ protein ∙ min⁻¹. Note: these calculations assume that mitochondria are approximately the same size.

In summary, the rate conversion constant used to estimate ionic current in functional mitochondria is the following: 1 nmol ∙ mg⁻¹protein ∙ min⁻¹ = 2 ∙ 10⁻¹⁶A (0.2 fA) for monovalent ions, and 4 ∙10⁻¹⁶ A (0.4 fA) for divalent ions per single mitochondrion.

What are the values of ion current in the intact isolated mitochondria?

The calculation derived in the previous section allows us to translate mitochondrial electrogenic ion (i.e., K⁺, Na⁺, Ca²⁺) fluxes from the units reported in the literature into units of current. As an example, we use typical values summarized in the review by Paolo Bernardi¹ and will use the value of 200 mV as an approximation for the typical values^16,17 of the mitochondrial membrane potential:

(1) Na⁺ uniporter: 40 nmol ∙ mg⁻¹ protein ∙ min⁻¹ = 80 ∙ 10⁻¹⁶ A = 0.8 ∙ 10⁻¹⁴ A = 0.008 pA at 200 mV of integral current per mitochondrion (channels unknown). (2)K⁺ uniporter: 22 nmol ∙ mg⁻¹ protein ∙ min⁻¹ = 0.004 pA at 200 mV of integral current per mitochondrion (several ion channels are proposed to play the role in electrogenic K⁺ uptake). (3) Ca²⁺ uniporter: 1400 nmol ∙ mg⁻¹ protein ∙ min⁻¹ = 0.6 pA, the theoretical maximum Ca²⁺ uniporter current per whole mitochondrion. Typical rates measured in isolated rat liver mitochondria are 50 to 640 nmol ∙ mg⁻¹ protein ∙ min⁻¹, with the estimated current less than 0.3 pA.^18-20

Mitochondrial ion channel current

Readers are referred to Table 1 of reference ³, which summarizes the sizes of mitochondrial ion channels. Overall, the smallest single channel identified by patch-clamp would generate about 1 pA at 200 mV, with some K⁺ channels generating currents of up to 200 pA per single ion channel. It should be noted that although it is somewhat problematic to estimate the number of single channels per single mitochondrion, it is clear that a single mitochondrion would have more than one channel of a certain type. For example, it has been estimated that a single mitochondrion would have ~40 single Ca²⁺ uniporter channels.²¹ Therefore, we can expect that in functional mitochondria under physiologically relevant conditions, the maximal ion flux across a single mitochondrial Ca²⁺ channel, which is believed to function as a uniporter, under conditions of high membrane potential (i.e., ~200 mV) to not exceed 0.03 pA.

What limits the rates of ion uptake by the mitochondria?

It is important to note that rate of K⁺ transport measured in the intact mitochondria might reflect so-called “leak” K⁺ conductance, as opposed to “induced” conductance (e.g., ATP-dependent K⁺ transport).²² The K⁺ channels described in the literature cannot explain such slow kinetics. However, it is conceivable that channels like the mitoK_ATP channel or large K⁺-Ca²⁺ channels might be activated for brief periods of time under specific conditions. While K⁺ transport rates in response to the opening of these channels cannot be easily quantified at the level of intact mitochondria, the upper limits of these rates can be estimated from the activity of the respiratory chain.

It should be noted that the mitochondrial ΔΨ generated by the respiratory chain, and not the Nernst equilibrium potential for each ion across the inner membrane, is the principal driving force responsible for mitochondrial ion transport. Active mitochondrial ion uptake in intact cells and isolated mitochondria has been observed without a significant change in the mitochondrial ΔΨ. This implies that the activity of the respiratory chain is greater than the rate of ion transport. Indeed, if this were not the case, electrogenic ion uptake would depolarize the mitochondria. This fact allows us to estimate the greatest rate of ionic uptake which could occur without depolarizing the mitochondria—more specifically, the maximal activity of the mitochondrial respiratory chain.

To estimate maximal mitochondrial ionic uptake, we assume that the maximal rate of the respiratory chain proton flux is the limiting step for maximal ion transport. The maximal rate of the proton flux has been estimated to approximate 40 nmol ∙ mg⁻¹ protein ∙ min⁻¹.¹ Applying the calculations presented earlier in the present study, such a proton flux is enough to sustain a current of 0.008 pA per single mitochondrion.

Obviously, if a channel with current greater than 0.008 pA opens in the inner mitochondrial membrane, it would depolarize the membrane. As an example, we can calculate the charge necessary to depolarize the mitochondrial membrane by 100 mV of a single mitochondrion with capacitance equivalent to ~1 pF. For our calculations, we can use the following relationship: V = Q ∙ C⁻¹; or Q = V ∙ C, the standard “charging capacitor” formula. This relationship will give us a charge needed to flow through the membrane with capacitance C to depolarize it by V volts: Q = 0.1 V ∙ 10⁻¹² f = 10⁻¹³ coulombs 1 A = 1 coulomb ∙ s⁻¹

Thus, for example, a current of 0.1 pA would depolarize the mitochondrial membrane within 1 s. We therefore conclude that in mitochondrial ion uptake experiments which do not show detectable membrane depolarization, the rates of mitochondrial ion uptake cannot exceed 0.016 pA.

The rate of ion transport by mitochondria in intact cells

While the measured rates of ion transport of mitochondria in intact cells is indirect in nature, and cannot be readily quantified, it is still possible to estimate its order of magnitude during physiological Ca²⁺ signaling conditions. Under conditions intended to mimic a physiological Ca²⁺ load, the increase in the Ca²⁺ concentration in the mitochondrial matrix is proportional to the amount of Ca²⁺ transported by the mitochondria, with no significant buffering taking place.²³ It has also been shown that, for example, during ATP-stimulated Ca²⁺ uptake in the mitochondria of HeLa cells, the concentration of free Ca²⁺ inside the mitochondrial matrix rises from a level below 1 μM to approximately 10 μM in under 5 s.²⁴ Morphological studies estimate the volume of the mitochondrial matrix to approximate 1 μL per 1 mg protein, and equate 1 mg of protein with between 7 and 9 billion single mitochondria. The volume of a single mitochondrion is therefore estimated to be on the order of 10⁻¹⁵ to 10⁻¹⁶ L. Thus, it is relatively simple to estimate that in order for free Ca²⁺ to increase from 1 to 10 μM, the total Ca²⁺ uptake is expected to be between 1000 and 10,000 Ca²⁺ ions. If this mitochondrial Ca²⁺ uptake were to occur in 1 s, this would mean the ionic current of intact cells linked to the integral activity of the uniporter is about 50 fA per mitochondrion, or about 5 fA per single uniporter channel. Interestingly, this number is several orders of magnitude less than expected based on measured currents through the uniporter channel. However, it is on the same order of magnitude as the rate obtained for the integral uniporter current per whole mitochondrion observed in isolated mitochondria, where the rate of 100–200 nmol ∙ mg⁻¹ protein ∙ min⁻¹ translates into a rate of 40–80 fA.

Potential Explanations for the Discrepancies between Directly and Indirectly Determined Rates of Mitochondrial Ion Flux

Among the original postulates of the Mitchell chemiosmotic theory of mitochondrial energy transduction was the relative impermeability of the mitochondrial inner membrane to ions: “The charge-impermeable membrane would…be an absolute requirement for tight coupling.”²⁵ Our calculations are consistent with the idea that ionic currents in intact mitochondria are indeed very small. Based on experimental data available in the literature, it is difficult to identify specific explanations for the observed discrepancy in the rates of ion fluxes among methodologies. The central goal of the present work was to provide a quantitative comparison between 2 approaches, rather than outline potential mechanisms underlying the differences. However, we can offer 2 important possibilities.

The most obvious explanation is that the probability of an ion channel opening is dramatically lower in the experimental conditions used to assess the intact mitochondria vs. those used to assess mitoplasts (i.e., patch-clamp). If this assumption is correct, one would expect that most of the mitochondrial channels in the intact, native condition will be closed most of the time, with only transient opening events. While this explanation may appear self-evident, we should point out that currently, there is no direct experimental means of detecting such a transient channel opening in the intact organelle. Theoretically, these brief channel opening events in intact mitochondria could be detected using microscopic imaging approaches to monitor fast voltage-sensitive fluorescent probes. Based on the calculations presented in the current report, we predict that channel opening would result in transient mitochondrial membrane depolarization; this would be similar to the depolarizing effect of channel openings involved in the generation of action potentials on cell membranes. However, this mitochondrial membrane depolarization is expected to be very brief due to the fast restoration of the membrane potential following channel closure by the activity of the respiratory chain. Such short depolarization events cannot be detected by currently available mitochondrial membrane potential-sensitive probes (e.g., TMRM). However, recent advances in the development of fast voltage-sensitive probes allow detection of relatively brief “spiking” depolarization events in bacteria.²⁶ If targeted to the mitochondria, perhaps these probes might permit the detection of transient channel openings, and in turn allow direct experimental investigation of channel function in the intact organelle.

Another possible explanation for the discrepancy among intact mitochondria vs. mitoplasts is that in many cases, channel activity observed via patch-clamp pipette might be specific to the mitoplast configuration. Indeed, the mitochondrial inner membrane is known to contain multiple transporting proteins which can potentially undergo conformational changes during mitochondrial swelling and/or channel purification, thereby exhibiting ion “channel-like” activity, which is not necessarily present in the intact mitochondria. Thus, perhaps additional means of mitochondrial ion transport and/or regulation that have yet to be discovered or popularized, and which are not currently detectable using conventional electrophysiological approaches. Endogenous non-channel ionophores are among the potential means of mediating and/or regulating mitochondrial ionic flux in vivo.^27,28 Ultimately, testing these hypotheses electrophysiologically will require new methodologies capable of detecting ionic currents at the sub-pA level.

Summary

Using simple calculations, we have directly compared the rates of mitochondrial ion transport measured by different experimental approaches. We conclude that the rates of ion transport in intact mitochondria are an orders of magnitude lower than can be expected from the estimates based on electrophysiological data. Specifically: (1) based on direct patch-clamp assays, the Ca²⁺ uniporter is expected to generate a current equivalent to approximately 50 pA per single mitochondrion,²¹ with some recent papers reporting even higher values.^29,30 The estimated maximal uniporter current across the membrane of the functional, intact organelle is expected to be only about 0.1 pA. Furthermore, the uniporter Ca²⁺ flux in the mitochondria of intact cells is estimated to be on the order of 0.005 pA. (2) Electrophysiological investigations of K⁺ transport indicates the presence of ion channels capable of conductance currents in the range of 1–2 pA, to upwards of 100s pA. However, in intact mitochondria, K⁺ transport is estimated to generate currents on the order of 0.004 pA. Moreover, these channels (e.g., mitoK_ATP) are likely open only upon specific stimuli (e.g., ATP) and cannot account for slow mitochondrial K⁺ uptake. (3) While it is difficult to quantify K⁺ transport in intact cells, maximal mitochondrial ion transport is limited by the activity of the respiratory chain. Therefore, electrogenic transport of K⁺ by the mitochondria exceeding 0.008 pA would inevitably result in mitochondrial membrane depolarization.

10.4161/chan.26290