Energy storage inherent in large tidal turbine farms

Abstract

While wind farms have no inherent storage to supply power in calm conditions, this paper demonstrates that large tidal turbine farms in channels have short-term energy storage. This storage lies in the inertia of the oscillating flow and can be used to exceed the previously published upper limit for power production by currents in a tidal channel, while simultaneously maintaining stronger currents. Inertial storage exploits the ability of large farms to manipulate the phase of the oscillating currents by varying the farm's drag coefficient. This work shows that by optimizing how a large farm's drag coefficient varies during the tidal cycle it is possible to have some flexibility about when power is produced. This flexibility can be used in many ways, e.g. producing more power, or to better meet short predictable peaks in demand. This flexibility also allows trading total power production off against meeting peak demand, or mitigating the flow speed reduction owing to power extraction. The effectiveness of inertial storage is governed by the frictional time scale relative to either the duration of a half tidal cycle or the duration of a peak in power demand, thus has greater benefits in larger channels.

1. Introduction

A big challenge for many renewable energy sources is being able to deliver power when it is required. While energy from wind and solar farms can meet a substantial fraction of the need for renewable alternatives to fossil fuels, these renewable energy sources have no inherent way to store energy that can be used to meet demand during calm periods or at night. To use such sources during these times requires expensive and inefficient secondary storage systems, such as batteries, otherwise demand must be met by supplementing supply from other sources, such as fossil fuels. Underwater turbines in the strong flows through tidal channels have the potential to produce significant power to meet the demand for renewable energy [1]. While the timing of power production by tidal turbines is highly predictable, they cannot produce power when currents are weak during the change between ebb and flood tides. Like wind turbines, tidal turbines appear to lack any inherent storage and thus also appear to be dependent on expensive and inefficient secondary storage to meet demand during periods of weak tidal flows.

While a single tidal turbine produces power at times determined by the prevailing tidal currents, surprisingly, this paper shows that large tidal turbine farms in channels have a degree of energy storage which allows some control over when power is produced. This short-term storage lies in the inertia of the oscillating tidal flow. Inertial storage is much more complex than just retaining the energy until it is needed, i.e. ‘fly wheel’ storage. For tidal inertial storage, the longer the delay in extracting the energy, the greater the total energy that can be extracted, though the maximum delay is limited by bottom frictional losses and the reversal of the tidal forcing. In large channels, it is theoretically possible to use inertial storage to significantly exceed the limit on tidal current power production given by Garrett & Cummins [2], hereafter GC05 ([3] extends their result to two-dimensions). To achieve the GC05 limit with a constant drag coefficient farm requires flow speeds to be reduced by 29–42% throughout the tidal channel. Thus, there is an inherent compromise between the fraction of the GC05 limit which can be extracted from the channel and the environmental impacts of the associated flow speed reduction [4], such as reduced sediment transport [5]. This work shows that farms can both exceed the GC05 limit and have average flow speeds stronger than those at the GC05 limit. Thus, along with the possibility of generating more power, or better meeting the timing of demand, inertial storage could also be used to mitigate the environmental effects of large tidal farms by maintaining higher tidal flow speeds along a channel than those of a GC05 farm.

This ability to generate more power or meet peaks in demand comes from optimizing how the farm's drag coefficient varies with time, which manipulates the phase of the tidal currents. Given the scale of the ocean, manipulating the tides sounds fanciful, however, this manipulation occurs within the confines of narrow channels, rather than within the open ocean. Even a small manipulation could give a large tidal turbine farm an advantage over a similarly sized wind farm, when a 1.5% improvement in wind farm output owing to dinosaur-inspired blade modifications is considered significant [6]. To date, two works have considered time-variable farm drag coefficients. Adcock [7] pointed out it is possible to exceed the GC05 potential with a time-variable drag coefficient, whereas in reference [8], Adcock showed that it is possible to produce more power from a channel connected to a lagoon by only operating the tidal turbines during the ebb tide. Here, we present many more benefits of time-variable farm drag coefficients, e.g. maintaining higher flows or meeting peaks in demand, along with providing physical explanations for these potential benefits. This short paper is a first step in outlining the conditions under which inertial energy storage can give a large tidal turbine farm advantages over a large wind farm.

2. Model

This work uses the GC05 model for a channel with a constant rectangular cross section. GC05 models the tidal turbine farm as an enhanced drag coefficient in a short narrow channel which connects two large water bodies, so large that they are unaffected by power extraction within the channel (figure 1). As in [12] (hereafter V10), the starting point for the model is the along-channel, depth-averaged shallow water momentum balance

$$\frac{\mathrm{\partial }u}{\mathrm{\partial }t}+u\frac{\mathrm{\partial }u}{\mathrm{\partial }x}=-g\frac{\mathrm{\partial }\eta }{\mathrm{\partial }x}-\frac{C_{\mathrm{D}}|u|u}{h}-F,$$ 2.1

where u is the tidal velocity, η the free surface elevation and F the additional drag owing to the turbine farm. h is the water depth and C_D the bottom drag coefficient. In dynamically short channels, the mass flow rate does not vary along the channel [9]. Even large channels, such as the 100 km long, 25 km wide Cook Strait NZ, can be dynamically short [10]. Integrating (2.1) across a uniform rectangular channel cross section, where lateral friction can be ignored, and then integrating along a short channel gives a simplified equation ∂u/∂t=g(η|_x=0−η|_x=L)/L−(C_D/h+C_F/L)|u|u. Here, C_F is the drag coefficient owing to the farm based on channel cross-sectional area, and the flow is forced by the water-level difference between the ends of the channel. This can be non-dimensionalized to give GC05's model for short channels which can be written as (see reference [11] for details)

$$\frac{\mathrm{\partial }{u}^{\prime }}{\mathrm{\partial }t}=\sin (t^{\prime })-({\lambda }_0+{\lambda }_{\mathrm{F}}(t^{\prime }))|u^{\prime }|u^{\prime },$$ 2.2

where u′ is the non-dimensional tidal velocity relative to the maximum velocity along the channel without any drag, i.e. relative to the velocity at the inertial limit u_I. λ₀=gΔC_D/ω²h, is a constant rescaled bottom drag coefficient (table 1) and λ_F is the drag coefficient owing to power extraction by the farm. Non-dimensional time, t′, is measured in radians (2π=one tidal cycle), though times will be presented as either a fraction of the tidal cycle or in hours within a 12.42 h long semi-diurnal tidal cycle. Within (2.2), the first term is the acceleration of the flow, and the second is the periodic forcing owing to the water-level difference between the ends of the channel. The last term is the combined drag owing to background bottom friction, and the drag owing to power extraction by the farm. The likely small effects of power extraction on the water levels at the ends of the channel and nonlinear distortion of these water levels are discussed in §5.

Figure 1.

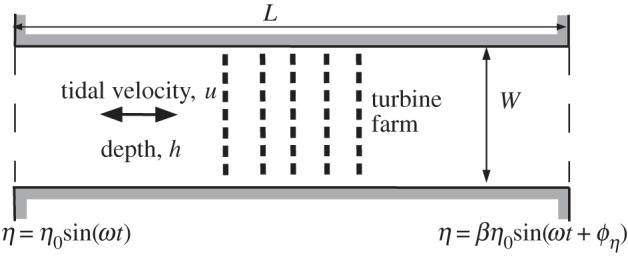
Schematic of tidal channel connecting two large water bodies. The channel has length L and a rectangular cross section with width W and depth h. Flow, u(t) is forced along the channel by a difference in the relative amplitude of tidal water levels β in the two water bodies and/or a difference in the phase of their surface tides ϕ_η.

Table 1.

Example channels loosely based on Cook Strait, NZ and the Pentland Firth, UK plus a hypothetical small tidal channel. More details on the example channels are given in Vennell [4,12,13]. Examples are for semi-diurnal tides ω=1.4×10⁻⁴ rad s⁻¹. η_L is the tidal elevation amplitude at the left hand end of the channel, $\mathrm{\Delta }=\sqrt{1-2\beta \cos {\varphi }_{\eta }+{\beta }^2}$, β is the ratio of the tidal amplitudes at the right- and left-hand ends and ϕ_η is the phase difference in the tidal elevation between the ends of the channel (figure 1).

	large channel, Cook Strait NZ	medium channel, Pentland Firth UK	small tidal channel
length, L (km)	100	20	5
width, W (km)	25	9	1
depth, h (m)	150	50	20
amplitude of head loss between ends ηLΔ (m)	1.6	1.0	0.26
standard drag coeff., CD	0.0025	0.0025	0.0025
rescaled bottom drag coeff., λ0=gΔCD/ω2h	0.1	1.0	2.8
undisturbed channel
peak flow, u0 (m s−1)	1.1	2.7	2.0
velocities phase lag behind forcing (°)	83	51	33
frictional time scale, TD0 (h)	17	2.4	1.3
at GCO5 potential
potential, ${\overline{P}}_{\mathrm{GC}05}$ (MW)	14 000	2300	20
optimal constant drag coeff., λGC05F	1.7	3.5	6.9
importance of farm, λGC05F/λ0	14.6	3.5	2.5
peak velocity, $u_{max}\hspace{0.17em}({\text{ms}}^{-1}$)	0.7	1.5	1.2
frictional time scale (h)	1.7	1.0	0.7
400 m2 turbines to fill cross section	9500	1200	50

The only difference between (2.2) and GC05's model is that the farm's drag coefficient is allowed to vary with time. Existing turbines can vary their blade pitch using motors to limit loads or to stop production when marine mammals approach [14]. It is this ability to vary blade pitch, or the related tip speed ratio, which could be used to vary a farm's drag coefficient. The variation of λ_F with time is optimized to maximize the output of the farm or its ability to meet the demand for electricity. Here, the solutions are presented relative to other solutions, often those from GC05's constant λ_F model, thus using the non-dimensional form of the momentum equation (2.2) makes discussion of the results simpler. Equation (2.2) was solved numerically for the velocity, u′(t′), using the Runge–Kutta fourth-order algorithm with 300 time steps per tidal cycle. Convergence of the numerical solution was tested by solving examples with between 50 and 500 steps per tidal cycle. Above 300, the step size had minimal effect on the solution's maximum velocity, average velocity or the average power output. Vennell [12]'s approximate analytical solution to GC05's constant λ_F model was used as an initial condition, and the model was run repeatedly for a number of tidal cycles until the velocity was periodic.

The non-dimensional power extracted by the farm is expressed as P(t′)=λ_F(t′)|u(t′)|³ and, in this work, the initial interest is in maximizing the power averaged over a tidal cycle

$$\overline{P}=\frac{1}{2\pi }{\int }_0^{2\pi }{\lambda }_{\mathrm{F}}(t^{\prime })|u(t^{\prime }){|}^3\hspace{0.17em}\mathrm{d}{t}^{\prime }.$$ 2.3

In order to maximize the average power output, λ_F(t′) needs to be expressed as a function of a set of coefficients which can then be optimized. As the tidal flow is periodic, λ_F(t′) is expressed as a Fourier series, i.e.

$${\lambda }_{\mathrm{F}}(t^{\prime })=a_0+\sum _{n=1}^N{a}_n\sin (n{t}^{\prime })+b_n\cos (n{t}^{\prime }).$$ 2.4

However, physically, λ_F(t′) cannot be negative. In addition, λ_F(t′) cannot be unrealistically large, as it will be limited by the number of turbines in the farm. Thus, farm optimization is done by maximizing average power (2.3) with constraints, i.e.

$$max\{\frac{1}{2\pi }{\int }_0^{2\pi }[{\lambda }_{\mathrm{F}}(t^{\prime })|u(t){|}^3]\hspace{0.17em}\mathrm{d}{t}^{\prime }\},\text{subjected to}\hspace{0.17em}0\le {\lambda }_{\mathrm{F}}(t^{\prime })\le {\lambda }_{\mathrm{F}}^{max},$$ 2.5

where the constant ${\lambda }_{\mathrm{F}}^{max}$ is a specified maximum permitted farm drag coefficient. This restriction on λ_F(t′) was enforced by optimizing (2.3) subjected to a set of linear inequality constraints on the coefficients based on (2.4) evaluated at the 300 time steps within the model's tidal cycle. Typically, 30 terms were used in the Fourier series representation of λ_F(t′). To speed up the search for the optimal set of coefficients, adjoint methods were used to calculate the components of the partial derivatives of (2.3) with respect to the coefficients in (2.4) [15]. Typically, the maximum ${\lambda }_{\mathrm{F}}^{max}$ was set at the optimal farm drag coefficient for GC05's constant drag coefficient model, i.e. ${\lambda }_{\mathrm{F}}^{max}={\lambda }_{\mathrm{F}}^{\mathrm{GC}05}$, where λ^GC05_F was found by optimizing (2.5) with a_n=b_n=0.

(a). Example channels

Table 1 presents three channels which are used as examples in this paper. The first is loosely based on Cook Strait that separates New Zealand's two main islands and was chosen as an example of a large channel, with λ₀=0.1. Its 14 000 MW GC05 potential is large. This results from the semi-diurnal tide having a 130° phase difference between the ends of the 100 km long Strait driving strong flows over a large cross-sectional area [4,16]. These flows can exceed 3 m s⁻¹ on the eastern side during spring tides. The 20 km long Pentland Firth, UK was chosen as an example of a medium-sized channel. The Firth has several islands and connected channels [17], thus the simplified one-dimensional channel version used here should be seen as a channel of the same scale as the Firth, rather than as an accurate model for power extraction from the complex set of channels which make up the Firth. The strong tidal currents through the Firth, which lies to the south of the Orkney Islands, have a considerable potential for tidal current power generation Bryden & Couch [18], Adcock et al. [17], Draper et al. [19]. The values in the table 1 are based on a bottom drag coefficient of 0.0025 which Adcock et al. [17] found best fit the observations in the Firth. This value matches the standard bottom drag coefficient, though for their definition of bottom drag the standard value is 0.005. Recent works have modelled the Firth estimating the undisturbed volume transport owing to the M2 tide at 1.1×10⁶ m³ s⁻¹ and for M2 tides λ₀≈1.0 [19,20]. The dimensions of the example loosely based on the Firth in table 1 have been chosen to match these values for C_D, volume transport and λ₀. The result is peak undisturbed flows of 2.7 m s⁻¹ which is reasonable, but the estimated potential of 2.3 GW is less than the 4 GW based on the more realistic two-dimensional model of Draper et al. [19]. However, a value of λ₀=1.0 provides an example representative of a channel where inertia and bottom friction are of equal importance in the undisturbed channel. The third example is a hypothetical small channel just 5 km long and 20 m deep, with λ₀=2.8. The results in this work are presented for an average tide, i.e. the M2 constituent which dominates within these channels, thus the λ₀ for the channels are only indicative and may vary over the spring–neap tidal cycle. The relative importance of the farm within the channel's dynamical balance can be gauged by the ratio λ^GC05_F/λ₀, which is given in table 1. Values range from around 15 for Cook Strait to around 3 for the Firth and the small channel. Thus, in all three examples, the force exerted by an optimal GC05 farm is significantly larger than the force owing to background bottom friction.

3. Exceeding the GCO5 limit on power production

(a). The extreme case

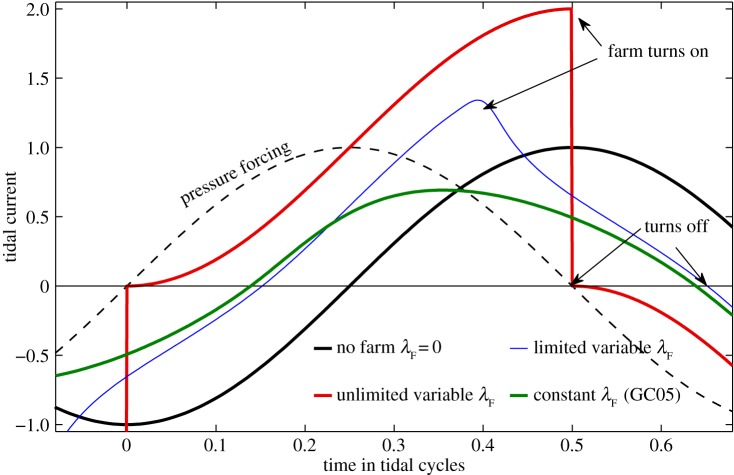
It is useful to consider the extreme case of a farm in a channel with no bottom friction when there is no constraint on the size of the farm and its drag coefficient, i.e. λ₀=0 and ${\lambda }_{\mathrm{F}}^{max}=\mathrm{\infty }$. In this case, it is possible to intuitively derive the optimal time-dependent farm drag coefficient and the velocity along the channel, which is given by the red curve in figure 2. For the extreme case, the farm is so large that power extraction can be used to reduce the velocity to zero at t=0. No more power is extracted until the end of the half tidal cycle at t=0.5. During the half tidal cycle, the flow is accelerated by the forcing owing to the water-level difference between the ends of the channel given by the black dashed line, resulting in the red velocity curve in figure 2. The acceleration of the flow is exactly the same as that for the flow in the undisturbed channel, whose velocity is shown by the solid black curve. The only difference is that the extreme farm has changed the phase of the velocity by reducing the starting velocity to zero. Flows in both the extreme case and the undisturbed channel undergo an acceleration of two units during the half tidal cycle, with the final velocity in the extreme case being twice that of the undisturbed channel. The average power generated by the extreme case is easily calculated by multiplying (2.2) by the velocity and integrating to give the average rate of work done on the flow by the forcing over the half tidal cycle ${\int }_0^{\pi }(1-\cos (t))\sin (t)\hspace{0.17em}\mathrm{d}t/\pi$, which is equal to 2/π.

Figure 2.

Velocity solutions to (2.2) which maximize average power (2.3) for λ₀=0. Red curve is the intuitively derived extreme case solution for ${\lambda }_{\mathrm{F}}^{max}=\mathrm{\infty }$, blue curve is the optimal solution to (2.2) for ${\lambda }_{\mathrm{F}}^{max}={\lambda }_{\mathrm{F}}^{\mathrm{GC}05}$ and the green curve is GC05's optimal solution for constant λ_F. Velocities are relative to the peak flow in the channel when there is no farm.

GC05's model is shown by the green curve in figure 2. The constant drag coefficient which maximizes the average power (2.3) of a GC05 farm gives 0.24 units of power (slightly less than the 0.25 from Vennell [12]'s approximate analytical solution to (2.2), for which the peak non-dimensional flow speed is $1/\sqrt{2}$). The extreme variable λ_F farm can produce around 8/π or 2.5 times more power than a GC05 farm with its constant λ_F.

Not only does the extreme case significantly exceed the GC05 limit on power production, the peak tidal flow in the channel is around $2\sqrt{2}$, or 2.8 times stronger. In addition, the average current speed during the half cycle in the extreme case is one unit, over twice as strong as the average speed of 0.45 for a GC05 farm. Superficially, this appears to violate the laws of physics, producing more energy from the currents, while making the average current speed much stronger. So strong, that peak flow speed is twice that in the channel with no farm, whereas the speed averaged over the half cycle equals the peak flow in the undisturbed channel (figure 2). The resolution of this paradox lies in realizing that the extreme farm's energy source lies in the changing of the phase of the velocity relative to the forcing by extracting power only at the end of each half tidal cycle.

The inertial storage mechanism is more than a simple fly wheel, as the forcing continues to accelerate the flow through the half cycle. Delaying extraction increases the total power that can be extracted. It is possible to generate additional power only in channels where inertia in the undisturbed channel's dynamical balance results in a lag between the velocity and the forcing, providing scope to manipulate the velocity's phase using a variable farm drag coefficient. In the extreme case, λ₀=0 and, the lag is 90° in the undisturbed channel. Extracting power increases the total drag and shifts the velocity phase to be closer to that of the forcing. A variable λ_F farm manipulates this shift to extract more power. There is little scope to manipulate the phase in order to extract more power in quasi-steady-state channels, λ₀>2, as inertia is not important and forcing and velocity are already almost in phase.

Inertial storage in a channel connecting two very large water bodies is very different to a tidal barrage across a channel linking an ocean to a lagoon. A lagoon can be used to store potential energy, as opposed to storage in the flow's inertia as discussed here for channels without lagoons. An extreme barrage in a channel as used here could exploit potential energy stored within the channel by allowing water to rapidly flow through turbines within the barrage when the water level difference is greatest. However, the short channels used here have no lagoon and have a tidal prism which is small compared with the volume of water flowing along the channel during a half tidal cycle [9]. Thus, for short channels, the potential energy available within the channel from an extreme barrage will be much smaller than the kinetic energy available from the extreme inertial storage farm. Consequently, barrage and inertial storage are not directly comparable in the channels used here.

(b). Limited variable farm drag coefficient, λ_F, and the effect of bottom friction, λ₀

In the extreme case, the farm must have an extremely large drag coefficient and withstand huge loads in order to stop the flow at the end of the half cycle. Clearly, such a large farm would not be built. A more useful question is: is it possible to exceed the GC05 limit if the farm's drag coefficient is limited to the same value as that required to optimize power production in GC05's constant λ_F model? i.e. if ${\lambda }_{\mathrm{F}}^{max}={\lambda }_{\mathrm{F}}^{\mathrm{GC}05}$. The blue curve in figure 2 shows that the peak velocity, in this case, still significantly exceeds the GC05's peak flow speed and is also stronger than the peak flow in the channel without a farm.

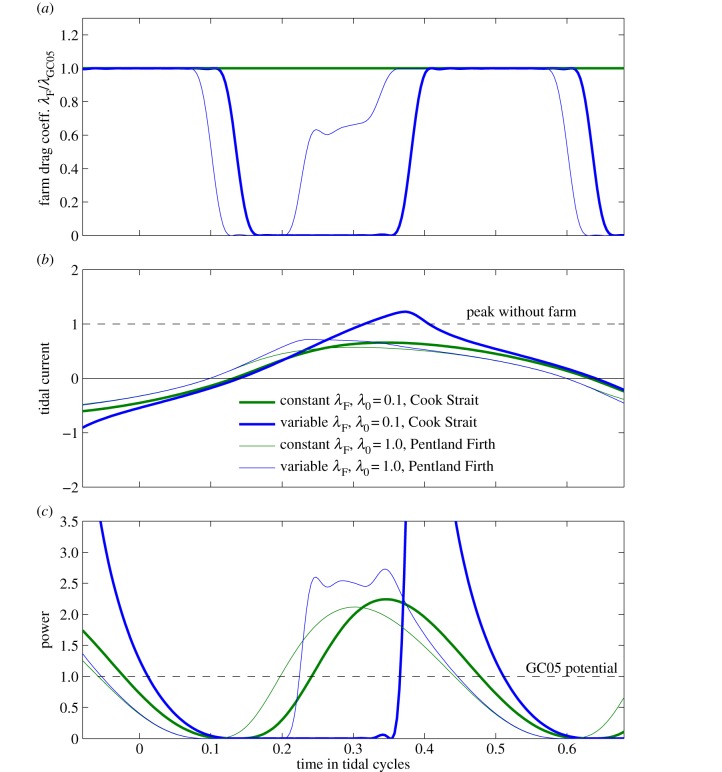
The Cook Strait example, λ₀=0.1, in figure 3, is near to the extreme case. Optimal farms in the Strait have only ‘on’ and ‘off’ phases (figure 3a). The ‘on’ phase of λ_F(t′) extracts power near the end of the half cycle. The power-extracted curve is a smoothed version of the extreme case, rapidly rising, with a slower decay in power production at the end of the ‘on’ phase (figure 3c). The average of this spike in power production is 1.3 times GC05's potential, which is less than in the extreme case, owing to the limit on λ_F. However, delaying extraction still allows the limited variable drag coefficient farm to exceed GC05's limit. For the Pentland Firth, example peak power for a variable λ_F farm is slightly higher than that of the GC05 farm, and spread over a longer period, thus also exceeds the GC05 limit. For the Firth, the optimal drag coefficient appears to have two steps with small oscillations (figure 3d). These small oscillations were reduced if more terms were used in the Fourier series (2.4), suggesting the oscillations may be a Gibbs' phenomenon associated with a step change in λ_F(t′). The two-step optimal drag coefficient occurred only around λ₀=1, becoming a single step above λ₀=2. This suggests that for high and low λ₀ the optimal λ_F(t′) is simply ‘on’ or ‘off’. More work is needed to understand this two-step character of λ_F(t′) for intermediate values of λ₀.

Figure 3.

Limited variable drag coefficient and constant drag coefficient farms which maximize average farm output (2.3) in two of the example channels. Blue lines are for optimal variable drag coefficient with ${\lambda }_{\mathrm{F}}^{max}={\lambda }_{\mathrm{F}}^{\mathrm{GC}05}$ and green lines are for GC05's optimal constant drag coefficient. Thick lines are for Cook Strait, and thin lines are for the Pentland Firth. (a) Optimal variable farm drag coefficient λ^opt_F(t′) relative to λ^GC05_F for each channel. (b) Tidal current relative to the peak flow in the undisturbed channel. (c) Instantaneous power production of the farm relative to GC05's potential for each channel, ${\overline{P}}_{\mathrm{GC}05}$.

Figure 4a shows that as bottom friction becomes more important in the channel's dynamical balance, the average power production achieved by optimizing a variable λ_F decreases asymptotically towards the power from a constant λ_F farm. Adcock [7] used a figure similar to figure 4a, based on a Fourier series (2.4) with two to six terms, to demonstrate how it is possible to exceed the GC05 limit. The additional power from the variable λ_F farm in Cook Strait with ${\lambda }_{\mathrm{F}}^{max}={\lambda }_{\mathrm{F}}^{\mathrm{GC}05}$ is large, around 30%. However, this falls to 5% if the farm is only large enough to have ${\lambda }_{\mathrm{F}}^{max}=0.5{\lambda }_{\mathrm{F}}^{\mathrm{GC}05}$. For the Firth, the benefits are small, 3 and 1% for the given cases of ${\lambda }_{\mathrm{F}}^{max}$. Although for λ₀>1 the additional power from a variable λ_F farm is modest, figure 4b demonstrates that they can be used to maintain significantly higher peak and average flow speeds across a wide range of λ₀, despite producing more power than a constant λ_F farm. For λ₀<0.4, peak flows for an inertial storage farm even exceed those in the channel without a farm. Not only are peak flow speeds higher in an inertial storage farm than those in a constant λ_F farm, the dashed lines in figure 4b show that current speeds averaged over a half tidal cycle are also higher. Thus, while any additional power production in a variable λ_F farm is limited to large channels, with λ₀<1, surprisingly, the inertial storage farm has average flows significantly stronger than a constant λ_F farm for channels with λ₀<2. Thus, over a wide range of channel sizes a variable λ_F farm can still be used to reduce flow speeds less than those of a constant λ_F farm.

Figure 4.

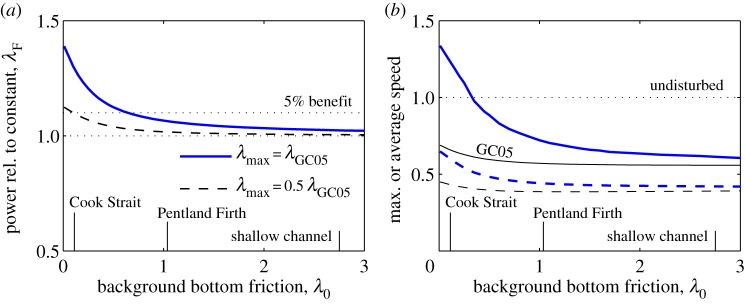
The effect of increasing bottom friction on power production by farm with optimal variable drag coefficient. Labels show λ₀ for the three example channels. (a) Average power relative to a constant drag coefficient farm with given ${\lambda }_{\mathrm{F}}^{max}$; (b) velocities relative to the velocity in channel with no farm at given λ₀. Solid lines show peak flow and the dashed lines the flow speed averaged over a tidal cycle. (Online version in colour.)

4. Meeting the timing of demand

The use of inertial storage to increase power production exploits the ability to delay power extraction until the end of the half tidal cycle. Any delay is limited by the time scale of frictional dissipation, which for larger channels, with λ₀<1 is longer than the half cycle, (5.2) and table 1. Here, we demonstrate that inertial storage can be used to better meet predictable peaks in demand which have time scales shorter than the half tidal cycle. For example, peaks in demand owing to domestic use of electricity. These peaks typically occur around 07.00 and 19.00 and span approximately 2 h. Meeting as much of the demand as possible is simply achieved in the model of §2 by including additional constraints on the coefficient of λ_F(t′) in (2.4), with (2.3) now being maximized subject to nonlinear constraints which require power production to be less than or equal to a specified demand at each time step of the numerical model, i.e.

$$max\{\frac{1}{2\pi }{\int }_0^{2\pi }[{\lambda }_{\mathrm{F}}(t^{\prime })|u(t^{\prime }){|}^3]\hspace{0.17em}\mathrm{d}{t}^{\prime }\},\text{subjected to}\hspace{0.17em}0\le {\lambda }_{\mathrm{F}}(t^{\prime })\le {\lambda }_{\mathrm{F}}^{max}$$ 4.1

and λ_F(t′)|u(t′)|³≤D(t′), where D(t′) is the specified power demand.

The grey curve in figure 5 is an idealized example of a demand curve, with a constant base load or background demand $B={\overline{P}}_{\mathrm{GC}05}$ and a Gaussian-shaped peak in demand of height $2{\overline{P}}_{\mathrm{GC}05}$ and half width 0.6 h. This example is used in the remainder of this paper, though the timing of peak demand will vary. The example is in itself demanding, asking the farm to best meet both a background power demand equal to the current upper limit for production, GC05's potential, and a short peak demand of twice the GC05 potential.

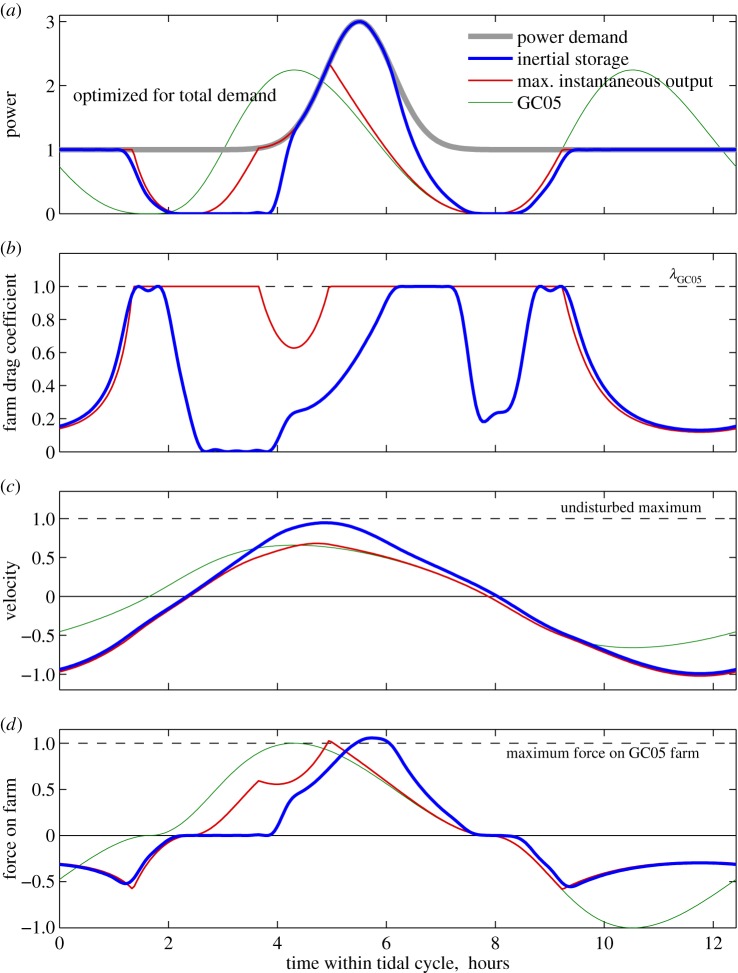
Figure 5.

Example of a farm in the Cook Strait example channel optimized to meet the total demand (4.1) given by the grey curve with ${\lambda }_{\mathrm{F}}^{max}={\lambda }_{\mathrm{F}}^{\mathrm{GC}05}$. The peak in the Gaussian demand curve is at 5.5 h. (a) Power and demand relative to ${\overline{P}}_{\mathrm{GC}05}$. An inertial storage farm meets 68% of total demand and 90% of peak demand, whereas a MIOF meets 63% of total demand but only 40% of peak demand. (b) Optimized variable farm drag coefficient relative to λ^GC05_F. (c) Velocity along the channel relative to velocity when there is no farm. (d) Total force on the farms relative to the maximum force on a GC05 farm.

Optimizing the farm to meet the total demand, while never exceeding instantaneous demand, is one possible strategy (4.1). The turbine farm could also be optimized to meet the peak demand, i.e altering (4.1) to only include the power produced above the background demand B

$$max\{\frac{1}{2\pi }{\int }_0^{2\pi }[{\lambda }_{\mathrm{F}}(t^{\prime })|u(t^{\prime }){|}^3]\hspace{0.17em}\mathrm{d}{t}^{\prime }\ge B\},\text{subjected to}\hspace{0.17em}0\le {\lambda }_{\mathrm{F}}(t^{\prime })\le {\lambda }_{\mathrm{F}}^{max}$$ 4.2

and λ_F(t′)|u(t′)|³≤D(t′). The farm could also be used to maximize meeting the base load component of a variable demand. However, exploiting inertial storage to do this produces only modest benefits, so optimizing for base load demand will not be discussed further.

The GC05 farm is no longer useful as a reference case as it may exceed demand for part of the tidal cycle. The new reference case is a ‘maximum instantaneous output farm’ (MIOF), where at each time step ${\lambda }_{\mathrm{F}}={\lambda }_{\mathrm{F}}^{max}$ or a smaller value which gives a power output matching the demand at that time step. The difference between a MIOF and (4.1) is that a MIOF optimizes the output to best meet instantaneous demand, whereas (4.1) optimizes the total demand met over the whole tidal cycle, and (4.2) optimizes the demand met during periods of peak demand. These optimizations use inertial storage to allow excess energy in one part of the tidal cycle to be used to better meet demand later in the half tidal cycle.

(a). Example of meeting demand

Figure 5 shows an example of optimizing to meet total demand (4.1). Remarkably, inertial storage can be used to match much of the peak demand curve, at a time 1.2 h later than the maximum production by a GC05 farm. While a MIOF can meet only 40% of peak demand, the inertial storage farm can meet 90% of peak demand. In the example, both the inertial storage farm and a MIOF meet a similar fraction of the total demand, around 65%. Thus, inertial storage can make the timing of farm output malleable. This gives farm operators some flexibility about when power is produced, around 1–2 h in this example, giving them some choice about which part of the demand the farm is used to meet.

The drag coefficient of the MIOF farm is maximized over much of the tidal cycle, only reducing at the ends so as to not exceed the background demand (figure 5b). The inertial storage farm has a more complex drag coefficient, which is maximized at three distinct periods during the tidal cycle. Despite meeting more of the peak demand, the inertial storage farm has much stronger peak flows than either a GC05 farm or a MIOF (figure 5c). In this example, peak flows for an inertial storage farm almost equal those in the channel with no farm.

Meeting the single demand peak in the tidal cycle creates an asymmetry between ebb and flood flows. This can be seen in the MIOF's velocities, where the positive peak flood flow speed is 20% weaker than the peak negative ebb flow. This asymmetry will result in a mean velocity through the channel (see figure 6b), which may have environmental impacts, such as creating a strong net drift of sediment along the channel in the direction of the mean flow. In this example, an inertial storage farm gives a much smaller asymmetry than a MIOF farm. Figure 5b shows that the maximum force on the inertial storage farm is similar to that in a MIOF, suggesting that design specifications for turbine loads will be similar in the two types of farm.

Figure 6.

Example of the effect of sliding the timing of peak demand relative to the tidal forcing for a farm in the Cook Strait, with λ₀=0.1. The farm is optimized to meet the total demand with ${\lambda }_{\mathrm{F}}^{max}={\lambda }_{\mathrm{F}}^{\mathrm{GC}05}$. (a) Solid lines are fraction of peak demand met, and dashed lines are the fraction of total demand met. (b) Tidal current along the channel. Upper curves are the peak positive flood flow. Lower curves give the mean velocity over a tidal cycle, a measure of the flood/ebb asymmetry which results from power extraction within a tidal cycle. Thick blue lines are inertial storage farm and thin red lines the MIOF. (Online version in colour.)

(b). Sliding peak demand relative to the tidal forcing

Peak domestic demand often has a 12 h cycle, with peaks around 07.00 and 19.00, whereas the tidal cycle is typically 12.42 h long. Peak tidal flow shifts approximately an hour later each day, thus peak demand slides relative to the tidal forcing over a 14 day cycle, with a greater or lesser correspondence between the timing of production and demand over this cycle (there is also a 14 day neap–spring tidal cycle which will not be considered here in order to simplify the interpretation).

To understand the effect of sliding peak demand, a periodic demand curve was moved relative to the forcing through a full tidal cycle, simulating power production over a 14 day period. The result is figure 6a which shows that while both MIOF and inertial storage farms meet a similar fraction of the total demand, an inertial storage farm can meet up to 90% of the peak demand, whereas a MIOF can meet less than 40% of the peak demand. Interestingly, for the inertial storage farm, the peak flood flow in figure 6b is generally stronger and its mean flow weaker than the MIOF. Thus, the inertial storage farm is better able to mitigate any impacts of both flow speed reduction and tidal asymmetry resulting from power extraction to meet peak demand.

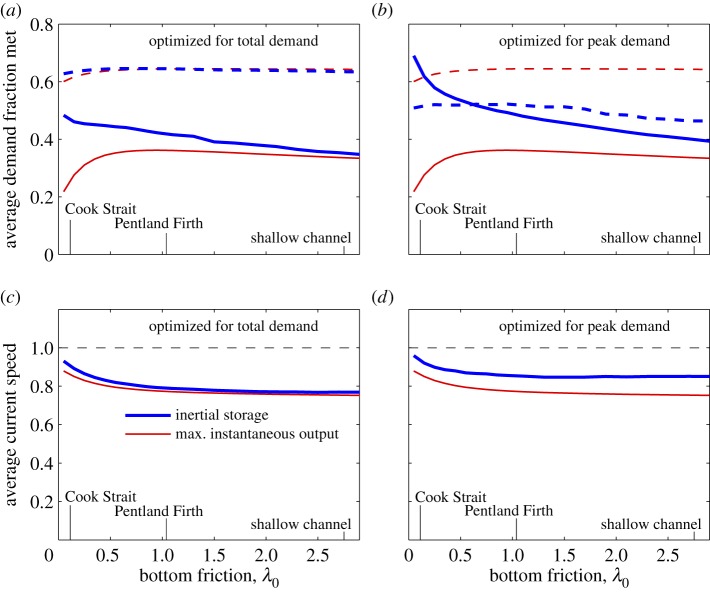
Figure 7a shows the effect of bottom friction on the fraction of demand met, averaged over a 14 day period. For the Cook Strait example, the up to 90% of peak demand met by an inertial storage farm in figure 6a averages out as 58% over 14 days, meeting 30% more of the peak demand than a MIOF. Across the range of λ₀, inertial storage and MIOF farms both meet a similar fraction of the total demand, with the average fraction of peak demand met being significantly higher for inertial storage than MIOF farms for medium to large channels, λ₀<2.

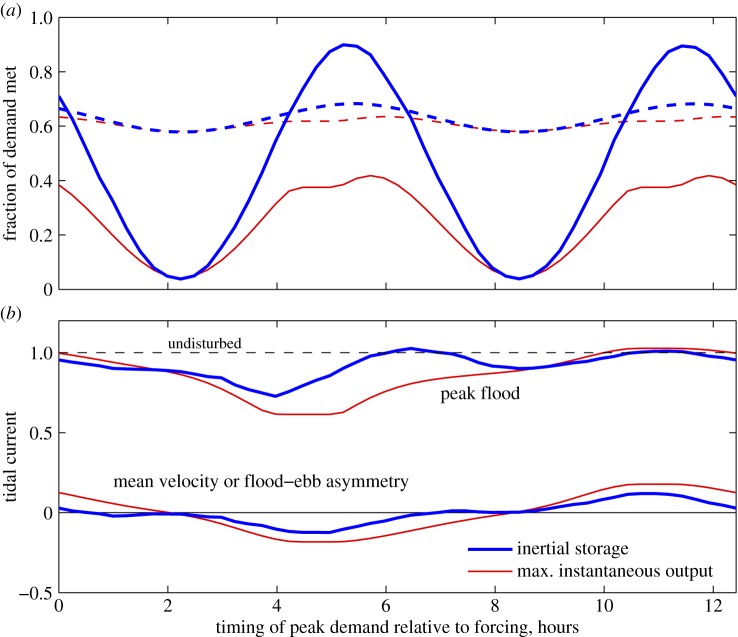
Figure 7.

Fraction of demand met averaged over 14 days for inertial storage farms and MIOF farms in a range of channel sizes with ${\lambda }_{\mathrm{F}}^{max}={\lambda }_{\mathrm{F}}^{\mathrm{GC}05}$. Dashed lines give fraction of total demand met and solid lines give the fraction of peak demand met. (a) Farms optimized to meet total demand (4.1). (b) Farms optimized to meet peak demand (4.2) are able to trade meeting more peak demand for meeting less of the total demand. (c,d) Average current speed, relative to average current speed in the undisturbed channel, for farms optimized to meet total demand and peak demand, respectively. Thick blue lines are inertial storage farm and thin red lines the MIOF. (Online version in colour.)

Although the farms in figure 7a are optimized to meet total demand, those in figure 7b are optimized to meet peak demand. Figure 7 demonstrates the flexibility of inertial storage, which can trade meeting a reduced fraction of total demand for meeting a larger fraction of peak demand. This flexibility can even be exploited to a degree in small channels, with a relaxed threshold of λ₀<3. The average current speed for both MIOF and inertial storage farms are similar when optimized to meet total demand, figure 7c, with both below the average speed in the undisturbed channel. For the farms optimized to meet peak demand, average current speeds for the inertial storage farm are around 10% higher than for the MIOF across the full range of channel sizes (figure 7d). This is likely a consequence of the inertial storage farm meeting less of the total demand and hence having a smaller time-averaged farm drag coefficient.

5. Discussion

Inertial storage works by delaying power extraction until later in the half tidal cycle, allowing the forcing to further increase the flow speed. The stored energy's lifetime is limited by dissipation owing to bottom friction. If the farm is turned off and in the absence of further forcing, (2.2) gives the velocity as u(t)=u_int/(u_intλ₀ωt/u_I+1), where u_int is the velocity at the time the farm turns off, and u_I is the velocity along the channel with no drag (which was used to non-dimensionalize u, §2 and (2.2)). Thus, velocity in a farm which is turned off at peak flow would decay with a time scale, or storage time, of order

$$T_{\mathrm{D}0}\approx \frac{u_{\mathrm{I}}}{{\lambda }_0\omega |u_{max}|}.$$ 5.1

Table 1 shows that this frictional time scale for the example channels ranges between 17 and 0.7 h. The scale T_D0 determines how beneficial delaying production is, because it indicates how long energy can persist within the flow before it is dissipated by background bottom friction. Owing to the nonlinear drag law, turning the farm off at a lower initial velocity would give a longer time scale, i.e. increase storage times. Thus, T_D0 varies over the tidal cycle, with energy persisting longer for flows weaker than the maximum velocity. Consequently, T_D0 indicates a lower limit for how long energy can persist within the flow when the farm is turned off. For Cook Strait, this lower limit T_D0=17 h, which is much longer than the half tidal–tidal cycle, thus delayed production can result in significantly higher total power production (figure 4a). For Pentland Firth, the lower limit is T_D0=2.4 h, less than half a tidal cycle, thus delayed production has more modest benefits.

In addition to switching off the farm, it could under produce by having ${\lambda }_{\mathrm{F}}<{\lambda }_{\mathrm{F}}^{max}$, storing some energy for later in the cycle. Energy stored owing to under production has a shorter storage time

$$T_{\mathrm{D}}\approx \frac{u_{\mathrm{I}}}{({\lambda }_0+{\lambda }_{\mathrm{F}}(t^{\prime }))\omega |u_{max}|}.$$ 5.2

Table 1 gives values of T_D at peak flow based on a constant λ_F equal to the GC05 optimal value. Table 1 shows that storage times for under production are longer than 1.7, 1.0 and 0.7 h for the three examples.

Using inertial storage to exceed the GC05 limit relies on a combination of two aspects of the physics. First, using inertial storage to retain energy in the oscillating flow allows extraction to be delayed until as late as possible in the half tidal cycle. Second, it relies on the forcing continuing to accelerate the flow during the delay. This continued acceleration creates stronger flows, which generate more power because of the cubic dependence of power on velocity. As noted above, to effectively use inertial storage to increase production, the bottom friction time scale needs to be comparable with, or longer than, the half tidal cycle. This delays extraction as long as possible, taking full advantage of the acceleration owing to forcing which continues throughout the half cycle. Thus, it is no surprise that using inertial storage to increase production is only really effective in large channels which have longer frictional time scales, with λ₀≤1 in figure 4a. What is surprising is that in both large and small channels a variable drag coefficient can be used to maintain higher average flow speeds than those for a GC05 farm (figure 4b). Using the farm to maintain flow speeds closer to those in the undisturbed channel does not necessarily mean environmental effects are mitigated, but raises the possibility that it may be possible to do so. Much more work on the effects of the change in strength of the flow over a full tidal cycle is needed in order to understand how to mitigate effects, such as those on sediment transport along the channel.

An inertial storage farm in Cook Strait can meet up to 90% of the example peak demand curve, or 58% of peak demand when averaged over 14 days, even though this peak demand is on top of a background demand equal to the channel's GC05 potential. The ability to meet peaks in power demand is determined by the duration of the peak relative to the frictional time scale. The example demand peaks have a width of 1.2 h, a duration comparable with the frictional time scale in the Pentland Firth, where on average an inertial storage farm meets 15% more of peak demand than a MIOF. Using inertial storage to delay peak production by 1–2 h gives the farm the ability to better align with peak demand on more tidal cycles within a 14 day period (figure 7). Thus, inertial storage can be used over a much wider range of channel sizes to meet predictable peak demand than the range for which it can be used to increase total power production. Consequently, tidal turbine farms in a wide range of channel sizes could have a role in producing short bursts of power to meet predictable peaks in demand.

Another important time scale is the resonant period of the channel. Rapid changes in the farm's drag coefficient may set up destructive seiching within the channel. The fundamental seiche periods in the example channels are 85, 30 and 5 min, respectively, however, a high drag coefficient farm may effectively halve the length of the channel, with seiches developing between the farm and the ends of the channel with fundamental periods of half these values. Although channels are ‘short’ for tidal oscillations, they are not short for these seiche periods, thus more work is needed to understand the dynamic effects of shallow water waves generated by rapid changes in farm drag coefficient. At the very least, any large change in the farm's drag coefficient must be made more gradually than the fundamental seiche period in order to minimize any seiching within the channel.

The dynamical equation (2.2) used to solve for the velocity has an electrical analogue. Inertia, which provides the storage here, is analogous to inductance, and the drag is equivalent to a nonlinear resistor [21]. This electrical circuit analogy could be used to understand how inertial storage could be exploited for arrays of tidal turbines within a network of interconnected channels, such as the Pentland Firth.

In the channel model of GC05, and that used here, it is assumed that the headloss between the ends of the channel is not affected by power extraction. Models for farms in the open ocean have shown power extraction can have regional effects [3,22]. Here, the channels are assumed to have a volume that is small compared with the volume of the oceans they connect, thus any exchange of water between the channel and the oceans will not significantly affect tidal patterns within the oceans. A recent regional tidal model of the Pentland Firth has demonstrated that power extraction affects the water-level difference between the ends of the Firth by less than 10% [19]. Another effect of power extraction is to generate higher harmonics of the M2 tide through the nonlinear effects of the quadratic drag law (2.2) [20]. This distortion of water level, both at the ends and within the channel, is not part of the GC05 short channel model. However, its importance can be gauged from tidal analysis of velocity solutions to (2.2). For the examples in figure 3, this nonlinear effect is small. Both the variable and constant λ_F farms create M4 tidal currents which are only 5–10% of the amplitude of the M2 constituent, slightly larger than the M4 of 5% for the undisturbed velocity. While the model used here may not allow for the small effects of power extraction on water levels at the ends of the channel and nonlinear distortion of water levels, these effects are likely to be similar for farms with variable λ_F, constant λ_F and for MIOF farms. The advantages of variable λ_F farms presented here are given relative to these latter two types of reference farm, thus the relative advantages are unlikely to be sensitive to these effects. However, regional two-dimensional depth-average models which tackle the computationally challenging problem of optimizing the farm drag coefficient in time must be developed to confirm this. These could exploit adjoint methods [23].

(a). Limitation of farm size and turbine efficiency

All the previous results assume that the farm is large enough to have a drag coefficient as large as that required for a GC05 farm to realize the potential of the tidal channel.

However, economics or the available space within the channel may limit the size of the farm [24]. Figure 4a demonstrated that halving the maximum drag coefficient restricts the ability to use inertial storage to exceed the GC05 limit. Inertial storage is likely to be more useful in better meeting short duration peaks in demand as seen in figure 7. Figure 8 plots the fraction of total and peak demand met by inertial storage farms with ${\lambda }_{\mathrm{F}}^{max}\le {\lambda }_{\mathrm{F}}^{\mathrm{GC}05}$ in the example channels. In figure 8, both the inertial storage farms and the MIOFs had ${\lambda }_{\mathrm{F}}^{max}$ restricted to the fraction of λ^GC05_F given on the x-axis. To enable a fair comparison the demand was set in proportion to farm size. Background demand was set equal to that from a constant drag coefficient farm with the given ${\lambda }_{\mathrm{F}}^{max}$ and, as in previous examples, peak demand was set at three times background demand. In Cook Strait, farms optimized to meet total demand can meet much more of peak demand than MIOFs, while meeting a similar fraction of total demand (figure 8a). Even a farm only one-fifth, the size of a GC05 farm still meets 10% more of peak demand than a MIOF. For the Firth, the benefits when optimized to meet total demand are more modest, with inertial storage farms half the size of the GC05 farm meeting around 1% more of peak demand, a figure which will be useful when seeking many small improvements from mature tidal turbine technology.

Figure 8.

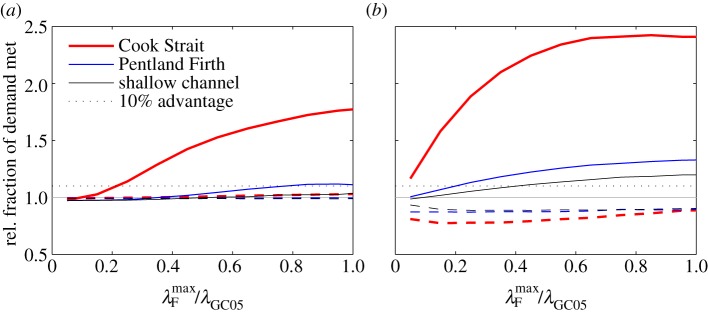
Effect of varying ${\lambda }_{\mathrm{F}}^{max}$ on the fraction of demand met by an inertial storage farm averaged over 14 days relative to a MIOF in the three example channels. Solid lines are ratio of the fraction of peak demand met by an inertial storage farm to the fraction met by a MIOF with the same ${\lambda }_{\mathrm{F}}^{max}$. Dashed lines give the ratio for the fractions of total demand met. Horizontal dotted line indicates ratio giving an inertial storage farm a 10% advantage over a MIOF. (a) Farms optimized to meet total demand (4.1). (b) Farms optimized to meet peak demand (4.2). (Online version in colour.)

Farms optimized to meet peak demand, figure 8b, show significant benefits for inertial storage farms across a wide range of farm sizes. In Cook Strait, inertial storage farms one-quarter the size of a GC05 farm can meet twice the fraction of peak demand met by a MIOF. At ${\lambda }_{\mathrm{F}}^{max}=0.1{\lambda }_{\mathrm{F}}^{\mathrm{GC}05}$, a small inertial storage farm in the Strait still meets 12% more of peak demand than a MIOF. The additional peak demand met results in a reduced fraction of total demand being met, demonstrating the ability to trade peak and total demand across a wide range of farm sizes in the Strait. In the Firth, an inertial storage farm has at least a 10% advantage over a MIOF for farms larger than one-fifth the size of a GC05 farm. Even inertial storage farms in the shallow channel have more than a 10% advantage for farms half the size of a GC05 farm. Thus, the malleability to trade meeting total demand with meeting peak demand exists across a wide range of channel sizes and farm sizes. Much more work is required to estimate the number of turbines required to exploit this malleability.

To exploit inertial storage, turbines will need to be built with the ability to rapidly change their drag coefficient and power output. This would most likely be done by adjusting blade pitch or by varying the tip speed ratio. Existing tidal turbines already use changes in blade pitch to limit loads on the structure at flows above a rated velocity, or to rapidly stop production when marine mammals are nearby [14]. The turbines in an inertial storage farm will likely need different design criteria, for example rapidly turning turbines on and off several times per tidal cycle may increase the risk of metal fatigue within the structure. This fatigue risk may also be compounded by oscillating loads owing to any seiching associated with rapid changes in drag coefficient. Another design consideration which will impact on both inertial storage and MIOF farms is minimum operating flow speeds. A further consideration is the need for maximum operating speeds to limit structural load. However, figure 5d suggests that loads on inertial storage farms are similar to those on MIOFs.

To maintain navigation along the channel, tidal turbines will often only be permitted to fill part of a channel's cross section. The mixing of high-speed flow which bypasses the turbines, with slower flow passing through the turbines results in mixing losses [25]. This mixing converts some of the flow's energy into heat [26]. This energy loss, and that owing to drag on any structures supporting the turbines, reduces the energy available from the channel for electricity production [11]. The power lost to mixing and support structure drags is not accounted for in the simple model given by (2.2) and (2.3). These losses will occur in both inertial storage farms and MIOFs, thus more work is needed to determine how these losses affect the relative performance of these two farms. These losses would likely affect both farms to a similar degree, thus the relative benefits of inertial storage presented here may be reasonable. An obvious next step is to extend the farm drag model to one built on actuator disc theory [12,25]. More work is also required to understand the impacts of support structure drag, which may significantly affect the flow's phase and magnitude, even if the turbines are not producing power.

6. Conclusion

This work shows that a variable farm drag coefficient can be used to make the timing of output from large tidal farms malleable. This malleability exploits the inertia of the oscillating tidal flow and can be used to produce more power, or better meet total or peak power demand. This will give farm operators some flexibility about how they optimize the farm's output. For example, trading total power production off against meeting more of the peak demand. They could also optimize the farm to minimize any environmental effects owing to the flow speed reduction caused by power extraction.

For larger channels, it is possible to exceed the GC05 limit on power production, while maintaining stronger currents. In some cases, peak flows even exceed that in the undisturbed channel. This is possible, because more power can be produced in larger channels by manipulating the phase of the currents relative to the forcing owing to the head loss between the ends of the channel. Extracting more power is limited to medium to large channels, with λ₀<1 (figure 4a). However, the benefit of maintaining higher average flow speeds over the half tidal cycle than those for a GC05 farm, extends across most channel sizes (figure 4b). Thus, using inertial storage to maintain higher average speeds along the channel, in order to minimize environmental impacts, may be more significant than producing more power.

While producing more power is important, it is essential to generate power when it is required. Inertial storage can be used to delay production by 1–2 h to better meet predictable daily peaks in power demand in medium to large channels, with λ₀<2 (figure 7a). Over a wider range of channel sizes, when λ₀<3, inertial storage can be used to trade off meeting total demand against meeting more of the peak demand (figure 7b), or maintaining higher current speeds (figure 7d).

The example demand curve used here required the farm to attempt to meet a background demand equal to the previous upper limit for production, GC05's potential, plus an additional peak demand of twice the channel's potential. This is a challenging demand to meet. However, inertial storage can be useful only if the farm is large enough to influence the flow's amplitude and phase. Farms of this scale can meet up to 90% of this peak demand, depending on the timing of the demand relative to the phase of the tidal forcing in the channel (figure 6). How useful an inertial storage farm is depends on the size of the channel and the size of the farm (figures 4, 7 and 8). In particular, inertial storage is useful in exceeding the GC05 limit for channels where the frictional time scale (5.2) is comparable with or longer than the half tidal cycle and useful in providing malleability to meet peaks in demand if the frictional time scale is comparable with or longer than the duration of those peaks.

This paper presents only the possibility that large tidal farms have some storage which could be used in a number of ways by farm operators. The simple one-dimensional model used here illustrates the mechanisms, but more sophisticated two- and three-dimensional models must be developed in order to properly quantify the benefits. In addition, more work is needed to determine how many turbines are required in a particular channel to make a farm large enough to be able to develop a drag coefficient capable of manipulating the phase of the tidal currents. Clearly, the farms must be large, though figure 8 demonstrates that inertial storage farms much smaller than a GC05 farm have a significant ability to trade peak power production for total power production. For large channels, such as Cook Strait, the number of turbines required is of order 1000 one MW turbines, one-tenth that required to fill its cross section (table 1). For medium-sized channels, such as the Pentland Firth, the number required could be around 300 one MW turbines, one-fifth that required to fill its cross section. Thus, tidal turbine farms comparable in size to the largest wind farms may be able to exploit inertial storage. When tidal turbine technology matures even a 1% benefit from exploiting inertial storage would be significant, as improvements of this size are already significant to large wind farms [6]. However, the turbines would need to form a ‘tidal fence’, spanning much of the channel's width and have a high channel blockage ratio. Tidal turbine farms of this scale are well off in the future, but this work presents ways large farms could be better used to meet varying energy demand when they are developed. Much further work is also needed to estimate the number of turbines required and how best to arrange turbines within an inertial storage farm, along with work to estimate the loads on the turbines in order to develop designs suitable for these farms.

Funding statement

This work was supported by New Zealand Marsden Fund (grant number 12-UO-101).