The impact of the certainty context on the process of choice

Abstract

In this study we examine how the introduction of a reference lottery with nonrandom outcomes alters the way in which choices among pairs of lotteries are made, even if it does not alter the choices. We use different domains (some of the lotteries produce gains, other losses) and different contexts (one member of the pair, the reference lottery, may be either risky or certain). In our experiment, the change from gain to loss domain affects choices: subjects are risk averse in the gain domain, but not in the loss domain. On the contrary, the context effect of the certain lottery does not affect choices. However, the introduction of the certainty reference lottery affects two behavioral variables, response time and brain activation, in a dramatic way. This result suggests that the certainty lottery promotes a different process through which preferences are revealed, even if the differences among lotteries may not be large enough to induce different choices.

We study behavioral and neuronal responses associated with economic choices. We manipulated the nature of one of the two lotteries (called the reference lottery) in a choice task between pairs of lotteries. In one condition the reference lottery was risky; in the other condition it was certain: that is, the outcome won or lost was fixed. We demonstrate that although choice behavior is relatively insensitive to the type of reference lottery, the case is dramatically different for response times and neuronal activation: these two strongly depend on it. Thus, very different neuro-physiologic processes appear to govern similar choice behavior. This study unequivocally indicates that, in humans, choice behavior alone does not reveal completely how choices are made. Our findings also show how the process of choice is distributed throughout the brain and that the activation of different functional units is sensitive to minute differences in environmental conditions, in particular the structure of comparison lotteries.

Two lines of inquiry are related to and inspired our study: the research on the effect of certainty on choice (as found in the Allais paradox, ref. 1), and on a context effect on ordering (2). Like most studies of choice, both studies rely strictly on subjects' announced preferences to hypothesize indirectly that choice processes themselves will change as a function of the alternatives that are being compared; however, no evidence is gathered to indicate directly how the choice processes are different. By gathering evidence on reaction time as well as brain activation, we directly assess how decision processes differ.

The Certainty Effect

We briefly recall the Allais paradox (1). We denote by (x, p; y, q; z, r) a lottery giving the monetary amount x with probability p, y with probability q and z with r; similarly, the notation (x, p; y, q) describes a lottery with two outcomes. In the standard setup of the Allais paradox the experimenter asks subjects to choose between lottery A = (1M, 1) (that is, one million dollars, M, with probability 1) and B = (5M, 0.1; 1M, 0.89, 0, 0.01). Then subjects are asked to choose between C = (1M, 0.11; 0, 0.89) and D = (5M, 0.1; 0, 0.9). The behavior consistent with Expected Utility Theory is (A, C) (A in the first choice and C in the second) or (B, D), because a pair of lottery can be obtained from the other by randomly combining two identical lotteries.††

A pattern commonly observed instead is (A, D). This deviation from the standard theory is the Allais paradox. This deviation is systematic because (A, D) is more commonly observed than (B, C). One interpretation of this behavior is called the certainty effect (^“people overweight outcomes that are considered certain, relative to outcomes that are merely possible—a phenomenon which we label the certainty effect,” ref. 3, page 265). Intuitively, in the first choice (A versus B) one million dollars is attractive because it is sure; in the second choice of C versus D this attractiveness is lost, because the million is no longer certain. In other words, the tradeoff between expected value and riskiness is not the same when one of the two outcomes is certain, compared with the case where both are risky. Later studies have called into question the certainty effect. Both Conlisk (4) and Carlin (5) demonstrate that seemingly minor variations in the way the choices are described to the subjects bring out large changes in the behavior, and less frequent violations of the Expected Utility Theory. Conlisk asks subjects to make the same choice as Allais, but decomposes C and D to make explicit their relationship with A and B (as described in ††). Because the role of the Independence axiom is now explicit, its effect may be stronger. Similarly, Carlin asks subjects to choose between the Allais lotteries, but in a control treatment the probability of the different outcomes is described by using a spinning wheel with 100 numbers. The violations of the Expected Utility patterns in these two new treatments are significantly smaller. In both cases, different setups seem to induce subjects to different ways of dealing with the choice. Both studies suggest that the process of choice (which can be influenced by different formulation of the choice) is the real determinant of the observed choice behavior. Unfortunately, standard laboratory experiments can tell us little about this process: our study involves techniques that try to fill this gap.

The Context Effect

A different line of inquiry that is related to our study is that in MacCrimmon et al. (2). The subjects in this study were to order sets of five options with equal expected values, one with a certain outcome and four with risky outcomes. In one set, the value of the best outcome in all five options was held constant and the probability of its occurrence varied. In a second set, the probabilities were held constant and value of the best outcome in all five options varied. Analyzing their data, Luce (6) notes that more than one-quarter of their subjects preferred a risky option to the one with certain outcome in the second condition, but preferred the option with certain outcome to the same risky one on the first condition. Their choices violated the basic assumption of independence of the order between two lotteries from the other alternatives (the authors of the study also demonstrated a context effect with a more indirect method; see pages 167–169 of ref. 2).

Choices and Choice Processes.

Our study examines two of the fundamental features of the choice process, response time and brain activation, to determine the factors responsible for the behavior in the studies we have described. If the presence of a certainty reference lottery affects these features, then these very features may be associated with, and explain, the different choice patterns exhibited in different experimental implementations of the Allais paradox, and in the context effect found in the MacCrimmon et al. (2) study. The results support this hypothesis.

This research is based partially on data reported by Smith et al. (7). That study examines fundamental economic forces in the environment: risk, ambiguity, gains, and losses. It is shown that there is an interaction in the choice data between payoffs (gains and losses) and the information condition (ambiguity, risk). Furthermore, this interaction is paralleled by an interaction in the statistics underlying the generation of brain images. At the same time additional data were gathered, which allowed us to assess the contextual role of certainty lotteries.

Experimental Stimuli.

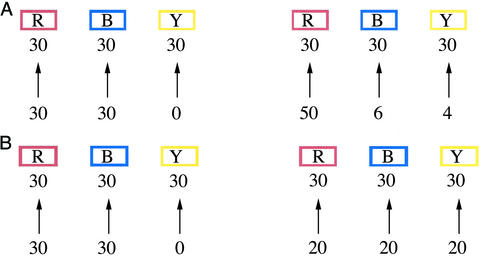
The participants were asked to choose between two lotteries of the type presented in Fig. 1A. There the lottery on the left is described as a container with 30 red, 30 blue, and 30 yellow marbles: the numbers below the arrows indicate that every red and blue marble is worth $30 and every yellow marble is worth nothing. The lottery on the right is described as a container with 30 red, 30 blue, and 30 yellow marbles, where every red marble is worth $50, every blue marble is worth $6, and every yellow marble is worth $4. The two lotteries have the same expected value, but the one on the right has higher variance in payoff. Variance is an index of riskiness: a lottery with smaller variance is less risky. A participant who prefers the lottery with the smaller variance is said to avoid risk. Because both choices are risky, the condition is called Risky, denoted by R. Participants were also asked to choose between two lotteries of the type presented in Fig. 1B. There the lottery on the right, described as a container with 30 red, 30 blue, and 30 yellow marbles, each worth $20, has no variance at all. In this case the condition of choice between the two lotteries is called Certainty (denoted by C). Inspection of Fig. 1 shows that the only differences between the risky and certainty conditions are the numbers in the payoff column. These minimal changes were intended to capture the difference between risk and certainty but to avoid visual differences in the presentation of the lotteries that might generate a confounding factor in the positron-emission tomography (PET) images. The full set of stimuli is available on request from J.V.P.

Fig 1.

(A) A sample stimulus for a pair of risky lotteries posing gains (condition RG). The groups of squares, numbers, and arrows indicate the distribution of red, blue, and yellow marbles in two containers. The numbers below the arrows signify the payoff in dollars of each of the marbles at the arrowhead. After an initial endowment of $190 cash, the participant's task is to choose the container from which one marble would be drawn. The lottery on the left has the lower payoff variance and is considered to be less risky. (B) A sample stimulus contrasting a risky lottery (on the left) and a certainty lottery posing gains (condition CG).

In the examples of choices shown in Fig. 1, the monetary payoffs were positive, so the subject could only gain. In a different set of choices, outcomes were all negative, so the subject could only lose money. We call the first condition Gain, denoted by G, and the second Loss, denoted by L. The stimuli in the loss conditions were identical to those in Fig. 1 with the addition of minus signs (−) in the row of numbers representing payoffs. The different combinations give four conditions: RG, CG, RL, and CL; for instance RG denotes the risk and gain condition.

Hypotheses

We have formulated three formal hypotheses.

Hypothesis 1.

Gain-loss effect: risk aversion in gains will not persist in the loss domain.

Hypothesis 2.

No effect of context on choice: context will not result in differences in the inferred preferences.

Hypothesis 3.

Effect of context on behavior: context will result in observed differences in process as reflected in both response time as well as brain scans.

Methods

Human Participants.

Nine healthy, right-handed medical students (three females and six males with a mean age of 27 years, standard deviation = 3 years) participated in the study. The volunteers gave written informed consent according to guidelines of the University of Minnesota Institutional Review Board and the Veterans Affairs Radioactive Drug Research Committee. Medical students were chosen because their familiarity with medical equipment was expected to minimize confounds that might be introduced by the PET imaging environment.

Task Paradigm.

After reading the instructions to participants and engaging in a series of practice trials, a participant received an initial endowment of $190 cash. Participants undertook choice tasks in the conditions we have described, using button presses to denote their choice. Each experimental condition consisted of 27 choice pairs presented in random order. The lotteries with certain outcomes were displayed as the right member of each pair.

After all scans had been conducted, one of the gains trials was chosen at random. The lottery chosen by the participant for that trial during the scan was played with real marbles in a plastic container. Similarly, one loss trial was randomly chosen and the lottery chosen by the participant was played. The participant inspected the container to verify its contents and then held the urn above the experimenter's head while the experimenter selected a marble. The colors of the selected marbles, one from a gains trial and one from a losses trial, determined the participant's additional gain and loss. The participant's total payoff was the initial endowment of $190 plus any additional gain less any loss. On average, participants earned $193 (standard deviation $20).

Several features of the task paradigm are noteworthy: a randomized block design, an absence of feedback after each trial (and a lack of varying wealth effects), and a link between performance and feedback at the end of the study.

Imaging.

In addition to the record of choices made by the subjects, we used PET and a tracer (H₂¹⁵O) to estimate regional cerebral blood flow (rCBF, a standard indicator for brain activity). rCBF was estimated from tissue radioactivity (after correction with measured two-dimensional attenuation) by using a Siemens ECAT 953B scanner (Knoxville, TN) with septae retracted, i.e., three-dimensional acquisition (8). An arm vein was used for access. The participant's head position was stabilized with a vacuum-molded pillow. A slow-bolus of H₂¹⁵O was injected intravenously (9.25 Mbq or 0.25 mCi/kg initially, infused at a constant speed over 30 s; 1 Ci = 37 GBq). Data acquisition (correcting for randoms and electronic dead time only) commenced on arrival of activity into the head as evidenced by consistently rising true counts. Each experimental scan of 90 s contained data from one type of lottery, e.g., CG or RG. The interval between scans was about 10 min. Images were reconstructed by filtered back projection including nonorthogonal angles to a final image resolution of 10 mm full-width at half-maximum.

Analysis.

Image analysis was performed with software provided by S. Minoshima (see refs. 9 and 10). Data were normalized to whole-brain average blood flow; image fiducials were used to localize the intercommissural plane; images were coregistered; anatomical standardization followed nonlinear transformation into a standard stereotaxic space (11). Voxel-by-voxel statistics (z scores) were computed as the difference in condition means divided by the adjusted pooled standard deviation.

A threshold of z = 3.3 reflects a significance level of 0.001, which corrects for multiple comparisons. Several standard atlases were use to determine anatomical designations and approximate Brodmann areas (11–13).

Results

Behavioral Results.

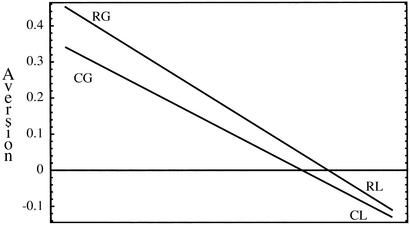
We first show the choice data in a simple graphical form and then conduct a more formal examination using a Logit regression. Fig. 2 identifies the four conditions. The measure represented on the vertical axis is a measure of the relative risk aversion exhibited in the four cases, RG, CG, RL, and CL. This measure is the difference in the proportion of choices that were risk-averse choices and risk-preferring choices in each setting. Note that for both CG and RG, the differences in percentage of proportion of risk averse and risk preferring choices is larger than 0. For RL and CL, the differences are slightly less than 0.

Fig 2.

The plotted points indicate the percentage difference between risk averse and risk preferring choices in the four conditions, RG, CG, RL, and CL. The figure shows that for both a Risky and Certainty comparison lottery subjects consistently show risk aversion. On the other hand, for Losses, risk aversion is less common than risk seeking for both risky and certainty reference lotteries.

To analyze these differences we performed a Logit analysis. The dependent variable of our statistical model is the probability of one of the lotteries being chosen. Independent variables are relevant features of these lotteries: exp, the difference between the expected values of the lotteries; std, the difference in the standard deviation of the lotteries; gain, a 0–1 variable equal to one when the outcomes are in the gain domain; cert, a 0–1 variable equal to one when the reference lottery is certain; expg, equal to the product of exp and gain; expc, equal to the product of exp and cert; and similarly for stg and stc. The results of this analysis are shown in Table 1.

Table 1.

Logit analysis

ch	Coefficient	SE	z	P > |z|	95% confidence interval
exp	0.4839094	0.0669722	7.226	0.000	0.3526464	0.6151724
std	0.0022734	0.0160675	0.141	0.887	−0.0292183	0.0337651
cert	0.1530257	0.2994381	0.511	0.609	−0.4338622	0.7399136
gain	0.3223414	0.1797661	1.793	0.073	−0.0299937	0.6746765
stc	0.0065275	0.0252911	0.258	0.796	−0.0430422	0.0560972
stg	−0.0915636	0.0177079	−5.171	0.000	−0.1262704	−0.0568568
expg	0.0664631	0.1028511	0.646	0.518	−0.1351214	0.2680475
cons	−0.1087111	0.1322396	−0.822	0.411	−0.3678959	0.1504737

For the overall grouped regression, the only variables that are significant are exp and stg, indicating that the only condition where standard deviation plays a role is in the gain domain. The potential context variables stc and cert have no impact. When the Logit regression is run on individual subjects, all nine show the expected value to be significant (P < 0.05) and five of the nine show the stg variable to be significant (P < 0.05). For those subjects for whom stg is not significant, three show std to be significant. Only one subject has data consistent with a context effect. The expc variable is dropped because of collinearity. Log likelihood = −512.76171; no. of obs = 905; LR χ²(7) = 227.87; Prob > χ² = 0.0000; Pseudo R² = 0.1818.

Response Time.

A second behavioral variable of interest is the response time, namely the length of the time interval between the presentation of the choice to the subjects and their choice. Table 2 shows that both context and gain have significant effects on average response time. For precise results regarding the regression of response time, see Table 3.

Table 2.

Response times for different treatments

	Gains	Losses
Certainty	2.391 (2.250, 2.531)	2.825 (2.669, 2.98)
Risky	3.090 (2.923, 3.258)	3.448 (3.285, 3.611)

The data are in seconds. In parentheses we report the 95% confidence interval. The table shows that choices among lotteries involving losses consistently require more average time than those that involve gains. Also, the risky condition requires consistently more average time than certainty condition. As with the choice data, we augment the table with a regression analysis. The dependent variable response time (sec) was regressed on the gain and cert variables. The estimated coefficients show that the choices under loss required more time to evaluate than those involving gains, and the choices with a risky reference lottery required more time. The precise results are shown in Table 3. (We also attempted to control for the relative importance of difference in lotteries, by approximating this difference by an estimate of the subjective value of the two lotteries. We assess this subjective value by taking the sum of the difference in expected values times the estimated coefficient for that subject plus the difference in standard deviations times the estimated coefficient for the subject on that variable. The coefficient of this variable is not significant.)

Table 3.

Regression of the response time (sec)

Source	SS	df	MS
Model	133.61820	2	66.8091033
Residual	1280.02093	902	1.41909195
Total	1413.63914	904	1.563760

sec	Coefficient	SE	t	P > |t|	95% confidence interval
gain	−0.398263	0.0792085	−5.028	0.000	−0.5537179	−0.2428089
cert	−0.662035	0.0793579	−8.342	0.000	−0.8177834	−0.5062883
cons	3.469154	0.0713755	48.109	0.000	3.3305120	3.607795

The variables describing the effects of certainty/uncertainty (cert) and gain/loss (gain) both have significant coefficients. No. of observations = 905; F(3,901) = 47.08, prob. > F = 0.0000; R² = 0.0945; adjusted R² = 0.0925; root MSE = 1.1913.

Changes in rCBF.

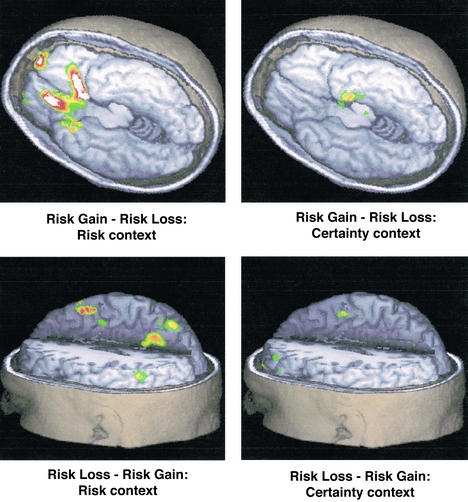
Fig. 3 illustrates key differences in rCBF changes during the contrast between gains and losses depending on the context in which the risky lottery is evaluated, i.e., when another risky lottery is offered as the alternative, or when a fixed amount of money is offered as the alternative. A detailed description of the location of the region of rCBF changes is reported in Tables 4 and 5. When subjects must choose between two risky lotteries (Risk/Risk, R), then a predominantly ventral pattern arises when the subjects can gain money relative to when they can lose money (Fig. 3 Upper Left; Table 4), and a predominantly dorsal pattern arises in the reverse contrast (Fig. 3 Lower Left; Table 5). However, when subjects must choose between a risky lottery and a fixed sum of money Risk/Certainty (C), the characteristic patterns seen in the Risk/Risk (R) contrasts virtually disappear (Fig. 3 Right; Tables 4 and 5).

Fig 3.

Changes in rCBF across conditions. (Upper Left) Brain locations more activated under gains than losses when risky stimuli are used as the comparison lottery. (Upper Right) The same contrast when the comparison lottery is certain rather than risky. (Lower Left) Brain locations more activated under losses than gains when risky stimuli are used as the comparison lottery. (Lower Right) The same contrast when the comparison lottery is certain rather than risky.

Table 4.

rCBF changes during Risk/Gain–Risk/Loss

x	y	z	Location		Brodmann Area	Z	P value
Comparison lottery is Risky
−6	10	−18	L	Orbital frontal: medial	BA 25	6.0	0.00000
−17	23	−18	L	Orbital frontal: medial	BA 13	5.1	0.00000
12	39	−20	R	Orbital frontal: medial	BA 11	4.8	0.00000
24	−35	52	R	Precun/paracen sulcus	BA 5/7	4.1	0.00002
−15	23	58	L	Premotor	BA 6/8	4.0	0.00003
−26	1	−36	L	Uncus	BA 20/38	3.8	0.00008
−10	71	11	L	Frontal pole	BA 10	3.7	0.00011
10	21	−20	R	Gyrus rectus	BA 13/14	3.7	0.00013
−1	−17	−38	L	Pons		3.6	0.00016
−60	−10	−11	L	Middle temporal	BA 21	3.5	0.00023
−3	−15	−32	L	Pons		3.4	0.00030
12	−24	50	R	Paracentral lobule	BA 6	3.4	0.00031
−3	68	−2	L	Frontal pole	BA 10	3.4	0.00036
Comparison lottery is Certainty
−26	1	63	L	Premotor	BA 6	4.4	0.00000
26	−40	−38	R	Cerebellar superior semilunar lobule	Crus I	4.2	0.00001
28	−49	−38	R	Cerebellar superior semilunar lobule	Crus I	4.2	0.00002
−8	−89	32	L	Cuneus	BA 19	3.9	0.00005
19	−31	50	R	Central sulcus	BA 3/1/2/4	3.8	0.00007
26	−51	−43	R	Cerebellar posterior lobe		3.8	0.00008
−30	−49	50	L	Precuneus	BA 7	3.7	0.00011
−24	−67	50	L	Precuneus	BA 7	3.4	0.00032

Table 5.

rCBF changes during Risk/Loss–Risk/Gain

x	y	z	Location		Brodmann Area	Z	P value
Comparision lottery is Risky
−44	−60	43	L	Inferior parietal lobule	BA 40	4.7	0.00000
−42	−53	43	L	Inferior parietal lobule	BA 40	4.6	0.00000
−10	−73	36	L	Precuneus: ventral	BA 7	4.3	0.00001
8	12	56	R	Pre-SMA	BA 6	4.2	0.00001
3	−60	34	R	Precuneus: ventral	BA 7	3.9	0.00005
−35	−60	−45	L	Cerebellar Gracile/inferior semilunar	VIIB	3.9	0.00005
−48	−1	−20	L	Middle temporal	BA 21	3.8	0.00008
46	−24	56	R	Central sulcus	BA 3/1/2	3.7	0.00009
8	−78	−36	R	Cerebellar inferior semilunar lobule	Crus II	3.6	0.00019
1	−6	43	R	Cingulate: motor	BA 24	3.6	0.00019
−37	30	36	L	Middle frontal	BA 9	3.5	0.00022
−28	−8	52	L	Precentral gyrus	BA 4/6	3.4	0.00031
−33	−71	27	L	Intraparietal sulcus	BA 39/19	3.3	0.00046
Comparison lottery is Certainty
−3	1	52	L	Medial frontal	BA 6	4.2	0.00001
37	−22	56	R	Primary motor	BA 4	3.8	0.00007
−44	32	29	L	Middle frontal	BA 9/46	3.6	0.00020
−3	17	−18	L	Gyrus rectus	BA 11	3.4	0.00031
33	−15	58	R	Primary motor	BA 4	3.4	0.00033

Risk-Gain Minus Risk-Loss.

Table 4 displays loci of significantly higher activation for gain than for loss stimuli under risk and certainty. Important differences in activation are in the orbital, frontal, and more ventral areas of the brain, including the pons, uncus, and gyrus rectus locations. These are absent in the certainty image.

Risk-Loss Minus Risk-Gain.

Table 5 reports loci of significantly higher activation for losses than gain stimuli under risk and certainty. Prevalent differences in activation are the inferior parietal lobule and parietal sulcus, which are not significant for certainty.

Discussion

We have shown that even when decision behavior, described by choices, is the same in different settings, the choices made by the subjects provide an incomplete account of how decisions are made. Regardless of the reference lottery, risky or certain, subjects are risk averse in the gain domain, and such risk aversion disappears in the loss domain. Yet reaction time and brain activation differ across these contexts. Given that reaction time and brain activation provide new information when decision behavior is the same, more than one system may govern how lotteries are evaluated. Proposing such parallel processing systems began with work by James (14) and has found increased interest in explaining different forms of reasoning, as well as explaining the presence of different forms of decision biases. Recently, work has focused on the ideas that there may be one system associated with quick and associative types of responses and one system that is more associated with more detached and reasoned responses: see ref. 15. Although the current work is consistent with the idea of multiple systems, additional research is required to determine whether the different systems isolated here fit neatly into categories that were previously derived. Certainly the results have this flavor. When there are certainty comparisons the time taken to make decisions is less and the areas of activation invoked have traditionally been associated with less computational and evaluative processes. However the results are far from conclusive. The ventro-medial area differentially activated in the Risk Gain–Risk Loss subtraction is also the area that plays a crucial role in the research centered around the Somatic Marker Hypothesis (16). An interesting difference emerging in our study is that this area is activated only in one of the decision environments, and does not seem for example to be important in decisions involving losses. This difference will require further study. A natural initial conjecture is that the difference in the decision setup adopted here and in the Damasio and colleagues (16) studies is important. The subjects in our study do not have a problem learning or estimating the distribution of gains and losses, and always make static choices; whereas subjects in the studies described in Bechara et al. (16) always have to learn in a dynamic context.

This research has potential implications for the study and design of social and economic institutions. It is possible that being more aware of the process by which decisions are made play a role in our understanding of policy choices. Our results suggest that the type of lottery being evaluated affects what processes are invoked to make decisions. To suggest that there are policy implications would mean that we need to find real-world institutions that are sensitive to the type of gamble being traded. But this is exactly the case. The over-the-counter nature of fixed government securities differs from the pit trading for options which differs from the enormous variety of different institutional arrangements for trading in corporate shares. Currently, we do not have a detailed understanding of why such institutional forms have evolved. A plausible proposition is that they evolved to deal with the contextual differences of environment that characterize the nature of gambles being traded.